Dataset Viewer
problem
stringlengths 1.19k
65.4k
| solution
stringlengths 1.19k
67.5k
| topic
stringlengths 5
80
|
|---|---|---|
---
title
intersecting_segments
---
# Search for a pair of intersecting segments
Given $n$ line segments on the plane. It is required to check whether at least two of them intersect with each other.
If the answer is yes, then print this pair of intersecting segments; it is enough to choose any of them among several answers.
The naive solution algorithm is to iterate over all pairs of segments in $O(n^2)$ and check for each pair whether they intersect or not. This article describes an algorithm with the runtime time $O(n \log n)$, which is based on the **sweep line algorithm**.
## Algorithm
Let's draw a vertical line $x = -\infty$ mentally and start moving this line to the right.
In the course of its movement, this line will meet with segments, and at each time a segment intersect with our line it intersects in exactly one point (we will assume that there are no vertical segments).
<center></center>
Thus, for each segment, at some point in time, its point will appear on the sweep line, then with the movement of the line, this point will move, and finally, at some point, the segment will disappear from the line.
We are interested in the **relative order of the segments** along the vertical.
Namely, we will store a list of segments crossing the sweep line at a given time, where the segments will be sorted by their $y$-coordinate on the sweep line.
<center></center>
This order is interesting because intersecting segments will have the same $y$-coordinate at least at one time:
<center></center>
We formulate key statements:
- To find an intersecting pair, it is sufficient to consider **only adjacent segments** at each fixed position of the sweep line.
- It is enough to consider the sweep line not in all possible real positions $(-\infty \ldots +\infty)$, but **only in those positions when new segments appear or old ones disappear**. In other words, it is enough to limit yourself only to the positions equal to the abscissas of the end points of the segments.
- When a new line segment appears, it is enough to **insert** it to the desired location in the list obtained for the previous sweep line. We should only check for the intersection of the **added segment with its immediate neighbors in the list above and below**.
- If the segment disappears, it is enough to **remove** it from the current list. After that, it is necessary **check for the intersection of the upper and lower neighbors in the list**.
- Other changes in the sequence of segments in the list, except for those described, do not exist. No other intersection checks are required.
To understand the truth of these statements, the following remarks are sufficient:
- Two disjoint segments never change their **relative order**.<br>
In fact, if one segment was first higher than the other, and then became lower, then between these two moments there was an intersection of these two segments.
- Two non-intersecting segments also cannot have the same $y$-coordinates.
- From this it follows that at the moment of the segment appearance we can find the position for this segment in the queue, and we will not have to rearrange this segment in the queue any more: **its order relative to other segments in the queue will not change**.
- Two intersecting segments at the moment of their intersection point will be neighbors of each other in the queue.
- Therefore, for finding pairs of intersecting line segments is sufficient to check the intersection of all and only those pairs of segments that sometime during the movement of the sweep line at least once were neighbors to each other. <br>
It is easy to notice that it is enough only to check the added segment with its upper and lower neighbors, as well as when removing the segment — its upper and lower neighbors (which after removal will become neighbors of each other).<br>
- It should be noted that at a fixed position of the sweep line, we must **first add all the segments** that start at this x-coordinate, and only **then remove all the segments** that end here.<br>
Thus, we do not miss the intersection of segments on the vertex: i.e. such cases when two segments have a common vertex.
- Note that **vertical segments** do not actually affect the correctness of the algorithm.<br>
These segments are distinguished by the fact that they appear and disappear at the same time. However, due to the previous comment, we know that all segments will be added to the queue first, and only then they will be deleted. Therefore, if the vertical segment intersects with some other segment opened at that moment (including the vertical one), it will be detected.<br>
**In what place of the queue to place vertical segments?** After all, a vertical segment does not have one specific $y$-coordinate, it extends for an entire segment along the $y$-coordinate. However, it is easy to understand that any coordinate from this segment can be taken as a $y$-coordinate.
Thus, the entire algorithm will perform no more than $2n$ tests on the intersection of a pair of segments, and will perform $O(n)$ operations with a queue of segments ($O(1)$ operations at the time of appearance and disappearance of each segment).
The final **asymptotic behavior of the algorithm** is thus $O(n \log n)$.
## Implementation
We present the full implementation of the described algorithm:
```cpp
const double EPS = 1E-9;
struct pt {
double x, y;
};
struct seg {
pt p, q;
int id;
double get_y(double x) const {
if (abs(p.x - q.x) < EPS)
return p.y;
return p.y + (q.y - p.y) * (x - p.x) / (q.x - p.x);
}
};
bool intersect1d(double l1, double r1, double l2, double r2) {
if (l1 > r1)
swap(l1, r1);
if (l2 > r2)
swap(l2, r2);
return max(l1, l2) <= min(r1, r2) + EPS;
}
int vec(const pt& a, const pt& b, const pt& c) {
double s = (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
return abs(s) < EPS ? 0 : s > 0 ? +1 : -1;
}
bool intersect(const seg& a, const seg& b)
{
return intersect1d(a.p.x, a.q.x, b.p.x, b.q.x) &&
intersect1d(a.p.y, a.q.y, b.p.y, b.q.y) &&
vec(a.p, a.q, b.p) * vec(a.p, a.q, b.q) <= 0 &&
vec(b.p, b.q, a.p) * vec(b.p, b.q, a.q) <= 0;
}
bool operator<(const seg& a, const seg& b)
{
double x = max(min(a.p.x, a.q.x), min(b.p.x, b.q.x));
return a.get_y(x) < b.get_y(x) - EPS;
}
struct event {
double x;
int tp, id;
event() {}
event(double x, int tp, int id) : x(x), tp(tp), id(id) {}
bool operator<(const event& e) const {
if (abs(x - e.x) > EPS)
return x < e.x;
return tp > e.tp;
}
};
set<seg> s;
vector<set<seg>::iterator> where;
set<seg>::iterator prev(set<seg>::iterator it) {
return it == s.begin() ? s.end() : --it;
}
set<seg>::iterator next(set<seg>::iterator it) {
return ++it;
}
pair<int, int> solve(const vector<seg>& a) {
int n = (int)a.size();
vector<event> e;
for (int i = 0; i < n; ++i) {
e.push_back(event(min(a[i].p.x, a[i].q.x), +1, i));
e.push_back(event(max(a[i].p.x, a[i].q.x), -1, i));
}
sort(e.begin(), e.end());
s.clear();
where.resize(a.size());
for (size_t i = 0; i < e.size(); ++i) {
int id = e[i].id;
if (e[i].tp == +1) {
set<seg>::iterator nxt = s.lower_bound(a[id]), prv = prev(nxt);
if (nxt != s.end() && intersect(*nxt, a[id]))
return make_pair(nxt->id, id);
if (prv != s.end() && intersect(*prv, a[id]))
return make_pair(prv->id, id);
where[id] = s.insert(nxt, a[id]);
} else {
set<seg>::iterator nxt = next(where[id]), prv = prev(where[id]);
if (nxt != s.end() && prv != s.end() && intersect(*nxt, *prv))
return make_pair(prv->id, nxt->id);
s.erase(where[id]);
}
}
return make_pair(-1, -1);
}
```
The main function here is `solve()`, which returns the number of found intersecting segments, or $(-1, -1)$, if there are no intersections.
Checking for the intersection of two segments is carried out by the `intersect ()` function, using an **algorithm based on the oriented area of the triangle**.
The queue of segments is the global variable `s`, a `set<event>`. Iterators that specify the position of each segment in the queue (for convenient removal of segments from the queue) are stored in the global array `where`.
Two auxiliary functions `prev()` and `next()` are also introduced, which return iterators to the previous and next elements (or `end()`, if one does not exist).
The constant `EPS` denotes the error of comparing two real numbers (it is mainly used when checking two segments for intersection).
|
---
title
intersecting_segments
---
# Search for a pair of intersecting segments
Given $n$ line segments on the plane. It is required to check whether at least two of them intersect with each other.
If the answer is yes, then print this pair of intersecting segments; it is enough to choose any of them among several answers.
The naive solution algorithm is to iterate over all pairs of segments in $O(n^2)$ and check for each pair whether they intersect or not. This article describes an algorithm with the runtime time $O(n \log n)$, which is based on the **sweep line algorithm**.
## Algorithm
Let's draw a vertical line $x = -\infty$ mentally and start moving this line to the right.
In the course of its movement, this line will meet with segments, and at each time a segment intersect with our line it intersects in exactly one point (we will assume that there are no vertical segments).
<center></center>
Thus, for each segment, at some point in time, its point will appear on the sweep line, then with the movement of the line, this point will move, and finally, at some point, the segment will disappear from the line.
We are interested in the **relative order of the segments** along the vertical.
Namely, we will store a list of segments crossing the sweep line at a given time, where the segments will be sorted by their $y$-coordinate on the sweep line.
<center></center>
This order is interesting because intersecting segments will have the same $y$-coordinate at least at one time:
<center></center>
We formulate key statements:
- To find an intersecting pair, it is sufficient to consider **only adjacent segments** at each fixed position of the sweep line.
- It is enough to consider the sweep line not in all possible real positions $(-\infty \ldots +\infty)$, but **only in those positions when new segments appear or old ones disappear**. In other words, it is enough to limit yourself only to the positions equal to the abscissas of the end points of the segments.
- When a new line segment appears, it is enough to **insert** it to the desired location in the list obtained for the previous sweep line. We should only check for the intersection of the **added segment with its immediate neighbors in the list above and below**.
- If the segment disappears, it is enough to **remove** it from the current list. After that, it is necessary **check for the intersection of the upper and lower neighbors in the list**.
- Other changes in the sequence of segments in the list, except for those described, do not exist. No other intersection checks are required.
To understand the truth of these statements, the following remarks are sufficient:
- Two disjoint segments never change their **relative order**.<br>
In fact, if one segment was first higher than the other, and then became lower, then between these two moments there was an intersection of these two segments.
- Two non-intersecting segments also cannot have the same $y$-coordinates.
- From this it follows that at the moment of the segment appearance we can find the position for this segment in the queue, and we will not have to rearrange this segment in the queue any more: **its order relative to other segments in the queue will not change**.
- Two intersecting segments at the moment of their intersection point will be neighbors of each other in the queue.
- Therefore, for finding pairs of intersecting line segments is sufficient to check the intersection of all and only those pairs of segments that sometime during the movement of the sweep line at least once were neighbors to each other. <br>
It is easy to notice that it is enough only to check the added segment with its upper and lower neighbors, as well as when removing the segment — its upper and lower neighbors (which after removal will become neighbors of each other).<br>
- It should be noted that at a fixed position of the sweep line, we must **first add all the segments** that start at this x-coordinate, and only **then remove all the segments** that end here.<br>
Thus, we do not miss the intersection of segments on the vertex: i.e. such cases when two segments have a common vertex.
- Note that **vertical segments** do not actually affect the correctness of the algorithm.<br>
These segments are distinguished by the fact that they appear and disappear at the same time. However, due to the previous comment, we know that all segments will be added to the queue first, and only then they will be deleted. Therefore, if the vertical segment intersects with some other segment opened at that moment (including the vertical one), it will be detected.<br>
**In what place of the queue to place vertical segments?** After all, a vertical segment does not have one specific $y$-coordinate, it extends for an entire segment along the $y$-coordinate. However, it is easy to understand that any coordinate from this segment can be taken as a $y$-coordinate.
Thus, the entire algorithm will perform no more than $2n$ tests on the intersection of a pair of segments, and will perform $O(n)$ operations with a queue of segments ($O(1)$ operations at the time of appearance and disappearance of each segment).
The final **asymptotic behavior of the algorithm** is thus $O(n \log n)$.
## Implementation
We present the full implementation of the described algorithm:
```cpp
const double EPS = 1E-9;
struct pt {
double x, y;
};
struct seg {
pt p, q;
int id;
double get_y(double x) const {
if (abs(p.x - q.x) < EPS)
return p.y;
return p.y + (q.y - p.y) * (x - p.x) / (q.x - p.x);
}
};
bool intersect1d(double l1, double r1, double l2, double r2) {
if (l1 > r1)
swap(l1, r1);
if (l2 > r2)
swap(l2, r2);
return max(l1, l2) <= min(r1, r2) + EPS;
}
int vec(const pt& a, const pt& b, const pt& c) {
double s = (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
return abs(s) < EPS ? 0 : s > 0 ? +1 : -1;
}
bool intersect(const seg& a, const seg& b)
{
return intersect1d(a.p.x, a.q.x, b.p.x, b.q.x) &&
intersect1d(a.p.y, a.q.y, b.p.y, b.q.y) &&
vec(a.p, a.q, b.p) * vec(a.p, a.q, b.q) <= 0 &&
vec(b.p, b.q, a.p) * vec(b.p, b.q, a.q) <= 0;
}
bool operator<(const seg& a, const seg& b)
{
double x = max(min(a.p.x, a.q.x), min(b.p.x, b.q.x));
return a.get_y(x) < b.get_y(x) - EPS;
}
struct event {
double x;
int tp, id;
event() {}
event(double x, int tp, int id) : x(x), tp(tp), id(id) {}
bool operator<(const event& e) const {
if (abs(x - e.x) > EPS)
return x < e.x;
return tp > e.tp;
}
};
set<seg> s;
vector<set<seg>::iterator> where;
set<seg>::iterator prev(set<seg>::iterator it) {
return it == s.begin() ? s.end() : --it;
}
set<seg>::iterator next(set<seg>::iterator it) {
return ++it;
}
pair<int, int> solve(const vector<seg>& a) {
int n = (int)a.size();
vector<event> e;
for (int i = 0; i < n; ++i) {
e.push_back(event(min(a[i].p.x, a[i].q.x), +1, i));
e.push_back(event(max(a[i].p.x, a[i].q.x), -1, i));
}
sort(e.begin(), e.end());
s.clear();
where.resize(a.size());
for (size_t i = 0; i < e.size(); ++i) {
int id = e[i].id;
if (e[i].tp == +1) {
set<seg>::iterator nxt = s.lower_bound(a[id]), prv = prev(nxt);
if (nxt != s.end() && intersect(*nxt, a[id]))
return make_pair(nxt->id, id);
if (prv != s.end() && intersect(*prv, a[id]))
return make_pair(prv->id, id);
where[id] = s.insert(nxt, a[id]);
} else {
set<seg>::iterator nxt = next(where[id]), prv = prev(where[id]);
if (nxt != s.end() && prv != s.end() && intersect(*nxt, *prv))
return make_pair(prv->id, nxt->id);
s.erase(where[id]);
}
}
return make_pair(-1, -1);
}
```
The main function here is `solve()`, which returns the number of found intersecting segments, or $(-1, -1)$, if there are no intersections.
Checking for the intersection of two segments is carried out by the `intersect ()` function, using an **algorithm based on the oriented area of the triangle**.
The queue of segments is the global variable `s`, a `set<event>`. Iterators that specify the position of each segment in the queue (for convenient removal of segments from the queue) are stored in the global array `where`.
Two auxiliary functions `prev()` and `next()` are also introduced, which return iterators to the previous and next elements (or `end()`, if one does not exist).
The constant `EPS` denotes the error of comparing two real numbers (it is mainly used when checking two segments for intersection).
## Problems
* [TIMUS 1469 No Smoking!](https://acm.timus.ru/problem.aspx?space=1&num=1469)
|
Search for a pair of intersecting segments
|
---
title
segments_intersection_checking
---
# Check if two segments intersect
You are given two segments $(a, b)$ and $(c, d)$.
You have to check if they intersect.
Of course, you may find their intersection and check if it isn't empty, but this can't be done in integers for segments with integer coordinates.
The approach described here can work in integers.
## Algorithm
Firstly, consider the case when the segments are part of the same line.
In this case it is sufficient to check if their projections on $Ox$ and $Oy$ intersect.
In the other case $a$ and $b$ must not lie on the same side of line $(c, d)$, and $c$ and $d$ must not lie on the same side of line $(a, b)$.
It can be checked with a couple of cross products.
## Implementation
The given algorithm is implemented for integer points. Of course, it can be easily modified to work with doubles.
```{.cpp file=check-segments-inter}
struct pt {
long long x, y;
pt() {}
pt(long long _x, long long _y) : x(_x), y(_y) {}
pt operator-(const pt& p) const { return pt(x - p.x, y - p.y); }
long long cross(const pt& p) const { return x * p.y - y * p.x; }
long long cross(const pt& a, const pt& b) const { return (a - *this).cross(b - *this); }
};
int sgn(const long long& x) { return x >= 0 ? x ? 1 : 0 : -1; }
bool inter1(long long a, long long b, long long c, long long d) {
if (a > b)
swap(a, b);
if (c > d)
swap(c, d);
return max(a, c) <= min(b, d);
}
bool check_inter(const pt& a, const pt& b, const pt& c, const pt& d) {
if (c.cross(a, d) == 0 && c.cross(b, d) == 0)
return inter1(a.x, b.x, c.x, d.x) && inter1(a.y, b.y, c.y, d.y);
return sgn(a.cross(b, c)) != sgn(a.cross(b, d)) &&
sgn(c.cross(d, a)) != sgn(c.cross(d, b));
}
```
|
---
title
segments_intersection_checking
---
# Check if two segments intersect
You are given two segments $(a, b)$ and $(c, d)$.
You have to check if they intersect.
Of course, you may find their intersection and check if it isn't empty, but this can't be done in integers for segments with integer coordinates.
The approach described here can work in integers.
## Algorithm
Firstly, consider the case when the segments are part of the same line.
In this case it is sufficient to check if their projections on $Ox$ and $Oy$ intersect.
In the other case $a$ and $b$ must not lie on the same side of line $(c, d)$, and $c$ and $d$ must not lie on the same side of line $(a, b)$.
It can be checked with a couple of cross products.
## Implementation
The given algorithm is implemented for integer points. Of course, it can be easily modified to work with doubles.
```{.cpp file=check-segments-inter}
struct pt {
long long x, y;
pt() {}
pt(long long _x, long long _y) : x(_x), y(_y) {}
pt operator-(const pt& p) const { return pt(x - p.x, y - p.y); }
long long cross(const pt& p) const { return x * p.y - y * p.x; }
long long cross(const pt& a, const pt& b) const { return (a - *this).cross(b - *this); }
};
int sgn(const long long& x) { return x >= 0 ? x ? 1 : 0 : -1; }
bool inter1(long long a, long long b, long long c, long long d) {
if (a > b)
swap(a, b);
if (c > d)
swap(c, d);
return max(a, c) <= min(b, d);
}
bool check_inter(const pt& a, const pt& b, const pt& c, const pt& d) {
if (c.cross(a, d) == 0 && c.cross(b, d) == 0)
return inter1(a.x, b.x, c.x, d.x) && inter1(a.y, b.y, c.y, d.y);
return sgn(a.cross(b, c)) != sgn(a.cross(b, d)) &&
sgn(c.cross(d, a)) != sgn(c.cross(d, b));
}
```
|
Check if two segments intersect
|
---
title
- Original
---
# Convex hull trick and Li Chao tree
Consider the following problem. There are $n$ cities. You want to travel from city $1$ to city $n$ by car. To do this you have to buy some gasoline. It is known that a liter of gasoline costs $cost_k$ in the $k^{th}$ city. Initially your fuel tank is empty and you spend one liter of gasoline per kilometer. Cities are located on the same line in ascending order with $k^{th}$ city having coordinate $x_k$. Also you have to pay $toll_k$ to enter $k^{th}$ city. Your task is to make the trip with minimum possible cost. It's obvious that the solution can be calculated via dynamic programming:
$$dp_i = toll_i+\min\limits_{j<i}(cost_j \cdot (x_i - x_j)+dp_j)$$
Naive approach will give you $O(n^2)$ complexity which can be improved to $O(n \log n)$ or $O(n \log [C \varepsilon^{-1}])$ where $C$ is largest possible $|x_i|$ and $\varepsilon$ is precision with which $x_i$ is considered ($\varepsilon = 1$ for integers which is usually the case). To do this one should note that the problem can be reduced to adding linear functions $k \cdot x + b$ to the set and finding minimum value of the functions in some particular point $x$. There are two main approaches one can use here.
## Convex hull trick
The idea of this approach is to maintain a lower convex hull of linear functions.
Actually it would be a bit more convenient to consider them not as linear functions, but as points $(k;b)$ on the plane such that we will have to find the point which has the least dot product with a given point $(x;1)$, that is, for this point $kx+b$ is minimized which is the same as initial problem.
Such minimum will necessarily be on lower convex envelope of these points as can be seen below:
<center>  </center>
One has to keep points on the convex hull and normal vectors of the hull's edges.
When you have a $(x;1)$ query you'll have to find the normal vector closest to it in terms of angles between them, then the optimum linear function will correspond to one of its endpoints.
To see that, one should note that points having a constant dot product with $(x;1)$ lie on a line which is orthogonal to $(x;1)$, so the optimum linear function will be the one in which tangent to convex hull which is collinear with normal to $(x;1)$ touches the hull.
This point is the one such that normals of edges lying to the left and to the right of it are headed in different sides of $(x;1)$.
This approach is useful when queries of adding linear functions are monotone in terms of $k$ or if we work offline, i.e. we may firstly add all linear functions and answer queries afterwards.
So we cannot solve the cities/gasoline problems using this way.
That would require handling online queries.
When it comes to deal with online queries however, things will go tough and one will have to use some kind of set data structure to implement a proper convex hull.
Online approach will however not be considered in this article due to its hardness and because second approach (which is Li Chao tree) allows to solve the problem way more simply.
Worth mentioning that one can still use this approach online without complications by square-root-decomposition.
That is, rebuild convex hull from scratch each $\sqrt n$ new lines.
To implement this approach one should begin with some geometric utility functions, here we suggest to use the C++ complex number type.
```cpp
typedef int ftype;
typedef complex<ftype> point;
#define x real
#define y imag
ftype dot(point a, point b) {
return (conj(a) * b).x();
}
ftype cross(point a, point b) {
return (conj(a) * b).y();
}
```
Here we will assume that when linear functions are added, their $k$ only increases and we want to find minimum values.
We will keep points in vector $hull$ and normal vectors in vector $vecs$.
When we add a new point, we have to look at the angle formed between last edge in convex hull and vector from last point in convex hull to new point.
This angle has to be directed counter-clockwise, that is the dot product of the last normal vector in the hull (directed inside hull) and the vector from the last point to the new one has to be non-negative.
As long as this isn't true, we should erase the last point in the convex hull alongside with the corresponding edge.
```cpp
vector<point> hull, vecs;
void add_line(ftype k, ftype b) {
point nw = {k, b};
while(!vecs.empty() && dot(vecs.back(), nw - hull.back()) < 0) {
hull.pop_back();
vecs.pop_back();
}
if(!hull.empty()) {
vecs.push_back(1i * (nw - hull.back()));
}
hull.push_back(nw);
}
```
Now to get the minimum value in some point we will find the first normal vector in the convex hull that is directed counter-clockwise from $(x;1)$. The left endpoint of such edge will be the answer. To check if vector $a$ is not directed counter-clockwise of vector $b$, we should check if their cross product $[a,b]$ is positive.
```cpp
int get(ftype x) {
point query = {x, 1};
auto it = lower_bound(vecs.begin(), vecs.end(), query, [](point a, point b) {
return cross(a, b) > 0;
});
return dot(query, hull[it - vecs.begin()]);
}
```
## Li Chao tree
Assume you're given a set of functions such that each two can intersect at most once. Let's keep in each vertex of a segment tree some function in such way, that if we go from root to the leaf it will be guaranteed that one of the functions we met on the path will be the one giving the minimum value in that leaf. Let's see how to construct it.
Assume we're in some vertex corresponding to half-segment $[l,r)$ and the function $f_{old}$ is kept there and we add the function $f_{new}$. Then the intersection point will be either in $[l;m)$ or in $[m;r)$ where $m=\left\lfloor\tfrac{l+r}{2}\right\rfloor$. We can efficiently find that out by comparing the values of the functions in points $l$ and $m$. If the dominating function changes, then it is in $[l;m)$ otherwise it is in $[m;r)$. Now for the half of the segment with no intersection we will pick the lower function and write it in the current vertex. You can see that it will always be the one which is lower in point $m$. After that we recursively go to the other half of the segment with the function which was the upper one. As you can see this will keep correctness on the first half of segment and in the other one correctness will be maintained during the recursive call. Thus we can add functions and check the minimum value in the point in $O(\log [C\varepsilon^{-1}])$.
Here is the illustration of what is going on in the vertex when we add new function:
<center></center>
Let's go to implementation now. Once again we will use complex numbers to keep linear functions.
```{.cpp file=lichaotree_line_definition}
typedef long long ftype;
typedef complex<ftype> point;
#define x real
#define y imag
ftype dot(point a, point b) {
return (conj(a) * b).x();
}
ftype f(point a, ftype x) {
return dot(a, {x, 1});
}
```
We will keep functions in the array $line$ and use binary indexing of the segment tree. If you want to use it on large numbers or doubles, you should use a dynamic segment tree.
The segment tree should be initialized with default values, e.g. with lines $0x + \infty$.
```{.cpp file=lichaotree_addline}
const int maxn = 2e5;
point line[4 * maxn];
void add_line(point nw, int v = 1, int l = 0, int r = maxn) {
int m = (l + r) / 2;
bool lef = f(nw, l) < f(line[v], l);
bool mid = f(nw, m) < f(line[v], m);
if(mid) {
swap(line[v], nw);
}
if(r - l == 1) {
return;
} else if(lef != mid) {
add_line(nw, 2 * v, l, m);
} else {
add_line(nw, 2 * v + 1, m, r);
}
}
```
Now to get the minimum in some point $x$ we simply choose the minimum value along the path to the point.
```{.cpp file=lichaotree_getminimum}
ftype get(int x, int v = 1, int l = 0, int r = maxn) {
int m = (l + r) / 2;
if(r - l == 1) {
return f(line[v], x);
} else if(x < m) {
return min(f(line[v], x), get(x, 2 * v, l, m));
} else {
return min(f(line[v], x), get(x, 2 * v + 1, m, r));
}
}
```
|
---
title
- Original
---
# Convex hull trick and Li Chao tree
Consider the following problem. There are $n$ cities. You want to travel from city $1$ to city $n$ by car. To do this you have to buy some gasoline. It is known that a liter of gasoline costs $cost_k$ in the $k^{th}$ city. Initially your fuel tank is empty and you spend one liter of gasoline per kilometer. Cities are located on the same line in ascending order with $k^{th}$ city having coordinate $x_k$. Also you have to pay $toll_k$ to enter $k^{th}$ city. Your task is to make the trip with minimum possible cost. It's obvious that the solution can be calculated via dynamic programming:
$$dp_i = toll_i+\min\limits_{j<i}(cost_j \cdot (x_i - x_j)+dp_j)$$
Naive approach will give you $O(n^2)$ complexity which can be improved to $O(n \log n)$ or $O(n \log [C \varepsilon^{-1}])$ where $C$ is largest possible $|x_i|$ and $\varepsilon$ is precision with which $x_i$ is considered ($\varepsilon = 1$ for integers which is usually the case). To do this one should note that the problem can be reduced to adding linear functions $k \cdot x + b$ to the set and finding minimum value of the functions in some particular point $x$. There are two main approaches one can use here.
## Convex hull trick
The idea of this approach is to maintain a lower convex hull of linear functions.
Actually it would be a bit more convenient to consider them not as linear functions, but as points $(k;b)$ on the plane such that we will have to find the point which has the least dot product with a given point $(x;1)$, that is, for this point $kx+b$ is minimized which is the same as initial problem.
Such minimum will necessarily be on lower convex envelope of these points as can be seen below:
<center>  </center>
One has to keep points on the convex hull and normal vectors of the hull's edges.
When you have a $(x;1)$ query you'll have to find the normal vector closest to it in terms of angles between them, then the optimum linear function will correspond to one of its endpoints.
To see that, one should note that points having a constant dot product with $(x;1)$ lie on a line which is orthogonal to $(x;1)$, so the optimum linear function will be the one in which tangent to convex hull which is collinear with normal to $(x;1)$ touches the hull.
This point is the one such that normals of edges lying to the left and to the right of it are headed in different sides of $(x;1)$.
This approach is useful when queries of adding linear functions are monotone in terms of $k$ or if we work offline, i.e. we may firstly add all linear functions and answer queries afterwards.
So we cannot solve the cities/gasoline problems using this way.
That would require handling online queries.
When it comes to deal with online queries however, things will go tough and one will have to use some kind of set data structure to implement a proper convex hull.
Online approach will however not be considered in this article due to its hardness and because second approach (which is Li Chao tree) allows to solve the problem way more simply.
Worth mentioning that one can still use this approach online without complications by square-root-decomposition.
That is, rebuild convex hull from scratch each $\sqrt n$ new lines.
To implement this approach one should begin with some geometric utility functions, here we suggest to use the C++ complex number type.
```cpp
typedef int ftype;
typedef complex<ftype> point;
#define x real
#define y imag
ftype dot(point a, point b) {
return (conj(a) * b).x();
}
ftype cross(point a, point b) {
return (conj(a) * b).y();
}
```
Here we will assume that when linear functions are added, their $k$ only increases and we want to find minimum values.
We will keep points in vector $hull$ and normal vectors in vector $vecs$.
When we add a new point, we have to look at the angle formed between last edge in convex hull and vector from last point in convex hull to new point.
This angle has to be directed counter-clockwise, that is the dot product of the last normal vector in the hull (directed inside hull) and the vector from the last point to the new one has to be non-negative.
As long as this isn't true, we should erase the last point in the convex hull alongside with the corresponding edge.
```cpp
vector<point> hull, vecs;
void add_line(ftype k, ftype b) {
point nw = {k, b};
while(!vecs.empty() && dot(vecs.back(), nw - hull.back()) < 0) {
hull.pop_back();
vecs.pop_back();
}
if(!hull.empty()) {
vecs.push_back(1i * (nw - hull.back()));
}
hull.push_back(nw);
}
```
Now to get the minimum value in some point we will find the first normal vector in the convex hull that is directed counter-clockwise from $(x;1)$. The left endpoint of such edge will be the answer. To check if vector $a$ is not directed counter-clockwise of vector $b$, we should check if their cross product $[a,b]$ is positive.
```cpp
int get(ftype x) {
point query = {x, 1};
auto it = lower_bound(vecs.begin(), vecs.end(), query, [](point a, point b) {
return cross(a, b) > 0;
});
return dot(query, hull[it - vecs.begin()]);
}
```
## Li Chao tree
Assume you're given a set of functions such that each two can intersect at most once. Let's keep in each vertex of a segment tree some function in such way, that if we go from root to the leaf it will be guaranteed that one of the functions we met on the path will be the one giving the minimum value in that leaf. Let's see how to construct it.
Assume we're in some vertex corresponding to half-segment $[l,r)$ and the function $f_{old}$ is kept there and we add the function $f_{new}$. Then the intersection point will be either in $[l;m)$ or in $[m;r)$ where $m=\left\lfloor\tfrac{l+r}{2}\right\rfloor$. We can efficiently find that out by comparing the values of the functions in points $l$ and $m$. If the dominating function changes, then it is in $[l;m)$ otherwise it is in $[m;r)$. Now for the half of the segment with no intersection we will pick the lower function and write it in the current vertex. You can see that it will always be the one which is lower in point $m$. After that we recursively go to the other half of the segment with the function which was the upper one. As you can see this will keep correctness on the first half of segment and in the other one correctness will be maintained during the recursive call. Thus we can add functions and check the minimum value in the point in $O(\log [C\varepsilon^{-1}])$.
Here is the illustration of what is going on in the vertex when we add new function:
<center></center>
Let's go to implementation now. Once again we will use complex numbers to keep linear functions.
```{.cpp file=lichaotree_line_definition}
typedef long long ftype;
typedef complex<ftype> point;
#define x real
#define y imag
ftype dot(point a, point b) {
return (conj(a) * b).x();
}
ftype f(point a, ftype x) {
return dot(a, {x, 1});
}
```
We will keep functions in the array $line$ and use binary indexing of the segment tree. If you want to use it on large numbers or doubles, you should use a dynamic segment tree.
The segment tree should be initialized with default values, e.g. with lines $0x + \infty$.
```{.cpp file=lichaotree_addline}
const int maxn = 2e5;
point line[4 * maxn];
void add_line(point nw, int v = 1, int l = 0, int r = maxn) {
int m = (l + r) / 2;
bool lef = f(nw, l) < f(line[v], l);
bool mid = f(nw, m) < f(line[v], m);
if(mid) {
swap(line[v], nw);
}
if(r - l == 1) {
return;
} else if(lef != mid) {
add_line(nw, 2 * v, l, m);
} else {
add_line(nw, 2 * v + 1, m, r);
}
}
```
Now to get the minimum in some point $x$ we simply choose the minimum value along the path to the point.
```{.cpp file=lichaotree_getminimum}
ftype get(int x, int v = 1, int l = 0, int r = maxn) {
int m = (l + r) / 2;
if(r - l == 1) {
return f(line[v], x);
} else if(x < m) {
return min(f(line[v], x), get(x, 2 * v, l, m));
} else {
return min(f(line[v], x), get(x, 2 * v + 1, m, r));
}
}
```
## Problems
* [Codebreaker - TROUBLES](https://codeforces.com/gym/103536/problem/B) (simple application of Convex Hull Trick after a couple of observations)
* [CS Academy - Squared Ends](https://csacademy.com/contest/archive/task/squared-ends)
* [Codeforces - Escape Through Leaf](http://codeforces.com/contest/932/problem/F)
* [CodeChef - Polynomials](https://www.codechef.com/NOV17/problems/POLY)
* [Codeforces - Kalila and Dimna in the Logging Industry](https://codeforces.com/problemset/problem/319/C)
* [Codeforces - Product Sum](https://codeforces.com/problemset/problem/631/E)
* [Codeforces - Bear and Bowling 4](https://codeforces.com/problemset/problem/660/F)
* [APIO 2010 - Commando](https://dmoj.ca/problem/apio10p1)
|
Convex hull trick and Li Chao tree
|
---
title
- Original
---
# Basic Geometry
In this article we will consider basic operations on points in Euclidean space which maintains the foundation of the whole analytical geometry.
We will consider for each point $\mathbf r$ the vector $\vec{\mathbf r}$ directed from $\mathbf 0$ to $\mathbf r$.
Later we will not distinguish between $\mathbf r$ and $\vec{\mathbf r}$ and use the term **point** as a synonym for **vector**.
## Linear operations
Both 2D and 3D points maintain linear space, which means that for them sum of points and multiplication of point by some number are defined. Here are those basic implementations for 2D:
```{.cpp file=point2d}
struct point2d {
ftype x, y;
point2d() {}
point2d(ftype x, ftype y): x(x), y(y) {}
point2d& operator+=(const point2d &t) {
x += t.x;
y += t.y;
return *this;
}
point2d& operator-=(const point2d &t) {
x -= t.x;
y -= t.y;
return *this;
}
point2d& operator*=(ftype t) {
x *= t;
y *= t;
return *this;
}
point2d& operator/=(ftype t) {
x /= t;
y /= t;
return *this;
}
point2d operator+(const point2d &t) const {
return point2d(*this) += t;
}
point2d operator-(const point2d &t) const {
return point2d(*this) -= t;
}
point2d operator*(ftype t) const {
return point2d(*this) *= t;
}
point2d operator/(ftype t) const {
return point2d(*this) /= t;
}
};
point2d operator*(ftype a, point2d b) {
return b * a;
}
```
And 3D points:
```{.cpp file=point3d}
struct point3d {
ftype x, y, z;
point3d() {}
point3d(ftype x, ftype y, ftype z): x(x), y(y), z(z) {}
point3d& operator+=(const point3d &t) {
x += t.x;
y += t.y;
z += t.z;
return *this;
}
point3d& operator-=(const point3d &t) {
x -= t.x;
y -= t.y;
z -= t.z;
return *this;
}
point3d& operator*=(ftype t) {
x *= t;
y *= t;
z *= t;
return *this;
}
point3d& operator/=(ftype t) {
x /= t;
y /= t;
z /= t;
return *this;
}
point3d operator+(const point3d &t) const {
return point3d(*this) += t;
}
point3d operator-(const point3d &t) const {
return point3d(*this) -= t;
}
point3d operator*(ftype t) const {
return point3d(*this) *= t;
}
point3d operator/(ftype t) const {
return point3d(*this) /= t;
}
};
point3d operator*(ftype a, point3d b) {
return b * a;
}
```
Here `ftype` is some type used for coordinates, usually `int`, `double` or `long long`.
## Dot product
### Definition
The dot (or scalar) product $\mathbf a \cdot \mathbf b$ for vectors $\mathbf a$ and $\mathbf b$ can be defined in two identical ways.
Geometrically it is product of the length of the first vector by the length of the projection of the second vector onto the first one.
As you may see from the image below this projection is nothing but $|\mathbf a| \cos \theta$ where $\theta$ is the angle between $\mathbf a$ and $\mathbf b$. Thus $\mathbf a\cdot \mathbf b = |\mathbf a| \cos \theta \cdot |\mathbf b|$.
<center>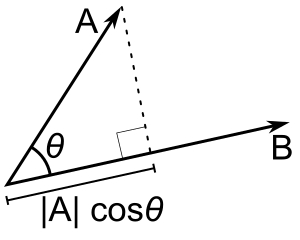</center>
The dot product holds some notable properties:
1. $\mathbf a \cdot \mathbf b = \mathbf b \cdot \mathbf a$
2. $(\alpha \cdot \mathbf a)\cdot \mathbf b = \alpha \cdot (\mathbf a \cdot \mathbf b)$
3. $(\mathbf a + \mathbf b)\cdot \mathbf c = \mathbf a \cdot \mathbf c + \mathbf b \cdot \mathbf c$
I.e. it is a commutative function which is linear with respect to both arguments.
Let's denote the unit vectors as
$$\mathbf e_x = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, \mathbf e_y = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, \mathbf e_z = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}.$$
With this notation we can write the vector $\mathbf r = (x;y;z)$ as $r = x \cdot \mathbf e_x + y \cdot \mathbf e_y + z \cdot \mathbf e_z$.
And since for unit vectors
$$\mathbf e_x\cdot \mathbf e_x = \mathbf e_y\cdot \mathbf e_y = \mathbf e_z\cdot \mathbf e_z = 1,\\
\mathbf e_x\cdot \mathbf e_y = \mathbf e_y\cdot \mathbf e_z = \mathbf e_z\cdot \mathbf e_x = 0$$
we can see that in terms of coordinates for $\mathbf a = (x_1;y_1;z_1)$ and $\mathbf b = (x_2;y_2;z_2)$ holds
$$\mathbf a\cdot \mathbf b = (x_1 \cdot \mathbf e_x + y_1 \cdot\mathbf e_y + z_1 \cdot\mathbf e_z)\cdot( x_2 \cdot\mathbf e_x + y_2 \cdot\mathbf e_y + z_2 \cdot\mathbf e_z) = x_1 x_2 + y_1 y_2 + z_1 z_2$$
That is also the algebraic definition of the dot product.
From this we can write functions which calculate it.
```{.cpp file=dotproduct}
ftype dot(point2d a, point2d b) {
return a.x * b.x + a.y * b.y;
}
ftype dot(point3d a, point3d b) {
return a.x * b.x + a.y * b.y + a.z * b.z;
}
```
When solving problems one should use algebraic definition to calculate dot products, but keep in mind geometric definition and properties to use it.
### Properties
We can define many geometrical properties via the dot product.
For example
1. Norm of $\mathbf a$ (squared length): $|\mathbf a|^2 = \mathbf a\cdot \mathbf a$
2. Length of $\mathbf a$: $|\mathbf a| = \sqrt{\mathbf a\cdot \mathbf a}$
3. Projection of $\mathbf a$ onto $\mathbf b$: $\dfrac{\mathbf a\cdot\mathbf b}{|\mathbf b|}$
4. Angle between vectors: $\arccos \left(\dfrac{\mathbf a\cdot \mathbf b}{|\mathbf a| \cdot |\mathbf b|}\right)$
5. From the previous point we may see that the dot product is positive if the angle between them is acute, negative if it is obtuse and it equals zero if they are orthogonal, i.e. they form a right angle.
Note that all these functions do not depend on the number of dimensions, hence they will be the same for the 2D and 3D case:
```{.cpp file=dotproperties}
ftype norm(point2d a) {
return dot(a, a);
}
double abs(point2d a) {
return sqrt(norm(a));
}
double proj(point2d a, point2d b) {
return dot(a, b) / abs(b);
}
double angle(point2d a, point2d b) {
return acos(dot(a, b) / abs(a) / abs(b));
}
```
To see the next important property we should take a look at the set of points $\mathbf r$ for which $\mathbf r\cdot \mathbf a = C$ for some fixed constant $C$.
You can see that this set of points is exactly the set of points for which the projection onto $\mathbf a$ is the point $C \cdot \dfrac{\mathbf a}{|\mathbf a|}$ and they form a hyperplane orthogonal to $\mathbf a$.
You can see the vector $\mathbf a$ alongside with several such vectors having same dot product with it in 2D on the picture below:
<center></center>
In 2D these vectors will form a line, in 3D they will form a plane.
Note that this result allows us to define a line in 2D as $\mathbf r\cdot \mathbf n=C$ or $(\mathbf r - \mathbf r_0)\cdot \mathbf n=0$ where $\mathbf n$ is vector orthogonal to the line and $\mathbf r_0$ is any vector already present on the line and $C = \mathbf r_0\cdot \mathbf n$.
In the same manner a plane can be defined in 3D.
## Cross product
### Definition
Assume you have three vectors $\mathbf a$, $\mathbf b$ and $\mathbf c$ in 3D space joined in a parallelepiped as in the picture below:
<center></center>
How would you calculate its volume?
From school we know that we should multiply the area of the base with the height, which is projection of $\mathbf a$ onto direction orthogonal to base.
That means that if we define $\mathbf b \times \mathbf c$ as the vector which is orthogonal to both $\mathbf b$ and $\mathbf c$ and which length is equal to the area of the parallelogram formed by $\mathbf b$ and $\mathbf c$ then $|\mathbf a\cdot (\mathbf b\times\mathbf c)|$ will be equal to the volume of the parallelepiped.
For integrity we will say that $\mathbf b\times \mathbf c$ will be always directed in such way that the rotation from the vector $\mathbf b$ to the vector $\mathbf c$ from the point of $\mathbf b\times \mathbf c$ is always counter-clockwise (see the picture below).
<center></center>
This defines the cross (or vector) product $\mathbf b\times \mathbf c$ of the vectors $\mathbf b$ and $\mathbf c$ and the triple product $\mathbf a\cdot(\mathbf b\times \mathbf c)$ of the vectors $\mathbf a$, $\mathbf b$ and $\mathbf c$.
Some notable properties of cross and triple products:
1. $\mathbf a\times \mathbf b = -\mathbf b\times \mathbf a$
2. $(\alpha \cdot \mathbf a)\times \mathbf b = \alpha \cdot (\mathbf a\times \mathbf b)$
3. For any $\mathbf b$ and $\mathbf c$ there is exactly one vector $\mathbf r$ such that $\mathbf a\cdot (\mathbf b\times \mathbf c) = \mathbf a\cdot\mathbf r$ for any vector $\mathbf a$. <br>Indeed if there are two such vectors $\mathbf r_1$ and $\mathbf r_2$ then $\mathbf a\cdot (\mathbf r_1 - \mathbf r_2)=0$ for all vectors $\mathbf a$ which is possible only when $\mathbf r_1 = \mathbf r_2$.
4. $\mathbf a\cdot (\mathbf b\times \mathbf c) = \mathbf b\cdot (\mathbf c\times \mathbf a) = -\mathbf a\cdot( \mathbf c\times \mathbf b)$
5. $(\mathbf a + \mathbf b)\times \mathbf c = \mathbf a\times \mathbf c + \mathbf b\times \mathbf c$.
Indeed for all vectors $\mathbf r$ the chain of equations holds:
\[\mathbf r\cdot( (\mathbf a + \mathbf b)\times \mathbf c) = (\mathbf a + \mathbf b) \cdot (\mathbf c\times \mathbf r) = \mathbf a \cdot(\mathbf c\times \mathbf r) + \mathbf b\cdot(\mathbf c\times \mathbf r) = \mathbf r\cdot (\mathbf a\times \mathbf c) + \mathbf r\cdot(\mathbf b\times \mathbf c) = \mathbf r\cdot(\mathbf a\times \mathbf c + \mathbf b\times \mathbf c)\]
Which proves $(\mathbf a + \mathbf b)\times \mathbf c = \mathbf a\times \mathbf c + \mathbf b\times \mathbf c$ due to point 3.
6. $|\mathbf a\times \mathbf b|=|\mathbf a| \cdot |\mathbf b| \sin \theta$ where $\theta$ is angle between $\mathbf a$ and $\mathbf b$, since $|\mathbf a\times \mathbf b|$ equals to the area of the parallelogram formed by $\mathbf a$ and $\mathbf b$.
Given all this and that the following equation holds for the unit vectors
$$\mathbf e_x\times \mathbf e_x = \mathbf e_y\times \mathbf e_y = \mathbf e_z\times \mathbf e_z = \mathbf 0,\\
\mathbf e_x\times \mathbf e_y = \mathbf e_z,~\mathbf e_y\times \mathbf e_z = \mathbf e_x,~\mathbf e_z\times \mathbf e_x = \mathbf e_y$$
we can calculate the cross product of $\mathbf a = (x_1;y_1;z_1)$ and $\mathbf b = (x_2;y_2;z_2)$ in coordinate form:
$$\mathbf a\times \mathbf b = (x_1 \cdot \mathbf e_x + y_1 \cdot \mathbf e_y + z_1 \cdot \mathbf e_z)\times (x_2 \cdot \mathbf e_x + y_2 \cdot \mathbf e_y + z_2 \cdot \mathbf e_z) =$$
$$(y_1 z_2 - z_1 y_2)\mathbf e_x + (z_1 x_2 - x_1 z_2)\mathbf e_y + (x_1 y_2 - y_1 x_2)$$
Which also can be written in the more elegant form:
$$\mathbf a\times \mathbf b = \begin{vmatrix}\mathbf e_x & \mathbf e_y & \mathbf e_z \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix},~a\cdot(b\times c) = \begin{vmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{vmatrix}$$
Here $| \cdot |$ stands for the determinant of a matrix.
Some kind of cross product (namely the pseudo-scalar product) can also be implemented in the 2D case.
If we would like to calculate the area of parallelogram formed by vectors $\mathbf a$ and $\mathbf b$ we would compute $|\mathbf e_z\cdot(\mathbf a\times \mathbf b)| = |x_1 y_2 - y_1 x_2|$.
Another way to obtain the same result is to multiply $|\mathbf a|$ (base of parallelogram) with the height, which is the projection of vector $\mathbf b$ onto vector $\mathbf a$ rotated by $90^\circ$ which in turn is $\widehat{\mathbf a}=(-y_1;x_1)$.
That is, to calculate $|\widehat{\mathbf a}\cdot\mathbf b|=|x_1y_2 - y_1 x_2|$.
If we will take the sign into consideration then the area will be positive if the rotation from $\mathbf a$ to $\mathbf b$ (i.e. from the view of the point of $\mathbf e_z$) is performed counter-clockwise and negative otherwise.
That defines the pseudo-scalar product.
Note that it also equals $|\mathbf a| \cdot |\mathbf b| \sin \theta$ where $\theta$ is angle from $\mathbf a$ to $\mathbf b$ count counter-clockwise (and negative if rotation is clockwise).
Let's implement all this stuff!
```{.cpp file=crossproduct}
point3d cross(point3d a, point3d b) {
return point3d(a.y * b.z - a.z * b.y,
a.z * b.x - a.x * b.z,
a.x * b.y - a.y * b.x);
}
ftype triple(point3d a, point3d b, point3d c) {
return dot(a, cross(b, c));
}
ftype cross(point2d a, point2d b) {
return a.x * b.y - a.y * b.x;
}
```
### Properties
As for the cross product, it equals to the zero vector iff the vectors $\mathbf a$ and $\mathbf b$ are collinear (they form a common line, i.e. they are parallel).
The same thing holds for the triple product, it is equal to zero iff the vectors $\mathbf a$, $\mathbf b$ and $\mathbf c$ are coplanar (they form a common plane).
From this we can obtain universal equations defining lines and planes.
A line can be defined via its direction vector $\mathbf d$ and an initial point $\mathbf r_0$ or by two points $\mathbf a$ and $\mathbf b$.
It is defined as $(\mathbf r - \mathbf r_0)\times\mathbf d=0$ or as $(\mathbf r - \mathbf a)\times (\mathbf b - \mathbf a) = 0$.
As for planes, it can be defined by three points $\mathbf a$, $\mathbf b$ and $\mathbf c$ as $(\mathbf r - \mathbf a)\cdot((\mathbf b - \mathbf a)\times (\mathbf c - \mathbf a))=0$ or by initial point $\mathbf r_0$ and two direction vectors lying in this plane $\mathbf d_1$ and $\mathbf d_2$: $(\mathbf r - \mathbf r_0)\cdot(\mathbf d_1\times \mathbf d_2)=0$.
In 2D the pseudo-scalar product also may be used to check the orientation between two vectors because it is positive if the rotation from the first to the second vector is clockwise and negative otherwise.
And, of course, it can be used to calculate areas of polygons, which is described in a different article.
A triple product can be used for the same purpose in 3D space.
## Exercises
### Line intersection
There are many possible ways to define a line in 2D and you shouldn't hesitate to combine them.
For example we have two lines and we want to find their intersection points.
We can say that all points from first line can be parameterized as $\mathbf r = \mathbf a_1 + t \cdot \mathbf d_1$ where $\mathbf a_1$ is initial point, $\mathbf d_1$ is direction and $t$ is some real parameter.
As for second line all its points must satisfy $(\mathbf r - \mathbf a_2)\times \mathbf d_2=0$. From this we can easily find parameter $t$:
$$(\mathbf a_1 + t \cdot \mathbf d_1 - \mathbf a_2)\times \mathbf d_2=0 \quad\Rightarrow\quad t = \dfrac{(\mathbf a_2 - \mathbf a_1)\times\mathbf d_2}{\mathbf d_1\times \mathbf d_2}$$
Let's implement function to intersect two lines.
```{.cpp file=basic_line_intersection}
point2d intersect(point2d a1, point2d d1, point2d a2, point2d d2) {
return a1 + cross(a2 - a1, d2) / cross(d1, d2) * d1;
}
```
### Planes intersection
However sometimes it might be hard to use some geometric insights.
For example, you're given three planes defined by initial points $\mathbf a_i$ and directions $\mathbf d_i$ and you want to find their intersection point.
You may note that you just have to solve the system of equations:
$$\begin{cases}\mathbf r\cdot \mathbf n_1 = \mathbf a_1\cdot \mathbf n_1, \\ \mathbf r\cdot \mathbf n_2 = \mathbf a_2\cdot \mathbf n_2, \\ \mathbf r\cdot \mathbf n_3 = \mathbf a_3\cdot \mathbf n_3\end{cases}$$
Instead of thinking on geometric approach, you can work out an algebraic one which can be obtained immediately.
For example, given that you already implemented a point class, it will be easy for you to solve this system using Cramer's rule because the triple product is simply the determinant of the matrix obtained from the vectors being its columns:
```{.cpp file=plane_intersection}
point3d intersect(point3d a1, point3d n1, point3d a2, point3d n2, point3d a3, point3d n3) {
point3d x(n1.x, n2.x, n3.x);
point3d y(n1.y, n2.y, n3.y);
point3d z(n1.z, n2.z, n3.z);
point3d d(dot(a1, n1), dot(a2, n2), dot(a3, n3));
return point3d(triple(d, y, z),
triple(x, d, z),
triple(x, y, d)) / triple(n1, n2, n3);
}
```
Now you may try to find out approaches for common geometric operations yourself to get used to all this stuff.
|
---
title
- Original
---
# Basic Geometry
In this article we will consider basic operations on points in Euclidean space which maintains the foundation of the whole analytical geometry.
We will consider for each point $\mathbf r$ the vector $\vec{\mathbf r}$ directed from $\mathbf 0$ to $\mathbf r$.
Later we will not distinguish between $\mathbf r$ and $\vec{\mathbf r}$ and use the term **point** as a synonym for **vector**.
## Linear operations
Both 2D and 3D points maintain linear space, which means that for them sum of points and multiplication of point by some number are defined. Here are those basic implementations for 2D:
```{.cpp file=point2d}
struct point2d {
ftype x, y;
point2d() {}
point2d(ftype x, ftype y): x(x), y(y) {}
point2d& operator+=(const point2d &t) {
x += t.x;
y += t.y;
return *this;
}
point2d& operator-=(const point2d &t) {
x -= t.x;
y -= t.y;
return *this;
}
point2d& operator*=(ftype t) {
x *= t;
y *= t;
return *this;
}
point2d& operator/=(ftype t) {
x /= t;
y /= t;
return *this;
}
point2d operator+(const point2d &t) const {
return point2d(*this) += t;
}
point2d operator-(const point2d &t) const {
return point2d(*this) -= t;
}
point2d operator*(ftype t) const {
return point2d(*this) *= t;
}
point2d operator/(ftype t) const {
return point2d(*this) /= t;
}
};
point2d operator*(ftype a, point2d b) {
return b * a;
}
```
And 3D points:
```{.cpp file=point3d}
struct point3d {
ftype x, y, z;
point3d() {}
point3d(ftype x, ftype y, ftype z): x(x), y(y), z(z) {}
point3d& operator+=(const point3d &t) {
x += t.x;
y += t.y;
z += t.z;
return *this;
}
point3d& operator-=(const point3d &t) {
x -= t.x;
y -= t.y;
z -= t.z;
return *this;
}
point3d& operator*=(ftype t) {
x *= t;
y *= t;
z *= t;
return *this;
}
point3d& operator/=(ftype t) {
x /= t;
y /= t;
z /= t;
return *this;
}
point3d operator+(const point3d &t) const {
return point3d(*this) += t;
}
point3d operator-(const point3d &t) const {
return point3d(*this) -= t;
}
point3d operator*(ftype t) const {
return point3d(*this) *= t;
}
point3d operator/(ftype t) const {
return point3d(*this) /= t;
}
};
point3d operator*(ftype a, point3d b) {
return b * a;
}
```
Here `ftype` is some type used for coordinates, usually `int`, `double` or `long long`.
## Dot product
### Definition
The dot (or scalar) product $\mathbf a \cdot \mathbf b$ for vectors $\mathbf a$ and $\mathbf b$ can be defined in two identical ways.
Geometrically it is product of the length of the first vector by the length of the projection of the second vector onto the first one.
As you may see from the image below this projection is nothing but $|\mathbf a| \cos \theta$ where $\theta$ is the angle between $\mathbf a$ and $\mathbf b$. Thus $\mathbf a\cdot \mathbf b = |\mathbf a| \cos \theta \cdot |\mathbf b|$.
<center></center>
The dot product holds some notable properties:
1. $\mathbf a \cdot \mathbf b = \mathbf b \cdot \mathbf a$
2. $(\alpha \cdot \mathbf a)\cdot \mathbf b = \alpha \cdot (\mathbf a \cdot \mathbf b)$
3. $(\mathbf a + \mathbf b)\cdot \mathbf c = \mathbf a \cdot \mathbf c + \mathbf b \cdot \mathbf c$
I.e. it is a commutative function which is linear with respect to both arguments.
Let's denote the unit vectors as
$$\mathbf e_x = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, \mathbf e_y = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, \mathbf e_z = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}.$$
With this notation we can write the vector $\mathbf r = (x;y;z)$ as $r = x \cdot \mathbf e_x + y \cdot \mathbf e_y + z \cdot \mathbf e_z$.
And since for unit vectors
$$\mathbf e_x\cdot \mathbf e_x = \mathbf e_y\cdot \mathbf e_y = \mathbf e_z\cdot \mathbf e_z = 1,\\
\mathbf e_x\cdot \mathbf e_y = \mathbf e_y\cdot \mathbf e_z = \mathbf e_z\cdot \mathbf e_x = 0$$
we can see that in terms of coordinates for $\mathbf a = (x_1;y_1;z_1)$ and $\mathbf b = (x_2;y_2;z_2)$ holds
$$\mathbf a\cdot \mathbf b = (x_1 \cdot \mathbf e_x + y_1 \cdot\mathbf e_y + z_1 \cdot\mathbf e_z)\cdot( x_2 \cdot\mathbf e_x + y_2 \cdot\mathbf e_y + z_2 \cdot\mathbf e_z) = x_1 x_2 + y_1 y_2 + z_1 z_2$$
That is also the algebraic definition of the dot product.
From this we can write functions which calculate it.
```{.cpp file=dotproduct}
ftype dot(point2d a, point2d b) {
return a.x * b.x + a.y * b.y;
}
ftype dot(point3d a, point3d b) {
return a.x * b.x + a.y * b.y + a.z * b.z;
}
```
When solving problems one should use algebraic definition to calculate dot products, but keep in mind geometric definition and properties to use it.
### Properties
We can define many geometrical properties via the dot product.
For example
1. Norm of $\mathbf a$ (squared length): $|\mathbf a|^2 = \mathbf a\cdot \mathbf a$
2. Length of $\mathbf a$: $|\mathbf a| = \sqrt{\mathbf a\cdot \mathbf a}$
3. Projection of $\mathbf a$ onto $\mathbf b$: $\dfrac{\mathbf a\cdot\mathbf b}{|\mathbf b|}$
4. Angle between vectors: $\arccos \left(\dfrac{\mathbf a\cdot \mathbf b}{|\mathbf a| \cdot |\mathbf b|}\right)$
5. From the previous point we may see that the dot product is positive if the angle between them is acute, negative if it is obtuse and it equals zero if they are orthogonal, i.e. they form a right angle.
Note that all these functions do not depend on the number of dimensions, hence they will be the same for the 2D and 3D case:
```{.cpp file=dotproperties}
ftype norm(point2d a) {
return dot(a, a);
}
double abs(point2d a) {
return sqrt(norm(a));
}
double proj(point2d a, point2d b) {
return dot(a, b) / abs(b);
}
double angle(point2d a, point2d b) {
return acos(dot(a, b) / abs(a) / abs(b));
}
```
To see the next important property we should take a look at the set of points $\mathbf r$ for which $\mathbf r\cdot \mathbf a = C$ for some fixed constant $C$.
You can see that this set of points is exactly the set of points for which the projection onto $\mathbf a$ is the point $C \cdot \dfrac{\mathbf a}{|\mathbf a|}$ and they form a hyperplane orthogonal to $\mathbf a$.
You can see the vector $\mathbf a$ alongside with several such vectors having same dot product with it in 2D on the picture below:
<center></center>
In 2D these vectors will form a line, in 3D they will form a plane.
Note that this result allows us to define a line in 2D as $\mathbf r\cdot \mathbf n=C$ or $(\mathbf r - \mathbf r_0)\cdot \mathbf n=0$ where $\mathbf n$ is vector orthogonal to the line and $\mathbf r_0$ is any vector already present on the line and $C = \mathbf r_0\cdot \mathbf n$.
In the same manner a plane can be defined in 3D.
## Cross product
### Definition
Assume you have three vectors $\mathbf a$, $\mathbf b$ and $\mathbf c$ in 3D space joined in a parallelepiped as in the picture below:
<center></center>
How would you calculate its volume?
From school we know that we should multiply the area of the base with the height, which is projection of $\mathbf a$ onto direction orthogonal to base.
That means that if we define $\mathbf b \times \mathbf c$ as the vector which is orthogonal to both $\mathbf b$ and $\mathbf c$ and which length is equal to the area of the parallelogram formed by $\mathbf b$ and $\mathbf c$ then $|\mathbf a\cdot (\mathbf b\times\mathbf c)|$ will be equal to the volume of the parallelepiped.
For integrity we will say that $\mathbf b\times \mathbf c$ will be always directed in such way that the rotation from the vector $\mathbf b$ to the vector $\mathbf c$ from the point of $\mathbf b\times \mathbf c$ is always counter-clockwise (see the picture below).
<center></center>
This defines the cross (or vector) product $\mathbf b\times \mathbf c$ of the vectors $\mathbf b$ and $\mathbf c$ and the triple product $\mathbf a\cdot(\mathbf b\times \mathbf c)$ of the vectors $\mathbf a$, $\mathbf b$ and $\mathbf c$.
Some notable properties of cross and triple products:
1. $\mathbf a\times \mathbf b = -\mathbf b\times \mathbf a$
2. $(\alpha \cdot \mathbf a)\times \mathbf b = \alpha \cdot (\mathbf a\times \mathbf b)$
3. For any $\mathbf b$ and $\mathbf c$ there is exactly one vector $\mathbf r$ such that $\mathbf a\cdot (\mathbf b\times \mathbf c) = \mathbf a\cdot\mathbf r$ for any vector $\mathbf a$. <br>Indeed if there are two such vectors $\mathbf r_1$ and $\mathbf r_2$ then $\mathbf a\cdot (\mathbf r_1 - \mathbf r_2)=0$ for all vectors $\mathbf a$ which is possible only when $\mathbf r_1 = \mathbf r_2$.
4. $\mathbf a\cdot (\mathbf b\times \mathbf c) = \mathbf b\cdot (\mathbf c\times \mathbf a) = -\mathbf a\cdot( \mathbf c\times \mathbf b)$
5. $(\mathbf a + \mathbf b)\times \mathbf c = \mathbf a\times \mathbf c + \mathbf b\times \mathbf c$.
Indeed for all vectors $\mathbf r$ the chain of equations holds:
\[\mathbf r\cdot( (\mathbf a + \mathbf b)\times \mathbf c) = (\mathbf a + \mathbf b) \cdot (\mathbf c\times \mathbf r) = \mathbf a \cdot(\mathbf c\times \mathbf r) + \mathbf b\cdot(\mathbf c\times \mathbf r) = \mathbf r\cdot (\mathbf a\times \mathbf c) + \mathbf r\cdot(\mathbf b\times \mathbf c) = \mathbf r\cdot(\mathbf a\times \mathbf c + \mathbf b\times \mathbf c)\]
Which proves $(\mathbf a + \mathbf b)\times \mathbf c = \mathbf a\times \mathbf c + \mathbf b\times \mathbf c$ due to point 3.
6. $|\mathbf a\times \mathbf b|=|\mathbf a| \cdot |\mathbf b| \sin \theta$ where $\theta$ is angle between $\mathbf a$ and $\mathbf b$, since $|\mathbf a\times \mathbf b|$ equals to the area of the parallelogram formed by $\mathbf a$ and $\mathbf b$.
Given all this and that the following equation holds for the unit vectors
$$\mathbf e_x\times \mathbf e_x = \mathbf e_y\times \mathbf e_y = \mathbf e_z\times \mathbf e_z = \mathbf 0,\\
\mathbf e_x\times \mathbf e_y = \mathbf e_z,~\mathbf e_y\times \mathbf e_z = \mathbf e_x,~\mathbf e_z\times \mathbf e_x = \mathbf e_y$$
we can calculate the cross product of $\mathbf a = (x_1;y_1;z_1)$ and $\mathbf b = (x_2;y_2;z_2)$ in coordinate form:
$$\mathbf a\times \mathbf b = (x_1 \cdot \mathbf e_x + y_1 \cdot \mathbf e_y + z_1 \cdot \mathbf e_z)\times (x_2 \cdot \mathbf e_x + y_2 \cdot \mathbf e_y + z_2 \cdot \mathbf e_z) =$$
$$(y_1 z_2 - z_1 y_2)\mathbf e_x + (z_1 x_2 - x_1 z_2)\mathbf e_y + (x_1 y_2 - y_1 x_2)$$
Which also can be written in the more elegant form:
$$\mathbf a\times \mathbf b = \begin{vmatrix}\mathbf e_x & \mathbf e_y & \mathbf e_z \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix},~a\cdot(b\times c) = \begin{vmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{vmatrix}$$
Here $| \cdot |$ stands for the determinant of a matrix.
Some kind of cross product (namely the pseudo-scalar product) can also be implemented in the 2D case.
If we would like to calculate the area of parallelogram formed by vectors $\mathbf a$ and $\mathbf b$ we would compute $|\mathbf e_z\cdot(\mathbf a\times \mathbf b)| = |x_1 y_2 - y_1 x_2|$.
Another way to obtain the same result is to multiply $|\mathbf a|$ (base of parallelogram) with the height, which is the projection of vector $\mathbf b$ onto vector $\mathbf a$ rotated by $90^\circ$ which in turn is $\widehat{\mathbf a}=(-y_1;x_1)$.
That is, to calculate $|\widehat{\mathbf a}\cdot\mathbf b|=|x_1y_2 - y_1 x_2|$.
If we will take the sign into consideration then the area will be positive if the rotation from $\mathbf a$ to $\mathbf b$ (i.e. from the view of the point of $\mathbf e_z$) is performed counter-clockwise and negative otherwise.
That defines the pseudo-scalar product.
Note that it also equals $|\mathbf a| \cdot |\mathbf b| \sin \theta$ where $\theta$ is angle from $\mathbf a$ to $\mathbf b$ count counter-clockwise (and negative if rotation is clockwise).
Let's implement all this stuff!
```{.cpp file=crossproduct}
point3d cross(point3d a, point3d b) {
return point3d(a.y * b.z - a.z * b.y,
a.z * b.x - a.x * b.z,
a.x * b.y - a.y * b.x);
}
ftype triple(point3d a, point3d b, point3d c) {
return dot(a, cross(b, c));
}
ftype cross(point2d a, point2d b) {
return a.x * b.y - a.y * b.x;
}
```
### Properties
As for the cross product, it equals to the zero vector iff the vectors $\mathbf a$ and $\mathbf b$ are collinear (they form a common line, i.e. they are parallel).
The same thing holds for the triple product, it is equal to zero iff the vectors $\mathbf a$, $\mathbf b$ and $\mathbf c$ are coplanar (they form a common plane).
From this we can obtain universal equations defining lines and planes.
A line can be defined via its direction vector $\mathbf d$ and an initial point $\mathbf r_0$ or by two points $\mathbf a$ and $\mathbf b$.
It is defined as $(\mathbf r - \mathbf r_0)\times\mathbf d=0$ or as $(\mathbf r - \mathbf a)\times (\mathbf b - \mathbf a) = 0$.
As for planes, it can be defined by three points $\mathbf a$, $\mathbf b$ and $\mathbf c$ as $(\mathbf r - \mathbf a)\cdot((\mathbf b - \mathbf a)\times (\mathbf c - \mathbf a))=0$ or by initial point $\mathbf r_0$ and two direction vectors lying in this plane $\mathbf d_1$ and $\mathbf d_2$: $(\mathbf r - \mathbf r_0)\cdot(\mathbf d_1\times \mathbf d_2)=0$.
In 2D the pseudo-scalar product also may be used to check the orientation between two vectors because it is positive if the rotation from the first to the second vector is clockwise and negative otherwise.
And, of course, it can be used to calculate areas of polygons, which is described in a different article.
A triple product can be used for the same purpose in 3D space.
## Exercises
### Line intersection
There are many possible ways to define a line in 2D and you shouldn't hesitate to combine them.
For example we have two lines and we want to find their intersection points.
We can say that all points from first line can be parameterized as $\mathbf r = \mathbf a_1 + t \cdot \mathbf d_1$ where $\mathbf a_1$ is initial point, $\mathbf d_1$ is direction and $t$ is some real parameter.
As for second line all its points must satisfy $(\mathbf r - \mathbf a_2)\times \mathbf d_2=0$. From this we can easily find parameter $t$:
$$(\mathbf a_1 + t \cdot \mathbf d_1 - \mathbf a_2)\times \mathbf d_2=0 \quad\Rightarrow\quad t = \dfrac{(\mathbf a_2 - \mathbf a_1)\times\mathbf d_2}{\mathbf d_1\times \mathbf d_2}$$
Let's implement function to intersect two lines.
```{.cpp file=basic_line_intersection}
point2d intersect(point2d a1, point2d d1, point2d a2, point2d d2) {
return a1 + cross(a2 - a1, d2) / cross(d1, d2) * d1;
}
```
### Planes intersection
However sometimes it might be hard to use some geometric insights.
For example, you're given three planes defined by initial points $\mathbf a_i$ and directions $\mathbf d_i$ and you want to find their intersection point.
You may note that you just have to solve the system of equations:
$$\begin{cases}\mathbf r\cdot \mathbf n_1 = \mathbf a_1\cdot \mathbf n_1, \\ \mathbf r\cdot \mathbf n_2 = \mathbf a_2\cdot \mathbf n_2, \\ \mathbf r\cdot \mathbf n_3 = \mathbf a_3\cdot \mathbf n_3\end{cases}$$
Instead of thinking on geometric approach, you can work out an algebraic one which can be obtained immediately.
For example, given that you already implemented a point class, it will be easy for you to solve this system using Cramer's rule because the triple product is simply the determinant of the matrix obtained from the vectors being its columns:
```{.cpp file=plane_intersection}
point3d intersect(point3d a1, point3d n1, point3d a2, point3d n2, point3d a3, point3d n3) {
point3d x(n1.x, n2.x, n3.x);
point3d y(n1.y, n2.y, n3.y);
point3d z(n1.z, n2.z, n3.z);
point3d d(dot(a1, n1), dot(a2, n2), dot(a3, n3));
return point3d(triple(d, y, z),
triple(x, d, z),
triple(x, y, d)) / triple(n1, n2, n3);
}
```
Now you may try to find out approaches for common geometric operations yourself to get used to all this stuff.
|
Basic Geometry
|
---
title
circles_intersection
---
# Circle-Circle Intersection
You are given two circles on a 2D plane, each one described as coordinates of its center and its radius. Find the points of their intersection (possible cases: one or two points, no intersection or circles coincide).
## Solution
Let's reduce this problem to the [circle-line intersection problem](circle-line-intersection.md).
Assume without loss of generality that the first circle is centered at the origin (if this is not true, we can move the origin to the center of the first circle and adjust the coordinates of intersection points accordingly at output time). We have a system of two equations:
$$x^2+y^2=r_1^2$$
$$(x - x_2)^2 + (y - y_2)^2 = r_2^2$$
Subtract the first equation from the second one to get rid of the second powers of variables:
$$x^2+y^2=r_1^2$$
$$x \cdot (-2x_2) + y \cdot (-2y_2) + (x_2^2+y_2^2+r_1^2-r_2^2) = 0$$
Thus, we've reduced the original problem to the problem of finding intersections of the first circle and a line:
$$Ax + By + C = 0$$
$$\begin{align}
A &= -2x_2 \\
B &= -2y_2 \\
C &= x_2^2+y_2^2+r_1^2-r_2^2
\end{align}$$
And this problem can be solved as described in the [corresponding article](circle-line-intersection.md).
The only degenerate case we need to consider separately is when the centers of the circles coincide. In this case $x_2=y_2=0$, and the line equation will be $C = r_1^2-r_2^2 = 0$. If the radii of the circles are the same, there are infinitely many intersection points, if they differ, there are no intersections.
|
---
title
circles_intersection
---
# Circle-Circle Intersection
You are given two circles on a 2D plane, each one described as coordinates of its center and its radius. Find the points of their intersection (possible cases: one or two points, no intersection or circles coincide).
## Solution
Let's reduce this problem to the [circle-line intersection problem](circle-line-intersection.md).
Assume without loss of generality that the first circle is centered at the origin (if this is not true, we can move the origin to the center of the first circle and adjust the coordinates of intersection points accordingly at output time). We have a system of two equations:
$$x^2+y^2=r_1^2$$
$$(x - x_2)^2 + (y - y_2)^2 = r_2^2$$
Subtract the first equation from the second one to get rid of the second powers of variables:
$$x^2+y^2=r_1^2$$
$$x \cdot (-2x_2) + y \cdot (-2y_2) + (x_2^2+y_2^2+r_1^2-r_2^2) = 0$$
Thus, we've reduced the original problem to the problem of finding intersections of the first circle and a line:
$$Ax + By + C = 0$$
$$\begin{align}
A &= -2x_2 \\
B &= -2y_2 \\
C &= x_2^2+y_2^2+r_1^2-r_2^2
\end{align}$$
And this problem can be solved as described in the [corresponding article](circle-line-intersection.md).
The only degenerate case we need to consider separately is when the centers of the circles coincide. In this case $x_2=y_2=0$, and the line equation will be $C = r_1^2-r_2^2 = 0$. If the radii of the circles are the same, there are infinitely many intersection points, if they differ, there are no intersections.
## Practice Problems
- [RadarFinder](https://community.topcoder.com/stat?c=problem_statement&pm=7766)
- [Runaway to a shadow - Codeforces Round #357](http://codeforces.com/problemset/problem/681/E)
- [ASC 1 Problem F "Get out!"](http://codeforces.com/gym/100199/problem/F)
- [SPOJ: CIRCINT](http://www.spoj.com/problems/CIRCINT/)
- [UVA - 10301 - Rings and Glue](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=1242)
- [Codeforces 933C A Colorful Prospect](https://codeforces.com/problemset/problem/933/C)
- [TIMUS 1429 Biscuits](https://acm.timus.ru/problem.aspx?space=1&num=1429)
|
Circle-Circle Intersection
|
---
title
segments_intersection
---
# Finding intersection of two segments
You are given two segments AB and CD, described as pairs of their endpoints. Each segment can be a single point if its endpoints are the same.
You have to find the intersection of these segments, which can be empty (if the segments don't intersect), a single point or a segment (if the given segments overlap).
## Solution
We can find the intersection point of segments in the same way as [the intersection of lines](lines-intersection.md):
reconstruct line equations from the segments' endpoints and check whether they are parallel.
If the lines are not parallel, we need to find their point of intersection and check whether it belongs to both segments
(to do this it's sufficient to verify that the intersection point belongs to each segment projected on X and Y axes).
In this case the answer will be either "no intersection" or the single point of lines' intersection.
The case of parallel lines is slightly more complicated (the case of one or more segments being a single point also belongs here).
In this case we need to check that both segments belong to the same line.
If they don't, the answer is "no intersection".
If they do, the answer is the intersection of the segments belonging to the same line, which is obtained by
ordering the endpoints of both segments in the increasing order of certain coordinate and taking the rightmost of left endpoints and the leftmost of right endpoints.
If both segments are single points, these points have to be identical, and it makes sense to perform this check separately.
In the beginning of the algorithm let's add a bounding box check - it is necessary for the case when the segments belong to the same line,
and (being a lightweight check) it allows the algorithm to work faster on average on random tests.
## Implementation
Here is the implementation, including all helper functions for lines and segments processing.
The main function `intersect` returns true if the segments have a non-empty intersection,
and stores endpoints of the intersection segment in arguments `left` and `right`.
If the answer is a single point, the values written to `left` and `right` will be the same.
```{.cpp file=segment_intersection}
const double EPS = 1E-9;
struct pt {
double x, y;
bool operator<(const pt& p) const
{
return x < p.x - EPS || (abs(x - p.x) < EPS && y < p.y - EPS);
}
};
struct line {
double a, b, c;
line() {}
line(pt p, pt q)
{
a = p.y - q.y;
b = q.x - p.x;
c = -a * p.x - b * p.y;
norm();
}
void norm()
{
double z = sqrt(a * a + b * b);
if (abs(z) > EPS)
a /= z, b /= z, c /= z;
}
double dist(pt p) const { return a * p.x + b * p.y + c; }
};
double det(double a, double b, double c, double d)
{
return a * d - b * c;
}
inline bool betw(double l, double r, double x)
{
return min(l, r) <= x + EPS && x <= max(l, r) + EPS;
}
inline bool intersect_1d(double a, double b, double c, double d)
{
if (a > b)
swap(a, b);
if (c > d)
swap(c, d);
return max(a, c) <= min(b, d) + EPS;
}
bool intersect(pt a, pt b, pt c, pt d, pt& left, pt& right)
{
if (!intersect_1d(a.x, b.x, c.x, d.x) || !intersect_1d(a.y, b.y, c.y, d.y))
return false;
line m(a, b);
line n(c, d);
double zn = det(m.a, m.b, n.a, n.b);
if (abs(zn) < EPS) {
if (abs(m.dist(c)) > EPS || abs(n.dist(a)) > EPS)
return false;
if (b < a)
swap(a, b);
if (d < c)
swap(c, d);
left = max(a, c);
right = min(b, d);
return true;
} else {
left.x = right.x = -det(m.c, m.b, n.c, n.b) / zn;
left.y = right.y = -det(m.a, m.c, n.a, n.c) / zn;
return betw(a.x, b.x, left.x) && betw(a.y, b.y, left.y) &&
betw(c.x, d.x, left.x) && betw(c.y, d.y, left.y);
}
}
```
|
---
title
segments_intersection
---
# Finding intersection of two segments
You are given two segments AB and CD, described as pairs of their endpoints. Each segment can be a single point if its endpoints are the same.
You have to find the intersection of these segments, which can be empty (if the segments don't intersect), a single point or a segment (if the given segments overlap).
## Solution
We can find the intersection point of segments in the same way as [the intersection of lines](lines-intersection.md):
reconstruct line equations from the segments' endpoints and check whether they are parallel.
If the lines are not parallel, we need to find their point of intersection and check whether it belongs to both segments
(to do this it's sufficient to verify that the intersection point belongs to each segment projected on X and Y axes).
In this case the answer will be either "no intersection" or the single point of lines' intersection.
The case of parallel lines is slightly more complicated (the case of one or more segments being a single point also belongs here).
In this case we need to check that both segments belong to the same line.
If they don't, the answer is "no intersection".
If they do, the answer is the intersection of the segments belonging to the same line, which is obtained by
ordering the endpoints of both segments in the increasing order of certain coordinate and taking the rightmost of left endpoints and the leftmost of right endpoints.
If both segments are single points, these points have to be identical, and it makes sense to perform this check separately.
In the beginning of the algorithm let's add a bounding box check - it is necessary for the case when the segments belong to the same line,
and (being a lightweight check) it allows the algorithm to work faster on average on random tests.
## Implementation
Here is the implementation, including all helper functions for lines and segments processing.
The main function `intersect` returns true if the segments have a non-empty intersection,
and stores endpoints of the intersection segment in arguments `left` and `right`.
If the answer is a single point, the values written to `left` and `right` will be the same.
```{.cpp file=segment_intersection}
const double EPS = 1E-9;
struct pt {
double x, y;
bool operator<(const pt& p) const
{
return x < p.x - EPS || (abs(x - p.x) < EPS && y < p.y - EPS);
}
};
struct line {
double a, b, c;
line() {}
line(pt p, pt q)
{
a = p.y - q.y;
b = q.x - p.x;
c = -a * p.x - b * p.y;
norm();
}
void norm()
{
double z = sqrt(a * a + b * b);
if (abs(z) > EPS)
a /= z, b /= z, c /= z;
}
double dist(pt p) const { return a * p.x + b * p.y + c; }
};
double det(double a, double b, double c, double d)
{
return a * d - b * c;
}
inline bool betw(double l, double r, double x)
{
return min(l, r) <= x + EPS && x <= max(l, r) + EPS;
}
inline bool intersect_1d(double a, double b, double c, double d)
{
if (a > b)
swap(a, b);
if (c > d)
swap(c, d);
return max(a, c) <= min(b, d) + EPS;
}
bool intersect(pt a, pt b, pt c, pt d, pt& left, pt& right)
{
if (!intersect_1d(a.x, b.x, c.x, d.x) || !intersect_1d(a.y, b.y, c.y, d.y))
return false;
line m(a, b);
line n(c, d);
double zn = det(m.a, m.b, n.a, n.b);
if (abs(zn) < EPS) {
if (abs(m.dist(c)) > EPS || abs(n.dist(a)) > EPS)
return false;
if (b < a)
swap(a, b);
if (d < c)
swap(c, d);
left = max(a, c);
right = min(b, d);
return true;
} else {
left.x = right.x = -det(m.c, m.b, n.c, n.b) / zn;
left.y = right.y = -det(m.a, m.c, n.a, n.c) / zn;
return betw(a.x, b.x, left.x) && betw(a.y, b.y, left.y) &&
betw(c.x, d.x, left.x) && betw(c.y, d.y, left.y);
}
}
```
|
Finding intersection of two segments
|
---
title
convex_hull_graham
---
# Convex Hull construction
In this article we will discuss the problem of constructing a convex hull from a set of points.
Consider $N$ points given on a plane, and the objective is to generate a convex hull, i.e. the smallest
convex polygon that contains all the given points.
We will see the **Graham's scan** algorithm published in 1972 by Graham, and
also the **Monotone chain** algorithm published in 1979 by Andrew. Both
are $\mathcal{O}(N \log N)$, and are asymptotically optimal (as it is proven that there
is no algorithm asymptotically better), with the exception of a few problems where
parallel or online processing is involved.
## Graham's scan Algorithm
The algorithm first finds the bottom-most point $P_0$. If there are multiple points
with the same Y coordinate, the one with the smaller X coordinate is considered. This
step takes $\mathcal{O}(N)$ time.
Next, all the other points are sorted by polar angle in clockwise order.
If the polar angle between two or more points is the same, the tie should be broken by distance from $P_0$, in increasing order.
Then we iterate through each point one by one, and make sure that the current
point and the two before it make a clockwise turn, otherwise the previous
point is discarded, since it would make a non-convex shape. Checking for clockwise or anticlockwise
nature can be done by checking the [orientation](oriented-triangle-area.md).
We use a stack to store the points, and once we reach the original point $P_0$,
the algorithm is done and we return the stack containing all the points of the
convex hull in clockwise order.
If you need to include the collinear points while doing a Graham scan, you need
another step after sorting. You need to get the points that have the biggest
polar distance from $P_0$ (these should be at the end of the sorted vector) and are collinear.
The points in this line should be reversed so that we can output all the
collinear points, otherwise the algorithm would get the nearest point in this
line and bail. This step shouldn't be included in the non-collinear version
of the algorithm, otherwise you wouldn't get the smallest convex hull.
### Implementation
```{.cpp file=graham_scan}
struct pt {
double x, y;
};
int orientation(pt a, pt b, pt c) {
double v = a.x*(b.y-c.y)+b.x*(c.y-a.y)+c.x*(a.y-b.y);
if (v < 0) return -1; // clockwise
if (v > 0) return +1; // counter-clockwise
return 0;
}
bool cw(pt a, pt b, pt c, bool include_collinear) {
int o = orientation(a, b, c);
return o < 0 || (include_collinear && o == 0);
}
bool collinear(pt a, pt b, pt c) { return orientation(a, b, c) == 0; }
void convex_hull(vector<pt>& a, bool include_collinear = false) {
pt p0 = *min_element(a.begin(), a.end(), [](pt a, pt b) {
return make_pair(a.y, a.x) < make_pair(b.y, b.x);
});
sort(a.begin(), a.end(), [&p0](const pt& a, const pt& b) {
int o = orientation(p0, a, b);
if (o == 0)
return (p0.x-a.x)*(p0.x-a.x) + (p0.y-a.y)*(p0.y-a.y)
< (p0.x-b.x)*(p0.x-b.x) + (p0.y-b.y)*(p0.y-b.y);
return o < 0;
});
if (include_collinear) {
int i = (int)a.size()-1;
while (i >= 0 && collinear(p0, a[i], a.back())) i--;
reverse(a.begin()+i+1, a.end());
}
vector<pt> st;
for (int i = 0; i < (int)a.size(); i++) {
while (st.size() > 1 && !cw(st[st.size()-2], st.back(), a[i], include_collinear))
st.pop_back();
st.push_back(a[i]);
}
a = st;
}
```
## Monotone chain Algorithm
The algorithm first finds the leftmost and rightmost points A and B. In the event multiple such points exist,
the lowest among the left (lowest Y-coordinate) is taken as A, and the highest among the right (highest Y-coordinate)
is taken as B. Clearly, A and B must both belong to the convex hull as they are the farthest away and they cannot be contained
by any line formed by a pair among the given points.
Now, draw a line through AB. This divides all the other points into two sets, S1 and S2, where S1 contains all the points
above the line connecting A and B, and S2 contains all the points below the line joining A and B. The points that lie on
the line joining A and B may belong to either set. The points A and B belong to both sets. Now the algorithm
constructs the upper set S1 and the lower set S2 and then combines them to obtain the answer.
To get the upper set, we sort all points by the x-coordinate. For each point we check if either - the current point is the last point,
(which we defined as B), or if the orientation between the line between A and the current point and the line between the current point and B is clockwise. In those cases the
current point belongs to the upper set S1. Checking for clockwise or anticlockwise nature can be done by checking the [orientation](oriented-triangle-area.md).
If the given point belongs to the upper set, we check the angle made by the line connecting the second last point and the last point in the upper convex hull,
with the line connecting the last point in the upper convex hull and the current point. If the angle is not clockwise, we remove the most recent point added
to the upper convex hull as the current point will be able to contain the previous point once it is added to the convex
hull.
The same logic applies for the lower set S2. If either - the current point is B, or the orientation of the lines, formed by A and the
current point and the current point and B, is counterclockwise - then it belongs to S2.
If the given point belongs to the lower set, we act similarly as for a point on the upper set except we check for a counterclockwise
orientation instead of a clockwise orientation. Thus, if the angle made by the line connecting the second last point and the last point in the lower convex hull,
with the line connecting the last point in the lower convex hull and the current point is not counterclockwise, we remove the most recent point added to the lower convex hull as the current point will be able to contain
the previous point once added to the hull.
The final convex hull is obtained from the union of the upper and lower convex hull, forming a clockwise hull, and the implementation is as follows.
If you need collinear points, you just need to check for them in the clockwise/counterclockwise routines.
However, this allows for a degenerate case where all the input points are collinear in a single line, and the algorithm would output repeated points.
To solve this, we check whether the upper hull contains all the points, and if it does, we just return the points in reverse, as that
is what Graham's implementation would return in this case.
### Implementation
```{.cpp file=monotone_chain}
struct pt {
double x, y;
};
int orientation(pt a, pt b, pt c) {
double v = a.x*(b.y-c.y)+b.x*(c.y-a.y)+c.x*(a.y-b.y);
if (v < 0) return -1; // clockwise
if (v > 0) return +1; // counter-clockwise
return 0;
}
bool cw(pt a, pt b, pt c, bool include_collinear) {
int o = orientation(a, b, c);
return o < 0 || (include_collinear && o == 0);
}
bool ccw(pt a, pt b, pt c, bool include_collinear) {
int o = orientation(a, b, c);
return o > 0 || (include_collinear && o == 0);
}
void convex_hull(vector<pt>& a, bool include_collinear = false) {
if (a.size() == 1)
return;
sort(a.begin(), a.end(), [](pt a, pt b) {
return make_pair(a.x, a.y) < make_pair(b.x, b.y);
});
pt p1 = a[0], p2 = a.back();
vector<pt> up, down;
up.push_back(p1);
down.push_back(p1);
for (int i = 1; i < (int)a.size(); i++) {
if (i == a.size() - 1 || cw(p1, a[i], p2, include_collinear)) {
while (up.size() >= 2 && !cw(up[up.size()-2], up[up.size()-1], a[i], include_collinear))
up.pop_back();
up.push_back(a[i]);
}
if (i == a.size() - 1 || ccw(p1, a[i], p2, include_collinear)) {
while (down.size() >= 2 && !ccw(down[down.size()-2], down[down.size()-1], a[i], include_collinear))
down.pop_back();
down.push_back(a[i]);
}
}
if (include_collinear && up.size() == a.size()) {
reverse(a.begin(), a.end());
return;
}
a.clear();
for (int i = 0; i < (int)up.size(); i++)
a.push_back(up[i]);
for (int i = down.size() - 2; i > 0; i--)
a.push_back(down[i]);
}
```
|
---
title
convex_hull_graham
---
# Convex Hull construction
In this article we will discuss the problem of constructing a convex hull from a set of points.
Consider $N$ points given on a plane, and the objective is to generate a convex hull, i.e. the smallest
convex polygon that contains all the given points.
We will see the **Graham's scan** algorithm published in 1972 by Graham, and
also the **Monotone chain** algorithm published in 1979 by Andrew. Both
are $\mathcal{O}(N \log N)$, and are asymptotically optimal (as it is proven that there
is no algorithm asymptotically better), with the exception of a few problems where
parallel or online processing is involved.
## Graham's scan Algorithm
The algorithm first finds the bottom-most point $P_0$. If there are multiple points
with the same Y coordinate, the one with the smaller X coordinate is considered. This
step takes $\mathcal{O}(N)$ time.
Next, all the other points are sorted by polar angle in clockwise order.
If the polar angle between two or more points is the same, the tie should be broken by distance from $P_0$, in increasing order.
Then we iterate through each point one by one, and make sure that the current
point and the two before it make a clockwise turn, otherwise the previous
point is discarded, since it would make a non-convex shape. Checking for clockwise or anticlockwise
nature can be done by checking the [orientation](oriented-triangle-area.md).
We use a stack to store the points, and once we reach the original point $P_0$,
the algorithm is done and we return the stack containing all the points of the
convex hull in clockwise order.
If you need to include the collinear points while doing a Graham scan, you need
another step after sorting. You need to get the points that have the biggest
polar distance from $P_0$ (these should be at the end of the sorted vector) and are collinear.
The points in this line should be reversed so that we can output all the
collinear points, otherwise the algorithm would get the nearest point in this
line and bail. This step shouldn't be included in the non-collinear version
of the algorithm, otherwise you wouldn't get the smallest convex hull.
### Implementation
```{.cpp file=graham_scan}
struct pt {
double x, y;
};
int orientation(pt a, pt b, pt c) {
double v = a.x*(b.y-c.y)+b.x*(c.y-a.y)+c.x*(a.y-b.y);
if (v < 0) return -1; // clockwise
if (v > 0) return +1; // counter-clockwise
return 0;
}
bool cw(pt a, pt b, pt c, bool include_collinear) {
int o = orientation(a, b, c);
return o < 0 || (include_collinear && o == 0);
}
bool collinear(pt a, pt b, pt c) { return orientation(a, b, c) == 0; }
void convex_hull(vector<pt>& a, bool include_collinear = false) {
pt p0 = *min_element(a.begin(), a.end(), [](pt a, pt b) {
return make_pair(a.y, a.x) < make_pair(b.y, b.x);
});
sort(a.begin(), a.end(), [&p0](const pt& a, const pt& b) {
int o = orientation(p0, a, b);
if (o == 0)
return (p0.x-a.x)*(p0.x-a.x) + (p0.y-a.y)*(p0.y-a.y)
< (p0.x-b.x)*(p0.x-b.x) + (p0.y-b.y)*(p0.y-b.y);
return o < 0;
});
if (include_collinear) {
int i = (int)a.size()-1;
while (i >= 0 && collinear(p0, a[i], a.back())) i--;
reverse(a.begin()+i+1, a.end());
}
vector<pt> st;
for (int i = 0; i < (int)a.size(); i++) {
while (st.size() > 1 && !cw(st[st.size()-2], st.back(), a[i], include_collinear))
st.pop_back();
st.push_back(a[i]);
}
a = st;
}
```
## Monotone chain Algorithm
The algorithm first finds the leftmost and rightmost points A and B. In the event multiple such points exist,
the lowest among the left (lowest Y-coordinate) is taken as A, and the highest among the right (highest Y-coordinate)
is taken as B. Clearly, A and B must both belong to the convex hull as they are the farthest away and they cannot be contained
by any line formed by a pair among the given points.
Now, draw a line through AB. This divides all the other points into two sets, S1 and S2, where S1 contains all the points
above the line connecting A and B, and S2 contains all the points below the line joining A and B. The points that lie on
the line joining A and B may belong to either set. The points A and B belong to both sets. Now the algorithm
constructs the upper set S1 and the lower set S2 and then combines them to obtain the answer.
To get the upper set, we sort all points by the x-coordinate. For each point we check if either - the current point is the last point,
(which we defined as B), or if the orientation between the line between A and the current point and the line between the current point and B is clockwise. In those cases the
current point belongs to the upper set S1. Checking for clockwise or anticlockwise nature can be done by checking the [orientation](oriented-triangle-area.md).
If the given point belongs to the upper set, we check the angle made by the line connecting the second last point and the last point in the upper convex hull,
with the line connecting the last point in the upper convex hull and the current point. If the angle is not clockwise, we remove the most recent point added
to the upper convex hull as the current point will be able to contain the previous point once it is added to the convex
hull.
The same logic applies for the lower set S2. If either - the current point is B, or the orientation of the lines, formed by A and the
current point and the current point and B, is counterclockwise - then it belongs to S2.
If the given point belongs to the lower set, we act similarly as for a point on the upper set except we check for a counterclockwise
orientation instead of a clockwise orientation. Thus, if the angle made by the line connecting the second last point and the last point in the lower convex hull,
with the line connecting the last point in the lower convex hull and the current point is not counterclockwise, we remove the most recent point added to the lower convex hull as the current point will be able to contain
the previous point once added to the hull.
The final convex hull is obtained from the union of the upper and lower convex hull, forming a clockwise hull, and the implementation is as follows.
If you need collinear points, you just need to check for them in the clockwise/counterclockwise routines.
However, this allows for a degenerate case where all the input points are collinear in a single line, and the algorithm would output repeated points.
To solve this, we check whether the upper hull contains all the points, and if it does, we just return the points in reverse, as that
is what Graham's implementation would return in this case.
### Implementation
```{.cpp file=monotone_chain}
struct pt {
double x, y;
};
int orientation(pt a, pt b, pt c) {
double v = a.x*(b.y-c.y)+b.x*(c.y-a.y)+c.x*(a.y-b.y);
if (v < 0) return -1; // clockwise
if (v > 0) return +1; // counter-clockwise
return 0;
}
bool cw(pt a, pt b, pt c, bool include_collinear) {
int o = orientation(a, b, c);
return o < 0 || (include_collinear && o == 0);
}
bool ccw(pt a, pt b, pt c, bool include_collinear) {
int o = orientation(a, b, c);
return o > 0 || (include_collinear && o == 0);
}
void convex_hull(vector<pt>& a, bool include_collinear = false) {
if (a.size() == 1)
return;
sort(a.begin(), a.end(), [](pt a, pt b) {
return make_pair(a.x, a.y) < make_pair(b.x, b.y);
});
pt p1 = a[0], p2 = a.back();
vector<pt> up, down;
up.push_back(p1);
down.push_back(p1);
for (int i = 1; i < (int)a.size(); i++) {
if (i == a.size() - 1 || cw(p1, a[i], p2, include_collinear)) {
while (up.size() >= 2 && !cw(up[up.size()-2], up[up.size()-1], a[i], include_collinear))
up.pop_back();
up.push_back(a[i]);
}
if (i == a.size() - 1 || ccw(p1, a[i], p2, include_collinear)) {
while (down.size() >= 2 && !ccw(down[down.size()-2], down[down.size()-1], a[i], include_collinear))
down.pop_back();
down.push_back(a[i]);
}
}
if (include_collinear && up.size() == a.size()) {
reverse(a.begin(), a.end());
return;
}
a.clear();
for (int i = 0; i < (int)up.size(); i++)
a.push_back(up[i]);
for (int i = down.size() - 2; i > 0; i--)
a.push_back(down[i]);
}
```
## Practice Problems
* [Kattis - Convex Hull](https://open.kattis.com/problems/convexhull)
* [Kattis - Keep the Parade Safe](https://open.kattis.com/problems/parade)
* [URI 1464 - Onion Layers](https://www.urionlinejudge.com.br/judge/en/problems/view/1464)
* [Timus 1185: Wall](http://acm.timus.ru/problem.aspx?space=1&num=1185)
* [Usaco 2014 January Contest, Gold - Cow Curling](http://usaco.org/index.php?page=viewproblem2&cpid=382)
|
Convex Hull construction
|
---
title
voronoi_diagram_2d_n4
---
# Delaunay triangulation and Voronoi diagram
Consider a set $\{p_i\}$ of points on the plane.
A **Voronoi diagram** $V(\{p_i\})$ of $\{p_i\}$ is a partition of the plane into $n$ regions $V_i$, where $V_i = \{p\in\mathbb{R}^2;\ \rho(p, p_i) = \min\ \rho(p, p_k)\}$.
The cells of the Voronoi diagram are polygons (possibly infinite).
A **Delaunay triangulation** $D(\{p_i\})$ of $\{p_i\}$ is a triangulation where every point $p_i$ is outside or on the boundary of the circumcircle of each triangle $T \in D(\{p_i\})$.
There is a nasty degenerated case when the Voronoi diagram isn't connected and Delaunay triangulation doesn't exist. This case is when all points are collinear.
## Properties
The Delaunay triangulation maximizes the minimum angle among all possible triangulations.
The Minimum Euclidean spanning tree of a point set is a subset of edges of its' Delaunay triangulation.
## Duality
Suppose that $\{p_i\}$ is not collinear and among $\{p_i\}$ no four points lie on one circle. Then $V(\{p_i\})$ and $D(\{p_i\})$ are dual, so if we obtain one of them, we may obtain the other in $O(n)$. What to do if it's not the case? The collinear case may be processed easily. Otherwise, $V$ and $D'$ are dual, where $D'$ is obtained from $D$ by removing all the edges such that two triangles on this edge share the circumcircle.
## Building Delaunay and Voronoi
Because of the duality, we only need a fast algorithm to compute only one of $V$ and $D$. We will describe how to build $D(\{p_i\})$ in $O(n\log n)$. The triangulation will be built via divide-and-conquer algorithm due to Guibas and Stolfi.
## Quad-edge data structure
During the algorithm $D$ will be stored inside the quad-edge data structure. This structure is described in the picture:
<center></center>
In the algorithm we will use the following functions on edges:
1. `make_edge(a, b)`<br>
This function creates an isolated edge from point `a` to point `b` together with its' reverse edge and both dual edges.
2. `splice(a, b)`<br>
This is a key function of the algorithm. It swaps `a->Onext` with `b->Onext` and `a->Onext->Rot->Onext` with `b->Onext->Rot->Onext`.
3. `delete_edge(e)`<br>
This function deletes e from the triangulation. To delete `e`, we may simply call `splice(e, e->Oprev)` and `splice(e->Rev, e->Rev->Oprev)`.
4. `connect(a, b)`<br>
This function creates a new edge `e` from `a->Dest` to `b->Org` in such a way that `a`, `b`, `e` all have the same left face. To do this, we call `e = make_edge(a->Dest, b->Org)`, `splice(e, a->Lnext)` and `splice(e->Rev, b)`.
## Algorithm
The algorithm will compute the triangulation and return two quad-edges: the counterclockwise convex hull edge out of the leftmost vertex and the clockwise convex hull edge out of the rightmost vertex.
Let's sort all points by x, and if $x_1 = x_2$ then by y. Let's solve the problem for some segment $(l, r)$ (initially $(l, r) = (0, n - 1)$). If $r - l + 1 = 2$, we will add an edge $(p[l], p[r])$ and return. If $r - l + 1 = 3$, we will firstly add the edges $(p[l], p[l + 1])$ and $(p[l + 1], p[r])$. We must also connect them using `splice(a->Rev, b)`. Now we must close the triangle. Our next action will depend on the orientation of $p[l], p[l + 1], p[r]$. If they are collinear, we can't make a triangle, so we simply return `(a, b->Rev)`. Otherwise, we create a new edge `c` by calling `connect(b, a)`. If the points are oriented counter-clockwise, we return `(a, b->Rev)`. Otherwise we return `(c->Rev, c)`.
Now suppose that $r - l + 1 \ge 4$. Firstly, let's solve $L = (l, \frac{l + r}{2})$ and $R = (\frac{l + r}{2} + 1, r)$ recursively. Now we have to merge these triangulations into one triangulation. Note that our points are sorted, so while merging we will add edges from L to R (so-called _cross_ edges) and remove some edges from L to L and from R to R.
What is the structure of the cross edges? All these edges must cross a line parallel to the y-axis and placed at the splitting x value. This establishes a linear ordering of the cross edges, so we can talk about successive cross edges, the bottom-most cross edge, etc. The algorithm will add the cross edges in ascending order. Note that any two adjacent cross edges will have a common endpoint, and the third side of the triangle they define goes from L to L or from R to R. Let's call the current cross edge the base. The successor of the base will either go from the left endpoint of the base to one of the R-neighbors of the right endpoint or vice versa.
Consider the circumcircle of base and the previous cross edge.
Suppose this circle is transformed into other circles having base as a chord but lying further into the Oy direction.
Our circle will go up for a while, but unless base is an upper tangent of L and R we will encounter a point belonging either to L or to R giving rise to a new triangle without any points in the circumcircle.
The new L-R edge of this triangle is the next cross edge added.
To do this efficiently, we compute two edges `lcand` and `rcand` so that `lcand` points to the first L point encountered in this process, and `rcand` points to the first R point.
Then we choose the one that would be encountered first. Initially base points to the lower tangent of L and R.
## Implementation
Note that the implementation of the in_circle function is GCC-specific.
```{.cpp file=delaunay}
typedef long long ll;
bool ge(const ll& a, const ll& b) { return a >= b; }
bool le(const ll& a, const ll& b) { return a <= b; }
bool eq(const ll& a, const ll& b) { return a == b; }
bool gt(const ll& a, const ll& b) { return a > b; }
bool lt(const ll& a, const ll& b) { return a < b; }
int sgn(const ll& a) { return a >= 0 ? a ? 1 : 0 : -1; }
struct pt {
ll x, y;
pt() { }
pt(ll _x, ll _y) : x(_x), y(_y) { }
pt operator-(const pt& p) const {
return pt(x - p.x, y - p.y);
}
ll cross(const pt& p) const {
return x * p.y - y * p.x;
}
ll cross(const pt& a, const pt& b) const {
return (a - *this).cross(b - *this);
}
ll dot(const pt& p) const {
return x * p.x + y * p.y;
}
ll dot(const pt& a, const pt& b) const {
return (a - *this).dot(b - *this);
}
ll sqrLength() const {
return this->dot(*this);
}
bool operator==(const pt& p) const {
return eq(x, p.x) && eq(y, p.y);
}
};
const pt inf_pt = pt(1e18, 1e18);
struct QuadEdge {
pt origin;
QuadEdge* rot = nullptr;
QuadEdge* onext = nullptr;
bool used = false;
QuadEdge* rev() const {
return rot->rot;
}
QuadEdge* lnext() const {
return rot->rev()->onext->rot;
}
QuadEdge* oprev() const {
return rot->onext->rot;
}
pt dest() const {
return rev()->origin;
}
};
QuadEdge* make_edge(pt from, pt to) {
QuadEdge* e1 = new QuadEdge;
QuadEdge* e2 = new QuadEdge;
QuadEdge* e3 = new QuadEdge;
QuadEdge* e4 = new QuadEdge;
e1->origin = from;
e2->origin = to;
e3->origin = e4->origin = inf_pt;
e1->rot = e3;
e2->rot = e4;
e3->rot = e2;
e4->rot = e1;
e1->onext = e1;
e2->onext = e2;
e3->onext = e4;
e4->onext = e3;
return e1;
}
void splice(QuadEdge* a, QuadEdge* b) {
swap(a->onext->rot->onext, b->onext->rot->onext);
swap(a->onext, b->onext);
}
void delete_edge(QuadEdge* e) {
splice(e, e->oprev());
splice(e->rev(), e->rev()->oprev());
delete e->rev()->rot;
delete e->rev();
delete e->rot;
delete e;
}
QuadEdge* connect(QuadEdge* a, QuadEdge* b) {
QuadEdge* e = make_edge(a->dest(), b->origin);
splice(e, a->lnext());
splice(e->rev(), b);
return e;
}
bool left_of(pt p, QuadEdge* e) {
return gt(p.cross(e->origin, e->dest()), 0);
}
bool right_of(pt p, QuadEdge* e) {
return lt(p.cross(e->origin, e->dest()), 0);
}
template <class T>
T det3(T a1, T a2, T a3, T b1, T b2, T b3, T c1, T c2, T c3) {
return a1 * (b2 * c3 - c2 * b3) - a2 * (b1 * c3 - c1 * b3) +
a3 * (b1 * c2 - c1 * b2);
}
bool in_circle(pt a, pt b, pt c, pt d) {
// If there is __int128, calculate directly.
// Otherwise, calculate angles.
#if defined(__LP64__) || defined(_WIN64)
__int128 det = -det3<__int128>(b.x, b.y, b.sqrLength(), c.x, c.y,
c.sqrLength(), d.x, d.y, d.sqrLength());
det += det3<__int128>(a.x, a.y, a.sqrLength(), c.x, c.y, c.sqrLength(), d.x,
d.y, d.sqrLength());
det -= det3<__int128>(a.x, a.y, a.sqrLength(), b.x, b.y, b.sqrLength(), d.x,
d.y, d.sqrLength());
det += det3<__int128>(a.x, a.y, a.sqrLength(), b.x, b.y, b.sqrLength(), c.x,
c.y, c.sqrLength());
return det > 0;
#else
auto ang = [](pt l, pt mid, pt r) {
ll x = mid.dot(l, r);
ll y = mid.cross(l, r);
long double res = atan2((long double)x, (long double)y);
return res;
};
long double kek = ang(a, b, c) + ang(c, d, a) - ang(b, c, d) - ang(d, a, b);
if (kek > 1e-8)
return true;
else
return false;
#endif
}
pair<QuadEdge*, QuadEdge*> build_tr(int l, int r, vector<pt>& p) {
if (r - l + 1 == 2) {
QuadEdge* res = make_edge(p[l], p[r]);
return make_pair(res, res->rev());
}
if (r - l + 1 == 3) {
QuadEdge *a = make_edge(p[l], p[l + 1]), *b = make_edge(p[l + 1], p[r]);
splice(a->rev(), b);
int sg = sgn(p[l].cross(p[l + 1], p[r]));
if (sg == 0)
return make_pair(a, b->rev());
QuadEdge* c = connect(b, a);
if (sg == 1)
return make_pair(a, b->rev());
else
return make_pair(c->rev(), c);
}
int mid = (l + r) / 2;
QuadEdge *ldo, *ldi, *rdo, *rdi;
tie(ldo, ldi) = build_tr(l, mid, p);
tie(rdi, rdo) = build_tr(mid + 1, r, p);
while (true) {
if (left_of(rdi->origin, ldi)) {
ldi = ldi->lnext();
continue;
}
if (right_of(ldi->origin, rdi)) {
rdi = rdi->rev()->onext;
continue;
}
break;
}
QuadEdge* basel = connect(rdi->rev(), ldi);
auto valid = [&basel](QuadEdge* e) { return right_of(e->dest(), basel); };
if (ldi->origin == ldo->origin)
ldo = basel->rev();
if (rdi->origin == rdo->origin)
rdo = basel;
while (true) {
QuadEdge* lcand = basel->rev()->onext;
if (valid(lcand)) {
while (in_circle(basel->dest(), basel->origin, lcand->dest(),
lcand->onext->dest())) {
QuadEdge* t = lcand->onext;
delete_edge(lcand);
lcand = t;
}
}
QuadEdge* rcand = basel->oprev();
if (valid(rcand)) {
while (in_circle(basel->dest(), basel->origin, rcand->dest(),
rcand->oprev()->dest())) {
QuadEdge* t = rcand->oprev();
delete_edge(rcand);
rcand = t;
}
}
if (!valid(lcand) && !valid(rcand))
break;
if (!valid(lcand) ||
(valid(rcand) && in_circle(lcand->dest(), lcand->origin,
rcand->origin, rcand->dest())))
basel = connect(rcand, basel->rev());
else
basel = connect(basel->rev(), lcand->rev());
}
return make_pair(ldo, rdo);
}
vector<tuple<pt, pt, pt>> delaunay(vector<pt> p) {
sort(p.begin(), p.end(), [](const pt& a, const pt& b) {
return lt(a.x, b.x) || (eq(a.x, b.x) && lt(a.y, b.y));
});
auto res = build_tr(0, (int)p.size() - 1, p);
QuadEdge* e = res.first;
vector<QuadEdge*> edges = {e};
while (lt(e->onext->dest().cross(e->dest(), e->origin), 0))
e = e->onext;
auto add = [&p, &e, &edges]() {
QuadEdge* curr = e;
do {
curr->used = true;
p.push_back(curr->origin);
edges.push_back(curr->rev());
curr = curr->lnext();
} while (curr != e);
};
add();
p.clear();
int kek = 0;
while (kek < (int)edges.size()) {
if (!(e = edges[kek++])->used)
add();
}
vector<tuple<pt, pt, pt>> ans;
for (int i = 0; i < (int)p.size(); i += 3) {
ans.push_back(make_tuple(p[i], p[i + 1], p[i + 2]));
}
return ans;
}
```
|
---
title
voronoi_diagram_2d_n4
---
# Delaunay triangulation and Voronoi diagram
Consider a set $\{p_i\}$ of points on the plane.
A **Voronoi diagram** $V(\{p_i\})$ of $\{p_i\}$ is a partition of the plane into $n$ regions $V_i$, where $V_i = \{p\in\mathbb{R}^2;\ \rho(p, p_i) = \min\ \rho(p, p_k)\}$.
The cells of the Voronoi diagram are polygons (possibly infinite).
A **Delaunay triangulation** $D(\{p_i\})$ of $\{p_i\}$ is a triangulation where every point $p_i$ is outside or on the boundary of the circumcircle of each triangle $T \in D(\{p_i\})$.
There is a nasty degenerated case when the Voronoi diagram isn't connected and Delaunay triangulation doesn't exist. This case is when all points are collinear.
## Properties
The Delaunay triangulation maximizes the minimum angle among all possible triangulations.
The Minimum Euclidean spanning tree of a point set is a subset of edges of its' Delaunay triangulation.
## Duality
Suppose that $\{p_i\}$ is not collinear and among $\{p_i\}$ no four points lie on one circle. Then $V(\{p_i\})$ and $D(\{p_i\})$ are dual, so if we obtain one of them, we may obtain the other in $O(n)$. What to do if it's not the case? The collinear case may be processed easily. Otherwise, $V$ and $D'$ are dual, where $D'$ is obtained from $D$ by removing all the edges such that two triangles on this edge share the circumcircle.
## Building Delaunay and Voronoi
Because of the duality, we only need a fast algorithm to compute only one of $V$ and $D$. We will describe how to build $D(\{p_i\})$ in $O(n\log n)$. The triangulation will be built via divide-and-conquer algorithm due to Guibas and Stolfi.
## Quad-edge data structure
During the algorithm $D$ will be stored inside the quad-edge data structure. This structure is described in the picture:
<center></center>
In the algorithm we will use the following functions on edges:
1. `make_edge(a, b)`<br>
This function creates an isolated edge from point `a` to point `b` together with its' reverse edge and both dual edges.
2. `splice(a, b)`<br>
This is a key function of the algorithm. It swaps `a->Onext` with `b->Onext` and `a->Onext->Rot->Onext` with `b->Onext->Rot->Onext`.
3. `delete_edge(e)`<br>
This function deletes e from the triangulation. To delete `e`, we may simply call `splice(e, e->Oprev)` and `splice(e->Rev, e->Rev->Oprev)`.
4. `connect(a, b)`<br>
This function creates a new edge `e` from `a->Dest` to `b->Org` in such a way that `a`, `b`, `e` all have the same left face. To do this, we call `e = make_edge(a->Dest, b->Org)`, `splice(e, a->Lnext)` and `splice(e->Rev, b)`.
## Algorithm
The algorithm will compute the triangulation and return two quad-edges: the counterclockwise convex hull edge out of the leftmost vertex and the clockwise convex hull edge out of the rightmost vertex.
Let's sort all points by x, and if $x_1 = x_2$ then by y. Let's solve the problem for some segment $(l, r)$ (initially $(l, r) = (0, n - 1)$). If $r - l + 1 = 2$, we will add an edge $(p[l], p[r])$ and return. If $r - l + 1 = 3$, we will firstly add the edges $(p[l], p[l + 1])$ and $(p[l + 1], p[r])$. We must also connect them using `splice(a->Rev, b)`. Now we must close the triangle. Our next action will depend on the orientation of $p[l], p[l + 1], p[r]$. If they are collinear, we can't make a triangle, so we simply return `(a, b->Rev)`. Otherwise, we create a new edge `c` by calling `connect(b, a)`. If the points are oriented counter-clockwise, we return `(a, b->Rev)`. Otherwise we return `(c->Rev, c)`.
Now suppose that $r - l + 1 \ge 4$. Firstly, let's solve $L = (l, \frac{l + r}{2})$ and $R = (\frac{l + r}{2} + 1, r)$ recursively. Now we have to merge these triangulations into one triangulation. Note that our points are sorted, so while merging we will add edges from L to R (so-called _cross_ edges) and remove some edges from L to L and from R to R.
What is the structure of the cross edges? All these edges must cross a line parallel to the y-axis and placed at the splitting x value. This establishes a linear ordering of the cross edges, so we can talk about successive cross edges, the bottom-most cross edge, etc. The algorithm will add the cross edges in ascending order. Note that any two adjacent cross edges will have a common endpoint, and the third side of the triangle they define goes from L to L or from R to R. Let's call the current cross edge the base. The successor of the base will either go from the left endpoint of the base to one of the R-neighbors of the right endpoint or vice versa.
Consider the circumcircle of base and the previous cross edge.
Suppose this circle is transformed into other circles having base as a chord but lying further into the Oy direction.
Our circle will go up for a while, but unless base is an upper tangent of L and R we will encounter a point belonging either to L or to R giving rise to a new triangle without any points in the circumcircle.
The new L-R edge of this triangle is the next cross edge added.
To do this efficiently, we compute two edges `lcand` and `rcand` so that `lcand` points to the first L point encountered in this process, and `rcand` points to the first R point.
Then we choose the one that would be encountered first. Initially base points to the lower tangent of L and R.
## Implementation
Note that the implementation of the in_circle function is GCC-specific.
```{.cpp file=delaunay}
typedef long long ll;
bool ge(const ll& a, const ll& b) { return a >= b; }
bool le(const ll& a, const ll& b) { return a <= b; }
bool eq(const ll& a, const ll& b) { return a == b; }
bool gt(const ll& a, const ll& b) { return a > b; }
bool lt(const ll& a, const ll& b) { return a < b; }
int sgn(const ll& a) { return a >= 0 ? a ? 1 : 0 : -1; }
struct pt {
ll x, y;
pt() { }
pt(ll _x, ll _y) : x(_x), y(_y) { }
pt operator-(const pt& p) const {
return pt(x - p.x, y - p.y);
}
ll cross(const pt& p) const {
return x * p.y - y * p.x;
}
ll cross(const pt& a, const pt& b) const {
return (a - *this).cross(b - *this);
}
ll dot(const pt& p) const {
return x * p.x + y * p.y;
}
ll dot(const pt& a, const pt& b) const {
return (a - *this).dot(b - *this);
}
ll sqrLength() const {
return this->dot(*this);
}
bool operator==(const pt& p) const {
return eq(x, p.x) && eq(y, p.y);
}
};
const pt inf_pt = pt(1e18, 1e18);
struct QuadEdge {
pt origin;
QuadEdge* rot = nullptr;
QuadEdge* onext = nullptr;
bool used = false;
QuadEdge* rev() const {
return rot->rot;
}
QuadEdge* lnext() const {
return rot->rev()->onext->rot;
}
QuadEdge* oprev() const {
return rot->onext->rot;
}
pt dest() const {
return rev()->origin;
}
};
QuadEdge* make_edge(pt from, pt to) {
QuadEdge* e1 = new QuadEdge;
QuadEdge* e2 = new QuadEdge;
QuadEdge* e3 = new QuadEdge;
QuadEdge* e4 = new QuadEdge;
e1->origin = from;
e2->origin = to;
e3->origin = e4->origin = inf_pt;
e1->rot = e3;
e2->rot = e4;
e3->rot = e2;
e4->rot = e1;
e1->onext = e1;
e2->onext = e2;
e3->onext = e4;
e4->onext = e3;
return e1;
}
void splice(QuadEdge* a, QuadEdge* b) {
swap(a->onext->rot->onext, b->onext->rot->onext);
swap(a->onext, b->onext);
}
void delete_edge(QuadEdge* e) {
splice(e, e->oprev());
splice(e->rev(), e->rev()->oprev());
delete e->rev()->rot;
delete e->rev();
delete e->rot;
delete e;
}
QuadEdge* connect(QuadEdge* a, QuadEdge* b) {
QuadEdge* e = make_edge(a->dest(), b->origin);
splice(e, a->lnext());
splice(e->rev(), b);
return e;
}
bool left_of(pt p, QuadEdge* e) {
return gt(p.cross(e->origin, e->dest()), 0);
}
bool right_of(pt p, QuadEdge* e) {
return lt(p.cross(e->origin, e->dest()), 0);
}
template <class T>
T det3(T a1, T a2, T a3, T b1, T b2, T b3, T c1, T c2, T c3) {
return a1 * (b2 * c3 - c2 * b3) - a2 * (b1 * c3 - c1 * b3) +
a3 * (b1 * c2 - c1 * b2);
}
bool in_circle(pt a, pt b, pt c, pt d) {
// If there is __int128, calculate directly.
// Otherwise, calculate angles.
#if defined(__LP64__) || defined(_WIN64)
__int128 det = -det3<__int128>(b.x, b.y, b.sqrLength(), c.x, c.y,
c.sqrLength(), d.x, d.y, d.sqrLength());
det += det3<__int128>(a.x, a.y, a.sqrLength(), c.x, c.y, c.sqrLength(), d.x,
d.y, d.sqrLength());
det -= det3<__int128>(a.x, a.y, a.sqrLength(), b.x, b.y, b.sqrLength(), d.x,
d.y, d.sqrLength());
det += det3<__int128>(a.x, a.y, a.sqrLength(), b.x, b.y, b.sqrLength(), c.x,
c.y, c.sqrLength());
return det > 0;
#else
auto ang = [](pt l, pt mid, pt r) {
ll x = mid.dot(l, r);
ll y = mid.cross(l, r);
long double res = atan2((long double)x, (long double)y);
return res;
};
long double kek = ang(a, b, c) + ang(c, d, a) - ang(b, c, d) - ang(d, a, b);
if (kek > 1e-8)
return true;
else
return false;
#endif
}
pair<QuadEdge*, QuadEdge*> build_tr(int l, int r, vector<pt>& p) {
if (r - l + 1 == 2) {
QuadEdge* res = make_edge(p[l], p[r]);
return make_pair(res, res->rev());
}
if (r - l + 1 == 3) {
QuadEdge *a = make_edge(p[l], p[l + 1]), *b = make_edge(p[l + 1], p[r]);
splice(a->rev(), b);
int sg = sgn(p[l].cross(p[l + 1], p[r]));
if (sg == 0)
return make_pair(a, b->rev());
QuadEdge* c = connect(b, a);
if (sg == 1)
return make_pair(a, b->rev());
else
return make_pair(c->rev(), c);
}
int mid = (l + r) / 2;
QuadEdge *ldo, *ldi, *rdo, *rdi;
tie(ldo, ldi) = build_tr(l, mid, p);
tie(rdi, rdo) = build_tr(mid + 1, r, p);
while (true) {
if (left_of(rdi->origin, ldi)) {
ldi = ldi->lnext();
continue;
}
if (right_of(ldi->origin, rdi)) {
rdi = rdi->rev()->onext;
continue;
}
break;
}
QuadEdge* basel = connect(rdi->rev(), ldi);
auto valid = [&basel](QuadEdge* e) { return right_of(e->dest(), basel); };
if (ldi->origin == ldo->origin)
ldo = basel->rev();
if (rdi->origin == rdo->origin)
rdo = basel;
while (true) {
QuadEdge* lcand = basel->rev()->onext;
if (valid(lcand)) {
while (in_circle(basel->dest(), basel->origin, lcand->dest(),
lcand->onext->dest())) {
QuadEdge* t = lcand->onext;
delete_edge(lcand);
lcand = t;
}
}
QuadEdge* rcand = basel->oprev();
if (valid(rcand)) {
while (in_circle(basel->dest(), basel->origin, rcand->dest(),
rcand->oprev()->dest())) {
QuadEdge* t = rcand->oprev();
delete_edge(rcand);
rcand = t;
}
}
if (!valid(lcand) && !valid(rcand))
break;
if (!valid(lcand) ||
(valid(rcand) && in_circle(lcand->dest(), lcand->origin,
rcand->origin, rcand->dest())))
basel = connect(rcand, basel->rev());
else
basel = connect(basel->rev(), lcand->rev());
}
return make_pair(ldo, rdo);
}
vector<tuple<pt, pt, pt>> delaunay(vector<pt> p) {
sort(p.begin(), p.end(), [](const pt& a, const pt& b) {
return lt(a.x, b.x) || (eq(a.x, b.x) && lt(a.y, b.y));
});
auto res = build_tr(0, (int)p.size() - 1, p);
QuadEdge* e = res.first;
vector<QuadEdge*> edges = {e};
while (lt(e->onext->dest().cross(e->dest(), e->origin), 0))
e = e->onext;
auto add = [&p, &e, &edges]() {
QuadEdge* curr = e;
do {
curr->used = true;
p.push_back(curr->origin);
edges.push_back(curr->rev());
curr = curr->lnext();
} while (curr != e);
};
add();
p.clear();
int kek = 0;
while (kek < (int)edges.size()) {
if (!(e = edges[kek++])->used)
add();
}
vector<tuple<pt, pt, pt>> ans;
for (int i = 0; i < (int)p.size(); i += 3) {
ans.push_back(make_tuple(p[i], p[i + 1], p[i + 2]));
}
return ans;
}
```
## Problems
* [TIMUS 1504 Good Manners](http://acm.timus.ru/problem.aspx?space=1&num=1504)
* [TIMUS 1520 Empire Strikes Back](http://acm.timus.ru/problem.aspx?space=1&num=1520)
* [SGU 383 Caravans](https://codeforces.com/problemsets/acmsguru/problem/99999/383)
|
Delaunay triangulation and Voronoi diagram
|
---
title
nearest_points
---
# Finding the nearest pair of points
## Problem statement
Given $n$ points on the plane. Each point $p_i$ is defined by its coordinates $(x_i,y_i)$. It is required to find among them two such points, such that the distance between them is minimal:
$$ \min_{\scriptstyle i, j=0 \ldots n-1,\atop \scriptstyle i \neq j } \rho (p_i, p_j). $$
We take the usual Euclidean distances:
$$ \rho (p_i,p_j) = \sqrt{(x_i-x_j)^2 + (y_i-y_j)^2} .$$
The trivial algorithm - iterating over all pairs and calculating the distance for each — works in $O(n^2)$.
The algorithm running in time $O(n \log n)$ is described below. This algorithm was proposed by Shamos and Hoey in 1975. (Source: Ch. 5 Notes of _Algorithm Design_ by Kleinberg & Tardos, also see [here](https://ieeexplore.ieee.org/abstract/document/4567872)) Preparata and Shamos also showed that this algorithm is optimal in the decision tree model.
## Algorithm
We construct an algorithm according to the general scheme of **divide-and-conquer** algorithms: the algorithm is designed as a recursive function, to which we pass a set of points; this recursive function splits this set in half, calls itself recursively on each half, and then performs some operations to combine the answers. The operation of combining consist of detecting the cases when one point of the optimal solution fell into one half, and the other point into the other (in this case, recursive calls from each of the halves cannot detect this pair separately). The main difficulty, as always in case of divide and conquer algorithms, lies in the effective implementation of the merging stage. If a set of $n$ points is passed to the recursive function, then the merge stage should work no more than $O(n)$, then the asymptotics of the whole algorithm $T(n)$ will be found from the equation:
$$T(n) = 2T(n/2) + O(n).$$
The solution to this equation, as is known, is $T(n) = O(n \log n).$
So, we proceed on to the construction of the algorithm. In order to come to an effective implementation of the merge stage in the future, we will divide the set of points into two subsets, according to their $x$-coordinates: In fact, we draw some vertical line dividing the set of points into two subsets of approximately the same size. It is convenient to make such a partition as follows: We sort the points in the standard way as pairs of numbers, ie.:
$$p_i < p_j \Longleftrightarrow (x_i < x_j) \lor \Big(\left(x_i = x_j\right) \wedge \left(y_i < y_j \right) \Big) $$
Then take the middle point after sorting $p_m (m = \lfloor n/2 \rfloor)$, and all the points before it and the $p_m$ itself are assigned to the first half, and all the points after it - to the second half:
$$A_1 = \{p_i \ | \ i = 0 \ldots m \}$$
$$A_2 = \{p_i \ | \ i = m + 1 \ldots n-1 \}.$$
Now, calling recursively on each of the sets $A_1$ and $A_2$, we will find the answers $h_1$ and $h_2$ for each of the halves. And take the best of them: $h = \min(h_1, h_2)$.
Now we need to make a **merge stage**, i.e. we try to find such pairs of points, for which the distance between which is less than $h$ and one point is lying in $A_1$ and the other in $A_2$.
It is obvious that it is sufficient to consider only those points that are separated from the vertical line by a distance less than $h$, i.e. the set $B$ of the points considered at this stage is equal to:
$$B = \{ p_i\ | \ | x_i - x_m\ | < h \}.$$
For each point in the set $B$, we try to find the points that are closer to it than $h$. For example, it is sufficient to consider only those points whose $y$-coordinate differs by no more than $h$. Moreover, it makes no sense to consider those points whose $y$-coordinate is greater than the $y$-coordinate of the current point. Thus, for each point $p_i$ we define the set of considered points $C(p_i)$ as follows:
$$C(p_i) = \{ p_j\ |\ p_j \in B,\ \ y_i - h < y_j \le y_i \}.$$
If we sort the points of the set $B$ by $y$-coordinate, it will be very easy to find $C(p_i)$: these are several points in a row ahead to the point $p_i$.
So, in the new notation, the **merging stage** looks like this: build a set $B$, sort the points in it by $y$-coordinate, then for each point $p_i \in B$ consider all points $p_j \in C(p_i)$, and for each pair $(p_i,p_j)$ calculate the distance and compare with the current best distance.
At first glance, this is still a non-optimal algorithm: it seems that the sizes of sets $C(p_i)$ will be of order $n$, and the required asymptotics will not work. However, surprisingly, it can be proved that the size of each of the sets $C(p_i)$ is a quantity $O(1)$, i.e. it does not exceed some small constant regardless of the points themselves. Proof of this fact is given in the next section.
Finally, we pay attention to the sorting, which the above algorithm contains: first,sorting by pairs $(x, y)$, and then second, sorting the elements of the set $B$ by $y$. In fact, both of these sorts inside the recursive function can be eliminated (otherwise we would not reach the $O(n)$ estimate for the **merging stage**, and the general asymptotics of the algorithm would be $O(n \log^2 n)$). It is easy to get rid of the first sort — it is enough to perform this sort before starting the recursion: after all, the elements themselves do not change inside the recursion, so there is no need to sort again. With the second sorting a little more difficult to perform, performing it previously will not work. But, remembering the merge sort, which also works on the principle of divide-and-conquer, we can simply embed this sort in our recursion. Let recursion, taking some set of points (as we remember,ordered by pairs $(x, y)$), return the same set, but sorted by the $y$-coordinate. To do this, simply merge (in $O(n)$) the two results returned by recursive calls. This will result in a set sorted by $y$-coordinate.
## Evaluation of the asymptotics
To show that the above algorithm is actually executed in $O(n \log n)$, we need to prove the following fact: $|C(p_i)| = O(1)$.
So, let us consider some point $p_i$; recall that the set $C(p_i)$ is a set of points whose $y$-coordinate lies in the segment $[y_i-h; y_i]$, and, moreover, along the $x$ coordinate, the point $p_i$ itself, and all the points of the set $C(p_i)$ lie in the band width $2h$. In other words, the points we are considering $p_i$ and $C(p_i)$ lie in a rectangle of size $2h \times h$.
Our task is to estimate the maximum number of points that can lie in this rectangle $2h \times h$; thus, we estimate the maximum size of the set $C(p_i)$. At the same time, when evaluating, we must not forget that there may be repeated points.
Remember that $h$ was obtained from the results of two recursive calls — on sets $A_1$ and $A_2$, and $A_1$ contains points to the left of the partition line and partially on it, $A_2$ contains the remaining points of the partition line and points to the right of it. For any pair of points from $A_1$, as well as from $A_2$, the distance can not be less than $h$ — otherwise it would mean incorrect operation of the recursive function.
To estimate the maximum number of points in the rectangle $2h \times h$ we divide it into two squares $h \times h$, the first square include all points $C(p_i) \cap A_1$, and the second contains all the others, i.e. $C(p_i) \cap A_2$. It follows from the above considerations that in each of these squares the distance between any two points is at least $h$.
We show that there are at most four points in each square. For example, this can be done as follows: divide the square into $4$ sub-squares with sides $h/2$. Then there can be no more than one point in each of these sub-squares (since even the diagonal is equal to $h / \sqrt{2}$, which is less than $h$). Therefore, there can be no more than $4$ points in the whole square.
So, we have proved that in a rectangle $2h \times h$ can not be more than $4 \cdot 2 = 8$ points, and, therefore, the size of the set $C(p_i)$ cannot exceed $7$, as required.
## Implementation
We introduce a data structure to store a point (its coordinates and a number) and comparison operators required for two types of sorting:
```{.cpp file=nearest_pair_def}
struct pt {
int x, y, id;
};
struct cmp_x {
bool operator()(const pt & a, const pt & b) const {
return a.x < b.x || (a.x == b.x && a.y < b.y);
}
};
struct cmp_y {
bool operator()(const pt & a, const pt & b) const {
return a.y < b.y;
}
};
int n;
vector<pt> a;
```
For a convenient implementation of recursion, we introduce an auxiliary function upd_ans(), which will calculate the distance between two points and check whether it is better than the current answer:
```{.cpp file=nearest_pair_update}
double mindist;
pair<int, int> best_pair;
void upd_ans(const pt & a, const pt & b) {
double dist = sqrt((a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y));
if (dist < mindist) {
mindist = dist;
best_pair = {a.id, b.id};
}
}
```
Finally, the implementation of the recursion itself. It is assumed that before calling it, the array $a[]$ is already sorted by $x$-coordinate. In recursion we pass just two pointers $l, r$, which indicate that it should look for the answer for $a[l \ldots r)$. If the distance between $r$ and $l$ is too small, the recursion must be stopped, and perform a trivial algorithm to find the nearest pair and then sort the subarray by $y$-coordinate.
To merge two sets of points received from recursive calls into one (ordered by $y$-coordinate), we use the standard STL $merge()$ function, and create an auxiliary buffer $t[]$(one for all recursive calls). (Using inplace_merge () is impractical because it generally does not work in linear time.)
Finally, the set $B$ is stored in the same array $t$.
```{.cpp file=nearest_pair_rec}
vector<pt> t;
void rec(int l, int r) {
if (r - l <= 3) {
for (int i = l; i < r; ++i) {
for (int j = i + 1; j < r; ++j) {
upd_ans(a[i], a[j]);
}
}
sort(a.begin() + l, a.begin() + r, cmp_y());
return;
}
int m = (l + r) >> 1;
int midx = a[m].x;
rec(l, m);
rec(m, r);
merge(a.begin() + l, a.begin() + m, a.begin() + m, a.begin() + r, t.begin(), cmp_y());
copy(t.begin(), t.begin() + r - l, a.begin() + l);
int tsz = 0;
for (int i = l; i < r; ++i) {
if (abs(a[i].x - midx) < mindist) {
for (int j = tsz - 1; j >= 0 && a[i].y - t[j].y < mindist; --j)
upd_ans(a[i], t[j]);
t[tsz++] = a[i];
}
}
}
```
By the way, if all the coordinates are integer, then at the time of the recursion you can not move to fractional values, and store in $mindist$ the square of the minimum distance.
In the main program, recursion should be called as follows:
```{.cpp file=nearest_pair_main}
t.resize(n);
sort(a.begin(), a.end(), cmp_x());
mindist = 1E20;
rec(0, n);
```
## Generalization: finding a triangle with minimal perimeter
The algorithm described above is interestingly generalized to this problem: among a given set of points, choose three different points so that the sum of pairwise distances between them is the smallest.
In fact, to solve this problem, the algorithm remains the same: we divide the field into two halves of the vertical line, call the solution recursively on both halves, choose the minimum $minper$ from the found perimeters, build a strip with the thickness of $minper / 2$, and iterate through all triangles that can improve the answer. (Note that the triangle with perimeter $\le minper$ has the longest side $\le minper / 2$.)
|
---
title
nearest_points
---
# Finding the nearest pair of points
## Problem statement
Given $n$ points on the plane. Each point $p_i$ is defined by its coordinates $(x_i,y_i)$. It is required to find among them two such points, such that the distance between them is minimal:
$$ \min_{\scriptstyle i, j=0 \ldots n-1,\atop \scriptstyle i \neq j } \rho (p_i, p_j). $$
We take the usual Euclidean distances:
$$ \rho (p_i,p_j) = \sqrt{(x_i-x_j)^2 + (y_i-y_j)^2} .$$
The trivial algorithm - iterating over all pairs and calculating the distance for each — works in $O(n^2)$.
The algorithm running in time $O(n \log n)$ is described below. This algorithm was proposed by Shamos and Hoey in 1975. (Source: Ch. 5 Notes of _Algorithm Design_ by Kleinberg & Tardos, also see [here](https://ieeexplore.ieee.org/abstract/document/4567872)) Preparata and Shamos also showed that this algorithm is optimal in the decision tree model.
## Algorithm
We construct an algorithm according to the general scheme of **divide-and-conquer** algorithms: the algorithm is designed as a recursive function, to which we pass a set of points; this recursive function splits this set in half, calls itself recursively on each half, and then performs some operations to combine the answers. The operation of combining consist of detecting the cases when one point of the optimal solution fell into one half, and the other point into the other (in this case, recursive calls from each of the halves cannot detect this pair separately). The main difficulty, as always in case of divide and conquer algorithms, lies in the effective implementation of the merging stage. If a set of $n$ points is passed to the recursive function, then the merge stage should work no more than $O(n)$, then the asymptotics of the whole algorithm $T(n)$ will be found from the equation:
$$T(n) = 2T(n/2) + O(n).$$
The solution to this equation, as is known, is $T(n) = O(n \log n).$
So, we proceed on to the construction of the algorithm. In order to come to an effective implementation of the merge stage in the future, we will divide the set of points into two subsets, according to their $x$-coordinates: In fact, we draw some vertical line dividing the set of points into two subsets of approximately the same size. It is convenient to make such a partition as follows: We sort the points in the standard way as pairs of numbers, ie.:
$$p_i < p_j \Longleftrightarrow (x_i < x_j) \lor \Big(\left(x_i = x_j\right) \wedge \left(y_i < y_j \right) \Big) $$
Then take the middle point after sorting $p_m (m = \lfloor n/2 \rfloor)$, and all the points before it and the $p_m$ itself are assigned to the first half, and all the points after it - to the second half:
$$A_1 = \{p_i \ | \ i = 0 \ldots m \}$$
$$A_2 = \{p_i \ | \ i = m + 1 \ldots n-1 \}.$$
Now, calling recursively on each of the sets $A_1$ and $A_2$, we will find the answers $h_1$ and $h_2$ for each of the halves. And take the best of them: $h = \min(h_1, h_2)$.
Now we need to make a **merge stage**, i.e. we try to find such pairs of points, for which the distance between which is less than $h$ and one point is lying in $A_1$ and the other in $A_2$.
It is obvious that it is sufficient to consider only those points that are separated from the vertical line by a distance less than $h$, i.e. the set $B$ of the points considered at this stage is equal to:
$$B = \{ p_i\ | \ | x_i - x_m\ | < h \}.$$
For each point in the set $B$, we try to find the points that are closer to it than $h$. For example, it is sufficient to consider only those points whose $y$-coordinate differs by no more than $h$. Moreover, it makes no sense to consider those points whose $y$-coordinate is greater than the $y$-coordinate of the current point. Thus, for each point $p_i$ we define the set of considered points $C(p_i)$ as follows:
$$C(p_i) = \{ p_j\ |\ p_j \in B,\ \ y_i - h < y_j \le y_i \}.$$
If we sort the points of the set $B$ by $y$-coordinate, it will be very easy to find $C(p_i)$: these are several points in a row ahead to the point $p_i$.
So, in the new notation, the **merging stage** looks like this: build a set $B$, sort the points in it by $y$-coordinate, then for each point $p_i \in B$ consider all points $p_j \in C(p_i)$, and for each pair $(p_i,p_j)$ calculate the distance and compare with the current best distance.
At first glance, this is still a non-optimal algorithm: it seems that the sizes of sets $C(p_i)$ will be of order $n$, and the required asymptotics will not work. However, surprisingly, it can be proved that the size of each of the sets $C(p_i)$ is a quantity $O(1)$, i.e. it does not exceed some small constant regardless of the points themselves. Proof of this fact is given in the next section.
Finally, we pay attention to the sorting, which the above algorithm contains: first,sorting by pairs $(x, y)$, and then second, sorting the elements of the set $B$ by $y$. In fact, both of these sorts inside the recursive function can be eliminated (otherwise we would not reach the $O(n)$ estimate for the **merging stage**, and the general asymptotics of the algorithm would be $O(n \log^2 n)$). It is easy to get rid of the first sort — it is enough to perform this sort before starting the recursion: after all, the elements themselves do not change inside the recursion, so there is no need to sort again. With the second sorting a little more difficult to perform, performing it previously will not work. But, remembering the merge sort, which also works on the principle of divide-and-conquer, we can simply embed this sort in our recursion. Let recursion, taking some set of points (as we remember,ordered by pairs $(x, y)$), return the same set, but sorted by the $y$-coordinate. To do this, simply merge (in $O(n)$) the two results returned by recursive calls. This will result in a set sorted by $y$-coordinate.
## Evaluation of the asymptotics
To show that the above algorithm is actually executed in $O(n \log n)$, we need to prove the following fact: $|C(p_i)| = O(1)$.
So, let us consider some point $p_i$; recall that the set $C(p_i)$ is a set of points whose $y$-coordinate lies in the segment $[y_i-h; y_i]$, and, moreover, along the $x$ coordinate, the point $p_i$ itself, and all the points of the set $C(p_i)$ lie in the band width $2h$. In other words, the points we are considering $p_i$ and $C(p_i)$ lie in a rectangle of size $2h \times h$.
Our task is to estimate the maximum number of points that can lie in this rectangle $2h \times h$; thus, we estimate the maximum size of the set $C(p_i)$. At the same time, when evaluating, we must not forget that there may be repeated points.
Remember that $h$ was obtained from the results of two recursive calls — on sets $A_1$ and $A_2$, and $A_1$ contains points to the left of the partition line and partially on it, $A_2$ contains the remaining points of the partition line and points to the right of it. For any pair of points from $A_1$, as well as from $A_2$, the distance can not be less than $h$ — otherwise it would mean incorrect operation of the recursive function.
To estimate the maximum number of points in the rectangle $2h \times h$ we divide it into two squares $h \times h$, the first square include all points $C(p_i) \cap A_1$, and the second contains all the others, i.e. $C(p_i) \cap A_2$. It follows from the above considerations that in each of these squares the distance between any two points is at least $h$.
We show that there are at most four points in each square. For example, this can be done as follows: divide the square into $4$ sub-squares with sides $h/2$. Then there can be no more than one point in each of these sub-squares (since even the diagonal is equal to $h / \sqrt{2}$, which is less than $h$). Therefore, there can be no more than $4$ points in the whole square.
So, we have proved that in a rectangle $2h \times h$ can not be more than $4 \cdot 2 = 8$ points, and, therefore, the size of the set $C(p_i)$ cannot exceed $7$, as required.
## Implementation
We introduce a data structure to store a point (its coordinates and a number) and comparison operators required for two types of sorting:
```{.cpp file=nearest_pair_def}
struct pt {
int x, y, id;
};
struct cmp_x {
bool operator()(const pt & a, const pt & b) const {
return a.x < b.x || (a.x == b.x && a.y < b.y);
}
};
struct cmp_y {
bool operator()(const pt & a, const pt & b) const {
return a.y < b.y;
}
};
int n;
vector<pt> a;
```
For a convenient implementation of recursion, we introduce an auxiliary function upd_ans(), which will calculate the distance between two points and check whether it is better than the current answer:
```{.cpp file=nearest_pair_update}
double mindist;
pair<int, int> best_pair;
void upd_ans(const pt & a, const pt & b) {
double dist = sqrt((a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y));
if (dist < mindist) {
mindist = dist;
best_pair = {a.id, b.id};
}
}
```
Finally, the implementation of the recursion itself. It is assumed that before calling it, the array $a[]$ is already sorted by $x$-coordinate. In recursion we pass just two pointers $l, r$, which indicate that it should look for the answer for $a[l \ldots r)$. If the distance between $r$ and $l$ is too small, the recursion must be stopped, and perform a trivial algorithm to find the nearest pair and then sort the subarray by $y$-coordinate.
To merge two sets of points received from recursive calls into one (ordered by $y$-coordinate), we use the standard STL $merge()$ function, and create an auxiliary buffer $t[]$(one for all recursive calls). (Using inplace_merge () is impractical because it generally does not work in linear time.)
Finally, the set $B$ is stored in the same array $t$.
```{.cpp file=nearest_pair_rec}
vector<pt> t;
void rec(int l, int r) {
if (r - l <= 3) {
for (int i = l; i < r; ++i) {
for (int j = i + 1; j < r; ++j) {
upd_ans(a[i], a[j]);
}
}
sort(a.begin() + l, a.begin() + r, cmp_y());
return;
}
int m = (l + r) >> 1;
int midx = a[m].x;
rec(l, m);
rec(m, r);
merge(a.begin() + l, a.begin() + m, a.begin() + m, a.begin() + r, t.begin(), cmp_y());
copy(t.begin(), t.begin() + r - l, a.begin() + l);
int tsz = 0;
for (int i = l; i < r; ++i) {
if (abs(a[i].x - midx) < mindist) {
for (int j = tsz - 1; j >= 0 && a[i].y - t[j].y < mindist; --j)
upd_ans(a[i], t[j]);
t[tsz++] = a[i];
}
}
}
```
By the way, if all the coordinates are integer, then at the time of the recursion you can not move to fractional values, and store in $mindist$ the square of the minimum distance.
In the main program, recursion should be called as follows:
```{.cpp file=nearest_pair_main}
t.resize(n);
sort(a.begin(), a.end(), cmp_x());
mindist = 1E20;
rec(0, n);
```
## Generalization: finding a triangle with minimal perimeter
The algorithm described above is interestingly generalized to this problem: among a given set of points, choose three different points so that the sum of pairwise distances between them is the smallest.
In fact, to solve this problem, the algorithm remains the same: we divide the field into two halves of the vertical line, call the solution recursively on both halves, choose the minimum $minper$ from the found perimeters, build a strip with the thickness of $minper / 2$, and iterate through all triangles that can improve the answer. (Note that the triangle with perimeter $\le minper$ has the longest side $\le minper / 2$.)
## Practice problems
* [UVA 10245 "The Closest Pair Problem" [difficulty: low]](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=1186)
* [SPOJ #8725 CLOPPAIR "Closest Point Pair" [difficulty: low]](https://www.spoj.com/problems/CLOPPAIR/)
* [CODEFORCES Team Olympiad Saratov - 2011 "Minimum amount" [difficulty: medium]](http://codeforces.com/contest/120/problem/J)
* [Google CodeJam 2009 Final " Min Perimeter "[difficulty: medium]](https://code.google.com/codejam/contest/311101/dashboard#s=a&a=1)
* [SPOJ #7029 CLOSEST "Closest Triple" [difficulty: medium]](https://www.spoj.com/problems/CLOSEST/)
* [TIMUS 1514 National Park [difficulty: medium]](https://acm.timus.ru/problem.aspx?space=1&num=1514)
|
Finding the nearest pair of points
|
---
title: Point location in O(log n)
title
- Original
---
# Point location in $O(log n)$
Consider the following problem: you are given a [planar subdivision](https://en.wikipedia.org/wiki/Planar_straight-line_graph) without no vertices of degree one and zero, and a lot of queries.
Each query is a point, for which we should determine the face of the subdivision it belongs to.
We will answer each query in $O(\log n)$ offline.<br>
This problem may arise when you need to locate some points in a Voronoi diagram or in some simple polygon.
## Algorithm
Firstly, for each query point $p\ (x_0, y_0)$ we want to find such an edge that if the point belongs to any edge, the point lies on the edge we found, otherwise this edge must intersect the line $x = x_0$ at some unique point $(x_0, y)$ where $y < y_0$ and this $y$ is maximum among all such edges.
The following image shows both cases.
<center></center>
We will solve this problem offline using the sweep line algorithm. Let's iterate over x-coordinates of query points and edges' endpoints in increasing order and keep a set of edges $s$. For each x-coordinate we will add some events beforehand.
The events will be of four types: _add_, _remove_, _vertical_, _get_.
For each vertical edge (both endpoints have the same x-coordinate) we will add one _vertical_ event for the corresponding x-coordinate.
For every other edge we will add one _add_ event for the minimum of x-coordinates of the endpoints and one _remove_ event for the maximum of x-coordinates of the endpoints.
Finally, for each query point we will add one _get_ event for its x-coordinate.
For each x-coordinate we will sort the events by their types in order (_vertical_, _get_, _remove_, _add_).
The following image shows all events in sorted order for each x-coordinate.
<center></center>
We will keep two sets during the sweep-line process.
A set $t$ for all non-vertical edges, and one set $vert$ especially for the vertical ones.
We will clear the set $vert$ at the beginning of processing each x-coordinate.
Now let's process the events for a fixed x-coordinate.
- If we got a _vertical_ event, we will simply insert the minimum y-coordinate of the corresponding edge's endpoints to $vert$.
- If we got a _remove_ or _add_ event, we will remove the corresponding edge from $t$ or add it to $t$.
- Finally, for each _get_ event we must check if the point lies on some vertical edge by performing a binary search in $vert$.
If the point doesn't lie on any vertical edge, we must find the answer for this query in $t$.
To do this, we again make a binary search.
In order to handle some degenerate cases (e.g. in case of the triangle $(0,~0)$, $(0,~2)$, $(1, 1)$ when we query the point $(0,~0)$), we must answer all _get_ events again after we processed all the events for this x-coordinate and choose the best of two answers.
Now let's choose a comparator for the set $t$.
This comparator should check if one edge doesn't lie above other for every x-coordinate they both cover. Suppose that we have two edges $(a, b)$ and $(c, d)$. Then the comparator is (in pseudocode):<br>
$val = sgn((b - a)\times(c - a)) + sgn((b - a)\times(d - a))$<br>
<b>if</b> $val \neq 0$<br>
<b>then return</b> $val > 0$<br>
$val = sgn((d - c)\times(a - c)) + sgn((d - c)\times(b - c))$<br>
<b>return</b> $val < 0$<br>
Now for every query we have the corresponding edge.
How to find the face?
If we couldn't find the edge it means that the point is in the outer face.
If the point belongs to the edge we found, the face is not unique.
Otherwise, there are two candidates - the faces that are bounded by this edge.
How to check which one is the answer? Note that the edge is not vertical.
Then the answer is the face that is above this edge.
Let's find such a face for each non-vertical edge.
Consider a counter-clockwise traversal of each face.
If during this traversal we increased x-coordinate while passing through the edge, then this face is the face we need to find for this edge.
## Notes
Actually, with persistent trees this approach can be used to answer the queries online.
## Implementation
The following code is implemented for integers, but it can be easily modified to work with doubles (by changing the compare methods and the point type).
This implementation assumes that the subdivision is correctly stored inside a [DCEL](https://en.wikipedia.org/wiki/Doubly_connected_edge_list) and the outer face is numbered $-1$.<br>
For each query a pair $(1, i)$ is returned if the point lies strictly inside the face number $i$, and a pair $(0, i)$ is returned if the point lies on the edge number $i$.
```{.cpp file=point-location}
typedef long long ll;
bool ge(const ll& a, const ll& b) { return a >= b; }
bool le(const ll& a, const ll& b) { return a <= b; }
bool eq(const ll& a, const ll& b) { return a == b; }
bool gt(const ll& a, const ll& b) { return a > b; }
bool lt(const ll& a, const ll& b) { return a < b; }
int sgn(const ll& x) { return le(x, 0) ? eq(x, 0) ? 0 : -1 : 1; }
struct pt {
ll x, y;
pt() {}
pt(ll _x, ll _y) : x(_x), y(_y) {}
pt operator-(const pt& a) const { return pt(x - a.x, y - a.y); }
ll dot(const pt& a) const { return x * a.x + y * a.y; }
ll dot(const pt& a, const pt& b) const { return (a - *this).dot(b - *this); }
ll cross(const pt& a) const { return x * a.y - y * a.x; }
ll cross(const pt& a, const pt& b) const { return (a - *this).cross(b - *this); }
bool operator==(const pt& a) const { return a.x == x && a.y == y; }
};
struct Edge {
pt l, r;
};
bool edge_cmp(Edge* edge1, Edge* edge2)
{
const pt a = edge1->l, b = edge1->r;
const pt c = edge2->l, d = edge2->r;
int val = sgn(a.cross(b, c)) + sgn(a.cross(b, d));
if (val != 0)
return val > 0;
val = sgn(c.cross(d, a)) + sgn(c.cross(d, b));
return val < 0;
}
enum EventType { DEL = 2, ADD = 3, GET = 1, VERT = 0 };
struct Event {
EventType type;
int pos;
bool operator<(const Event& event) const { return type < event.type; }
};
vector<Edge*> sweepline(vector<Edge*> planar, vector<pt> queries)
{
using pt_type = decltype(pt::x);
// collect all x-coordinates
auto s =
set<pt_type, std::function<bool(const pt_type&, const pt_type&)>>(lt);
for (pt p : queries)
s.insert(p.x);
for (Edge* e : planar) {
s.insert(e->l.x);
s.insert(e->r.x);
}
// map all x-coordinates to ids
int cid = 0;
auto id =
map<pt_type, int, std::function<bool(const pt_type&, const pt_type&)>>(
lt);
for (auto x : s)
id[x] = cid++;
// create events
auto t = set<Edge*, decltype(*edge_cmp)>(edge_cmp);
auto vert_cmp = [](const pair<pt_type, int>& l,
const pair<pt_type, int>& r) {
if (!eq(l.first, r.first))
return lt(l.first, r.first);
return l.second < r.second;
};
auto vert = set<pair<pt_type, int>, decltype(vert_cmp)>(vert_cmp);
vector<vector<Event>> events(cid);
for (int i = 0; i < (int)queries.size(); i++) {
int x = id[queries[i].x];
events[x].push_back(Event{GET, i});
}
for (int i = 0; i < (int)planar.size(); i++) {
int lx = id[planar[i]->l.x], rx = id[planar[i]->r.x];
if (lx > rx) {
swap(lx, rx);
swap(planar[i]->l, planar[i]->r);
}
if (lx == rx) {
events[lx].push_back(Event{VERT, i});
} else {
events[lx].push_back(Event{ADD, i});
events[rx].push_back(Event{DEL, i});
}
}
// perform sweep line algorithm
vector<Edge*> ans(queries.size(), nullptr);
for (int x = 0; x < cid; x++) {
sort(events[x].begin(), events[x].end());
vert.clear();
for (Event event : events[x]) {
if (event.type == DEL) {
t.erase(planar[event.pos]);
}
if (event.type == VERT) {
vert.insert(make_pair(
min(planar[event.pos]->l.y, planar[event.pos]->r.y),
event.pos));
}
if (event.type == ADD) {
t.insert(planar[event.pos]);
}
if (event.type == GET) {
auto jt = vert.upper_bound(
make_pair(queries[event.pos].y, planar.size()));
if (jt != vert.begin()) {
--jt;
int i = jt->second;
if (ge(max(planar[i]->l.y, planar[i]->r.y),
queries[event.pos].y)) {
ans[event.pos] = planar[i];
continue;
}
}
Edge* e = new Edge;
e->l = e->r = queries[event.pos];
auto it = t.upper_bound(e);
if (it != t.begin())
ans[event.pos] = *(--it);
delete e;
}
}
for (Event event : events[x]) {
if (event.type != GET)
continue;
if (ans[event.pos] != nullptr &&
eq(ans[event.pos]->l.x, ans[event.pos]->r.x))
continue;
Edge* e = new Edge;
e->l = e->r = queries[event.pos];
auto it = t.upper_bound(e);
delete e;
if (it == t.begin())
e = nullptr;
else
e = *(--it);
if (ans[event.pos] == nullptr) {
ans[event.pos] = e;
continue;
}
if (e == nullptr)
continue;
if (e == ans[event.pos])
continue;
if (id[ans[event.pos]->r.x] == x) {
if (id[e->l.x] == x) {
if (gt(e->l.y, ans[event.pos]->r.y))
ans[event.pos] = e;
}
} else {
ans[event.pos] = e;
}
}
}
return ans;
}
struct DCEL {
struct Edge {
pt origin;
Edge* nxt = nullptr;
Edge* twin = nullptr;
int face;
};
vector<Edge*> body;
};
vector<pair<int, int>> point_location(DCEL planar, vector<pt> queries)
{
vector<pair<int, int>> ans(queries.size());
vector<Edge*> planar2;
map<intptr_t, int> pos;
map<intptr_t, int> added_on;
int n = planar.body.size();
for (int i = 0; i < n; i++) {
if (planar.body[i]->face > planar.body[i]->twin->face)
continue;
Edge* e = new Edge;
e->l = planar.body[i]->origin;
e->r = planar.body[i]->twin->origin;
added_on[(intptr_t)e] = i;
pos[(intptr_t)e] =
lt(planar.body[i]->origin.x, planar.body[i]->twin->origin.x)
? planar.body[i]->face
: planar.body[i]->twin->face;
planar2.push_back(e);
}
auto res = sweepline(planar2, queries);
for (int i = 0; i < (int)queries.size(); i++) {
if (res[i] == nullptr) {
ans[i] = make_pair(1, -1);
continue;
}
pt p = queries[i];
pt l = res[i]->l, r = res[i]->r;
if (eq(p.cross(l, r), 0) && le(p.dot(l, r), 0)) {
ans[i] = make_pair(0, added_on[(intptr_t)res[i]]);
continue;
}
ans[i] = make_pair(1, pos[(intptr_t)res[i]]);
}
for (auto e : planar2)
delete e;
return ans;
}
```
|
---
title: Point location in O(log n)
title
- Original
---
# Point location in $O(log n)$
Consider the following problem: you are given a [planar subdivision](https://en.wikipedia.org/wiki/Planar_straight-line_graph) without no vertices of degree one and zero, and a lot of queries.
Each query is a point, for which we should determine the face of the subdivision it belongs to.
We will answer each query in $O(\log n)$ offline.<br>
This problem may arise when you need to locate some points in a Voronoi diagram or in some simple polygon.
## Algorithm
Firstly, for each query point $p\ (x_0, y_0)$ we want to find such an edge that if the point belongs to any edge, the point lies on the edge we found, otherwise this edge must intersect the line $x = x_0$ at some unique point $(x_0, y)$ where $y < y_0$ and this $y$ is maximum among all such edges.
The following image shows both cases.
<center></center>
We will solve this problem offline using the sweep line algorithm. Let's iterate over x-coordinates of query points and edges' endpoints in increasing order and keep a set of edges $s$. For each x-coordinate we will add some events beforehand.
The events will be of four types: _add_, _remove_, _vertical_, _get_.
For each vertical edge (both endpoints have the same x-coordinate) we will add one _vertical_ event for the corresponding x-coordinate.
For every other edge we will add one _add_ event for the minimum of x-coordinates of the endpoints and one _remove_ event for the maximum of x-coordinates of the endpoints.
Finally, for each query point we will add one _get_ event for its x-coordinate.
For each x-coordinate we will sort the events by their types in order (_vertical_, _get_, _remove_, _add_).
The following image shows all events in sorted order for each x-coordinate.
<center></center>
We will keep two sets during the sweep-line process.
A set $t$ for all non-vertical edges, and one set $vert$ especially for the vertical ones.
We will clear the set $vert$ at the beginning of processing each x-coordinate.
Now let's process the events for a fixed x-coordinate.
- If we got a _vertical_ event, we will simply insert the minimum y-coordinate of the corresponding edge's endpoints to $vert$.
- If we got a _remove_ or _add_ event, we will remove the corresponding edge from $t$ or add it to $t$.
- Finally, for each _get_ event we must check if the point lies on some vertical edge by performing a binary search in $vert$.
If the point doesn't lie on any vertical edge, we must find the answer for this query in $t$.
To do this, we again make a binary search.
In order to handle some degenerate cases (e.g. in case of the triangle $(0,~0)$, $(0,~2)$, $(1, 1)$ when we query the point $(0,~0)$), we must answer all _get_ events again after we processed all the events for this x-coordinate and choose the best of two answers.
Now let's choose a comparator for the set $t$.
This comparator should check if one edge doesn't lie above other for every x-coordinate they both cover. Suppose that we have two edges $(a, b)$ and $(c, d)$. Then the comparator is (in pseudocode):<br>
$val = sgn((b - a)\times(c - a)) + sgn((b - a)\times(d - a))$<br>
<b>if</b> $val \neq 0$<br>
<b>then return</b> $val > 0$<br>
$val = sgn((d - c)\times(a - c)) + sgn((d - c)\times(b - c))$<br>
<b>return</b> $val < 0$<br>
Now for every query we have the corresponding edge.
How to find the face?
If we couldn't find the edge it means that the point is in the outer face.
If the point belongs to the edge we found, the face is not unique.
Otherwise, there are two candidates - the faces that are bounded by this edge.
How to check which one is the answer? Note that the edge is not vertical.
Then the answer is the face that is above this edge.
Let's find such a face for each non-vertical edge.
Consider a counter-clockwise traversal of each face.
If during this traversal we increased x-coordinate while passing through the edge, then this face is the face we need to find for this edge.
## Notes
Actually, with persistent trees this approach can be used to answer the queries online.
## Implementation
The following code is implemented for integers, but it can be easily modified to work with doubles (by changing the compare methods and the point type).
This implementation assumes that the subdivision is correctly stored inside a [DCEL](https://en.wikipedia.org/wiki/Doubly_connected_edge_list) and the outer face is numbered $-1$.<br>
For each query a pair $(1, i)$ is returned if the point lies strictly inside the face number $i$, and a pair $(0, i)$ is returned if the point lies on the edge number $i$.
```{.cpp file=point-location}
typedef long long ll;
bool ge(const ll& a, const ll& b) { return a >= b; }
bool le(const ll& a, const ll& b) { return a <= b; }
bool eq(const ll& a, const ll& b) { return a == b; }
bool gt(const ll& a, const ll& b) { return a > b; }
bool lt(const ll& a, const ll& b) { return a < b; }
int sgn(const ll& x) { return le(x, 0) ? eq(x, 0) ? 0 : -1 : 1; }
struct pt {
ll x, y;
pt() {}
pt(ll _x, ll _y) : x(_x), y(_y) {}
pt operator-(const pt& a) const { return pt(x - a.x, y - a.y); }
ll dot(const pt& a) const { return x * a.x + y * a.y; }
ll dot(const pt& a, const pt& b) const { return (a - *this).dot(b - *this); }
ll cross(const pt& a) const { return x * a.y - y * a.x; }
ll cross(const pt& a, const pt& b) const { return (a - *this).cross(b - *this); }
bool operator==(const pt& a) const { return a.x == x && a.y == y; }
};
struct Edge {
pt l, r;
};
bool edge_cmp(Edge* edge1, Edge* edge2)
{
const pt a = edge1->l, b = edge1->r;
const pt c = edge2->l, d = edge2->r;
int val = sgn(a.cross(b, c)) + sgn(a.cross(b, d));
if (val != 0)
return val > 0;
val = sgn(c.cross(d, a)) + sgn(c.cross(d, b));
return val < 0;
}
enum EventType { DEL = 2, ADD = 3, GET = 1, VERT = 0 };
struct Event {
EventType type;
int pos;
bool operator<(const Event& event) const { return type < event.type; }
};
vector<Edge*> sweepline(vector<Edge*> planar, vector<pt> queries)
{
using pt_type = decltype(pt::x);
// collect all x-coordinates
auto s =
set<pt_type, std::function<bool(const pt_type&, const pt_type&)>>(lt);
for (pt p : queries)
s.insert(p.x);
for (Edge* e : planar) {
s.insert(e->l.x);
s.insert(e->r.x);
}
// map all x-coordinates to ids
int cid = 0;
auto id =
map<pt_type, int, std::function<bool(const pt_type&, const pt_type&)>>(
lt);
for (auto x : s)
id[x] = cid++;
// create events
auto t = set<Edge*, decltype(*edge_cmp)>(edge_cmp);
auto vert_cmp = [](const pair<pt_type, int>& l,
const pair<pt_type, int>& r) {
if (!eq(l.first, r.first))
return lt(l.first, r.first);
return l.second < r.second;
};
auto vert = set<pair<pt_type, int>, decltype(vert_cmp)>(vert_cmp);
vector<vector<Event>> events(cid);
for (int i = 0; i < (int)queries.size(); i++) {
int x = id[queries[i].x];
events[x].push_back(Event{GET, i});
}
for (int i = 0; i < (int)planar.size(); i++) {
int lx = id[planar[i]->l.x], rx = id[planar[i]->r.x];
if (lx > rx) {
swap(lx, rx);
swap(planar[i]->l, planar[i]->r);
}
if (lx == rx) {
events[lx].push_back(Event{VERT, i});
} else {
events[lx].push_back(Event{ADD, i});
events[rx].push_back(Event{DEL, i});
}
}
// perform sweep line algorithm
vector<Edge*> ans(queries.size(), nullptr);
for (int x = 0; x < cid; x++) {
sort(events[x].begin(), events[x].end());
vert.clear();
for (Event event : events[x]) {
if (event.type == DEL) {
t.erase(planar[event.pos]);
}
if (event.type == VERT) {
vert.insert(make_pair(
min(planar[event.pos]->l.y, planar[event.pos]->r.y),
event.pos));
}
if (event.type == ADD) {
t.insert(planar[event.pos]);
}
if (event.type == GET) {
auto jt = vert.upper_bound(
make_pair(queries[event.pos].y, planar.size()));
if (jt != vert.begin()) {
--jt;
int i = jt->second;
if (ge(max(planar[i]->l.y, planar[i]->r.y),
queries[event.pos].y)) {
ans[event.pos] = planar[i];
continue;
}
}
Edge* e = new Edge;
e->l = e->r = queries[event.pos];
auto it = t.upper_bound(e);
if (it != t.begin())
ans[event.pos] = *(--it);
delete e;
}
}
for (Event event : events[x]) {
if (event.type != GET)
continue;
if (ans[event.pos] != nullptr &&
eq(ans[event.pos]->l.x, ans[event.pos]->r.x))
continue;
Edge* e = new Edge;
e->l = e->r = queries[event.pos];
auto it = t.upper_bound(e);
delete e;
if (it == t.begin())
e = nullptr;
else
e = *(--it);
if (ans[event.pos] == nullptr) {
ans[event.pos] = e;
continue;
}
if (e == nullptr)
continue;
if (e == ans[event.pos])
continue;
if (id[ans[event.pos]->r.x] == x) {
if (id[e->l.x] == x) {
if (gt(e->l.y, ans[event.pos]->r.y))
ans[event.pos] = e;
}
} else {
ans[event.pos] = e;
}
}
}
return ans;
}
struct DCEL {
struct Edge {
pt origin;
Edge* nxt = nullptr;
Edge* twin = nullptr;
int face;
};
vector<Edge*> body;
};
vector<pair<int, int>> point_location(DCEL planar, vector<pt> queries)
{
vector<pair<int, int>> ans(queries.size());
vector<Edge*> planar2;
map<intptr_t, int> pos;
map<intptr_t, int> added_on;
int n = planar.body.size();
for (int i = 0; i < n; i++) {
if (planar.body[i]->face > planar.body[i]->twin->face)
continue;
Edge* e = new Edge;
e->l = planar.body[i]->origin;
e->r = planar.body[i]->twin->origin;
added_on[(intptr_t)e] = i;
pos[(intptr_t)e] =
lt(planar.body[i]->origin.x, planar.body[i]->twin->origin.x)
? planar.body[i]->face
: planar.body[i]->twin->face;
planar2.push_back(e);
}
auto res = sweepline(planar2, queries);
for (int i = 0; i < (int)queries.size(); i++) {
if (res[i] == nullptr) {
ans[i] = make_pair(1, -1);
continue;
}
pt p = queries[i];
pt l = res[i]->l, r = res[i]->r;
if (eq(p.cross(l, r), 0) && le(p.dot(l, r), 0)) {
ans[i] = make_pair(0, added_on[(intptr_t)res[i]]);
continue;
}
ans[i] = make_pair(1, pos[(intptr_t)res[i]]);
}
for (auto e : planar2)
delete e;
return ans;
}
```
## Problems
* [TIMUS 1848 Fly Hunt](http://acm.timus.ru/problem.aspx?space=1&num=1848&locale=en)
* [UVA 12310 Point Location](https://onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=297&page=show_problem&problem=3732)
|
Point location in $O(log n)$
|
End of preview. Expand
in Data Studio
README.md exists but content is empty.
- Downloads last month
- 13