problem
stringlengths 1.19k
65.4k
| solution
stringlengths 1.19k
67.5k
| topic
stringlengths 5
80
|
|---|---|---|
---
title
intersecting_segments
---
# Search for a pair of intersecting segments
Given $n$ line segments on the plane. It is required to check whether at least two of them intersect with each other.
If the answer is yes, then print this pair of intersecting segments; it is enough to choose any of them among several answers.
The naive solution algorithm is to iterate over all pairs of segments in $O(n^2)$ and check for each pair whether they intersect or not. This article describes an algorithm with the runtime time $O(n \log n)$, which is based on the **sweep line algorithm**.
## Algorithm
Let's draw a vertical line $x = -\infty$ mentally and start moving this line to the right.
In the course of its movement, this line will meet with segments, and at each time a segment intersect with our line it intersects in exactly one point (we will assume that there are no vertical segments).
<center></center>
Thus, for each segment, at some point in time, its point will appear on the sweep line, then with the movement of the line, this point will move, and finally, at some point, the segment will disappear from the line.
We are interested in the **relative order of the segments** along the vertical.
Namely, we will store a list of segments crossing the sweep line at a given time, where the segments will be sorted by their $y$-coordinate on the sweep line.
<center></center>
This order is interesting because intersecting segments will have the same $y$-coordinate at least at one time:
<center></center>
We formulate key statements:
- To find an intersecting pair, it is sufficient to consider **only adjacent segments** at each fixed position of the sweep line.
- It is enough to consider the sweep line not in all possible real positions $(-\infty \ldots +\infty)$, but **only in those positions when new segments appear or old ones disappear**. In other words, it is enough to limit yourself only to the positions equal to the abscissas of the end points of the segments.
- When a new line segment appears, it is enough to **insert** it to the desired location in the list obtained for the previous sweep line. We should only check for the intersection of the **added segment with its immediate neighbors in the list above and below**.
- If the segment disappears, it is enough to **remove** it from the current list. After that, it is necessary **check for the intersection of the upper and lower neighbors in the list**.
- Other changes in the sequence of segments in the list, except for those described, do not exist. No other intersection checks are required.
To understand the truth of these statements, the following remarks are sufficient:
- Two disjoint segments never change their **relative order**.<br>
In fact, if one segment was first higher than the other, and then became lower, then between these two moments there was an intersection of these two segments.
- Two non-intersecting segments also cannot have the same $y$-coordinates.
- From this it follows that at the moment of the segment appearance we can find the position for this segment in the queue, and we will not have to rearrange this segment in the queue any more: **its order relative to other segments in the queue will not change**.
- Two intersecting segments at the moment of their intersection point will be neighbors of each other in the queue.
- Therefore, for finding pairs of intersecting line segments is sufficient to check the intersection of all and only those pairs of segments that sometime during the movement of the sweep line at least once were neighbors to each other. <br>
It is easy to notice that it is enough only to check the added segment with its upper and lower neighbors, as well as when removing the segment — its upper and lower neighbors (which after removal will become neighbors of each other).<br>
- It should be noted that at a fixed position of the sweep line, we must **first add all the segments** that start at this x-coordinate, and only **then remove all the segments** that end here.<br>
Thus, we do not miss the intersection of segments on the vertex: i.e. such cases when two segments have a common vertex.
- Note that **vertical segments** do not actually affect the correctness of the algorithm.<br>
These segments are distinguished by the fact that they appear and disappear at the same time. However, due to the previous comment, we know that all segments will be added to the queue first, and only then they will be deleted. Therefore, if the vertical segment intersects with some other segment opened at that moment (including the vertical one), it will be detected.<br>
**In what place of the queue to place vertical segments?** After all, a vertical segment does not have one specific $y$-coordinate, it extends for an entire segment along the $y$-coordinate. However, it is easy to understand that any coordinate from this segment can be taken as a $y$-coordinate.
Thus, the entire algorithm will perform no more than $2n$ tests on the intersection of a pair of segments, and will perform $O(n)$ operations with a queue of segments ($O(1)$ operations at the time of appearance and disappearance of each segment).
The final **asymptotic behavior of the algorithm** is thus $O(n \log n)$.
## Implementation
We present the full implementation of the described algorithm:
```cpp
const double EPS = 1E-9;
struct pt {
double x, y;
};
struct seg {
pt p, q;
int id;
double get_y(double x) const {
if (abs(p.x - q.x) < EPS)
return p.y;
return p.y + (q.y - p.y) * (x - p.x) / (q.x - p.x);
}
};
bool intersect1d(double l1, double r1, double l2, double r2) {
if (l1 > r1)
swap(l1, r1);
if (l2 > r2)
swap(l2, r2);
return max(l1, l2) <= min(r1, r2) + EPS;
}
int vec(const pt& a, const pt& b, const pt& c) {
double s = (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
return abs(s) < EPS ? 0 : s > 0 ? +1 : -1;
}
bool intersect(const seg& a, const seg& b)
{
return intersect1d(a.p.x, a.q.x, b.p.x, b.q.x) &&
intersect1d(a.p.y, a.q.y, b.p.y, b.q.y) &&
vec(a.p, a.q, b.p) * vec(a.p, a.q, b.q) <= 0 &&
vec(b.p, b.q, a.p) * vec(b.p, b.q, a.q) <= 0;
}
bool operator<(const seg& a, const seg& b)
{
double x = max(min(a.p.x, a.q.x), min(b.p.x, b.q.x));
return a.get_y(x) < b.get_y(x) - EPS;
}
struct event {
double x;
int tp, id;
event() {}
event(double x, int tp, int id) : x(x), tp(tp), id(id) {}
bool operator<(const event& e) const {
if (abs(x - e.x) > EPS)
return x < e.x;
return tp > e.tp;
}
};
set<seg> s;
vector<set<seg>::iterator> where;
set<seg>::iterator prev(set<seg>::iterator it) {
return it == s.begin() ? s.end() : --it;
}
set<seg>::iterator next(set<seg>::iterator it) {
return ++it;
}
pair<int, int> solve(const vector<seg>& a) {
int n = (int)a.size();
vector<event> e;
for (int i = 0; i < n; ++i) {
e.push_back(event(min(a[i].p.x, a[i].q.x), +1, i));
e.push_back(event(max(a[i].p.x, a[i].q.x), -1, i));
}
sort(e.begin(), e.end());
s.clear();
where.resize(a.size());
for (size_t i = 0; i < e.size(); ++i) {
int id = e[i].id;
if (e[i].tp == +1) {
set<seg>::iterator nxt = s.lower_bound(a[id]), prv = prev(nxt);
if (nxt != s.end() && intersect(*nxt, a[id]))
return make_pair(nxt->id, id);
if (prv != s.end() && intersect(*prv, a[id]))
return make_pair(prv->id, id);
where[id] = s.insert(nxt, a[id]);
} else {
set<seg>::iterator nxt = next(where[id]), prv = prev(where[id]);
if (nxt != s.end() && prv != s.end() && intersect(*nxt, *prv))
return make_pair(prv->id, nxt->id);
s.erase(where[id]);
}
}
return make_pair(-1, -1);
}
```
The main function here is `solve()`, which returns the number of found intersecting segments, or $(-1, -1)$, if there are no intersections.
Checking for the intersection of two segments is carried out by the `intersect ()` function, using an **algorithm based on the oriented area of the triangle**.
The queue of segments is the global variable `s`, a `set<event>`. Iterators that specify the position of each segment in the queue (for convenient removal of segments from the queue) are stored in the global array `where`.
Two auxiliary functions `prev()` and `next()` are also introduced, which return iterators to the previous and next elements (or `end()`, if one does not exist).
The constant `EPS` denotes the error of comparing two real numbers (it is mainly used when checking two segments for intersection).
|
---
title
intersecting_segments
---
# Search for a pair of intersecting segments
Given $n$ line segments on the plane. It is required to check whether at least two of them intersect with each other.
If the answer is yes, then print this pair of intersecting segments; it is enough to choose any of them among several answers.
The naive solution algorithm is to iterate over all pairs of segments in $O(n^2)$ and check for each pair whether they intersect or not. This article describes an algorithm with the runtime time $O(n \log n)$, which is based on the **sweep line algorithm**.
## Algorithm
Let's draw a vertical line $x = -\infty$ mentally and start moving this line to the right.
In the course of its movement, this line will meet with segments, and at each time a segment intersect with our line it intersects in exactly one point (we will assume that there are no vertical segments).
<center></center>
Thus, for each segment, at some point in time, its point will appear on the sweep line, then with the movement of the line, this point will move, and finally, at some point, the segment will disappear from the line.
We are interested in the **relative order of the segments** along the vertical.
Namely, we will store a list of segments crossing the sweep line at a given time, where the segments will be sorted by their $y$-coordinate on the sweep line.
<center></center>
This order is interesting because intersecting segments will have the same $y$-coordinate at least at one time:
<center></center>
We formulate key statements:
- To find an intersecting pair, it is sufficient to consider **only adjacent segments** at each fixed position of the sweep line.
- It is enough to consider the sweep line not in all possible real positions $(-\infty \ldots +\infty)$, but **only in those positions when new segments appear or old ones disappear**. In other words, it is enough to limit yourself only to the positions equal to the abscissas of the end points of the segments.
- When a new line segment appears, it is enough to **insert** it to the desired location in the list obtained for the previous sweep line. We should only check for the intersection of the **added segment with its immediate neighbors in the list above and below**.
- If the segment disappears, it is enough to **remove** it from the current list. After that, it is necessary **check for the intersection of the upper and lower neighbors in the list**.
- Other changes in the sequence of segments in the list, except for those described, do not exist. No other intersection checks are required.
To understand the truth of these statements, the following remarks are sufficient:
- Two disjoint segments never change their **relative order**.<br>
In fact, if one segment was first higher than the other, and then became lower, then between these two moments there was an intersection of these two segments.
- Two non-intersecting segments also cannot have the same $y$-coordinates.
- From this it follows that at the moment of the segment appearance we can find the position for this segment in the queue, and we will not have to rearrange this segment in the queue any more: **its order relative to other segments in the queue will not change**.
- Two intersecting segments at the moment of their intersection point will be neighbors of each other in the queue.
- Therefore, for finding pairs of intersecting line segments is sufficient to check the intersection of all and only those pairs of segments that sometime during the movement of the sweep line at least once were neighbors to each other. <br>
It is easy to notice that it is enough only to check the added segment with its upper and lower neighbors, as well as when removing the segment — its upper and lower neighbors (which after removal will become neighbors of each other).<br>
- It should be noted that at a fixed position of the sweep line, we must **first add all the segments** that start at this x-coordinate, and only **then remove all the segments** that end here.<br>
Thus, we do not miss the intersection of segments on the vertex: i.e. such cases when two segments have a common vertex.
- Note that **vertical segments** do not actually affect the correctness of the algorithm.<br>
These segments are distinguished by the fact that they appear and disappear at the same time. However, due to the previous comment, we know that all segments will be added to the queue first, and only then they will be deleted. Therefore, if the vertical segment intersects with some other segment opened at that moment (including the vertical one), it will be detected.<br>
**In what place of the queue to place vertical segments?** After all, a vertical segment does not have one specific $y$-coordinate, it extends for an entire segment along the $y$-coordinate. However, it is easy to understand that any coordinate from this segment can be taken as a $y$-coordinate.
Thus, the entire algorithm will perform no more than $2n$ tests on the intersection of a pair of segments, and will perform $O(n)$ operations with a queue of segments ($O(1)$ operations at the time of appearance and disappearance of each segment).
The final **asymptotic behavior of the algorithm** is thus $O(n \log n)$.
## Implementation
We present the full implementation of the described algorithm:
```cpp
const double EPS = 1E-9;
struct pt {
double x, y;
};
struct seg {
pt p, q;
int id;
double get_y(double x) const {
if (abs(p.x - q.x) < EPS)
return p.y;
return p.y + (q.y - p.y) * (x - p.x) / (q.x - p.x);
}
};
bool intersect1d(double l1, double r1, double l2, double r2) {
if (l1 > r1)
swap(l1, r1);
if (l2 > r2)
swap(l2, r2);
return max(l1, l2) <= min(r1, r2) + EPS;
}
int vec(const pt& a, const pt& b, const pt& c) {
double s = (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
return abs(s) < EPS ? 0 : s > 0 ? +1 : -1;
}
bool intersect(const seg& a, const seg& b)
{
return intersect1d(a.p.x, a.q.x, b.p.x, b.q.x) &&
intersect1d(a.p.y, a.q.y, b.p.y, b.q.y) &&
vec(a.p, a.q, b.p) * vec(a.p, a.q, b.q) <= 0 &&
vec(b.p, b.q, a.p) * vec(b.p, b.q, a.q) <= 0;
}
bool operator<(const seg& a, const seg& b)
{
double x = max(min(a.p.x, a.q.x), min(b.p.x, b.q.x));
return a.get_y(x) < b.get_y(x) - EPS;
}
struct event {
double x;
int tp, id;
event() {}
event(double x, int tp, int id) : x(x), tp(tp), id(id) {}
bool operator<(const event& e) const {
if (abs(x - e.x) > EPS)
return x < e.x;
return tp > e.tp;
}
};
set<seg> s;
vector<set<seg>::iterator> where;
set<seg>::iterator prev(set<seg>::iterator it) {
return it == s.begin() ? s.end() : --it;
}
set<seg>::iterator next(set<seg>::iterator it) {
return ++it;
}
pair<int, int> solve(const vector<seg>& a) {
int n = (int)a.size();
vector<event> e;
for (int i = 0; i < n; ++i) {
e.push_back(event(min(a[i].p.x, a[i].q.x), +1, i));
e.push_back(event(max(a[i].p.x, a[i].q.x), -1, i));
}
sort(e.begin(), e.end());
s.clear();
where.resize(a.size());
for (size_t i = 0; i < e.size(); ++i) {
int id = e[i].id;
if (e[i].tp == +1) {
set<seg>::iterator nxt = s.lower_bound(a[id]), prv = prev(nxt);
if (nxt != s.end() && intersect(*nxt, a[id]))
return make_pair(nxt->id, id);
if (prv != s.end() && intersect(*prv, a[id]))
return make_pair(prv->id, id);
where[id] = s.insert(nxt, a[id]);
} else {
set<seg>::iterator nxt = next(where[id]), prv = prev(where[id]);
if (nxt != s.end() && prv != s.end() && intersect(*nxt, *prv))
return make_pair(prv->id, nxt->id);
s.erase(where[id]);
}
}
return make_pair(-1, -1);
}
```
The main function here is `solve()`, which returns the number of found intersecting segments, or $(-1, -1)$, if there are no intersections.
Checking for the intersection of two segments is carried out by the `intersect ()` function, using an **algorithm based on the oriented area of the triangle**.
The queue of segments is the global variable `s`, a `set<event>`. Iterators that specify the position of each segment in the queue (for convenient removal of segments from the queue) are stored in the global array `where`.
Two auxiliary functions `prev()` and `next()` are also introduced, which return iterators to the previous and next elements (or `end()`, if one does not exist).
The constant `EPS` denotes the error of comparing two real numbers (it is mainly used when checking two segments for intersection).
## Problems
* [TIMUS 1469 No Smoking!](https://acm.timus.ru/problem.aspx?space=1&num=1469)
|
Search for a pair of intersecting segments
|
---
title
segments_intersection_checking
---
# Check if two segments intersect
You are given two segments $(a, b)$ and $(c, d)$.
You have to check if they intersect.
Of course, you may find their intersection and check if it isn't empty, but this can't be done in integers for segments with integer coordinates.
The approach described here can work in integers.
## Algorithm
Firstly, consider the case when the segments are part of the same line.
In this case it is sufficient to check if their projections on $Ox$ and $Oy$ intersect.
In the other case $a$ and $b$ must not lie on the same side of line $(c, d)$, and $c$ and $d$ must not lie on the same side of line $(a, b)$.
It can be checked with a couple of cross products.
## Implementation
The given algorithm is implemented for integer points. Of course, it can be easily modified to work with doubles.
```{.cpp file=check-segments-inter}
struct pt {
long long x, y;
pt() {}
pt(long long _x, long long _y) : x(_x), y(_y) {}
pt operator-(const pt& p) const { return pt(x - p.x, y - p.y); }
long long cross(const pt& p) const { return x * p.y - y * p.x; }
long long cross(const pt& a, const pt& b) const { return (a - *this).cross(b - *this); }
};
int sgn(const long long& x) { return x >= 0 ? x ? 1 : 0 : -1; }
bool inter1(long long a, long long b, long long c, long long d) {
if (a > b)
swap(a, b);
if (c > d)
swap(c, d);
return max(a, c) <= min(b, d);
}
bool check_inter(const pt& a, const pt& b, const pt& c, const pt& d) {
if (c.cross(a, d) == 0 && c.cross(b, d) == 0)
return inter1(a.x, b.x, c.x, d.x) && inter1(a.y, b.y, c.y, d.y);
return sgn(a.cross(b, c)) != sgn(a.cross(b, d)) &&
sgn(c.cross(d, a)) != sgn(c.cross(d, b));
}
```
|
---
title
segments_intersection_checking
---
# Check if two segments intersect
You are given two segments $(a, b)$ and $(c, d)$.
You have to check if they intersect.
Of course, you may find their intersection and check if it isn't empty, but this can't be done in integers for segments with integer coordinates.
The approach described here can work in integers.
## Algorithm
Firstly, consider the case when the segments are part of the same line.
In this case it is sufficient to check if their projections on $Ox$ and $Oy$ intersect.
In the other case $a$ and $b$ must not lie on the same side of line $(c, d)$, and $c$ and $d$ must not lie on the same side of line $(a, b)$.
It can be checked with a couple of cross products.
## Implementation
The given algorithm is implemented for integer points. Of course, it can be easily modified to work with doubles.
```{.cpp file=check-segments-inter}
struct pt {
long long x, y;
pt() {}
pt(long long _x, long long _y) : x(_x), y(_y) {}
pt operator-(const pt& p) const { return pt(x - p.x, y - p.y); }
long long cross(const pt& p) const { return x * p.y - y * p.x; }
long long cross(const pt& a, const pt& b) const { return (a - *this).cross(b - *this); }
};
int sgn(const long long& x) { return x >= 0 ? x ? 1 : 0 : -1; }
bool inter1(long long a, long long b, long long c, long long d) {
if (a > b)
swap(a, b);
if (c > d)
swap(c, d);
return max(a, c) <= min(b, d);
}
bool check_inter(const pt& a, const pt& b, const pt& c, const pt& d) {
if (c.cross(a, d) == 0 && c.cross(b, d) == 0)
return inter1(a.x, b.x, c.x, d.x) && inter1(a.y, b.y, c.y, d.y);
return sgn(a.cross(b, c)) != sgn(a.cross(b, d)) &&
sgn(c.cross(d, a)) != sgn(c.cross(d, b));
}
```
|
Check if two segments intersect
|
---
title
- Original
---
# Convex hull trick and Li Chao tree
Consider the following problem. There are $n$ cities. You want to travel from city $1$ to city $n$ by car. To do this you have to buy some gasoline. It is known that a liter of gasoline costs $cost_k$ in the $k^{th}$ city. Initially your fuel tank is empty and you spend one liter of gasoline per kilometer. Cities are located on the same line in ascending order with $k^{th}$ city having coordinate $x_k$. Also you have to pay $toll_k$ to enter $k^{th}$ city. Your task is to make the trip with minimum possible cost. It's obvious that the solution can be calculated via dynamic programming:
$$dp_i = toll_i+\min\limits_{j<i}(cost_j \cdot (x_i - x_j)+dp_j)$$
Naive approach will give you $O(n^2)$ complexity which can be improved to $O(n \log n)$ or $O(n \log [C \varepsilon^{-1}])$ where $C$ is largest possible $|x_i|$ and $\varepsilon$ is precision with which $x_i$ is considered ($\varepsilon = 1$ for integers which is usually the case). To do this one should note that the problem can be reduced to adding linear functions $k \cdot x + b$ to the set and finding minimum value of the functions in some particular point $x$. There are two main approaches one can use here.
## Convex hull trick
The idea of this approach is to maintain a lower convex hull of linear functions.
Actually it would be a bit more convenient to consider them not as linear functions, but as points $(k;b)$ on the plane such that we will have to find the point which has the least dot product with a given point $(x;1)$, that is, for this point $kx+b$ is minimized which is the same as initial problem.
Such minimum will necessarily be on lower convex envelope of these points as can be seen below:
<center>  </center>
One has to keep points on the convex hull and normal vectors of the hull's edges.
When you have a $(x;1)$ query you'll have to find the normal vector closest to it in terms of angles between them, then the optimum linear function will correspond to one of its endpoints.
To see that, one should note that points having a constant dot product with $(x;1)$ lie on a line which is orthogonal to $(x;1)$, so the optimum linear function will be the one in which tangent to convex hull which is collinear with normal to $(x;1)$ touches the hull.
This point is the one such that normals of edges lying to the left and to the right of it are headed in different sides of $(x;1)$.
This approach is useful when queries of adding linear functions are monotone in terms of $k$ or if we work offline, i.e. we may firstly add all linear functions and answer queries afterwards.
So we cannot solve the cities/gasoline problems using this way.
That would require handling online queries.
When it comes to deal with online queries however, things will go tough and one will have to use some kind of set data structure to implement a proper convex hull.
Online approach will however not be considered in this article due to its hardness and because second approach (which is Li Chao tree) allows to solve the problem way more simply.
Worth mentioning that one can still use this approach online without complications by square-root-decomposition.
That is, rebuild convex hull from scratch each $\sqrt n$ new lines.
To implement this approach one should begin with some geometric utility functions, here we suggest to use the C++ complex number type.
```cpp
typedef int ftype;
typedef complex<ftype> point;
#define x real
#define y imag
ftype dot(point a, point b) {
return (conj(a) * b).x();
}
ftype cross(point a, point b) {
return (conj(a) * b).y();
}
```
Here we will assume that when linear functions are added, their $k$ only increases and we want to find minimum values.
We will keep points in vector $hull$ and normal vectors in vector $vecs$.
When we add a new point, we have to look at the angle formed between last edge in convex hull and vector from last point in convex hull to new point.
This angle has to be directed counter-clockwise, that is the dot product of the last normal vector in the hull (directed inside hull) and the vector from the last point to the new one has to be non-negative.
As long as this isn't true, we should erase the last point in the convex hull alongside with the corresponding edge.
```cpp
vector<point> hull, vecs;
void add_line(ftype k, ftype b) {
point nw = {k, b};
while(!vecs.empty() && dot(vecs.back(), nw - hull.back()) < 0) {
hull.pop_back();
vecs.pop_back();
}
if(!hull.empty()) {
vecs.push_back(1i * (nw - hull.back()));
}
hull.push_back(nw);
}
```
Now to get the minimum value in some point we will find the first normal vector in the convex hull that is directed counter-clockwise from $(x;1)$. The left endpoint of such edge will be the answer. To check if vector $a$ is not directed counter-clockwise of vector $b$, we should check if their cross product $[a,b]$ is positive.
```cpp
int get(ftype x) {
point query = {x, 1};
auto it = lower_bound(vecs.begin(), vecs.end(), query, [](point a, point b) {
return cross(a, b) > 0;
});
return dot(query, hull[it - vecs.begin()]);
}
```
## Li Chao tree
Assume you're given a set of functions such that each two can intersect at most once. Let's keep in each vertex of a segment tree some function in such way, that if we go from root to the leaf it will be guaranteed that one of the functions we met on the path will be the one giving the minimum value in that leaf. Let's see how to construct it.
Assume we're in some vertex corresponding to half-segment $[l,r)$ and the function $f_{old}$ is kept there and we add the function $f_{new}$. Then the intersection point will be either in $[l;m)$ or in $[m;r)$ where $m=\left\lfloor\tfrac{l+r}{2}\right\rfloor$. We can efficiently find that out by comparing the values of the functions in points $l$ and $m$. If the dominating function changes, then it is in $[l;m)$ otherwise it is in $[m;r)$. Now for the half of the segment with no intersection we will pick the lower function and write it in the current vertex. You can see that it will always be the one which is lower in point $m$. After that we recursively go to the other half of the segment with the function which was the upper one. As you can see this will keep correctness on the first half of segment and in the other one correctness will be maintained during the recursive call. Thus we can add functions and check the minimum value in the point in $O(\log [C\varepsilon^{-1}])$.
Here is the illustration of what is going on in the vertex when we add new function:
<center></center>
Let's go to implementation now. Once again we will use complex numbers to keep linear functions.
```{.cpp file=lichaotree_line_definition}
typedef long long ftype;
typedef complex<ftype> point;
#define x real
#define y imag
ftype dot(point a, point b) {
return (conj(a) * b).x();
}
ftype f(point a, ftype x) {
return dot(a, {x, 1});
}
```
We will keep functions in the array $line$ and use binary indexing of the segment tree. If you want to use it on large numbers or doubles, you should use a dynamic segment tree.
The segment tree should be initialized with default values, e.g. with lines $0x + \infty$.
```{.cpp file=lichaotree_addline}
const int maxn = 2e5;
point line[4 * maxn];
void add_line(point nw, int v = 1, int l = 0, int r = maxn) {
int m = (l + r) / 2;
bool lef = f(nw, l) < f(line[v], l);
bool mid = f(nw, m) < f(line[v], m);
if(mid) {
swap(line[v], nw);
}
if(r - l == 1) {
return;
} else if(lef != mid) {
add_line(nw, 2 * v, l, m);
} else {
add_line(nw, 2 * v + 1, m, r);
}
}
```
Now to get the minimum in some point $x$ we simply choose the minimum value along the path to the point.
```{.cpp file=lichaotree_getminimum}
ftype get(int x, int v = 1, int l = 0, int r = maxn) {
int m = (l + r) / 2;
if(r - l == 1) {
return f(line[v], x);
} else if(x < m) {
return min(f(line[v], x), get(x, 2 * v, l, m));
} else {
return min(f(line[v], x), get(x, 2 * v + 1, m, r));
}
}
```
|
---
title
- Original
---
# Convex hull trick and Li Chao tree
Consider the following problem. There are $n$ cities. You want to travel from city $1$ to city $n$ by car. To do this you have to buy some gasoline. It is known that a liter of gasoline costs $cost_k$ in the $k^{th}$ city. Initially your fuel tank is empty and you spend one liter of gasoline per kilometer. Cities are located on the same line in ascending order with $k^{th}$ city having coordinate $x_k$. Also you have to pay $toll_k$ to enter $k^{th}$ city. Your task is to make the trip with minimum possible cost. It's obvious that the solution can be calculated via dynamic programming:
$$dp_i = toll_i+\min\limits_{j<i}(cost_j \cdot (x_i - x_j)+dp_j)$$
Naive approach will give you $O(n^2)$ complexity which can be improved to $O(n \log n)$ or $O(n \log [C \varepsilon^{-1}])$ where $C$ is largest possible $|x_i|$ and $\varepsilon$ is precision with which $x_i$ is considered ($\varepsilon = 1$ for integers which is usually the case). To do this one should note that the problem can be reduced to adding linear functions $k \cdot x + b$ to the set and finding minimum value of the functions in some particular point $x$. There are two main approaches one can use here.
## Convex hull trick
The idea of this approach is to maintain a lower convex hull of linear functions.
Actually it would be a bit more convenient to consider them not as linear functions, but as points $(k;b)$ on the plane such that we will have to find the point which has the least dot product with a given point $(x;1)$, that is, for this point $kx+b$ is minimized which is the same as initial problem.
Such minimum will necessarily be on lower convex envelope of these points as can be seen below:
<center>  </center>
One has to keep points on the convex hull and normal vectors of the hull's edges.
When you have a $(x;1)$ query you'll have to find the normal vector closest to it in terms of angles between them, then the optimum linear function will correspond to one of its endpoints.
To see that, one should note that points having a constant dot product with $(x;1)$ lie on a line which is orthogonal to $(x;1)$, so the optimum linear function will be the one in which tangent to convex hull which is collinear with normal to $(x;1)$ touches the hull.
This point is the one such that normals of edges lying to the left and to the right of it are headed in different sides of $(x;1)$.
This approach is useful when queries of adding linear functions are monotone in terms of $k$ or if we work offline, i.e. we may firstly add all linear functions and answer queries afterwards.
So we cannot solve the cities/gasoline problems using this way.
That would require handling online queries.
When it comes to deal with online queries however, things will go tough and one will have to use some kind of set data structure to implement a proper convex hull.
Online approach will however not be considered in this article due to its hardness and because second approach (which is Li Chao tree) allows to solve the problem way more simply.
Worth mentioning that one can still use this approach online without complications by square-root-decomposition.
That is, rebuild convex hull from scratch each $\sqrt n$ new lines.
To implement this approach one should begin with some geometric utility functions, here we suggest to use the C++ complex number type.
```cpp
typedef int ftype;
typedef complex<ftype> point;
#define x real
#define y imag
ftype dot(point a, point b) {
return (conj(a) * b).x();
}
ftype cross(point a, point b) {
return (conj(a) * b).y();
}
```
Here we will assume that when linear functions are added, their $k$ only increases and we want to find minimum values.
We will keep points in vector $hull$ and normal vectors in vector $vecs$.
When we add a new point, we have to look at the angle formed between last edge in convex hull and vector from last point in convex hull to new point.
This angle has to be directed counter-clockwise, that is the dot product of the last normal vector in the hull (directed inside hull) and the vector from the last point to the new one has to be non-negative.
As long as this isn't true, we should erase the last point in the convex hull alongside with the corresponding edge.
```cpp
vector<point> hull, vecs;
void add_line(ftype k, ftype b) {
point nw = {k, b};
while(!vecs.empty() && dot(vecs.back(), nw - hull.back()) < 0) {
hull.pop_back();
vecs.pop_back();
}
if(!hull.empty()) {
vecs.push_back(1i * (nw - hull.back()));
}
hull.push_back(nw);
}
```
Now to get the minimum value in some point we will find the first normal vector in the convex hull that is directed counter-clockwise from $(x;1)$. The left endpoint of such edge will be the answer. To check if vector $a$ is not directed counter-clockwise of vector $b$, we should check if their cross product $[a,b]$ is positive.
```cpp
int get(ftype x) {
point query = {x, 1};
auto it = lower_bound(vecs.begin(), vecs.end(), query, [](point a, point b) {
return cross(a, b) > 0;
});
return dot(query, hull[it - vecs.begin()]);
}
```
## Li Chao tree
Assume you're given a set of functions such that each two can intersect at most once. Let's keep in each vertex of a segment tree some function in such way, that if we go from root to the leaf it will be guaranteed that one of the functions we met on the path will be the one giving the minimum value in that leaf. Let's see how to construct it.
Assume we're in some vertex corresponding to half-segment $[l,r)$ and the function $f_{old}$ is kept there and we add the function $f_{new}$. Then the intersection point will be either in $[l;m)$ or in $[m;r)$ where $m=\left\lfloor\tfrac{l+r}{2}\right\rfloor$. We can efficiently find that out by comparing the values of the functions in points $l$ and $m$. If the dominating function changes, then it is in $[l;m)$ otherwise it is in $[m;r)$. Now for the half of the segment with no intersection we will pick the lower function and write it in the current vertex. You can see that it will always be the one which is lower in point $m$. After that we recursively go to the other half of the segment with the function which was the upper one. As you can see this will keep correctness on the first half of segment and in the other one correctness will be maintained during the recursive call. Thus we can add functions and check the minimum value in the point in $O(\log [C\varepsilon^{-1}])$.
Here is the illustration of what is going on in the vertex when we add new function:
<center></center>
Let's go to implementation now. Once again we will use complex numbers to keep linear functions.
```{.cpp file=lichaotree_line_definition}
typedef long long ftype;
typedef complex<ftype> point;
#define x real
#define y imag
ftype dot(point a, point b) {
return (conj(a) * b).x();
}
ftype f(point a, ftype x) {
return dot(a, {x, 1});
}
```
We will keep functions in the array $line$ and use binary indexing of the segment tree. If you want to use it on large numbers or doubles, you should use a dynamic segment tree.
The segment tree should be initialized with default values, e.g. with lines $0x + \infty$.
```{.cpp file=lichaotree_addline}
const int maxn = 2e5;
point line[4 * maxn];
void add_line(point nw, int v = 1, int l = 0, int r = maxn) {
int m = (l + r) / 2;
bool lef = f(nw, l) < f(line[v], l);
bool mid = f(nw, m) < f(line[v], m);
if(mid) {
swap(line[v], nw);
}
if(r - l == 1) {
return;
} else if(lef != mid) {
add_line(nw, 2 * v, l, m);
} else {
add_line(nw, 2 * v + 1, m, r);
}
}
```
Now to get the minimum in some point $x$ we simply choose the minimum value along the path to the point.
```{.cpp file=lichaotree_getminimum}
ftype get(int x, int v = 1, int l = 0, int r = maxn) {
int m = (l + r) / 2;
if(r - l == 1) {
return f(line[v], x);
} else if(x < m) {
return min(f(line[v], x), get(x, 2 * v, l, m));
} else {
return min(f(line[v], x), get(x, 2 * v + 1, m, r));
}
}
```
## Problems
* [Codebreaker - TROUBLES](https://codeforces.com/gym/103536/problem/B) (simple application of Convex Hull Trick after a couple of observations)
* [CS Academy - Squared Ends](https://csacademy.com/contest/archive/task/squared-ends)
* [Codeforces - Escape Through Leaf](http://codeforces.com/contest/932/problem/F)
* [CodeChef - Polynomials](https://www.codechef.com/NOV17/problems/POLY)
* [Codeforces - Kalila and Dimna in the Logging Industry](https://codeforces.com/problemset/problem/319/C)
* [Codeforces - Product Sum](https://codeforces.com/problemset/problem/631/E)
* [Codeforces - Bear and Bowling 4](https://codeforces.com/problemset/problem/660/F)
* [APIO 2010 - Commando](https://dmoj.ca/problem/apio10p1)
|
Convex hull trick and Li Chao tree
|
---
title
- Original
---
# Basic Geometry
In this article we will consider basic operations on points in Euclidean space which maintains the foundation of the whole analytical geometry.
We will consider for each point $\mathbf r$ the vector $\vec{\mathbf r}$ directed from $\mathbf 0$ to $\mathbf r$.
Later we will not distinguish between $\mathbf r$ and $\vec{\mathbf r}$ and use the term **point** as a synonym for **vector**.
## Linear operations
Both 2D and 3D points maintain linear space, which means that for them sum of points and multiplication of point by some number are defined. Here are those basic implementations for 2D:
```{.cpp file=point2d}
struct point2d {
ftype x, y;
point2d() {}
point2d(ftype x, ftype y): x(x), y(y) {}
point2d& operator+=(const point2d &t) {
x += t.x;
y += t.y;
return *this;
}
point2d& operator-=(const point2d &t) {
x -= t.x;
y -= t.y;
return *this;
}
point2d& operator*=(ftype t) {
x *= t;
y *= t;
return *this;
}
point2d& operator/=(ftype t) {
x /= t;
y /= t;
return *this;
}
point2d operator+(const point2d &t) const {
return point2d(*this) += t;
}
point2d operator-(const point2d &t) const {
return point2d(*this) -= t;
}
point2d operator*(ftype t) const {
return point2d(*this) *= t;
}
point2d operator/(ftype t) const {
return point2d(*this) /= t;
}
};
point2d operator*(ftype a, point2d b) {
return b * a;
}
```
And 3D points:
```{.cpp file=point3d}
struct point3d {
ftype x, y, z;
point3d() {}
point3d(ftype x, ftype y, ftype z): x(x), y(y), z(z) {}
point3d& operator+=(const point3d &t) {
x += t.x;
y += t.y;
z += t.z;
return *this;
}
point3d& operator-=(const point3d &t) {
x -= t.x;
y -= t.y;
z -= t.z;
return *this;
}
point3d& operator*=(ftype t) {
x *= t;
y *= t;
z *= t;
return *this;
}
point3d& operator/=(ftype t) {
x /= t;
y /= t;
z /= t;
return *this;
}
point3d operator+(const point3d &t) const {
return point3d(*this) += t;
}
point3d operator-(const point3d &t) const {
return point3d(*this) -= t;
}
point3d operator*(ftype t) const {
return point3d(*this) *= t;
}
point3d operator/(ftype t) const {
return point3d(*this) /= t;
}
};
point3d operator*(ftype a, point3d b) {
return b * a;
}
```
Here `ftype` is some type used for coordinates, usually `int`, `double` or `long long`.
## Dot product
### Definition
The dot (or scalar) product $\mathbf a \cdot \mathbf b$ for vectors $\mathbf a$ and $\mathbf b$ can be defined in two identical ways.
Geometrically it is product of the length of the first vector by the length of the projection of the second vector onto the first one.
As you may see from the image below this projection is nothing but $|\mathbf a| \cos \theta$ where $\theta$ is the angle between $\mathbf a$ and $\mathbf b$. Thus $\mathbf a\cdot \mathbf b = |\mathbf a| \cos \theta \cdot |\mathbf b|$.
<center>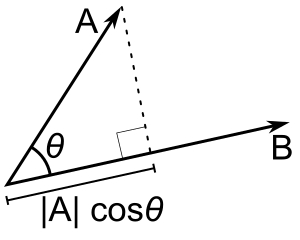</center>
The dot product holds some notable properties:
1. $\mathbf a \cdot \mathbf b = \mathbf b \cdot \mathbf a$
2. $(\alpha \cdot \mathbf a)\cdot \mathbf b = \alpha \cdot (\mathbf a \cdot \mathbf b)$
3. $(\mathbf a + \mathbf b)\cdot \mathbf c = \mathbf a \cdot \mathbf c + \mathbf b \cdot \mathbf c$
I.e. it is a commutative function which is linear with respect to both arguments.
Let's denote the unit vectors as
$$\mathbf e_x = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, \mathbf e_y = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, \mathbf e_z = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}.$$
With this notation we can write the vector $\mathbf r = (x;y;z)$ as $r = x \cdot \mathbf e_x + y \cdot \mathbf e_y + z \cdot \mathbf e_z$.
And since for unit vectors
$$\mathbf e_x\cdot \mathbf e_x = \mathbf e_y\cdot \mathbf e_y = \mathbf e_z\cdot \mathbf e_z = 1,\\
\mathbf e_x\cdot \mathbf e_y = \mathbf e_y\cdot \mathbf e_z = \mathbf e_z\cdot \mathbf e_x = 0$$
we can see that in terms of coordinates for $\mathbf a = (x_1;y_1;z_1)$ and $\mathbf b = (x_2;y_2;z_2)$ holds
$$\mathbf a\cdot \mathbf b = (x_1 \cdot \mathbf e_x + y_1 \cdot\mathbf e_y + z_1 \cdot\mathbf e_z)\cdot( x_2 \cdot\mathbf e_x + y_2 \cdot\mathbf e_y + z_2 \cdot\mathbf e_z) = x_1 x_2 + y_1 y_2 + z_1 z_2$$
That is also the algebraic definition of the dot product.
From this we can write functions which calculate it.
```{.cpp file=dotproduct}
ftype dot(point2d a, point2d b) {
return a.x * b.x + a.y * b.y;
}
ftype dot(point3d a, point3d b) {
return a.x * b.x + a.y * b.y + a.z * b.z;
}
```
When solving problems one should use algebraic definition to calculate dot products, but keep in mind geometric definition and properties to use it.
### Properties
We can define many geometrical properties via the dot product.
For example
1. Norm of $\mathbf a$ (squared length): $|\mathbf a|^2 = \mathbf a\cdot \mathbf a$
2. Length of $\mathbf a$: $|\mathbf a| = \sqrt{\mathbf a\cdot \mathbf a}$
3. Projection of $\mathbf a$ onto $\mathbf b$: $\dfrac{\mathbf a\cdot\mathbf b}{|\mathbf b|}$
4. Angle between vectors: $\arccos \left(\dfrac{\mathbf a\cdot \mathbf b}{|\mathbf a| \cdot |\mathbf b|}\right)$
5. From the previous point we may see that the dot product is positive if the angle between them is acute, negative if it is obtuse and it equals zero if they are orthogonal, i.e. they form a right angle.
Note that all these functions do not depend on the number of dimensions, hence they will be the same for the 2D and 3D case:
```{.cpp file=dotproperties}
ftype norm(point2d a) {
return dot(a, a);
}
double abs(point2d a) {
return sqrt(norm(a));
}
double proj(point2d a, point2d b) {
return dot(a, b) / abs(b);
}
double angle(point2d a, point2d b) {
return acos(dot(a, b) / abs(a) / abs(b));
}
```
To see the next important property we should take a look at the set of points $\mathbf r$ for which $\mathbf r\cdot \mathbf a = C$ for some fixed constant $C$.
You can see that this set of points is exactly the set of points for which the projection onto $\mathbf a$ is the point $C \cdot \dfrac{\mathbf a}{|\mathbf a|}$ and they form a hyperplane orthogonal to $\mathbf a$.
You can see the vector $\mathbf a$ alongside with several such vectors having same dot product with it in 2D on the picture below:
<center></center>
In 2D these vectors will form a line, in 3D they will form a plane.
Note that this result allows us to define a line in 2D as $\mathbf r\cdot \mathbf n=C$ or $(\mathbf r - \mathbf r_0)\cdot \mathbf n=0$ where $\mathbf n$ is vector orthogonal to the line and $\mathbf r_0$ is any vector already present on the line and $C = \mathbf r_0\cdot \mathbf n$.
In the same manner a plane can be defined in 3D.
## Cross product
### Definition
Assume you have three vectors $\mathbf a$, $\mathbf b$ and $\mathbf c$ in 3D space joined in a parallelepiped as in the picture below:
<center></center>
How would you calculate its volume?
From school we know that we should multiply the area of the base with the height, which is projection of $\mathbf a$ onto direction orthogonal to base.
That means that if we define $\mathbf b \times \mathbf c$ as the vector which is orthogonal to both $\mathbf b$ and $\mathbf c$ and which length is equal to the area of the parallelogram formed by $\mathbf b$ and $\mathbf c$ then $|\mathbf a\cdot (\mathbf b\times\mathbf c)|$ will be equal to the volume of the parallelepiped.
For integrity we will say that $\mathbf b\times \mathbf c$ will be always directed in such way that the rotation from the vector $\mathbf b$ to the vector $\mathbf c$ from the point of $\mathbf b\times \mathbf c$ is always counter-clockwise (see the picture below).
<center></center>
This defines the cross (or vector) product $\mathbf b\times \mathbf c$ of the vectors $\mathbf b$ and $\mathbf c$ and the triple product $\mathbf a\cdot(\mathbf b\times \mathbf c)$ of the vectors $\mathbf a$, $\mathbf b$ and $\mathbf c$.
Some notable properties of cross and triple products:
1. $\mathbf a\times \mathbf b = -\mathbf b\times \mathbf a$
2. $(\alpha \cdot \mathbf a)\times \mathbf b = \alpha \cdot (\mathbf a\times \mathbf b)$
3. For any $\mathbf b$ and $\mathbf c$ there is exactly one vector $\mathbf r$ such that $\mathbf a\cdot (\mathbf b\times \mathbf c) = \mathbf a\cdot\mathbf r$ for any vector $\mathbf a$. <br>Indeed if there are two such vectors $\mathbf r_1$ and $\mathbf r_2$ then $\mathbf a\cdot (\mathbf r_1 - \mathbf r_2)=0$ for all vectors $\mathbf a$ which is possible only when $\mathbf r_1 = \mathbf r_2$.
4. $\mathbf a\cdot (\mathbf b\times \mathbf c) = \mathbf b\cdot (\mathbf c\times \mathbf a) = -\mathbf a\cdot( \mathbf c\times \mathbf b)$
5. $(\mathbf a + \mathbf b)\times \mathbf c = \mathbf a\times \mathbf c + \mathbf b\times \mathbf c$.
Indeed for all vectors $\mathbf r$ the chain of equations holds:
\[\mathbf r\cdot( (\mathbf a + \mathbf b)\times \mathbf c) = (\mathbf a + \mathbf b) \cdot (\mathbf c\times \mathbf r) = \mathbf a \cdot(\mathbf c\times \mathbf r) + \mathbf b\cdot(\mathbf c\times \mathbf r) = \mathbf r\cdot (\mathbf a\times \mathbf c) + \mathbf r\cdot(\mathbf b\times \mathbf c) = \mathbf r\cdot(\mathbf a\times \mathbf c + \mathbf b\times \mathbf c)\]
Which proves $(\mathbf a + \mathbf b)\times \mathbf c = \mathbf a\times \mathbf c + \mathbf b\times \mathbf c$ due to point 3.
6. $|\mathbf a\times \mathbf b|=|\mathbf a| \cdot |\mathbf b| \sin \theta$ where $\theta$ is angle between $\mathbf a$ and $\mathbf b$, since $|\mathbf a\times \mathbf b|$ equals to the area of the parallelogram formed by $\mathbf a$ and $\mathbf b$.
Given all this and that the following equation holds for the unit vectors
$$\mathbf e_x\times \mathbf e_x = \mathbf e_y\times \mathbf e_y = \mathbf e_z\times \mathbf e_z = \mathbf 0,\\
\mathbf e_x\times \mathbf e_y = \mathbf e_z,~\mathbf e_y\times \mathbf e_z = \mathbf e_x,~\mathbf e_z\times \mathbf e_x = \mathbf e_y$$
we can calculate the cross product of $\mathbf a = (x_1;y_1;z_1)$ and $\mathbf b = (x_2;y_2;z_2)$ in coordinate form:
$$\mathbf a\times \mathbf b = (x_1 \cdot \mathbf e_x + y_1 \cdot \mathbf e_y + z_1 \cdot \mathbf e_z)\times (x_2 \cdot \mathbf e_x + y_2 \cdot \mathbf e_y + z_2 \cdot \mathbf e_z) =$$
$$(y_1 z_2 - z_1 y_2)\mathbf e_x + (z_1 x_2 - x_1 z_2)\mathbf e_y + (x_1 y_2 - y_1 x_2)$$
Which also can be written in the more elegant form:
$$\mathbf a\times \mathbf b = \begin{vmatrix}\mathbf e_x & \mathbf e_y & \mathbf e_z \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix},~a\cdot(b\times c) = \begin{vmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{vmatrix}$$
Here $| \cdot |$ stands for the determinant of a matrix.
Some kind of cross product (namely the pseudo-scalar product) can also be implemented in the 2D case.
If we would like to calculate the area of parallelogram formed by vectors $\mathbf a$ and $\mathbf b$ we would compute $|\mathbf e_z\cdot(\mathbf a\times \mathbf b)| = |x_1 y_2 - y_1 x_2|$.
Another way to obtain the same result is to multiply $|\mathbf a|$ (base of parallelogram) with the height, which is the projection of vector $\mathbf b$ onto vector $\mathbf a$ rotated by $90^\circ$ which in turn is $\widehat{\mathbf a}=(-y_1;x_1)$.
That is, to calculate $|\widehat{\mathbf a}\cdot\mathbf b|=|x_1y_2 - y_1 x_2|$.
If we will take the sign into consideration then the area will be positive if the rotation from $\mathbf a$ to $\mathbf b$ (i.e. from the view of the point of $\mathbf e_z$) is performed counter-clockwise and negative otherwise.
That defines the pseudo-scalar product.
Note that it also equals $|\mathbf a| \cdot |\mathbf b| \sin \theta$ where $\theta$ is angle from $\mathbf a$ to $\mathbf b$ count counter-clockwise (and negative if rotation is clockwise).
Let's implement all this stuff!
```{.cpp file=crossproduct}
point3d cross(point3d a, point3d b) {
return point3d(a.y * b.z - a.z * b.y,
a.z * b.x - a.x * b.z,
a.x * b.y - a.y * b.x);
}
ftype triple(point3d a, point3d b, point3d c) {
return dot(a, cross(b, c));
}
ftype cross(point2d a, point2d b) {
return a.x * b.y - a.y * b.x;
}
```
### Properties
As for the cross product, it equals to the zero vector iff the vectors $\mathbf a$ and $\mathbf b$ are collinear (they form a common line, i.e. they are parallel).
The same thing holds for the triple product, it is equal to zero iff the vectors $\mathbf a$, $\mathbf b$ and $\mathbf c$ are coplanar (they form a common plane).
From this we can obtain universal equations defining lines and planes.
A line can be defined via its direction vector $\mathbf d$ and an initial point $\mathbf r_0$ or by two points $\mathbf a$ and $\mathbf b$.
It is defined as $(\mathbf r - \mathbf r_0)\times\mathbf d=0$ or as $(\mathbf r - \mathbf a)\times (\mathbf b - \mathbf a) = 0$.
As for planes, it can be defined by three points $\mathbf a$, $\mathbf b$ and $\mathbf c$ as $(\mathbf r - \mathbf a)\cdot((\mathbf b - \mathbf a)\times (\mathbf c - \mathbf a))=0$ or by initial point $\mathbf r_0$ and two direction vectors lying in this plane $\mathbf d_1$ and $\mathbf d_2$: $(\mathbf r - \mathbf r_0)\cdot(\mathbf d_1\times \mathbf d_2)=0$.
In 2D the pseudo-scalar product also may be used to check the orientation between two vectors because it is positive if the rotation from the first to the second vector is clockwise and negative otherwise.
And, of course, it can be used to calculate areas of polygons, which is described in a different article.
A triple product can be used for the same purpose in 3D space.
## Exercises
### Line intersection
There are many possible ways to define a line in 2D and you shouldn't hesitate to combine them.
For example we have two lines and we want to find their intersection points.
We can say that all points from first line can be parameterized as $\mathbf r = \mathbf a_1 + t \cdot \mathbf d_1$ where $\mathbf a_1$ is initial point, $\mathbf d_1$ is direction and $t$ is some real parameter.
As for second line all its points must satisfy $(\mathbf r - \mathbf a_2)\times \mathbf d_2=0$. From this we can easily find parameter $t$:
$$(\mathbf a_1 + t \cdot \mathbf d_1 - \mathbf a_2)\times \mathbf d_2=0 \quad\Rightarrow\quad t = \dfrac{(\mathbf a_2 - \mathbf a_1)\times\mathbf d_2}{\mathbf d_1\times \mathbf d_2}$$
Let's implement function to intersect two lines.
```{.cpp file=basic_line_intersection}
point2d intersect(point2d a1, point2d d1, point2d a2, point2d d2) {
return a1 + cross(a2 - a1, d2) / cross(d1, d2) * d1;
}
```
### Planes intersection
However sometimes it might be hard to use some geometric insights.
For example, you're given three planes defined by initial points $\mathbf a_i$ and directions $\mathbf d_i$ and you want to find their intersection point.
You may note that you just have to solve the system of equations:
$$\begin{cases}\mathbf r\cdot \mathbf n_1 = \mathbf a_1\cdot \mathbf n_1, \\ \mathbf r\cdot \mathbf n_2 = \mathbf a_2\cdot \mathbf n_2, \\ \mathbf r\cdot \mathbf n_3 = \mathbf a_3\cdot \mathbf n_3\end{cases}$$
Instead of thinking on geometric approach, you can work out an algebraic one which can be obtained immediately.
For example, given that you already implemented a point class, it will be easy for you to solve this system using Cramer's rule because the triple product is simply the determinant of the matrix obtained from the vectors being its columns:
```{.cpp file=plane_intersection}
point3d intersect(point3d a1, point3d n1, point3d a2, point3d n2, point3d a3, point3d n3) {
point3d x(n1.x, n2.x, n3.x);
point3d y(n1.y, n2.y, n3.y);
point3d z(n1.z, n2.z, n3.z);
point3d d(dot(a1, n1), dot(a2, n2), dot(a3, n3));
return point3d(triple(d, y, z),
triple(x, d, z),
triple(x, y, d)) / triple(n1, n2, n3);
}
```
Now you may try to find out approaches for common geometric operations yourself to get used to all this stuff.
|
---
title
- Original
---
# Basic Geometry
In this article we will consider basic operations on points in Euclidean space which maintains the foundation of the whole analytical geometry.
We will consider for each point $\mathbf r$ the vector $\vec{\mathbf r}$ directed from $\mathbf 0$ to $\mathbf r$.
Later we will not distinguish between $\mathbf r$ and $\vec{\mathbf r}$ and use the term **point** as a synonym for **vector**.
## Linear operations
Both 2D and 3D points maintain linear space, which means that for them sum of points and multiplication of point by some number are defined. Here are those basic implementations for 2D:
```{.cpp file=point2d}
struct point2d {
ftype x, y;
point2d() {}
point2d(ftype x, ftype y): x(x), y(y) {}
point2d& operator+=(const point2d &t) {
x += t.x;
y += t.y;
return *this;
}
point2d& operator-=(const point2d &t) {
x -= t.x;
y -= t.y;
return *this;
}
point2d& operator*=(ftype t) {
x *= t;
y *= t;
return *this;
}
point2d& operator/=(ftype t) {
x /= t;
y /= t;
return *this;
}
point2d operator+(const point2d &t) const {
return point2d(*this) += t;
}
point2d operator-(const point2d &t) const {
return point2d(*this) -= t;
}
point2d operator*(ftype t) const {
return point2d(*this) *= t;
}
point2d operator/(ftype t) const {
return point2d(*this) /= t;
}
};
point2d operator*(ftype a, point2d b) {
return b * a;
}
```
And 3D points:
```{.cpp file=point3d}
struct point3d {
ftype x, y, z;
point3d() {}
point3d(ftype x, ftype y, ftype z): x(x), y(y), z(z) {}
point3d& operator+=(const point3d &t) {
x += t.x;
y += t.y;
z += t.z;
return *this;
}
point3d& operator-=(const point3d &t) {
x -= t.x;
y -= t.y;
z -= t.z;
return *this;
}
point3d& operator*=(ftype t) {
x *= t;
y *= t;
z *= t;
return *this;
}
point3d& operator/=(ftype t) {
x /= t;
y /= t;
z /= t;
return *this;
}
point3d operator+(const point3d &t) const {
return point3d(*this) += t;
}
point3d operator-(const point3d &t) const {
return point3d(*this) -= t;
}
point3d operator*(ftype t) const {
return point3d(*this) *= t;
}
point3d operator/(ftype t) const {
return point3d(*this) /= t;
}
};
point3d operator*(ftype a, point3d b) {
return b * a;
}
```
Here `ftype` is some type used for coordinates, usually `int`, `double` or `long long`.
## Dot product
### Definition
The dot (or scalar) product $\mathbf a \cdot \mathbf b$ for vectors $\mathbf a$ and $\mathbf b$ can be defined in two identical ways.
Geometrically it is product of the length of the first vector by the length of the projection of the second vector onto the first one.
As you may see from the image below this projection is nothing but $|\mathbf a| \cos \theta$ where $\theta$ is the angle between $\mathbf a$ and $\mathbf b$. Thus $\mathbf a\cdot \mathbf b = |\mathbf a| \cos \theta \cdot |\mathbf b|$.
<center></center>
The dot product holds some notable properties:
1. $\mathbf a \cdot \mathbf b = \mathbf b \cdot \mathbf a$
2. $(\alpha \cdot \mathbf a)\cdot \mathbf b = \alpha \cdot (\mathbf a \cdot \mathbf b)$
3. $(\mathbf a + \mathbf b)\cdot \mathbf c = \mathbf a \cdot \mathbf c + \mathbf b \cdot \mathbf c$
I.e. it is a commutative function which is linear with respect to both arguments.
Let's denote the unit vectors as
$$\mathbf e_x = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, \mathbf e_y = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, \mathbf e_z = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}.$$
With this notation we can write the vector $\mathbf r = (x;y;z)$ as $r = x \cdot \mathbf e_x + y \cdot \mathbf e_y + z \cdot \mathbf e_z$.
And since for unit vectors
$$\mathbf e_x\cdot \mathbf e_x = \mathbf e_y\cdot \mathbf e_y = \mathbf e_z\cdot \mathbf e_z = 1,\\
\mathbf e_x\cdot \mathbf e_y = \mathbf e_y\cdot \mathbf e_z = \mathbf e_z\cdot \mathbf e_x = 0$$
we can see that in terms of coordinates for $\mathbf a = (x_1;y_1;z_1)$ and $\mathbf b = (x_2;y_2;z_2)$ holds
$$\mathbf a\cdot \mathbf b = (x_1 \cdot \mathbf e_x + y_1 \cdot\mathbf e_y + z_1 \cdot\mathbf e_z)\cdot( x_2 \cdot\mathbf e_x + y_2 \cdot\mathbf e_y + z_2 \cdot\mathbf e_z) = x_1 x_2 + y_1 y_2 + z_1 z_2$$
That is also the algebraic definition of the dot product.
From this we can write functions which calculate it.
```{.cpp file=dotproduct}
ftype dot(point2d a, point2d b) {
return a.x * b.x + a.y * b.y;
}
ftype dot(point3d a, point3d b) {
return a.x * b.x + a.y * b.y + a.z * b.z;
}
```
When solving problems one should use algebraic definition to calculate dot products, but keep in mind geometric definition and properties to use it.
### Properties
We can define many geometrical properties via the dot product.
For example
1. Norm of $\mathbf a$ (squared length): $|\mathbf a|^2 = \mathbf a\cdot \mathbf a$
2. Length of $\mathbf a$: $|\mathbf a| = \sqrt{\mathbf a\cdot \mathbf a}$
3. Projection of $\mathbf a$ onto $\mathbf b$: $\dfrac{\mathbf a\cdot\mathbf b}{|\mathbf b|}$
4. Angle between vectors: $\arccos \left(\dfrac{\mathbf a\cdot \mathbf b}{|\mathbf a| \cdot |\mathbf b|}\right)$
5. From the previous point we may see that the dot product is positive if the angle between them is acute, negative if it is obtuse and it equals zero if they are orthogonal, i.e. they form a right angle.
Note that all these functions do not depend on the number of dimensions, hence they will be the same for the 2D and 3D case:
```{.cpp file=dotproperties}
ftype norm(point2d a) {
return dot(a, a);
}
double abs(point2d a) {
return sqrt(norm(a));
}
double proj(point2d a, point2d b) {
return dot(a, b) / abs(b);
}
double angle(point2d a, point2d b) {
return acos(dot(a, b) / abs(a) / abs(b));
}
```
To see the next important property we should take a look at the set of points $\mathbf r$ for which $\mathbf r\cdot \mathbf a = C$ for some fixed constant $C$.
You can see that this set of points is exactly the set of points for which the projection onto $\mathbf a$ is the point $C \cdot \dfrac{\mathbf a}{|\mathbf a|}$ and they form a hyperplane orthogonal to $\mathbf a$.
You can see the vector $\mathbf a$ alongside with several such vectors having same dot product with it in 2D on the picture below:
<center></center>
In 2D these vectors will form a line, in 3D they will form a plane.
Note that this result allows us to define a line in 2D as $\mathbf r\cdot \mathbf n=C$ or $(\mathbf r - \mathbf r_0)\cdot \mathbf n=0$ where $\mathbf n$ is vector orthogonal to the line and $\mathbf r_0$ is any vector already present on the line and $C = \mathbf r_0\cdot \mathbf n$.
In the same manner a plane can be defined in 3D.
## Cross product
### Definition
Assume you have three vectors $\mathbf a$, $\mathbf b$ and $\mathbf c$ in 3D space joined in a parallelepiped as in the picture below:
<center></center>
How would you calculate its volume?
From school we know that we should multiply the area of the base with the height, which is projection of $\mathbf a$ onto direction orthogonal to base.
That means that if we define $\mathbf b \times \mathbf c$ as the vector which is orthogonal to both $\mathbf b$ and $\mathbf c$ and which length is equal to the area of the parallelogram formed by $\mathbf b$ and $\mathbf c$ then $|\mathbf a\cdot (\mathbf b\times\mathbf c)|$ will be equal to the volume of the parallelepiped.
For integrity we will say that $\mathbf b\times \mathbf c$ will be always directed in such way that the rotation from the vector $\mathbf b$ to the vector $\mathbf c$ from the point of $\mathbf b\times \mathbf c$ is always counter-clockwise (see the picture below).
<center></center>
This defines the cross (or vector) product $\mathbf b\times \mathbf c$ of the vectors $\mathbf b$ and $\mathbf c$ and the triple product $\mathbf a\cdot(\mathbf b\times \mathbf c)$ of the vectors $\mathbf a$, $\mathbf b$ and $\mathbf c$.
Some notable properties of cross and triple products:
1. $\mathbf a\times \mathbf b = -\mathbf b\times \mathbf a$
2. $(\alpha \cdot \mathbf a)\times \mathbf b = \alpha \cdot (\mathbf a\times \mathbf b)$
3. For any $\mathbf b$ and $\mathbf c$ there is exactly one vector $\mathbf r$ such that $\mathbf a\cdot (\mathbf b\times \mathbf c) = \mathbf a\cdot\mathbf r$ for any vector $\mathbf a$. <br>Indeed if there are two such vectors $\mathbf r_1$ and $\mathbf r_2$ then $\mathbf a\cdot (\mathbf r_1 - \mathbf r_2)=0$ for all vectors $\mathbf a$ which is possible only when $\mathbf r_1 = \mathbf r_2$.
4. $\mathbf a\cdot (\mathbf b\times \mathbf c) = \mathbf b\cdot (\mathbf c\times \mathbf a) = -\mathbf a\cdot( \mathbf c\times \mathbf b)$
5. $(\mathbf a + \mathbf b)\times \mathbf c = \mathbf a\times \mathbf c + \mathbf b\times \mathbf c$.
Indeed for all vectors $\mathbf r$ the chain of equations holds:
\[\mathbf r\cdot( (\mathbf a + \mathbf b)\times \mathbf c) = (\mathbf a + \mathbf b) \cdot (\mathbf c\times \mathbf r) = \mathbf a \cdot(\mathbf c\times \mathbf r) + \mathbf b\cdot(\mathbf c\times \mathbf r) = \mathbf r\cdot (\mathbf a\times \mathbf c) + \mathbf r\cdot(\mathbf b\times \mathbf c) = \mathbf r\cdot(\mathbf a\times \mathbf c + \mathbf b\times \mathbf c)\]
Which proves $(\mathbf a + \mathbf b)\times \mathbf c = \mathbf a\times \mathbf c + \mathbf b\times \mathbf c$ due to point 3.
6. $|\mathbf a\times \mathbf b|=|\mathbf a| \cdot |\mathbf b| \sin \theta$ where $\theta$ is angle between $\mathbf a$ and $\mathbf b$, since $|\mathbf a\times \mathbf b|$ equals to the area of the parallelogram formed by $\mathbf a$ and $\mathbf b$.
Given all this and that the following equation holds for the unit vectors
$$\mathbf e_x\times \mathbf e_x = \mathbf e_y\times \mathbf e_y = \mathbf e_z\times \mathbf e_z = \mathbf 0,\\
\mathbf e_x\times \mathbf e_y = \mathbf e_z,~\mathbf e_y\times \mathbf e_z = \mathbf e_x,~\mathbf e_z\times \mathbf e_x = \mathbf e_y$$
we can calculate the cross product of $\mathbf a = (x_1;y_1;z_1)$ and $\mathbf b = (x_2;y_2;z_2)$ in coordinate form:
$$\mathbf a\times \mathbf b = (x_1 \cdot \mathbf e_x + y_1 \cdot \mathbf e_y + z_1 \cdot \mathbf e_z)\times (x_2 \cdot \mathbf e_x + y_2 \cdot \mathbf e_y + z_2 \cdot \mathbf e_z) =$$
$$(y_1 z_2 - z_1 y_2)\mathbf e_x + (z_1 x_2 - x_1 z_2)\mathbf e_y + (x_1 y_2 - y_1 x_2)$$
Which also can be written in the more elegant form:
$$\mathbf a\times \mathbf b = \begin{vmatrix}\mathbf e_x & \mathbf e_y & \mathbf e_z \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix},~a\cdot(b\times c) = \begin{vmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{vmatrix}$$
Here $| \cdot |$ stands for the determinant of a matrix.
Some kind of cross product (namely the pseudo-scalar product) can also be implemented in the 2D case.
If we would like to calculate the area of parallelogram formed by vectors $\mathbf a$ and $\mathbf b$ we would compute $|\mathbf e_z\cdot(\mathbf a\times \mathbf b)| = |x_1 y_2 - y_1 x_2|$.
Another way to obtain the same result is to multiply $|\mathbf a|$ (base of parallelogram) with the height, which is the projection of vector $\mathbf b$ onto vector $\mathbf a$ rotated by $90^\circ$ which in turn is $\widehat{\mathbf a}=(-y_1;x_1)$.
That is, to calculate $|\widehat{\mathbf a}\cdot\mathbf b|=|x_1y_2 - y_1 x_2|$.
If we will take the sign into consideration then the area will be positive if the rotation from $\mathbf a$ to $\mathbf b$ (i.e. from the view of the point of $\mathbf e_z$) is performed counter-clockwise and negative otherwise.
That defines the pseudo-scalar product.
Note that it also equals $|\mathbf a| \cdot |\mathbf b| \sin \theta$ where $\theta$ is angle from $\mathbf a$ to $\mathbf b$ count counter-clockwise (and negative if rotation is clockwise).
Let's implement all this stuff!
```{.cpp file=crossproduct}
point3d cross(point3d a, point3d b) {
return point3d(a.y * b.z - a.z * b.y,
a.z * b.x - a.x * b.z,
a.x * b.y - a.y * b.x);
}
ftype triple(point3d a, point3d b, point3d c) {
return dot(a, cross(b, c));
}
ftype cross(point2d a, point2d b) {
return a.x * b.y - a.y * b.x;
}
```
### Properties
As for the cross product, it equals to the zero vector iff the vectors $\mathbf a$ and $\mathbf b$ are collinear (they form a common line, i.e. they are parallel).
The same thing holds for the triple product, it is equal to zero iff the vectors $\mathbf a$, $\mathbf b$ and $\mathbf c$ are coplanar (they form a common plane).
From this we can obtain universal equations defining lines and planes.
A line can be defined via its direction vector $\mathbf d$ and an initial point $\mathbf r_0$ or by two points $\mathbf a$ and $\mathbf b$.
It is defined as $(\mathbf r - \mathbf r_0)\times\mathbf d=0$ or as $(\mathbf r - \mathbf a)\times (\mathbf b - \mathbf a) = 0$.
As for planes, it can be defined by three points $\mathbf a$, $\mathbf b$ and $\mathbf c$ as $(\mathbf r - \mathbf a)\cdot((\mathbf b - \mathbf a)\times (\mathbf c - \mathbf a))=0$ or by initial point $\mathbf r_0$ and two direction vectors lying in this plane $\mathbf d_1$ and $\mathbf d_2$: $(\mathbf r - \mathbf r_0)\cdot(\mathbf d_1\times \mathbf d_2)=0$.
In 2D the pseudo-scalar product also may be used to check the orientation between two vectors because it is positive if the rotation from the first to the second vector is clockwise and negative otherwise.
And, of course, it can be used to calculate areas of polygons, which is described in a different article.
A triple product can be used for the same purpose in 3D space.
## Exercises
### Line intersection
There are many possible ways to define a line in 2D and you shouldn't hesitate to combine them.
For example we have two lines and we want to find their intersection points.
We can say that all points from first line can be parameterized as $\mathbf r = \mathbf a_1 + t \cdot \mathbf d_1$ where $\mathbf a_1$ is initial point, $\mathbf d_1$ is direction and $t$ is some real parameter.
As for second line all its points must satisfy $(\mathbf r - \mathbf a_2)\times \mathbf d_2=0$. From this we can easily find parameter $t$:
$$(\mathbf a_1 + t \cdot \mathbf d_1 - \mathbf a_2)\times \mathbf d_2=0 \quad\Rightarrow\quad t = \dfrac{(\mathbf a_2 - \mathbf a_1)\times\mathbf d_2}{\mathbf d_1\times \mathbf d_2}$$
Let's implement function to intersect two lines.
```{.cpp file=basic_line_intersection}
point2d intersect(point2d a1, point2d d1, point2d a2, point2d d2) {
return a1 + cross(a2 - a1, d2) / cross(d1, d2) * d1;
}
```
### Planes intersection
However sometimes it might be hard to use some geometric insights.
For example, you're given three planes defined by initial points $\mathbf a_i$ and directions $\mathbf d_i$ and you want to find their intersection point.
You may note that you just have to solve the system of equations:
$$\begin{cases}\mathbf r\cdot \mathbf n_1 = \mathbf a_1\cdot \mathbf n_1, \\ \mathbf r\cdot \mathbf n_2 = \mathbf a_2\cdot \mathbf n_2, \\ \mathbf r\cdot \mathbf n_3 = \mathbf a_3\cdot \mathbf n_3\end{cases}$$
Instead of thinking on geometric approach, you can work out an algebraic one which can be obtained immediately.
For example, given that you already implemented a point class, it will be easy for you to solve this system using Cramer's rule because the triple product is simply the determinant of the matrix obtained from the vectors being its columns:
```{.cpp file=plane_intersection}
point3d intersect(point3d a1, point3d n1, point3d a2, point3d n2, point3d a3, point3d n3) {
point3d x(n1.x, n2.x, n3.x);
point3d y(n1.y, n2.y, n3.y);
point3d z(n1.z, n2.z, n3.z);
point3d d(dot(a1, n1), dot(a2, n2), dot(a3, n3));
return point3d(triple(d, y, z),
triple(x, d, z),
triple(x, y, d)) / triple(n1, n2, n3);
}
```
Now you may try to find out approaches for common geometric operations yourself to get used to all this stuff.
|
Basic Geometry
|
---
title
circles_intersection
---
# Circle-Circle Intersection
You are given two circles on a 2D plane, each one described as coordinates of its center and its radius. Find the points of their intersection (possible cases: one or two points, no intersection or circles coincide).
## Solution
Let's reduce this problem to the [circle-line intersection problem](circle-line-intersection.md).
Assume without loss of generality that the first circle is centered at the origin (if this is not true, we can move the origin to the center of the first circle and adjust the coordinates of intersection points accordingly at output time). We have a system of two equations:
$$x^2+y^2=r_1^2$$
$$(x - x_2)^2 + (y - y_2)^2 = r_2^2$$
Subtract the first equation from the second one to get rid of the second powers of variables:
$$x^2+y^2=r_1^2$$
$$x \cdot (-2x_2) + y \cdot (-2y_2) + (x_2^2+y_2^2+r_1^2-r_2^2) = 0$$
Thus, we've reduced the original problem to the problem of finding intersections of the first circle and a line:
$$Ax + By + C = 0$$
$$\begin{align}
A &= -2x_2 \\
B &= -2y_2 \\
C &= x_2^2+y_2^2+r_1^2-r_2^2
\end{align}$$
And this problem can be solved as described in the [corresponding article](circle-line-intersection.md).
The only degenerate case we need to consider separately is when the centers of the circles coincide. In this case $x_2=y_2=0$, and the line equation will be $C = r_1^2-r_2^2 = 0$. If the radii of the circles are the same, there are infinitely many intersection points, if they differ, there are no intersections.
|
---
title
circles_intersection
---
# Circle-Circle Intersection
You are given two circles on a 2D plane, each one described as coordinates of its center and its radius. Find the points of their intersection (possible cases: one or two points, no intersection or circles coincide).
## Solution
Let's reduce this problem to the [circle-line intersection problem](circle-line-intersection.md).
Assume without loss of generality that the first circle is centered at the origin (if this is not true, we can move the origin to the center of the first circle and adjust the coordinates of intersection points accordingly at output time). We have a system of two equations:
$$x^2+y^2=r_1^2$$
$$(x - x_2)^2 + (y - y_2)^2 = r_2^2$$
Subtract the first equation from the second one to get rid of the second powers of variables:
$$x^2+y^2=r_1^2$$
$$x \cdot (-2x_2) + y \cdot (-2y_2) + (x_2^2+y_2^2+r_1^2-r_2^2) = 0$$
Thus, we've reduced the original problem to the problem of finding intersections of the first circle and a line:
$$Ax + By + C = 0$$
$$\begin{align}
A &= -2x_2 \\
B &= -2y_2 \\
C &= x_2^2+y_2^2+r_1^2-r_2^2
\end{align}$$
And this problem can be solved as described in the [corresponding article](circle-line-intersection.md).
The only degenerate case we need to consider separately is when the centers of the circles coincide. In this case $x_2=y_2=0$, and the line equation will be $C = r_1^2-r_2^2 = 0$. If the radii of the circles are the same, there are infinitely many intersection points, if they differ, there are no intersections.
## Practice Problems
- [RadarFinder](https://community.topcoder.com/stat?c=problem_statement&pm=7766)
- [Runaway to a shadow - Codeforces Round #357](http://codeforces.com/problemset/problem/681/E)
- [ASC 1 Problem F "Get out!"](http://codeforces.com/gym/100199/problem/F)
- [SPOJ: CIRCINT](http://www.spoj.com/problems/CIRCINT/)
- [UVA - 10301 - Rings and Glue](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=1242)
- [Codeforces 933C A Colorful Prospect](https://codeforces.com/problemset/problem/933/C)
- [TIMUS 1429 Biscuits](https://acm.timus.ru/problem.aspx?space=1&num=1429)
|
Circle-Circle Intersection
|
---
title
segments_intersection
---
# Finding intersection of two segments
You are given two segments AB and CD, described as pairs of their endpoints. Each segment can be a single point if its endpoints are the same.
You have to find the intersection of these segments, which can be empty (if the segments don't intersect), a single point or a segment (if the given segments overlap).
## Solution
We can find the intersection point of segments in the same way as [the intersection of lines](lines-intersection.md):
reconstruct line equations from the segments' endpoints and check whether they are parallel.
If the lines are not parallel, we need to find their point of intersection and check whether it belongs to both segments
(to do this it's sufficient to verify that the intersection point belongs to each segment projected on X and Y axes).
In this case the answer will be either "no intersection" or the single point of lines' intersection.
The case of parallel lines is slightly more complicated (the case of one or more segments being a single point also belongs here).
In this case we need to check that both segments belong to the same line.
If they don't, the answer is "no intersection".
If they do, the answer is the intersection of the segments belonging to the same line, which is obtained by
ordering the endpoints of both segments in the increasing order of certain coordinate and taking the rightmost of left endpoints and the leftmost of right endpoints.
If both segments are single points, these points have to be identical, and it makes sense to perform this check separately.
In the beginning of the algorithm let's add a bounding box check - it is necessary for the case when the segments belong to the same line,
and (being a lightweight check) it allows the algorithm to work faster on average on random tests.
## Implementation
Here is the implementation, including all helper functions for lines and segments processing.
The main function `intersect` returns true if the segments have a non-empty intersection,
and stores endpoints of the intersection segment in arguments `left` and `right`.
If the answer is a single point, the values written to `left` and `right` will be the same.
```{.cpp file=segment_intersection}
const double EPS = 1E-9;
struct pt {
double x, y;
bool operator<(const pt& p) const
{
return x < p.x - EPS || (abs(x - p.x) < EPS && y < p.y - EPS);
}
};
struct line {
double a, b, c;
line() {}
line(pt p, pt q)
{
a = p.y - q.y;
b = q.x - p.x;
c = -a * p.x - b * p.y;
norm();
}
void norm()
{
double z = sqrt(a * a + b * b);
if (abs(z) > EPS)
a /= z, b /= z, c /= z;
}
double dist(pt p) const { return a * p.x + b * p.y + c; }
};
double det(double a, double b, double c, double d)
{
return a * d - b * c;
}
inline bool betw(double l, double r, double x)
{
return min(l, r) <= x + EPS && x <= max(l, r) + EPS;
}
inline bool intersect_1d(double a, double b, double c, double d)
{
if (a > b)
swap(a, b);
if (c > d)
swap(c, d);
return max(a, c) <= min(b, d) + EPS;
}
bool intersect(pt a, pt b, pt c, pt d, pt& left, pt& right)
{
if (!intersect_1d(a.x, b.x, c.x, d.x) || !intersect_1d(a.y, b.y, c.y, d.y))
return false;
line m(a, b);
line n(c, d);
double zn = det(m.a, m.b, n.a, n.b);
if (abs(zn) < EPS) {
if (abs(m.dist(c)) > EPS || abs(n.dist(a)) > EPS)
return false;
if (b < a)
swap(a, b);
if (d < c)
swap(c, d);
left = max(a, c);
right = min(b, d);
return true;
} else {
left.x = right.x = -det(m.c, m.b, n.c, n.b) / zn;
left.y = right.y = -det(m.a, m.c, n.a, n.c) / zn;
return betw(a.x, b.x, left.x) && betw(a.y, b.y, left.y) &&
betw(c.x, d.x, left.x) && betw(c.y, d.y, left.y);
}
}
```
|
---
title
segments_intersection
---
# Finding intersection of two segments
You are given two segments AB and CD, described as pairs of their endpoints. Each segment can be a single point if its endpoints are the same.
You have to find the intersection of these segments, which can be empty (if the segments don't intersect), a single point or a segment (if the given segments overlap).
## Solution
We can find the intersection point of segments in the same way as [the intersection of lines](lines-intersection.md):
reconstruct line equations from the segments' endpoints and check whether they are parallel.
If the lines are not parallel, we need to find their point of intersection and check whether it belongs to both segments
(to do this it's sufficient to verify that the intersection point belongs to each segment projected on X and Y axes).
In this case the answer will be either "no intersection" or the single point of lines' intersection.
The case of parallel lines is slightly more complicated (the case of one or more segments being a single point also belongs here).
In this case we need to check that both segments belong to the same line.
If they don't, the answer is "no intersection".
If they do, the answer is the intersection of the segments belonging to the same line, which is obtained by
ordering the endpoints of both segments in the increasing order of certain coordinate and taking the rightmost of left endpoints and the leftmost of right endpoints.
If both segments are single points, these points have to be identical, and it makes sense to perform this check separately.
In the beginning of the algorithm let's add a bounding box check - it is necessary for the case when the segments belong to the same line,
and (being a lightweight check) it allows the algorithm to work faster on average on random tests.
## Implementation
Here is the implementation, including all helper functions for lines and segments processing.
The main function `intersect` returns true if the segments have a non-empty intersection,
and stores endpoints of the intersection segment in arguments `left` and `right`.
If the answer is a single point, the values written to `left` and `right` will be the same.
```{.cpp file=segment_intersection}
const double EPS = 1E-9;
struct pt {
double x, y;
bool operator<(const pt& p) const
{
return x < p.x - EPS || (abs(x - p.x) < EPS && y < p.y - EPS);
}
};
struct line {
double a, b, c;
line() {}
line(pt p, pt q)
{
a = p.y - q.y;
b = q.x - p.x;
c = -a * p.x - b * p.y;
norm();
}
void norm()
{
double z = sqrt(a * a + b * b);
if (abs(z) > EPS)
a /= z, b /= z, c /= z;
}
double dist(pt p) const { return a * p.x + b * p.y + c; }
};
double det(double a, double b, double c, double d)
{
return a * d - b * c;
}
inline bool betw(double l, double r, double x)
{
return min(l, r) <= x + EPS && x <= max(l, r) + EPS;
}
inline bool intersect_1d(double a, double b, double c, double d)
{
if (a > b)
swap(a, b);
if (c > d)
swap(c, d);
return max(a, c) <= min(b, d) + EPS;
}
bool intersect(pt a, pt b, pt c, pt d, pt& left, pt& right)
{
if (!intersect_1d(a.x, b.x, c.x, d.x) || !intersect_1d(a.y, b.y, c.y, d.y))
return false;
line m(a, b);
line n(c, d);
double zn = det(m.a, m.b, n.a, n.b);
if (abs(zn) < EPS) {
if (abs(m.dist(c)) > EPS || abs(n.dist(a)) > EPS)
return false;
if (b < a)
swap(a, b);
if (d < c)
swap(c, d);
left = max(a, c);
right = min(b, d);
return true;
} else {
left.x = right.x = -det(m.c, m.b, n.c, n.b) / zn;
left.y = right.y = -det(m.a, m.c, n.a, n.c) / zn;
return betw(a.x, b.x, left.x) && betw(a.y, b.y, left.y) &&
betw(c.x, d.x, left.x) && betw(c.y, d.y, left.y);
}
}
```
|
Finding intersection of two segments
|
---
title
convex_hull_graham
---
# Convex Hull construction
In this article we will discuss the problem of constructing a convex hull from a set of points.
Consider $N$ points given on a plane, and the objective is to generate a convex hull, i.e. the smallest
convex polygon that contains all the given points.
We will see the **Graham's scan** algorithm published in 1972 by Graham, and
also the **Monotone chain** algorithm published in 1979 by Andrew. Both
are $\mathcal{O}(N \log N)$, and are asymptotically optimal (as it is proven that there
is no algorithm asymptotically better), with the exception of a few problems where
parallel or online processing is involved.
## Graham's scan Algorithm
The algorithm first finds the bottom-most point $P_0$. If there are multiple points
with the same Y coordinate, the one with the smaller X coordinate is considered. This
step takes $\mathcal{O}(N)$ time.
Next, all the other points are sorted by polar angle in clockwise order.
If the polar angle between two or more points is the same, the tie should be broken by distance from $P_0$, in increasing order.
Then we iterate through each point one by one, and make sure that the current
point and the two before it make a clockwise turn, otherwise the previous
point is discarded, since it would make a non-convex shape. Checking for clockwise or anticlockwise
nature can be done by checking the [orientation](oriented-triangle-area.md).
We use a stack to store the points, and once we reach the original point $P_0$,
the algorithm is done and we return the stack containing all the points of the
convex hull in clockwise order.
If you need to include the collinear points while doing a Graham scan, you need
another step after sorting. You need to get the points that have the biggest
polar distance from $P_0$ (these should be at the end of the sorted vector) and are collinear.
The points in this line should be reversed so that we can output all the
collinear points, otherwise the algorithm would get the nearest point in this
line and bail. This step shouldn't be included in the non-collinear version
of the algorithm, otherwise you wouldn't get the smallest convex hull.
### Implementation
```{.cpp file=graham_scan}
struct pt {
double x, y;
};
int orientation(pt a, pt b, pt c) {
double v = a.x*(b.y-c.y)+b.x*(c.y-a.y)+c.x*(a.y-b.y);
if (v < 0) return -1; // clockwise
if (v > 0) return +1; // counter-clockwise
return 0;
}
bool cw(pt a, pt b, pt c, bool include_collinear) {
int o = orientation(a, b, c);
return o < 0 || (include_collinear && o == 0);
}
bool collinear(pt a, pt b, pt c) { return orientation(a, b, c) == 0; }
void convex_hull(vector<pt>& a, bool include_collinear = false) {
pt p0 = *min_element(a.begin(), a.end(), [](pt a, pt b) {
return make_pair(a.y, a.x) < make_pair(b.y, b.x);
});
sort(a.begin(), a.end(), [&p0](const pt& a, const pt& b) {
int o = orientation(p0, a, b);
if (o == 0)
return (p0.x-a.x)*(p0.x-a.x) + (p0.y-a.y)*(p0.y-a.y)
< (p0.x-b.x)*(p0.x-b.x) + (p0.y-b.y)*(p0.y-b.y);
return o < 0;
});
if (include_collinear) {
int i = (int)a.size()-1;
while (i >= 0 && collinear(p0, a[i], a.back())) i--;
reverse(a.begin()+i+1, a.end());
}
vector<pt> st;
for (int i = 0; i < (int)a.size(); i++) {
while (st.size() > 1 && !cw(st[st.size()-2], st.back(), a[i], include_collinear))
st.pop_back();
st.push_back(a[i]);
}
a = st;
}
```
## Monotone chain Algorithm
The algorithm first finds the leftmost and rightmost points A and B. In the event multiple such points exist,
the lowest among the left (lowest Y-coordinate) is taken as A, and the highest among the right (highest Y-coordinate)
is taken as B. Clearly, A and B must both belong to the convex hull as they are the farthest away and they cannot be contained
by any line formed by a pair among the given points.
Now, draw a line through AB. This divides all the other points into two sets, S1 and S2, where S1 contains all the points
above the line connecting A and B, and S2 contains all the points below the line joining A and B. The points that lie on
the line joining A and B may belong to either set. The points A and B belong to both sets. Now the algorithm
constructs the upper set S1 and the lower set S2 and then combines them to obtain the answer.
To get the upper set, we sort all points by the x-coordinate. For each point we check if either - the current point is the last point,
(which we defined as B), or if the orientation between the line between A and the current point and the line between the current point and B is clockwise. In those cases the
current point belongs to the upper set S1. Checking for clockwise or anticlockwise nature can be done by checking the [orientation](oriented-triangle-area.md).
If the given point belongs to the upper set, we check the angle made by the line connecting the second last point and the last point in the upper convex hull,
with the line connecting the last point in the upper convex hull and the current point. If the angle is not clockwise, we remove the most recent point added
to the upper convex hull as the current point will be able to contain the previous point once it is added to the convex
hull.
The same logic applies for the lower set S2. If either - the current point is B, or the orientation of the lines, formed by A and the
current point and the current point and B, is counterclockwise - then it belongs to S2.
If the given point belongs to the lower set, we act similarly as for a point on the upper set except we check for a counterclockwise
orientation instead of a clockwise orientation. Thus, if the angle made by the line connecting the second last point and the last point in the lower convex hull,
with the line connecting the last point in the lower convex hull and the current point is not counterclockwise, we remove the most recent point added to the lower convex hull as the current point will be able to contain
the previous point once added to the hull.
The final convex hull is obtained from the union of the upper and lower convex hull, forming a clockwise hull, and the implementation is as follows.
If you need collinear points, you just need to check for them in the clockwise/counterclockwise routines.
However, this allows for a degenerate case where all the input points are collinear in a single line, and the algorithm would output repeated points.
To solve this, we check whether the upper hull contains all the points, and if it does, we just return the points in reverse, as that
is what Graham's implementation would return in this case.
### Implementation
```{.cpp file=monotone_chain}
struct pt {
double x, y;
};
int orientation(pt a, pt b, pt c) {
double v = a.x*(b.y-c.y)+b.x*(c.y-a.y)+c.x*(a.y-b.y);
if (v < 0) return -1; // clockwise
if (v > 0) return +1; // counter-clockwise
return 0;
}
bool cw(pt a, pt b, pt c, bool include_collinear) {
int o = orientation(a, b, c);
return o < 0 || (include_collinear && o == 0);
}
bool ccw(pt a, pt b, pt c, bool include_collinear) {
int o = orientation(a, b, c);
return o > 0 || (include_collinear && o == 0);
}
void convex_hull(vector<pt>& a, bool include_collinear = false) {
if (a.size() == 1)
return;
sort(a.begin(), a.end(), [](pt a, pt b) {
return make_pair(a.x, a.y) < make_pair(b.x, b.y);
});
pt p1 = a[0], p2 = a.back();
vector<pt> up, down;
up.push_back(p1);
down.push_back(p1);
for (int i = 1; i < (int)a.size(); i++) {
if (i == a.size() - 1 || cw(p1, a[i], p2, include_collinear)) {
while (up.size() >= 2 && !cw(up[up.size()-2], up[up.size()-1], a[i], include_collinear))
up.pop_back();
up.push_back(a[i]);
}
if (i == a.size() - 1 || ccw(p1, a[i], p2, include_collinear)) {
while (down.size() >= 2 && !ccw(down[down.size()-2], down[down.size()-1], a[i], include_collinear))
down.pop_back();
down.push_back(a[i]);
}
}
if (include_collinear && up.size() == a.size()) {
reverse(a.begin(), a.end());
return;
}
a.clear();
for (int i = 0; i < (int)up.size(); i++)
a.push_back(up[i]);
for (int i = down.size() - 2; i > 0; i--)
a.push_back(down[i]);
}
```
|
---
title
convex_hull_graham
---
# Convex Hull construction
In this article we will discuss the problem of constructing a convex hull from a set of points.
Consider $N$ points given on a plane, and the objective is to generate a convex hull, i.e. the smallest
convex polygon that contains all the given points.
We will see the **Graham's scan** algorithm published in 1972 by Graham, and
also the **Monotone chain** algorithm published in 1979 by Andrew. Both
are $\mathcal{O}(N \log N)$, and are asymptotically optimal (as it is proven that there
is no algorithm asymptotically better), with the exception of a few problems where
parallel or online processing is involved.
## Graham's scan Algorithm
The algorithm first finds the bottom-most point $P_0$. If there are multiple points
with the same Y coordinate, the one with the smaller X coordinate is considered. This
step takes $\mathcal{O}(N)$ time.
Next, all the other points are sorted by polar angle in clockwise order.
If the polar angle between two or more points is the same, the tie should be broken by distance from $P_0$, in increasing order.
Then we iterate through each point one by one, and make sure that the current
point and the two before it make a clockwise turn, otherwise the previous
point is discarded, since it would make a non-convex shape. Checking for clockwise or anticlockwise
nature can be done by checking the [orientation](oriented-triangle-area.md).
We use a stack to store the points, and once we reach the original point $P_0$,
the algorithm is done and we return the stack containing all the points of the
convex hull in clockwise order.
If you need to include the collinear points while doing a Graham scan, you need
another step after sorting. You need to get the points that have the biggest
polar distance from $P_0$ (these should be at the end of the sorted vector) and are collinear.
The points in this line should be reversed so that we can output all the
collinear points, otherwise the algorithm would get the nearest point in this
line and bail. This step shouldn't be included in the non-collinear version
of the algorithm, otherwise you wouldn't get the smallest convex hull.
### Implementation
```{.cpp file=graham_scan}
struct pt {
double x, y;
};
int orientation(pt a, pt b, pt c) {
double v = a.x*(b.y-c.y)+b.x*(c.y-a.y)+c.x*(a.y-b.y);
if (v < 0) return -1; // clockwise
if (v > 0) return +1; // counter-clockwise
return 0;
}
bool cw(pt a, pt b, pt c, bool include_collinear) {
int o = orientation(a, b, c);
return o < 0 || (include_collinear && o == 0);
}
bool collinear(pt a, pt b, pt c) { return orientation(a, b, c) == 0; }
void convex_hull(vector<pt>& a, bool include_collinear = false) {
pt p0 = *min_element(a.begin(), a.end(), [](pt a, pt b) {
return make_pair(a.y, a.x) < make_pair(b.y, b.x);
});
sort(a.begin(), a.end(), [&p0](const pt& a, const pt& b) {
int o = orientation(p0, a, b);
if (o == 0)
return (p0.x-a.x)*(p0.x-a.x) + (p0.y-a.y)*(p0.y-a.y)
< (p0.x-b.x)*(p0.x-b.x) + (p0.y-b.y)*(p0.y-b.y);
return o < 0;
});
if (include_collinear) {
int i = (int)a.size()-1;
while (i >= 0 && collinear(p0, a[i], a.back())) i--;
reverse(a.begin()+i+1, a.end());
}
vector<pt> st;
for (int i = 0; i < (int)a.size(); i++) {
while (st.size() > 1 && !cw(st[st.size()-2], st.back(), a[i], include_collinear))
st.pop_back();
st.push_back(a[i]);
}
a = st;
}
```
## Monotone chain Algorithm
The algorithm first finds the leftmost and rightmost points A and B. In the event multiple such points exist,
the lowest among the left (lowest Y-coordinate) is taken as A, and the highest among the right (highest Y-coordinate)
is taken as B. Clearly, A and B must both belong to the convex hull as they are the farthest away and they cannot be contained
by any line formed by a pair among the given points.
Now, draw a line through AB. This divides all the other points into two sets, S1 and S2, where S1 contains all the points
above the line connecting A and B, and S2 contains all the points below the line joining A and B. The points that lie on
the line joining A and B may belong to either set. The points A and B belong to both sets. Now the algorithm
constructs the upper set S1 and the lower set S2 and then combines them to obtain the answer.
To get the upper set, we sort all points by the x-coordinate. For each point we check if either - the current point is the last point,
(which we defined as B), or if the orientation between the line between A and the current point and the line between the current point and B is clockwise. In those cases the
current point belongs to the upper set S1. Checking for clockwise or anticlockwise nature can be done by checking the [orientation](oriented-triangle-area.md).
If the given point belongs to the upper set, we check the angle made by the line connecting the second last point and the last point in the upper convex hull,
with the line connecting the last point in the upper convex hull and the current point. If the angle is not clockwise, we remove the most recent point added
to the upper convex hull as the current point will be able to contain the previous point once it is added to the convex
hull.
The same logic applies for the lower set S2. If either - the current point is B, or the orientation of the lines, formed by A and the
current point and the current point and B, is counterclockwise - then it belongs to S2.
If the given point belongs to the lower set, we act similarly as for a point on the upper set except we check for a counterclockwise
orientation instead of a clockwise orientation. Thus, if the angle made by the line connecting the second last point and the last point in the lower convex hull,
with the line connecting the last point in the lower convex hull and the current point is not counterclockwise, we remove the most recent point added to the lower convex hull as the current point will be able to contain
the previous point once added to the hull.
The final convex hull is obtained from the union of the upper and lower convex hull, forming a clockwise hull, and the implementation is as follows.
If you need collinear points, you just need to check for them in the clockwise/counterclockwise routines.
However, this allows for a degenerate case where all the input points are collinear in a single line, and the algorithm would output repeated points.
To solve this, we check whether the upper hull contains all the points, and if it does, we just return the points in reverse, as that
is what Graham's implementation would return in this case.
### Implementation
```{.cpp file=monotone_chain}
struct pt {
double x, y;
};
int orientation(pt a, pt b, pt c) {
double v = a.x*(b.y-c.y)+b.x*(c.y-a.y)+c.x*(a.y-b.y);
if (v < 0) return -1; // clockwise
if (v > 0) return +1; // counter-clockwise
return 0;
}
bool cw(pt a, pt b, pt c, bool include_collinear) {
int o = orientation(a, b, c);
return o < 0 || (include_collinear && o == 0);
}
bool ccw(pt a, pt b, pt c, bool include_collinear) {
int o = orientation(a, b, c);
return o > 0 || (include_collinear && o == 0);
}
void convex_hull(vector<pt>& a, bool include_collinear = false) {
if (a.size() == 1)
return;
sort(a.begin(), a.end(), [](pt a, pt b) {
return make_pair(a.x, a.y) < make_pair(b.x, b.y);
});
pt p1 = a[0], p2 = a.back();
vector<pt> up, down;
up.push_back(p1);
down.push_back(p1);
for (int i = 1; i < (int)a.size(); i++) {
if (i == a.size() - 1 || cw(p1, a[i], p2, include_collinear)) {
while (up.size() >= 2 && !cw(up[up.size()-2], up[up.size()-1], a[i], include_collinear))
up.pop_back();
up.push_back(a[i]);
}
if (i == a.size() - 1 || ccw(p1, a[i], p2, include_collinear)) {
while (down.size() >= 2 && !ccw(down[down.size()-2], down[down.size()-1], a[i], include_collinear))
down.pop_back();
down.push_back(a[i]);
}
}
if (include_collinear && up.size() == a.size()) {
reverse(a.begin(), a.end());
return;
}
a.clear();
for (int i = 0; i < (int)up.size(); i++)
a.push_back(up[i]);
for (int i = down.size() - 2; i > 0; i--)
a.push_back(down[i]);
}
```
## Practice Problems
* [Kattis - Convex Hull](https://open.kattis.com/problems/convexhull)
* [Kattis - Keep the Parade Safe](https://open.kattis.com/problems/parade)
* [URI 1464 - Onion Layers](https://www.urionlinejudge.com.br/judge/en/problems/view/1464)
* [Timus 1185: Wall](http://acm.timus.ru/problem.aspx?space=1&num=1185)
* [Usaco 2014 January Contest, Gold - Cow Curling](http://usaco.org/index.php?page=viewproblem2&cpid=382)
|
Convex Hull construction
|
---
title
voronoi_diagram_2d_n4
---
# Delaunay triangulation and Voronoi diagram
Consider a set $\{p_i\}$ of points on the plane.
A **Voronoi diagram** $V(\{p_i\})$ of $\{p_i\}$ is a partition of the plane into $n$ regions $V_i$, where $V_i = \{p\in\mathbb{R}^2;\ \rho(p, p_i) = \min\ \rho(p, p_k)\}$.
The cells of the Voronoi diagram are polygons (possibly infinite).
A **Delaunay triangulation** $D(\{p_i\})$ of $\{p_i\}$ is a triangulation where every point $p_i$ is outside or on the boundary of the circumcircle of each triangle $T \in D(\{p_i\})$.
There is a nasty degenerated case when the Voronoi diagram isn't connected and Delaunay triangulation doesn't exist. This case is when all points are collinear.
## Properties
The Delaunay triangulation maximizes the minimum angle among all possible triangulations.
The Minimum Euclidean spanning tree of a point set is a subset of edges of its' Delaunay triangulation.
## Duality
Suppose that $\{p_i\}$ is not collinear and among $\{p_i\}$ no four points lie on one circle. Then $V(\{p_i\})$ and $D(\{p_i\})$ are dual, so if we obtain one of them, we may obtain the other in $O(n)$. What to do if it's not the case? The collinear case may be processed easily. Otherwise, $V$ and $D'$ are dual, where $D'$ is obtained from $D$ by removing all the edges such that two triangles on this edge share the circumcircle.
## Building Delaunay and Voronoi
Because of the duality, we only need a fast algorithm to compute only one of $V$ and $D$. We will describe how to build $D(\{p_i\})$ in $O(n\log n)$. The triangulation will be built via divide-and-conquer algorithm due to Guibas and Stolfi.
## Quad-edge data structure
During the algorithm $D$ will be stored inside the quad-edge data structure. This structure is described in the picture:
<center></center>
In the algorithm we will use the following functions on edges:
1. `make_edge(a, b)`<br>
This function creates an isolated edge from point `a` to point `b` together with its' reverse edge and both dual edges.
2. `splice(a, b)`<br>
This is a key function of the algorithm. It swaps `a->Onext` with `b->Onext` and `a->Onext->Rot->Onext` with `b->Onext->Rot->Onext`.
3. `delete_edge(e)`<br>
This function deletes e from the triangulation. To delete `e`, we may simply call `splice(e, e->Oprev)` and `splice(e->Rev, e->Rev->Oprev)`.
4. `connect(a, b)`<br>
This function creates a new edge `e` from `a->Dest` to `b->Org` in such a way that `a`, `b`, `e` all have the same left face. To do this, we call `e = make_edge(a->Dest, b->Org)`, `splice(e, a->Lnext)` and `splice(e->Rev, b)`.
## Algorithm
The algorithm will compute the triangulation and return two quad-edges: the counterclockwise convex hull edge out of the leftmost vertex and the clockwise convex hull edge out of the rightmost vertex.
Let's sort all points by x, and if $x_1 = x_2$ then by y. Let's solve the problem for some segment $(l, r)$ (initially $(l, r) = (0, n - 1)$). If $r - l + 1 = 2$, we will add an edge $(p[l], p[r])$ and return. If $r - l + 1 = 3$, we will firstly add the edges $(p[l], p[l + 1])$ and $(p[l + 1], p[r])$. We must also connect them using `splice(a->Rev, b)`. Now we must close the triangle. Our next action will depend on the orientation of $p[l], p[l + 1], p[r]$. If they are collinear, we can't make a triangle, so we simply return `(a, b->Rev)`. Otherwise, we create a new edge `c` by calling `connect(b, a)`. If the points are oriented counter-clockwise, we return `(a, b->Rev)`. Otherwise we return `(c->Rev, c)`.
Now suppose that $r - l + 1 \ge 4$. Firstly, let's solve $L = (l, \frac{l + r}{2})$ and $R = (\frac{l + r}{2} + 1, r)$ recursively. Now we have to merge these triangulations into one triangulation. Note that our points are sorted, so while merging we will add edges from L to R (so-called _cross_ edges) and remove some edges from L to L and from R to R.
What is the structure of the cross edges? All these edges must cross a line parallel to the y-axis and placed at the splitting x value. This establishes a linear ordering of the cross edges, so we can talk about successive cross edges, the bottom-most cross edge, etc. The algorithm will add the cross edges in ascending order. Note that any two adjacent cross edges will have a common endpoint, and the third side of the triangle they define goes from L to L or from R to R. Let's call the current cross edge the base. The successor of the base will either go from the left endpoint of the base to one of the R-neighbors of the right endpoint or vice versa.
Consider the circumcircle of base and the previous cross edge.
Suppose this circle is transformed into other circles having base as a chord but lying further into the Oy direction.
Our circle will go up for a while, but unless base is an upper tangent of L and R we will encounter a point belonging either to L or to R giving rise to a new triangle without any points in the circumcircle.
The new L-R edge of this triangle is the next cross edge added.
To do this efficiently, we compute two edges `lcand` and `rcand` so that `lcand` points to the first L point encountered in this process, and `rcand` points to the first R point.
Then we choose the one that would be encountered first. Initially base points to the lower tangent of L and R.
## Implementation
Note that the implementation of the in_circle function is GCC-specific.
```{.cpp file=delaunay}
typedef long long ll;
bool ge(const ll& a, const ll& b) { return a >= b; }
bool le(const ll& a, const ll& b) { return a <= b; }
bool eq(const ll& a, const ll& b) { return a == b; }
bool gt(const ll& a, const ll& b) { return a > b; }
bool lt(const ll& a, const ll& b) { return a < b; }
int sgn(const ll& a) { return a >= 0 ? a ? 1 : 0 : -1; }
struct pt {
ll x, y;
pt() { }
pt(ll _x, ll _y) : x(_x), y(_y) { }
pt operator-(const pt& p) const {
return pt(x - p.x, y - p.y);
}
ll cross(const pt& p) const {
return x * p.y - y * p.x;
}
ll cross(const pt& a, const pt& b) const {
return (a - *this).cross(b - *this);
}
ll dot(const pt& p) const {
return x * p.x + y * p.y;
}
ll dot(const pt& a, const pt& b) const {
return (a - *this).dot(b - *this);
}
ll sqrLength() const {
return this->dot(*this);
}
bool operator==(const pt& p) const {
return eq(x, p.x) && eq(y, p.y);
}
};
const pt inf_pt = pt(1e18, 1e18);
struct QuadEdge {
pt origin;
QuadEdge* rot = nullptr;
QuadEdge* onext = nullptr;
bool used = false;
QuadEdge* rev() const {
return rot->rot;
}
QuadEdge* lnext() const {
return rot->rev()->onext->rot;
}
QuadEdge* oprev() const {
return rot->onext->rot;
}
pt dest() const {
return rev()->origin;
}
};
QuadEdge* make_edge(pt from, pt to) {
QuadEdge* e1 = new QuadEdge;
QuadEdge* e2 = new QuadEdge;
QuadEdge* e3 = new QuadEdge;
QuadEdge* e4 = new QuadEdge;
e1->origin = from;
e2->origin = to;
e3->origin = e4->origin = inf_pt;
e1->rot = e3;
e2->rot = e4;
e3->rot = e2;
e4->rot = e1;
e1->onext = e1;
e2->onext = e2;
e3->onext = e4;
e4->onext = e3;
return e1;
}
void splice(QuadEdge* a, QuadEdge* b) {
swap(a->onext->rot->onext, b->onext->rot->onext);
swap(a->onext, b->onext);
}
void delete_edge(QuadEdge* e) {
splice(e, e->oprev());
splice(e->rev(), e->rev()->oprev());
delete e->rev()->rot;
delete e->rev();
delete e->rot;
delete e;
}
QuadEdge* connect(QuadEdge* a, QuadEdge* b) {
QuadEdge* e = make_edge(a->dest(), b->origin);
splice(e, a->lnext());
splice(e->rev(), b);
return e;
}
bool left_of(pt p, QuadEdge* e) {
return gt(p.cross(e->origin, e->dest()), 0);
}
bool right_of(pt p, QuadEdge* e) {
return lt(p.cross(e->origin, e->dest()), 0);
}
template <class T>
T det3(T a1, T a2, T a3, T b1, T b2, T b3, T c1, T c2, T c3) {
return a1 * (b2 * c3 - c2 * b3) - a2 * (b1 * c3 - c1 * b3) +
a3 * (b1 * c2 - c1 * b2);
}
bool in_circle(pt a, pt b, pt c, pt d) {
// If there is __int128, calculate directly.
// Otherwise, calculate angles.
#if defined(__LP64__) || defined(_WIN64)
__int128 det = -det3<__int128>(b.x, b.y, b.sqrLength(), c.x, c.y,
c.sqrLength(), d.x, d.y, d.sqrLength());
det += det3<__int128>(a.x, a.y, a.sqrLength(), c.x, c.y, c.sqrLength(), d.x,
d.y, d.sqrLength());
det -= det3<__int128>(a.x, a.y, a.sqrLength(), b.x, b.y, b.sqrLength(), d.x,
d.y, d.sqrLength());
det += det3<__int128>(a.x, a.y, a.sqrLength(), b.x, b.y, b.sqrLength(), c.x,
c.y, c.sqrLength());
return det > 0;
#else
auto ang = [](pt l, pt mid, pt r) {
ll x = mid.dot(l, r);
ll y = mid.cross(l, r);
long double res = atan2((long double)x, (long double)y);
return res;
};
long double kek = ang(a, b, c) + ang(c, d, a) - ang(b, c, d) - ang(d, a, b);
if (kek > 1e-8)
return true;
else
return false;
#endif
}
pair<QuadEdge*, QuadEdge*> build_tr(int l, int r, vector<pt>& p) {
if (r - l + 1 == 2) {
QuadEdge* res = make_edge(p[l], p[r]);
return make_pair(res, res->rev());
}
if (r - l + 1 == 3) {
QuadEdge *a = make_edge(p[l], p[l + 1]), *b = make_edge(p[l + 1], p[r]);
splice(a->rev(), b);
int sg = sgn(p[l].cross(p[l + 1], p[r]));
if (sg == 0)
return make_pair(a, b->rev());
QuadEdge* c = connect(b, a);
if (sg == 1)
return make_pair(a, b->rev());
else
return make_pair(c->rev(), c);
}
int mid = (l + r) / 2;
QuadEdge *ldo, *ldi, *rdo, *rdi;
tie(ldo, ldi) = build_tr(l, mid, p);
tie(rdi, rdo) = build_tr(mid + 1, r, p);
while (true) {
if (left_of(rdi->origin, ldi)) {
ldi = ldi->lnext();
continue;
}
if (right_of(ldi->origin, rdi)) {
rdi = rdi->rev()->onext;
continue;
}
break;
}
QuadEdge* basel = connect(rdi->rev(), ldi);
auto valid = [&basel](QuadEdge* e) { return right_of(e->dest(), basel); };
if (ldi->origin == ldo->origin)
ldo = basel->rev();
if (rdi->origin == rdo->origin)
rdo = basel;
while (true) {
QuadEdge* lcand = basel->rev()->onext;
if (valid(lcand)) {
while (in_circle(basel->dest(), basel->origin, lcand->dest(),
lcand->onext->dest())) {
QuadEdge* t = lcand->onext;
delete_edge(lcand);
lcand = t;
}
}
QuadEdge* rcand = basel->oprev();
if (valid(rcand)) {
while (in_circle(basel->dest(), basel->origin, rcand->dest(),
rcand->oprev()->dest())) {
QuadEdge* t = rcand->oprev();
delete_edge(rcand);
rcand = t;
}
}
if (!valid(lcand) && !valid(rcand))
break;
if (!valid(lcand) ||
(valid(rcand) && in_circle(lcand->dest(), lcand->origin,
rcand->origin, rcand->dest())))
basel = connect(rcand, basel->rev());
else
basel = connect(basel->rev(), lcand->rev());
}
return make_pair(ldo, rdo);
}
vector<tuple<pt, pt, pt>> delaunay(vector<pt> p) {
sort(p.begin(), p.end(), [](const pt& a, const pt& b) {
return lt(a.x, b.x) || (eq(a.x, b.x) && lt(a.y, b.y));
});
auto res = build_tr(0, (int)p.size() - 1, p);
QuadEdge* e = res.first;
vector<QuadEdge*> edges = {e};
while (lt(e->onext->dest().cross(e->dest(), e->origin), 0))
e = e->onext;
auto add = [&p, &e, &edges]() {
QuadEdge* curr = e;
do {
curr->used = true;
p.push_back(curr->origin);
edges.push_back(curr->rev());
curr = curr->lnext();
} while (curr != e);
};
add();
p.clear();
int kek = 0;
while (kek < (int)edges.size()) {
if (!(e = edges[kek++])->used)
add();
}
vector<tuple<pt, pt, pt>> ans;
for (int i = 0; i < (int)p.size(); i += 3) {
ans.push_back(make_tuple(p[i], p[i + 1], p[i + 2]));
}
return ans;
}
```
|
---
title
voronoi_diagram_2d_n4
---
# Delaunay triangulation and Voronoi diagram
Consider a set $\{p_i\}$ of points on the plane.
A **Voronoi diagram** $V(\{p_i\})$ of $\{p_i\}$ is a partition of the plane into $n$ regions $V_i$, where $V_i = \{p\in\mathbb{R}^2;\ \rho(p, p_i) = \min\ \rho(p, p_k)\}$.
The cells of the Voronoi diagram are polygons (possibly infinite).
A **Delaunay triangulation** $D(\{p_i\})$ of $\{p_i\}$ is a triangulation where every point $p_i$ is outside or on the boundary of the circumcircle of each triangle $T \in D(\{p_i\})$.
There is a nasty degenerated case when the Voronoi diagram isn't connected and Delaunay triangulation doesn't exist. This case is when all points are collinear.
## Properties
The Delaunay triangulation maximizes the minimum angle among all possible triangulations.
The Minimum Euclidean spanning tree of a point set is a subset of edges of its' Delaunay triangulation.
## Duality
Suppose that $\{p_i\}$ is not collinear and among $\{p_i\}$ no four points lie on one circle. Then $V(\{p_i\})$ and $D(\{p_i\})$ are dual, so if we obtain one of them, we may obtain the other in $O(n)$. What to do if it's not the case? The collinear case may be processed easily. Otherwise, $V$ and $D'$ are dual, where $D'$ is obtained from $D$ by removing all the edges such that two triangles on this edge share the circumcircle.
## Building Delaunay and Voronoi
Because of the duality, we only need a fast algorithm to compute only one of $V$ and $D$. We will describe how to build $D(\{p_i\})$ in $O(n\log n)$. The triangulation will be built via divide-and-conquer algorithm due to Guibas and Stolfi.
## Quad-edge data structure
During the algorithm $D$ will be stored inside the quad-edge data structure. This structure is described in the picture:
<center></center>
In the algorithm we will use the following functions on edges:
1. `make_edge(a, b)`<br>
This function creates an isolated edge from point `a` to point `b` together with its' reverse edge and both dual edges.
2. `splice(a, b)`<br>
This is a key function of the algorithm. It swaps `a->Onext` with `b->Onext` and `a->Onext->Rot->Onext` with `b->Onext->Rot->Onext`.
3. `delete_edge(e)`<br>
This function deletes e from the triangulation. To delete `e`, we may simply call `splice(e, e->Oprev)` and `splice(e->Rev, e->Rev->Oprev)`.
4. `connect(a, b)`<br>
This function creates a new edge `e` from `a->Dest` to `b->Org` in such a way that `a`, `b`, `e` all have the same left face. To do this, we call `e = make_edge(a->Dest, b->Org)`, `splice(e, a->Lnext)` and `splice(e->Rev, b)`.
## Algorithm
The algorithm will compute the triangulation and return two quad-edges: the counterclockwise convex hull edge out of the leftmost vertex and the clockwise convex hull edge out of the rightmost vertex.
Let's sort all points by x, and if $x_1 = x_2$ then by y. Let's solve the problem for some segment $(l, r)$ (initially $(l, r) = (0, n - 1)$). If $r - l + 1 = 2$, we will add an edge $(p[l], p[r])$ and return. If $r - l + 1 = 3$, we will firstly add the edges $(p[l], p[l + 1])$ and $(p[l + 1], p[r])$. We must also connect them using `splice(a->Rev, b)`. Now we must close the triangle. Our next action will depend on the orientation of $p[l], p[l + 1], p[r]$. If they are collinear, we can't make a triangle, so we simply return `(a, b->Rev)`. Otherwise, we create a new edge `c` by calling `connect(b, a)`. If the points are oriented counter-clockwise, we return `(a, b->Rev)`. Otherwise we return `(c->Rev, c)`.
Now suppose that $r - l + 1 \ge 4$. Firstly, let's solve $L = (l, \frac{l + r}{2})$ and $R = (\frac{l + r}{2} + 1, r)$ recursively. Now we have to merge these triangulations into one triangulation. Note that our points are sorted, so while merging we will add edges from L to R (so-called _cross_ edges) and remove some edges from L to L and from R to R.
What is the structure of the cross edges? All these edges must cross a line parallel to the y-axis and placed at the splitting x value. This establishes a linear ordering of the cross edges, so we can talk about successive cross edges, the bottom-most cross edge, etc. The algorithm will add the cross edges in ascending order. Note that any two adjacent cross edges will have a common endpoint, and the third side of the triangle they define goes from L to L or from R to R. Let's call the current cross edge the base. The successor of the base will either go from the left endpoint of the base to one of the R-neighbors of the right endpoint or vice versa.
Consider the circumcircle of base and the previous cross edge.
Suppose this circle is transformed into other circles having base as a chord but lying further into the Oy direction.
Our circle will go up for a while, but unless base is an upper tangent of L and R we will encounter a point belonging either to L or to R giving rise to a new triangle without any points in the circumcircle.
The new L-R edge of this triangle is the next cross edge added.
To do this efficiently, we compute two edges `lcand` and `rcand` so that `lcand` points to the first L point encountered in this process, and `rcand` points to the first R point.
Then we choose the one that would be encountered first. Initially base points to the lower tangent of L and R.
## Implementation
Note that the implementation of the in_circle function is GCC-specific.
```{.cpp file=delaunay}
typedef long long ll;
bool ge(const ll& a, const ll& b) { return a >= b; }
bool le(const ll& a, const ll& b) { return a <= b; }
bool eq(const ll& a, const ll& b) { return a == b; }
bool gt(const ll& a, const ll& b) { return a > b; }
bool lt(const ll& a, const ll& b) { return a < b; }
int sgn(const ll& a) { return a >= 0 ? a ? 1 : 0 : -1; }
struct pt {
ll x, y;
pt() { }
pt(ll _x, ll _y) : x(_x), y(_y) { }
pt operator-(const pt& p) const {
return pt(x - p.x, y - p.y);
}
ll cross(const pt& p) const {
return x * p.y - y * p.x;
}
ll cross(const pt& a, const pt& b) const {
return (a - *this).cross(b - *this);
}
ll dot(const pt& p) const {
return x * p.x + y * p.y;
}
ll dot(const pt& a, const pt& b) const {
return (a - *this).dot(b - *this);
}
ll sqrLength() const {
return this->dot(*this);
}
bool operator==(const pt& p) const {
return eq(x, p.x) && eq(y, p.y);
}
};
const pt inf_pt = pt(1e18, 1e18);
struct QuadEdge {
pt origin;
QuadEdge* rot = nullptr;
QuadEdge* onext = nullptr;
bool used = false;
QuadEdge* rev() const {
return rot->rot;
}
QuadEdge* lnext() const {
return rot->rev()->onext->rot;
}
QuadEdge* oprev() const {
return rot->onext->rot;
}
pt dest() const {
return rev()->origin;
}
};
QuadEdge* make_edge(pt from, pt to) {
QuadEdge* e1 = new QuadEdge;
QuadEdge* e2 = new QuadEdge;
QuadEdge* e3 = new QuadEdge;
QuadEdge* e4 = new QuadEdge;
e1->origin = from;
e2->origin = to;
e3->origin = e4->origin = inf_pt;
e1->rot = e3;
e2->rot = e4;
e3->rot = e2;
e4->rot = e1;
e1->onext = e1;
e2->onext = e2;
e3->onext = e4;
e4->onext = e3;
return e1;
}
void splice(QuadEdge* a, QuadEdge* b) {
swap(a->onext->rot->onext, b->onext->rot->onext);
swap(a->onext, b->onext);
}
void delete_edge(QuadEdge* e) {
splice(e, e->oprev());
splice(e->rev(), e->rev()->oprev());
delete e->rev()->rot;
delete e->rev();
delete e->rot;
delete e;
}
QuadEdge* connect(QuadEdge* a, QuadEdge* b) {
QuadEdge* e = make_edge(a->dest(), b->origin);
splice(e, a->lnext());
splice(e->rev(), b);
return e;
}
bool left_of(pt p, QuadEdge* e) {
return gt(p.cross(e->origin, e->dest()), 0);
}
bool right_of(pt p, QuadEdge* e) {
return lt(p.cross(e->origin, e->dest()), 0);
}
template <class T>
T det3(T a1, T a2, T a3, T b1, T b2, T b3, T c1, T c2, T c3) {
return a1 * (b2 * c3 - c2 * b3) - a2 * (b1 * c3 - c1 * b3) +
a3 * (b1 * c2 - c1 * b2);
}
bool in_circle(pt a, pt b, pt c, pt d) {
// If there is __int128, calculate directly.
// Otherwise, calculate angles.
#if defined(__LP64__) || defined(_WIN64)
__int128 det = -det3<__int128>(b.x, b.y, b.sqrLength(), c.x, c.y,
c.sqrLength(), d.x, d.y, d.sqrLength());
det += det3<__int128>(a.x, a.y, a.sqrLength(), c.x, c.y, c.sqrLength(), d.x,
d.y, d.sqrLength());
det -= det3<__int128>(a.x, a.y, a.sqrLength(), b.x, b.y, b.sqrLength(), d.x,
d.y, d.sqrLength());
det += det3<__int128>(a.x, a.y, a.sqrLength(), b.x, b.y, b.sqrLength(), c.x,
c.y, c.sqrLength());
return det > 0;
#else
auto ang = [](pt l, pt mid, pt r) {
ll x = mid.dot(l, r);
ll y = mid.cross(l, r);
long double res = atan2((long double)x, (long double)y);
return res;
};
long double kek = ang(a, b, c) + ang(c, d, a) - ang(b, c, d) - ang(d, a, b);
if (kek > 1e-8)
return true;
else
return false;
#endif
}
pair<QuadEdge*, QuadEdge*> build_tr(int l, int r, vector<pt>& p) {
if (r - l + 1 == 2) {
QuadEdge* res = make_edge(p[l], p[r]);
return make_pair(res, res->rev());
}
if (r - l + 1 == 3) {
QuadEdge *a = make_edge(p[l], p[l + 1]), *b = make_edge(p[l + 1], p[r]);
splice(a->rev(), b);
int sg = sgn(p[l].cross(p[l + 1], p[r]));
if (sg == 0)
return make_pair(a, b->rev());
QuadEdge* c = connect(b, a);
if (sg == 1)
return make_pair(a, b->rev());
else
return make_pair(c->rev(), c);
}
int mid = (l + r) / 2;
QuadEdge *ldo, *ldi, *rdo, *rdi;
tie(ldo, ldi) = build_tr(l, mid, p);
tie(rdi, rdo) = build_tr(mid + 1, r, p);
while (true) {
if (left_of(rdi->origin, ldi)) {
ldi = ldi->lnext();
continue;
}
if (right_of(ldi->origin, rdi)) {
rdi = rdi->rev()->onext;
continue;
}
break;
}
QuadEdge* basel = connect(rdi->rev(), ldi);
auto valid = [&basel](QuadEdge* e) { return right_of(e->dest(), basel); };
if (ldi->origin == ldo->origin)
ldo = basel->rev();
if (rdi->origin == rdo->origin)
rdo = basel;
while (true) {
QuadEdge* lcand = basel->rev()->onext;
if (valid(lcand)) {
while (in_circle(basel->dest(), basel->origin, lcand->dest(),
lcand->onext->dest())) {
QuadEdge* t = lcand->onext;
delete_edge(lcand);
lcand = t;
}
}
QuadEdge* rcand = basel->oprev();
if (valid(rcand)) {
while (in_circle(basel->dest(), basel->origin, rcand->dest(),
rcand->oprev()->dest())) {
QuadEdge* t = rcand->oprev();
delete_edge(rcand);
rcand = t;
}
}
if (!valid(lcand) && !valid(rcand))
break;
if (!valid(lcand) ||
(valid(rcand) && in_circle(lcand->dest(), lcand->origin,
rcand->origin, rcand->dest())))
basel = connect(rcand, basel->rev());
else
basel = connect(basel->rev(), lcand->rev());
}
return make_pair(ldo, rdo);
}
vector<tuple<pt, pt, pt>> delaunay(vector<pt> p) {
sort(p.begin(), p.end(), [](const pt& a, const pt& b) {
return lt(a.x, b.x) || (eq(a.x, b.x) && lt(a.y, b.y));
});
auto res = build_tr(0, (int)p.size() - 1, p);
QuadEdge* e = res.first;
vector<QuadEdge*> edges = {e};
while (lt(e->onext->dest().cross(e->dest(), e->origin), 0))
e = e->onext;
auto add = [&p, &e, &edges]() {
QuadEdge* curr = e;
do {
curr->used = true;
p.push_back(curr->origin);
edges.push_back(curr->rev());
curr = curr->lnext();
} while (curr != e);
};
add();
p.clear();
int kek = 0;
while (kek < (int)edges.size()) {
if (!(e = edges[kek++])->used)
add();
}
vector<tuple<pt, pt, pt>> ans;
for (int i = 0; i < (int)p.size(); i += 3) {
ans.push_back(make_tuple(p[i], p[i + 1], p[i + 2]));
}
return ans;
}
```
## Problems
* [TIMUS 1504 Good Manners](http://acm.timus.ru/problem.aspx?space=1&num=1504)
* [TIMUS 1520 Empire Strikes Back](http://acm.timus.ru/problem.aspx?space=1&num=1520)
* [SGU 383 Caravans](https://codeforces.com/problemsets/acmsguru/problem/99999/383)
|
Delaunay triangulation and Voronoi diagram
|
---
title
nearest_points
---
# Finding the nearest pair of points
## Problem statement
Given $n$ points on the plane. Each point $p_i$ is defined by its coordinates $(x_i,y_i)$. It is required to find among them two such points, such that the distance between them is minimal:
$$ \min_{\scriptstyle i, j=0 \ldots n-1,\atop \scriptstyle i \neq j } \rho (p_i, p_j). $$
We take the usual Euclidean distances:
$$ \rho (p_i,p_j) = \sqrt{(x_i-x_j)^2 + (y_i-y_j)^2} .$$
The trivial algorithm - iterating over all pairs and calculating the distance for each — works in $O(n^2)$.
The algorithm running in time $O(n \log n)$ is described below. This algorithm was proposed by Shamos and Hoey in 1975. (Source: Ch. 5 Notes of _Algorithm Design_ by Kleinberg & Tardos, also see [here](https://ieeexplore.ieee.org/abstract/document/4567872)) Preparata and Shamos also showed that this algorithm is optimal in the decision tree model.
## Algorithm
We construct an algorithm according to the general scheme of **divide-and-conquer** algorithms: the algorithm is designed as a recursive function, to which we pass a set of points; this recursive function splits this set in half, calls itself recursively on each half, and then performs some operations to combine the answers. The operation of combining consist of detecting the cases when one point of the optimal solution fell into one half, and the other point into the other (in this case, recursive calls from each of the halves cannot detect this pair separately). The main difficulty, as always in case of divide and conquer algorithms, lies in the effective implementation of the merging stage. If a set of $n$ points is passed to the recursive function, then the merge stage should work no more than $O(n)$, then the asymptotics of the whole algorithm $T(n)$ will be found from the equation:
$$T(n) = 2T(n/2) + O(n).$$
The solution to this equation, as is known, is $T(n) = O(n \log n).$
So, we proceed on to the construction of the algorithm. In order to come to an effective implementation of the merge stage in the future, we will divide the set of points into two subsets, according to their $x$-coordinates: In fact, we draw some vertical line dividing the set of points into two subsets of approximately the same size. It is convenient to make such a partition as follows: We sort the points in the standard way as pairs of numbers, ie.:
$$p_i < p_j \Longleftrightarrow (x_i < x_j) \lor \Big(\left(x_i = x_j\right) \wedge \left(y_i < y_j \right) \Big) $$
Then take the middle point after sorting $p_m (m = \lfloor n/2 \rfloor)$, and all the points before it and the $p_m$ itself are assigned to the first half, and all the points after it - to the second half:
$$A_1 = \{p_i \ | \ i = 0 \ldots m \}$$
$$A_2 = \{p_i \ | \ i = m + 1 \ldots n-1 \}.$$
Now, calling recursively on each of the sets $A_1$ and $A_2$, we will find the answers $h_1$ and $h_2$ for each of the halves. And take the best of them: $h = \min(h_1, h_2)$.
Now we need to make a **merge stage**, i.e. we try to find such pairs of points, for which the distance between which is less than $h$ and one point is lying in $A_1$ and the other in $A_2$.
It is obvious that it is sufficient to consider only those points that are separated from the vertical line by a distance less than $h$, i.e. the set $B$ of the points considered at this stage is equal to:
$$B = \{ p_i\ | \ | x_i - x_m\ | < h \}.$$
For each point in the set $B$, we try to find the points that are closer to it than $h$. For example, it is sufficient to consider only those points whose $y$-coordinate differs by no more than $h$. Moreover, it makes no sense to consider those points whose $y$-coordinate is greater than the $y$-coordinate of the current point. Thus, for each point $p_i$ we define the set of considered points $C(p_i)$ as follows:
$$C(p_i) = \{ p_j\ |\ p_j \in B,\ \ y_i - h < y_j \le y_i \}.$$
If we sort the points of the set $B$ by $y$-coordinate, it will be very easy to find $C(p_i)$: these are several points in a row ahead to the point $p_i$.
So, in the new notation, the **merging stage** looks like this: build a set $B$, sort the points in it by $y$-coordinate, then for each point $p_i \in B$ consider all points $p_j \in C(p_i)$, and for each pair $(p_i,p_j)$ calculate the distance and compare with the current best distance.
At first glance, this is still a non-optimal algorithm: it seems that the sizes of sets $C(p_i)$ will be of order $n$, and the required asymptotics will not work. However, surprisingly, it can be proved that the size of each of the sets $C(p_i)$ is a quantity $O(1)$, i.e. it does not exceed some small constant regardless of the points themselves. Proof of this fact is given in the next section.
Finally, we pay attention to the sorting, which the above algorithm contains: first,sorting by pairs $(x, y)$, and then second, sorting the elements of the set $B$ by $y$. In fact, both of these sorts inside the recursive function can be eliminated (otherwise we would not reach the $O(n)$ estimate for the **merging stage**, and the general asymptotics of the algorithm would be $O(n \log^2 n)$). It is easy to get rid of the first sort — it is enough to perform this sort before starting the recursion: after all, the elements themselves do not change inside the recursion, so there is no need to sort again. With the second sorting a little more difficult to perform, performing it previously will not work. But, remembering the merge sort, which also works on the principle of divide-and-conquer, we can simply embed this sort in our recursion. Let recursion, taking some set of points (as we remember,ordered by pairs $(x, y)$), return the same set, but sorted by the $y$-coordinate. To do this, simply merge (in $O(n)$) the two results returned by recursive calls. This will result in a set sorted by $y$-coordinate.
## Evaluation of the asymptotics
To show that the above algorithm is actually executed in $O(n \log n)$, we need to prove the following fact: $|C(p_i)| = O(1)$.
So, let us consider some point $p_i$; recall that the set $C(p_i)$ is a set of points whose $y$-coordinate lies in the segment $[y_i-h; y_i]$, and, moreover, along the $x$ coordinate, the point $p_i$ itself, and all the points of the set $C(p_i)$ lie in the band width $2h$. In other words, the points we are considering $p_i$ and $C(p_i)$ lie in a rectangle of size $2h \times h$.
Our task is to estimate the maximum number of points that can lie in this rectangle $2h \times h$; thus, we estimate the maximum size of the set $C(p_i)$. At the same time, when evaluating, we must not forget that there may be repeated points.
Remember that $h$ was obtained from the results of two recursive calls — on sets $A_1$ and $A_2$, and $A_1$ contains points to the left of the partition line and partially on it, $A_2$ contains the remaining points of the partition line and points to the right of it. For any pair of points from $A_1$, as well as from $A_2$, the distance can not be less than $h$ — otherwise it would mean incorrect operation of the recursive function.
To estimate the maximum number of points in the rectangle $2h \times h$ we divide it into two squares $h \times h$, the first square include all points $C(p_i) \cap A_1$, and the second contains all the others, i.e. $C(p_i) \cap A_2$. It follows from the above considerations that in each of these squares the distance between any two points is at least $h$.
We show that there are at most four points in each square. For example, this can be done as follows: divide the square into $4$ sub-squares with sides $h/2$. Then there can be no more than one point in each of these sub-squares (since even the diagonal is equal to $h / \sqrt{2}$, which is less than $h$). Therefore, there can be no more than $4$ points in the whole square.
So, we have proved that in a rectangle $2h \times h$ can not be more than $4 \cdot 2 = 8$ points, and, therefore, the size of the set $C(p_i)$ cannot exceed $7$, as required.
## Implementation
We introduce a data structure to store a point (its coordinates and a number) and comparison operators required for two types of sorting:
```{.cpp file=nearest_pair_def}
struct pt {
int x, y, id;
};
struct cmp_x {
bool operator()(const pt & a, const pt & b) const {
return a.x < b.x || (a.x == b.x && a.y < b.y);
}
};
struct cmp_y {
bool operator()(const pt & a, const pt & b) const {
return a.y < b.y;
}
};
int n;
vector<pt> a;
```
For a convenient implementation of recursion, we introduce an auxiliary function upd_ans(), which will calculate the distance between two points and check whether it is better than the current answer:
```{.cpp file=nearest_pair_update}
double mindist;
pair<int, int> best_pair;
void upd_ans(const pt & a, const pt & b) {
double dist = sqrt((a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y));
if (dist < mindist) {
mindist = dist;
best_pair = {a.id, b.id};
}
}
```
Finally, the implementation of the recursion itself. It is assumed that before calling it, the array $a[]$ is already sorted by $x$-coordinate. In recursion we pass just two pointers $l, r$, which indicate that it should look for the answer for $a[l \ldots r)$. If the distance between $r$ and $l$ is too small, the recursion must be stopped, and perform a trivial algorithm to find the nearest pair and then sort the subarray by $y$-coordinate.
To merge two sets of points received from recursive calls into one (ordered by $y$-coordinate), we use the standard STL $merge()$ function, and create an auxiliary buffer $t[]$(one for all recursive calls). (Using inplace_merge () is impractical because it generally does not work in linear time.)
Finally, the set $B$ is stored in the same array $t$.
```{.cpp file=nearest_pair_rec}
vector<pt> t;
void rec(int l, int r) {
if (r - l <= 3) {
for (int i = l; i < r; ++i) {
for (int j = i + 1; j < r; ++j) {
upd_ans(a[i], a[j]);
}
}
sort(a.begin() + l, a.begin() + r, cmp_y());
return;
}
int m = (l + r) >> 1;
int midx = a[m].x;
rec(l, m);
rec(m, r);
merge(a.begin() + l, a.begin() + m, a.begin() + m, a.begin() + r, t.begin(), cmp_y());
copy(t.begin(), t.begin() + r - l, a.begin() + l);
int tsz = 0;
for (int i = l; i < r; ++i) {
if (abs(a[i].x - midx) < mindist) {
for (int j = tsz - 1; j >= 0 && a[i].y - t[j].y < mindist; --j)
upd_ans(a[i], t[j]);
t[tsz++] = a[i];
}
}
}
```
By the way, if all the coordinates are integer, then at the time of the recursion you can not move to fractional values, and store in $mindist$ the square of the minimum distance.
In the main program, recursion should be called as follows:
```{.cpp file=nearest_pair_main}
t.resize(n);
sort(a.begin(), a.end(), cmp_x());
mindist = 1E20;
rec(0, n);
```
## Generalization: finding a triangle with minimal perimeter
The algorithm described above is interestingly generalized to this problem: among a given set of points, choose three different points so that the sum of pairwise distances between them is the smallest.
In fact, to solve this problem, the algorithm remains the same: we divide the field into two halves of the vertical line, call the solution recursively on both halves, choose the minimum $minper$ from the found perimeters, build a strip with the thickness of $minper / 2$, and iterate through all triangles that can improve the answer. (Note that the triangle with perimeter $\le minper$ has the longest side $\le minper / 2$.)
|
---
title
nearest_points
---
# Finding the nearest pair of points
## Problem statement
Given $n$ points on the plane. Each point $p_i$ is defined by its coordinates $(x_i,y_i)$. It is required to find among them two such points, such that the distance between them is minimal:
$$ \min_{\scriptstyle i, j=0 \ldots n-1,\atop \scriptstyle i \neq j } \rho (p_i, p_j). $$
We take the usual Euclidean distances:
$$ \rho (p_i,p_j) = \sqrt{(x_i-x_j)^2 + (y_i-y_j)^2} .$$
The trivial algorithm - iterating over all pairs and calculating the distance for each — works in $O(n^2)$.
The algorithm running in time $O(n \log n)$ is described below. This algorithm was proposed by Shamos and Hoey in 1975. (Source: Ch. 5 Notes of _Algorithm Design_ by Kleinberg & Tardos, also see [here](https://ieeexplore.ieee.org/abstract/document/4567872)) Preparata and Shamos also showed that this algorithm is optimal in the decision tree model.
## Algorithm
We construct an algorithm according to the general scheme of **divide-and-conquer** algorithms: the algorithm is designed as a recursive function, to which we pass a set of points; this recursive function splits this set in half, calls itself recursively on each half, and then performs some operations to combine the answers. The operation of combining consist of detecting the cases when one point of the optimal solution fell into one half, and the other point into the other (in this case, recursive calls from each of the halves cannot detect this pair separately). The main difficulty, as always in case of divide and conquer algorithms, lies in the effective implementation of the merging stage. If a set of $n$ points is passed to the recursive function, then the merge stage should work no more than $O(n)$, then the asymptotics of the whole algorithm $T(n)$ will be found from the equation:
$$T(n) = 2T(n/2) + O(n).$$
The solution to this equation, as is known, is $T(n) = O(n \log n).$
So, we proceed on to the construction of the algorithm. In order to come to an effective implementation of the merge stage in the future, we will divide the set of points into two subsets, according to their $x$-coordinates: In fact, we draw some vertical line dividing the set of points into two subsets of approximately the same size. It is convenient to make such a partition as follows: We sort the points in the standard way as pairs of numbers, ie.:
$$p_i < p_j \Longleftrightarrow (x_i < x_j) \lor \Big(\left(x_i = x_j\right) \wedge \left(y_i < y_j \right) \Big) $$
Then take the middle point after sorting $p_m (m = \lfloor n/2 \rfloor)$, and all the points before it and the $p_m$ itself are assigned to the first half, and all the points after it - to the second half:
$$A_1 = \{p_i \ | \ i = 0 \ldots m \}$$
$$A_2 = \{p_i \ | \ i = m + 1 \ldots n-1 \}.$$
Now, calling recursively on each of the sets $A_1$ and $A_2$, we will find the answers $h_1$ and $h_2$ for each of the halves. And take the best of them: $h = \min(h_1, h_2)$.
Now we need to make a **merge stage**, i.e. we try to find such pairs of points, for which the distance between which is less than $h$ and one point is lying in $A_1$ and the other in $A_2$.
It is obvious that it is sufficient to consider only those points that are separated from the vertical line by a distance less than $h$, i.e. the set $B$ of the points considered at this stage is equal to:
$$B = \{ p_i\ | \ | x_i - x_m\ | < h \}.$$
For each point in the set $B$, we try to find the points that are closer to it than $h$. For example, it is sufficient to consider only those points whose $y$-coordinate differs by no more than $h$. Moreover, it makes no sense to consider those points whose $y$-coordinate is greater than the $y$-coordinate of the current point. Thus, for each point $p_i$ we define the set of considered points $C(p_i)$ as follows:
$$C(p_i) = \{ p_j\ |\ p_j \in B,\ \ y_i - h < y_j \le y_i \}.$$
If we sort the points of the set $B$ by $y$-coordinate, it will be very easy to find $C(p_i)$: these are several points in a row ahead to the point $p_i$.
So, in the new notation, the **merging stage** looks like this: build a set $B$, sort the points in it by $y$-coordinate, then for each point $p_i \in B$ consider all points $p_j \in C(p_i)$, and for each pair $(p_i,p_j)$ calculate the distance and compare with the current best distance.
At first glance, this is still a non-optimal algorithm: it seems that the sizes of sets $C(p_i)$ will be of order $n$, and the required asymptotics will not work. However, surprisingly, it can be proved that the size of each of the sets $C(p_i)$ is a quantity $O(1)$, i.e. it does not exceed some small constant regardless of the points themselves. Proof of this fact is given in the next section.
Finally, we pay attention to the sorting, which the above algorithm contains: first,sorting by pairs $(x, y)$, and then second, sorting the elements of the set $B$ by $y$. In fact, both of these sorts inside the recursive function can be eliminated (otherwise we would not reach the $O(n)$ estimate for the **merging stage**, and the general asymptotics of the algorithm would be $O(n \log^2 n)$). It is easy to get rid of the first sort — it is enough to perform this sort before starting the recursion: after all, the elements themselves do not change inside the recursion, so there is no need to sort again. With the second sorting a little more difficult to perform, performing it previously will not work. But, remembering the merge sort, which also works on the principle of divide-and-conquer, we can simply embed this sort in our recursion. Let recursion, taking some set of points (as we remember,ordered by pairs $(x, y)$), return the same set, but sorted by the $y$-coordinate. To do this, simply merge (in $O(n)$) the two results returned by recursive calls. This will result in a set sorted by $y$-coordinate.
## Evaluation of the asymptotics
To show that the above algorithm is actually executed in $O(n \log n)$, we need to prove the following fact: $|C(p_i)| = O(1)$.
So, let us consider some point $p_i$; recall that the set $C(p_i)$ is a set of points whose $y$-coordinate lies in the segment $[y_i-h; y_i]$, and, moreover, along the $x$ coordinate, the point $p_i$ itself, and all the points of the set $C(p_i)$ lie in the band width $2h$. In other words, the points we are considering $p_i$ and $C(p_i)$ lie in a rectangle of size $2h \times h$.
Our task is to estimate the maximum number of points that can lie in this rectangle $2h \times h$; thus, we estimate the maximum size of the set $C(p_i)$. At the same time, when evaluating, we must not forget that there may be repeated points.
Remember that $h$ was obtained from the results of two recursive calls — on sets $A_1$ and $A_2$, and $A_1$ contains points to the left of the partition line and partially on it, $A_2$ contains the remaining points of the partition line and points to the right of it. For any pair of points from $A_1$, as well as from $A_2$, the distance can not be less than $h$ — otherwise it would mean incorrect operation of the recursive function.
To estimate the maximum number of points in the rectangle $2h \times h$ we divide it into two squares $h \times h$, the first square include all points $C(p_i) \cap A_1$, and the second contains all the others, i.e. $C(p_i) \cap A_2$. It follows from the above considerations that in each of these squares the distance between any two points is at least $h$.
We show that there are at most four points in each square. For example, this can be done as follows: divide the square into $4$ sub-squares with sides $h/2$. Then there can be no more than one point in each of these sub-squares (since even the diagonal is equal to $h / \sqrt{2}$, which is less than $h$). Therefore, there can be no more than $4$ points in the whole square.
So, we have proved that in a rectangle $2h \times h$ can not be more than $4 \cdot 2 = 8$ points, and, therefore, the size of the set $C(p_i)$ cannot exceed $7$, as required.
## Implementation
We introduce a data structure to store a point (its coordinates and a number) and comparison operators required for two types of sorting:
```{.cpp file=nearest_pair_def}
struct pt {
int x, y, id;
};
struct cmp_x {
bool operator()(const pt & a, const pt & b) const {
return a.x < b.x || (a.x == b.x && a.y < b.y);
}
};
struct cmp_y {
bool operator()(const pt & a, const pt & b) const {
return a.y < b.y;
}
};
int n;
vector<pt> a;
```
For a convenient implementation of recursion, we introduce an auxiliary function upd_ans(), which will calculate the distance between two points and check whether it is better than the current answer:
```{.cpp file=nearest_pair_update}
double mindist;
pair<int, int> best_pair;
void upd_ans(const pt & a, const pt & b) {
double dist = sqrt((a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y));
if (dist < mindist) {
mindist = dist;
best_pair = {a.id, b.id};
}
}
```
Finally, the implementation of the recursion itself. It is assumed that before calling it, the array $a[]$ is already sorted by $x$-coordinate. In recursion we pass just two pointers $l, r$, which indicate that it should look for the answer for $a[l \ldots r)$. If the distance between $r$ and $l$ is too small, the recursion must be stopped, and perform a trivial algorithm to find the nearest pair and then sort the subarray by $y$-coordinate.
To merge two sets of points received from recursive calls into one (ordered by $y$-coordinate), we use the standard STL $merge()$ function, and create an auxiliary buffer $t[]$(one for all recursive calls). (Using inplace_merge () is impractical because it generally does not work in linear time.)
Finally, the set $B$ is stored in the same array $t$.
```{.cpp file=nearest_pair_rec}
vector<pt> t;
void rec(int l, int r) {
if (r - l <= 3) {
for (int i = l; i < r; ++i) {
for (int j = i + 1; j < r; ++j) {
upd_ans(a[i], a[j]);
}
}
sort(a.begin() + l, a.begin() + r, cmp_y());
return;
}
int m = (l + r) >> 1;
int midx = a[m].x;
rec(l, m);
rec(m, r);
merge(a.begin() + l, a.begin() + m, a.begin() + m, a.begin() + r, t.begin(), cmp_y());
copy(t.begin(), t.begin() + r - l, a.begin() + l);
int tsz = 0;
for (int i = l; i < r; ++i) {
if (abs(a[i].x - midx) < mindist) {
for (int j = tsz - 1; j >= 0 && a[i].y - t[j].y < mindist; --j)
upd_ans(a[i], t[j]);
t[tsz++] = a[i];
}
}
}
```
By the way, if all the coordinates are integer, then at the time of the recursion you can not move to fractional values, and store in $mindist$ the square of the minimum distance.
In the main program, recursion should be called as follows:
```{.cpp file=nearest_pair_main}
t.resize(n);
sort(a.begin(), a.end(), cmp_x());
mindist = 1E20;
rec(0, n);
```
## Generalization: finding a triangle with minimal perimeter
The algorithm described above is interestingly generalized to this problem: among a given set of points, choose three different points so that the sum of pairwise distances between them is the smallest.
In fact, to solve this problem, the algorithm remains the same: we divide the field into two halves of the vertical line, call the solution recursively on both halves, choose the minimum $minper$ from the found perimeters, build a strip with the thickness of $minper / 2$, and iterate through all triangles that can improve the answer. (Note that the triangle with perimeter $\le minper$ has the longest side $\le minper / 2$.)
## Practice problems
* [UVA 10245 "The Closest Pair Problem" [difficulty: low]](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=1186)
* [SPOJ #8725 CLOPPAIR "Closest Point Pair" [difficulty: low]](https://www.spoj.com/problems/CLOPPAIR/)
* [CODEFORCES Team Olympiad Saratov - 2011 "Minimum amount" [difficulty: medium]](http://codeforces.com/contest/120/problem/J)
* [Google CodeJam 2009 Final " Min Perimeter "[difficulty: medium]](https://code.google.com/codejam/contest/311101/dashboard#s=a&a=1)
* [SPOJ #7029 CLOSEST "Closest Triple" [difficulty: medium]](https://www.spoj.com/problems/CLOSEST/)
* [TIMUS 1514 National Park [difficulty: medium]](https://acm.timus.ru/problem.aspx?space=1&num=1514)
|
Finding the nearest pair of points
|
---
title: Point location in O(log n)
title
- Original
---
# Point location in $O(log n)$
Consider the following problem: you are given a [planar subdivision](https://en.wikipedia.org/wiki/Planar_straight-line_graph) without no vertices of degree one and zero, and a lot of queries.
Each query is a point, for which we should determine the face of the subdivision it belongs to.
We will answer each query in $O(\log n)$ offline.<br>
This problem may arise when you need to locate some points in a Voronoi diagram or in some simple polygon.
## Algorithm
Firstly, for each query point $p\ (x_0, y_0)$ we want to find such an edge that if the point belongs to any edge, the point lies on the edge we found, otherwise this edge must intersect the line $x = x_0$ at some unique point $(x_0, y)$ where $y < y_0$ and this $y$ is maximum among all such edges.
The following image shows both cases.
<center></center>
We will solve this problem offline using the sweep line algorithm. Let's iterate over x-coordinates of query points and edges' endpoints in increasing order and keep a set of edges $s$. For each x-coordinate we will add some events beforehand.
The events will be of four types: _add_, _remove_, _vertical_, _get_.
For each vertical edge (both endpoints have the same x-coordinate) we will add one _vertical_ event for the corresponding x-coordinate.
For every other edge we will add one _add_ event for the minimum of x-coordinates of the endpoints and one _remove_ event for the maximum of x-coordinates of the endpoints.
Finally, for each query point we will add one _get_ event for its x-coordinate.
For each x-coordinate we will sort the events by their types in order (_vertical_, _get_, _remove_, _add_).
The following image shows all events in sorted order for each x-coordinate.
<center></center>
We will keep two sets during the sweep-line process.
A set $t$ for all non-vertical edges, and one set $vert$ especially for the vertical ones.
We will clear the set $vert$ at the beginning of processing each x-coordinate.
Now let's process the events for a fixed x-coordinate.
- If we got a _vertical_ event, we will simply insert the minimum y-coordinate of the corresponding edge's endpoints to $vert$.
- If we got a _remove_ or _add_ event, we will remove the corresponding edge from $t$ or add it to $t$.
- Finally, for each _get_ event we must check if the point lies on some vertical edge by performing a binary search in $vert$.
If the point doesn't lie on any vertical edge, we must find the answer for this query in $t$.
To do this, we again make a binary search.
In order to handle some degenerate cases (e.g. in case of the triangle $(0,~0)$, $(0,~2)$, $(1, 1)$ when we query the point $(0,~0)$), we must answer all _get_ events again after we processed all the events for this x-coordinate and choose the best of two answers.
Now let's choose a comparator for the set $t$.
This comparator should check if one edge doesn't lie above other for every x-coordinate they both cover. Suppose that we have two edges $(a, b)$ and $(c, d)$. Then the comparator is (in pseudocode):<br>
$val = sgn((b - a)\times(c - a)) + sgn((b - a)\times(d - a))$<br>
<b>if</b> $val \neq 0$<br>
<b>then return</b> $val > 0$<br>
$val = sgn((d - c)\times(a - c)) + sgn((d - c)\times(b - c))$<br>
<b>return</b> $val < 0$<br>
Now for every query we have the corresponding edge.
How to find the face?
If we couldn't find the edge it means that the point is in the outer face.
If the point belongs to the edge we found, the face is not unique.
Otherwise, there are two candidates - the faces that are bounded by this edge.
How to check which one is the answer? Note that the edge is not vertical.
Then the answer is the face that is above this edge.
Let's find such a face for each non-vertical edge.
Consider a counter-clockwise traversal of each face.
If during this traversal we increased x-coordinate while passing through the edge, then this face is the face we need to find for this edge.
## Notes
Actually, with persistent trees this approach can be used to answer the queries online.
## Implementation
The following code is implemented for integers, but it can be easily modified to work with doubles (by changing the compare methods and the point type).
This implementation assumes that the subdivision is correctly stored inside a [DCEL](https://en.wikipedia.org/wiki/Doubly_connected_edge_list) and the outer face is numbered $-1$.<br>
For each query a pair $(1, i)$ is returned if the point lies strictly inside the face number $i$, and a pair $(0, i)$ is returned if the point lies on the edge number $i$.
```{.cpp file=point-location}
typedef long long ll;
bool ge(const ll& a, const ll& b) { return a >= b; }
bool le(const ll& a, const ll& b) { return a <= b; }
bool eq(const ll& a, const ll& b) { return a == b; }
bool gt(const ll& a, const ll& b) { return a > b; }
bool lt(const ll& a, const ll& b) { return a < b; }
int sgn(const ll& x) { return le(x, 0) ? eq(x, 0) ? 0 : -1 : 1; }
struct pt {
ll x, y;
pt() {}
pt(ll _x, ll _y) : x(_x), y(_y) {}
pt operator-(const pt& a) const { return pt(x - a.x, y - a.y); }
ll dot(const pt& a) const { return x * a.x + y * a.y; }
ll dot(const pt& a, const pt& b) const { return (a - *this).dot(b - *this); }
ll cross(const pt& a) const { return x * a.y - y * a.x; }
ll cross(const pt& a, const pt& b) const { return (a - *this).cross(b - *this); }
bool operator==(const pt& a) const { return a.x == x && a.y == y; }
};
struct Edge {
pt l, r;
};
bool edge_cmp(Edge* edge1, Edge* edge2)
{
const pt a = edge1->l, b = edge1->r;
const pt c = edge2->l, d = edge2->r;
int val = sgn(a.cross(b, c)) + sgn(a.cross(b, d));
if (val != 0)
return val > 0;
val = sgn(c.cross(d, a)) + sgn(c.cross(d, b));
return val < 0;
}
enum EventType { DEL = 2, ADD = 3, GET = 1, VERT = 0 };
struct Event {
EventType type;
int pos;
bool operator<(const Event& event) const { return type < event.type; }
};
vector<Edge*> sweepline(vector<Edge*> planar, vector<pt> queries)
{
using pt_type = decltype(pt::x);
// collect all x-coordinates
auto s =
set<pt_type, std::function<bool(const pt_type&, const pt_type&)>>(lt);
for (pt p : queries)
s.insert(p.x);
for (Edge* e : planar) {
s.insert(e->l.x);
s.insert(e->r.x);
}
// map all x-coordinates to ids
int cid = 0;
auto id =
map<pt_type, int, std::function<bool(const pt_type&, const pt_type&)>>(
lt);
for (auto x : s)
id[x] = cid++;
// create events
auto t = set<Edge*, decltype(*edge_cmp)>(edge_cmp);
auto vert_cmp = [](const pair<pt_type, int>& l,
const pair<pt_type, int>& r) {
if (!eq(l.first, r.first))
return lt(l.first, r.first);
return l.second < r.second;
};
auto vert = set<pair<pt_type, int>, decltype(vert_cmp)>(vert_cmp);
vector<vector<Event>> events(cid);
for (int i = 0; i < (int)queries.size(); i++) {
int x = id[queries[i].x];
events[x].push_back(Event{GET, i});
}
for (int i = 0; i < (int)planar.size(); i++) {
int lx = id[planar[i]->l.x], rx = id[planar[i]->r.x];
if (lx > rx) {
swap(lx, rx);
swap(planar[i]->l, planar[i]->r);
}
if (lx == rx) {
events[lx].push_back(Event{VERT, i});
} else {
events[lx].push_back(Event{ADD, i});
events[rx].push_back(Event{DEL, i});
}
}
// perform sweep line algorithm
vector<Edge*> ans(queries.size(), nullptr);
for (int x = 0; x < cid; x++) {
sort(events[x].begin(), events[x].end());
vert.clear();
for (Event event : events[x]) {
if (event.type == DEL) {
t.erase(planar[event.pos]);
}
if (event.type == VERT) {
vert.insert(make_pair(
min(planar[event.pos]->l.y, planar[event.pos]->r.y),
event.pos));
}
if (event.type == ADD) {
t.insert(planar[event.pos]);
}
if (event.type == GET) {
auto jt = vert.upper_bound(
make_pair(queries[event.pos].y, planar.size()));
if (jt != vert.begin()) {
--jt;
int i = jt->second;
if (ge(max(planar[i]->l.y, planar[i]->r.y),
queries[event.pos].y)) {
ans[event.pos] = planar[i];
continue;
}
}
Edge* e = new Edge;
e->l = e->r = queries[event.pos];
auto it = t.upper_bound(e);
if (it != t.begin())
ans[event.pos] = *(--it);
delete e;
}
}
for (Event event : events[x]) {
if (event.type != GET)
continue;
if (ans[event.pos] != nullptr &&
eq(ans[event.pos]->l.x, ans[event.pos]->r.x))
continue;
Edge* e = new Edge;
e->l = e->r = queries[event.pos];
auto it = t.upper_bound(e);
delete e;
if (it == t.begin())
e = nullptr;
else
e = *(--it);
if (ans[event.pos] == nullptr) {
ans[event.pos] = e;
continue;
}
if (e == nullptr)
continue;
if (e == ans[event.pos])
continue;
if (id[ans[event.pos]->r.x] == x) {
if (id[e->l.x] == x) {
if (gt(e->l.y, ans[event.pos]->r.y))
ans[event.pos] = e;
}
} else {
ans[event.pos] = e;
}
}
}
return ans;
}
struct DCEL {
struct Edge {
pt origin;
Edge* nxt = nullptr;
Edge* twin = nullptr;
int face;
};
vector<Edge*> body;
};
vector<pair<int, int>> point_location(DCEL planar, vector<pt> queries)
{
vector<pair<int, int>> ans(queries.size());
vector<Edge*> planar2;
map<intptr_t, int> pos;
map<intptr_t, int> added_on;
int n = planar.body.size();
for (int i = 0; i < n; i++) {
if (planar.body[i]->face > planar.body[i]->twin->face)
continue;
Edge* e = new Edge;
e->l = planar.body[i]->origin;
e->r = planar.body[i]->twin->origin;
added_on[(intptr_t)e] = i;
pos[(intptr_t)e] =
lt(planar.body[i]->origin.x, planar.body[i]->twin->origin.x)
? planar.body[i]->face
: planar.body[i]->twin->face;
planar2.push_back(e);
}
auto res = sweepline(planar2, queries);
for (int i = 0; i < (int)queries.size(); i++) {
if (res[i] == nullptr) {
ans[i] = make_pair(1, -1);
continue;
}
pt p = queries[i];
pt l = res[i]->l, r = res[i]->r;
if (eq(p.cross(l, r), 0) && le(p.dot(l, r), 0)) {
ans[i] = make_pair(0, added_on[(intptr_t)res[i]]);
continue;
}
ans[i] = make_pair(1, pos[(intptr_t)res[i]]);
}
for (auto e : planar2)
delete e;
return ans;
}
```
|
---
title: Point location in O(log n)
title
- Original
---
# Point location in $O(log n)$
Consider the following problem: you are given a [planar subdivision](https://en.wikipedia.org/wiki/Planar_straight-line_graph) without no vertices of degree one and zero, and a lot of queries.
Each query is a point, for which we should determine the face of the subdivision it belongs to.
We will answer each query in $O(\log n)$ offline.<br>
This problem may arise when you need to locate some points in a Voronoi diagram or in some simple polygon.
## Algorithm
Firstly, for each query point $p\ (x_0, y_0)$ we want to find such an edge that if the point belongs to any edge, the point lies on the edge we found, otherwise this edge must intersect the line $x = x_0$ at some unique point $(x_0, y)$ where $y < y_0$ and this $y$ is maximum among all such edges.
The following image shows both cases.
<center></center>
We will solve this problem offline using the sweep line algorithm. Let's iterate over x-coordinates of query points and edges' endpoints in increasing order and keep a set of edges $s$. For each x-coordinate we will add some events beforehand.
The events will be of four types: _add_, _remove_, _vertical_, _get_.
For each vertical edge (both endpoints have the same x-coordinate) we will add one _vertical_ event for the corresponding x-coordinate.
For every other edge we will add one _add_ event for the minimum of x-coordinates of the endpoints and one _remove_ event for the maximum of x-coordinates of the endpoints.
Finally, for each query point we will add one _get_ event for its x-coordinate.
For each x-coordinate we will sort the events by their types in order (_vertical_, _get_, _remove_, _add_).
The following image shows all events in sorted order for each x-coordinate.
<center></center>
We will keep two sets during the sweep-line process.
A set $t$ for all non-vertical edges, and one set $vert$ especially for the vertical ones.
We will clear the set $vert$ at the beginning of processing each x-coordinate.
Now let's process the events for a fixed x-coordinate.
- If we got a _vertical_ event, we will simply insert the minimum y-coordinate of the corresponding edge's endpoints to $vert$.
- If we got a _remove_ or _add_ event, we will remove the corresponding edge from $t$ or add it to $t$.
- Finally, for each _get_ event we must check if the point lies on some vertical edge by performing a binary search in $vert$.
If the point doesn't lie on any vertical edge, we must find the answer for this query in $t$.
To do this, we again make a binary search.
In order to handle some degenerate cases (e.g. in case of the triangle $(0,~0)$, $(0,~2)$, $(1, 1)$ when we query the point $(0,~0)$), we must answer all _get_ events again after we processed all the events for this x-coordinate and choose the best of two answers.
Now let's choose a comparator for the set $t$.
This comparator should check if one edge doesn't lie above other for every x-coordinate they both cover. Suppose that we have two edges $(a, b)$ and $(c, d)$. Then the comparator is (in pseudocode):<br>
$val = sgn((b - a)\times(c - a)) + sgn((b - a)\times(d - a))$<br>
<b>if</b> $val \neq 0$<br>
<b>then return</b> $val > 0$<br>
$val = sgn((d - c)\times(a - c)) + sgn((d - c)\times(b - c))$<br>
<b>return</b> $val < 0$<br>
Now for every query we have the corresponding edge.
How to find the face?
If we couldn't find the edge it means that the point is in the outer face.
If the point belongs to the edge we found, the face is not unique.
Otherwise, there are two candidates - the faces that are bounded by this edge.
How to check which one is the answer? Note that the edge is not vertical.
Then the answer is the face that is above this edge.
Let's find such a face for each non-vertical edge.
Consider a counter-clockwise traversal of each face.
If during this traversal we increased x-coordinate while passing through the edge, then this face is the face we need to find for this edge.
## Notes
Actually, with persistent trees this approach can be used to answer the queries online.
## Implementation
The following code is implemented for integers, but it can be easily modified to work with doubles (by changing the compare methods and the point type).
This implementation assumes that the subdivision is correctly stored inside a [DCEL](https://en.wikipedia.org/wiki/Doubly_connected_edge_list) and the outer face is numbered $-1$.<br>
For each query a pair $(1, i)$ is returned if the point lies strictly inside the face number $i$, and a pair $(0, i)$ is returned if the point lies on the edge number $i$.
```{.cpp file=point-location}
typedef long long ll;
bool ge(const ll& a, const ll& b) { return a >= b; }
bool le(const ll& a, const ll& b) { return a <= b; }
bool eq(const ll& a, const ll& b) { return a == b; }
bool gt(const ll& a, const ll& b) { return a > b; }
bool lt(const ll& a, const ll& b) { return a < b; }
int sgn(const ll& x) { return le(x, 0) ? eq(x, 0) ? 0 : -1 : 1; }
struct pt {
ll x, y;
pt() {}
pt(ll _x, ll _y) : x(_x), y(_y) {}
pt operator-(const pt& a) const { return pt(x - a.x, y - a.y); }
ll dot(const pt& a) const { return x * a.x + y * a.y; }
ll dot(const pt& a, const pt& b) const { return (a - *this).dot(b - *this); }
ll cross(const pt& a) const { return x * a.y - y * a.x; }
ll cross(const pt& a, const pt& b) const { return (a - *this).cross(b - *this); }
bool operator==(const pt& a) const { return a.x == x && a.y == y; }
};
struct Edge {
pt l, r;
};
bool edge_cmp(Edge* edge1, Edge* edge2)
{
const pt a = edge1->l, b = edge1->r;
const pt c = edge2->l, d = edge2->r;
int val = sgn(a.cross(b, c)) + sgn(a.cross(b, d));
if (val != 0)
return val > 0;
val = sgn(c.cross(d, a)) + sgn(c.cross(d, b));
return val < 0;
}
enum EventType { DEL = 2, ADD = 3, GET = 1, VERT = 0 };
struct Event {
EventType type;
int pos;
bool operator<(const Event& event) const { return type < event.type; }
};
vector<Edge*> sweepline(vector<Edge*> planar, vector<pt> queries)
{
using pt_type = decltype(pt::x);
// collect all x-coordinates
auto s =
set<pt_type, std::function<bool(const pt_type&, const pt_type&)>>(lt);
for (pt p : queries)
s.insert(p.x);
for (Edge* e : planar) {
s.insert(e->l.x);
s.insert(e->r.x);
}
// map all x-coordinates to ids
int cid = 0;
auto id =
map<pt_type, int, std::function<bool(const pt_type&, const pt_type&)>>(
lt);
for (auto x : s)
id[x] = cid++;
// create events
auto t = set<Edge*, decltype(*edge_cmp)>(edge_cmp);
auto vert_cmp = [](const pair<pt_type, int>& l,
const pair<pt_type, int>& r) {
if (!eq(l.first, r.first))
return lt(l.first, r.first);
return l.second < r.second;
};
auto vert = set<pair<pt_type, int>, decltype(vert_cmp)>(vert_cmp);
vector<vector<Event>> events(cid);
for (int i = 0; i < (int)queries.size(); i++) {
int x = id[queries[i].x];
events[x].push_back(Event{GET, i});
}
for (int i = 0; i < (int)planar.size(); i++) {
int lx = id[planar[i]->l.x], rx = id[planar[i]->r.x];
if (lx > rx) {
swap(lx, rx);
swap(planar[i]->l, planar[i]->r);
}
if (lx == rx) {
events[lx].push_back(Event{VERT, i});
} else {
events[lx].push_back(Event{ADD, i});
events[rx].push_back(Event{DEL, i});
}
}
// perform sweep line algorithm
vector<Edge*> ans(queries.size(), nullptr);
for (int x = 0; x < cid; x++) {
sort(events[x].begin(), events[x].end());
vert.clear();
for (Event event : events[x]) {
if (event.type == DEL) {
t.erase(planar[event.pos]);
}
if (event.type == VERT) {
vert.insert(make_pair(
min(planar[event.pos]->l.y, planar[event.pos]->r.y),
event.pos));
}
if (event.type == ADD) {
t.insert(planar[event.pos]);
}
if (event.type == GET) {
auto jt = vert.upper_bound(
make_pair(queries[event.pos].y, planar.size()));
if (jt != vert.begin()) {
--jt;
int i = jt->second;
if (ge(max(planar[i]->l.y, planar[i]->r.y),
queries[event.pos].y)) {
ans[event.pos] = planar[i];
continue;
}
}
Edge* e = new Edge;
e->l = e->r = queries[event.pos];
auto it = t.upper_bound(e);
if (it != t.begin())
ans[event.pos] = *(--it);
delete e;
}
}
for (Event event : events[x]) {
if (event.type != GET)
continue;
if (ans[event.pos] != nullptr &&
eq(ans[event.pos]->l.x, ans[event.pos]->r.x))
continue;
Edge* e = new Edge;
e->l = e->r = queries[event.pos];
auto it = t.upper_bound(e);
delete e;
if (it == t.begin())
e = nullptr;
else
e = *(--it);
if (ans[event.pos] == nullptr) {
ans[event.pos] = e;
continue;
}
if (e == nullptr)
continue;
if (e == ans[event.pos])
continue;
if (id[ans[event.pos]->r.x] == x) {
if (id[e->l.x] == x) {
if (gt(e->l.y, ans[event.pos]->r.y))
ans[event.pos] = e;
}
} else {
ans[event.pos] = e;
}
}
}
return ans;
}
struct DCEL {
struct Edge {
pt origin;
Edge* nxt = nullptr;
Edge* twin = nullptr;
int face;
};
vector<Edge*> body;
};
vector<pair<int, int>> point_location(DCEL planar, vector<pt> queries)
{
vector<pair<int, int>> ans(queries.size());
vector<Edge*> planar2;
map<intptr_t, int> pos;
map<intptr_t, int> added_on;
int n = planar.body.size();
for (int i = 0; i < n; i++) {
if (planar.body[i]->face > planar.body[i]->twin->face)
continue;
Edge* e = new Edge;
e->l = planar.body[i]->origin;
e->r = planar.body[i]->twin->origin;
added_on[(intptr_t)e] = i;
pos[(intptr_t)e] =
lt(planar.body[i]->origin.x, planar.body[i]->twin->origin.x)
? planar.body[i]->face
: planar.body[i]->twin->face;
planar2.push_back(e);
}
auto res = sweepline(planar2, queries);
for (int i = 0; i < (int)queries.size(); i++) {
if (res[i] == nullptr) {
ans[i] = make_pair(1, -1);
continue;
}
pt p = queries[i];
pt l = res[i]->l, r = res[i]->r;
if (eq(p.cross(l, r), 0) && le(p.dot(l, r), 0)) {
ans[i] = make_pair(0, added_on[(intptr_t)res[i]]);
continue;
}
ans[i] = make_pair(1, pos[(intptr_t)res[i]]);
}
for (auto e : planar2)
delete e;
return ans;
}
```
## Problems
* [TIMUS 1848 Fly Hunt](http://acm.timus.ru/problem.aspx?space=1&num=1848&locale=en)
* [UVA 12310 Point Location](https://onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=297&page=show_problem&problem=3732)
|
Point location in $O(log n)$
|
---
title: Finding faces of a planar graph
title
facets
---
# Finding faces of a planar graph
Consider a graph $G$ with $n$ vertices and $m$ edges, which can be drawn on a plane in such a way that two edges intersect only at a common vertex (if it exists).
Such graphs are called **planar**. Now suppose that we are given a planar graph together with its straight-line embedding, which means that for each vertex $v$ we have a corresponding point $(x, y)$ and all edges are drawn as line segments between these points without intersection (such embedding always exists). These line segments split the plane into several regions, which are called faces. Exactly one of the faces is unbounded. This face is called **outer**, while the other faces are called **inner**.
In this article we will deal with finding both inner and outer faces of a planar graph. We will assume that the graph is connected.
## Some facts about planar graphs
In this section we present several facts about planar graphs without proof. Readers who are interested in proofs should refer to [Graph Theory by R. Diestel](https://sites.math.washington.edu/~billey/classes/562.winter.2018/articles/GraphTheory.pdf) or some other book.
### Euler's theorem
Euler's theorem states that any correct embedding of a connected planar graph with $n$ vertices, $m$ edges and $f$ faces satisfies:
$$n - m + f = 2$$
And more generally, every planar graph with $k$ connected components satisfies:
$$n - m + f = 1 + k$$
### Number of edges of a planar graph.
If $n \ge 3$ then the maximum number of edges of a planar graph with $n$ vertices is $3n - 6$. This number is achieved by any connected planar graph where each face is bounded by a triangle. In terms of complexity this fact means that $m = O(n)$ for any planar graph.
### Number of faces of a planar graph.
As a direct consequence of the above fact, if $n \ge 3$ then the maximum number of faces of a planar graph with $n$ vertices is $2n - 4$.
### Minimum vertex degree in a planar graph.
Every planar graph has a vertex of degree 5 or less.
## The algorithm
Firstly, sort the adjacent edges for each vertex by polar angle.
Now let's traverse the graph in the following way. Suppose that we entered vertex $u$ through the edge $(v, u)$ and $(u, w)$ is the next edge after $(v, u)$ in the sorted adjacency list of $u$. Then the next vertex will be $w$. It turns out that if we start this traversal at some edge $(v, u)$, we will traverse exactly one of the faces adjacent to $(v, u)$, the exact face depending on whether our first step is from $u$ to $v$ or from $v$ to $u$.
Now the algorithm is quite obvious. We must iterate over all edges of the graph and start the traversal for each edge that wasn't visited by one of the previous traversals. This way we will find each face exactly once, and each edge will be traversed twice (once in each direction).
### Finding the next edge
During the traversal we have to find the next edge in counter-clockwise order. The most obvious way to find the next edge is binary search by angle. However, given the counter-clockwise order of adjacent edges for each vertex, we can precompute the next edges and store them in a hash table. If the edges are already sorted by angle, the complexity of finding all faces in this case becomes linear.
### Finding the outer face
It's not hard to see that the algorithm traverses each inner face in a clockwise order and the outer face in the counter-clockwise order, so the outer face can be found by checking the order of each face.
### Complexity
It's quite clear that the complexity of the algorithm is $O(m \log m)$ because of sorting, and since $m = O(n)$, it's actually $O(n \log n)$. As mentioned before, without sorting the complexity becomes $O(n)$.
## What if the graph isn't connected?
At the first glance it may seem that finding faces of a disconnected graph is not much harder because we can run the same algorithm for each connected component. However, the components may be drawn in a nested way, forming **holes** (see the image below). In this case the inner face of some component becomes the outer face of some other components and has a complex disconnected border. Dealing with such cases is quite hard, one possible approach is to identify nested components with [point location](point-location.md) algorithms.
<center></center>
## Implementation
The following implementation returns a vector of vertices for each face, outer face goes first.
Inner faces are returned in counter-clockwise orders and the outer face is returned in clockwise order.
For simplicity we find the next edge by doing binary search by angle.
```{.cpp file=planar}
struct Point {
int64_t x, y;
Point(int64_t x_, int64_t y_): x(x_), y(y_) {}
Point operator - (const Point & p) const {
return Point(x - p.x, y - p.y);
}
int64_t cross (const Point & p) const {
return x * p.y - y * p.x;
}
int64_t cross (const Point & p, const Point & q) const {
return (p - *this).cross(q - *this);
}
int half () const {
return int(y < 0 || (y == 0 && x < 0));
}
};
std::vector<std::vector<size_t>> find_faces(std::vector<Point> vertices, std::vector<std::vector<size_t>> adj) {
size_t n = vertices.size();
std::vector<std::vector<char>> used(n);
for (size_t i = 0; i < n; i++) {
used[i].resize(adj[i].size());
used[i].assign(adj[i].size(), 0);
auto compare = [&](size_t l, size_t r) {
Point pl = vertices[l] - vertices[i];
Point pr = vertices[r] - vertices[i];
if (pl.half() != pr.half())
return pl.half() < pr.half();
return pl.cross(pr) > 0;
};
std::sort(adj[i].begin(), adj[i].end(), compare);
}
std::vector<std::vector<size_t>> faces;
for (size_t i = 0; i < n; i++) {
for (size_t edge_id = 0; edge_id < adj[i].size(); edge_id++) {
if (used[i][edge_id]) {
continue;
}
std::vector<size_t> face;
size_t v = i;
size_t e = edge_id;
while (!used[v][e]) {
used[v][e] = true;
face.push_back(v);
size_t u = adj[v][e];
size_t e1 = std::lower_bound(adj[u].begin(), adj[u].end(), v, [&](size_t l, size_t r) {
Point pl = vertices[l] - vertices[u];
Point pr = vertices[r] - vertices[u];
if (pl.half() != pr.half())
return pl.half() < pr.half();
return pl.cross(pr) > 0;
}) - adj[u].begin() + 1;
if (e1 == adj[u].size()) {
e1 = 0;
}
v = u;
e = e1;
}
std::reverse(face.begin(), face.end());
int sign = 0;
for (size_t j = 0; j < face.size(); j++) {
size_t j1 = (j + 1) % face.size();
size_t j2 = (j + 2) % face.size();
int64_t val = vertices[face[j]].cross(vertices[face[j1]], vertices[face[j2]]);
if (val > 0) {
sign = 1;
break;
} else if (val < 0) {
sign = -1;
break;
}
}
if (sign <= 0) {
faces.insert(faces.begin(), face);
} else {
faces.emplace_back(face);
}
}
}
return faces;
}
```
## Building planar graph from line segments
Sometimes you are not given a graph explicitly, but rather as a set of line segments on a plane, and the actual graph is formed by intersecting those segments, as shown in the picture below. In this case you have to build the graph manually. The easiest way to do so is as follows. Fix a segment and intersect it with all other segments. Then sort all intersection points together with the two endpoints of the segment lexicographically and add them to the graph as vertices. Also link each two adjacent vertices in lexicographical order by an edge. After doing this procedure for all edges we will obtain the graph. Of course, we should ensure that two equal intersection points will always correspond to the same vertex. The easiest way to do this is to store the points in a map by their coordinates, regarding points whose coordinates differ by a small number (say, less than $10^{-9}$) as equal. This algorithm works in $O(n^2 \log n)$.
<center></center>
## Implementation
```{.cpp file=planar_implicit}
using dbl = long double;
const dbl eps = 1e-9;
struct Point {
dbl x, y;
Point(){}
Point(dbl x_, dbl y_): x(x_), y(y_) {}
Point operator * (dbl d) const {
return Point(x * d, y * d);
}
Point operator + (const Point & p) const {
return Point(x + p.x, y + p.y);
}
Point operator - (const Point & p) const {
return Point(x - p.x, y - p.y);
}
dbl cross (const Point & p) const {
return x * p.y - y * p.x;
}
dbl cross (const Point & p, const Point & q) const {
return (p - *this).cross(q - *this);
}
dbl dot (const Point & p) const {
return x * p.x + y * p.y;
}
dbl dot (const Point & p, const Point & q) const {
return (p - *this).dot(q - *this);
}
bool operator < (const Point & p) const {
if (fabs(x - p.x) < eps) {
if (fabs(y - p.y) < eps) {
return false;
} else {
return y < p.y;
}
} else {
return x < p.x;
}
}
bool operator == (const Point & p) const {
return fabs(x - p.x) < eps && fabs(y - p.y) < eps;
}
bool operator >= (const Point & p) const {
return !(*this < p);
}
};
struct Line{
Point p[2];
Line(Point l, Point r){p[0] = l; p[1] = r;}
Point& operator [](const int & i){return p[i];}
const Point& operator[](const int & i)const{return p[i];}
Line(const Line & l){
p[0] = l.p[0]; p[1] = l.p[1];
}
Point getOrth()const{
return Point(p[1].y - p[0].y, p[0].x - p[1].x);
}
bool hasPointLine(const Point & t)const{
return std::fabs(p[0].cross(p[1], t)) < eps;
}
bool hasPointSeg(const Point & t)const{
return hasPointLine(t) && t.dot(p[0], p[1]) < eps;
}
};
std::vector<Point> interLineLine(Line l1, Line l2){
if(std::fabs(l1.getOrth().cross(l2.getOrth())) < eps){
if(l1.hasPointLine(l2[0]))return {l1[0], l1[1]};
else return {};
}
Point u = l2[1] - l2[0];
Point v = l1[1] - l1[0];
dbl s = u.cross(l2[0] - l1[0])/u.cross(v);
return {Point(l1[0] + v * s)};
}
std::vector<Point> interSegSeg(Line l1, Line l2){
if (l1[0] == l1[1]) {
if (l2[0] == l2[1]) {
if (l1[0] == l2[0])
return {l1[0]};
else
return {};
} else {
if (l2.hasPointSeg(l1[0]))
return {l1[0]};
else
return {};
}
}
if (l2[0] == l2[1]) {
if (l1.hasPointSeg(l2[0]))
return {l2[0]};
else
return {};
}
auto li = interLineLine(l1, l2);
if (li.empty())
return li;
if (li.size() == 2) {
if (l1[0] >= l1[1])
std::swap(l1[0], l1[1]);
if (l2[0] >= l2[1])
std::swap(l2[0], l2[1]);
std::vector<Point> res(2);
if (l1[0] < l2[0])
res[0] = l2[0];
else
res[0] = l1[0];
if (l1[1] < l2[1])
res[1] = l1[1];
else
res[1] = l2[1];
if (res[0] == res[1])
res.pop_back();
if (res.size() == 2u && res[1] < res[0])
return {};
else
return res;
}
Point cand = li[0];
if (l1.hasPointSeg(cand) && l2.hasPointSeg(cand))
return {cand};
else
return {};
}
std::pair<std::vector<Point>, std::vector<std::vector<size_t>>> build_graph(std::vector<Line> segments) {
std::vector<Point> p;
std::vector<std::vector<size_t>> adj;
std::map<std::pair<int64_t, int64_t>, size_t> point_id;
auto get_point_id = [&](Point pt) {
auto repr = std::make_pair(
int64_t(std::round(pt.x * 1000000000) + 1e-6),
int64_t(std::round(pt.y * 1000000000) + 1e-6)
);
if (!point_id.count(repr)) {
adj.emplace_back();
size_t id = point_id.size();
point_id[repr] = id;
p.push_back(pt);
return id;
} else {
return point_id[repr];
}
};
for (size_t i = 0; i < segments.size(); i++) {
std::vector<size_t> curr = {
get_point_id(segments[i][0]),
get_point_id(segments[i][1])
};
for (size_t j = 0; j < segments.size(); j++) {
if (i == j)
continue;
auto inter = interSegSeg(segments[i], segments[j]);
for (auto pt: inter) {
curr.push_back(get_point_id(pt));
}
}
std::sort(curr.begin(), curr.end(), [&](size_t l, size_t r) { return p[l] < p[r]; });
curr.erase(std::unique(curr.begin(), curr.end()), curr.end());
for (size_t j = 0; j + 1 < curr.size(); j++) {
adj[curr[j]].push_back(curr[j + 1]);
adj[curr[j + 1]].push_back(curr[j]);
}
}
for (size_t i = 0; i < adj.size(); i++) {
std::sort(adj[i].begin(), adj[i].end());
// removing edges that were added multiple times
adj[i].erase(std::unique(adj[i].begin(), adj[i].end()), adj[i].end());
}
return {p, adj};
}
```
|
---
title: Finding faces of a planar graph
title
facets
---
# Finding faces of a planar graph
Consider a graph $G$ with $n$ vertices and $m$ edges, which can be drawn on a plane in such a way that two edges intersect only at a common vertex (if it exists).
Such graphs are called **planar**. Now suppose that we are given a planar graph together with its straight-line embedding, which means that for each vertex $v$ we have a corresponding point $(x, y)$ and all edges are drawn as line segments between these points without intersection (such embedding always exists). These line segments split the plane into several regions, which are called faces. Exactly one of the faces is unbounded. This face is called **outer**, while the other faces are called **inner**.
In this article we will deal with finding both inner and outer faces of a planar graph. We will assume that the graph is connected.
## Some facts about planar graphs
In this section we present several facts about planar graphs without proof. Readers who are interested in proofs should refer to [Graph Theory by R. Diestel](https://sites.math.washington.edu/~billey/classes/562.winter.2018/articles/GraphTheory.pdf) or some other book.
### Euler's theorem
Euler's theorem states that any correct embedding of a connected planar graph with $n$ vertices, $m$ edges and $f$ faces satisfies:
$$n - m + f = 2$$
And more generally, every planar graph with $k$ connected components satisfies:
$$n - m + f = 1 + k$$
### Number of edges of a planar graph.
If $n \ge 3$ then the maximum number of edges of a planar graph with $n$ vertices is $3n - 6$. This number is achieved by any connected planar graph where each face is bounded by a triangle. In terms of complexity this fact means that $m = O(n)$ for any planar graph.
### Number of faces of a planar graph.
As a direct consequence of the above fact, if $n \ge 3$ then the maximum number of faces of a planar graph with $n$ vertices is $2n - 4$.
### Minimum vertex degree in a planar graph.
Every planar graph has a vertex of degree 5 or less.
## The algorithm
Firstly, sort the adjacent edges for each vertex by polar angle.
Now let's traverse the graph in the following way. Suppose that we entered vertex $u$ through the edge $(v, u)$ and $(u, w)$ is the next edge after $(v, u)$ in the sorted adjacency list of $u$. Then the next vertex will be $w$. It turns out that if we start this traversal at some edge $(v, u)$, we will traverse exactly one of the faces adjacent to $(v, u)$, the exact face depending on whether our first step is from $u$ to $v$ or from $v$ to $u$.
Now the algorithm is quite obvious. We must iterate over all edges of the graph and start the traversal for each edge that wasn't visited by one of the previous traversals. This way we will find each face exactly once, and each edge will be traversed twice (once in each direction).
### Finding the next edge
During the traversal we have to find the next edge in counter-clockwise order. The most obvious way to find the next edge is binary search by angle. However, given the counter-clockwise order of adjacent edges for each vertex, we can precompute the next edges and store them in a hash table. If the edges are already sorted by angle, the complexity of finding all faces in this case becomes linear.
### Finding the outer face
It's not hard to see that the algorithm traverses each inner face in a clockwise order and the outer face in the counter-clockwise order, so the outer face can be found by checking the order of each face.
### Complexity
It's quite clear that the complexity of the algorithm is $O(m \log m)$ because of sorting, and since $m = O(n)$, it's actually $O(n \log n)$. As mentioned before, without sorting the complexity becomes $O(n)$.
## What if the graph isn't connected?
At the first glance it may seem that finding faces of a disconnected graph is not much harder because we can run the same algorithm for each connected component. However, the components may be drawn in a nested way, forming **holes** (see the image below). In this case the inner face of some component becomes the outer face of some other components and has a complex disconnected border. Dealing with such cases is quite hard, one possible approach is to identify nested components with [point location](point-location.md) algorithms.
<center></center>
## Implementation
The following implementation returns a vector of vertices for each face, outer face goes first.
Inner faces are returned in counter-clockwise orders and the outer face is returned in clockwise order.
For simplicity we find the next edge by doing binary search by angle.
```{.cpp file=planar}
struct Point {
int64_t x, y;
Point(int64_t x_, int64_t y_): x(x_), y(y_) {}
Point operator - (const Point & p) const {
return Point(x - p.x, y - p.y);
}
int64_t cross (const Point & p) const {
return x * p.y - y * p.x;
}
int64_t cross (const Point & p, const Point & q) const {
return (p - *this).cross(q - *this);
}
int half () const {
return int(y < 0 || (y == 0 && x < 0));
}
};
std::vector<std::vector<size_t>> find_faces(std::vector<Point> vertices, std::vector<std::vector<size_t>> adj) {
size_t n = vertices.size();
std::vector<std::vector<char>> used(n);
for (size_t i = 0; i < n; i++) {
used[i].resize(adj[i].size());
used[i].assign(adj[i].size(), 0);
auto compare = [&](size_t l, size_t r) {
Point pl = vertices[l] - vertices[i];
Point pr = vertices[r] - vertices[i];
if (pl.half() != pr.half())
return pl.half() < pr.half();
return pl.cross(pr) > 0;
};
std::sort(adj[i].begin(), adj[i].end(), compare);
}
std::vector<std::vector<size_t>> faces;
for (size_t i = 0; i < n; i++) {
for (size_t edge_id = 0; edge_id < adj[i].size(); edge_id++) {
if (used[i][edge_id]) {
continue;
}
std::vector<size_t> face;
size_t v = i;
size_t e = edge_id;
while (!used[v][e]) {
used[v][e] = true;
face.push_back(v);
size_t u = adj[v][e];
size_t e1 = std::lower_bound(adj[u].begin(), adj[u].end(), v, [&](size_t l, size_t r) {
Point pl = vertices[l] - vertices[u];
Point pr = vertices[r] - vertices[u];
if (pl.half() != pr.half())
return pl.half() < pr.half();
return pl.cross(pr) > 0;
}) - adj[u].begin() + 1;
if (e1 == adj[u].size()) {
e1 = 0;
}
v = u;
e = e1;
}
std::reverse(face.begin(), face.end());
int sign = 0;
for (size_t j = 0; j < face.size(); j++) {
size_t j1 = (j + 1) % face.size();
size_t j2 = (j + 2) % face.size();
int64_t val = vertices[face[j]].cross(vertices[face[j1]], vertices[face[j2]]);
if (val > 0) {
sign = 1;
break;
} else if (val < 0) {
sign = -1;
break;
}
}
if (sign <= 0) {
faces.insert(faces.begin(), face);
} else {
faces.emplace_back(face);
}
}
}
return faces;
}
```
## Building planar graph from line segments
Sometimes you are not given a graph explicitly, but rather as a set of line segments on a plane, and the actual graph is formed by intersecting those segments, as shown in the picture below. In this case you have to build the graph manually. The easiest way to do so is as follows. Fix a segment and intersect it with all other segments. Then sort all intersection points together with the two endpoints of the segment lexicographically and add them to the graph as vertices. Also link each two adjacent vertices in lexicographical order by an edge. After doing this procedure for all edges we will obtain the graph. Of course, we should ensure that two equal intersection points will always correspond to the same vertex. The easiest way to do this is to store the points in a map by their coordinates, regarding points whose coordinates differ by a small number (say, less than $10^{-9}$) as equal. This algorithm works in $O(n^2 \log n)$.
<center></center>
## Implementation
```{.cpp file=planar_implicit}
using dbl = long double;
const dbl eps = 1e-9;
struct Point {
dbl x, y;
Point(){}
Point(dbl x_, dbl y_): x(x_), y(y_) {}
Point operator * (dbl d) const {
return Point(x * d, y * d);
}
Point operator + (const Point & p) const {
return Point(x + p.x, y + p.y);
}
Point operator - (const Point & p) const {
return Point(x - p.x, y - p.y);
}
dbl cross (const Point & p) const {
return x * p.y - y * p.x;
}
dbl cross (const Point & p, const Point & q) const {
return (p - *this).cross(q - *this);
}
dbl dot (const Point & p) const {
return x * p.x + y * p.y;
}
dbl dot (const Point & p, const Point & q) const {
return (p - *this).dot(q - *this);
}
bool operator < (const Point & p) const {
if (fabs(x - p.x) < eps) {
if (fabs(y - p.y) < eps) {
return false;
} else {
return y < p.y;
}
} else {
return x < p.x;
}
}
bool operator == (const Point & p) const {
return fabs(x - p.x) < eps && fabs(y - p.y) < eps;
}
bool operator >= (const Point & p) const {
return !(*this < p);
}
};
struct Line{
Point p[2];
Line(Point l, Point r){p[0] = l; p[1] = r;}
Point& operator [](const int & i){return p[i];}
const Point& operator[](const int & i)const{return p[i];}
Line(const Line & l){
p[0] = l.p[0]; p[1] = l.p[1];
}
Point getOrth()const{
return Point(p[1].y - p[0].y, p[0].x - p[1].x);
}
bool hasPointLine(const Point & t)const{
return std::fabs(p[0].cross(p[1], t)) < eps;
}
bool hasPointSeg(const Point & t)const{
return hasPointLine(t) && t.dot(p[0], p[1]) < eps;
}
};
std::vector<Point> interLineLine(Line l1, Line l2){
if(std::fabs(l1.getOrth().cross(l2.getOrth())) < eps){
if(l1.hasPointLine(l2[0]))return {l1[0], l1[1]};
else return {};
}
Point u = l2[1] - l2[0];
Point v = l1[1] - l1[0];
dbl s = u.cross(l2[0] - l1[0])/u.cross(v);
return {Point(l1[0] + v * s)};
}
std::vector<Point> interSegSeg(Line l1, Line l2){
if (l1[0] == l1[1]) {
if (l2[0] == l2[1]) {
if (l1[0] == l2[0])
return {l1[0]};
else
return {};
} else {
if (l2.hasPointSeg(l1[0]))
return {l1[0]};
else
return {};
}
}
if (l2[0] == l2[1]) {
if (l1.hasPointSeg(l2[0]))
return {l2[0]};
else
return {};
}
auto li = interLineLine(l1, l2);
if (li.empty())
return li;
if (li.size() == 2) {
if (l1[0] >= l1[1])
std::swap(l1[0], l1[1]);
if (l2[0] >= l2[1])
std::swap(l2[0], l2[1]);
std::vector<Point> res(2);
if (l1[0] < l2[0])
res[0] = l2[0];
else
res[0] = l1[0];
if (l1[1] < l2[1])
res[1] = l1[1];
else
res[1] = l2[1];
if (res[0] == res[1])
res.pop_back();
if (res.size() == 2u && res[1] < res[0])
return {};
else
return res;
}
Point cand = li[0];
if (l1.hasPointSeg(cand) && l2.hasPointSeg(cand))
return {cand};
else
return {};
}
std::pair<std::vector<Point>, std::vector<std::vector<size_t>>> build_graph(std::vector<Line> segments) {
std::vector<Point> p;
std::vector<std::vector<size_t>> adj;
std::map<std::pair<int64_t, int64_t>, size_t> point_id;
auto get_point_id = [&](Point pt) {
auto repr = std::make_pair(
int64_t(std::round(pt.x * 1000000000) + 1e-6),
int64_t(std::round(pt.y * 1000000000) + 1e-6)
);
if (!point_id.count(repr)) {
adj.emplace_back();
size_t id = point_id.size();
point_id[repr] = id;
p.push_back(pt);
return id;
} else {
return point_id[repr];
}
};
for (size_t i = 0; i < segments.size(); i++) {
std::vector<size_t> curr = {
get_point_id(segments[i][0]),
get_point_id(segments[i][1])
};
for (size_t j = 0; j < segments.size(); j++) {
if (i == j)
continue;
auto inter = interSegSeg(segments[i], segments[j]);
for (auto pt: inter) {
curr.push_back(get_point_id(pt));
}
}
std::sort(curr.begin(), curr.end(), [&](size_t l, size_t r) { return p[l] < p[r]; });
curr.erase(std::unique(curr.begin(), curr.end()), curr.end());
for (size_t j = 0; j + 1 < curr.size(); j++) {
adj[curr[j]].push_back(curr[j + 1]);
adj[curr[j + 1]].push_back(curr[j]);
}
}
for (size_t i = 0; i < adj.size(); i++) {
std::sort(adj[i].begin(), adj[i].end());
// removing edges that were added multiple times
adj[i].erase(std::unique(adj[i].begin(), adj[i].end()), adj[i].end());
}
return {p, adj};
}
```
## Problems
* [TIMUS 1664 Pipeline Transportation](https://acm.timus.ru/problem.aspx?space=1&num=1664)
* [TIMUS 1681 Brother Bear's Garden](https://acm.timus.ru/problem.aspx?space=1&num=1681)
|
Finding faces of a planar graph
|
---
title
pick_grid_theorem
---
# Pick's Theorem
A polygon without self-intersections is called lattice if all its vertices have integer coordinates in some 2D grid. Pick's theorem provides a way to compute the area of this polygon through the number of vertices that are lying on the boundary and the number of vertices that lie strictly inside the polygon.
## Formula
Given a certain lattice polygon with non-zero area.
We denote its area by $S$, the number of points with integer coordinates lying strictly inside the polygon by $I$ and the number of points lying on polygon sides by $B$.
Then, the **Pick's formula** states:
$$S=I+\frac{B}{2}-1$$
In particular, if the values of $I$ and $B$ for a polygon are given, the area can be calculated in $O(1)$ without even knowing the vertices.
This formula was discovered and proven by Austrian mathematician Georg Alexander Pick in 1899.
## Proof
The proof is carried out in many stages: from simple polygons to arbitrary ones:
- A single square: $S=1, I=0, B=4$, which satisfies the formula.
- An arbitrary non-degenerate rectangle with sides parallel to coordinate axes: Assume $a$ and $b$ be the length of the sides of rectangle. Then, $S=ab, I=(a-1)(b-1), B=2(a+b)$. On substituting, we see that formula is true.
- A right angle with legs parallel to the axes: To prove this, note that any such triangle can be obtained by cutting off a rectangle by a diagonal. Denoting the number of integral points lying on diagonal by $c$, it can be shown that Pick's formula holds for this triangle regardless of $c$.
- An arbitrary triangle: Note that any such triangle can be turned into a rectangle by attaching it to sides of right-angled triangles with legs parallel to the axes (you will not need more than 3 such triangles). From here, we can get correct formula for any triangle.
- An arbitrary polygon: To prove this, triangulate it, ie, divide into triangles with integral coordinates. Further, it is possible to prove that Pick's theorem retains its validity when a polygon is added to a triangle. Thus, we have proven Pick's formula for arbitrary polygon.
## Generalization to higher dimensions
Unfortunately, this simple and beautiful formula cannot be generalized to higher dimensions.
John Reeve demonstrated this by proposing a tetrahedron (**Reeve tetrahedron**) with following vertices in 1957:
$$A=(0,0,0),
B=(1,0,0),
C=(0,1,0),
D=(1,1,k),$$
where $k$ can be any natural number. Then for any $k$, the tetrahedron $ABCD$ does not contain integer point inside it and has only $4$ points on its borders, $A, B, C, D$. Thus, the volume and surface area may vary in spite of unchanged number of points within and on boundary. Therefore, Pick's theorem doesn't allow generalizations.
However, higher dimensions still has a generalization using **Ehrhart polynomials** but they are quite complex and depends not only on points inside but also on the boundary of polytype.
## Extra Resources
A few simple examples and a simple proof of Pick's theorem can be found [here](http://www.geometer.org/mathcircles/pick.pdf).
|
---
title
pick_grid_theorem
---
# Pick's Theorem
A polygon without self-intersections is called lattice if all its vertices have integer coordinates in some 2D grid. Pick's theorem provides a way to compute the area of this polygon through the number of vertices that are lying on the boundary and the number of vertices that lie strictly inside the polygon.
## Formula
Given a certain lattice polygon with non-zero area.
We denote its area by $S$, the number of points with integer coordinates lying strictly inside the polygon by $I$ and the number of points lying on polygon sides by $B$.
Then, the **Pick's formula** states:
$$S=I+\frac{B}{2}-1$$
In particular, if the values of $I$ and $B$ for a polygon are given, the area can be calculated in $O(1)$ without even knowing the vertices.
This formula was discovered and proven by Austrian mathematician Georg Alexander Pick in 1899.
## Proof
The proof is carried out in many stages: from simple polygons to arbitrary ones:
- A single square: $S=1, I=0, B=4$, which satisfies the formula.
- An arbitrary non-degenerate rectangle with sides parallel to coordinate axes: Assume $a$ and $b$ be the length of the sides of rectangle. Then, $S=ab, I=(a-1)(b-1), B=2(a+b)$. On substituting, we see that formula is true.
- A right angle with legs parallel to the axes: To prove this, note that any such triangle can be obtained by cutting off a rectangle by a diagonal. Denoting the number of integral points lying on diagonal by $c$, it can be shown that Pick's formula holds for this triangle regardless of $c$.
- An arbitrary triangle: Note that any such triangle can be turned into a rectangle by attaching it to sides of right-angled triangles with legs parallel to the axes (you will not need more than 3 such triangles). From here, we can get correct formula for any triangle.
- An arbitrary polygon: To prove this, triangulate it, ie, divide into triangles with integral coordinates. Further, it is possible to prove that Pick's theorem retains its validity when a polygon is added to a triangle. Thus, we have proven Pick's formula for arbitrary polygon.
## Generalization to higher dimensions
Unfortunately, this simple and beautiful formula cannot be generalized to higher dimensions.
John Reeve demonstrated this by proposing a tetrahedron (**Reeve tetrahedron**) with following vertices in 1957:
$$A=(0,0,0),
B=(1,0,0),
C=(0,1,0),
D=(1,1,k),$$
where $k$ can be any natural number. Then for any $k$, the tetrahedron $ABCD$ does not contain integer point inside it and has only $4$ points on its borders, $A, B, C, D$. Thus, the volume and surface area may vary in spite of unchanged number of points within and on boundary. Therefore, Pick's theorem doesn't allow generalizations.
However, higher dimensions still has a generalization using **Ehrhart polynomials** but they are quite complex and depends not only on points inside but also on the boundary of polytype.
## Extra Resources
A few simple examples and a simple proof of Pick's theorem can be found [here](http://www.geometer.org/mathcircles/pick.pdf).
|
Pick's Theorem
|
---
title
oriented_area
---
# Oriented area of a triangle
Given three points $p_1$, $p_2$ and $p_3$, calculate an oriented (signed) area of a triangle formed by them. The sign of the area is determined in the following way: imagine you are standing in the plane at point $p_1$ and are facing $p_2$. You go to $p_2$ and if $p_3$ is to your right (then we say the three vectors turn "clockwise"), the sign of the area is negative, otherwise it is positive. If the three points are collinear, the area is zero.
Using this signed area, we can both get the regular unsigned area (as the absolute value of the signed area) and determine if the points lie clockwise or counterclockwise in their specified order (which is useful, for example, in convex hull algorithms).
## Calculation
We can use the fact that a determinant of a $2\times 2$ matrix is equal to the signed area of a parallelogram spanned by column (or row) vectors of the matrix.
This is analog to the definition of the cross product in 2D (see [Basic Geometry](basic-geometry.md)).
By dividing this area by two we get the area of a triangle that we are interested in.
We will use $\vec{p_1p_2}$ and $\vec{p_2p_3}$ as the column vectors and calculate a $2\times 2$ determinant:
$$2S=\left|\begin{matrix}x_2-x_1 & x_3-x_2\\y_2-y_1 & y_3-y_2\end{matrix}\right|=(x_2-x_1)(y_3-y_2)-(x_3-x_2)(y_2-y_1)$$
## Implementation
```cpp
int signed_area_parallelogram(point2d p1, point2d p2, point2d p3) {
return cross(p2 - p1, p3 - p2);
}
double triangle_area(point2d p1, point2d p2, point2d p3) {
return abs(signed_area_parallelogram(p1, p2, p3)) / 2.0;
}
bool clockwise(point2d p1, point2d p2, point2d p3) {
return signed_area_parallelogram(p1, p2, p3) < 0;
}
bool counter_clockwise(point2d p1, point2d p2, point2d p3) {
return signed_area_parallelogram(p1, p2, p3) > 0;
}
```
|
---
title
oriented_area
---
# Oriented area of a triangle
Given three points $p_1$, $p_2$ and $p_3$, calculate an oriented (signed) area of a triangle formed by them. The sign of the area is determined in the following way: imagine you are standing in the plane at point $p_1$ and are facing $p_2$. You go to $p_2$ and if $p_3$ is to your right (then we say the three vectors turn "clockwise"), the sign of the area is negative, otherwise it is positive. If the three points are collinear, the area is zero.
Using this signed area, we can both get the regular unsigned area (as the absolute value of the signed area) and determine if the points lie clockwise or counterclockwise in their specified order (which is useful, for example, in convex hull algorithms).
## Calculation
We can use the fact that a determinant of a $2\times 2$ matrix is equal to the signed area of a parallelogram spanned by column (or row) vectors of the matrix.
This is analog to the definition of the cross product in 2D (see [Basic Geometry](basic-geometry.md)).
By dividing this area by two we get the area of a triangle that we are interested in.
We will use $\vec{p_1p_2}$ and $\vec{p_2p_3}$ as the column vectors and calculate a $2\times 2$ determinant:
$$2S=\left|\begin{matrix}x_2-x_1 & x_3-x_2\\y_2-y_1 & y_3-y_2\end{matrix}\right|=(x_2-x_1)(y_3-y_2)-(x_3-x_2)(y_2-y_1)$$
## Implementation
```cpp
int signed_area_parallelogram(point2d p1, point2d p2, point2d p3) {
return cross(p2 - p1, p3 - p2);
}
double triangle_area(point2d p1, point2d p2, point2d p3) {
return abs(signed_area_parallelogram(p1, p2, p3)) / 2.0;
}
bool clockwise(point2d p1, point2d p2, point2d p3) {
return signed_area_parallelogram(p1, p2, p3) < 0;
}
bool counter_clockwise(point2d p1, point2d p2, point2d p3) {
return signed_area_parallelogram(p1, p2, p3) > 0;
}
```
## Practice Problems
* [Codechef - Chef and Polygons](https://www.codechef.com/problems/CHEFPOLY)
|
Oriented area of a triangle
|
---
title: Check if point belongs to the convex polygon in O(log N)
title
pt_in_polygon
---
# Check if point belongs to the convex polygon in $O(\log N)$
Consider the following problem: you are given a convex polygon with integer vertices and a lot of queries.
Each query is a point, for which we should determine whether it lies inside or on the boundary of the polygon or not.
Suppose the polygon is ordered counter-clockwise. We will answer each query in $O(\log n)$ online.
## Algorithm
Let's pick the point with the smallest x-coordinate. If there are several of them, we pick the one with the smallest y-coordinate. Let's denote it as $p_0$.
Now all other points $p_1,\dots,p_n$ of the polygon are ordered by their polar angle from the chosen point (because the polygon is ordered counter-clockwise).
If the point belongs to the polygon, it belongs to some triangle $p_0, p_i, p_{i + 1}$ (maybe more than one if it lies on the boundary of triangles).
Consider the triangle $p_0, p_i, p_{i + 1}$ such that $p$ belongs to this triangle and $i$ is maximum among all such triangles.
There is one special case. $p$ lies on the segment $(p_0, p_n)$. This case we will check separately.
Otherwise all points $p_j$ with $j \le i$ are counter-clockwise from $p$ with respect to $p_0$, and all other points are not counter-clockwise from $p$.
This means that we can apply binary search for the point $p_i$, such that $p_i$ is not counter-clockwise from $p$ with respect to $p_0$, and $i$ is maximum among all such points.
And afterwards we check if the points is actually in the determined triangle.
The sign of $(a - c) \times (b - c)$ will tell us, if the point $a$ is clockwise or counter-clockwise from the point $b$ with respect to the point $c$.
If $(a - c) \times (b - c) > 0$, then the point $a$ is to the right of the vector going from $c$ to $b$, which means clockwise from $b$ with respect to $c$.
And if $(a - c) \times (b - c) < 0$, then the point is to the left, or counter clockwise.
And it is exactly on the line between the points $b$ and $c$.
Back to the algorithm:
Consider a query point $p$.
Firstly, we must check if the point lies between $p_1$ and $p_n$.
Otherwise we already know that it cannot be part of the polygon.
This can be done by checking if the cross product $(p_1 - p_0)\times(p - p_0)$ is zero or has the same sign with $(p_1 - p_0)\times(p_n - p_0)$, and $(p_n - p_0)\times(p - p_0)$ is zero or has the same sign with $(p_n - p_0)\times(p_1 - p_0)$.
Then we handle the special case in which $p$ is part of the line $(p_0, p_1)$.
And then we can binary search the last point from $p_1,\dots p_n$ which is not counter-clockwise from $p$ with respect to $p_0$.
For a single point $p_i$ this condition can be checked by checking that $(p_i - p_0)\times(p - p_0) \le 0$. After we found such a point $p_i$, we must test if $p$ lies inside the triangle $p_0, p_i, p_{i + 1}$.
To test if it belongs to the triangle, we may simply check that $|(p_i - p_0)\times(p_{i + 1} - p_0)| = |(p_0 - p)\times(p_i - p)| + |(p_i - p)\times(p_{i + 1} - p)| + |(p_{i + 1} - p)\times(p_0 - p)|$.
This checks if the area of the triangle $p_0, p_i, p_{i+1}$ has to exact same size as the sum of the sizes of the triangle $p_0, p_i, p$, the triangle $p_0, p, p_{i+1}$ and the triangle $p_i, p_{i+1}, p$.
If $p$ is outside, then the sum of those three triangle will be bigger than the size of the triangle.
If it is inside, then it will be equal.
## Implementation
The function `prepare` will make sure that the lexicographical smallest point (smallest x value, and in ties smallest y value) will be $p_0$, and computes the vectors $p_i - p_0$.
Afterwards the function `pointInConvexPolygon` computes the result of a query.
We additionally remember the point $p_0$ and translate all queried points with it in order compute the correct distance, as vectors don't have an initial point.
By translating the query points we can assume that all vectors start at the origin $(0, 0)$, and simplify the computations for distances and lengths.
```{.cpp file=points_in_convex_polygon}
struct pt {
long long x, y;
pt() {}
pt(long long _x, long long _y) : x(_x), y(_y) {}
pt operator+(const pt &p) const { return pt(x + p.x, y + p.y); }
pt operator-(const pt &p) const { return pt(x - p.x, y - p.y); }
long long cross(const pt &p) const { return x * p.y - y * p.x; }
long long dot(const pt &p) const { return x * p.x + y * p.y; }
long long cross(const pt &a, const pt &b) const { return (a - *this).cross(b - *this); }
long long dot(const pt &a, const pt &b) const { return (a - *this).dot(b - *this); }
long long sqrLen() const { return this->dot(*this); }
};
bool lexComp(const pt &l, const pt &r) {
return l.x < r.x || (l.x == r.x && l.y < r.y);
}
int sgn(long long val) { return val > 0 ? 1 : (val == 0 ? 0 : -1); }
vector<pt> seq;
pt translation;
int n;
bool pointInTriangle(pt a, pt b, pt c, pt point) {
long long s1 = abs(a.cross(b, c));
long long s2 = abs(point.cross(a, b)) + abs(point.cross(b, c)) + abs(point.cross(c, a));
return s1 == s2;
}
void prepare(vector<pt> &points) {
n = points.size();
int pos = 0;
for (int i = 1; i < n; i++) {
if (lexComp(points[i], points[pos]))
pos = i;
}
rotate(points.begin(), points.begin() + pos, points.end());
n--;
seq.resize(n);
for (int i = 0; i < n; i++)
seq[i] = points[i + 1] - points[0];
translation = points[0];
}
bool pointInConvexPolygon(pt point) {
point = point - translation;
if (seq[0].cross(point) != 0 &&
sgn(seq[0].cross(point)) != sgn(seq[0].cross(seq[n - 1])))
return false;
if (seq[n - 1].cross(point) != 0 &&
sgn(seq[n - 1].cross(point)) != sgn(seq[n - 1].cross(seq[0])))
return false;
if (seq[0].cross(point) == 0)
return seq[0].sqrLen() >= point.sqrLen();
int l = 0, r = n - 1;
while (r - l > 1) {
int mid = (l + r) / 2;
int pos = mid;
if (seq[pos].cross(point) >= 0)
l = mid;
else
r = mid;
}
int pos = l;
return pointInTriangle(seq[pos], seq[pos + 1], pt(0, 0), point);
}
```
|
---
title: Check if point belongs to the convex polygon in O(log N)
title
pt_in_polygon
---
# Check if point belongs to the convex polygon in $O(\log N)$
Consider the following problem: you are given a convex polygon with integer vertices and a lot of queries.
Each query is a point, for which we should determine whether it lies inside or on the boundary of the polygon or not.
Suppose the polygon is ordered counter-clockwise. We will answer each query in $O(\log n)$ online.
## Algorithm
Let's pick the point with the smallest x-coordinate. If there are several of them, we pick the one with the smallest y-coordinate. Let's denote it as $p_0$.
Now all other points $p_1,\dots,p_n$ of the polygon are ordered by their polar angle from the chosen point (because the polygon is ordered counter-clockwise).
If the point belongs to the polygon, it belongs to some triangle $p_0, p_i, p_{i + 1}$ (maybe more than one if it lies on the boundary of triangles).
Consider the triangle $p_0, p_i, p_{i + 1}$ such that $p$ belongs to this triangle and $i$ is maximum among all such triangles.
There is one special case. $p$ lies on the segment $(p_0, p_n)$. This case we will check separately.
Otherwise all points $p_j$ with $j \le i$ are counter-clockwise from $p$ with respect to $p_0$, and all other points are not counter-clockwise from $p$.
This means that we can apply binary search for the point $p_i$, such that $p_i$ is not counter-clockwise from $p$ with respect to $p_0$, and $i$ is maximum among all such points.
And afterwards we check if the points is actually in the determined triangle.
The sign of $(a - c) \times (b - c)$ will tell us, if the point $a$ is clockwise or counter-clockwise from the point $b$ with respect to the point $c$.
If $(a - c) \times (b - c) > 0$, then the point $a$ is to the right of the vector going from $c$ to $b$, which means clockwise from $b$ with respect to $c$.
And if $(a - c) \times (b - c) < 0$, then the point is to the left, or counter clockwise.
And it is exactly on the line between the points $b$ and $c$.
Back to the algorithm:
Consider a query point $p$.
Firstly, we must check if the point lies between $p_1$ and $p_n$.
Otherwise we already know that it cannot be part of the polygon.
This can be done by checking if the cross product $(p_1 - p_0)\times(p - p_0)$ is zero or has the same sign with $(p_1 - p_0)\times(p_n - p_0)$, and $(p_n - p_0)\times(p - p_0)$ is zero or has the same sign with $(p_n - p_0)\times(p_1 - p_0)$.
Then we handle the special case in which $p$ is part of the line $(p_0, p_1)$.
And then we can binary search the last point from $p_1,\dots p_n$ which is not counter-clockwise from $p$ with respect to $p_0$.
For a single point $p_i$ this condition can be checked by checking that $(p_i - p_0)\times(p - p_0) \le 0$. After we found such a point $p_i$, we must test if $p$ lies inside the triangle $p_0, p_i, p_{i + 1}$.
To test if it belongs to the triangle, we may simply check that $|(p_i - p_0)\times(p_{i + 1} - p_0)| = |(p_0 - p)\times(p_i - p)| + |(p_i - p)\times(p_{i + 1} - p)| + |(p_{i + 1} - p)\times(p_0 - p)|$.
This checks if the area of the triangle $p_0, p_i, p_{i+1}$ has to exact same size as the sum of the sizes of the triangle $p_0, p_i, p$, the triangle $p_0, p, p_{i+1}$ and the triangle $p_i, p_{i+1}, p$.
If $p$ is outside, then the sum of those three triangle will be bigger than the size of the triangle.
If it is inside, then it will be equal.
## Implementation
The function `prepare` will make sure that the lexicographical smallest point (smallest x value, and in ties smallest y value) will be $p_0$, and computes the vectors $p_i - p_0$.
Afterwards the function `pointInConvexPolygon` computes the result of a query.
We additionally remember the point $p_0$ and translate all queried points with it in order compute the correct distance, as vectors don't have an initial point.
By translating the query points we can assume that all vectors start at the origin $(0, 0)$, and simplify the computations for distances and lengths.
```{.cpp file=points_in_convex_polygon}
struct pt {
long long x, y;
pt() {}
pt(long long _x, long long _y) : x(_x), y(_y) {}
pt operator+(const pt &p) const { return pt(x + p.x, y + p.y); }
pt operator-(const pt &p) const { return pt(x - p.x, y - p.y); }
long long cross(const pt &p) const { return x * p.y - y * p.x; }
long long dot(const pt &p) const { return x * p.x + y * p.y; }
long long cross(const pt &a, const pt &b) const { return (a - *this).cross(b - *this); }
long long dot(const pt &a, const pt &b) const { return (a - *this).dot(b - *this); }
long long sqrLen() const { return this->dot(*this); }
};
bool lexComp(const pt &l, const pt &r) {
return l.x < r.x || (l.x == r.x && l.y < r.y);
}
int sgn(long long val) { return val > 0 ? 1 : (val == 0 ? 0 : -1); }
vector<pt> seq;
pt translation;
int n;
bool pointInTriangle(pt a, pt b, pt c, pt point) {
long long s1 = abs(a.cross(b, c));
long long s2 = abs(point.cross(a, b)) + abs(point.cross(b, c)) + abs(point.cross(c, a));
return s1 == s2;
}
void prepare(vector<pt> &points) {
n = points.size();
int pos = 0;
for (int i = 1; i < n; i++) {
if (lexComp(points[i], points[pos]))
pos = i;
}
rotate(points.begin(), points.begin() + pos, points.end());
n--;
seq.resize(n);
for (int i = 0; i < n; i++)
seq[i] = points[i + 1] - points[0];
translation = points[0];
}
bool pointInConvexPolygon(pt point) {
point = point - translation;
if (seq[0].cross(point) != 0 &&
sgn(seq[0].cross(point)) != sgn(seq[0].cross(seq[n - 1])))
return false;
if (seq[n - 1].cross(point) != 0 &&
sgn(seq[n - 1].cross(point)) != sgn(seq[n - 1].cross(seq[0])))
return false;
if (seq[0].cross(point) == 0)
return seq[0].sqrLen() >= point.sqrLen();
int l = 0, r = n - 1;
while (r - l > 1) {
int mid = (l + r) / 2;
int pos = mid;
if (seq[pos].cross(point) >= 0)
l = mid;
else
r = mid;
}
int pos = l;
return pointInTriangle(seq[pos], seq[pos + 1], pt(0, 0), point);
}
```
## Problems
[SGU253 Theodore Roosevelt](https://codeforces.com/problemsets/acmsguru/problem/99999/253)
[Codeforces 55E Very simple problem](https://codeforces.com/contest/55/problem/E)
|
Check if point belongs to the convex polygon in $O(\log N)$
|
---
title
lines_intersection
---
# Intersection Point of Lines
You are given two lines, described via the equations $a_1 x + b_1 y + c_1 = 0$ and $a_2 x + b_2 y + c_2 = 0$.
We have to find the intersection point of the lines, or determine that the lines are parallel.
## Solution
If two lines are not parallel, they intersect.
To find their intersection point, we need to solve the following system of linear equations:
$$\begin{cases} a_1 x + b_1 y + c_1 = 0 \\
a_2 x + b_2 y + c_2 = 0
\end{cases}$$
Using Cramer's rule, we can immediately write down the solution for the system, which will give us the required intersection point of the lines:
$$x = - \frac{\begin{vmatrix}c_1 & b_1 \cr c_2 & b_2\end{vmatrix}}{\begin{vmatrix}a_1 & b_1 \cr a_2 & b_2\end{vmatrix} } = - \frac{c_1 b_2 - c_2 b_1}{a_1 b_2 - a_2 b_1},$$
$$y = - \frac{\begin{vmatrix}a_1 & c_1 \cr a_2 & c_2\end{vmatrix}}{\begin{vmatrix}a_1 & b_1 \cr a_2 & b_2\end{vmatrix}} = - \frac{a_1 c_2 - a_2 c_1}{a_1 b_2 - a_2 b_1}.$$
If the denominator equals $0$, i.e.
$$\begin{vmatrix}a_1 & b_1 \cr a_2 & b_2\end{vmatrix} = a_1 b_2 - a_2 b_1 = 0 $$
then either the system has no solutions (the lines are parallel and distinct) or there are infinitely many solutions (the lines overlap).
If we need to distinguish these two cases, we have to check if coefficients $c$ are proportional with the same ratio as the coefficients $a$ and $b$.
To do that we only have calculate the following determinants, and if they both equal $0$, the lines overlap:
$$\begin{vmatrix}a_1 & c_1 \cr a_2 & c_2\end{vmatrix}, \begin{vmatrix}b_1 & c_1 \cr b_2 & c_2\end{vmatrix} $$
Notice, a different approach for computing the intersection point is explained in the article [Basic Geometry](basic-geometry.md).
## Implementation
```{.cpp file=line_intersection}
struct pt {
double x, y;
};
struct line {
double a, b, c;
};
const double EPS = 1e-9;
double det(double a, double b, double c, double d) {
return a*d - b*c;
}
bool intersect(line m, line n, pt & res) {
double zn = det(m.a, m.b, n.a, n.b);
if (abs(zn) < EPS)
return false;
res.x = -det(m.c, m.b, n.c, n.b) / zn;
res.y = -det(m.a, m.c, n.a, n.c) / zn;
return true;
}
bool parallel(line m, line n) {
return abs(det(m.a, m.b, n.a, n.b)) < EPS;
}
bool equivalent(line m, line n) {
return abs(det(m.a, m.b, n.a, n.b)) < EPS
&& abs(det(m.a, m.c, n.a, n.c)) < EPS
&& abs(det(m.b, m.c, n.b, n.c)) < EPS;
}
```
|
---
title
lines_intersection
---
# Intersection Point of Lines
You are given two lines, described via the equations $a_1 x + b_1 y + c_1 = 0$ and $a_2 x + b_2 y + c_2 = 0$.
We have to find the intersection point of the lines, or determine that the lines are parallel.
## Solution
If two lines are not parallel, they intersect.
To find their intersection point, we need to solve the following system of linear equations:
$$\begin{cases} a_1 x + b_1 y + c_1 = 0 \\
a_2 x + b_2 y + c_2 = 0
\end{cases}$$
Using Cramer's rule, we can immediately write down the solution for the system, which will give us the required intersection point of the lines:
$$x = - \frac{\begin{vmatrix}c_1 & b_1 \cr c_2 & b_2\end{vmatrix}}{\begin{vmatrix}a_1 & b_1 \cr a_2 & b_2\end{vmatrix} } = - \frac{c_1 b_2 - c_2 b_1}{a_1 b_2 - a_2 b_1},$$
$$y = - \frac{\begin{vmatrix}a_1 & c_1 \cr a_2 & c_2\end{vmatrix}}{\begin{vmatrix}a_1 & b_1 \cr a_2 & b_2\end{vmatrix}} = - \frac{a_1 c_2 - a_2 c_1}{a_1 b_2 - a_2 b_1}.$$
If the denominator equals $0$, i.e.
$$\begin{vmatrix}a_1 & b_1 \cr a_2 & b_2\end{vmatrix} = a_1 b_2 - a_2 b_1 = 0 $$
then either the system has no solutions (the lines are parallel and distinct) or there are infinitely many solutions (the lines overlap).
If we need to distinguish these two cases, we have to check if coefficients $c$ are proportional with the same ratio as the coefficients $a$ and $b$.
To do that we only have calculate the following determinants, and if they both equal $0$, the lines overlap:
$$\begin{vmatrix}a_1 & c_1 \cr a_2 & c_2\end{vmatrix}, \begin{vmatrix}b_1 & c_1 \cr b_2 & c_2\end{vmatrix} $$
Notice, a different approach for computing the intersection point is explained in the article [Basic Geometry](basic-geometry.md).
## Implementation
```{.cpp file=line_intersection}
struct pt {
double x, y;
};
struct line {
double a, b, c;
};
const double EPS = 1e-9;
double det(double a, double b, double c, double d) {
return a*d - b*c;
}
bool intersect(line m, line n, pt & res) {
double zn = det(m.a, m.b, n.a, n.b);
if (abs(zn) < EPS)
return false;
res.x = -det(m.c, m.b, n.c, n.b) / zn;
res.y = -det(m.a, m.c, n.a, n.c) / zn;
return true;
}
bool parallel(line m, line n) {
return abs(det(m.a, m.b, n.a, n.b)) < EPS;
}
bool equivalent(line m, line n) {
return abs(det(m.a, m.b, n.a, n.b)) < EPS
&& abs(det(m.a, m.c, n.a, n.c)) < EPS
&& abs(det(m.b, m.c, n.b, n.c)) < EPS;
}
```
|
Intersection Point of Lines
|
---
title
- Original
---
# Half-plane intersection
In this article we will discuss the problem of computing the intersection of a set of half-planes. Such an intersection can be conveniently represented as a convex region/polygon, where every point inside of it is also inside all of the half-planes, and it is this polygon that we're trying to find or construct. We give some initial intuition for the problem, describe a $O(N \log N)$ approach known as the Sort-and-Incremental algorithm and give some sample applications of this technique.
It is strongly recommended for the reader to be familiar with basic geometrical primitives and operations (points, vectors, intersection of lines). Additionally, knowledge about [Convex Hulls](../geometry/convex-hull.md) or the [Convex Hull Trick](../geometry/convex_hull_trick.md) may help to better understand the concepts in this article, but they are not a prerequisite by any means.
## Initial clarifications and definitions
For the entire article, we will make some assumptions (unless specified otherwise):
1. We define $N$ to be the quantity of half-planes in the given set.
2. We will represent lines and half-planes by one point and one vector (any point that lies on the given line, and the direction vector of the line). In the case of half-planes, we assume that every half-plane allows the region to the left side of its direction vector. Additionally, we define the angle of a half-plane to be the polar angle of its direction vector. See image below for example.
3. We will assume that the resulting intersection is always either bounded or empty. If we need to handle the unbounded case, we can simply add 4 half-planes that define a large-enough bounding box.
4. We will assume, for simplicity, that there are no parallel half-planes in the given set. Towards the end of the article we will discuss how to deal with such cases.

The half-plane $y \geq 2x - 2$ can be represented as the point $P = (1, 0)$ with direction vector $PQ = Q - P = (1, 2)$
## Brute force approach - $O(N^3)$ {data-toc-label="Brute force approach - O(N^3)"}
One of the most straightforward and obvious solutions would be to compute the intersection point of the lines of all pairs of half-planes and, for each point, check if it is inside all of the other half-planes. Since there are $O(N^2)$ intersection points, and for each of them we have to check $O(N)$ half-planes, the total time complexity is $O(N^3)$. The actual region of the intersection can then be reconstructed using, for example, a Convex Hull algorithm on the set of intersection points that were included in all the half-planes.
It is fairly easy to see why this works: the vertices of the resulting convex polygon are all intersection points of the half-plane lines, and each of those vertices is obviously part of all the half-planes. The main advantage of this method is that its easy to understand, remember and code on-the-fly if you just need to check if the intersection is empty or not. However, it is awfully slow and unfit for most problems, so we need something faster.
## Incremental approach - $O(N^2)$ {data-toc-label="Incremental approach - O(N^2)"}
Another fairly straightforward approach is to incrementally construct the intersection of the half-planes, one at a time. This method is basically equivalent to cutting a convex polygon by a line $N$ times, and removing the redundant half-planes at every step. To do this, we can represent the convex polygon as a list of line segments, and to cut it with a half-plane we simply find the intersection points of the segments with the half-plane line (there will only be two intersection points if the line properly intersects the polygon), and replace all the line segments in-between with the new segment corresponding to the half-plane. Since such procedure can be implemented in linear time, we can simply start with a big bounding box and cut it down with each one of the half-planes, obtaining a total time complexity of $O(N^2)$.
This method is a big step in the right direction, but it does feel wasteful to have to iterate over $O(N)$ half-planes at every step. We will see next that, by making some clever observations, the ideas behind this incremental approach can be recycled to create a $O(N \log N)$ algorithm.
## Sort-and-Incremental algorithm - $O(N \log N)$ {data-toc-label="Sort-and-Incremental algorithm - O(N log N)"}
The first properly-documented source of this algorithm we could find was Zeyuan Zhu's thesis for Chinese Team Selecting Contest titled [New Algorithm for Half-plane Intersection and its Practical Value](http://people.csail.mit.edu/zeyuan/publications.htm), from the year 2006. The approach we'll describe next is based on this same algorithm, but instead of computing two separate intersections for the lower and upper halves of the intersections, we'll construct it all at once in one pass with a deque (double-ended queue).
The algorithm itself, as the name may spoil, takes advantage of the fact that the resulting region from the intersection of half-planes is convex, and thus it will consist of some segments of half-planes in order sorted by their angles. This leads to a crucial observation: if we incrementally intersect the half-planes in their order sorted by angle (as they would appear in the final, resulting shape of the intersection) and store them in a double-ended queue, then we will only ever need to remove half-planes from the front and the back of the deque.
To better visualize this fact, suppose we're performing the incremental approach described previously on a set of half-planes that is sorted by angle (in this case, we'll assume they're sorted from $-\pi$ to $\pi$), and suppose that we're about to start some arbitrary $k$'th step. This means we have already constructed the intersection of the first $k-1$ half-planes. Now, because the half-planes are sorted by angle, whatever the $k$'th half-plane is, we can be sure that it will form a convex turn with the $(K-1)$'th half-plane. For that reason, a few things may happen:
1. Some (possibly none) of the half-planes in the back of the intersection may become *redundant*. In this case, we need to pop these now-useless half-planes from the back of the deque.
2. Some (possibly none) of the half-planes at the front may become *redundant*. Analogous to case 1, we just pop them from the front of the deque.
3. The intersection may become empty (after handling cases 1 and/or 2). In this case, we just report the intersection is empty and terminate the algorithm.
*We say a half-plane is "redundant" if it does not contribute anything to the intersection. Such a half-plane could be removed and the resulting intersection would not change at all.*
Here's a small example with an illustration:
Let $H = \{ A, B, C, D, E \}$ be the set of half-planes currently present in the intersection. Additionally, let $P = \{ p, q, r, s \}$ be the set of intersection points of adjacent half-planes in H. Now, suppose we wish to intersect it with the half-plane $F$, as seen in the illustration below:

Notice the half-plane $F$ makes $A$ and $E$ redundant in the intersection. So we remove both $A$ and $E$ from the front and back of the intersection, respectively, and add $F$ at the end. And we finally obtain the new intersection $H = \{ B, C, D, F\}$ with $P = \{ q, r, t, u \}$.

With all of this in mind, we have almost everything we need to actually implement the algorithm, but we still need to talk about some special cases. At the beginning of the article we said we would add a bounding box to take care of the cases where the intersection could be unbounded, so the only tricky case we actually need to handle is parallel half-planes. We can have two sub-cases: two half-planes can be parallel with the same direction or with opposite direction. The reason this case needs to be handled separately is because we will need to compute intersection points of half-plane lines to be able to check if a half-plane is redundant or not, and two parallel lines have no intersection point, so we need a special way to deal with them.
For the case of parallel half-planes of opposite orientation: Notice that, because we're adding the bounding box to deal with the unbounded case, this also deals with the case where we have two adjacent parallel half-planes with opposite directions after sorting, since there will have to be at least one of the bounding-box half-planes in between these two (remember they are sorted by angle).
* However, it is possible that, after removing some half-planes from the back of the deque, two parallel half-planes of opposite direction end up together. This case only happens, specifically, when these two half-planes form an empty intersection, as this last half-plane will cause everything to be removed from the deque. To avoid this problem, we have to manually check for parallel half-planes, and if they have opposite direction, we just instantly stop the algorithm and return an empty intersection.
Thus the only case we actually need to handle is having multiple half-planes with the same angle, and it turns out this case is fairly easy to handle: we only have keep the leftmost half-plane and erase the rest, since they will be completely redundant anyways.
To sum up, the full algorithm will roughly look as follows:
1. We begin by sorting the set of half-planes by angle, which takes $O(N \log N)$ time.
2. We will iterate over the set of half-planes, and for each one, we will perform the incremental procedure, popping from the front and the back of the double-ended queue as necessary. This will take linear time in total, as every half-plane can only be added or removed once.
3. At the end, the convex polygon resulting from the intersection can be simply obtained by computing the intersection points of adjacent half-planes in the deque at the end of the procedure. This will take linear time as well. It is also possible to store such points during step 2 and skip this step entirely, but we believe it is slightly easier (in terms of implementation) to compute them on-the-fly.
In total, we have achieved a time complexity of $O(N \log N)$. Since sorting is clearly the bottleneck, the algorithm can be made to run in linear time in the special case where we are given half-planes sorted in advance by their angles (an example of such a case would be obtaining the half-planes that define a convex polygon).
### Direct implementation
Here is a sample, direct implementation of the algorithm, with comments explaining most parts:
Simple point/vector and half-plane structs:
```cpp
// Redefine epsilon and infinity as necessary. Be mindful of precision errors.
const long double eps = 1e-9, inf = 1e9;
// Basic point/vector struct.
struct Point {
long double x, y;
explicit Point(long double x = 0, long double y = 0) : x(x), y(y) {}
// Addition, substraction, multiply by constant, dot product, cross product.
friend Point operator + (const Point& p, const Point& q) {
return Point(p.x + q.x, p.y + q.y);
}
friend Point operator - (const Point& p, const Point& q) {
return Point(p.x - q.x, p.y - q.y);
}
friend Point operator * (const Point& p, const long double& k) {
return Point(p.x * k, p.y * k);
}
friend long double dot(const Point& p, const Point& q) {
return p.x * q.x + p.y * q.y;
}
friend long double cross(const Point& p, const Point& q) {
return p.x * q.y - p.y * q.x;
}
};
// Basic half-plane struct.
struct Halfplane {
// 'p' is a passing point of the line and 'pq' is the direction vector of the line.
Point p, pq;
long double angle;
Halfplane() {}
Halfplane(const Point& a, const Point& b) : p(a), pq(b - a) {
angle = atan2l(pq.y, pq.x);
}
// Check if point 'r' is outside this half-plane.
// Every half-plane allows the region to the LEFT of its line.
bool out(const Point& r) {
return cross(pq, r - p) < -eps;
}
// Comparator for sorting.
bool operator < (const Halfplane& e) const {
return angle < e.angle;
}
// Intersection point of the lines of two half-planes. It is assumed they're never parallel.
friend Point inter(const Halfplane& s, const Halfplane& t) {
long double alpha = cross((t.p - s.p), t.pq) / cross(s.pq, t.pq);
return s.p + (s.pq * alpha);
}
};
```
Algorithm:
```cpp
// Actual algorithm
vector<Point> hp_intersect(vector<Halfplane>& H) {
Point box[4] = { // Bounding box in CCW order
Point(inf, inf),
Point(-inf, inf),
Point(-inf, -inf),
Point(inf, -inf)
};
for(int i = 0; i<4; i++) { // Add bounding box half-planes.
Halfplane aux(box[i], box[(i+1) % 4]);
H.push_back(aux);
}
// Sort by angle and start algorithm
sort(H.begin(), H.end());
deque<Halfplane> dq;
int len = 0;
for(int i = 0; i < int(H.size()); i++) {
// Remove from the back of the deque while last half-plane is redundant
while (len > 1 && H[i].out(inter(dq[len-1], dq[len-2]))) {
dq.pop_back();
--len;
}
// Remove from the front of the deque while first half-plane is redundant
while (len > 1 && H[i].out(inter(dq[0], dq[1]))) {
dq.pop_front();
--len;
}
// Special case check: Parallel half-planes
if (len > 0 && fabsl(cross(H[i].pq, dq[len-1].pq)) < eps) {
// Opposite parallel half-planes that ended up checked against each other.
if (dot(H[i].pq, dq[len-1].pq) < 0.0)
return vector<Point>();
// Same direction half-plane: keep only the leftmost half-plane.
if (H[i].out(dq[len-1].p)) {
dq.pop_back();
--len;
}
else continue;
}
// Add new half-plane
dq.push_back(H[i]);
++len;
}
// Final cleanup: Check half-planes at the front against the back and vice-versa
while (len > 2 && dq[0].out(inter(dq[len-1], dq[len-2]))) {
dq.pop_back();
--len;
}
while (len > 2 && dq[len-1].out(inter(dq[0], dq[1]))) {
dq.pop_front();
--len;
}
// Report empty intersection if necessary
if (len < 3) return vector<Point>();
// Reconstruct the convex polygon from the remaining half-planes.
vector<Point> ret(len);
for(int i = 0; i+1 < len; i++) {
ret[i] = inter(dq[i], dq[i+1]);
}
ret.back() = inter(dq[len-1], dq[0]);
return ret;
}
```
### Implementation discussion
A special thing to note is that, in case there multiple half-planes that intersect at the same point, then this algorithm could return repeated adjacent points in the final polygon. However, this should not have any impact on judging correctly whether the intersection is empty or not, and it does not affect the polygon area at all either. You may want to remove these duplicates depending on what tasks you need to do after. You can do this very easily with std::unique. We want to keep the repeat points during the execution of the algorithm so that the intersections with area equal to zero can be computed correctly (for example, intersections that consist of a single point, line or line-segment). I encourage the reader to test some small hand-made cases where the intersection results in a single point or line.
One more thing that should be talked about is what to do if we are given half-planes in the form of a linear constraint (for example, $ax + by + c \leq 0$). In such case, there are two options. You can either implement the algorithm with the corresponding modifications to work with such representation (essentially create your own half-plane struct, should be fairly straightforward if you're familiar with the convex hull trick), or you can transform the lines into the representation we used in this article by taking any 2 points of each line. In general, it is recommended to work with the representation that you're given in the problem to avoid additional precision issues.
## Problems, tasks and applications
Many problems that can be solved with half-plane intersection can also be solved without it, but with (usually) more complicated or uncommon approaches. Generally, half-plane intersection can appear when dealing with problems related to polygons (mostly convex), visibility in the plane and two-dimensional linear programming. Here are some sample tasks that can be solved with this technique:
### Convex polygon intersection
One of the classical applications of half-plane intersection: Given $N$ polygons, compute the region that is included inside all of the polygons.
Since the intersection of a set of half-planes is a convex polygon, we can also represent a convex polygon as a set of half-planes (every edge of the polygon is a segment of a half-plane). Generate these half-planes for every polygon and compute the intersection of the whole set. The total time complexity is $O(S \log S)$, where S is the total number of sides of all the polygons. The problem can also theoretically be solved in $O(S \log N)$ by merging the $N$ sets of half-planes using a heap and then running the algorithm without the sorting step, but such solution has much worse constant factor than straightforward sorting and only provides minor speed gains for very small $N$.
### Visibility in the plane
Problems that require something among the lines of "determine if some line segments are visible from some point(s) in the plane" can usually be formulated as half-plane intersection problems. Take, for example, the following task: Given some simple polygon (not necessarily convex), determine if there's any point inside the polygon such that the whole boundary of the polygon can be observed from that point. This is also known as finding the [kernel of a polygon](https://en.wikipedia.org/wiki/Star-shaped_polygon) and can be solved by simple half-plane intersection, taking each edge of the polygon as a half-plane and then computing its intersection.
Here's a related, more interesting problem that was presented by Artem Vasilyev in one of his [Brazilian ICPC Summer School lectures](https://youtu.be/WKyZSitpm6M?t=6463):
Given a set $p$ of points $p_1, p_2\ \dots \ p_n$ in the plane, determine if there's any point $q$ you can stand at such that you can see all the points of $p$ from left to right in increasing order of their index.
Such problem can be solved by noticing that being able to see some point $p_i$ to the left of $p_j$ is the same as being able to see the right side of the line segment from $p_i$ to $p_j$ (or equivalently, being able to see the left side of the segment from $p_j$ to $p_i$). With that in mind, we can simply create a half-plane for every line segment $p_i p_{i+1}$ (or $p_{i+1} p_i$ depending on the orientation you choose) and check if the intersection of the whole set is empty or not.
### Half-plane intersection with binary search
Another common application is utilizing half-plane intersection as a tool to validate the predicate of a binary search procedure. Here's an example of such a problem, also presented by Artem Vasilyev in the same lecture that was previously mentioned: Given a **convex** polygon $P$, find the biggest circumference that can be inscribed inside of it.
Instead of looking for some sort of closed-form solution, annoying formulas or obscure algorithmic solutions, lets instead try to binary search on the answer. Notice that, for some fixed $r$, a circle with radius $r$ can be inscribed inside $P$ only if there exists some point inside $P$ that has distance greater or equal than $r$ to all the points of the boundary of $P$. This condition can be validated by "shrinking" the polygon inwards by a distance of $r$ and checking that the polygon remains non-degenerate (or is a point/segment itself). Such procedure can be simulated by taking the half-planes of the polygon sides in counter-clockwise order, translating each of them by a distance of $r$ in the direction of the region they allow (that is, orthogonal to the direction vector of the half-plane), and checking if the intersection is not empty.
Clearly, if we can inscribe a circle of radius $r$, we can also inscribe any other circle of radius smaller than $r$. So we can perform a binary search on the radius $r$ and validate every step using half-plane intersection. Also, note that the half-planes of a convex polygon are already sorted by angle, so the sorting step can be skipped in the algorithm. Thus we obtain a total time complexity of $O(NK)$, where $N$ is the number of polygon vertices and $K$ is the number of iterations of the binary search (the actual value will depend on the range of possible answers and the desired precision).
### Two-dimensional linear programming
One more application of half-plane intersection is linear programming in two variables. All linear constraints for two variables can be expressed in the form of $Ax + By + C \leq 0$ (inequality comparator may vary). Clearly, these are just half-planes, so checking if a feasible solution exists for a set of linear constraints can be done with half-plane intersection. Additionally, for a given set of linear constraints, it is possible to compute the region of feasible solutions (i.e. the intersection of the half-planes) and then answer multiple queries of maximizing/minimizing some linear function $f(x, y)$ subject to the constraints in $O(\log N)$ per query using binary search (very similar to the convex hull trick).
It is worth mentioning that there also exists a fairly simple randomized algorithm that can check whether a set of linear constraints has a feasible solution or not, and maximize/minimize some linear function subject to the given constraints. This randomized algorithm was also explained nicely by Artem Vasilyev in the lecture mentioned earlier. Here are some additional resources on it, should the reader be interested: [CG - Lecture 4, parts 4 and 5](https://youtu.be/5dfc355t2y4) and [Petr Mitrichev's blog (which includes the solution to the hardest problem in the practice problems list below)](https://petr-mitrichev.blogspot.com/2016/07/a-half-plane-week.html).
|
---
title
- Original
---
# Half-plane intersection
In this article we will discuss the problem of computing the intersection of a set of half-planes. Such an intersection can be conveniently represented as a convex region/polygon, where every point inside of it is also inside all of the half-planes, and it is this polygon that we're trying to find or construct. We give some initial intuition for the problem, describe a $O(N \log N)$ approach known as the Sort-and-Incremental algorithm and give some sample applications of this technique.
It is strongly recommended for the reader to be familiar with basic geometrical primitives and operations (points, vectors, intersection of lines). Additionally, knowledge about [Convex Hulls](../geometry/convex-hull.md) or the [Convex Hull Trick](../geometry/convex_hull_trick.md) may help to better understand the concepts in this article, but they are not a prerequisite by any means.
## Initial clarifications and definitions
For the entire article, we will make some assumptions (unless specified otherwise):
1. We define $N$ to be the quantity of half-planes in the given set.
2. We will represent lines and half-planes by one point and one vector (any point that lies on the given line, and the direction vector of the line). In the case of half-planes, we assume that every half-plane allows the region to the left side of its direction vector. Additionally, we define the angle of a half-plane to be the polar angle of its direction vector. See image below for example.
3. We will assume that the resulting intersection is always either bounded or empty. If we need to handle the unbounded case, we can simply add 4 half-planes that define a large-enough bounding box.
4. We will assume, for simplicity, that there are no parallel half-planes in the given set. Towards the end of the article we will discuss how to deal with such cases.

The half-plane $y \geq 2x - 2$ can be represented as the point $P = (1, 0)$ with direction vector $PQ = Q - P = (1, 2)$
## Brute force approach - $O(N^3)$ {data-toc-label="Brute force approach - O(N^3)"}
One of the most straightforward and obvious solutions would be to compute the intersection point of the lines of all pairs of half-planes and, for each point, check if it is inside all of the other half-planes. Since there are $O(N^2)$ intersection points, and for each of them we have to check $O(N)$ half-planes, the total time complexity is $O(N^3)$. The actual region of the intersection can then be reconstructed using, for example, a Convex Hull algorithm on the set of intersection points that were included in all the half-planes.
It is fairly easy to see why this works: the vertices of the resulting convex polygon are all intersection points of the half-plane lines, and each of those vertices is obviously part of all the half-planes. The main advantage of this method is that its easy to understand, remember and code on-the-fly if you just need to check if the intersection is empty or not. However, it is awfully slow and unfit for most problems, so we need something faster.
## Incremental approach - $O(N^2)$ {data-toc-label="Incremental approach - O(N^2)"}
Another fairly straightforward approach is to incrementally construct the intersection of the half-planes, one at a time. This method is basically equivalent to cutting a convex polygon by a line $N$ times, and removing the redundant half-planes at every step. To do this, we can represent the convex polygon as a list of line segments, and to cut it with a half-plane we simply find the intersection points of the segments with the half-plane line (there will only be two intersection points if the line properly intersects the polygon), and replace all the line segments in-between with the new segment corresponding to the half-plane. Since such procedure can be implemented in linear time, we can simply start with a big bounding box and cut it down with each one of the half-planes, obtaining a total time complexity of $O(N^2)$.
This method is a big step in the right direction, but it does feel wasteful to have to iterate over $O(N)$ half-planes at every step. We will see next that, by making some clever observations, the ideas behind this incremental approach can be recycled to create a $O(N \log N)$ algorithm.
## Sort-and-Incremental algorithm - $O(N \log N)$ {data-toc-label="Sort-and-Incremental algorithm - O(N log N)"}
The first properly-documented source of this algorithm we could find was Zeyuan Zhu's thesis for Chinese Team Selecting Contest titled [New Algorithm for Half-plane Intersection and its Practical Value](http://people.csail.mit.edu/zeyuan/publications.htm), from the year 2006. The approach we'll describe next is based on this same algorithm, but instead of computing two separate intersections for the lower and upper halves of the intersections, we'll construct it all at once in one pass with a deque (double-ended queue).
The algorithm itself, as the name may spoil, takes advantage of the fact that the resulting region from the intersection of half-planes is convex, and thus it will consist of some segments of half-planes in order sorted by their angles. This leads to a crucial observation: if we incrementally intersect the half-planes in their order sorted by angle (as they would appear in the final, resulting shape of the intersection) and store them in a double-ended queue, then we will only ever need to remove half-planes from the front and the back of the deque.
To better visualize this fact, suppose we're performing the incremental approach described previously on a set of half-planes that is sorted by angle (in this case, we'll assume they're sorted from $-\pi$ to $\pi$), and suppose that we're about to start some arbitrary $k$'th step. This means we have already constructed the intersection of the first $k-1$ half-planes. Now, because the half-planes are sorted by angle, whatever the $k$'th half-plane is, we can be sure that it will form a convex turn with the $(K-1)$'th half-plane. For that reason, a few things may happen:
1. Some (possibly none) of the half-planes in the back of the intersection may become *redundant*. In this case, we need to pop these now-useless half-planes from the back of the deque.
2. Some (possibly none) of the half-planes at the front may become *redundant*. Analogous to case 1, we just pop them from the front of the deque.
3. The intersection may become empty (after handling cases 1 and/or 2). In this case, we just report the intersection is empty and terminate the algorithm.
*We say a half-plane is "redundant" if it does not contribute anything to the intersection. Such a half-plane could be removed and the resulting intersection would not change at all.*
Here's a small example with an illustration:
Let $H = \{ A, B, C, D, E \}$ be the set of half-planes currently present in the intersection. Additionally, let $P = \{ p, q, r, s \}$ be the set of intersection points of adjacent half-planes in H. Now, suppose we wish to intersect it with the half-plane $F$, as seen in the illustration below:

Notice the half-plane $F$ makes $A$ and $E$ redundant in the intersection. So we remove both $A$ and $E$ from the front and back of the intersection, respectively, and add $F$ at the end. And we finally obtain the new intersection $H = \{ B, C, D, F\}$ with $P = \{ q, r, t, u \}$.

With all of this in mind, we have almost everything we need to actually implement the algorithm, but we still need to talk about some special cases. At the beginning of the article we said we would add a bounding box to take care of the cases where the intersection could be unbounded, so the only tricky case we actually need to handle is parallel half-planes. We can have two sub-cases: two half-planes can be parallel with the same direction or with opposite direction. The reason this case needs to be handled separately is because we will need to compute intersection points of half-plane lines to be able to check if a half-plane is redundant or not, and two parallel lines have no intersection point, so we need a special way to deal with them.
For the case of parallel half-planes of opposite orientation: Notice that, because we're adding the bounding box to deal with the unbounded case, this also deals with the case where we have two adjacent parallel half-planes with opposite directions after sorting, since there will have to be at least one of the bounding-box half-planes in between these two (remember they are sorted by angle).
* However, it is possible that, after removing some half-planes from the back of the deque, two parallel half-planes of opposite direction end up together. This case only happens, specifically, when these two half-planes form an empty intersection, as this last half-plane will cause everything to be removed from the deque. To avoid this problem, we have to manually check for parallel half-planes, and if they have opposite direction, we just instantly stop the algorithm and return an empty intersection.
Thus the only case we actually need to handle is having multiple half-planes with the same angle, and it turns out this case is fairly easy to handle: we only have keep the leftmost half-plane and erase the rest, since they will be completely redundant anyways.
To sum up, the full algorithm will roughly look as follows:
1. We begin by sorting the set of half-planes by angle, which takes $O(N \log N)$ time.
2. We will iterate over the set of half-planes, and for each one, we will perform the incremental procedure, popping from the front and the back of the double-ended queue as necessary. This will take linear time in total, as every half-plane can only be added or removed once.
3. At the end, the convex polygon resulting from the intersection can be simply obtained by computing the intersection points of adjacent half-planes in the deque at the end of the procedure. This will take linear time as well. It is also possible to store such points during step 2 and skip this step entirely, but we believe it is slightly easier (in terms of implementation) to compute them on-the-fly.
In total, we have achieved a time complexity of $O(N \log N)$. Since sorting is clearly the bottleneck, the algorithm can be made to run in linear time in the special case where we are given half-planes sorted in advance by their angles (an example of such a case would be obtaining the half-planes that define a convex polygon).
### Direct implementation
Here is a sample, direct implementation of the algorithm, with comments explaining most parts:
Simple point/vector and half-plane structs:
```cpp
// Redefine epsilon and infinity as necessary. Be mindful of precision errors.
const long double eps = 1e-9, inf = 1e9;
// Basic point/vector struct.
struct Point {
long double x, y;
explicit Point(long double x = 0, long double y = 0) : x(x), y(y) {}
// Addition, substraction, multiply by constant, dot product, cross product.
friend Point operator + (const Point& p, const Point& q) {
return Point(p.x + q.x, p.y + q.y);
}
friend Point operator - (const Point& p, const Point& q) {
return Point(p.x - q.x, p.y - q.y);
}
friend Point operator * (const Point& p, const long double& k) {
return Point(p.x * k, p.y * k);
}
friend long double dot(const Point& p, const Point& q) {
return p.x * q.x + p.y * q.y;
}
friend long double cross(const Point& p, const Point& q) {
return p.x * q.y - p.y * q.x;
}
};
// Basic half-plane struct.
struct Halfplane {
// 'p' is a passing point of the line and 'pq' is the direction vector of the line.
Point p, pq;
long double angle;
Halfplane() {}
Halfplane(const Point& a, const Point& b) : p(a), pq(b - a) {
angle = atan2l(pq.y, pq.x);
}
// Check if point 'r' is outside this half-plane.
// Every half-plane allows the region to the LEFT of its line.
bool out(const Point& r) {
return cross(pq, r - p) < -eps;
}
// Comparator for sorting.
bool operator < (const Halfplane& e) const {
return angle < e.angle;
}
// Intersection point of the lines of two half-planes. It is assumed they're never parallel.
friend Point inter(const Halfplane& s, const Halfplane& t) {
long double alpha = cross((t.p - s.p), t.pq) / cross(s.pq, t.pq);
return s.p + (s.pq * alpha);
}
};
```
Algorithm:
```cpp
// Actual algorithm
vector<Point> hp_intersect(vector<Halfplane>& H) {
Point box[4] = { // Bounding box in CCW order
Point(inf, inf),
Point(-inf, inf),
Point(-inf, -inf),
Point(inf, -inf)
};
for(int i = 0; i<4; i++) { // Add bounding box half-planes.
Halfplane aux(box[i], box[(i+1) % 4]);
H.push_back(aux);
}
// Sort by angle and start algorithm
sort(H.begin(), H.end());
deque<Halfplane> dq;
int len = 0;
for(int i = 0; i < int(H.size()); i++) {
// Remove from the back of the deque while last half-plane is redundant
while (len > 1 && H[i].out(inter(dq[len-1], dq[len-2]))) {
dq.pop_back();
--len;
}
// Remove from the front of the deque while first half-plane is redundant
while (len > 1 && H[i].out(inter(dq[0], dq[1]))) {
dq.pop_front();
--len;
}
// Special case check: Parallel half-planes
if (len > 0 && fabsl(cross(H[i].pq, dq[len-1].pq)) < eps) {
// Opposite parallel half-planes that ended up checked against each other.
if (dot(H[i].pq, dq[len-1].pq) < 0.0)
return vector<Point>();
// Same direction half-plane: keep only the leftmost half-plane.
if (H[i].out(dq[len-1].p)) {
dq.pop_back();
--len;
}
else continue;
}
// Add new half-plane
dq.push_back(H[i]);
++len;
}
// Final cleanup: Check half-planes at the front against the back and vice-versa
while (len > 2 && dq[0].out(inter(dq[len-1], dq[len-2]))) {
dq.pop_back();
--len;
}
while (len > 2 && dq[len-1].out(inter(dq[0], dq[1]))) {
dq.pop_front();
--len;
}
// Report empty intersection if necessary
if (len < 3) return vector<Point>();
// Reconstruct the convex polygon from the remaining half-planes.
vector<Point> ret(len);
for(int i = 0; i+1 < len; i++) {
ret[i] = inter(dq[i], dq[i+1]);
}
ret.back() = inter(dq[len-1], dq[0]);
return ret;
}
```
### Implementation discussion
A special thing to note is that, in case there multiple half-planes that intersect at the same point, then this algorithm could return repeated adjacent points in the final polygon. However, this should not have any impact on judging correctly whether the intersection is empty or not, and it does not affect the polygon area at all either. You may want to remove these duplicates depending on what tasks you need to do after. You can do this very easily with std::unique. We want to keep the repeat points during the execution of the algorithm so that the intersections with area equal to zero can be computed correctly (for example, intersections that consist of a single point, line or line-segment). I encourage the reader to test some small hand-made cases where the intersection results in a single point or line.
One more thing that should be talked about is what to do if we are given half-planes in the form of a linear constraint (for example, $ax + by + c \leq 0$). In such case, there are two options. You can either implement the algorithm with the corresponding modifications to work with such representation (essentially create your own half-plane struct, should be fairly straightforward if you're familiar with the convex hull trick), or you can transform the lines into the representation we used in this article by taking any 2 points of each line. In general, it is recommended to work with the representation that you're given in the problem to avoid additional precision issues.
## Problems, tasks and applications
Many problems that can be solved with half-plane intersection can also be solved without it, but with (usually) more complicated or uncommon approaches. Generally, half-plane intersection can appear when dealing with problems related to polygons (mostly convex), visibility in the plane and two-dimensional linear programming. Here are some sample tasks that can be solved with this technique:
### Convex polygon intersection
One of the classical applications of half-plane intersection: Given $N$ polygons, compute the region that is included inside all of the polygons.
Since the intersection of a set of half-planes is a convex polygon, we can also represent a convex polygon as a set of half-planes (every edge of the polygon is a segment of a half-plane). Generate these half-planes for every polygon and compute the intersection of the whole set. The total time complexity is $O(S \log S)$, where S is the total number of sides of all the polygons. The problem can also theoretically be solved in $O(S \log N)$ by merging the $N$ sets of half-planes using a heap and then running the algorithm without the sorting step, but such solution has much worse constant factor than straightforward sorting and only provides minor speed gains for very small $N$.
### Visibility in the plane
Problems that require something among the lines of "determine if some line segments are visible from some point(s) in the plane" can usually be formulated as half-plane intersection problems. Take, for example, the following task: Given some simple polygon (not necessarily convex), determine if there's any point inside the polygon such that the whole boundary of the polygon can be observed from that point. This is also known as finding the [kernel of a polygon](https://en.wikipedia.org/wiki/Star-shaped_polygon) and can be solved by simple half-plane intersection, taking each edge of the polygon as a half-plane and then computing its intersection.
Here's a related, more interesting problem that was presented by Artem Vasilyev in one of his [Brazilian ICPC Summer School lectures](https://youtu.be/WKyZSitpm6M?t=6463):
Given a set $p$ of points $p_1, p_2\ \dots \ p_n$ in the plane, determine if there's any point $q$ you can stand at such that you can see all the points of $p$ from left to right in increasing order of their index.
Such problem can be solved by noticing that being able to see some point $p_i$ to the left of $p_j$ is the same as being able to see the right side of the line segment from $p_i$ to $p_j$ (or equivalently, being able to see the left side of the segment from $p_j$ to $p_i$). With that in mind, we can simply create a half-plane for every line segment $p_i p_{i+1}$ (or $p_{i+1} p_i$ depending on the orientation you choose) and check if the intersection of the whole set is empty or not.
### Half-plane intersection with binary search
Another common application is utilizing half-plane intersection as a tool to validate the predicate of a binary search procedure. Here's an example of such a problem, also presented by Artem Vasilyev in the same lecture that was previously mentioned: Given a **convex** polygon $P$, find the biggest circumference that can be inscribed inside of it.
Instead of looking for some sort of closed-form solution, annoying formulas or obscure algorithmic solutions, lets instead try to binary search on the answer. Notice that, for some fixed $r$, a circle with radius $r$ can be inscribed inside $P$ only if there exists some point inside $P$ that has distance greater or equal than $r$ to all the points of the boundary of $P$. This condition can be validated by "shrinking" the polygon inwards by a distance of $r$ and checking that the polygon remains non-degenerate (or is a point/segment itself). Such procedure can be simulated by taking the half-planes of the polygon sides in counter-clockwise order, translating each of them by a distance of $r$ in the direction of the region they allow (that is, orthogonal to the direction vector of the half-plane), and checking if the intersection is not empty.
Clearly, if we can inscribe a circle of radius $r$, we can also inscribe any other circle of radius smaller than $r$. So we can perform a binary search on the radius $r$ and validate every step using half-plane intersection. Also, note that the half-planes of a convex polygon are already sorted by angle, so the sorting step can be skipped in the algorithm. Thus we obtain a total time complexity of $O(NK)$, where $N$ is the number of polygon vertices and $K$ is the number of iterations of the binary search (the actual value will depend on the range of possible answers and the desired precision).
### Two-dimensional linear programming
One more application of half-plane intersection is linear programming in two variables. All linear constraints for two variables can be expressed in the form of $Ax + By + C \leq 0$ (inequality comparator may vary). Clearly, these are just half-planes, so checking if a feasible solution exists for a set of linear constraints can be done with half-plane intersection. Additionally, for a given set of linear constraints, it is possible to compute the region of feasible solutions (i.e. the intersection of the half-planes) and then answer multiple queries of maximizing/minimizing some linear function $f(x, y)$ subject to the constraints in $O(\log N)$ per query using binary search (very similar to the convex hull trick).
It is worth mentioning that there also exists a fairly simple randomized algorithm that can check whether a set of linear constraints has a feasible solution or not, and maximize/minimize some linear function subject to the given constraints. This randomized algorithm was also explained nicely by Artem Vasilyev in the lecture mentioned earlier. Here are some additional resources on it, should the reader be interested: [CG - Lecture 4, parts 4 and 5](https://youtu.be/5dfc355t2y4) and [Petr Mitrichev's blog (which includes the solution to the hardest problem in the practice problems list below)](https://petr-mitrichev.blogspot.com/2016/07/a-half-plane-week.html).
## Practice problems
### Classic problems, direct application
* [Codechef - Animesh decides to settle down](https://www.codechef.com/problems/CHN02)
* [POJ - How I mathematician Wonder What You Are!](http://poj.org/problem?id=3130)
* [POJ - Rotating Scoreboard](http://poj.org/problem?id=3335)
* [POJ - Video Surveillance](http://poj.org/problem?id=1474)
* [POJ - Art Gallery](http://poj.org/problem?id=1279)
* [POJ - Uyuw's Concert](http://poj.org/problem?id=2451)
### Harder problems
* [POJ - Most Distant Point from the Sea - Medium](http://poj.org/problem?id=3525)
* [Baekjoon - Jeju's Island - Same as above but seemingly stronger test cases](https://www.acmicpc.net/problem/3903)
* [POJ - Feng Shui - Medium](http://poj.org/problem?id=3384)
* [POJ - Triathlon - Medium/hard](http://poj.org/problem?id=1755)
* [DMOJ - Arrow - Medium/hard](https://dmoj.ca/problem/ccoprep3p3)
* [POJ - Jungle Outpost - Hard](http://poj.org/problem?id=3968)
* [Codeforces - Jungle Outpost (alternative link, problem J) - Hard](https://codeforces.com/gym/101309/attachments?mobile=false)
* [Yandex - Asymmetry Value (need virtual contest to see, problem F) - Very Hard](https://contest.yandex.com/contest/2540/enter/)
### Additional problems
* 40th Petrozavodsk Programming Camp, Winter 2021 - Day 1: Jagiellonian U Contest, Grand Prix of Krakow - Problem B: (Almost) Fair Cake-Cutting. At the time of writing the article, this problem was private and only accessible by participants of the Programming Camp.
## References, bibliography and other sources
### Main sources
* [New Algorithm for Half-plane Intersection and its Practical Value.](http://people.csail.mit.edu/zeyuan/publications.htm) Original paper of the algorithm.
* [Artem Vasilyev's Brazilian ICPC Summer School 2020 lecture.](https://youtu.be/WKyZSitpm6M?t=6463) Amazing lecture on half-plane intersection. Also covers other geometry topics.
### Good blogs (Chinese)
* [Fundamentals of Computational Geometry - Intersection of Half-planes.](https://zhuanlan.zhihu.com/p/83499723)
* [Detailed introduction to the half-plane intersection algorithm.](https://blog.csdn.net/qq_40861916/article/details/83541403)
* [Summary of Half-plane intersection problems.](https://blog.csdn.net/qq_40482358/article/details/87921815)
* [Sorting incremental method of half-plane intersection.](https://blog.csdn.net/u012061345/article/details/23872929)
### Randomized algorithm
* [Linear Programming and Half-Plane intersection - Parts 4 and 5.](https://youtu.be/5dfc355t2y4)
* [Petr Mitrichev's Blog: A half-plane week.](https://petr-mitrichev.blogspot.com/2016/07/a-half-plane-week.html)
|
Half-plane intersection
|
---
title
circle_tangents
---
# Finding common tangents to two circles
Given two circles. It is required to find all their common tangents, i.e. all such lines that touch both circles simultaneously.
The described algorithm will also work in the case when one (or both) circles degenerate into points. Thus, this algorithm can also be used to find tangents to a circle passing through a given point.
## The number of common tangents
The number of common tangents to two circles can be **0,1,2,3,4** and **infinite**.
Look at the images for different cases.
<center></center>
Here, we won't be considering **degenerate** cases, i.e *when the circles coincide (in this case they have infinitely many common tangents), or one circle lies inside the other (in this case they have no common tangents, or if the circles are tangent, there is one common tangent).*
In most cases, two circles have **four** common tangents.
If the circles **are tangent** , then they will have three common tangents, but this can be understood as a degenerate case: as if the two tangents coincided.
Moreover, the algorithm described below will work in the case when one or both circles have zero radius: in this case there will be, respectively, two or one common tangent.
Summing up, we will always look for **four tangents** for all cases except infinite tangents case (The infinite tangents case needs to be handled separately and it is not discussed here). In degenerate cases, some of tangents will coincide, but nevertheless, these cases will also fit into the big picture.
## Algorithm
For the sake of simplicity of the algorithm, we will assume, without losing generality, that the center of the first circle has coordinates $(0, 0)$. (If this is not the case, then this can be achieved by simply shifting the whole picture, and after finding a solution, by shifting the obtained straight lines back.)
Denote $r_1$ and $r_2$ the radii of the first and second circles, and by $(v_x,v_y)$ the coordinates of the center of the second circle and point $v$ different from origin. (Note: we are not considering the case in which both the circles are same).
To solve the problem, we approach it purely **algebraically** . We need to find all the lines of the form $ax + by + c = 0$ that lie at a distance $r_1$ from the origin of coordinates, and at a distance $r_2$ from a point $v$. In addition, we impose the condition of normalization of the straight line: the sum of the squares of the coefficients and must be equal to one (this is necessary, otherwise the same straight line will correspond to infinitely many representations of the form $ax + by + c = 0$). Total we get such a system of equations for the desired $a, b, c$:
$$\begin{align}
a^2 + b^2 &= 1 \\
\mid a \cdot 0 + b \cdot 0 + c \mid &= r_1 \\
\mid a \cdot v_x + b \cdot v_y + c \mid &= r_2
\end{align}$$
To get rid of the modulus, note that there are only four ways to open the modulus in this system. All these methods can be considered by the general case, if we understand the opening of the modulus as the fact that the coefficient on the right-hand side may be multiplied by -1. In other words, we turn to this system:
$$\begin{align}
a^2 + b^2 &= 1 \\
c &= \pm r_1 \\
a \cdot v_x + b \cdot v_y + c &= \pm r_2
\end{align}$$
Entering the notation $d_1 = \pm r_1$ and $d_2 = \pm r_2$ , we come to the conclusion that the system must have four solutions:
$$\begin{align}
a^2 + b^2 &= 1 \\
c &= d_1 \\
a \cdot v_x + b \cdot v_y + c &= d_2
\end{align}$$
The solution of this system is reduced to solving a quadratic equation. We will omit all the cumbersome calculations, and immediately give a ready answer:
$$\begin{align}
a &= {( d_2 - d_1 ) v_x \pm v_y \sqrt{v_x^2 + v_y^2-(d_2-d_1)^2} \over {v_x^2 + v_y^2} } \\
b &= {( d_2 - d_1 ) v_y \pm v_x \sqrt{v_x^2 + v_y^2-(d_2-d_1)^2} \over {v_x^2 + v_y^2} } \\
c &= d_1
\end{align}$$
Total we got eight solutions instead four. However, it is easy to understand where superfluous decisions arise: in fact, in the latter system, it is enough to take only one solution (for example, the first). In fact, the geometric meaning of what we take $\pm r_1$ and $\pm r_2$ is clear: we are actually sorting out which side of each circle there is a straight line. Therefore, the two methods that arise when solving the latter system are redundant: it is enough to choose one of the two solutions (only, of course, in all four cases, you must choose the same family of solutions).
The last thing that we have not yet considered is **how to shift the straight lines** in the case when the first circle was not originally located at the origin. However, everything is simple here: it follows from the linearity of the equation of a straight line that the value $a \cdot x_0 + b \cdot y_0$ (where $x_0$ and $y_0$ are the coordinates of the original center of the first circle) must be subtracted from the coefficient $c$.
##Implementation
We first describe all the necessary data structures and other auxiliary definitions:
```point-line-circle-struct
struct pt {
double x, y;
pt operator- (pt p) {
pt res = { x-p.x, y-p.y };
return res;
}
};
struct circle : pt {
double r;
};
struct line {
double a, b, c;
};
const double EPS = 1E-9;
double sqr (double a) {
return a * a;
}
```
Then the solution itself can be written this way (where the main function for the call is the second; and the first function is an auxiliary):
```find-tangents-to-two-circles
void tangents (pt c, double r1, double r2, vector<line> & ans) {
double r = r2 - r1;
double z = sqr(c.x) + sqr(c.y);
double d = z - sqr(r);
if (d < -EPS) return;
d = sqrt (abs (d));
line l;
l.a = (c.x * r + c.y * d) / z;
l.b = (c.y * r - c.x * d) / z;
l.c = r1;
ans.push_back (l);
}
vector<line> tangents (circle a, circle b) {
vector<line> ans;
for (int i=-1; i<=1; i+=2)
for (int j=-1; j<=1; j+=2)
tangents (b-a, a.r*i, b.r*j, ans);
for (size_t i=0; i<ans.size(); ++i)
ans[i].c -= ans[i].a * a.x + ans[i].b * a.y;
return ans;
}
```
|
---
title
circle_tangents
---
# Finding common tangents to two circles
Given two circles. It is required to find all their common tangents, i.e. all such lines that touch both circles simultaneously.
The described algorithm will also work in the case when one (or both) circles degenerate into points. Thus, this algorithm can also be used to find tangents to a circle passing through a given point.
## The number of common tangents
The number of common tangents to two circles can be **0,1,2,3,4** and **infinite**.
Look at the images for different cases.
<center></center>
Here, we won't be considering **degenerate** cases, i.e *when the circles coincide (in this case they have infinitely many common tangents), or one circle lies inside the other (in this case they have no common tangents, or if the circles are tangent, there is one common tangent).*
In most cases, two circles have **four** common tangents.
If the circles **are tangent** , then they will have three common tangents, but this can be understood as a degenerate case: as if the two tangents coincided.
Moreover, the algorithm described below will work in the case when one or both circles have zero radius: in this case there will be, respectively, two or one common tangent.
Summing up, we will always look for **four tangents** for all cases except infinite tangents case (The infinite tangents case needs to be handled separately and it is not discussed here). In degenerate cases, some of tangents will coincide, but nevertheless, these cases will also fit into the big picture.
## Algorithm
For the sake of simplicity of the algorithm, we will assume, without losing generality, that the center of the first circle has coordinates $(0, 0)$. (If this is not the case, then this can be achieved by simply shifting the whole picture, and after finding a solution, by shifting the obtained straight lines back.)
Denote $r_1$ and $r_2$ the radii of the first and second circles, and by $(v_x,v_y)$ the coordinates of the center of the second circle and point $v$ different from origin. (Note: we are not considering the case in which both the circles are same).
To solve the problem, we approach it purely **algebraically** . We need to find all the lines of the form $ax + by + c = 0$ that lie at a distance $r_1$ from the origin of coordinates, and at a distance $r_2$ from a point $v$. In addition, we impose the condition of normalization of the straight line: the sum of the squares of the coefficients and must be equal to one (this is necessary, otherwise the same straight line will correspond to infinitely many representations of the form $ax + by + c = 0$). Total we get such a system of equations for the desired $a, b, c$:
$$\begin{align}
a^2 + b^2 &= 1 \\
\mid a \cdot 0 + b \cdot 0 + c \mid &= r_1 \\
\mid a \cdot v_x + b \cdot v_y + c \mid &= r_2
\end{align}$$
To get rid of the modulus, note that there are only four ways to open the modulus in this system. All these methods can be considered by the general case, if we understand the opening of the modulus as the fact that the coefficient on the right-hand side may be multiplied by -1. In other words, we turn to this system:
$$\begin{align}
a^2 + b^2 &= 1 \\
c &= \pm r_1 \\
a \cdot v_x + b \cdot v_y + c &= \pm r_2
\end{align}$$
Entering the notation $d_1 = \pm r_1$ and $d_2 = \pm r_2$ , we come to the conclusion that the system must have four solutions:
$$\begin{align}
a^2 + b^2 &= 1 \\
c &= d_1 \\
a \cdot v_x + b \cdot v_y + c &= d_2
\end{align}$$
The solution of this system is reduced to solving a quadratic equation. We will omit all the cumbersome calculations, and immediately give a ready answer:
$$\begin{align}
a &= {( d_2 - d_1 ) v_x \pm v_y \sqrt{v_x^2 + v_y^2-(d_2-d_1)^2} \over {v_x^2 + v_y^2} } \\
b &= {( d_2 - d_1 ) v_y \pm v_x \sqrt{v_x^2 + v_y^2-(d_2-d_1)^2} \over {v_x^2 + v_y^2} } \\
c &= d_1
\end{align}$$
Total we got eight solutions instead four. However, it is easy to understand where superfluous decisions arise: in fact, in the latter system, it is enough to take only one solution (for example, the first). In fact, the geometric meaning of what we take $\pm r_1$ and $\pm r_2$ is clear: we are actually sorting out which side of each circle there is a straight line. Therefore, the two methods that arise when solving the latter system are redundant: it is enough to choose one of the two solutions (only, of course, in all four cases, you must choose the same family of solutions).
The last thing that we have not yet considered is **how to shift the straight lines** in the case when the first circle was not originally located at the origin. However, everything is simple here: it follows from the linearity of the equation of a straight line that the value $a \cdot x_0 + b \cdot y_0$ (where $x_0$ and $y_0$ are the coordinates of the original center of the first circle) must be subtracted from the coefficient $c$.
##Implementation
We first describe all the necessary data structures and other auxiliary definitions:
```point-line-circle-struct
struct pt {
double x, y;
pt operator- (pt p) {
pt res = { x-p.x, y-p.y };
return res;
}
};
struct circle : pt {
double r;
};
struct line {
double a, b, c;
};
const double EPS = 1E-9;
double sqr (double a) {
return a * a;
}
```
Then the solution itself can be written this way (where the main function for the call is the second; and the first function is an auxiliary):
```find-tangents-to-two-circles
void tangents (pt c, double r1, double r2, vector<line> & ans) {
double r = r2 - r1;
double z = sqr(c.x) + sqr(c.y);
double d = z - sqr(r);
if (d < -EPS) return;
d = sqrt (abs (d));
line l;
l.a = (c.x * r + c.y * d) / z;
l.b = (c.y * r - c.x * d) / z;
l.c = r1;
ans.push_back (l);
}
vector<line> tangents (circle a, circle b) {
vector<line> ans;
for (int i=-1; i<=1; i+=2)
for (int j=-1; j<=1; j+=2)
tangents (b-a, a.r*i, b.r*j, ans);
for (size_t i=0; i<ans.size(); ++i)
ans[i].c -= ans[i].a * a.x + ans[i].b * a.y;
return ans;
}
```
## Problems
[TIMUS 1163 Chapaev](https://acm.timus.ru/problem.aspx?space=1&num=1163)
|
Finding common tangents to two circles
|
---
title: Finding area of simple polygon in O(N)
title
polygon_area
---
# Finding area of simple polygon in $O(N)$
Let a simple polygon (i.e. without self intersection, not necessarily convex) be given. It is required to calculate its area given its vertices.
## Method 1
This is easy to do if we go through all edges and add trapezoid areas bounded by each edge and x-axis. The area needs to be taken with sign so that the extra area will be reduced. Hence, the formula is as follows:
$$A = \sum_{(p,q)\in \text{edges}} \frac{(p_x - q_x) \cdot (p_y + q_y)}{2}$$
Code:
```cpp
double area(const vector<point>& fig) {
double res = 0;
for (unsigned i = 0; i < fig.size(); i++) {
point p = i ? fig[i - 1] : fig.back();
point q = fig[i];
res += (p.x - q.x) * (p.y + q.y);
}
return fabs(res) / 2;
}
```
## Method 2
We can choose a point $O$ arbitrarily, iterate over all edges adding the oriented area of the triangle formed by the edge and point $O$. Again, due to the sign of area, extra area will be reduced.
This method is better as it can be generalized to more complex cases (such as when some sides are arcs instead of straight lines)
|
---
title: Finding area of simple polygon in O(N)
title
polygon_area
---
# Finding area of simple polygon in $O(N)$
Let a simple polygon (i.e. without self intersection, not necessarily convex) be given. It is required to calculate its area given its vertices.
## Method 1
This is easy to do if we go through all edges and add trapezoid areas bounded by each edge and x-axis. The area needs to be taken with sign so that the extra area will be reduced. Hence, the formula is as follows:
$$A = \sum_{(p,q)\in \text{edges}} \frac{(p_x - q_x) \cdot (p_y + q_y)}{2}$$
Code:
```cpp
double area(const vector<point>& fig) {
double res = 0;
for (unsigned i = 0; i < fig.size(); i++) {
point p = i ? fig[i - 1] : fig.back();
point q = fig[i];
res += (p.x - q.x) * (p.y + q.y);
}
return fabs(res) / 2;
}
```
## Method 2
We can choose a point $O$ arbitrarily, iterate over all edges adding the oriented area of the triangle formed by the edge and point $O$. Again, due to the sign of area, extra area will be reduced.
This method is better as it can be generalized to more complex cases (such as when some sides are arcs instead of straight lines)
|
Finding area of simple polygon in $O(N)$
|
---
title
circle_line_intersection
---
# Circle-Line Intersection
Given the coordinates of the center of a circle and its radius, and the equation of a line, you're required to find the points of intersection.
## Solution
Instead of solving the system of two equations, we will approach the problem geometrically. This way we get a more accurate solution from the point of view of numerical stability.
We assume without loss of generality that the circle is centered at the origin. If it's not, we translate it there and correct the $C$ constant in the line equation. So we have a circle centered at $(0,0)$ of radius $r$ and a line with equation $Ax+By+C=0$.
Let's start by find the point on the line which is closest to the origin $(x_0, y_0)$. First, it has to be at a distance
$$ d_0 = \frac{|C|}{\sqrt{A^2+B^2}} $$
Second, since the vector $(A, B)$ is perpendicular to the line, the coordinates of the point must be proportional to the coordinates of this vector. Since we know the distance of the point to the origin, we just need to scale the vector $(A, B)$ to this length, and we'll get:
$$\begin{align}
x_0 &= - \frac{AC}{A^2 + B^2} \\
y_0 &= - \frac{BC}{A^2 + B^2}
\end{align}$$
The minus signs are not obvious, but they can be easily verified by substituting $x_0$ and $y_0$ in the equation of the line.
At this stage we can determine the number of intersection points, and even find the solution when there is one or zero points. Indeed, if the distance from $(x_0, y_0)$ to the origin $d_0$ is greater than the radius $r$, the answer is **zero points**. If $d_0=r$, the answer is **one point** $(x_0, y_0)$. If $d_0<r$, there are two points of intersection, and now we have to find their coordinates.
So, we know that the point $(x_0, y_0)$ is inside the circle. The two points of intersection, $(a_x, a_y)$ and $(b_x, b_y)$, must belong to the line $Ax+By+C=0$ and must be at the same distance $d$ from $(x_0, y_0)$, and this distance is easy to find:
$$ d = \sqrt{r^2 - \frac{C^2}{A^2 + B^2}} $$
Note that the vector $(-B, A)$ is collinear to the line, and thus we can find the points in question by adding and subtracting vector $(-B,A)$, scaled to the length $d$, to the point $(x_0, y_0)$.
Finally, the equations of the two points of intersection are:
$$\begin{align}
m &= \sqrt{\frac{d^2}{A^2 + B^2}} \\
a_x &= x_0 + B \cdot m, a_y = y_0 - A \cdot m \\
b_x &= x_0 - B \cdot m, b_y = y_0 + A \cdot m
\end{align}$$
Had we solved the original system of equations using algebraic methods, we would likely get an answer in a different form with a larger error. The geometric method described here is more graphic and more accurate.
## Implementation
As indicated at the outset, we assume that the circle is centered at the origin, and therefore the input to the program is the radius $r$ of the circle and the parameters $A$, $B$ and $C$ of the equation of the line.
```cpp
double r, a, b, c; // given as input
double x0 = -a*c/(a*a+b*b), y0 = -b*c/(a*a+b*b);
if (c*c > r*r*(a*a+b*b)+EPS)
puts ("no points");
else if (abs (c*c - r*r*(a*a+b*b)) < EPS) {
puts ("1 point");
cout << x0 << ' ' << y0 << '\n';
}
else {
double d = r*r - c*c/(a*a+b*b);
double mult = sqrt (d / (a*a+b*b));
double ax, ay, bx, by;
ax = x0 + b * mult;
bx = x0 - b * mult;
ay = y0 - a * mult;
by = y0 + a * mult;
puts ("2 points");
cout << ax << ' ' << ay << '\n' << bx << ' ' << by << '\n';
}
```
|
---
title
circle_line_intersection
---
# Circle-Line Intersection
Given the coordinates of the center of a circle and its radius, and the equation of a line, you're required to find the points of intersection.
## Solution
Instead of solving the system of two equations, we will approach the problem geometrically. This way we get a more accurate solution from the point of view of numerical stability.
We assume without loss of generality that the circle is centered at the origin. If it's not, we translate it there and correct the $C$ constant in the line equation. So we have a circle centered at $(0,0)$ of radius $r$ and a line with equation $Ax+By+C=0$.
Let's start by find the point on the line which is closest to the origin $(x_0, y_0)$. First, it has to be at a distance
$$ d_0 = \frac{|C|}{\sqrt{A^2+B^2}} $$
Second, since the vector $(A, B)$ is perpendicular to the line, the coordinates of the point must be proportional to the coordinates of this vector. Since we know the distance of the point to the origin, we just need to scale the vector $(A, B)$ to this length, and we'll get:
$$\begin{align}
x_0 &= - \frac{AC}{A^2 + B^2} \\
y_0 &= - \frac{BC}{A^2 + B^2}
\end{align}$$
The minus signs are not obvious, but they can be easily verified by substituting $x_0$ and $y_0$ in the equation of the line.
At this stage we can determine the number of intersection points, and even find the solution when there is one or zero points. Indeed, if the distance from $(x_0, y_0)$ to the origin $d_0$ is greater than the radius $r$, the answer is **zero points**. If $d_0=r$, the answer is **one point** $(x_0, y_0)$. If $d_0<r$, there are two points of intersection, and now we have to find their coordinates.
So, we know that the point $(x_0, y_0)$ is inside the circle. The two points of intersection, $(a_x, a_y)$ and $(b_x, b_y)$, must belong to the line $Ax+By+C=0$ and must be at the same distance $d$ from $(x_0, y_0)$, and this distance is easy to find:
$$ d = \sqrt{r^2 - \frac{C^2}{A^2 + B^2}} $$
Note that the vector $(-B, A)$ is collinear to the line, and thus we can find the points in question by adding and subtracting vector $(-B,A)$, scaled to the length $d$, to the point $(x_0, y_0)$.
Finally, the equations of the two points of intersection are:
$$\begin{align}
m &= \sqrt{\frac{d^2}{A^2 + B^2}} \\
a_x &= x_0 + B \cdot m, a_y = y_0 - A \cdot m \\
b_x &= x_0 - B \cdot m, b_y = y_0 + A \cdot m
\end{align}$$
Had we solved the original system of equations using algebraic methods, we would likely get an answer in a different form with a larger error. The geometric method described here is more graphic and more accurate.
## Implementation
As indicated at the outset, we assume that the circle is centered at the origin, and therefore the input to the program is the radius $r$ of the circle and the parameters $A$, $B$ and $C$ of the equation of the line.
```cpp
double r, a, b, c; // given as input
double x0 = -a*c/(a*a+b*b), y0 = -b*c/(a*a+b*b);
if (c*c > r*r*(a*a+b*b)+EPS)
puts ("no points");
else if (abs (c*c - r*r*(a*a+b*b)) < EPS) {
puts ("1 point");
cout << x0 << ' ' << y0 << '\n';
}
else {
double d = r*r - c*c/(a*a+b*b);
double mult = sqrt (d / (a*a+b*b));
double ax, ay, bx, by;
ax = x0 + b * mult;
bx = x0 - b * mult;
ay = y0 - a * mult;
by = y0 + a * mult;
puts ("2 points");
cout << ax << ' ' << ay << '\n' << bx << ' ' << by << '\n';
}
```
## Practice Problems
- [CODECHEF: ANDOOR](https://www.codechef.com/problems/ANDOOR)
|
Circle-Line Intersection
|
---
title
- Original
---
# Lattice points inside non-lattice polygon
For lattice polygons there is Pick's formula to enumerate the lattice points inside the polygon.
What about polygons with arbitrary vertices?
Let's process each of the polygon's edges individually, and after that we may sum up the amounts of lattice points under each edge considering its orientations to choose a sign (like in calculating the area of a polygon using trapezoids).
First of all we should note that if current edge has endpoints in $A=(x_1;y_1)$ and $B=(x_2;y_2)$ then it can be represented as a linear function:
$$y=y_1+(y_2-y_1) \cdot \dfrac{x-x_1}{x_2-x_1}=\left(\dfrac{y_2-y_1}{x_2-x_1}\right)\cdot x + \left(\dfrac{y_1x_2-x_1y_2}{x_2-x_1}\right)$$
$$y = k \cdot x + b,~k = \dfrac{y_2-y_1}{x_2-x_1},~b = \dfrac{y_1x_2-x_1y_2}{x_2-x_1}$$
Now we will perform a substitution $x=x'+\lceil x_1 \rceil$ so that $b' = b + k \cdot \lceil x_1 \rceil$.
This allows us to work with $x_1'=0$ and $x_2'=x_2 - \lceil x_1 \rceil$.
Let's denote $n = \lfloor x_2' \rfloor$.
We will not sum up points at $x = n$ and on $y = 0$ for the integrity of the algorithm.
They may be added manually afterwards.
Thus we have to sum up $\sum\limits_{x'=0}^{n - 1} \lfloor k' \cdot x' + b'\rfloor$. We also assume that $k' \geq 0$ and $b'\geq 0$.
Otherwise one should substitute $x'=-t$ and add $\lceil|b'|\rceil$ to $b'$.
Let's discuss how we can evaluate a sum $\sum\limits_{x=0}^{n - 1} \lfloor k \cdot x + b\rfloor$.
We have two cases:
- $k \geq 1$ or $b \geq 1$.
Then we should start with summing up points below $y=\lfloor k \rfloor \cdot x + \lfloor b \rfloor$. Their amount equals to
\[ \sum\limits_{x=0}^{n - 1} \lfloor k \rfloor \cdot x + \lfloor b \rfloor=\dfrac{(\lfloor k \rfloor(n-1)+2\lfloor b \rfloor) n}{2}. \]
Now we are interested only in points $(x;y)$ such that $\lfloor k \rfloor \cdot x + \lfloor b \rfloor < y \leq k\cdot x + b$.
This amount is the same as the number of points such that $0 < y \leq (k - \lfloor k \rfloor) \cdot x + (b - \lfloor b \rfloor)$.
So we reduced our problem to $k'= k - \lfloor k \rfloor$, $b' = b - \lfloor b \rfloor$ and both $k'$ and $b'$ less than $1$ now.
Here is a picture, we just summed up blue points and subtracted the blue linear function from the black one to reduce problem to smaller values for $k$ and $b$:
<center></center>
- $k < 1$ and $b < 1$.
If $\lfloor k \cdot n + b\rfloor$ equals $0$, we can safely return $0$.
If this is not the case, we can say that there are no lattice points such that $x < 0$ and $0 < y \leq k \cdot x + b$.
That means that we will have the same answer if we consider new reference system in which $O'=(n;\lfloor k\cdot n + b\rfloor)$, axis $x'$ is directed down and axis $y'$ is directed to the left.
For this reference system we are interested in lattice points on the set
\[ \left\{(x;y)~\bigg|~0 \leq x < \lfloor k \cdot n + b\rfloor,~ 0 < y \leq \dfrac{x+(k\cdot n+b)-\lfloor k\cdot n + b \rfloor}{k}\right\} \]
which returns us back to the case $k>1$.
You can see new reference point $O'$ and axes $X'$ and $Y'$ in the picture below:
<center></center>
As you see, in new reference system linear function will have coefficient $\tfrac 1 k$ and its zero will be in the point $\lfloor k\cdot n + b \rfloor-(k\cdot n+b)$ which makes formula above correct.
## Complexity analysis
We have to count at most $\dfrac{(k(n-1)+2b)n}{2}$ points.
Among them we will count $\dfrac{\lfloor k \rfloor (n-1)+2\lfloor b \rfloor}{2}$ on the very first step.
We may consider that $b$ is negligibly small because we can start with making it less than $1$.
In that case we cay say that we count about $\dfrac{\lfloor k \rfloor}{k} \geq \dfrac 1 2$ of all points.
Thus we will finish in $O(\log n)$ steps.
## Implementation
Here is simple function which calculates number of integer points $(x;y)$ such for $0 \leq x < n$ and $0 < y \leq \lfloor k x+b\rfloor$:
```cpp
int count_lattices(Fraction k, Fraction b, long long n) {
auto fk = k.floor();
auto fb = b.floor();
auto cnt = 0LL;
if (k >= 1 || b >= 1) {
cnt += (fk * (n - 1) + 2 * fb) * n / 2;
k -= fk;
b -= fb;
}
auto t = k * n + b;
auto ft = t.floor();
if (ft >= 1) {
cnt += count_lattices(1 / k, (t - t.floor()) / k, t.floor());
}
return cnt;
}
```
Here `Fraction` is some class handling rational numbers.
On practice it seems that if all denominators and numerators are at most $C$ by absolute value then in the recursive calls they will be at most $C^2$ if you keep dividing numerators and denominators by their greatest common divisor.
Given this assumption we can say that one may use doubles and require accuracy of $\varepsilon^2$ where $\varepsilon$ is accuracy with which $k$ and $b$ are given.
That means that in floor one should consider numbers as integer if they differs at most by $\varepsilon^2$ from an integer.
|
---
title
- Original
---
# Lattice points inside non-lattice polygon
For lattice polygons there is Pick's formula to enumerate the lattice points inside the polygon.
What about polygons with arbitrary vertices?
Let's process each of the polygon's edges individually, and after that we may sum up the amounts of lattice points under each edge considering its orientations to choose a sign (like in calculating the area of a polygon using trapezoids).
First of all we should note that if current edge has endpoints in $A=(x_1;y_1)$ and $B=(x_2;y_2)$ then it can be represented as a linear function:
$$y=y_1+(y_2-y_1) \cdot \dfrac{x-x_1}{x_2-x_1}=\left(\dfrac{y_2-y_1}{x_2-x_1}\right)\cdot x + \left(\dfrac{y_1x_2-x_1y_2}{x_2-x_1}\right)$$
$$y = k \cdot x + b,~k = \dfrac{y_2-y_1}{x_2-x_1},~b = \dfrac{y_1x_2-x_1y_2}{x_2-x_1}$$
Now we will perform a substitution $x=x'+\lceil x_1 \rceil$ so that $b' = b + k \cdot \lceil x_1 \rceil$.
This allows us to work with $x_1'=0$ and $x_2'=x_2 - \lceil x_1 \rceil$.
Let's denote $n = \lfloor x_2' \rfloor$.
We will not sum up points at $x = n$ and on $y = 0$ for the integrity of the algorithm.
They may be added manually afterwards.
Thus we have to sum up $\sum\limits_{x'=0}^{n - 1} \lfloor k' \cdot x' + b'\rfloor$. We also assume that $k' \geq 0$ and $b'\geq 0$.
Otherwise one should substitute $x'=-t$ and add $\lceil|b'|\rceil$ to $b'$.
Let's discuss how we can evaluate a sum $\sum\limits_{x=0}^{n - 1} \lfloor k \cdot x + b\rfloor$.
We have two cases:
- $k \geq 1$ or $b \geq 1$.
Then we should start with summing up points below $y=\lfloor k \rfloor \cdot x + \lfloor b \rfloor$. Their amount equals to
\[ \sum\limits_{x=0}^{n - 1} \lfloor k \rfloor \cdot x + \lfloor b \rfloor=\dfrac{(\lfloor k \rfloor(n-1)+2\lfloor b \rfloor) n}{2}. \]
Now we are interested only in points $(x;y)$ such that $\lfloor k \rfloor \cdot x + \lfloor b \rfloor < y \leq k\cdot x + b$.
This amount is the same as the number of points such that $0 < y \leq (k - \lfloor k \rfloor) \cdot x + (b - \lfloor b \rfloor)$.
So we reduced our problem to $k'= k - \lfloor k \rfloor$, $b' = b - \lfloor b \rfloor$ and both $k'$ and $b'$ less than $1$ now.
Here is a picture, we just summed up blue points and subtracted the blue linear function from the black one to reduce problem to smaller values for $k$ and $b$:
<center></center>
- $k < 1$ and $b < 1$.
If $\lfloor k \cdot n + b\rfloor$ equals $0$, we can safely return $0$.
If this is not the case, we can say that there are no lattice points such that $x < 0$ and $0 < y \leq k \cdot x + b$.
That means that we will have the same answer if we consider new reference system in which $O'=(n;\lfloor k\cdot n + b\rfloor)$, axis $x'$ is directed down and axis $y'$ is directed to the left.
For this reference system we are interested in lattice points on the set
\[ \left\{(x;y)~\bigg|~0 \leq x < \lfloor k \cdot n + b\rfloor,~ 0 < y \leq \dfrac{x+(k\cdot n+b)-\lfloor k\cdot n + b \rfloor}{k}\right\} \]
which returns us back to the case $k>1$.
You can see new reference point $O'$ and axes $X'$ and $Y'$ in the picture below:
<center></center>
As you see, in new reference system linear function will have coefficient $\tfrac 1 k$ and its zero will be in the point $\lfloor k\cdot n + b \rfloor-(k\cdot n+b)$ which makes formula above correct.
## Complexity analysis
We have to count at most $\dfrac{(k(n-1)+2b)n}{2}$ points.
Among them we will count $\dfrac{\lfloor k \rfloor (n-1)+2\lfloor b \rfloor}{2}$ on the very first step.
We may consider that $b$ is negligibly small because we can start with making it less than $1$.
In that case we cay say that we count about $\dfrac{\lfloor k \rfloor}{k} \geq \dfrac 1 2$ of all points.
Thus we will finish in $O(\log n)$ steps.
## Implementation
Here is simple function which calculates number of integer points $(x;y)$ such for $0 \leq x < n$ and $0 < y \leq \lfloor k x+b\rfloor$:
```cpp
int count_lattices(Fraction k, Fraction b, long long n) {
auto fk = k.floor();
auto fb = b.floor();
auto cnt = 0LL;
if (k >= 1 || b >= 1) {
cnt += (fk * (n - 1) + 2 * fb) * n / 2;
k -= fk;
b -= fb;
}
auto t = k * n + b;
auto ft = t.floor();
if (ft >= 1) {
cnt += count_lattices(1 / k, (t - t.floor()) / k, t.floor());
}
return cnt;
}
```
Here `Fraction` is some class handling rational numbers.
On practice it seems that if all denominators and numerators are at most $C$ by absolute value then in the recursive calls they will be at most $C^2$ if you keep dividing numerators and denominators by their greatest common divisor.
Given this assumption we can say that one may use doubles and require accuracy of $\varepsilon^2$ where $\varepsilon$ is accuracy with which $k$ and $b$ are given.
That means that in floor one should consider numbers as integer if they differs at most by $\varepsilon^2$ from an integer.
|
Lattice points inside non-lattice polygon
|
---
title
- Original
---
# Minkowski sum of convex polygons
## Definition
Consider two sets $A$ and $B$ of points on a plane. Minkowski sum $A + B$ is defined as $\{a + b| a \in A, b \in B\}$.
Here we will consider the case when $A$ and $B$ consist of convex polygons $P$ and $Q$ with their interiors.
Throughout this article we will identify polygons with ordered sequences of their vertices, so that notation like $|P|$ or
$P_i$ makes sense.
It turns out that the sum of convex polygons $P$ and $Q$ is a convex polygon with at most $|P| + |Q|$ vertices.
## Algorithm
Here we consider the polygons to be cyclically enumerated, i. e. $P_{|P|} = P_0,\ Q_{|Q|} = Q_0$ and so on.
Since the size of the sum is linear in terms of the sizes of initial polygons, we should aim at finding a linear-time algorithm.
Suppose that both polygons are ordered counter-clockwise. Consider sequences of edges $\{\overrightarrow{P_iP_{i+1}}\}$
and $\{\overrightarrow{Q_jQ_{j+1}}\}$ ordered by polar angle. We claim that the sequence of edges of $P + Q$ can be obtained by merging
these two sequences preserving polar angle order and replacing consequitive co-directed vectors with their sum. Straightforward usage of this idea results
in a linear-time algorithm, however, restoring the vertices of $P + Q$ from the sequence of sides requires repeated addition of vectors,
which may introduce unwanted precision issues if we're working with floating-point coordinates, so we will describe a slight
modification of this idea.
Firstly we should reorder the vertices in such a way that the first vertex
of each polygon has the lowest y-coordinate (in case of several such vertices pick the one with the smallest x-coordinate). After that the sides of both polygons
will become sorted by polar angle, so there is no need to sort them manually.
Now we create two pointers $i$ (pointing to a vertex of $P$) and $j$ (pointing to a vertex of $Q$), both initially set to 0.
We repeat the following steps while $i < |P|$ or $j < |Q|$.
1. Append $P_i + Q_j$ to $P + Q$.
2. Compare polar angles of $\overrightarrow{P_iP_{i + 1}}$ and $\overrightarrow{Q_jQ_{j+1}}$.
3. Increment the pointer which corresponds to the smallest angle (if the angles are equal, increment both).
## Visualization
Here is a nice visualization, which may help you understand what is going on.
<center></center>
## Distance between two polygons
One of the most common applications of Minkowski sum is computing the distance between two convex polygons (or simply checking whether they intersect).
The distance between two convex polygons $P$ and $Q$ is defined as $\min\limits_{a \in P, b \in Q} ||a - b||$. One can note that
the distance is always attained between two vertices or a vertex and an edge, so we can easily find the distance in $O(|P||Q|)$. However,
with clever usage of Minkowski sum we can reduce the complexity to $O(|P| + |Q|)$.
If we reflect $Q$ through the point $(0, 0)$ obtaining polygon $-Q$, the problem boils down to finding the smallest distance between a point in
$P + (-Q)$ and $(0, 0)$. We can find that distance in linear time using the following idea.
If $(0, 0)$ is inside or on the boundary of polygon, the distance is $0$, otherwise the distance is attained between $(0, 0)$ and some vertex or edge of the polygon.
Since Minkowski sum can be computed
in linear time, we obtain a linear-time algorithm for finding the distance between two convex polygons.
## Implementation
Below is the implementation of Minkowski sum for polygons with integer points. Note that in this case all computations can be done in integers since
instead of computing polar angles and directly comparing them we can look at the sign of cross product of two vectors.
```{.cpp file=minkowski}
struct pt{
long long x, y;
pt operator + (const pt & p) const {
return pt{x + p.x, y + p.y};
}
pt operator - (const pt & p) const {
return pt{x - p.x, y - p.y};
}
long long cross(const pt & p) const {
return x * p.y - y * p.x;
}
};
void reorder_polygon(vector<pt> & P){
size_t pos = 0;
for(size_t i = 1; i < P.size(); i++){
if(P[i].y < P[pos].y || (P[i].y == P[pos].y && P[i].x < P[pos].x))
pos = i;
}
rotate(P.begin(), P.begin() + pos, P.end());
}
vector<pt> minkowski(vector<pt> P, vector<pt> Q){
// the first vertex must be the lowest
reorder_polygon(P);
reorder_polygon(Q);
// we must ensure cyclic indexing
P.push_back(P[0]);
P.push_back(P[1]);
Q.push_back(Q[0]);
Q.push_back(Q[1]);
// main part
vector<pt> result;
size_t i = 0, j = 0;
while(i < P.size() - 2 || j < Q.size() - 2){
result.push_back(P[i] + Q[j]);
auto cross = (P[i + 1] - P[i]).cross(Q[j + 1] - Q[j]);
if(cross >= 0 && i < P.size() - 2)
++i;
if(cross <= 0 && j < Q.size() - 2)
++j;
}
return result;
}
```
|
---
title
- Original
---
# Minkowski sum of convex polygons
## Definition
Consider two sets $A$ and $B$ of points on a plane. Minkowski sum $A + B$ is defined as $\{a + b| a \in A, b \in B\}$.
Here we will consider the case when $A$ and $B$ consist of convex polygons $P$ and $Q$ with their interiors.
Throughout this article we will identify polygons with ordered sequences of their vertices, so that notation like $|P|$ or
$P_i$ makes sense.
It turns out that the sum of convex polygons $P$ and $Q$ is a convex polygon with at most $|P| + |Q|$ vertices.
## Algorithm
Here we consider the polygons to be cyclically enumerated, i. e. $P_{|P|} = P_0,\ Q_{|Q|} = Q_0$ and so on.
Since the size of the sum is linear in terms of the sizes of initial polygons, we should aim at finding a linear-time algorithm.
Suppose that both polygons are ordered counter-clockwise. Consider sequences of edges $\{\overrightarrow{P_iP_{i+1}}\}$
and $\{\overrightarrow{Q_jQ_{j+1}}\}$ ordered by polar angle. We claim that the sequence of edges of $P + Q$ can be obtained by merging
these two sequences preserving polar angle order and replacing consequitive co-directed vectors with their sum. Straightforward usage of this idea results
in a linear-time algorithm, however, restoring the vertices of $P + Q$ from the sequence of sides requires repeated addition of vectors,
which may introduce unwanted precision issues if we're working with floating-point coordinates, so we will describe a slight
modification of this idea.
Firstly we should reorder the vertices in such a way that the first vertex
of each polygon has the lowest y-coordinate (in case of several such vertices pick the one with the smallest x-coordinate). After that the sides of both polygons
will become sorted by polar angle, so there is no need to sort them manually.
Now we create two pointers $i$ (pointing to a vertex of $P$) and $j$ (pointing to a vertex of $Q$), both initially set to 0.
We repeat the following steps while $i < |P|$ or $j < |Q|$.
1. Append $P_i + Q_j$ to $P + Q$.
2. Compare polar angles of $\overrightarrow{P_iP_{i + 1}}$ and $\overrightarrow{Q_jQ_{j+1}}$.
3. Increment the pointer which corresponds to the smallest angle (if the angles are equal, increment both).
## Visualization
Here is a nice visualization, which may help you understand what is going on.
<center></center>
## Distance between two polygons
One of the most common applications of Minkowski sum is computing the distance between two convex polygons (or simply checking whether they intersect).
The distance between two convex polygons $P$ and $Q$ is defined as $\min\limits_{a \in P, b \in Q} ||a - b||$. One can note that
the distance is always attained between two vertices or a vertex and an edge, so we can easily find the distance in $O(|P||Q|)$. However,
with clever usage of Minkowski sum we can reduce the complexity to $O(|P| + |Q|)$.
If we reflect $Q$ through the point $(0, 0)$ obtaining polygon $-Q$, the problem boils down to finding the smallest distance between a point in
$P + (-Q)$ and $(0, 0)$. We can find that distance in linear time using the following idea.
If $(0, 0)$ is inside or on the boundary of polygon, the distance is $0$, otherwise the distance is attained between $(0, 0)$ and some vertex or edge of the polygon.
Since Minkowski sum can be computed
in linear time, we obtain a linear-time algorithm for finding the distance between two convex polygons.
## Implementation
Below is the implementation of Minkowski sum for polygons with integer points. Note that in this case all computations can be done in integers since
instead of computing polar angles and directly comparing them we can look at the sign of cross product of two vectors.
```{.cpp file=minkowski}
struct pt{
long long x, y;
pt operator + (const pt & p) const {
return pt{x + p.x, y + p.y};
}
pt operator - (const pt & p) const {
return pt{x - p.x, y - p.y};
}
long long cross(const pt & p) const {
return x * p.y - y * p.x;
}
};
void reorder_polygon(vector<pt> & P){
size_t pos = 0;
for(size_t i = 1; i < P.size(); i++){
if(P[i].y < P[pos].y || (P[i].y == P[pos].y && P[i].x < P[pos].x))
pos = i;
}
rotate(P.begin(), P.begin() + pos, P.end());
}
vector<pt> minkowski(vector<pt> P, vector<pt> Q){
// the first vertex must be the lowest
reorder_polygon(P);
reorder_polygon(Q);
// we must ensure cyclic indexing
P.push_back(P[0]);
P.push_back(P[1]);
Q.push_back(Q[0]);
Q.push_back(Q[1]);
// main part
vector<pt> result;
size_t i = 0, j = 0;
while(i < P.size() - 2 || j < Q.size() - 2){
result.push_back(P[i] + Q[j]);
auto cross = (P[i + 1] - P[i]).cross(Q[j + 1] - Q[j]);
if(cross >= 0 && i < P.size() - 2)
++i;
if(cross <= 0 && j < Q.size() - 2)
++j;
}
return result;
}
```
## Problems
* [Codeforces 87E Mogohu-Rea Idol](https://codeforces.com/problemset/problem/87/E)
* [Codeforces 1195F Geometers Anonymous Club](https://codeforces.com/contest/1195/problem/F)
* [TIMUS 1894 Non-Flying Weather](https://acm.timus.ru/problem.aspx?space=1&num=1894)
|
Minkowski sum of convex polygons
|
---
title
length_of_segments_union
---
# Length of the union of segments
Given $n$ segments on a line, each described by a pair of coordinates $(a_{i1}, a_{i2})$.
We have to find the length of their union.
The following algorithm was proposed by Klee in 1977.
It works in $O(n\log n)$ and has been proven to be the asymptotically optimal.
## Solution
We store in an array $x$ the endpoints of all the segments sorted by their values.
And additionally we store whether it is a left end or a right end of a segment.
Now we iterate over the array, keeping a counter $c$ of currently opened segments.
Whenever the current element is a left end, we increase this counter, and otherwise we decrease it.
To compute the answer, we take the length between the last to $x$ values $x_i - x_{i-1}$, whenever we come to a new coordinate, and there is currently at least one segment is open.
## Implementation
```cpp
int length_union(const vector<pair<int, int>> &a) {
int n = a.size();
vector<pair<int, bool>> x(n*2);
for (int i = 0; i < n; i++) {
x[i*2] = {a[i].first, false};
x[i*2+1] = {a[i].second, true};
}
sort(x.begin(), x.end());
int result = 0;
int c = 0;
for (int i = 0; i < n * 2; i++) {
if (i > 0 && x[i].first > x[i-1].first && c > 0)
result += x[i].first - x[i-1].first;
if (x[i].second)
c--;
else
c++;
}
return result;
}
```
|
---
title
length_of_segments_union
---
# Length of the union of segments
Given $n$ segments on a line, each described by a pair of coordinates $(a_{i1}, a_{i2})$.
We have to find the length of their union.
The following algorithm was proposed by Klee in 1977.
It works in $O(n\log n)$ and has been proven to be the asymptotically optimal.
## Solution
We store in an array $x$ the endpoints of all the segments sorted by their values.
And additionally we store whether it is a left end or a right end of a segment.
Now we iterate over the array, keeping a counter $c$ of currently opened segments.
Whenever the current element is a left end, we increase this counter, and otherwise we decrease it.
To compute the answer, we take the length between the last to $x$ values $x_i - x_{i-1}$, whenever we come to a new coordinate, and there is currently at least one segment is open.
## Implementation
```cpp
int length_union(const vector<pair<int, int>> &a) {
int n = a.size();
vector<pair<int, bool>> x(n*2);
for (int i = 0; i < n; i++) {
x[i*2] = {a[i].first, false};
x[i*2+1] = {a[i].second, true};
}
sort(x.begin(), x.end());
int result = 0;
int c = 0;
for (int i = 0; i < n * 2; i++) {
if (i > 0 && x[i].first > x[i-1].first && c > 0)
result += x[i].first - x[i-1].first;
if (x[i].second)
c--;
else
c++;
}
return result;
}
```
|
Length of the union of segments
|
---
title
segment_to_line
---
# Finding the equation of a line for a segment
The task is: given the coordinates of the ends of a segment, construct a line passing through it.
We assume that the segment is non-degenerate, i.e. has a length greater than zero (otherwise, of course, infinitely many different lines pass through it).
### Two-dimensional case
Let the given segment be $PQ$ i.e. the known coordinates of its ends $P_x , P_y , Q_x , Q_y$ .
It is necessary to construct **the equation of a line in the plane** passing through this segment, i.e. find the coefficients $A , B , C$ in the equation of a line:
$$A x + B y + C = 0.$$
Note that for the required triples $(A, B, C)$ there are **infinitely many** solutions which describe the given segment:
you can multiply all three coefficients by an arbitrary non-zero number and get the same straight line.
Therefore, our task is to find one of these triples.
It is easy to verify (by substitution of these expressions and the coordinates of the points $P$ and $Q$ into the equation of a straight line) that the following set of coefficients fits:
$$\begin{align}
A &= P_y - Q_y, \\
B &= Q_x - P_x, \\
C &= - A P_x - B P_y.
\end{align}$$
### Integer case
An important advantage of this method of constructing a straight line is that if the coordinates of the ends were integer, then the coefficients obtained will also be **integer** . In some cases, this allows one to perform geometric operations without resorting to real numbers at all.
However, there is a small drawback: for the same straight line different triples of coefficients can be obtained.
To avoid this, but do not go away from the integer coefficients, you can apply the following technique, often called **rationing**. Find the [greatest common divisor](../algebra/euclid-algorithm.md) of numbers $| A | , | B | , | C |$ , we divide all three coefficients by it, and then we make the normalization of the sign: if $A <0$ or $A = 0, B <0$ then multiply all three coefficients by $-1$ .
As a result, we will come to the conclusion that for identical straight lines, identical triples of coefficients will be obtained, which makes it easy to check straight lines for equality.
### Real case
When working with real numbers, you should always be aware of errors.
The coefficients $A$ and $B$ will have the order of the original coordinates, the coefficient $C$ is of the order of the square of them. This may already be quite large numbers, and, for example, when we [intersect straight lines](lines-intersection.md), they will become even larger, which can lead to large rounding errors already when the coordinates of the end points are of order $10^3$.
Therefore, when working with real numbers, it is desirable to produce the so-called **normalization**, this is straightforward: namely, to make the coefficients such that $A ^ 2 + B ^ 2 = 1$ . To do this, calculate the number $Z$ :
$$Z = \sqrt{A ^ 2 + B ^ 2},$$
and divide all three coefficients $A , B , C$ by it.
Thus, the order of the coefficients $A$ and $B$ will not depend on the order of the input coordinates, and the coefficient $C$ will be of the same order as the input coordinates. In practice, this leads to a significant improvement in the accuracy of calculations.
Finally, we mention the **comparison** of straight lines - in fact, after such a normalization, for the same straight line, only two triples of coefficients can be obtained: up to multiplication by $-1$.
Accordingly, if we make an additional normalization taking into account the sign (if $A < -\varepsilon$ or $| A | < \varepsilon$, $B <- \varepsilon$ then multiply by $-1$ ), the resulting coefficients will be unique.
### Three-dimensional and multidimensional case
Already in the three-dimensional case there is **no simple equation** describing a straight line (it can be defined as the intersection of two planes, that is, a system of two equations, but this is an inconvenient method).
Consequently, in the three-dimensional and multidimensional cases we must use the **parametric method of defining a straight line** , i.e. as a point $p$ and a vector $v$ :
$$p + v t, ~~~ t \in \mathbb{R}.$$
Those. a straight line is all points that can be obtained from a point $p$ adding a vector $v$ with an arbitrary coefficient.
The **construction** of a straight line in a parametric form along the coordinates of the ends of a segment is trivial, we just take one end of the segment for the point $p$, and the vector from the first to the second end — for the vector $v$.
|
---
title
segment_to_line
---
# Finding the equation of a line for a segment
The task is: given the coordinates of the ends of a segment, construct a line passing through it.
We assume that the segment is non-degenerate, i.e. has a length greater than zero (otherwise, of course, infinitely many different lines pass through it).
### Two-dimensional case
Let the given segment be $PQ$ i.e. the known coordinates of its ends $P_x , P_y , Q_x , Q_y$ .
It is necessary to construct **the equation of a line in the plane** passing through this segment, i.e. find the coefficients $A , B , C$ in the equation of a line:
$$A x + B y + C = 0.$$
Note that for the required triples $(A, B, C)$ there are **infinitely many** solutions which describe the given segment:
you can multiply all three coefficients by an arbitrary non-zero number and get the same straight line.
Therefore, our task is to find one of these triples.
It is easy to verify (by substitution of these expressions and the coordinates of the points $P$ and $Q$ into the equation of a straight line) that the following set of coefficients fits:
$$\begin{align}
A &= P_y - Q_y, \\
B &= Q_x - P_x, \\
C &= - A P_x - B P_y.
\end{align}$$
### Integer case
An important advantage of this method of constructing a straight line is that if the coordinates of the ends were integer, then the coefficients obtained will also be **integer** . In some cases, this allows one to perform geometric operations without resorting to real numbers at all.
However, there is a small drawback: for the same straight line different triples of coefficients can be obtained.
To avoid this, but do not go away from the integer coefficients, you can apply the following technique, often called **rationing**. Find the [greatest common divisor](../algebra/euclid-algorithm.md) of numbers $| A | , | B | , | C |$ , we divide all three coefficients by it, and then we make the normalization of the sign: if $A <0$ or $A = 0, B <0$ then multiply all three coefficients by $-1$ .
As a result, we will come to the conclusion that for identical straight lines, identical triples of coefficients will be obtained, which makes it easy to check straight lines for equality.
### Real case
When working with real numbers, you should always be aware of errors.
The coefficients $A$ and $B$ will have the order of the original coordinates, the coefficient $C$ is of the order of the square of them. This may already be quite large numbers, and, for example, when we [intersect straight lines](lines-intersection.md), they will become even larger, which can lead to large rounding errors already when the coordinates of the end points are of order $10^3$.
Therefore, when working with real numbers, it is desirable to produce the so-called **normalization**, this is straightforward: namely, to make the coefficients such that $A ^ 2 + B ^ 2 = 1$ . To do this, calculate the number $Z$ :
$$Z = \sqrt{A ^ 2 + B ^ 2},$$
and divide all three coefficients $A , B , C$ by it.
Thus, the order of the coefficients $A$ and $B$ will not depend on the order of the input coordinates, and the coefficient $C$ will be of the same order as the input coordinates. In practice, this leads to a significant improvement in the accuracy of calculations.
Finally, we mention the **comparison** of straight lines - in fact, after such a normalization, for the same straight line, only two triples of coefficients can be obtained: up to multiplication by $-1$.
Accordingly, if we make an additional normalization taking into account the sign (if $A < -\varepsilon$ or $| A | < \varepsilon$, $B <- \varepsilon$ then multiply by $-1$ ), the resulting coefficients will be unique.
### Three-dimensional and multidimensional case
Already in the three-dimensional case there is **no simple equation** describing a straight line (it can be defined as the intersection of two planes, that is, a system of two equations, but this is an inconvenient method).
Consequently, in the three-dimensional and multidimensional cases we must use the **parametric method of defining a straight line** , i.e. as a point $p$ and a vector $v$ :
$$p + v t, ~~~ t \in \mathbb{R}.$$
Those. a straight line is all points that can be obtained from a point $p$ adding a vector $v$ with an arbitrary coefficient.
The **construction** of a straight line in a parametric form along the coordinates of the ends of a segment is trivial, we just take one end of the segment for the point $p$, and the vector from the first to the second end — for the vector $v$.
|
Finding the equation of a line for a segment
|
---
title
triangles_union
---
# Vertical decomposition
## Overview
Vertical decomposition is a powerful technique used in various geometry problems. The general idea is to cut the plane into several vertical stripes
with some "good" properties and solve the problem for these stripes independently. We will illustrate the idea on some examples.
## Area of the union of triangles
Suppose that there are $n$ triangles on a plane and we are to find the area of their union. The problem would be easy if the triangles didn't intersect, so
let's get rid of these intersections by dividing the plane into vertical stripes by drawing vertical lines through all vertices and all points of intersection of
sides of different triangles. There may be $O(n^2)$ such lines so we obtained $O(n^2)$ stripes. Now consider some vertical stripe. Each non-vertical segment either crosses it from left to right or doesn't cross at all.
Also, no two segments intersect strictly inside the stripe. It means that the part of the union of triangles that lies inside this stripe is composed of disjoint trapezoids with bases lying on the sides of the stripe.
This property allows us to compute the area inside each stripe with a following scanline algorithm. Each segment crossing the stripe is either upper or lower, depending on whether the interior of the corresponding triangle
is above or below the segment. We can visualize each upper segment as an opening bracket and each lower segment as a closing bracket and decompose the stripe into trapezoids by decomposing the bracket sequence into smaller correct bracket sequences. This algorithm requires $O(n^3\log n)$ time and $O(n^2)$ memory.
### Optimization 1
Firstly we will reduce the runtime to $O(n^2\log n)$. Instead of generating trapezoids for each stripe let's fix some triangle side (segment $s = (s_0, s_1)$) and find the set of stripes where this segment is a side of some trapezoid. Note that in this case we only have to find the stripes where the balance of brackets below (or above, in case of a lower segment) $s$ is zero. It means that instead of running vertical scanline for each stripe we can run a horizontal scanline for all parts of other segments which affect the balance of brackets with respect to $s$.
For simplicity we will show how to do this for an upper segment, the algorithm for lower segments is similar. Consider some other non-vertical segment $t = (t_0, t_1)$ and find the intersection $[x_1, x_2]$ of projections of $s$ and $t$ on $Ox$. If this intersection is empty or consists of one point, $t$ can be discarded since $s$ and $t$ do not intersect the interior of the same stripe. Otherwise consider the intersection $I$ of $s$ and $t$. There are three cases.
1. $I = \varnothing$
In this case $t$ is either above or below $s$ on $[x_1, x_2]$. If $t$ is above, it doesn't affect whether $s$ is a side of some trapezoid or not.
If $t$ is below $s$, we should add $1$ or $-1$ to the balance of bracket sequences for all stripes in $[x_1, x_2]$, depending on whether $t$ is upper or lower.
2. $I$ consists of a single point $p$
This case can be reduced to the previous one by splitting $[x_1, x_2]$ into $[x_1, p_x]$ and $[p_x, x_2]$.
3. $I$ is some segment $l$
This case means that the parts of $s$ and $t$ for $x\in[x_1, x_2]$ coincide. If $t$ is lower, $s$ is clearly not a side of a trapezoid.
Otherwise, it could happen that both $s$ and $t$ can be considered as a side of some trapezoid. In order to resolve this ambiguity, we can
decide that only the segment with the lowest index should be considered as a side (here we suppose that triangle sides are enumerated in some way). So, if $index(s) < index(t)$, we should ignore this case,
otherwise we should mark that $s$ can never be a side on $[x_1, x_2]$ (for example, by adding a corresponding event with balance $-2$).
Here is a graphic representation of the three cases.
<center></center>
Finally we should remark on processing all the additions of $1$ or $-1$ on all stripes in $[x_1, x_2]$. For each addition of $w$ on $[x_1, x_2]$ we can create events $(x_1, w),\ (x_2, -w)$
and process all these events with a sweep line.
### Optimization 2
Note that if we apply the previous optimization, we no longer have to find all stripes explicitly. This reduces the memory consumption to $O(n)$.
## Intersection of convex polygons
Another usage of vertical decomposition is to compute the intersection of two convex polygons in linear time. Suppose the plane is split into vertical stripes by vertical lines passing through each
vertex of each polygon. Then if we consider one of the input polygons and some stripe, their intersection is either a trapezoid, a triangle or a point. Therefore we can simply intersect these shapes for each vertical stripe and merge these intersections into a single polygon.
## Implementation
Below is the code that calculates area of the union of a set of triangles in $O(n^2\log n)$ time and $O(n)$ memory.
```{.cpp file=triangle_union}
typedef double dbl;
const dbl eps = 1e-9;
inline bool eq(dbl x, dbl y){
return fabs(x - y) < eps;
}
inline bool lt(dbl x, dbl y){
return x < y - eps;
}
inline bool gt(dbl x, dbl y){
return x > y + eps;
}
inline bool le(dbl x, dbl y){
return x < y + eps;
}
inline bool ge(dbl x, dbl y){
return x > y - eps;
}
struct pt{
dbl x, y;
inline pt operator - (const pt & p)const{
return pt{x - p.x, y - p.y};
}
inline pt operator + (const pt & p)const{
return pt{x + p.x, y + p.y};
}
inline pt operator * (dbl a)const{
return pt{x * a, y * a};
}
inline dbl cross(const pt & p)const{
return x * p.y - y * p.x;
}
inline dbl dot(const pt & p)const{
return x * p.x + y * p.y;
}
inline bool operator == (const pt & p)const{
return eq(x, p.x) && eq(y, p.y);
}
};
struct Line{
pt p[2];
Line(){}
Line(pt a, pt b):p{a, b}{}
pt vec()const{
return p[1] - p[0];
}
pt& operator [](size_t i){
return p[i];
}
};
inline bool lexComp(const pt & l, const pt & r){
if(fabs(l.x - r.x) > eps){
return l.x < r.x;
}
else return l.y < r.y;
}
vector<pt> interSegSeg(Line l1, Line l2){
if(eq(l1.vec().cross(l2.vec()), 0)){
if(!eq(l1.vec().cross(l2[0] - l1[0]), 0))
return {};
if(!lexComp(l1[0], l1[1]))
swap(l1[0], l1[1]);
if(!lexComp(l2[0], l2[1]))
swap(l2[0], l2[1]);
pt l = lexComp(l1[0], l2[0]) ? l2[0] : l1[0];
pt r = lexComp(l1[1], l2[1]) ? l1[1] : l2[1];
if(l == r)
return {l};
else return lexComp(l, r) ? vector<pt>{l, r} : vector<pt>();
}
else{
dbl s = (l2[0] - l1[0]).cross(l2.vec()) / l1.vec().cross(l2.vec());
pt inter = l1[0] + l1.vec() * s;
if(ge(s, 0) && le(s, 1) && le((l2[0] - inter).dot(l2[1] - inter), 0))
return {inter};
else
return {};
}
}
inline char get_segtype(Line segment, pt other_point){
if(eq(segment[0].x, segment[1].x))
return 0;
if(!lexComp(segment[0], segment[1]))
swap(segment[0], segment[1]);
return (segment[1] - segment[0]).cross(other_point - segment[0]) > 0 ? 1 : -1;
}
dbl union_area(vector<tuple<pt, pt, pt> > triangles){
vector<Line> segments(3 * triangles.size());
vector<char> segtype(segments.size());
for(size_t i = 0; i < triangles.size(); i++){
pt a, b, c;
tie(a, b, c) = triangles[i];
segments[3 * i] = lexComp(a, b) ? Line(a, b) : Line(b, a);
segtype[3 * i] = get_segtype(segments[3 * i], c);
segments[3 * i + 1] = lexComp(b, c) ? Line(b, c) : Line(c, b);
segtype[3 * i + 1] = get_segtype(segments[3 * i + 1], a);
segments[3 * i + 2] = lexComp(c, a) ? Line(c, a) : Line(a, c);
segtype[3 * i + 2] = get_segtype(segments[3 * i + 2], b);
}
vector<dbl> k(segments.size()), b(segments.size());
for(size_t i = 0; i < segments.size(); i++){
if(segtype[i]){
k[i] = (segments[i][1].y - segments[i][0].y) / (segments[i][1].x - segments[i][0].x);
b[i] = segments[i][0].y - k[i] * segments[i][0].x;
}
}
dbl ans = 0;
for(size_t i = 0; i < segments.size(); i++){
if(!segtype[i])
continue;
dbl l = segments[i][0].x, r = segments[i][1].x;
vector<pair<dbl, int> > evts;
for(size_t j = 0; j < segments.size(); j++){
if(!segtype[j] || i == j)
continue;
dbl l1 = segments[j][0].x, r1 = segments[j][1].x;
if(ge(l1, r) || ge(l, r1))
continue;
dbl common_l = max(l, l1), common_r = min(r, r1);
auto pts = interSegSeg(segments[i], segments[j]);
if(pts.empty()){
dbl yl1 = k[j] * common_l + b[j];
dbl yl = k[i] * common_l + b[i];
if(lt(yl1, yl) == (segtype[i] == 1)){
int evt_type = -segtype[i] * segtype[j];
evts.emplace_back(common_l, evt_type);
evts.emplace_back(common_r, -evt_type);
}
}
else if(pts.size() == 1u){
dbl yl = k[i] * common_l + b[i], yl1 = k[j] * common_l + b[j];
int evt_type = -segtype[i] * segtype[j];
if(lt(yl1, yl) == (segtype[i] == 1)){
evts.emplace_back(common_l, evt_type);
evts.emplace_back(pts[0].x, -evt_type);
}
yl = k[i] * common_r + b[i], yl1 = k[j] * common_r + b[j];
if(lt(yl1, yl) == (segtype[i] == 1)){
evts.emplace_back(pts[0].x, evt_type);
evts.emplace_back(common_r, -evt_type);
}
}
else{
if(segtype[j] != segtype[i] || j > i){
evts.emplace_back(common_l, -2);
evts.emplace_back(common_r, 2);
}
}
}
evts.emplace_back(l, 0);
sort(evts.begin(), evts.end());
size_t j = 0;
int balance = 0;
while(j < evts.size()){
size_t ptr = j;
while(ptr < evts.size() && eq(evts[j].first, evts[ptr].first)){
balance += evts[ptr].second;
++ptr;
}
if(!balance && !eq(evts[j].first, r)){
dbl next_x = ptr == evts.size() ? r : evts[ptr].first;
ans -= segtype[i] * (k[i] * (next_x + evts[j].first) + 2 * b[i]) * (next_x - evts[j].first);
}
j = ptr;
}
}
return ans/2;
}
```
|
---
title
triangles_union
---
# Vertical decomposition
## Overview
Vertical decomposition is a powerful technique used in various geometry problems. The general idea is to cut the plane into several vertical stripes
with some "good" properties and solve the problem for these stripes independently. We will illustrate the idea on some examples.
## Area of the union of triangles
Suppose that there are $n$ triangles on a plane and we are to find the area of their union. The problem would be easy if the triangles didn't intersect, so
let's get rid of these intersections by dividing the plane into vertical stripes by drawing vertical lines through all vertices and all points of intersection of
sides of different triangles. There may be $O(n^2)$ such lines so we obtained $O(n^2)$ stripes. Now consider some vertical stripe. Each non-vertical segment either crosses it from left to right or doesn't cross at all.
Also, no two segments intersect strictly inside the stripe. It means that the part of the union of triangles that lies inside this stripe is composed of disjoint trapezoids with bases lying on the sides of the stripe.
This property allows us to compute the area inside each stripe with a following scanline algorithm. Each segment crossing the stripe is either upper or lower, depending on whether the interior of the corresponding triangle
is above or below the segment. We can visualize each upper segment as an opening bracket and each lower segment as a closing bracket and decompose the stripe into trapezoids by decomposing the bracket sequence into smaller correct bracket sequences. This algorithm requires $O(n^3\log n)$ time and $O(n^2)$ memory.
### Optimization 1
Firstly we will reduce the runtime to $O(n^2\log n)$. Instead of generating trapezoids for each stripe let's fix some triangle side (segment $s = (s_0, s_1)$) and find the set of stripes where this segment is a side of some trapezoid. Note that in this case we only have to find the stripes where the balance of brackets below (or above, in case of a lower segment) $s$ is zero. It means that instead of running vertical scanline for each stripe we can run a horizontal scanline for all parts of other segments which affect the balance of brackets with respect to $s$.
For simplicity we will show how to do this for an upper segment, the algorithm for lower segments is similar. Consider some other non-vertical segment $t = (t_0, t_1)$ and find the intersection $[x_1, x_2]$ of projections of $s$ and $t$ on $Ox$. If this intersection is empty or consists of one point, $t$ can be discarded since $s$ and $t$ do not intersect the interior of the same stripe. Otherwise consider the intersection $I$ of $s$ and $t$. There are three cases.
1. $I = \varnothing$
In this case $t$ is either above or below $s$ on $[x_1, x_2]$. If $t$ is above, it doesn't affect whether $s$ is a side of some trapezoid or not.
If $t$ is below $s$, we should add $1$ or $-1$ to the balance of bracket sequences for all stripes in $[x_1, x_2]$, depending on whether $t$ is upper or lower.
2. $I$ consists of a single point $p$
This case can be reduced to the previous one by splitting $[x_1, x_2]$ into $[x_1, p_x]$ and $[p_x, x_2]$.
3. $I$ is some segment $l$
This case means that the parts of $s$ and $t$ for $x\in[x_1, x_2]$ coincide. If $t$ is lower, $s$ is clearly not a side of a trapezoid.
Otherwise, it could happen that both $s$ and $t$ can be considered as a side of some trapezoid. In order to resolve this ambiguity, we can
decide that only the segment with the lowest index should be considered as a side (here we suppose that triangle sides are enumerated in some way). So, if $index(s) < index(t)$, we should ignore this case,
otherwise we should mark that $s$ can never be a side on $[x_1, x_2]$ (for example, by adding a corresponding event with balance $-2$).
Here is a graphic representation of the three cases.
<center></center>
Finally we should remark on processing all the additions of $1$ or $-1$ on all stripes in $[x_1, x_2]$. For each addition of $w$ on $[x_1, x_2]$ we can create events $(x_1, w),\ (x_2, -w)$
and process all these events with a sweep line.
### Optimization 2
Note that if we apply the previous optimization, we no longer have to find all stripes explicitly. This reduces the memory consumption to $O(n)$.
## Intersection of convex polygons
Another usage of vertical decomposition is to compute the intersection of two convex polygons in linear time. Suppose the plane is split into vertical stripes by vertical lines passing through each
vertex of each polygon. Then if we consider one of the input polygons and some stripe, their intersection is either a trapezoid, a triangle or a point. Therefore we can simply intersect these shapes for each vertical stripe and merge these intersections into a single polygon.
## Implementation
Below is the code that calculates area of the union of a set of triangles in $O(n^2\log n)$ time and $O(n)$ memory.
```{.cpp file=triangle_union}
typedef double dbl;
const dbl eps = 1e-9;
inline bool eq(dbl x, dbl y){
return fabs(x - y) < eps;
}
inline bool lt(dbl x, dbl y){
return x < y - eps;
}
inline bool gt(dbl x, dbl y){
return x > y + eps;
}
inline bool le(dbl x, dbl y){
return x < y + eps;
}
inline bool ge(dbl x, dbl y){
return x > y - eps;
}
struct pt{
dbl x, y;
inline pt operator - (const pt & p)const{
return pt{x - p.x, y - p.y};
}
inline pt operator + (const pt & p)const{
return pt{x + p.x, y + p.y};
}
inline pt operator * (dbl a)const{
return pt{x * a, y * a};
}
inline dbl cross(const pt & p)const{
return x * p.y - y * p.x;
}
inline dbl dot(const pt & p)const{
return x * p.x + y * p.y;
}
inline bool operator == (const pt & p)const{
return eq(x, p.x) && eq(y, p.y);
}
};
struct Line{
pt p[2];
Line(){}
Line(pt a, pt b):p{a, b}{}
pt vec()const{
return p[1] - p[0];
}
pt& operator [](size_t i){
return p[i];
}
};
inline bool lexComp(const pt & l, const pt & r){
if(fabs(l.x - r.x) > eps){
return l.x < r.x;
}
else return l.y < r.y;
}
vector<pt> interSegSeg(Line l1, Line l2){
if(eq(l1.vec().cross(l2.vec()), 0)){
if(!eq(l1.vec().cross(l2[0] - l1[0]), 0))
return {};
if(!lexComp(l1[0], l1[1]))
swap(l1[0], l1[1]);
if(!lexComp(l2[0], l2[1]))
swap(l2[0], l2[1]);
pt l = lexComp(l1[0], l2[0]) ? l2[0] : l1[0];
pt r = lexComp(l1[1], l2[1]) ? l1[1] : l2[1];
if(l == r)
return {l};
else return lexComp(l, r) ? vector<pt>{l, r} : vector<pt>();
}
else{
dbl s = (l2[0] - l1[0]).cross(l2.vec()) / l1.vec().cross(l2.vec());
pt inter = l1[0] + l1.vec() * s;
if(ge(s, 0) && le(s, 1) && le((l2[0] - inter).dot(l2[1] - inter), 0))
return {inter};
else
return {};
}
}
inline char get_segtype(Line segment, pt other_point){
if(eq(segment[0].x, segment[1].x))
return 0;
if(!lexComp(segment[0], segment[1]))
swap(segment[0], segment[1]);
return (segment[1] - segment[0]).cross(other_point - segment[0]) > 0 ? 1 : -1;
}
dbl union_area(vector<tuple<pt, pt, pt> > triangles){
vector<Line> segments(3 * triangles.size());
vector<char> segtype(segments.size());
for(size_t i = 0; i < triangles.size(); i++){
pt a, b, c;
tie(a, b, c) = triangles[i];
segments[3 * i] = lexComp(a, b) ? Line(a, b) : Line(b, a);
segtype[3 * i] = get_segtype(segments[3 * i], c);
segments[3 * i + 1] = lexComp(b, c) ? Line(b, c) : Line(c, b);
segtype[3 * i + 1] = get_segtype(segments[3 * i + 1], a);
segments[3 * i + 2] = lexComp(c, a) ? Line(c, a) : Line(a, c);
segtype[3 * i + 2] = get_segtype(segments[3 * i + 2], b);
}
vector<dbl> k(segments.size()), b(segments.size());
for(size_t i = 0; i < segments.size(); i++){
if(segtype[i]){
k[i] = (segments[i][1].y - segments[i][0].y) / (segments[i][1].x - segments[i][0].x);
b[i] = segments[i][0].y - k[i] * segments[i][0].x;
}
}
dbl ans = 0;
for(size_t i = 0; i < segments.size(); i++){
if(!segtype[i])
continue;
dbl l = segments[i][0].x, r = segments[i][1].x;
vector<pair<dbl, int> > evts;
for(size_t j = 0; j < segments.size(); j++){
if(!segtype[j] || i == j)
continue;
dbl l1 = segments[j][0].x, r1 = segments[j][1].x;
if(ge(l1, r) || ge(l, r1))
continue;
dbl common_l = max(l, l1), common_r = min(r, r1);
auto pts = interSegSeg(segments[i], segments[j]);
if(pts.empty()){
dbl yl1 = k[j] * common_l + b[j];
dbl yl = k[i] * common_l + b[i];
if(lt(yl1, yl) == (segtype[i] == 1)){
int evt_type = -segtype[i] * segtype[j];
evts.emplace_back(common_l, evt_type);
evts.emplace_back(common_r, -evt_type);
}
}
else if(pts.size() == 1u){
dbl yl = k[i] * common_l + b[i], yl1 = k[j] * common_l + b[j];
int evt_type = -segtype[i] * segtype[j];
if(lt(yl1, yl) == (segtype[i] == 1)){
evts.emplace_back(common_l, evt_type);
evts.emplace_back(pts[0].x, -evt_type);
}
yl = k[i] * common_r + b[i], yl1 = k[j] * common_r + b[j];
if(lt(yl1, yl) == (segtype[i] == 1)){
evts.emplace_back(pts[0].x, evt_type);
evts.emplace_back(common_r, -evt_type);
}
}
else{
if(segtype[j] != segtype[i] || j > i){
evts.emplace_back(common_l, -2);
evts.emplace_back(common_r, 2);
}
}
}
evts.emplace_back(l, 0);
sort(evts.begin(), evts.end());
size_t j = 0;
int balance = 0;
while(j < evts.size()){
size_t ptr = j;
while(ptr < evts.size() && eq(evts[j].first, evts[ptr].first)){
balance += evts[ptr].second;
++ptr;
}
if(!balance && !eq(evts[j].first, r)){
dbl next_x = ptr == evts.size() ? r : evts[ptr].first;
ans -= segtype[i] * (k[i] * (next_x + evts[j].first) + 2 * b[i]) * (next_x - evts[j].first);
}
j = ptr;
}
}
return ans/2;
}
```
## Problems
* [Codeforces 62C Inquisition](https://codeforces.com/contest/62/problem/C)
* [Codeforces 107E Darts](https://codeforces.com/contest/107/problem/E)
|
Vertical decomposition
|
---
title
- Original
---
# Knuth's Optimization
Knuth's optimization, also known as the Knuth-Yao Speedup, is a special case of dynamic programming on ranges, that can optimize the time complexity of solutions by a linear factor, from $O(n^3)$ for standard range DP to $O(n^2)$.
## Conditions
The Speedup is applied for transitions of the form
$$dp(i, j) = \min_{i \leq k < j} [ dp(i, k) + dp(k+1, j) + C(i, j) ].$$
Similar to [divide and conquer DP](./divide-and-conquer-dp.md), let $opt(i, j)$ be the value of $k$ that minimizes the expression in the transition ($opt$ is referred to as the "optimal splitting point" further in this article). The optimization requires that the following holds:
$$opt(i, j-1) \leq opt(i, j) \leq opt(i+1, j).$$
We can show that it is true when the cost function $C$ satisfies the following conditions for $a \leq b \leq c \leq d$:
1. $C(b, c) \leq C(a, d)$;
2. $C(a, c) + C(b, d) \leq C(a, d) + C(b, c)$ (the quadrangle inequality [QI]).
This result is proved further below.
## Algorithm
Let's process the dp states in such a way that we calculate $dp(i, j-1)$ and $dp(i+1, j)$ before $dp(i, j)$, and in doing so we also calculate $opt(i, j-1)$ and $opt(i+1, j)$. Then for calculating $opt(i, j)$, instead of testing values of $k$ from $i$ to $j-1$, we only need to test from $opt(i, j-1)$ to $opt(i+1, j)$. To process $(i,j)$ pairs in this order it is sufficient to use nested for loops in which $i$ goes from the maximum value to the minimum one and $j$ goes from $i+1$ to the maximum value.
### Generic implementation
Though implementation varies, here's a fairly generic
example. The structure of the code is almost identical to that of Range DP.
```{.cpp file=knuth_optimization}
int solve() {
int N;
... // read N and input
int dp[N][N], opt[N][N];
auto C = [&](int i, int j) {
... // Implement cost function C.
};
for (int i = 0; i < N; i++) {
opt[i][i] = i;
... // Initialize dp[i][i] according to the problem
}
for (int i = N-2; i >= 0; i--) {
for (int j = i+1; j < N; j++) {
int mn = INT_MAX;
int cost = C(i, j);
for (int k = opt[i][j-1]; k <= min(j-1, opt[i+1][j]); k++) {
if (mn >= dp[i][k] + dp[k+1][j] + cost) {
opt[i][j] = k;
mn = dp[i][k] + dp[k+1][j] + cost;
}
}
dp[i][j] = mn;
}
}
cout << dp[0][N-1] << endl;
}
```
### Complexity
A complexity of the algorithm can be estimated as the following sum:
$$
\sum\limits_{i=1}^N \sum\limits_{j=i+1}^N [opt(i+1,j)-opt(i,j-1)] =
\sum\limits_{i=1}^N \sum\limits_{j=i}^{N-1} [opt(i+1,j+1)-opt(i,j)].
$$
As you see, most of the terms in this expression cancel each other out, except for positive terms with $j=N$ and negative terms with $i=1$. Thus, the whole sum can be estimated as
$$
\sum\limits_{k=1}^N[opt(k,N)-opt(1,k)] = O(n^2),
$$
rather than $O(n^3)$ as it would be if we were using a regular range DP.
### On practice
The most common application of Knuth's optimization is in Range DP, with the given transition. The only difficulty is in proving that the cost function satisfies the given conditions. The simplest case is when the cost function $C(i, j)$ is simply the sum of the elements of the subarray $S[i, i+1, ..., j]$ for some array (depending on the question). However, they can be more complicated at times.
Note that more than the conditions on the dp transition and the cost function, the key to this optimization is the inequality on the optimum splitting point. In some problems, such as the optimal binary search tree problem (which is, incidentally, the original problem for which this optimization was developed), the transitions and cost functions will be less obvious, however, one can still prove that $opt(i, j-1) \leq opt(i, j) \leq opt(i+1, j)$, and thus, use this optimization.
### Proof of correctness
To prove the correctness of this algorithm in terms of $C(i,j)$ conditions, it suffices to prove that
$$
opt(i, j-1) \leq opt(i, j) \leq opt(i+1, j)
$$
assuming the given conditions are satisfied.
!!! lemma "Lemma"
$dp(i, j)$ also satisfies the quadrangle inequality, given the conditions of the problem are satisfied.
??? hint "Proof"
The proof for this lemma uses strong induction. It has been taken from the paper <a href="https://dl.acm.org/doi/pdf/10.1145/800141.804691">Efficient Dynamic Programming Using Quadrangle Inequalities</a>, authored by F. Frances Yao, which introduced the Knuth-Yao Speedup (this particular statement is Lemma 2.1 in the paper). The idea is to induct on the length $l = d - a$. The case where $l = 1$ is trivial. For $l > 1$ consider 2 cases:
1. $b = c$
The inequality reduces to $dp(a, b) + dp(b, d) \leq dp(a, d)$ (This assumes that $dp(i, i) = 0$ for all $i$, which is the case for all problems using this optimization). Let $opt(a,d) = z$.
- If $z < j$,
Note that
$$
dp(a, b) \leq dp_{z}(a, b) = dp(a, z) + dp(z+1, b) + C(a, b).
$$
Therefore,
$$
dp(a, b) + dp(b, d) \leq dp(a, z) + dp(z+1, b) + dp(b, d) + C(a, b)
$$
From the induction hypothesis, $dp(z+1, b) + dp(b, d) \leq dp(z+1, d)$. Also, it is given that $C(a, b) \leq C(a, d)$. Combining these 2 facts with above inequality yields the desired result.
- If $z \geq j$, the proof of this case is symmetric to the previous case.
2. $b < c$
Let $opt(b, c) = z$ and $opt(a, d) = y$.
- If $z \leq y$,
$$
dp(a, c) + dp(b, d) \leq dp_{z}(a, c) + dp_{y}(b, d)
$$
where
$$
dp_{z}(a, c) + dp_{y}(b, d) = C(a, c) + C(b, d) + dp(a, z) + dp(z+1, c) + dp(b, y) + dp(y+1, d).
$$
Using the QI on $C$ and on the dp state for the indices $z+1 \leq y+1 \leq c \leq d$ (from the induction hypothesis) yields the desired result.
- If $z > y$, the proof of this case is symmetric to the previous case.
This completes the proof of the lemma.
Now, consider the following setup. We have 2 indices $i \leq p \leq q < j$. Set $dp_{k} = C(i, j) + dp(i, k) + dp(k+1, j)$.
Suppose we show that
$$
dp_{p}(i, j-1) \geq dp_{q}(i, j-1) \implies dp_{p}(i, j) \geq dp_{q}(i, j).
$$
Setting $q = opt(i, j-1)$, by definition, $dp_{p}(i, j-1) \geq dp_{q}(i, j-1)$. Therefore, applying the inequality to all $i \leq p \leq q$, we can infer that $opt(i, j)$ is at least as much as $opt(i, j-1)$, proving the first half of the inequality.
Now, using the QI on some indices $p+1 \leq q+1 \leq j-1 \leq j$, we get
$$\begin{align}
&dp(p+1, j-1) + dp(q+1, j) ≤ dp(q+1, j-1) + dp(p+1, j) \\
\implies& (dp(i, p) + dp(p+1, j-1) + C(i, j-1)) + (dp(i, q) + dp(q+1, j) + C(i, j)) \\
\leq& (dp(i, q) + dp(q+1, j-1) + C(i, j-1)) + (dp(i, p) + dp(p+1, j) + C(i, j)) \\
\implies& dp_{p}(i, j-1) + dp_{q}(i, j) ≤ dp_{p}(i, j) + dp_{q}(i, j-1) \\
\implies& dp_{p}(i, j-1) - dp_{q}(i, j-1) ≤ dp_{p}(i, j) - dp_{q}(i, j) \\
\end{align}$$
Finally,
$$\begin{align}
&dp_{p}(i, j-1) \geq dp_{q}(i, j-1) \\
&\implies 0 \leq dp_{p}(i, j-1) - dp_{q}(i, j-1) \leq dp_{p}(i, j) - dp_{q}(i, j) \\
&\implies dp_{p}(i, j) \geq dp_{q}(i, j)
\end{align}$$
This proves the first part of the inequality, i.e., $opt(i, j-1) \leq opt(i, j)$. The second part $opt(i, j) \leq opt(i+1, j)$ can be shown with the same idea, starting with the inequality
$dp(i, p) + dp(i+1, q) ≤ dp(i+1, p) + dp(i, q)$.
This completes the proof.
|
---
title
- Original
---
# Knuth's Optimization
Knuth's optimization, also known as the Knuth-Yao Speedup, is a special case of dynamic programming on ranges, that can optimize the time complexity of solutions by a linear factor, from $O(n^3)$ for standard range DP to $O(n^2)$.
## Conditions
The Speedup is applied for transitions of the form
$$dp(i, j) = \min_{i \leq k < j} [ dp(i, k) + dp(k+1, j) + C(i, j) ].$$
Similar to [divide and conquer DP](./divide-and-conquer-dp.md), let $opt(i, j)$ be the value of $k$ that minimizes the expression in the transition ($opt$ is referred to as the "optimal splitting point" further in this article). The optimization requires that the following holds:
$$opt(i, j-1) \leq opt(i, j) \leq opt(i+1, j).$$
We can show that it is true when the cost function $C$ satisfies the following conditions for $a \leq b \leq c \leq d$:
1. $C(b, c) \leq C(a, d)$;
2. $C(a, c) + C(b, d) \leq C(a, d) + C(b, c)$ (the quadrangle inequality [QI]).
This result is proved further below.
## Algorithm
Let's process the dp states in such a way that we calculate $dp(i, j-1)$ and $dp(i+1, j)$ before $dp(i, j)$, and in doing so we also calculate $opt(i, j-1)$ and $opt(i+1, j)$. Then for calculating $opt(i, j)$, instead of testing values of $k$ from $i$ to $j-1$, we only need to test from $opt(i, j-1)$ to $opt(i+1, j)$. To process $(i,j)$ pairs in this order it is sufficient to use nested for loops in which $i$ goes from the maximum value to the minimum one and $j$ goes from $i+1$ to the maximum value.
### Generic implementation
Though implementation varies, here's a fairly generic
example. The structure of the code is almost identical to that of Range DP.
```{.cpp file=knuth_optimization}
int solve() {
int N;
... // read N and input
int dp[N][N], opt[N][N];
auto C = [&](int i, int j) {
... // Implement cost function C.
};
for (int i = 0; i < N; i++) {
opt[i][i] = i;
... // Initialize dp[i][i] according to the problem
}
for (int i = N-2; i >= 0; i--) {
for (int j = i+1; j < N; j++) {
int mn = INT_MAX;
int cost = C(i, j);
for (int k = opt[i][j-1]; k <= min(j-1, opt[i+1][j]); k++) {
if (mn >= dp[i][k] + dp[k+1][j] + cost) {
opt[i][j] = k;
mn = dp[i][k] + dp[k+1][j] + cost;
}
}
dp[i][j] = mn;
}
}
cout << dp[0][N-1] << endl;
}
```
### Complexity
A complexity of the algorithm can be estimated as the following sum:
$$
\sum\limits_{i=1}^N \sum\limits_{j=i+1}^N [opt(i+1,j)-opt(i,j-1)] =
\sum\limits_{i=1}^N \sum\limits_{j=i}^{N-1} [opt(i+1,j+1)-opt(i,j)].
$$
As you see, most of the terms in this expression cancel each other out, except for positive terms with $j=N$ and negative terms with $i=1$. Thus, the whole sum can be estimated as
$$
\sum\limits_{k=1}^N[opt(k,N)-opt(1,k)] = O(n^2),
$$
rather than $O(n^3)$ as it would be if we were using a regular range DP.
### On practice
The most common application of Knuth's optimization is in Range DP, with the given transition. The only difficulty is in proving that the cost function satisfies the given conditions. The simplest case is when the cost function $C(i, j)$ is simply the sum of the elements of the subarray $S[i, i+1, ..., j]$ for some array (depending on the question). However, they can be more complicated at times.
Note that more than the conditions on the dp transition and the cost function, the key to this optimization is the inequality on the optimum splitting point. In some problems, such as the optimal binary search tree problem (which is, incidentally, the original problem for which this optimization was developed), the transitions and cost functions will be less obvious, however, one can still prove that $opt(i, j-1) \leq opt(i, j) \leq opt(i+1, j)$, and thus, use this optimization.
### Proof of correctness
To prove the correctness of this algorithm in terms of $C(i,j)$ conditions, it suffices to prove that
$$
opt(i, j-1) \leq opt(i, j) \leq opt(i+1, j)
$$
assuming the given conditions are satisfied.
!!! lemma "Lemma"
$dp(i, j)$ also satisfies the quadrangle inequality, given the conditions of the problem are satisfied.
??? hint "Proof"
The proof for this lemma uses strong induction. It has been taken from the paper <a href="https://dl.acm.org/doi/pdf/10.1145/800141.804691">Efficient Dynamic Programming Using Quadrangle Inequalities</a>, authored by F. Frances Yao, which introduced the Knuth-Yao Speedup (this particular statement is Lemma 2.1 in the paper). The idea is to induct on the length $l = d - a$. The case where $l = 1$ is trivial. For $l > 1$ consider 2 cases:
1. $b = c$
The inequality reduces to $dp(a, b) + dp(b, d) \leq dp(a, d)$ (This assumes that $dp(i, i) = 0$ for all $i$, which is the case for all problems using this optimization). Let $opt(a,d) = z$.
- If $z < j$,
Note that
$$
dp(a, b) \leq dp_{z}(a, b) = dp(a, z) + dp(z+1, b) + C(a, b).
$$
Therefore,
$$
dp(a, b) + dp(b, d) \leq dp(a, z) + dp(z+1, b) + dp(b, d) + C(a, b)
$$
From the induction hypothesis, $dp(z+1, b) + dp(b, d) \leq dp(z+1, d)$. Also, it is given that $C(a, b) \leq C(a, d)$. Combining these 2 facts with above inequality yields the desired result.
- If $z \geq j$, the proof of this case is symmetric to the previous case.
2. $b < c$
Let $opt(b, c) = z$ and $opt(a, d) = y$.
- If $z \leq y$,
$$
dp(a, c) + dp(b, d) \leq dp_{z}(a, c) + dp_{y}(b, d)
$$
where
$$
dp_{z}(a, c) + dp_{y}(b, d) = C(a, c) + C(b, d) + dp(a, z) + dp(z+1, c) + dp(b, y) + dp(y+1, d).
$$
Using the QI on $C$ and on the dp state for the indices $z+1 \leq y+1 \leq c \leq d$ (from the induction hypothesis) yields the desired result.
- If $z > y$, the proof of this case is symmetric to the previous case.
This completes the proof of the lemma.
Now, consider the following setup. We have 2 indices $i \leq p \leq q < j$. Set $dp_{k} = C(i, j) + dp(i, k) + dp(k+1, j)$.
Suppose we show that
$$
dp_{p}(i, j-1) \geq dp_{q}(i, j-1) \implies dp_{p}(i, j) \geq dp_{q}(i, j).
$$
Setting $q = opt(i, j-1)$, by definition, $dp_{p}(i, j-1) \geq dp_{q}(i, j-1)$. Therefore, applying the inequality to all $i \leq p \leq q$, we can infer that $opt(i, j)$ is at least as much as $opt(i, j-1)$, proving the first half of the inequality.
Now, using the QI on some indices $p+1 \leq q+1 \leq j-1 \leq j$, we get
$$\begin{align}
&dp(p+1, j-1) + dp(q+1, j) ≤ dp(q+1, j-1) + dp(p+1, j) \\
\implies& (dp(i, p) + dp(p+1, j-1) + C(i, j-1)) + (dp(i, q) + dp(q+1, j) + C(i, j)) \\
\leq& (dp(i, q) + dp(q+1, j-1) + C(i, j-1)) + (dp(i, p) + dp(p+1, j) + C(i, j)) \\
\implies& dp_{p}(i, j-1) + dp_{q}(i, j) ≤ dp_{p}(i, j) + dp_{q}(i, j-1) \\
\implies& dp_{p}(i, j-1) - dp_{q}(i, j-1) ≤ dp_{p}(i, j) - dp_{q}(i, j) \\
\end{align}$$
Finally,
$$\begin{align}
&dp_{p}(i, j-1) \geq dp_{q}(i, j-1) \\
&\implies 0 \leq dp_{p}(i, j-1) - dp_{q}(i, j-1) \leq dp_{p}(i, j) - dp_{q}(i, j) \\
&\implies dp_{p}(i, j) \geq dp_{q}(i, j)
\end{align}$$
This proves the first part of the inequality, i.e., $opt(i, j-1) \leq opt(i, j)$. The second part $opt(i, j) \leq opt(i+1, j)$ can be shown with the same idea, starting with the inequality
$dp(i, p) + dp(i+1, q) ≤ dp(i+1, p) + dp(i, q)$.
This completes the proof.
## Practice Problems
- [UVA - Cutting Sticks](https://onlinejudge.org/external/100/10003.pdf)
- [UVA - Prefix Codes](https://onlinejudge.org/external/120/12057.pdf)
- [SPOJ - Breaking String](https://www.spoj.com/problems/BRKSTRNG/)
- [UVA - Optimal Binary Search Tree](https://onlinejudge.org/external/103/10304.pdf)
## References
- [Geeksforgeeks Article](https://www.geeksforgeeks.org/knuths-optimization-in-dynamic-programming/)
- [Doc on DP Speedups](https://home.cse.ust.hk/~golin/COMP572/Notes/DP_speedup.pdf)
- [Efficient Dynamic Programming Using Quadrangle Inequalities](https://dl.acm.org/doi/pdf/10.1145/800141.804691)
|
Knuth's Optimization
|
---
title
maximum_zero_submatrix
---
# Finding the largest zero submatrix
You are given a matrix with `n` rows and `m` columns. Find the largest submatrix consisting of only zeros (a submatrix is a rectangular area of the matrix).
## Algorithm
Elements of the matrix will be `a[i][j]`, where `i = 0...n - 1`, `j = 0... m - 1`. For simplicity, we will consider all non-zero elements equal to 1.
### Step 1: Auxiliary dynamic
First, we calculate the following auxiliary matrix: `d[i][j]`, nearest row that has a 1 above `a[i][j]`. Formally speaking, `d[i][j]` is the largest row number (from `0` to `i - 1`), in which there is a element equal to `1` in the `j`-th column.
While iterating from top-left to bottom-right, when we stand in row `i`, we know the values from the previous row, so, it is enough to update just the elements with value `1`. We can save the values in a simple array `d[i]`, `i = 1...m - 1`, because in the further algorithm we will process the matrix one row at a time and only need the values of the current row.
```cpp
vector<int> d(m, -1);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (a[i][j] == 1) {
d[j] = i;
}
}
}
```
### Step 2: Problem solving
We can solve the problem in $O(n m^2)$ iterating through rows, considering every possible left and right columns for a submatrix. The bottom of the rectangle will be the current row, and using `d[i][j]` we can find the top row. However, it is possible to go further and significantly improve the complexity of the solution.
It is clear that the desired zero submatrix is bounded on all four sides by some ones, which prevent it from increasing in size and improving the answer. Therefore, we will not miss the answer if we act as follows: for every cell `j` in row `i` (the bottom row of a potential zero submatrix) we will have `d[i][j]` as the top row of the current zero submatrix. It now remains to determine the optimal left and right boundaries of the zero submatrix, i.e. maximally push this submatrix to the left and right of the `j`-th column.
What does it mean to push the maximum to the left? It means to find an index `k1` for which `d[i][k1] > d[i][j]`, and at the same time `k1` - the closest one to the left of the index `j`. It is clear that then `k1 + 1` gives the number of the left column of the required zero submatrix. If there is no such index at all, then put `k1` = `-1`(this means that we were able to extend the current zero submatrix to the left all the way to the border of matrix `a`).
Symmetrically, you can define an index `k2` for the right border: this is the closest index to the right of `j` such that `d[i][k2] > d[i][j]` (or `m`, if there is no such index).
So, the indices `k1` and `k2`, if we learn to search for them effectively, will give us all the necessary information about the current zero submatrix. In particular, its area will be equal to `(i - d[i][j]) * (k2 - k1 - 1)`.
How to look for these indexes `k1` and `k2` effectively with fixed `i` and `j`? We can do that in $O(1)$ on average.
To achieve such complexity, you can use the stack as follows. Let's first learn how to search for an index `k1`, and save its value for each index `j` within the current row `i` in matrix `d1[i][j]`. To do this, we will look through all the columns `j` from left to right, and we will store in the stack only those columns that have `d[][]` strictly greater than `d[i][j]`. It is clear that when moving from a column `j` to the next column, it is necessary to update the content of the stack. When there is an inappropriate element at the top of the stack (i.e. `d[][] <= d[i][j]`) pop it. It is easy to understand that it is enough to remove from the stack only from its top, and from none of its other places (because the stack will contain an increasing `d` sequence of columns).
The value `d1[i][j]` for each `j` will be equal to the value lying at that moment on top of the stack.
The dynamics `d2[i][j]` for finding the indices `k2` is considered similar, only you need to view the columns from right to left.
It is clear that since there are exactly `m` pieces added to the stack on each line, there could not be more deletions either, the sum of complexities will be linear, so the final complexity of the algorithm is $O(nm)$.
It should also be noted that this algorithm consumes $O(m)$ memory (not counting the input data - the matrix `a[][]`).
### Implementation
```cpp
int zero_matrix(vector<vector<int>> a) {
int n = a.size();
int m = a[0].size();
int ans = 0;
vector<int> d(m, -1), d1(m), d2(m);
stack<int> st;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (a[i][j] == 1)
d[j] = i;
}
for (int j = 0; j < m; ++j) {
while (!st.empty() && d[st.top()] <= d[j])
st.pop();
d1[j] = st.empty() ? -1 : st.top();
st.push(j);
}
while (!st.empty())
st.pop();
for (int j = m - 1; j >= 0; --j) {
while (!st.empty() && d[st.top()] <= d[j])
st.pop();
d2[j] = st.empty() ? m : st.top();
st.push(j);
}
while (!st.empty())
st.pop();
for (int j = 0; j < m; ++j)
ans = max(ans, (i - d[j]) * (d2[j] - d1[j] - 1));
}
return ans;
}
```
|
---
title
maximum_zero_submatrix
---
# Finding the largest zero submatrix
You are given a matrix with `n` rows and `m` columns. Find the largest submatrix consisting of only zeros (a submatrix is a rectangular area of the matrix).
## Algorithm
Elements of the matrix will be `a[i][j]`, where `i = 0...n - 1`, `j = 0... m - 1`. For simplicity, we will consider all non-zero elements equal to 1.
### Step 1: Auxiliary dynamic
First, we calculate the following auxiliary matrix: `d[i][j]`, nearest row that has a 1 above `a[i][j]`. Formally speaking, `d[i][j]` is the largest row number (from `0` to `i - 1`), in which there is a element equal to `1` in the `j`-th column.
While iterating from top-left to bottom-right, when we stand in row `i`, we know the values from the previous row, so, it is enough to update just the elements with value `1`. We can save the values in a simple array `d[i]`, `i = 1...m - 1`, because in the further algorithm we will process the matrix one row at a time and only need the values of the current row.
```cpp
vector<int> d(m, -1);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (a[i][j] == 1) {
d[j] = i;
}
}
}
```
### Step 2: Problem solving
We can solve the problem in $O(n m^2)$ iterating through rows, considering every possible left and right columns for a submatrix. The bottom of the rectangle will be the current row, and using `d[i][j]` we can find the top row. However, it is possible to go further and significantly improve the complexity of the solution.
It is clear that the desired zero submatrix is bounded on all four sides by some ones, which prevent it from increasing in size and improving the answer. Therefore, we will not miss the answer if we act as follows: for every cell `j` in row `i` (the bottom row of a potential zero submatrix) we will have `d[i][j]` as the top row of the current zero submatrix. It now remains to determine the optimal left and right boundaries of the zero submatrix, i.e. maximally push this submatrix to the left and right of the `j`-th column.
What does it mean to push the maximum to the left? It means to find an index `k1` for which `d[i][k1] > d[i][j]`, and at the same time `k1` - the closest one to the left of the index `j`. It is clear that then `k1 + 1` gives the number of the left column of the required zero submatrix. If there is no such index at all, then put `k1` = `-1`(this means that we were able to extend the current zero submatrix to the left all the way to the border of matrix `a`).
Symmetrically, you can define an index `k2` for the right border: this is the closest index to the right of `j` such that `d[i][k2] > d[i][j]` (or `m`, if there is no such index).
So, the indices `k1` and `k2`, if we learn to search for them effectively, will give us all the necessary information about the current zero submatrix. In particular, its area will be equal to `(i - d[i][j]) * (k2 - k1 - 1)`.
How to look for these indexes `k1` and `k2` effectively with fixed `i` and `j`? We can do that in $O(1)$ on average.
To achieve such complexity, you can use the stack as follows. Let's first learn how to search for an index `k1`, and save its value for each index `j` within the current row `i` in matrix `d1[i][j]`. To do this, we will look through all the columns `j` from left to right, and we will store in the stack only those columns that have `d[][]` strictly greater than `d[i][j]`. It is clear that when moving from a column `j` to the next column, it is necessary to update the content of the stack. When there is an inappropriate element at the top of the stack (i.e. `d[][] <= d[i][j]`) pop it. It is easy to understand that it is enough to remove from the stack only from its top, and from none of its other places (because the stack will contain an increasing `d` sequence of columns).
The value `d1[i][j]` for each `j` will be equal to the value lying at that moment on top of the stack.
The dynamics `d2[i][j]` for finding the indices `k2` is considered similar, only you need to view the columns from right to left.
It is clear that since there are exactly `m` pieces added to the stack on each line, there could not be more deletions either, the sum of complexities will be linear, so the final complexity of the algorithm is $O(nm)$.
It should also be noted that this algorithm consumes $O(m)$ memory (not counting the input data - the matrix `a[][]`).
### Implementation
```cpp
int zero_matrix(vector<vector<int>> a) {
int n = a.size();
int m = a[0].size();
int ans = 0;
vector<int> d(m, -1), d1(m), d2(m);
stack<int> st;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (a[i][j] == 1)
d[j] = i;
}
for (int j = 0; j < m; ++j) {
while (!st.empty() && d[st.top()] <= d[j])
st.pop();
d1[j] = st.empty() ? -1 : st.top();
st.push(j);
}
while (!st.empty())
st.pop();
for (int j = m - 1; j >= 0; --j) {
while (!st.empty() && d[st.top()] <= d[j])
st.pop();
d2[j] = st.empty() ? m : st.top();
st.push(j);
}
while (!st.empty())
st.pop();
for (int j = 0; j < m; ++j)
ans = max(ans, (i - d[j]) * (d2[j] - d1[j] - 1));
}
return ans;
}
```
|
Finding the largest zero submatrix
|
---
title
profile_dynamics
---
# Dynamic Programming on Broken Profile. Problem "Parquet"
Common problems solved using DP on broken profile include:
- finding number of ways to fully fill an area (e.g. chessboard/grid) with some figures (e.g. dominoes)
- finding a way to fill an area with minimum number of figures
- finding a partial fill with minimum number of unfilled space (or cells, in case of grid)
- finding a partial fill with the minimum number of figures, such that no more figures can be added
## Problem "Parquet"
**Problem description.** Given a grid of size $N \times M$. Find number of ways to fill the grid with figures of size $2 \times 1$ (no cell should be left unfilled, and figures should not overlap each other).
Let the DP state be: $dp[i, mask]$, where $i = 1, \ldots N$ and $mask = 0, \ldots 2^M - 1$.
$i$ represents number of rows in the current grid, and $mask$ is the state of last row of current grid. If $j$-th bit of $mask$ is $0$ then the corresponding cell is filled, otherwise it is unfilled.
Clearly, the answer to the problem will be $dp[N, 0]$.
We will be building the DP state by iterating over each $i = 1, \cdots N$ and each $mask = 0, \ldots 2^M - 1$, and for each $mask$ we will be only transitioning forward, that is, we will be _adding_ figures to the current grid.
### Implementation
```cpp
int n, m;
vector < vector<long long> > dp;
void calc (int x = 0, int y = 0, int mask = 0, int next_mask = 0)
{
if (x == n)
return;
if (y >= m)
dp[x+1][next_mask] += dp[x][mask];
else
{
int my_mask = 1 << y;
if (mask & my_mask)
calc (x, y+1, mask, next_mask);
else
{
calc (x, y+1, mask, next_mask | my_mask);
if (y+1 < m && ! (mask & my_mask) && ! (mask & (my_mask << 1)))
calc (x, y+2, mask, next_mask);
}
}
}
int main()
{
cin >> n >> m;
dp.resize (n+1, vector<long long> (1<<m));
dp[0][0] = 1;
for (int x=0; x<n; ++x)
for (int mask=0; mask<(1<<m); ++mask)
calc (x, 0, mask, 0);
cout << dp[n][0];
}
```
|
---
title
profile_dynamics
---
# Dynamic Programming on Broken Profile. Problem "Parquet"
Common problems solved using DP on broken profile include:
- finding number of ways to fully fill an area (e.g. chessboard/grid) with some figures (e.g. dominoes)
- finding a way to fill an area with minimum number of figures
- finding a partial fill with minimum number of unfilled space (or cells, in case of grid)
- finding a partial fill with the minimum number of figures, such that no more figures can be added
## Problem "Parquet"
**Problem description.** Given a grid of size $N \times M$. Find number of ways to fill the grid with figures of size $2 \times 1$ (no cell should be left unfilled, and figures should not overlap each other).
Let the DP state be: $dp[i, mask]$, where $i = 1, \ldots N$ and $mask = 0, \ldots 2^M - 1$.
$i$ represents number of rows in the current grid, and $mask$ is the state of last row of current grid. If $j$-th bit of $mask$ is $0$ then the corresponding cell is filled, otherwise it is unfilled.
Clearly, the answer to the problem will be $dp[N, 0]$.
We will be building the DP state by iterating over each $i = 1, \cdots N$ and each $mask = 0, \ldots 2^M - 1$, and for each $mask$ we will be only transitioning forward, that is, we will be _adding_ figures to the current grid.
### Implementation
```cpp
int n, m;
vector < vector<long long> > dp;
void calc (int x = 0, int y = 0, int mask = 0, int next_mask = 0)
{
if (x == n)
return;
if (y >= m)
dp[x+1][next_mask] += dp[x][mask];
else
{
int my_mask = 1 << y;
if (mask & my_mask)
calc (x, y+1, mask, next_mask);
else
{
calc (x, y+1, mask, next_mask | my_mask);
if (y+1 < m && ! (mask & my_mask) && ! (mask & (my_mask << 1)))
calc (x, y+2, mask, next_mask);
}
}
}
int main()
{
cin >> n >> m;
dp.resize (n+1, vector<long long> (1<<m));
dp[0][0] = 1;
for (int x=0; x<n; ++x)
for (int mask=0; mask<(1<<m); ++mask)
calc (x, 0, mask, 0);
cout << dp[n][0];
}
```
## Practice Problems
- [UVA 10359 - Tiling](https://onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1300)
- [UVA 10918 - Tri Tiling](https://onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1859)
- [SPOJ GNY07H (Four Tiling)](https://www.spoj.com/problems/GNY07H/)
- [SPOJ M5TILE (Five Tiling)](https://www.spoj.com/problems/M5TILE/)
- [SPOJ MNTILE (MxN Tiling)](https://www.spoj.com/problems/MNTILE/)
- [SPOJ DOJ1](https://www.spoj.com/problems/DOJ1/)
- [SPOJ DOJ2](https://www.spoj.com/problems/DOJ2/)
- [SPOJ BTCODE_J](https://www.spoj.com/problems/BTCODE_J/)
- [SPOJ PBOARD](https://www.spoj.com/problems/PBOARD/)
- [ACM HDU 4285 - Circuits](http://acm.hdu.edu.cn/showproblem.php?pid=4285)
- [LiveArchive 4608 - Mosaic](https://icpcarchive.ecs.baylor.edu/index.php?option=onlinejudge&page=show_problem&problem=2609)
- [Timus 1519 - Formula 1](https://acm.timus.ru/problem.aspx?space=1&num=1519)
- [Codeforces Parquet](https://codeforces.com/problemset/problem/26/C)
## References
- [Blog by EvilBunny](https://web.archive.org/web/20180712171735/https://blog.evilbuggy.com/2018/05/broken-profile-dynamic-programming.html)
- [TopCoder Recipe by "syg96"](https://apps.topcoder.com/forums/?module=Thread&start=0&threadID=697369)
- [Blogpost by sk765](http://sk765.blogspot.com/2012/02/dynamic-programming-with-profile.html)
|
Dynamic Programming on Broken Profile. Problem "Parquet"
|
---
title
- Original
---
# Divide and Conquer DP
Divide and Conquer is a dynamic programming optimization.
### Preconditions
Some dynamic programming problems have a recurrence of this form:
$$
dp(i, j) = \min_{0 \leq k \leq j} \\{ dp(i - 1, k - 1) + C(k, j) \\}
$$
where $C(k, j)$ is a cost function and $dp(i, j) = 0$ when $j \lt 0$.
Say $0 \leq i \lt m$ and $0 \leq j \lt n$, and evaluating $C$ takes $O(1)$
time. Then the straightforward evaluation of the above recurrence is $O(m n^2)$. There
are $m \times n$ states, and $n$ transitions for each state.
Let $opt(i, j)$ be the value of $k$ that minimizes the above expression. Assuming that the
cost function satisfies the quadrangle inequality, we can show that
$opt(i, j) \leq opt(i, j + 1)$ for all $i, j$. This is known as the _monotonicity condition_.
Then, we can apply divide and conquer DP. The optimal
"splitting point" for a fixed $i$ increases as $j$ increases.
This lets us solve for all states more efficiently. Say we compute $opt(i, j)$
for some fixed $i$ and $j$. Then for any $j' < j$ we know that $opt(i, j') \leq opt(i, j)$.
This means when computing $opt(i, j')$, we don't have to consider as many
splitting points!
To minimize the runtime, we apply the idea behind divide and conquer. First,
compute $opt(i, n / 2)$. Then, compute $opt(i, n / 4)$, knowing that it is less
than or equal to $opt(i, n / 2)$ and $opt(i, 3 n / 4)$ knowing that it is
greater than or equal to $opt(i, n / 2)$. By recursively keeping track of the
lower and upper bounds on $opt$, we reach a $O(m n \log n)$ runtime. Each
possible value of $opt(i, j)$ only appears in $\log n$ different nodes.
Note that it doesn't matter how "balanced" $opt(i, j)$ is. Across a fixed
level, each value of $k$ is used at most twice, and there are at most $\log n$
levels.
## Generic implementation
Even though implementation varies based on problem, here's a fairly generic
template.
The function `compute` computes one row $i$ of states `dp_cur`, given the previous row $i-1$ of states `dp_before`.
It has to be called with `compute(0, n-1, 0, n-1)`. The function `solve` computes `m` rows and returns the result.
```{.cpp file=divide_and_conquer_dp}
int m, n;
vector<long long> dp_before(n), dp_cur(n);
long long C(int i, int j);
// compute dp_cur[l], ... dp_cur[r] (inclusive)
void compute(int l, int r, int optl, int optr) {
if (l > r)
return;
int mid = (l + r) >> 1;
pair<long long, int> best = {LLONG_MAX, -1};
for (int k = optl; k <= min(mid, optr); k++) {
best = min(best, {(k ? dp_before[k - 1] : 0) + C(k, mid), k});
}
dp_cur[mid] = best.first;
int opt = best.second;
compute(l, mid - 1, optl, opt);
compute(mid + 1, r, opt, optr);
}
int solve() {
for (int i = 0; i < n; i++)
dp_before[i] = C(0, i);
for (int i = 1; i < m; i++) {
compute(0, n - 1, 0, n - 1);
dp_before = dp_cur;
}
return dp_before[n - 1];
}
```
### Things to look out for
The greatest difficulty with Divide and Conquer DP problems is proving the
monotonicity of $opt$. One special case where this is true is when the cost function satisfies the quadrangle inequality, i.e., $C(a, c) + C(b, d) \leq C(a, d) + C(b, c)$ for all $a \leq b \leq c \leq d$.
Many Divide and Conquer DP problems can also be solved with the Convex Hull trick or vice-versa. It is useful to know and understand
both!
|
---
title
- Original
---
# Divide and Conquer DP
Divide and Conquer is a dynamic programming optimization.
### Preconditions
Some dynamic programming problems have a recurrence of this form:
$$
dp(i, j) = \min_{0 \leq k \leq j} \\{ dp(i - 1, k - 1) + C(k, j) \\}
$$
where $C(k, j)$ is a cost function and $dp(i, j) = 0$ when $j \lt 0$.
Say $0 \leq i \lt m$ and $0 \leq j \lt n$, and evaluating $C$ takes $O(1)$
time. Then the straightforward evaluation of the above recurrence is $O(m n^2)$. There
are $m \times n$ states, and $n$ transitions for each state.
Let $opt(i, j)$ be the value of $k$ that minimizes the above expression. Assuming that the
cost function satisfies the quadrangle inequality, we can show that
$opt(i, j) \leq opt(i, j + 1)$ for all $i, j$. This is known as the _monotonicity condition_.
Then, we can apply divide and conquer DP. The optimal
"splitting point" for a fixed $i$ increases as $j$ increases.
This lets us solve for all states more efficiently. Say we compute $opt(i, j)$
for some fixed $i$ and $j$. Then for any $j' < j$ we know that $opt(i, j') \leq opt(i, j)$.
This means when computing $opt(i, j')$, we don't have to consider as many
splitting points!
To minimize the runtime, we apply the idea behind divide and conquer. First,
compute $opt(i, n / 2)$. Then, compute $opt(i, n / 4)$, knowing that it is less
than or equal to $opt(i, n / 2)$ and $opt(i, 3 n / 4)$ knowing that it is
greater than or equal to $opt(i, n / 2)$. By recursively keeping track of the
lower and upper bounds on $opt$, we reach a $O(m n \log n)$ runtime. Each
possible value of $opt(i, j)$ only appears in $\log n$ different nodes.
Note that it doesn't matter how "balanced" $opt(i, j)$ is. Across a fixed
level, each value of $k$ is used at most twice, and there are at most $\log n$
levels.
## Generic implementation
Even though implementation varies based on problem, here's a fairly generic
template.
The function `compute` computes one row $i$ of states `dp_cur`, given the previous row $i-1$ of states `dp_before`.
It has to be called with `compute(0, n-1, 0, n-1)`. The function `solve` computes `m` rows and returns the result.
```{.cpp file=divide_and_conquer_dp}
int m, n;
vector<long long> dp_before(n), dp_cur(n);
long long C(int i, int j);
// compute dp_cur[l], ... dp_cur[r] (inclusive)
void compute(int l, int r, int optl, int optr) {
if (l > r)
return;
int mid = (l + r) >> 1;
pair<long long, int> best = {LLONG_MAX, -1};
for (int k = optl; k <= min(mid, optr); k++) {
best = min(best, {(k ? dp_before[k - 1] : 0) + C(k, mid), k});
}
dp_cur[mid] = best.first;
int opt = best.second;
compute(l, mid - 1, optl, opt);
compute(mid + 1, r, opt, optr);
}
int solve() {
for (int i = 0; i < n; i++)
dp_before[i] = C(0, i);
for (int i = 1; i < m; i++) {
compute(0, n - 1, 0, n - 1);
dp_before = dp_cur;
}
return dp_before[n - 1];
}
```
### Things to look out for
The greatest difficulty with Divide and Conquer DP problems is proving the
monotonicity of $opt$. One special case where this is true is when the cost function satisfies the quadrangle inequality, i.e., $C(a, c) + C(b, d) \leq C(a, d) + C(b, c)$ for all $a \leq b \leq c \leq d$.
Many Divide and Conquer DP problems can also be solved with the Convex Hull trick or vice-versa. It is useful to know and understand
both!
## Practice Problems
- [AtCoder - Yakiniku Restaurants](https://atcoder.jp/contests/arc067/tasks/arc067_d)
- [CodeForces - Ciel and Gondolas](https://codeforces.com/contest/321/problem/E) (Be careful with I/O!)
- [CodeForces - Levels And Regions](https://codeforces.com/problemset/problem/673/E)
- [CodeForces - Partition Game](https://codeforces.com/contest/1527/problem/E)
- [CodeForces - The Bakery](https://codeforces.com/problemset/problem/834/D)
- [CodeForces - Yet Another Minimization Problem](https://codeforces.com/contest/868/problem/F)
- [Codechef - CHEFAOR](https://www.codechef.com/problems/CHEFAOR)
- [CodeForces - GUARDS](https://codeforces.com/gym/103536/problem/A) (This is the exact problem in this article.)
- [Hackerrank - Guardians of the Lunatics](https://www.hackerrank.com/contests/ioi-2014-practice-contest-2/challenges/guardians-lunatics-ioi14)
- [Hackerrank - Mining](https://www.hackerrank.com/contests/world-codesprint-5/challenges/mining)
- [Kattis - Money (ACM ICPC World Finals 2017)](https://open.kattis.com/problems/money)
- [SPOJ - ADAMOLD](https://www.spoj.com/problems/ADAMOLD/)
- [SPOJ - LARMY](https://www.spoj.com/problems/LARMY/)
- [SPOJ - NKLEAVES](https://www.spoj.com/problems/NKLEAVES/)
- [Timus - Bicolored Horses](https://acm.timus.ru/problem.aspx?space=1&num=1167)
- [USACO - Circular Barn](http://www.usaco.org/index.php?page=viewproblem2&cpid=616)
- [UVA - Arranging Heaps](https://onlinejudge.org/external/125/12524.pdf)
- [UVA - Naming Babies](https://onlinejudge.org/external/125/12594.pdf)
## References
- [Quora Answer by Michael Levin](https://www.quora.com/What-is-divide-and-conquer-optimization-in-dynamic-programming)
- [Video Tutorial by "Sothe" the Algorithm Wolf](https://www.youtube.com/watch?v=wLXEWuDWnzI)
|
Divide and Conquer DP
|
---
title
maximum_average_segment
---
# Search the subarray with the maximum/minimum sum
Here, we consider the problem of finding a subarray with maximum sum, as well as some of its variations (including the algorithm for solving this problem online).
## Problem statement
Given an array of numbers $a[1 \ldots n]$. It is required to find a subarray $a[l \ldots r]$ with the maximal sum:
$$ \max_{ 1 \le l \le r \le n } \sum_{i=l}^{r} a[i].$$
For example, if all integers in array $a[]$ were non-negative, then the answer would be the array itself.
However, the solution is non-trivial when the array can contain both positive and negative numbers.
It is clear that the problem of finding the **minimum** subarray is essentially the same, you just need to change the signs of all numbers.
## Algorithm 1
Here we consider an almost obvious algorithm. (Next, we'll look at another algorithm, which is a little harder to come up with, but its implementation is even shorter.)
### Algorithm description
The algorithm is very simple.
We introduce for convenience the **notation**: $s[i] = \sum_{j=1}^{i} a[j]$. That is, the array $s[i]$ is an array of partial sums of array $a[]$. Also, set $s[0] = 0$.
Let us now iterate over the index $r = 1 \ldots n$, and learn how to quickly find the optimal $l$ for each current value $r$, at which the maximum sum is reached on the subarray $[l, r]$.
Formally, this means that for the current $r$ we need to find an $l$ (not exceeding $r$), so that the value of $s[r] - s[l-1]$ is maximal. After a trivial transformation, we can see that we need to find in the array $s[]$ a minimum on the segment $[0, r-1]$.
From here, we immediately obtain a solution: we simply store where the current minimum is in the array $s[]$. Using this minimum, we find the current optimal index $l$ in $O(1)$, and when moving from the current index $r$ to the next one, we simply update this minimum.
Obviously, this algorithm works in $O(n)$ and is asymptotically optimal.
### Implementation
To implement it, we don't even need to explicitly store an array of partial sums $s[]$ — we will only need the current element from it.
The implementation is given in 0-indexed arrays, not in 1-numbering as described above.
We first give a solution that finds a simple numerical answer without finding the indices of the desired segment:
```cpp
int ans = a[0], sum = 0, min_sum = 0;
for (int r = 0; r < n; ++r) {
sum += a[r];
ans = max(ans, sum - min_sum);
min_sum = min(min_sum, sum);
}
```
Now we give a full version of the solution, which additionally also finds the boundaries of the desired segment:
```cpp
int ans = a[0], ans_l = 0, ans_r = 0;
int sum = 0, min_sum = 0, min_pos = -1;
for (int r = 0; r < n; ++r) {
sum += a[r];
int cur = sum - min_sum;
if (cur > ans) {
ans = cur;
ans_l = min_pos + 1;
ans_r = r;
}
if (sum < min_sum) {
min_sum = sum;
min_pos = r;
}
}
```
## Algorithm 2
Here we consider a different algorithm. It is a little more difficult to understand, but it is more elegant than the above, and its implementation is a little bit shorter. This algorithm was proposed by Jay Kadane in 1984.
### Algorithm description
The algorithm itself is as follows. Let's go through the array and accumulate the current partial sum in some variable $s$. If at some point $s$ is negative, we just assign $s=0$. It is argued that the maximum all the values that the variable $s$ is assigned to during the algorithm will be the answer to the problem.
**Proof:**
Consider the first index when the sum of $s$ becomes negative. This means that starting with a zero partial sum, we eventually obtain a negative partial sum — so this whole prefix of the array, as well as any suffix, has a negative sum. Therefore, this subarray never contributes to the partial sum of any subarray of which it is a prefix, and can simply be dropped.
However, this is not enough to prove the algorithm. In the algorithm, we are actually limited in finding the answer only to such segments that begin immediately after the places when $s<0$ happened.
But, in fact, consider an arbitrary segment $[l, r]$, and $l$ is not in such a "critical" position (i.e. $l > p+1$, where $p$ is the last such position, in which $s<0$). Since the last critical position is strictly earlier than in $l-1$, it turns out that the sum of $a[p+1 \ldots l-1]$ is non-negative. This means that by moving $l$ to position $p+1$, we will increase the answer or, in extreme cases, we will not change it.
One way or another, it turns out that when searching for an answer, you can limit yourself to only segments that begin immediately after the positions in which $s<0$ appeared. This proves that the algorithm is correct.
### Implementation
As in algorithm 1, we first gave a simplified implementation that looks for only a numerical answer without finding the boundaries of the desired segment:
```cpp
int ans = a[0], sum = 0;
for (int r = 0; r < n; ++r) {
sum += a[r];
ans = max(ans, sum);
sum = max(sum, 0);
}
```
A complete solution, maintaining the indexes of the boundaries of the corresponding segment:
```cpp
int ans = a[0], ans_l = 0, ans_r = 0;
int sum = 0, minus_pos = -1;
for (int r = 0; r < n; ++r) {
sum += a[r];
if (sum > ans) {
ans = sum;
ans_l = minus_pos + 1;
ans_r = r;
}
if (sum < 0) {
sum = 0;
minus_pos = r;
}
}
```
## Related tasks
### Finding the maximum/minimum subarray with constraints
If the problem condition imposes additional restrictions on the required segment $[l, r]$ (for example, that the length $r-l+1$ of the segment must be within the specified limits), then the described algorithm is likely to be easily generalized to these cases — anyway, the problem will still be to find the minimum in the array $s[]$ with the specified additional restrictions.
### Two-dimensional case of the problem: search for maximum/minimum submatrix
The problem described in this article is naturally generalized to large dimensions. For example, in a two-dimensional case, it turns into a search for such a submatrix $[l_1 \ldots r_1, l_2 \ldots r_2]$ of a given matrix, which has the maximum sum of numbers in it.
Using the solution for the one-dimensional case, it is easy to obtain a solution in $O(n^3)$ for the two-dimensions case:
we iterate over all possible values of $l_1$ and $r_1$, and calculate the sums from $l_1$ to $r_1$ in each row of the matrix. Now we have the one-dimensional problem of finding the indices $l_2$ and $r_2$ in this array, which can already be solved in linear time.
**Faster** algorithms for solving this problem are known, but they are not much faster than $O(n^3)$, and are very complex (so complex that many of them are inferior to the trivial algorithm for all reasonable constraints by the hidden constant). Currently, the best known algorithm works in $O\left(n^3 \frac{ \log^3 \log n }{ \log^2 n} \right)$ time (T. Chan 2007 "More algorithms for all-pairs shortest paths in weighted graphs")
This algorithm by Chan, as well as many other results in this area, actually describe **fast matrix multiplication** (where matrix multiplication means modified multiplication: minimum is used instead of addition, and addition is used instead of multiplication). The problem of finding the submatrix with the largest sum can be reduced to the problem of finding the shortest paths between all pairs of vertices, and this problem, in turn, can be reduced to such a multiplication of matrices.
### Search for a subarray with a maximum/minimum average
This problem lies in finding such a segment $a[l, r]$, such that the average value is maximal:
$$ \max_{l \le r} \frac{ 1 }{ r-l+1 } \sum_{i=l}^{r} a[i].$$
Of course, if no other conditions are imposed on the required segment $[l, r]$, then the solution will always be a segment of length $1$ at the maximum element of the array.
The problem only makes sense, if there are additional restrictions (for example, the length of the desired segment is bounded below).
In this case, we apply the **standard technique** when working with the problems of the average value: we will select the desired maximum average value by **binary search**.
To do this, we need to learn how to solve the following subproblem: given the number $x$, and we need to check whether there is a subarray of array $a[]$ (of course, satisfying all additional constraints of the problem), where the average value is greater than $x$.
To solve this subproblem, subtract $x$ from each element of array $a[]$. Then our subproblem actually turns into this one: whether or not there are positive sum subarrays in this array. And we already know how to solve this problem.
Thus, we obtained the solution for the asymptotic $O(T(n) \log W)$, where $W$ is the required accuracy, $T(n)$ is the time of solving the subtask for an array of length $n$ (which may vary depending on the specific additional restrictions imposed).
### Solving the online problem
The condition of the problem is as follows: given an array of $n$ numbers, and a number $L$. There are queries of the form $(l,r)$, and in response to each query, it is required to find a subarray of the segment $[l, r]$ of length not less than $L$ with the maximum possible arithmetic mean.
The algorithm for solving this problem is quite complex. KADR (Yaroslav Tverdokhleb) described his algorithm on the [Russian forum](http://e-maxx.ru/forum/viewtopic.php?id=410).
|
---
title
maximum_average_segment
---
# Search the subarray with the maximum/minimum sum
Here, we consider the problem of finding a subarray with maximum sum, as well as some of its variations (including the algorithm for solving this problem online).
## Problem statement
Given an array of numbers $a[1 \ldots n]$. It is required to find a subarray $a[l \ldots r]$ with the maximal sum:
$$ \max_{ 1 \le l \le r \le n } \sum_{i=l}^{r} a[i].$$
For example, if all integers in array $a[]$ were non-negative, then the answer would be the array itself.
However, the solution is non-trivial when the array can contain both positive and negative numbers.
It is clear that the problem of finding the **minimum** subarray is essentially the same, you just need to change the signs of all numbers.
## Algorithm 1
Here we consider an almost obvious algorithm. (Next, we'll look at another algorithm, which is a little harder to come up with, but its implementation is even shorter.)
### Algorithm description
The algorithm is very simple.
We introduce for convenience the **notation**: $s[i] = \sum_{j=1}^{i} a[j]$. That is, the array $s[i]$ is an array of partial sums of array $a[]$. Also, set $s[0] = 0$.
Let us now iterate over the index $r = 1 \ldots n$, and learn how to quickly find the optimal $l$ for each current value $r$, at which the maximum sum is reached on the subarray $[l, r]$.
Formally, this means that for the current $r$ we need to find an $l$ (not exceeding $r$), so that the value of $s[r] - s[l-1]$ is maximal. After a trivial transformation, we can see that we need to find in the array $s[]$ a minimum on the segment $[0, r-1]$.
From here, we immediately obtain a solution: we simply store where the current minimum is in the array $s[]$. Using this minimum, we find the current optimal index $l$ in $O(1)$, and when moving from the current index $r$ to the next one, we simply update this minimum.
Obviously, this algorithm works in $O(n)$ and is asymptotically optimal.
### Implementation
To implement it, we don't even need to explicitly store an array of partial sums $s[]$ — we will only need the current element from it.
The implementation is given in 0-indexed arrays, not in 1-numbering as described above.
We first give a solution that finds a simple numerical answer without finding the indices of the desired segment:
```cpp
int ans = a[0], sum = 0, min_sum = 0;
for (int r = 0; r < n; ++r) {
sum += a[r];
ans = max(ans, sum - min_sum);
min_sum = min(min_sum, sum);
}
```
Now we give a full version of the solution, which additionally also finds the boundaries of the desired segment:
```cpp
int ans = a[0], ans_l = 0, ans_r = 0;
int sum = 0, min_sum = 0, min_pos = -1;
for (int r = 0; r < n; ++r) {
sum += a[r];
int cur = sum - min_sum;
if (cur > ans) {
ans = cur;
ans_l = min_pos + 1;
ans_r = r;
}
if (sum < min_sum) {
min_sum = sum;
min_pos = r;
}
}
```
## Algorithm 2
Here we consider a different algorithm. It is a little more difficult to understand, but it is more elegant than the above, and its implementation is a little bit shorter. This algorithm was proposed by Jay Kadane in 1984.
### Algorithm description
The algorithm itself is as follows. Let's go through the array and accumulate the current partial sum in some variable $s$. If at some point $s$ is negative, we just assign $s=0$. It is argued that the maximum all the values that the variable $s$ is assigned to during the algorithm will be the answer to the problem.
**Proof:**
Consider the first index when the sum of $s$ becomes negative. This means that starting with a zero partial sum, we eventually obtain a negative partial sum — so this whole prefix of the array, as well as any suffix, has a negative sum. Therefore, this subarray never contributes to the partial sum of any subarray of which it is a prefix, and can simply be dropped.
However, this is not enough to prove the algorithm. In the algorithm, we are actually limited in finding the answer only to such segments that begin immediately after the places when $s<0$ happened.
But, in fact, consider an arbitrary segment $[l, r]$, and $l$ is not in such a "critical" position (i.e. $l > p+1$, where $p$ is the last such position, in which $s<0$). Since the last critical position is strictly earlier than in $l-1$, it turns out that the sum of $a[p+1 \ldots l-1]$ is non-negative. This means that by moving $l$ to position $p+1$, we will increase the answer or, in extreme cases, we will not change it.
One way or another, it turns out that when searching for an answer, you can limit yourself to only segments that begin immediately after the positions in which $s<0$ appeared. This proves that the algorithm is correct.
### Implementation
As in algorithm 1, we first gave a simplified implementation that looks for only a numerical answer without finding the boundaries of the desired segment:
```cpp
int ans = a[0], sum = 0;
for (int r = 0; r < n; ++r) {
sum += a[r];
ans = max(ans, sum);
sum = max(sum, 0);
}
```
A complete solution, maintaining the indexes of the boundaries of the corresponding segment:
```cpp
int ans = a[0], ans_l = 0, ans_r = 0;
int sum = 0, minus_pos = -1;
for (int r = 0; r < n; ++r) {
sum += a[r];
if (sum > ans) {
ans = sum;
ans_l = minus_pos + 1;
ans_r = r;
}
if (sum < 0) {
sum = 0;
minus_pos = r;
}
}
```
## Related tasks
### Finding the maximum/minimum subarray with constraints
If the problem condition imposes additional restrictions on the required segment $[l, r]$ (for example, that the length $r-l+1$ of the segment must be within the specified limits), then the described algorithm is likely to be easily generalized to these cases — anyway, the problem will still be to find the minimum in the array $s[]$ with the specified additional restrictions.
### Two-dimensional case of the problem: search for maximum/minimum submatrix
The problem described in this article is naturally generalized to large dimensions. For example, in a two-dimensional case, it turns into a search for such a submatrix $[l_1 \ldots r_1, l_2 \ldots r_2]$ of a given matrix, which has the maximum sum of numbers in it.
Using the solution for the one-dimensional case, it is easy to obtain a solution in $O(n^3)$ for the two-dimensions case:
we iterate over all possible values of $l_1$ and $r_1$, and calculate the sums from $l_1$ to $r_1$ in each row of the matrix. Now we have the one-dimensional problem of finding the indices $l_2$ and $r_2$ in this array, which can already be solved in linear time.
**Faster** algorithms for solving this problem are known, but they are not much faster than $O(n^3)$, and are very complex (so complex that many of them are inferior to the trivial algorithm for all reasonable constraints by the hidden constant). Currently, the best known algorithm works in $O\left(n^3 \frac{ \log^3 \log n }{ \log^2 n} \right)$ time (T. Chan 2007 "More algorithms for all-pairs shortest paths in weighted graphs")
This algorithm by Chan, as well as many other results in this area, actually describe **fast matrix multiplication** (where matrix multiplication means modified multiplication: minimum is used instead of addition, and addition is used instead of multiplication). The problem of finding the submatrix with the largest sum can be reduced to the problem of finding the shortest paths between all pairs of vertices, and this problem, in turn, can be reduced to such a multiplication of matrices.
### Search for a subarray with a maximum/minimum average
This problem lies in finding such a segment $a[l, r]$, such that the average value is maximal:
$$ \max_{l \le r} \frac{ 1 }{ r-l+1 } \sum_{i=l}^{r} a[i].$$
Of course, if no other conditions are imposed on the required segment $[l, r]$, then the solution will always be a segment of length $1$ at the maximum element of the array.
The problem only makes sense, if there are additional restrictions (for example, the length of the desired segment is bounded below).
In this case, we apply the **standard technique** when working with the problems of the average value: we will select the desired maximum average value by **binary search**.
To do this, we need to learn how to solve the following subproblem: given the number $x$, and we need to check whether there is a subarray of array $a[]$ (of course, satisfying all additional constraints of the problem), where the average value is greater than $x$.
To solve this subproblem, subtract $x$ from each element of array $a[]$. Then our subproblem actually turns into this one: whether or not there are positive sum subarrays in this array. And we already know how to solve this problem.
Thus, we obtained the solution for the asymptotic $O(T(n) \log W)$, where $W$ is the required accuracy, $T(n)$ is the time of solving the subtask for an array of length $n$ (which may vary depending on the specific additional restrictions imposed).
### Solving the online problem
The condition of the problem is as follows: given an array of $n$ numbers, and a number $L$. There are queries of the form $(l,r)$, and in response to each query, it is required to find a subarray of the segment $[l, r]$ of length not less than $L$ with the maximum possible arithmetic mean.
The algorithm for solving this problem is quite complex. KADR (Yaroslav Tverdokhleb) described his algorithm on the [Russian forum](http://e-maxx.ru/forum/viewtopic.php?id=410).
|
Search the subarray with the maximum/minimum sum
|
---
title
joseph_problem
---
# Josephus Problem
## Statement
We are given the natural numbers $n$ and $k$.
All natural numbers from $1$ to $n$ are written in a circle.
First, count the $k$-th number starting from the first one and delete it.
Then $k$ numbers are counted starting from the next one and the $k$-th one is removed again, and so on.
The process stops when one number remains.
It is required to find the last number.
This task was set by **Flavius Josephus** in the 1st century (though in a somewhat narrower formulation: for $k = 2$).
This problem can be solved by modeling the procedure.
Brute force modeling will work $O(n^{2})$. Using a [Segment Tree](/data_structures/segment_tree.html), we can improve it to $O(n \log n)$.
We want something better though.
## Modeling a $O(n)$ solution
We will try to find a pattern expressing the answer for the problem $J_{n, k}$ through the solution of the previous problems.
Using brute force modeling we can construct a table of values, for example, the following:
$$\begin{array}{ccccccccccc}
n\setminus k & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
2 & 2 & 1 & 2 & 1 & 2 & 1 & 2 & 1 & 2 & 1 \\
3 & 3 & 3 & 2 & 2 & 1 & 1 & 3 & 3 & 2 & 2 \\
4 & 4 & 1 & 1 & 2 & 2 & 3 & 2 & 3 & 3 & 4 \\
5 & 5 & 3 & 4 & 1 & 2 & 4 & 4 & 1 & 2 & 4 \\
6 & 6 & 5 & 1 & 5 & 1 & 4 & 5 & 3 & 5 & 2 \\
7 & 7 & 7 & 4 & 2 & 6 & 3 & 5 & 4 & 7 & 5 \\
8 & 8 & 1 & 7 & 6 & 3 & 1 & 4 & 4 & 8 & 7 \\
9 & 9 & 3 & 1 & 1 & 8 & 7 & 2 & 3 & 8 & 8 \\
10 & 10 & 5 & 4 & 5 & 3 & 3 & 9 & 1 & 7 & 8 \\
\end{array}$$
And here we can clearly see the following **pattern**:
$$J_{n,k} = \left( (J_{n-1,k} + k - 1) \bmod n \right) + 1$$
$$J_{1,k} = 1$$
Here, 1-indexing makes for a somewhat messy formula; if you instead number the positions from 0, you get a very elegant formula:
$$J_{n,k} = (J_{n-1,k} + k) \bmod n$$
So, we found a solution to the problem of Josephus, working in $O(n)$ operations.
## Implementation
Simple **recursive implementation** (in 1-indexing)
```{.cpp file=josephus_rec}
int josephus(int n, int k) {
return n > 1 ? (josephus(n-1, k) + k - 1) % n + 1 : 1;
}
```
**Non-recursive form** :
```{.cpp file=josephus_iter}
int josephus(int n, int k) {
int res = 0;
for (int i = 1; i <= n; ++i)
res = (res + k) % i;
return res + 1;
}
```
This formula can also be found analytically.
Again here we assume 0-indexing.
After we delete the first number, we have $n-1$ numbers left.
When we repeat the procedure, we will start with the number that had originally the index $k \bmod n$.
$J_{n-1, k}$ would be the answer for the remaining circle, if we start counting at $0$, but because we actually start with $k$ we have $J_{n, k} = (J_{n-1,k} + k) \ \bmod n$.
## Modeling a $O(k \log n)$ solution
For relatively small $k$ we can come up with a better solution than the above recursive solution in $O(n)$.
If $k$ is a lot smaller than $n$, then we can delete multiple numbers ($\lfloor \frac{n}{k} \rfloor$) in one run without looping over.
Afterwards we have $n - \lfloor \frac{n}{k} \rfloor$ numbers left, and we start with the $(\lfloor \frac{n}{k} \rfloor \cdot k)$-th number.
So we have to shift by that many.
We can notice that $\lfloor \frac{n}{k} \rfloor \cdot k$ is simply $-n \bmod k$.
And because we removed every $k$-th number, we have to add the number of numbers that we removed before the result index.
Which we can compute by dividing the result index by $k - 1$.
Also, we need to handle the case when $n$ becomes less than $k$. In this case, the above optimization would cause an infinite loop.
**Implementation** (for convenience in 0-indexing):
```{.cpp file=josephus_fast0}
int josephus(int n, int k) {
if (n == 1)
return 0;
if (k == 1)
return n-1;
if (k > n)
return (josephus(n-1, k) + k) % n;
int cnt = n / k;
int res = josephus(n - cnt, k);
res -= n % k;
if (res < 0)
res += n;
else
res += res / (k - 1);
return res;
}
```
Let us estimate the **complexity** of this algorithm. Immediately note that the case $n < k$ is analyzed by the old solution, which will work in this case for $O(k)$. Now consider the algorithm itself. In fact, after every iteration, instead of $n$ numbers, we are left with $n \left( 1 - \frac{1}{k} \right)$ numbers, so the total number of iterations $x$ of the algorithm can be found roughly from the following equation:
$$ n \left(1 - \frac{1}{k} \right) ^ x = 1, $$
on taking logarithm on both sides, we obtain:
$$\ln n + x \ln \left(1 - \frac{1}{k} \right) = 0,$$
$$x = - \frac{\ln n}{\ln \left(1 - \frac{1}{k} \right)},$$
using the decomposition of the logarithm into Taylor series, we obtain an approximate estimate:
$$x \approx k \ln n$$
Thus, the complexity of the algorithm is actually $O (k \log n)$.
## Analytical solution for $k = 2$
In this particular case (in which this task was set by Josephus Flavius) the problem is solved much easier.
In the case of even $n$ we get that all even numbers will be crossed out, and then there will be a problem remaining for $\frac{n}{2}$, then the answer for $n$ will be obtained from the answer for $\frac{n}{2}$ by multiplying by two and subtracting one (by shifting positions):
$$ J_{2n, 2} = 2 J_{n, 2} - 1 $$
Similarly, in the case of an odd $n$, all even numbers will be crossed out, then the first number, and the problem for $\frac{n-1}{2}$ will remain, and taking into account the shift of positions, we obtain the second formula:
$$J_{2n+1,2} = 2 J_{n, 2} + 1 $$
We can use this recurrent dependency directly in our implementation. This pattern can be translated into another form: $J_{n, 2}$ represents a sequence of all odd numbers, "restarting" from one whenever $n$ turns out to be a power of two. This can be written as a single formula:
$$J_{n, 2} = 1 + 2 \left(n-2^{\lfloor \log_2 n \rfloor} \right)$$
## Analytical solution for $k > 2$
Despite the simple form of the problem and a large number of articles on this and related problems, a simple analytical representation of the solution of Josephus' problem has not yet been found. For small $k$, some formulas are derived, but apparently they are all difficult to apply in practice (for example, see Halbeisen, Hungerbuhler "The Josephus Problem" and Odlyzko, Wilf "Functional iteration and the Josephus problem").
|
---
title
joseph_problem
---
# Josephus Problem
## Statement
We are given the natural numbers $n$ and $k$.
All natural numbers from $1$ to $n$ are written in a circle.
First, count the $k$-th number starting from the first one and delete it.
Then $k$ numbers are counted starting from the next one and the $k$-th one is removed again, and so on.
The process stops when one number remains.
It is required to find the last number.
This task was set by **Flavius Josephus** in the 1st century (though in a somewhat narrower formulation: for $k = 2$).
This problem can be solved by modeling the procedure.
Brute force modeling will work $O(n^{2})$. Using a [Segment Tree](/data_structures/segment_tree.html), we can improve it to $O(n \log n)$.
We want something better though.
## Modeling a $O(n)$ solution
We will try to find a pattern expressing the answer for the problem $J_{n, k}$ through the solution of the previous problems.
Using brute force modeling we can construct a table of values, for example, the following:
$$\begin{array}{ccccccccccc}
n\setminus k & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
2 & 2 & 1 & 2 & 1 & 2 & 1 & 2 & 1 & 2 & 1 \\
3 & 3 & 3 & 2 & 2 & 1 & 1 & 3 & 3 & 2 & 2 \\
4 & 4 & 1 & 1 & 2 & 2 & 3 & 2 & 3 & 3 & 4 \\
5 & 5 & 3 & 4 & 1 & 2 & 4 & 4 & 1 & 2 & 4 \\
6 & 6 & 5 & 1 & 5 & 1 & 4 & 5 & 3 & 5 & 2 \\
7 & 7 & 7 & 4 & 2 & 6 & 3 & 5 & 4 & 7 & 5 \\
8 & 8 & 1 & 7 & 6 & 3 & 1 & 4 & 4 & 8 & 7 \\
9 & 9 & 3 & 1 & 1 & 8 & 7 & 2 & 3 & 8 & 8 \\
10 & 10 & 5 & 4 & 5 & 3 & 3 & 9 & 1 & 7 & 8 \\
\end{array}$$
And here we can clearly see the following **pattern**:
$$J_{n,k} = \left( (J_{n-1,k} + k - 1) \bmod n \right) + 1$$
$$J_{1,k} = 1$$
Here, 1-indexing makes for a somewhat messy formula; if you instead number the positions from 0, you get a very elegant formula:
$$J_{n,k} = (J_{n-1,k} + k) \bmod n$$
So, we found a solution to the problem of Josephus, working in $O(n)$ operations.
## Implementation
Simple **recursive implementation** (in 1-indexing)
```{.cpp file=josephus_rec}
int josephus(int n, int k) {
return n > 1 ? (josephus(n-1, k) + k - 1) % n + 1 : 1;
}
```
**Non-recursive form** :
```{.cpp file=josephus_iter}
int josephus(int n, int k) {
int res = 0;
for (int i = 1; i <= n; ++i)
res = (res + k) % i;
return res + 1;
}
```
This formula can also be found analytically.
Again here we assume 0-indexing.
After we delete the first number, we have $n-1$ numbers left.
When we repeat the procedure, we will start with the number that had originally the index $k \bmod n$.
$J_{n-1, k}$ would be the answer for the remaining circle, if we start counting at $0$, but because we actually start with $k$ we have $J_{n, k} = (J_{n-1,k} + k) \ \bmod n$.
## Modeling a $O(k \log n)$ solution
For relatively small $k$ we can come up with a better solution than the above recursive solution in $O(n)$.
If $k$ is a lot smaller than $n$, then we can delete multiple numbers ($\lfloor \frac{n}{k} \rfloor$) in one run without looping over.
Afterwards we have $n - \lfloor \frac{n}{k} \rfloor$ numbers left, and we start with the $(\lfloor \frac{n}{k} \rfloor \cdot k)$-th number.
So we have to shift by that many.
We can notice that $\lfloor \frac{n}{k} \rfloor \cdot k$ is simply $-n \bmod k$.
And because we removed every $k$-th number, we have to add the number of numbers that we removed before the result index.
Which we can compute by dividing the result index by $k - 1$.
Also, we need to handle the case when $n$ becomes less than $k$. In this case, the above optimization would cause an infinite loop.
**Implementation** (for convenience in 0-indexing):
```{.cpp file=josephus_fast0}
int josephus(int n, int k) {
if (n == 1)
return 0;
if (k == 1)
return n-1;
if (k > n)
return (josephus(n-1, k) + k) % n;
int cnt = n / k;
int res = josephus(n - cnt, k);
res -= n % k;
if (res < 0)
res += n;
else
res += res / (k - 1);
return res;
}
```
Let us estimate the **complexity** of this algorithm. Immediately note that the case $n < k$ is analyzed by the old solution, which will work in this case for $O(k)$. Now consider the algorithm itself. In fact, after every iteration, instead of $n$ numbers, we are left with $n \left( 1 - \frac{1}{k} \right)$ numbers, so the total number of iterations $x$ of the algorithm can be found roughly from the following equation:
$$ n \left(1 - \frac{1}{k} \right) ^ x = 1, $$
on taking logarithm on both sides, we obtain:
$$\ln n + x \ln \left(1 - \frac{1}{k} \right) = 0,$$
$$x = - \frac{\ln n}{\ln \left(1 - \frac{1}{k} \right)},$$
using the decomposition of the logarithm into Taylor series, we obtain an approximate estimate:
$$x \approx k \ln n$$
Thus, the complexity of the algorithm is actually $O (k \log n)$.
## Analytical solution for $k = 2$
In this particular case (in which this task was set by Josephus Flavius) the problem is solved much easier.
In the case of even $n$ we get that all even numbers will be crossed out, and then there will be a problem remaining for $\frac{n}{2}$, then the answer for $n$ will be obtained from the answer for $\frac{n}{2}$ by multiplying by two and subtracting one (by shifting positions):
$$ J_{2n, 2} = 2 J_{n, 2} - 1 $$
Similarly, in the case of an odd $n$, all even numbers will be crossed out, then the first number, and the problem for $\frac{n-1}{2}$ will remain, and taking into account the shift of positions, we obtain the second formula:
$$J_{2n+1,2} = 2 J_{n, 2} + 1 $$
We can use this recurrent dependency directly in our implementation. This pattern can be translated into another form: $J_{n, 2}$ represents a sequence of all odd numbers, "restarting" from one whenever $n$ turns out to be a power of two. This can be written as a single formula:
$$J_{n, 2} = 1 + 2 \left(n-2^{\lfloor \log_2 n \rfloor} \right)$$
## Analytical solution for $k > 2$
Despite the simple form of the problem and a large number of articles on this and related problems, a simple analytical representation of the solution of Josephus' problem has not yet been found. For small $k$, some formulas are derived, but apparently they are all difficult to apply in practice (for example, see Halbeisen, Hungerbuhler "The Josephus Problem" and Odlyzko, Wilf "Functional iteration and the Josephus problem").
|
Josephus Problem
|
---
title
stern_brocot_farey
---
# The Stern-Brocot tree and Farey sequences
## Stern-Brocot tree
The Stern-Brocot tree is an elegant construction to represent the set of all positive fractions. It was independently discovered by German mathematician Moritz Stern in 1858 and by French watchmaker Achille Brocot in 1861. However, some sources attribute the discovery to ancient Greek mathematician Eratosthenes.
The construction starts at the zeroth iteration with the two fractions
$$
\frac{0}{1}, \frac{1}{0}
$$
where it should be noted that the second quantity is not strictly a fraction, but it can be interpreted as an irreducible fraction representing infinity.
At every subsequent iteration, consider all adjacent fractions $\frac{a}{b}$ and $\frac{c}{d}$ and insert their [mediant](https://en.wikipedia.org/wiki/Mediant_(mathematics)) $\frac{a+c}{b+d}$ between them.
The first few iterations look like this:
$$
\begin{array}{c}
\dfrac{0}{1}, \dfrac{1}{1}, \dfrac{1}{0} \\
\dfrac{0}{1}, \dfrac{1}{2}, \dfrac{1}{1}, \dfrac{2}{1}, \dfrac{1}{0} \\
\dfrac{0}{1}, \dfrac{1}{3}, \dfrac{1}{2}, \dfrac{2}{3}, \dfrac{1}{1}, \dfrac{3}{2}, \dfrac{2}{1}, \dfrac{3}{1}, \dfrac{1}{0}
\end{array}
$$
Continuing this process to infinity this covers *all* positive fractions. Additionally, all fractions will be *unique* and *irreducible*. Finally, the fractions will also appear in ascending order.
Before proving these properties, let us actually show a visualization of the Stern-Brocot tree, rather than the list representation. Every fraction in the tree has two children. Each child is the mediant of the closest ancestor on the left and closest ancestor to the right.
<center></center>
## Proofs
**Ordering.** Proving ordering is simple. We note that the mediant of two fractions is always in-between the fractions
$$
\frac{a}{b} \le \frac{a+c}{b+d} \le \frac{c}{d}
$$
given that
$$
\frac{a}{b} \le \frac{c}{d}.
$$
The two inequalities can be easily shown by rewriting the fractions with common denominators.
As the ordering is ascending in the zeroth iteration, it will be maintained at every subsequent iteration.
**Irreducibility.** To prove this we will show that for any two adjacent fractions $\frac{a}{b}$ and $\frac{c}{d}$ we have that
$$
bc - ad = 1.
$$
Recall that a Diophantine equation with two variables $ax+by=c$ has a solution iff $c$ is a multiple of $\gcd(a,b)$. In our case this implies that $\gcd(a,b) = \gcd(c,d) = 1$, which is what we want to show.
Clearly at the zeroth iteration $bc - ad = 1$. What remains to be shown is that mediants retain this property.
Assume our two adjacent fractions uphold $bc - ad = 1$, after the mediant is added to the list
$$
\frac{a}{b}, \frac{a+c}{b+d}, \frac{c}{d}
$$
the new expressions become
$$\begin{align}
b(a+c) - a(b+d) &= 1 \\
c(b+d) - d(a+c) &= 1
\end{align}$$
which, using that $bc-ad=1$, can be easily shown to be true.
From this we see that the property is always maintained and thus all fractions are irreducible.
**The presence of all fractions.** This proof is closely related to locating a fraction in the Stern-Brocot tree. From the ordering property we have that left subtree of a fraction contains only fractions smaller than the parent fraction, and the right subtree contains only fractions larger than the parent fraction. This means we can search for a fraction by traversing the tree from the root, going left if the target is smaller than the fraction and going right if the target is larger.
Pick an arbitrary positive target fraction $\frac{x}{y}$. It is obviously between $\frac{0}{1}$ and $\frac{1}{0}$, so the only way for the fraction to not be in the tree is if it takes an infinite number of steps to get to it.
If that is the case we would at all iterations have
$$
\frac{a}{b} \lt \frac{x}{y} \lt \frac{c}{d}
$$
which (using the fact than an integer $z \gt 0 \iff z \ge 1$) can be rewritten as
$$
\begin{align}
bx - ay &\ge 1 \\
cy - dx &\ge 1.
\end{align}
$$
Now multiply the first inequality by $c+d$ and the second with $a+b$ and add them to get
$$
(c+d)(bx - ay) + (a+b)(cy - dx) \ge a+b+c+d.
$$
Expanding this and using the previously shown property $bc-ad=1$ we get that
$$
x+y \ge a+b+c+d.
$$
And given that at every iteration at least one of $a,b,c,d$ will increase, the fraction searching process will contain no more than $x+y$ iterations. This contradicts the assumption that the path to $\frac{x}{y}$ was infinite and hence $\frac{x}{y}$ must be part of the tree.
## Tree Building Algorithm
To build any subtree of the Stern-Brocot tree, it suffices to know the left and right ancestor. On the first level, the left and right ancestors are $\frac{0}{1}$ and $\frac{1}{0}$ respectively. Using these, we calculate the mediant and proceed one level deeper, with the mediant replacing the right ancestor in the left subtree, and vice versa.
This pseudocode tries to build the entire infinite tree:
```cpp
void build(int a = 0, int b = 1, int c = 1, int d = 0, int level = 1) {
int x = a + c, y = b + d;
... output the current fraction x/y at the current level in the tree
build(a, b, x, y, level + 1);
build(x, y, c, d, level + 1);
}
```
## Fraction Search Algorithm
The search algorithm was already described in the proof that all fractions appear in the tree, but we will repeat it here. The algorithm is a binary search algorithm. Initially we stand at the root of the tree and we compare our target with the current fraction. If they are the same we are done and stop the process. If our target is smaller we move to the left child, otherwise we move to the right child.
### Naive search
Here is an implementation that returns the path to a given fraction $\frac{p}{q}$ as a sequence of `'L'` and `'R'` characters, meaning traversal to the left and right child respectively. This sequence of characters uniquely defines all positive fractions and is called the Stern-Brocot number system.
```cpp
string find(int p, int q) {
int pL = 0, qL = 1;
int pR = 1, qR = 0;
int pM = 1, qM = 1;
string res;
while(pM != p || qM != q) {
if(p * qM < pM * q) {
res += 'L';
tie(pR, qR) = {pM, qM};
} else {
res += 'R';
tie(pL, qL) = {pM, qM};
}
tie(pM, qM) = pair{pL + pR, qL + qR};
}
return res;
}
```
Irrational numbers in the Stern-Brocot number system corresponds to infinite sequences of characters. Along the endless path towards the irrational number the algorithm will find reduced fractions with gradually increasing denominators that provides increasingly better approximations of the irrational number. So by taking a prefix of the infinite sequence approximations with any desired precision can be achieved. This application is important in watch-making, which explains why the tree was discovered in that domain.
Note that for a fraction $\frac{p}{q}$, the length of the resulting sequence could be as large as $O(p+q)$, for example when the fraction is of form $\frac{p}{1}$. This means that the algorithm above **should not be used, unless this is an acceptable complexity**!
### Logarithmic search
Fortunately, it is possible to enhance the algorithm above to guarantee $O(\log (p+q))$ complexity. For this we should note that if the current boundary fractions are $\frac{p_L}{q_L}$ and $\frac{p_R}{q_R}$, then by doing $a$ steps to the right we move to the fraction $\frac{p_L + a p_R}{q_L + a q_R}$, and by doing $a$ steps to the left, we move to the fraction $\frac{a p_L + p_R}{a q_L + q_R}$.
Therefore, instead of doing steps of `L` or `R` one by one, we can do $k$ steps in the same direction at once, after which we would switch to going into other direction, and so on. In this way, we can find the path to the fraction $\frac{p}{q}$ as its run-length encoding.
As the directions alternate this way, we will always know which one to take. So, for convenience we may represent a path to a fraction $\frac{p}{q}$ as a sequence of fractions
$$
\frac{p_0}{q_0}, \frac{p_1}{q_1}, \frac{p_2}{q_2}, \dots, \frac{p_n}{q_n}, \frac{p_{n+1}}{q_{n+1}} = \frac{p}{q}
$$
such that $\frac{p_{k-1}}{q_{k-1}}$ and $\frac{p_k}{q_k}$ are the boundaries of the search interval on the $k$-th step, starting with $\frac{p_0}{q_0} = \frac{0}{1}$ and $\frac{p_1}{q_1} = \frac{1}{0}$. Then, after the $k$-th step we move to a fraction
$$
\frac{p_{k+1}}{q_{k+1}} = \frac{p_{k-1} + a_k p_k}{q_{k-1} + a_k q_k},
$$
where $a_k$ is a positive integer number. If you're familiar with [continued fractions](), you would recognize that the sequence $\frac{p_i}{q_i}$ is the sequence of the convergent fractions of $\frac{p}{q}$ and the sequence $[a_1; a_2, \dots, a_{n}, 1]$ represents the continued fraction of $\frac{p}{q}$.
This allows to find the run-length encoding of the path to $\frac{p}{q}$ in the manner which follows the algorithm for computing continued fraction representation of the fraction $\frac{p}{q}$:
```cpp
auto find(int p, int q) {
bool right = true;
vector<pair<int, char>> res;
while(q) {
res.emplace_back(p / q, right ? 'R' : 'L');
tie(p, q) = pair{q, p % q};
right ^= 1;
}
res.back().first--;
return res;
}
```
However, this approach only works if we already know $\frac{p}{q}$ and want to find its place in the Stern-Brocot tree.
On practice, it is often the case that $\frac{p}{q}$ is not known in advance, but we are able to check for specific $\frac{x}{y}$ whether $\frac{x}{y} < \frac{p}{q}$.
Knowing this, we can emulate the search on Stern-Brocot tree by maintaining the current boundaries $\frac{p_{k-1}}{q_{k-1}}$ and $\frac{p_k}{q_k}$, and finding each $a_k$ via binary search. The algorithm then is a bit more technical and potentially have a complexity of $O(\log^2(x+y))$, unless the problem formulation allows you to find $a_k$ faster (for example, using `floor` of some known expression).
## Farey Sequence
The Farey sequence of order $n$ is the sorted sequence of fractions between $0$ and $1$ whose denominators do not exceed $n$.
The sequences are named after English geologist John Farey, who in 1816 conjectured that any fraction in a Farey sequence is the mediant of its neighbors. This was proven some time later by Cauchy, but independent of both of them, the mathematician Haros had come to almost the same conclusion in 1802.
The Farey sequences have many interesting properties on their own, but the connection to the Stern-Brocot tree is the most obvious. In fact, the Farey sequences can be obtained by trimming branches from the tree.
From the algorithm for building the Stern-Brocot tree, we get an algorithm for the Farey sequences. Start with the list of fractions $\frac{0}{1}, \frac{1}{0}$. At every subsequent iteration, insert the mediant only if the denominator does not exceed $n$. At some point the list will stop changing and the desired Farey sequence will have been found.
### Length of a Farey Sequence
A Farey sequence of order $n$ contains all elements of the Farey sequence of order $n-1$ as well as all irreducible fractions with denominator $n$, but the latter is just the totient $\varphi(n)$. So the length $L_n$ of the Farey sequence of order $n$ is
$$
L_n = L_{n-1} + \varphi(n)
$$
or equivalently, by unraveling the recursion we get
$$
L_n = 1 + \sum_{k=1}^n \varphi(k).
$$
|
---
title
stern_brocot_farey
---
# The Stern-Brocot tree and Farey sequences
## Stern-Brocot tree
The Stern-Brocot tree is an elegant construction to represent the set of all positive fractions. It was independently discovered by German mathematician Moritz Stern in 1858 and by French watchmaker Achille Brocot in 1861. However, some sources attribute the discovery to ancient Greek mathematician Eratosthenes.
The construction starts at the zeroth iteration with the two fractions
$$
\frac{0}{1}, \frac{1}{0}
$$
where it should be noted that the second quantity is not strictly a fraction, but it can be interpreted as an irreducible fraction representing infinity.
At every subsequent iteration, consider all adjacent fractions $\frac{a}{b}$ and $\frac{c}{d}$ and insert their [mediant](https://en.wikipedia.org/wiki/Mediant_(mathematics)) $\frac{a+c}{b+d}$ between them.
The first few iterations look like this:
$$
\begin{array}{c}
\dfrac{0}{1}, \dfrac{1}{1}, \dfrac{1}{0} \\
\dfrac{0}{1}, \dfrac{1}{2}, \dfrac{1}{1}, \dfrac{2}{1}, \dfrac{1}{0} \\
\dfrac{0}{1}, \dfrac{1}{3}, \dfrac{1}{2}, \dfrac{2}{3}, \dfrac{1}{1}, \dfrac{3}{2}, \dfrac{2}{1}, \dfrac{3}{1}, \dfrac{1}{0}
\end{array}
$$
Continuing this process to infinity this covers *all* positive fractions. Additionally, all fractions will be *unique* and *irreducible*. Finally, the fractions will also appear in ascending order.
Before proving these properties, let us actually show a visualization of the Stern-Brocot tree, rather than the list representation. Every fraction in the tree has two children. Each child is the mediant of the closest ancestor on the left and closest ancestor to the right.
<center></center>
## Proofs
**Ordering.** Proving ordering is simple. We note that the mediant of two fractions is always in-between the fractions
$$
\frac{a}{b} \le \frac{a+c}{b+d} \le \frac{c}{d}
$$
given that
$$
\frac{a}{b} \le \frac{c}{d}.
$$
The two inequalities can be easily shown by rewriting the fractions with common denominators.
As the ordering is ascending in the zeroth iteration, it will be maintained at every subsequent iteration.
**Irreducibility.** To prove this we will show that for any two adjacent fractions $\frac{a}{b}$ and $\frac{c}{d}$ we have that
$$
bc - ad = 1.
$$
Recall that a Diophantine equation with two variables $ax+by=c$ has a solution iff $c$ is a multiple of $\gcd(a,b)$. In our case this implies that $\gcd(a,b) = \gcd(c,d) = 1$, which is what we want to show.
Clearly at the zeroth iteration $bc - ad = 1$. What remains to be shown is that mediants retain this property.
Assume our two adjacent fractions uphold $bc - ad = 1$, after the mediant is added to the list
$$
\frac{a}{b}, \frac{a+c}{b+d}, \frac{c}{d}
$$
the new expressions become
$$\begin{align}
b(a+c) - a(b+d) &= 1 \\
c(b+d) - d(a+c) &= 1
\end{align}$$
which, using that $bc-ad=1$, can be easily shown to be true.
From this we see that the property is always maintained and thus all fractions are irreducible.
**The presence of all fractions.** This proof is closely related to locating a fraction in the Stern-Brocot tree. From the ordering property we have that left subtree of a fraction contains only fractions smaller than the parent fraction, and the right subtree contains only fractions larger than the parent fraction. This means we can search for a fraction by traversing the tree from the root, going left if the target is smaller than the fraction and going right if the target is larger.
Pick an arbitrary positive target fraction $\frac{x}{y}$. It is obviously between $\frac{0}{1}$ and $\frac{1}{0}$, so the only way for the fraction to not be in the tree is if it takes an infinite number of steps to get to it.
If that is the case we would at all iterations have
$$
\frac{a}{b} \lt \frac{x}{y} \lt \frac{c}{d}
$$
which (using the fact than an integer $z \gt 0 \iff z \ge 1$) can be rewritten as
$$
\begin{align}
bx - ay &\ge 1 \\
cy - dx &\ge 1.
\end{align}
$$
Now multiply the first inequality by $c+d$ and the second with $a+b$ and add them to get
$$
(c+d)(bx - ay) + (a+b)(cy - dx) \ge a+b+c+d.
$$
Expanding this and using the previously shown property $bc-ad=1$ we get that
$$
x+y \ge a+b+c+d.
$$
And given that at every iteration at least one of $a,b,c,d$ will increase, the fraction searching process will contain no more than $x+y$ iterations. This contradicts the assumption that the path to $\frac{x}{y}$ was infinite and hence $\frac{x}{y}$ must be part of the tree.
## Tree Building Algorithm
To build any subtree of the Stern-Brocot tree, it suffices to know the left and right ancestor. On the first level, the left and right ancestors are $\frac{0}{1}$ and $\frac{1}{0}$ respectively. Using these, we calculate the mediant and proceed one level deeper, with the mediant replacing the right ancestor in the left subtree, and vice versa.
This pseudocode tries to build the entire infinite tree:
```cpp
void build(int a = 0, int b = 1, int c = 1, int d = 0, int level = 1) {
int x = a + c, y = b + d;
... output the current fraction x/y at the current level in the tree
build(a, b, x, y, level + 1);
build(x, y, c, d, level + 1);
}
```
## Fraction Search Algorithm
The search algorithm was already described in the proof that all fractions appear in the tree, but we will repeat it here. The algorithm is a binary search algorithm. Initially we stand at the root of the tree and we compare our target with the current fraction. If they are the same we are done and stop the process. If our target is smaller we move to the left child, otherwise we move to the right child.
### Naive search
Here is an implementation that returns the path to a given fraction $\frac{p}{q}$ as a sequence of `'L'` and `'R'` characters, meaning traversal to the left and right child respectively. This sequence of characters uniquely defines all positive fractions and is called the Stern-Brocot number system.
```cpp
string find(int p, int q) {
int pL = 0, qL = 1;
int pR = 1, qR = 0;
int pM = 1, qM = 1;
string res;
while(pM != p || qM != q) {
if(p * qM < pM * q) {
res += 'L';
tie(pR, qR) = {pM, qM};
} else {
res += 'R';
tie(pL, qL) = {pM, qM};
}
tie(pM, qM) = pair{pL + pR, qL + qR};
}
return res;
}
```
Irrational numbers in the Stern-Brocot number system corresponds to infinite sequences of characters. Along the endless path towards the irrational number the algorithm will find reduced fractions with gradually increasing denominators that provides increasingly better approximations of the irrational number. So by taking a prefix of the infinite sequence approximations with any desired precision can be achieved. This application is important in watch-making, which explains why the tree was discovered in that domain.
Note that for a fraction $\frac{p}{q}$, the length of the resulting sequence could be as large as $O(p+q)$, for example when the fraction is of form $\frac{p}{1}$. This means that the algorithm above **should not be used, unless this is an acceptable complexity**!
### Logarithmic search
Fortunately, it is possible to enhance the algorithm above to guarantee $O(\log (p+q))$ complexity. For this we should note that if the current boundary fractions are $\frac{p_L}{q_L}$ and $\frac{p_R}{q_R}$, then by doing $a$ steps to the right we move to the fraction $\frac{p_L + a p_R}{q_L + a q_R}$, and by doing $a$ steps to the left, we move to the fraction $\frac{a p_L + p_R}{a q_L + q_R}$.
Therefore, instead of doing steps of `L` or `R` one by one, we can do $k$ steps in the same direction at once, after which we would switch to going into other direction, and so on. In this way, we can find the path to the fraction $\frac{p}{q}$ as its run-length encoding.
As the directions alternate this way, we will always know which one to take. So, for convenience we may represent a path to a fraction $\frac{p}{q}$ as a sequence of fractions
$$
\frac{p_0}{q_0}, \frac{p_1}{q_1}, \frac{p_2}{q_2}, \dots, \frac{p_n}{q_n}, \frac{p_{n+1}}{q_{n+1}} = \frac{p}{q}
$$
such that $\frac{p_{k-1}}{q_{k-1}}$ and $\frac{p_k}{q_k}$ are the boundaries of the search interval on the $k$-th step, starting with $\frac{p_0}{q_0} = \frac{0}{1}$ and $\frac{p_1}{q_1} = \frac{1}{0}$. Then, after the $k$-th step we move to a fraction
$$
\frac{p_{k+1}}{q_{k+1}} = \frac{p_{k-1} + a_k p_k}{q_{k-1} + a_k q_k},
$$
where $a_k$ is a positive integer number. If you're familiar with [continued fractions](), you would recognize that the sequence $\frac{p_i}{q_i}$ is the sequence of the convergent fractions of $\frac{p}{q}$ and the sequence $[a_1; a_2, \dots, a_{n}, 1]$ represents the continued fraction of $\frac{p}{q}$.
This allows to find the run-length encoding of the path to $\frac{p}{q}$ in the manner which follows the algorithm for computing continued fraction representation of the fraction $\frac{p}{q}$:
```cpp
auto find(int p, int q) {
bool right = true;
vector<pair<int, char>> res;
while(q) {
res.emplace_back(p / q, right ? 'R' : 'L');
tie(p, q) = pair{q, p % q};
right ^= 1;
}
res.back().first--;
return res;
}
```
However, this approach only works if we already know $\frac{p}{q}$ and want to find its place in the Stern-Brocot tree.
On practice, it is often the case that $\frac{p}{q}$ is not known in advance, but we are able to check for specific $\frac{x}{y}$ whether $\frac{x}{y} < \frac{p}{q}$.
Knowing this, we can emulate the search on Stern-Brocot tree by maintaining the current boundaries $\frac{p_{k-1}}{q_{k-1}}$ and $\frac{p_k}{q_k}$, and finding each $a_k$ via binary search. The algorithm then is a bit more technical and potentially have a complexity of $O(\log^2(x+y))$, unless the problem formulation allows you to find $a_k$ faster (for example, using `floor` of some known expression).
## Farey Sequence
The Farey sequence of order $n$ is the sorted sequence of fractions between $0$ and $1$ whose denominators do not exceed $n$.
The sequences are named after English geologist John Farey, who in 1816 conjectured that any fraction in a Farey sequence is the mediant of its neighbors. This was proven some time later by Cauchy, but independent of both of them, the mathematician Haros had come to almost the same conclusion in 1802.
The Farey sequences have many interesting properties on their own, but the connection to the Stern-Brocot tree is the most obvious. In fact, the Farey sequences can be obtained by trimming branches from the tree.
From the algorithm for building the Stern-Brocot tree, we get an algorithm for the Farey sequences. Start with the list of fractions $\frac{0}{1}, \frac{1}{0}$. At every subsequent iteration, insert the mediant only if the denominator does not exceed $n$. At some point the list will stop changing and the desired Farey sequence will have been found.
### Length of a Farey Sequence
A Farey sequence of order $n$ contains all elements of the Farey sequence of order $n-1$ as well as all irreducible fractions with denominator $n$, but the latter is just the totient $\varphi(n)$. So the length $L_n$ of the Farey sequence of order $n$ is
$$
L_n = L_{n-1} + \varphi(n)
$$
or equivalently, by unraveling the recursion we get
$$
L_n = 1 + \sum_{k=1}^n \varphi(k).
$$
|
The Stern-Brocot tree and Farey sequences
|
---
title
15_puzzle
---
# 15 Puzzle Game: Existence Of The Solution
This game is played on a $4 \times 4$ board. On this board there are $15$ playing tiles numbered from 1 to 15. One cell is left empty (denoted by 0). You need to get the board to the position presented below by repeatedly moving one of the tiles to the free space:
$$\begin{matrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 0 \end{matrix}$$
The game "15 Puzzle” was created by Noyes Chapman in 1880.
## Existence Of The Solution
Let's consider this problem: given a position on the board, determine whether a sequence of moves which leads to a solution exists.
Suppose we have some position on the board:
$$\begin{matrix} a_1 & a_2 & a_3 & a_4 \\ a_5 & a_6 & a_7 & a_8 \\ a_9 & a_{10} & a_{11} & a_{12} \\ a_{13} & a_{14} & a_{15} & a_{16} \end{matrix}$$
where one of the elements equals zero and indicates an empty cell $a_z = 0$
Let’s consider the permutation:
$$a_1 a_2 ... a_{z-1} a_{z+1} ... a_{15} a_{16}$$
i.e. the permutation of numbers corresponding to the position on the board without a zero element
Let $N$ be the number of inversions in this permutation (i.e. the number of such elements $a_i$ and $a_j$ that $i < j$, but $a_i > a_j$).
Suppose $K$ is an index of a row where the empty element is located (i.e. using our convention, $K = (z - 1) \div \ 4 + 1$).
Then, **the solution exists iff $N + K$ is even**.
## Implementation
The algorithm above can be illustrated with the following program code:
```cpp
int a[16];
for (int i=0; i<16; ++i)
cin >> a[i];
int inv = 0;
for (int i=0; i<16; ++i)
if (a[i])
for (int j=0; j<i; ++j)
if (a[j] > a[i])
++inv;
for (int i=0; i<16; ++i)
if (a[i] == 0)
inv += 1 + i / 4;
puts ((inv & 1) ? "No Solution" : "Solution Exists");
```
## Proof
In 1879 Johnson proved that if $N + K$ is odd, then the solution doesn’t exist, and in the same year Story proved that all positions when $N + K$ is even have a solution.
However, all these proofs were quite complex.
In 1999 Archer proposed a much simpler proof (you can download his article [here](http://www.cs.cmu.edu/afs/cs/academic/class/15859-f01/www/notes/15-puzzle.pdf)).
|
---
title
15_puzzle
---
# 15 Puzzle Game: Existence Of The Solution
This game is played on a $4 \times 4$ board. On this board there are $15$ playing tiles numbered from 1 to 15. One cell is left empty (denoted by 0). You need to get the board to the position presented below by repeatedly moving one of the tiles to the free space:
$$\begin{matrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 0 \end{matrix}$$
The game "15 Puzzle” was created by Noyes Chapman in 1880.
## Existence Of The Solution
Let's consider this problem: given a position on the board, determine whether a sequence of moves which leads to a solution exists.
Suppose we have some position on the board:
$$\begin{matrix} a_1 & a_2 & a_3 & a_4 \\ a_5 & a_6 & a_7 & a_8 \\ a_9 & a_{10} & a_{11} & a_{12} \\ a_{13} & a_{14} & a_{15} & a_{16} \end{matrix}$$
where one of the elements equals zero and indicates an empty cell $a_z = 0$
Let’s consider the permutation:
$$a_1 a_2 ... a_{z-1} a_{z+1} ... a_{15} a_{16}$$
i.e. the permutation of numbers corresponding to the position on the board without a zero element
Let $N$ be the number of inversions in this permutation (i.e. the number of such elements $a_i$ and $a_j$ that $i < j$, but $a_i > a_j$).
Suppose $K$ is an index of a row where the empty element is located (i.e. using our convention, $K = (z - 1) \div \ 4 + 1$).
Then, **the solution exists iff $N + K$ is even**.
## Implementation
The algorithm above can be illustrated with the following program code:
```cpp
int a[16];
for (int i=0; i<16; ++i)
cin >> a[i];
int inv = 0;
for (int i=0; i<16; ++i)
if (a[i])
for (int j=0; j<i; ++j)
if (a[j] > a[i])
++inv;
for (int i=0; i<16; ++i)
if (a[i] == 0)
inv += 1 + i / 4;
puts ((inv & 1) ? "No Solution" : "Solution Exists");
```
## Proof
In 1879 Johnson proved that if $N + K$ is odd, then the solution doesn’t exist, and in the same year Story proved that all positions when $N + K$ is even have a solution.
However, all these proofs were quite complex.
In 1999 Archer proposed a much simpler proof (you can download his article [here](http://www.cs.cmu.edu/afs/cs/academic/class/15859-f01/www/notes/15-puzzle.pdf)).
## Practice Problems
* [Hackerrank - N-puzzle](https://www.hackerrank.com/challenges/n-puzzle)
|
15 Puzzle Game: Existence Of The Solution
|
---
title
dijkstra
---
# Dijkstra Algorithm
You are given a directed or undirected weighted graph with $n$ vertices and $m$ edges. The weights of all edges are non-negative. You are also given a starting vertex $s$. This article discusses finding the lengths of the shortest paths from a starting vertex $s$ to all other vertices, and output the shortest paths themselves.
This problem is also called **single-source shortest paths problem**.
## Algorithm
Here is an algorithm described by the Dutch computer scientist Edsger W. Dijkstra in 1959.
Let's create an array $d[]$ where for each vertex $v$ we store the current length of the shortest path from $s$ to $v$ in $d[v]$.
Initially $d[s] = 0$, and for all other vertices this length equals infinity.
In the implementation a sufficiently large number (which is guaranteed to be greater than any possible path length) is chosen as infinity.
$$d[v] = \infty,~ v \ne s$$
In addition, we maintain a Boolean array $u[]$ which stores for each vertex $v$ whether it's marked. Initially all vertices are unmarked:
$$u[v] = {\rm false}$$
The Dijkstra's algorithm runs for $n$ iterations. At each iteration a vertex $v$ is chosen as unmarked vertex which has the least value $d[v]$:
Evidently, in the first iteration the starting vertex $s$ will be selected.
The selected vertex $v$ is marked. Next, from vertex $v$ **relaxations** are performed: all edges of the form $(v,\text{to})$ are considered, and for each vertex $\text{to}$ the algorithm tries to improve the value $d[\text{to}]$. If the length of the current edge equals $len$, the code for relaxation is:
$$d[\text{to}] = \min (d[\text{to}], d[v] + len)$$
After all such edges are considered, the current iteration ends. Finally, after $n$ iterations, all vertices will be marked, and the algorithm terminates. We claim that the found values $d[v]$ are the lengths of shortest paths from $s$ to all vertices $v$.
Note that if some vertices are unreachable from the starting vertex $s$, the values $d[v]$ for them will remain infinite. Obviously, the last few iterations of the algorithm will choose those vertices, but no useful work will be done for them. Therefore, the algorithm can be stopped as soon as the selected vertex has infinite distance to it.
### Restoring Shortest Paths
Usually one needs to know not only the lengths of shortest paths but also the shortest paths themselves. Let's see how to maintain sufficient information to restore the shortest path from $s$ to any vertex. We'll maintain an array of predecessors $p[]$ in which for each vertex $v \ne s$, $p[v]$ is the penultimate vertex in the shortest path from $s$ to $v$. Here we use the fact that if we take the shortest path to some vertex $v$ and remove $v$ from this path, we'll get a path ending in at vertex $p[v]$, and this path will be the shortest for the vertex $p[v]$. This array of predecessors can be used to restore the shortest path to any vertex: starting with $v$, repeatedly take the predecessor of the current vertex until we reach the starting vertex $s$ to get the required shortest path with vertices listed in reverse order. So, the shortest path $P$ to the vertex $v$ is equal to:
$$P = (s, \ldots, p[p[p[v]]], p[p[v]], p[v], v)$$
Building this array of predecessors is very simple: for each successful relaxation, i.e. when for some selected vertex $v$, there is an improvement in the distance to some vertex $\text{to}$, we update the predecessor vertex for $\text{to}$ with vertex $v$:
$$p[\text{to}] = v$$
## Proof
The main assertion on which Dijkstra's algorithm correctness is based is the following:
**After any vertex $v$ becomes marked, the current distance to it $d[v]$ is the shortest, and will no longer change.**
The proof is done by induction. For the first iteration this statement is obvious: the only marked vertex is $s$, and the distance to is $d[s] = 0$ is indeed the length of the shortest path to $s$. Now suppose this statement is true for all previous iterations, i.e. for all already marked vertices; let's prove that it is not violated after the current iteration completes. Let $v$ be the vertex selected in the current iteration, i.e. $v$ is the vertex that the algorithm will mark. Now we have to prove that $d[v]$ is indeed equal to the length of the shortest path to it $l[v]$.
Consider the shortest path $P$ to the vertex $v$. This path can be split into two parts: $P_1$ which consists of only marked nodes (at least the starting vertex $s$ is part of $P_1$), and the rest of the path $P_2$ (it may include a marked vertex, but it always starts with an unmarked vertex). Let's denote the first vertex of the path $P_2$ as $p$, and the last vertex of the path $P_1$ as $q$.
First we prove our statement for the vertex $p$, i.e. let's prove that $d[p] = l[p]$.
This is almost obvious: on one of the previous iterations we chose the vertex $q$ and performed relaxation from it.
Since (by virtue of the choice of vertex $p$) the shortest path to $p$ is the shortest path to $q$ plus edge $(p,q)$, the relaxation from $q$ set the value of $d[p]$ to the length of the shortest path $l[p]$.
Since the edges' weights are non-negative, the length of the shortest path $l[p]$ (which we just proved to be equal to $d[p]$) does not exceed the length $l[v]$ of the shortest path to the vertex $v$. Given that $l[v] \le d[v]$ (because Dijkstra's algorithm could not have found a shorter way than the shortest possible one), we get the inequality:
$$d[p] = l[p] \le l[v] \le d[v]$$
On the other hand, since both vertices $p$ and $v$ are unmarked, and the current iteration chose vertex $v$, not $p$, we get another inequality:
$$d[p] \ge d[v]$$
From these two inequalities we conclude that $d[p] = d[v]$, and then from previously found equations we get:
$$d[v] = l[v]$$
Q.E.D.
## Implementation
Dijkstra's algorithm performs $n$ iterations. On each iteration it selects an unmarked vertex $v$ with the lowest value $d[v]$, marks it and checks all the edges $(v, \text{to})$ attempting to improve the value $d[\text{to}]$.
The running time of the algorithm consists of:
* $n$ searches for a vertex with the smallest value $d[v]$ among $O(n)$ unmarked vertices
* $m$ relaxation attempts
For the simplest implementation of these operations on each iteration vertex search requires $O(n)$ operations, and each relaxation can be performed in $O(1)$. Hence, the resulting asymptotic behavior of the algorithm is:
$$O(n^2+m)$$
This complexity is optimal for dense graph, i.e. when $m \approx n^2$.
However in sparse graphs, when $m$ is much smaller than the maximal number of edges $n^2$, the problem can be solved in $O(n \log n + m)$ complexity. The algorithm and implementation can be found on the article [Dijkstra on sparse graphs](dijkstra_sparse.md).
```{.cpp file=dijkstra_dense}
const int INF = 1000000000;
vector<vector<pair<int, int>>> adj;
void dijkstra(int s, vector<int> & d, vector<int> & p) {
int n = adj.size();
d.assign(n, INF);
p.assign(n, -1);
vector<bool> u(n, false);
d[s] = 0;
for (int i = 0; i < n; i++) {
int v = -1;
for (int j = 0; j < n; j++) {
if (!u[j] && (v == -1 || d[j] < d[v]))
v = j;
}
if (d[v] == INF)
break;
u[v] = true;
for (auto edge : adj[v]) {
int to = edge.first;
int len = edge.second;
if (d[v] + len < d[to]) {
d[to] = d[v] + len;
p[to] = v;
}
}
}
}
```
Here the graph $\text{adj}$ is stored as adjacency list: for each vertex $v$ $\text{adj}[v]$ contains the list of edges going from this vertex, i.e. the list of `pair<int,int>` where the first element in the pair is the vertex at the other end of the edge, and the second element is the edge weight.
The function takes the starting vertex $s$ and two vectors that will be used as return values.
First of all, the code initializes arrays: distances $d[]$, labels $u[]$ and predecessors $p[]$. Then it performs $n$ iterations. At each iteration the vertex $v$ is selected which has the smallest distance $d[v]$ among all the unmarked vertices. If the distance to selected vertex $v$ is equal to infinity, the algorithm stops. Otherwise the vertex is marked, and all the edges going out from this vertex are checked. If relaxation along the edge is possible (i.e. distance $d[\text{to}]$ can be improved), the distance $d[\text{to}]$ and predecessor $p[\text{to}]$ are updated.
After performing all the iterations array $d[]$ stores the lengths of the shortest paths to all vertices, and array $p[]$ stores the predecessors of all vertices (except starting vertex $s$). The path to any vertex $t$ can be restored in the following way:
```{.cpp file=dijkstra_restore_path}
vector<int> restore_path(int s, int t, vector<int> const& p) {
vector<int> path;
for (int v = t; v != s; v = p[v])
path.push_back(v);
path.push_back(s);
reverse(path.begin(), path.end());
return path;
}
```
## References
* Edsger Dijkstra. A note on two problems in connexion with graphs [1959]
* Thomas Cormen, Charles Leiserson, Ronald Rivest, Clifford Stein. Introduction to Algorithms [2005]
|
---
title
dijkstra
---
# Dijkstra Algorithm
You are given a directed or undirected weighted graph with $n$ vertices and $m$ edges. The weights of all edges are non-negative. You are also given a starting vertex $s$. This article discusses finding the lengths of the shortest paths from a starting vertex $s$ to all other vertices, and output the shortest paths themselves.
This problem is also called **single-source shortest paths problem**.
## Algorithm
Here is an algorithm described by the Dutch computer scientist Edsger W. Dijkstra in 1959.
Let's create an array $d[]$ where for each vertex $v$ we store the current length of the shortest path from $s$ to $v$ in $d[v]$.
Initially $d[s] = 0$, and for all other vertices this length equals infinity.
In the implementation a sufficiently large number (which is guaranteed to be greater than any possible path length) is chosen as infinity.
$$d[v] = \infty,~ v \ne s$$
In addition, we maintain a Boolean array $u[]$ which stores for each vertex $v$ whether it's marked. Initially all vertices are unmarked:
$$u[v] = {\rm false}$$
The Dijkstra's algorithm runs for $n$ iterations. At each iteration a vertex $v$ is chosen as unmarked vertex which has the least value $d[v]$:
Evidently, in the first iteration the starting vertex $s$ will be selected.
The selected vertex $v$ is marked. Next, from vertex $v$ **relaxations** are performed: all edges of the form $(v,\text{to})$ are considered, and for each vertex $\text{to}$ the algorithm tries to improve the value $d[\text{to}]$. If the length of the current edge equals $len$, the code for relaxation is:
$$d[\text{to}] = \min (d[\text{to}], d[v] + len)$$
After all such edges are considered, the current iteration ends. Finally, after $n$ iterations, all vertices will be marked, and the algorithm terminates. We claim that the found values $d[v]$ are the lengths of shortest paths from $s$ to all vertices $v$.
Note that if some vertices are unreachable from the starting vertex $s$, the values $d[v]$ for them will remain infinite. Obviously, the last few iterations of the algorithm will choose those vertices, but no useful work will be done for them. Therefore, the algorithm can be stopped as soon as the selected vertex has infinite distance to it.
### Restoring Shortest Paths
Usually one needs to know not only the lengths of shortest paths but also the shortest paths themselves. Let's see how to maintain sufficient information to restore the shortest path from $s$ to any vertex. We'll maintain an array of predecessors $p[]$ in which for each vertex $v \ne s$, $p[v]$ is the penultimate vertex in the shortest path from $s$ to $v$. Here we use the fact that if we take the shortest path to some vertex $v$ and remove $v$ from this path, we'll get a path ending in at vertex $p[v]$, and this path will be the shortest for the vertex $p[v]$. This array of predecessors can be used to restore the shortest path to any vertex: starting with $v$, repeatedly take the predecessor of the current vertex until we reach the starting vertex $s$ to get the required shortest path with vertices listed in reverse order. So, the shortest path $P$ to the vertex $v$ is equal to:
$$P = (s, \ldots, p[p[p[v]]], p[p[v]], p[v], v)$$
Building this array of predecessors is very simple: for each successful relaxation, i.e. when for some selected vertex $v$, there is an improvement in the distance to some vertex $\text{to}$, we update the predecessor vertex for $\text{to}$ with vertex $v$:
$$p[\text{to}] = v$$
## Proof
The main assertion on which Dijkstra's algorithm correctness is based is the following:
**After any vertex $v$ becomes marked, the current distance to it $d[v]$ is the shortest, and will no longer change.**
The proof is done by induction. For the first iteration this statement is obvious: the only marked vertex is $s$, and the distance to is $d[s] = 0$ is indeed the length of the shortest path to $s$. Now suppose this statement is true for all previous iterations, i.e. for all already marked vertices; let's prove that it is not violated after the current iteration completes. Let $v$ be the vertex selected in the current iteration, i.e. $v$ is the vertex that the algorithm will mark. Now we have to prove that $d[v]$ is indeed equal to the length of the shortest path to it $l[v]$.
Consider the shortest path $P$ to the vertex $v$. This path can be split into two parts: $P_1$ which consists of only marked nodes (at least the starting vertex $s$ is part of $P_1$), and the rest of the path $P_2$ (it may include a marked vertex, but it always starts with an unmarked vertex). Let's denote the first vertex of the path $P_2$ as $p$, and the last vertex of the path $P_1$ as $q$.
First we prove our statement for the vertex $p$, i.e. let's prove that $d[p] = l[p]$.
This is almost obvious: on one of the previous iterations we chose the vertex $q$ and performed relaxation from it.
Since (by virtue of the choice of vertex $p$) the shortest path to $p$ is the shortest path to $q$ plus edge $(p,q)$, the relaxation from $q$ set the value of $d[p]$ to the length of the shortest path $l[p]$.
Since the edges' weights are non-negative, the length of the shortest path $l[p]$ (which we just proved to be equal to $d[p]$) does not exceed the length $l[v]$ of the shortest path to the vertex $v$. Given that $l[v] \le d[v]$ (because Dijkstra's algorithm could not have found a shorter way than the shortest possible one), we get the inequality:
$$d[p] = l[p] \le l[v] \le d[v]$$
On the other hand, since both vertices $p$ and $v$ are unmarked, and the current iteration chose vertex $v$, not $p$, we get another inequality:
$$d[p] \ge d[v]$$
From these two inequalities we conclude that $d[p] = d[v]$, and then from previously found equations we get:
$$d[v] = l[v]$$
Q.E.D.
## Implementation
Dijkstra's algorithm performs $n$ iterations. On each iteration it selects an unmarked vertex $v$ with the lowest value $d[v]$, marks it and checks all the edges $(v, \text{to})$ attempting to improve the value $d[\text{to}]$.
The running time of the algorithm consists of:
* $n$ searches for a vertex with the smallest value $d[v]$ among $O(n)$ unmarked vertices
* $m$ relaxation attempts
For the simplest implementation of these operations on each iteration vertex search requires $O(n)$ operations, and each relaxation can be performed in $O(1)$. Hence, the resulting asymptotic behavior of the algorithm is:
$$O(n^2+m)$$
This complexity is optimal for dense graph, i.e. when $m \approx n^2$.
However in sparse graphs, when $m$ is much smaller than the maximal number of edges $n^2$, the problem can be solved in $O(n \log n + m)$ complexity. The algorithm and implementation can be found on the article [Dijkstra on sparse graphs](dijkstra_sparse.md).
```{.cpp file=dijkstra_dense}
const int INF = 1000000000;
vector<vector<pair<int, int>>> adj;
void dijkstra(int s, vector<int> & d, vector<int> & p) {
int n = adj.size();
d.assign(n, INF);
p.assign(n, -1);
vector<bool> u(n, false);
d[s] = 0;
for (int i = 0; i < n; i++) {
int v = -1;
for (int j = 0; j < n; j++) {
if (!u[j] && (v == -1 || d[j] < d[v]))
v = j;
}
if (d[v] == INF)
break;
u[v] = true;
for (auto edge : adj[v]) {
int to = edge.first;
int len = edge.second;
if (d[v] + len < d[to]) {
d[to] = d[v] + len;
p[to] = v;
}
}
}
}
```
Here the graph $\text{adj}$ is stored as adjacency list: for each vertex $v$ $\text{adj}[v]$ contains the list of edges going from this vertex, i.e. the list of `pair<int,int>` where the first element in the pair is the vertex at the other end of the edge, and the second element is the edge weight.
The function takes the starting vertex $s$ and two vectors that will be used as return values.
First of all, the code initializes arrays: distances $d[]$, labels $u[]$ and predecessors $p[]$. Then it performs $n$ iterations. At each iteration the vertex $v$ is selected which has the smallest distance $d[v]$ among all the unmarked vertices. If the distance to selected vertex $v$ is equal to infinity, the algorithm stops. Otherwise the vertex is marked, and all the edges going out from this vertex are checked. If relaxation along the edge is possible (i.e. distance $d[\text{to}]$ can be improved), the distance $d[\text{to}]$ and predecessor $p[\text{to}]$ are updated.
After performing all the iterations array $d[]$ stores the lengths of the shortest paths to all vertices, and array $p[]$ stores the predecessors of all vertices (except starting vertex $s$). The path to any vertex $t$ can be restored in the following way:
```{.cpp file=dijkstra_restore_path}
vector<int> restore_path(int s, int t, vector<int> const& p) {
vector<int> path;
for (int v = t; v != s; v = p[v])
path.push_back(v);
path.push_back(s);
reverse(path.begin(), path.end());
return path;
}
```
## References
* Edsger Dijkstra. A note on two problems in connexion with graphs [1959]
* Thomas Cormen, Charles Leiserson, Ronald Rivest, Clifford Stein. Introduction to Algorithms [2005]
## Practice Problems
* [Timus - Ivan's Car](http://acm.timus.ru/problem.aspx?space=1&num=1930) [Difficulty:Medium]
* [Timus - Sightseeing Trip](http://acm.timus.ru/problem.aspx?space=1&num=1004)
* [SPOJ - SHPATH](http://www.spoj.com/problems/SHPATH/) [Difficulty:Easy]
* [Codeforces - Dijkstra?](http://codeforces.com/problemset/problem/20/C) [Difficulty:Easy]
* [Codeforces - Shortest Path](http://codeforces.com/problemset/problem/59/E)
* [Codeforces - Jzzhu and Cities](http://codeforces.com/problemset/problem/449/B)
* [Codeforces - The Classic Problem](http://codeforces.com/problemset/problem/464/E)
* [Codeforces - President and Roads](http://codeforces.com/problemset/problem/567/E)
* [Codeforces - Complete The Graph](http://codeforces.com/problemset/problem/715/B)
* [TopCoder - SkiResorts](https://community.topcoder.com/stat?c=problem_statement&pm=12468)
* [TopCoder - MaliciousPath](https://community.topcoder.com/stat?c=problem_statement&pm=13596)
* [SPOJ - Ada and Trip](http://www.spoj.com/problems/ADATRIP/)
* [LA - 3850 - Here We Go(relians) Again](https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1851)
* [GYM - Destination Unknown (D)](http://codeforces.com/gym/100625)
* [UVA 12950 - Even Obsession](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=4829)
* [GYM - Journey to Grece (A)](http://codeforces.com/gym/100753)
* [UVA 13030 - Brain Fry](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=866&page=show_problem&problem=4918)
* [UVA 1027 - Toll](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=3468)
* [UVA 11377 - Airport Setup](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=2372)
* [Codeforces - Dynamic Shortest Path](http://codeforces.com/problemset/problem/843/D)
* [UVA 11813 - Shopping](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2913)
* [UVA 11833 - Route Change](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=226&page=show_problem&problem=2933)
* [SPOJ - Easy Dijkstra Problem](http://www.spoj.com/problems/EZDIJKST/en/)
* [LA - 2819 - Cave Raider](https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=820)
* [UVA 12144 - Almost Shortest Path](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=3296)
* [UVA 12047 - Highest Paid Toll](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=3198)
* [UVA 11514 - Batman](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=2509)
* [Codeforces - Team Rocket Rises Again](http://codeforces.com/contest/757/problem/F)
* [UVA - 11338 - Minefield](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2313)
* [UVA 11374 - Airport Express](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2369)
* [UVA 11097 - Poor My Problem](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2038)
* [UVA 13172 - The music teacher](https://uva.onlinejudge.org/index.php?option=onlinejudge&Itemid=8&page=show_problem&problem=5083)
* [Codeforces - Dirty Arkady's Kitchen](http://codeforces.com/contest/827/problem/F)
* [SPOJ - Delivery Route](http://www.spoj.com/problems/DELIVER/)
* [SPOJ - Costly Chess](http://www.spoj.com/problems/CCHESS/)
* [CSES - Shortest Routes 1](https://cses.fi/problemset/task/1671)
* [CSES - Flight Discount](https://cses.fi/problemset/task/1195)
* [CSES - Flight Routes](https://cses.fi/problemset/task/1196)
|
Dijkstra Algorithm
|
---
title
tree_painting
---
# Paint the edges of the tree
This is a fairly common task. Given a tree $G$ with $N$ vertices. There are two types of queries: the first one is to paint an edge, the second one is to query the number of colored edges between two vertices.
Here we will describe a fairly simple solution (using a [segment tree](../data_structures/segment_tree.md)) that will answer each query in $O(\log N)$ time.
The preprocessing step will take $O(N)$ time.
## Algorithm
First, we need to find the [LCA](lca.md) to reduce each query of the second kind $(i,j)$ into two queries $(l,i)$ and $(l,j)$, where $l$ is the LCA of $i$ and $j$.
The answer of the query $(i,j)$ will be the sum of both subqueries.
Both these queries have a special structure, the first vertex is an ancestor of the second one.
For the rest of the article we will only talk about these special kind of queries.
We will start by describing the **preprocessing** step.
Run a depth-first search from the root of the tree and record the Euler tour of this depth-first search (each vertex is added to the list when the search visits it first and every time we return from one of its children).
The same technique can be used in the LCA preprocessing.
This list will contain each edge (in the sense that if $i$ and $j$ are the ends of the edge, then there will be a place in the list where $i$ and $j$ are neighbors in the list), and it appear exactly two times: in the forward direction (from $i$ to $j$, where vertex $i$ is closer to the root than vertex $j$) and in the opposite direction (from $j$ to $i$).
We will build two lists for these edges.
The first one will store the color of all edges in the forward direction, and the second one the color of all edges in the opposite direction.
We will use $1$ if the edge is colored, and $0$ otherwise.
Over these two lists we will build each a segment tree (for sum with a single modification), let's call them $T1$ and $T2$.
Let us answer a query of the form $(i,j)$, where $i$ is the ancestor of $j$.
We need to determine how many edges are painted on the path between $i$ and $j$.
Let's find $i$ and $j$ in the Euler tour for the first time, let it be the positions $p$ and $q$ (this can be done in $O(1)$ if we calculate these positions in advance during preprocessing).
Then the **answer** to the query is the sum $T1[p..q-1]$ minus the sum $T2[p..q-1]$.
**Why?**
Consider the segment $[p;q]$ in the Euler tour.
It contains all edges of the path we need from $i$ to $j$ but also contains a set of edges that lie on other paths from $i$.
However there is one big difference between the edges we need and the rest of the edges: the edges we need will be listed only once in the forward direction, and all the other edges appear twice: once in the forward and once in the opposite direction.
Hence, the difference $T1[p..q-1] - T2[p..q-1]$ will give us the correct answer (minus one is necessary because otherwise, we will capture an extra edge going out from vertex $j$).
The sum query in the segment tree is executed in $O(\log N)$.
Answering the **first type of query** (painting an edge) is even easier - we just need to update $T1$ and $T2$, namely to perform a single update of the element that corresponds to our edge (finding the edge in the list, again, is possible in $O(1)$, if you perform this search during preprocessing).
A single modification in the segment tree is performed in $O(\log N)$.
## Implementation
Here is the full implementation of the solution, including LCA computation:
```cpp
const int INF = 1000 * 1000 * 1000;
typedef vector<vector<int>> graph;
vector<int> dfs_list;
vector<int> edges_list;
vector<int> h;
void dfs(int v, const graph& g, const graph& edge_ids, int cur_h = 1) {
h[v] = cur_h;
dfs_list.push_back(v);
for (size_t i = 0; i < g[v].size(); ++i) {
if (h[g[v][i]] == -1) {
edges_list.push_back(edge_ids[v][i]);
dfs(g[v][i], g, edge_ids, cur_h + 1);
edges_list.push_back(edge_ids[v][i]);
dfs_list.push_back(v);
}
}
}
vector<int> lca_tree;
vector<int> first;
void lca_tree_build(int i, int l, int r) {
if (l == r) {
lca_tree[i] = dfs_list[l];
} else {
int m = (l + r) >> 1;
lca_tree_build(i + i, l, m);
lca_tree_build(i + i + 1, m + 1, r);
int lt = lca_tree[i + i], rt = lca_tree[i + i + 1];
lca_tree[i] = h[lt] < h[rt] ? lt : rt;
}
}
void lca_prepare(int n) {
lca_tree.assign(dfs_list.size() * 8, -1);
lca_tree_build(1, 0, (int)dfs_list.size() - 1);
first.assign(n, -1);
for (int i = 0; i < (int)dfs_list.size(); ++i) {
int v = dfs_list[i];
if (first[v] == -1)
first[v] = i;
}
}
int lca_tree_query(int i, int tl, int tr, int l, int r) {
if (tl == l && tr == r)
return lca_tree[i];
int m = (tl + tr) >> 1;
if (r <= m)
return lca_tree_query(i + i, tl, m, l, r);
if (l > m)
return lca_tree_query(i + i + 1, m + 1, tr, l, r);
int lt = lca_tree_query(i + i, tl, m, l, m);
int rt = lca_tree_query(i + i + 1, m + 1, tr, m + 1, r);
return h[lt] < h[rt] ? lt : rt;
}
int lca(int a, int b) {
if (first[a] > first[b])
swap(a, b);
return lca_tree_query(1, 0, (int)dfs_list.size() - 1, first[a], first[b]);
}
vector<int> first1, first2;
vector<char> edge_used;
vector<int> tree1, tree2;
void query_prepare(int n) {
first1.resize(n - 1, -1);
first2.resize(n - 1, -1);
for (int i = 0; i < (int)edges_list.size(); ++i) {
int j = edges_list[i];
if (first1[j] == -1)
first1[j] = i;
else
first2[j] = i;
}
edge_used.resize(n - 1);
tree1.resize(edges_list.size() * 8);
tree2.resize(edges_list.size() * 8);
}
void sum_tree_update(vector<int>& tree, int i, int l, int r, int j, int delta) {
tree[i] += delta;
if (l < r) {
int m = (l + r) >> 1;
if (j <= m)
sum_tree_update(tree, i + i, l, m, j, delta);
else
sum_tree_update(tree, i + i + 1, m + 1, r, j, delta);
}
}
int sum_tree_query(const vector<int>& tree, int i, int tl, int tr, int l, int r) {
if (l > r || tl > tr)
return 0;
if (tl == l && tr == r)
return tree[i];
int m = (tl + tr) >> 1;
if (r <= m)
return sum_tree_query(tree, i + i, tl, m, l, r);
if (l > m)
return sum_tree_query(tree, i + i + 1, m + 1, tr, l, r);
return sum_tree_query(tree, i + i, tl, m, l, m) +
sum_tree_query(tree, i + i + 1, m + 1, tr, m + 1, r);
}
int query(int v1, int v2) {
return sum_tree_query(tree1, 1, 0, (int)edges_list.size() - 1, first[v1], first[v2] - 1) -
sum_tree_query(tree2, 1, 0, (int)edges_list.size() - 1, first[v1], first[v2] - 1);
}
int main() {
// reading the graph
int n;
scanf("%d", &n);
graph g(n), edge_ids(n);
for (int i = 0; i < n - 1; ++i) {
int v1, v2;
scanf("%d%d", &v1, &v2);
--v1, --v2;
g[v1].push_back(v2);
g[v2].push_back(v1);
edge_ids[v1].push_back(i);
edge_ids[v2].push_back(i);
}
h.assign(n, -1);
dfs(0, g, edge_ids);
lca_prepare(n);
query_prepare(n);
for (;;) {
if () {
// request for painting edge x;
// if start = true, then the edge is painted, otherwise the painting
// is removed
edge_used[x] = start;
sum_tree_update(tree1, 1, 0, (int)edges_list.size() - 1, first1[x],
start ? 1 : -1);
sum_tree_update(tree2, 1, 0, (int)edges_list.size() - 1, first2[x],
start ? 1 : -1);
} else {
// query the number of colored edges on the path between v1 and v2
int l = lca(v1, v2);
int result = query(l, v1) + query(l, v2);
// result - the answer to the request
}
}
}
```
|
---
title
tree_painting
---
# Paint the edges of the tree
This is a fairly common task. Given a tree $G$ with $N$ vertices. There are two types of queries: the first one is to paint an edge, the second one is to query the number of colored edges between two vertices.
Here we will describe a fairly simple solution (using a [segment tree](../data_structures/segment_tree.md)) that will answer each query in $O(\log N)$ time.
The preprocessing step will take $O(N)$ time.
## Algorithm
First, we need to find the [LCA](lca.md) to reduce each query of the second kind $(i,j)$ into two queries $(l,i)$ and $(l,j)$, where $l$ is the LCA of $i$ and $j$.
The answer of the query $(i,j)$ will be the sum of both subqueries.
Both these queries have a special structure, the first vertex is an ancestor of the second one.
For the rest of the article we will only talk about these special kind of queries.
We will start by describing the **preprocessing** step.
Run a depth-first search from the root of the tree and record the Euler tour of this depth-first search (each vertex is added to the list when the search visits it first and every time we return from one of its children).
The same technique can be used in the LCA preprocessing.
This list will contain each edge (in the sense that if $i$ and $j$ are the ends of the edge, then there will be a place in the list where $i$ and $j$ are neighbors in the list), and it appear exactly two times: in the forward direction (from $i$ to $j$, where vertex $i$ is closer to the root than vertex $j$) and in the opposite direction (from $j$ to $i$).
We will build two lists for these edges.
The first one will store the color of all edges in the forward direction, and the second one the color of all edges in the opposite direction.
We will use $1$ if the edge is colored, and $0$ otherwise.
Over these two lists we will build each a segment tree (for sum with a single modification), let's call them $T1$ and $T2$.
Let us answer a query of the form $(i,j)$, where $i$ is the ancestor of $j$.
We need to determine how many edges are painted on the path between $i$ and $j$.
Let's find $i$ and $j$ in the Euler tour for the first time, let it be the positions $p$ and $q$ (this can be done in $O(1)$ if we calculate these positions in advance during preprocessing).
Then the **answer** to the query is the sum $T1[p..q-1]$ minus the sum $T2[p..q-1]$.
**Why?**
Consider the segment $[p;q]$ in the Euler tour.
It contains all edges of the path we need from $i$ to $j$ but also contains a set of edges that lie on other paths from $i$.
However there is one big difference between the edges we need and the rest of the edges: the edges we need will be listed only once in the forward direction, and all the other edges appear twice: once in the forward and once in the opposite direction.
Hence, the difference $T1[p..q-1] - T2[p..q-1]$ will give us the correct answer (minus one is necessary because otherwise, we will capture an extra edge going out from vertex $j$).
The sum query in the segment tree is executed in $O(\log N)$.
Answering the **first type of query** (painting an edge) is even easier - we just need to update $T1$ and $T2$, namely to perform a single update of the element that corresponds to our edge (finding the edge in the list, again, is possible in $O(1)$, if you perform this search during preprocessing).
A single modification in the segment tree is performed in $O(\log N)$.
## Implementation
Here is the full implementation of the solution, including LCA computation:
```cpp
const int INF = 1000 * 1000 * 1000;
typedef vector<vector<int>> graph;
vector<int> dfs_list;
vector<int> edges_list;
vector<int> h;
void dfs(int v, const graph& g, const graph& edge_ids, int cur_h = 1) {
h[v] = cur_h;
dfs_list.push_back(v);
for (size_t i = 0; i < g[v].size(); ++i) {
if (h[g[v][i]] == -1) {
edges_list.push_back(edge_ids[v][i]);
dfs(g[v][i], g, edge_ids, cur_h + 1);
edges_list.push_back(edge_ids[v][i]);
dfs_list.push_back(v);
}
}
}
vector<int> lca_tree;
vector<int> first;
void lca_tree_build(int i, int l, int r) {
if (l == r) {
lca_tree[i] = dfs_list[l];
} else {
int m = (l + r) >> 1;
lca_tree_build(i + i, l, m);
lca_tree_build(i + i + 1, m + 1, r);
int lt = lca_tree[i + i], rt = lca_tree[i + i + 1];
lca_tree[i] = h[lt] < h[rt] ? lt : rt;
}
}
void lca_prepare(int n) {
lca_tree.assign(dfs_list.size() * 8, -1);
lca_tree_build(1, 0, (int)dfs_list.size() - 1);
first.assign(n, -1);
for (int i = 0; i < (int)dfs_list.size(); ++i) {
int v = dfs_list[i];
if (first[v] == -1)
first[v] = i;
}
}
int lca_tree_query(int i, int tl, int tr, int l, int r) {
if (tl == l && tr == r)
return lca_tree[i];
int m = (tl + tr) >> 1;
if (r <= m)
return lca_tree_query(i + i, tl, m, l, r);
if (l > m)
return lca_tree_query(i + i + 1, m + 1, tr, l, r);
int lt = lca_tree_query(i + i, tl, m, l, m);
int rt = lca_tree_query(i + i + 1, m + 1, tr, m + 1, r);
return h[lt] < h[rt] ? lt : rt;
}
int lca(int a, int b) {
if (first[a] > first[b])
swap(a, b);
return lca_tree_query(1, 0, (int)dfs_list.size() - 1, first[a], first[b]);
}
vector<int> first1, first2;
vector<char> edge_used;
vector<int> tree1, tree2;
void query_prepare(int n) {
first1.resize(n - 1, -1);
first2.resize(n - 1, -1);
for (int i = 0; i < (int)edges_list.size(); ++i) {
int j = edges_list[i];
if (first1[j] == -1)
first1[j] = i;
else
first2[j] = i;
}
edge_used.resize(n - 1);
tree1.resize(edges_list.size() * 8);
tree2.resize(edges_list.size() * 8);
}
void sum_tree_update(vector<int>& tree, int i, int l, int r, int j, int delta) {
tree[i] += delta;
if (l < r) {
int m = (l + r) >> 1;
if (j <= m)
sum_tree_update(tree, i + i, l, m, j, delta);
else
sum_tree_update(tree, i + i + 1, m + 1, r, j, delta);
}
}
int sum_tree_query(const vector<int>& tree, int i, int tl, int tr, int l, int r) {
if (l > r || tl > tr)
return 0;
if (tl == l && tr == r)
return tree[i];
int m = (tl + tr) >> 1;
if (r <= m)
return sum_tree_query(tree, i + i, tl, m, l, r);
if (l > m)
return sum_tree_query(tree, i + i + 1, m + 1, tr, l, r);
return sum_tree_query(tree, i + i, tl, m, l, m) +
sum_tree_query(tree, i + i + 1, m + 1, tr, m + 1, r);
}
int query(int v1, int v2) {
return sum_tree_query(tree1, 1, 0, (int)edges_list.size() - 1, first[v1], first[v2] - 1) -
sum_tree_query(tree2, 1, 0, (int)edges_list.size() - 1, first[v1], first[v2] - 1);
}
int main() {
// reading the graph
int n;
scanf("%d", &n);
graph g(n), edge_ids(n);
for (int i = 0; i < n - 1; ++i) {
int v1, v2;
scanf("%d%d", &v1, &v2);
--v1, --v2;
g[v1].push_back(v2);
g[v2].push_back(v1);
edge_ids[v1].push_back(i);
edge_ids[v2].push_back(i);
}
h.assign(n, -1);
dfs(0, g, edge_ids);
lca_prepare(n);
query_prepare(n);
for (;;) {
if () {
// request for painting edge x;
// if start = true, then the edge is painted, otherwise the painting
// is removed
edge_used[x] = start;
sum_tree_update(tree1, 1, 0, (int)edges_list.size() - 1, first1[x],
start ? 1 : -1);
sum_tree_update(tree2, 1, 0, (int)edges_list.size() - 1, first2[x],
start ? 1 : -1);
} else {
// query the number of colored edges on the path between v1 and v2
int l = lca(v1, v2);
int result = query(l, v1) + query(l, v2);
// result - the answer to the request
}
}
}
```
|
Paint the edges of the tree
|
---
title
flow_with_limits
---
# Flows with demands
In a normal flow network the flow of an edge is only limited by the capacity $c(e)$ from above and by 0 from below.
In this article we will discuss flow networks, where we additionally require the flow of each edge to have a certain amount, i.e. we bound the flow from below by a **demand** function $d(e)$:
$$ d(e) \le f(e) \le c(e)$$
So next each edge has a minimal flow value, that we have to pass along the edge.
This is a generalization of the normal flow problem, since setting $d(e) = 0$ for all edges $e$ gives a normal flow network.
Notice, that in the normal flow network it is extremely trivial to find a valid flow, just setting $f(e) = 0$ is already a valid one.
However if the flow of each edge has to satisfy a demand, than suddenly finding a valid flow is already pretty complicated.
We will consider two problems:
1. finding an arbitrary flow that satisfies all constraints
2. finding a minimal flow that satisfies all constraints
## Finding an arbitrary flow
We make the following changes in the network.
We add a new source $s'$ and a new sink $t'$, a new edge from the source $s'$ to every other vertex, a new edge for every vertex to the sink $t'$, and one edge from $t$ to $s$.
Additionally we define the new capacity function $c'$ as:
- $c'((s', v)) = \sum_{u \in V} d((u, v))$ for each edge $(s', v)$.
- $c'((v, t')) = \sum_{w \in V} d((v, w))$ for each edge $(v, t')$.
- $c'((u, v)) = c((u, v)) - d((u, v))$ for each edge $(u, v)$ in the old network.
- $c'((t, s)) = \infty$
If the new network has a saturating flow (a flow where each edge outgoing from $s'$ is completely filled, which is equivalent to every edge incoming to $t'$ is completely filled), then the network with demands has a valid flow, and the actual flow can be easily reconstructed from the new network.
Otherwise there doesn't exist a flow that satisfies all conditions.
Since a saturating flow has to be a maximum flow, it can be found by any maximum flow algorithm, like the [Edmonds-Karp algorithm](edmonds_karp.md) or the [Push-relabel algorithm](push-relabel.md).
The correctness of these transformations is more difficult to understand.
We can think of it in the following way:
Each edge $e = (u, v)$ with $d(e) > 0$ is originally replaced by two edges: one with the capacity $d(i)$ , and the other with $c(i) - d(i)$.
We want to find a flow that saturates the first edge (i.e. the flow along this edge must be equal to its capacity).
The second edge is less important - the flow along it can be anything, assuming that it doesn't exceed its capacity.
Consider each edge that has to be saturated, and we perform the following operation:
we draw the edge from the new source $s'$ to its end $v$, draw the edge from its start $u$ to the new sink $t'$, remove the edge itself, and from the old sink $t$ to the old source $s$ we draw an edge of infinite capacity.
By these actions we simulate the fact that this edge is saturated - from $v$ there will be an additionally $d(e)$ flow outgoing (we simulate it with a new source that feeds the right amount of flow to $v$), and $u$ will also push $d(e)$ additional flow (but instead along the old edge, this flow will go directly to the new sink $t'$).
A flow with the value $d(e)$, that originally flowed along the path $s - \dots - u - v - \dots t$ can now take the new path $s' - v - \dots - t - s - \dots - u - t'$.
The only thing that got simplified in the definition of the new network, is that if procedure created multiple edges between the same pair of vertices, then they are combined to one single edge with the summed capacity.
## Minimal flow
Note that along the edge $(t, s)$ (from the old sink to the old source) with the capacity $\infty$ flows the entire flow of the corresponding old network.
I.e. the capacity of this edge effects the flow value of the old network.
By giving this edge a sufficient large capacity (i.e. $\infty$), the flow of the old network is unlimited.
By limiting this edge by smaller capacities, the flow value will decrease.
However if we limit this edge by a too small value, than the network will not have a saturated solution, e.g. the corresponding solution for the original network will not satisfy the demand of the edges.
Obviously here can use a binary search to find the lowest value with which all constraints are still satisfied.
This gives the minimal flow of the original network.
|
---
title
flow_with_limits
---
# Flows with demands
In a normal flow network the flow of an edge is only limited by the capacity $c(e)$ from above and by 0 from below.
In this article we will discuss flow networks, where we additionally require the flow of each edge to have a certain amount, i.e. we bound the flow from below by a **demand** function $d(e)$:
$$ d(e) \le f(e) \le c(e)$$
So next each edge has a minimal flow value, that we have to pass along the edge.
This is a generalization of the normal flow problem, since setting $d(e) = 0$ for all edges $e$ gives a normal flow network.
Notice, that in the normal flow network it is extremely trivial to find a valid flow, just setting $f(e) = 0$ is already a valid one.
However if the flow of each edge has to satisfy a demand, than suddenly finding a valid flow is already pretty complicated.
We will consider two problems:
1. finding an arbitrary flow that satisfies all constraints
2. finding a minimal flow that satisfies all constraints
## Finding an arbitrary flow
We make the following changes in the network.
We add a new source $s'$ and a new sink $t'$, a new edge from the source $s'$ to every other vertex, a new edge for every vertex to the sink $t'$, and one edge from $t$ to $s$.
Additionally we define the new capacity function $c'$ as:
- $c'((s', v)) = \sum_{u \in V} d((u, v))$ for each edge $(s', v)$.
- $c'((v, t')) = \sum_{w \in V} d((v, w))$ for each edge $(v, t')$.
- $c'((u, v)) = c((u, v)) - d((u, v))$ for each edge $(u, v)$ in the old network.
- $c'((t, s)) = \infty$
If the new network has a saturating flow (a flow where each edge outgoing from $s'$ is completely filled, which is equivalent to every edge incoming to $t'$ is completely filled), then the network with demands has a valid flow, and the actual flow can be easily reconstructed from the new network.
Otherwise there doesn't exist a flow that satisfies all conditions.
Since a saturating flow has to be a maximum flow, it can be found by any maximum flow algorithm, like the [Edmonds-Karp algorithm](edmonds_karp.md) or the [Push-relabel algorithm](push-relabel.md).
The correctness of these transformations is more difficult to understand.
We can think of it in the following way:
Each edge $e = (u, v)$ with $d(e) > 0$ is originally replaced by two edges: one with the capacity $d(i)$ , and the other with $c(i) - d(i)$.
We want to find a flow that saturates the first edge (i.e. the flow along this edge must be equal to its capacity).
The second edge is less important - the flow along it can be anything, assuming that it doesn't exceed its capacity.
Consider each edge that has to be saturated, and we perform the following operation:
we draw the edge from the new source $s'$ to its end $v$, draw the edge from its start $u$ to the new sink $t'$, remove the edge itself, and from the old sink $t$ to the old source $s$ we draw an edge of infinite capacity.
By these actions we simulate the fact that this edge is saturated - from $v$ there will be an additionally $d(e)$ flow outgoing (we simulate it with a new source that feeds the right amount of flow to $v$), and $u$ will also push $d(e)$ additional flow (but instead along the old edge, this flow will go directly to the new sink $t'$).
A flow with the value $d(e)$, that originally flowed along the path $s - \dots - u - v - \dots t$ can now take the new path $s' - v - \dots - t - s - \dots - u - t'$.
The only thing that got simplified in the definition of the new network, is that if procedure created multiple edges between the same pair of vertices, then they are combined to one single edge with the summed capacity.
## Minimal flow
Note that along the edge $(t, s)$ (from the old sink to the old source) with the capacity $\infty$ flows the entire flow of the corresponding old network.
I.e. the capacity of this edge effects the flow value of the old network.
By giving this edge a sufficient large capacity (i.e. $\infty$), the flow of the old network is unlimited.
By limiting this edge by smaller capacities, the flow value will decrease.
However if we limit this edge by a too small value, than the network will not have a saturated solution, e.g. the corresponding solution for the original network will not satisfy the demand of the edges.
Obviously here can use a binary search to find the lowest value with which all constraints are still satisfied.
This gives the minimal flow of the original network.
|
Flows with demands
|
---
title
fixed_length_paths
---
# Number of paths of fixed length / Shortest paths of fixed length
The following article describes solutions to these two problems built on the same idea:
reduce the problem to the construction of matrix and compute the solution with the usual matrix multiplication or with a modified multiplication.
## Number of paths of a fixed length
We are given a directed, unweighted graph $G$ with $n$ vertices and we are given an integer $k$.
The task is the following:
for each pair of vertices $(i, j)$ we have to find the number of paths of length $k$ between these vertices.
Paths don't have to be simple, i.e. vertices and edges can be visited any number of times in a single path.
We assume that the graph is specified with an adjacency matrix, i.e. the matrix $G[][]$ of size $n \times n$, where each element $G[i][j]$ equal to $1$ if the vertex $i$ is connected with $j$ by an edge, and $0$ is they are not connected by an edge.
The following algorithm works also in the case of multiple edges:
if some pair of vertices $(i, j)$ is connected with $m$ edges, then we can record this in the adjacency matrix by setting $G[i][j] = m$.
Also the algorithm works if the graph contains loops (a loop is an edge that connect a vertex with itself).
It is obvious that the constructed adjacency matrix if the answer to the problem for the case $k = 1$.
It contains the number of paths of length $1$ between each pair of vertices.
We will build the solution iteratively:
Let's assume we know the answer for some $k$.
Here we describe a method how we can construct the answer for $k + 1$.
Denote by $C_k$ the matrix for the case $k$, and by $C_{k+1}$ the matrix we want to construct.
With the following formula we can compute every entry of $C_{k+1}$:
$$C_{k+1}[i][j] = \sum_{p = 1}^{n} C_k[i][p] \cdot G[p][j]$$
It is easy to see that the formula computes nothing other than the product of the matrices $C_k$ and $G$:
$$C_{k+1} = C_k \cdot G$$
Thus the solution of the problem can be represented as follows:
$$C_k = \underbrace{G \cdot G \cdots G}_{k \text{ times}} = G^k$$
It remains to note that the matrix products can be raised to a high power efficiently using [Binary exponentiation](../algebra/binary-exp.md).
This gives a solution with $O(n^3 \log k)$ complexity.
## Shortest paths of a fixed length
We are given a directed weighted graph $G$ with $n$ vertices and an integer $k$.
For each pair of vertices $(i, j)$ we have to find the length of the shortest path between $i$ and $j$ that consists of exactly $k$ edges.
We assume that the graph is specified by an adjacency matrix, i.e. via the matrix $G[][]$ of size $n \times n$ where each element $G[i][j]$ contains the length of the edges from the vertex $i$ to the vertex $j$.
If there is no edge between two vertices, then the corresponding element of the matrix will be assigned to infinity $\infty$.
It is obvious that in this form the adjacency matrix is the answer to the problem for $k = 1$.
It contains the lengths of shortest paths between each pair of vertices, or $\infty$ if a path consisting of one edge doesn't exist.
Again we can build the solution to the problem iteratively:
Let's assume we know the answer for some $k$.
We show how we can compute the answer for $k+1$.
Let us denote $L_k$ the matrix for $k$ and $L_{k+1}$ the matrix we want to build.
Then the following formula computes each entry of $L_{k+1}$:
$$L_{k+1}[i][j] = \min_{p = 1 \ldots n} \left(L_k[i][p] + G[p][j]\right)$$
When looking closer at this formula, we can draw an analogy with the matrix multiplication:
in fact the matrix $L_k$ is multiplied by the matrix $G$, the only difference is that instead in the multiplication operation we take the minimum instead of the sum.
$$L_{k+1} = L_k \odot G,$$
where the operation $\odot$ is defined as follows:
$$A \odot B = C~~\Longleftrightarrow~~C_{i j} = \min_{p = 1 \ldots n}\left(A_{i p} + B_{p j}\right)$$
Thus the solution of the task can be represented using the modified multiplication:
$$L_k = \underbrace{G \odot \ldots \odot G}_{k~\text{times}} = G^{\odot k}$$
It remains to note that we also can compute this exponentiation efficiently with [Binary exponentiation](../algebra/binary-exp.md), because the modified multiplication is obviously associative.
So also this solution has $O(n^3 \log k)$ complexity.
## Generalization of the problems for paths with length up to $k$ {data-toc-label="Generalization of the problems for paths with length up to k"}
The above solutions solve the problems for a fixed $k$.
However the solutions can be adapted for solving problems for which the paths are allowed to contain no more than $k$ edges.
This can be done by slightly modifying the input graph.
We duplicate each vertex:
for each vertex $v$ we create one more vertex $v'$ and add the edge $(v, v')$ and the loop $(v', v')$.
The number of paths between $i$ and $j$ with at most $k$ edges is the same number as the number of paths between $i$ and $j'$ with exactly $k + 1$ edges, since there is a bijection that maps every path $[p_0 = i,~p_1,~\ldots,~p_{m-1},~p_m = j]$ of length $m \le k$ to the path $[p_0 = i,~p_1,~\ldots,~p_{m-1},~p_m = j, j', \ldots, j']$ of length $k + 1$.
The same trick can be applied to compute the shortest paths with at most $k$ edges.
We again duplicate each vertex and add the two mentioned edges with weight $0$.
|
---
title
fixed_length_paths
---
# Number of paths of fixed length / Shortest paths of fixed length
The following article describes solutions to these two problems built on the same idea:
reduce the problem to the construction of matrix and compute the solution with the usual matrix multiplication or with a modified multiplication.
## Number of paths of a fixed length
We are given a directed, unweighted graph $G$ with $n$ vertices and we are given an integer $k$.
The task is the following:
for each pair of vertices $(i, j)$ we have to find the number of paths of length $k$ between these vertices.
Paths don't have to be simple, i.e. vertices and edges can be visited any number of times in a single path.
We assume that the graph is specified with an adjacency matrix, i.e. the matrix $G[][]$ of size $n \times n$, where each element $G[i][j]$ equal to $1$ if the vertex $i$ is connected with $j$ by an edge, and $0$ is they are not connected by an edge.
The following algorithm works also in the case of multiple edges:
if some pair of vertices $(i, j)$ is connected with $m$ edges, then we can record this in the adjacency matrix by setting $G[i][j] = m$.
Also the algorithm works if the graph contains loops (a loop is an edge that connect a vertex with itself).
It is obvious that the constructed adjacency matrix if the answer to the problem for the case $k = 1$.
It contains the number of paths of length $1$ between each pair of vertices.
We will build the solution iteratively:
Let's assume we know the answer for some $k$.
Here we describe a method how we can construct the answer for $k + 1$.
Denote by $C_k$ the matrix for the case $k$, and by $C_{k+1}$ the matrix we want to construct.
With the following formula we can compute every entry of $C_{k+1}$:
$$C_{k+1}[i][j] = \sum_{p = 1}^{n} C_k[i][p] \cdot G[p][j]$$
It is easy to see that the formula computes nothing other than the product of the matrices $C_k$ and $G$:
$$C_{k+1} = C_k \cdot G$$
Thus the solution of the problem can be represented as follows:
$$C_k = \underbrace{G \cdot G \cdots G}_{k \text{ times}} = G^k$$
It remains to note that the matrix products can be raised to a high power efficiently using [Binary exponentiation](../algebra/binary-exp.md).
This gives a solution with $O(n^3 \log k)$ complexity.
## Shortest paths of a fixed length
We are given a directed weighted graph $G$ with $n$ vertices and an integer $k$.
For each pair of vertices $(i, j)$ we have to find the length of the shortest path between $i$ and $j$ that consists of exactly $k$ edges.
We assume that the graph is specified by an adjacency matrix, i.e. via the matrix $G[][]$ of size $n \times n$ where each element $G[i][j]$ contains the length of the edges from the vertex $i$ to the vertex $j$.
If there is no edge between two vertices, then the corresponding element of the matrix will be assigned to infinity $\infty$.
It is obvious that in this form the adjacency matrix is the answer to the problem for $k = 1$.
It contains the lengths of shortest paths between each pair of vertices, or $\infty$ if a path consisting of one edge doesn't exist.
Again we can build the solution to the problem iteratively:
Let's assume we know the answer for some $k$.
We show how we can compute the answer for $k+1$.
Let us denote $L_k$ the matrix for $k$ and $L_{k+1}$ the matrix we want to build.
Then the following formula computes each entry of $L_{k+1}$:
$$L_{k+1}[i][j] = \min_{p = 1 \ldots n} \left(L_k[i][p] + G[p][j]\right)$$
When looking closer at this formula, we can draw an analogy with the matrix multiplication:
in fact the matrix $L_k$ is multiplied by the matrix $G$, the only difference is that instead in the multiplication operation we take the minimum instead of the sum.
$$L_{k+1} = L_k \odot G,$$
where the operation $\odot$ is defined as follows:
$$A \odot B = C~~\Longleftrightarrow~~C_{i j} = \min_{p = 1 \ldots n}\left(A_{i p} + B_{p j}\right)$$
Thus the solution of the task can be represented using the modified multiplication:
$$L_k = \underbrace{G \odot \ldots \odot G}_{k~\text{times}} = G^{\odot k}$$
It remains to note that we also can compute this exponentiation efficiently with [Binary exponentiation](../algebra/binary-exp.md), because the modified multiplication is obviously associative.
So also this solution has $O(n^3 \log k)$ complexity.
## Generalization of the problems for paths with length up to $k$ {data-toc-label="Generalization of the problems for paths with length up to k"}
The above solutions solve the problems for a fixed $k$.
However the solutions can be adapted for solving problems for which the paths are allowed to contain no more than $k$ edges.
This can be done by slightly modifying the input graph.
We duplicate each vertex:
for each vertex $v$ we create one more vertex $v'$ and add the edge $(v, v')$ and the loop $(v', v')$.
The number of paths between $i$ and $j$ with at most $k$ edges is the same number as the number of paths between $i$ and $j'$ with exactly $k + 1$ edges, since there is a bijection that maps every path $[p_0 = i,~p_1,~\ldots,~p_{m-1},~p_m = j]$ of length $m \le k$ to the path $[p_0 = i,~p_1,~\ldots,~p_{m-1},~p_m = j, j', \ldots, j']$ of length $k + 1$.
The same trick can be applied to compute the shortest paths with at most $k$ edges.
We again duplicate each vertex and add the two mentioned edges with weight $0$.
|
Number of paths of fixed length / Shortest paths of fixed length
|
---
title
kuhn_matching
---
# Kuhn's Algorithm for Maximum Bipartite Matching
## Problem
You are given a bipartite graph $G$ containing $n$ vertices and $m$ edges. Find the maximum matching, i.e., select as many edges as possible so
that no selected edge shares a vertex with any other selected edge.
## Algorithm Description
### Required Definitions
* A **matching** $M$ is a set of pairwise non-adjacent edges of a graph (in other words, no more than one edge from the set should be incident to any vertex of the graph $M$).
The **cardinality** of a matching is the number of edges in it.
All those vertices that have an adjacent edge from the matching (i.e., which have degree exactly one in the subgraph formed by $M$) are called **saturated**
by this matching.
* A **maximal matching** is a matching $M$ of a graph $G$ that is not a subset of any other matching.
* A **maximum matching** (also known as maximum-cardinality matching) is a matching that contains the largest possible number of edges. Every maximum matching is a maximal matching.
* A **path** of length $k$ here means a *simple* path (i.e. not containing repeated vertices or edges) containing $k$ edges, unless specified otherwise.
* An **alternating path** (in a bipartite graph, with respect to some matching) is a path in which the edges alternately belong / do not belong to the matching.
* An **augmenting path** (in a bipartite graph, with respect to some matching) is an alternating path whose initial and final vertices are unsaturated, i.e.,
they do not belong in the matching.
* The **symmetric difference** (also known as the **disjunctive union**) of sets $A$ and $B$, represented by $A \oplus B$, is the set of all elements that belong to exactly one of $A$ or $B$, but not to both.
That is, $A \oplus B = (A - B) \cup (B - A) = (A \cup B) - (A \cap B)$.
### Berge's lemma
This lemma was proven by the French mathematician **Claude Berge** in 1957, although it already was observed by the Danish mathematician **Julius Petersen** in 1891 and
the Hungarian mathematician **Denés Kőnig** in 1931.
#### Formulation
A matching $M$ is maximum $\Leftrightarrow$ there is no augmenting path relative to the matching $M$.
#### Proof
Both sides of the bi-implication will be proven by contradiction.
1. A matching $M$ is maximum $\Rightarrow$ there is no augmenting path relative to the matching $M$.
Let there be an augmenting path $P$ relative to the given maximum matching $M$. This augmenting path $P$ will necessarily be of odd length, having one more edge not in $M$ than the number of edges it has that are also in $M$.
We create a new matching $M'$ by including all edges in the original matching $M$ except those also in the $P$, and the edges in $P$ that are not in $M$.
This is a valid matching because the initial and final vertices of $P$ are unsaturated by $M$, and the rest of the vertices are saturated only by the matching $P \cap M$.
This new matching $M'$ will have one more edge than $M$, and so $M$ could not have been maximum.
Formally, given an augmenting path $P$ w.r.t. some maximum matching $M$, the matching $M' = P \oplus M$ is such that $|M'| = |M| + 1$, a contradiction.
2. A matching $M$ is maximum $\Leftarrow$ there is no augmenting path relative to the matching $M$.
Let there be a matching $M'$ of greater cardinality than $M$. We consider the symmetric difference $Q = M \oplus M'$. The subgraph $Q$ is no longer necessarily a matching.
Any vertex in $Q$ has a maximum degree of $2$, which means that all connected components in it are one of the three -
* an isolated vertex
* a (simple) path whose edges are alternately from $M$ and $M'$
* a cycle of even length whose edges are alternately from $M$ and $M'$
Since $M'$ has a cardinality greater than $M$, $Q$ has more edges from $M'$ than $M$. By the Pigeonhole principle, at least one connected component will be a path having
more edges from $M'$ than $M$. Because any such path is alternating, it will have initial and final vertices unsaturated by $M$, making it an augmenting path for $M$,
which contradicts the premise.   $\blacksquare$
### Kuhn's algorithm
Kuhn's algorithm is a direct application of Berge's lemma. It is essentially described as follows:
First, we take an empty matching. Then, while the algorithm is able to find an augmenting path, we update the matching by alternating it along this path and repeat the process of finding the augmenting path. As soon as it is not possible to find such a path, we stop the process - the current matching is the maximum.
It remains to detail the way to find augmenting paths. Kuhn's algorithm simply searches for any of these paths using [depth-first](depth-first-search.md) or [breadth-first](breadth-first-search.md) traversal. The algorithm
looks through all the vertices of the graph in turn, starting each traversal from it, trying to find an augmenting path starting at this vertex.
The algorithm is more convenient to describe if we assume that the input graph is already split into two parts (although, in fact, the algorithm can be implemented in such a way
that the input graph is not explicitly split into two parts).
The algorithm looks at all the vertices $v$ of the first part of the graph: $v = 1 \ldots n_1$. If the current vertex $v$ is already saturated with the current matching
(i.e., some edge adjacent to it has already been selected), then skip this vertex. Otherwise, the algorithm tries to saturate this vertex, for which it starts
a search for an augmenting path starting from this vertex.
The search for an augmenting path is carried out using a special depth-first or breadth-first traversal (usually depth-first traversal is used for ease of implementation).
Initially, the depth-first traversal is at the current unsaturated vertex $v$ of the first part. Let's look through all edges from this vertex. Let the current edge be an edge
$(v, to)$. If the vertex $to$ is not yet saturated with matching, then we have succeeded in finding an augmenting path: it consists of a single edge $(v, to)$;
in this case, we simply include this edge in the matching and stop searching for the augmenting path from the vertex $v$. Otherwise, if $to$ is already saturated with some edge
$(to, p)$,
then will go along this edge: thus we will try to find an augmenting path passing through the edges $(v, to),(to, p), \ldots$.
To do this, simply go to the vertex $p$ in our traversal - now we try to find an augmenting path from this vertex.
So, this traversal, launched from the vertex $v$, will either find an augmenting path, and thereby saturate the vertex $v$, or it will not find such an augmenting path (and, therefore, this vertex $v$ cannot be saturated).
After all the vertices $v = 1 \ldots n_1$ have been scanned, the current matching will be maximum.
### Running time
Kuhn's algorithm can be thought of as a series of $n$ depth/breadth-first traversal runs on the entire graph. Therefore, the whole algorithm is executed in time $O(nm)$, which
in the worst case is $O(n^3)$.
However, this estimate can be improved slightly. It turns out that for Kuhn's algorithm, it is important which part of the graph is chosen as the first and which as the second.
Indeed, in the implementation described above, the depth/breadth-first traversal starts only from the vertices of the first part, so the entire algorithm is executed in
time $O(n_1m)$, where $n_1$ is the number of vertices of the first part. In the worst case, this is $O(n_1 ^ 2 n_2)$ (where $n_2$ is the number of vertices of the second part).
This shows that it is more profitable when the first part contains fewer vertices than the second. On very unbalanced graphs (when $n_1$ and $n_2$ are very different),
this translates into a significant difference in runtimes.
## Implementation
### Standard implementation
Let us present here an implementation of the above algorithm based on depth-first traversal and accepting a bipartite graph in the form of a graph explicitly split into two parts.
This implementation is very concise, and perhaps it should be remembered in this form.
Here $n$ is the number of vertices in the first part, $k$ - in the second part, $g[v]$ is the list of edges from the top of the first part (i.e. the list of numbers of the
vertices to which these edges lead from $v$). The vertices in both parts are numbered independently, i.e. vertices in the first part are numbered $1 \ldots n$, and those in the
second are numbered $1 \ldots k$.
Then there are two auxiliary arrays: $\rm mt$ and $\rm used$. The first - $\rm mt$ - contains information about the current matching. For convenience of programming,
this information is contained only for the vertices of the second part: $\textrm{mt[} i \rm]$ - this is the number of the vertex of the first part connected by an edge with the vertex $i$ of
the second part (or $-1$, if no matching edge comes out of it). The second array is $\rm used$: the usual array of "visits" to the vertices in the depth-first traversal
(it is needed just so that the depth-first traversal does not enter the same vertex twice).
A function $\textrm{try_kuhn}$ is a depth-first traversal. It returns $\rm true$ if it was able to find an augmenting path from the vertex $v$, and it is considered that this
function has already performed the alternation of matching along the found chain.
Inside the function, all the edges outgoing from the vertex $v$ of the first part are scanned, and then the following is checked: if this edge leads to an unsaturated vertex
$to$, or if this vertex $to$ is saturated, but it is possible to find an increasing chain by recursively starting from $\textrm{mt[}to \rm ]$, then we say that we have found an
augmenting path, and before returning from the function with the result $\rm true$, we alternate the current edge: we redirect the edge adjacent to $to$ to the vertex $v$.
The main program first indicates that the current matching is empty (the list $\rm mt$ is filled with numbers $-1$). Then the vertex $v$ of the first part is searched by $\textrm{try_kuhn}$,
and a depth-first traversal is started from it, having previously zeroed the array $\rm used$.
It is worth noting that the size of the matching is easy to get as the number of calls $\textrm{try_kuhn}$ in the main program that returned the result $\rm true$. The desired
maximum matching itself is contained in the array $\rm mt$.
```cpp
int n, k;
vector<vector<int>> g;
vector<int> mt;
vector<bool> used;
bool try_kuhn(int v) {
if (used[v])
return false;
used[v] = true;
for (int to : g[v]) {
if (mt[to] == -1 || try_kuhn(mt[to])) {
mt[to] = v;
return true;
}
}
return false;
}
int main() {
//... reading the graph ...
mt.assign(k, -1);
for (int v = 0; v < n; ++v) {
used.assign(n, false);
try_kuhn(v);
}
for (int i = 0; i < k; ++i)
if (mt[i] != -1)
printf("%d %d\n", mt[i] + 1, i + 1);
}
```
We repeat once again that Kuhn's algorithm is easy to implement in such a way that it works on graphs that are known to be bipartite, but their explicit splitting into two parts
has not been given. In this case, it will be necessary to abandon the convenient division into two parts, and store all the information for all vertices of the graph. For this,
an array of lists $g$ is now specified not only for the vertices of the first part, but for all the vertices of the graph (of course, now the vertices of both parts are numbered
in a common numbering - from $1$ to $n$). Arrays $\rm mt$ and are $\rm used$ are now also defined for the vertices of both parts, and, accordingly, they need to be kept in this state.
### Improved implementation
Let us modify the algorithm as follows. Before the main loop of the algorithm, we will find an **arbitrary matching** by some simple algorithm (a simple **heuristic algorithm**),
and only then we will execute a loop with calls to the $\textrm{try_kuhn}()$ function, which will improve this matching. As a result, the algorithm will work noticeably faster on
random graphs - because in most graphs, you can easily find a matching of a sufficiently large size using heuristics, and then improve the found matching to the maximum using
the usual Kuhn's algorithm. Thus, we will save on launching a depth-first traversal from those vertices that we have already included using the heuristic into the current matching.
For example, you can simply iterate over all the vertices of the first part, and for each of them, find an arbitrary edge that can be added to the matching, and add it.
Even such a simple heuristic can speed up Kuhn's algorithm several times.
Please note that the main loop will have to be slightly modified. Since when calling the function $\textrm{try_kuhn}$ in the main loop, it is assumed that the current vertex is
not yet included in the matching, you need to add an appropriate check.
In the implementation, only the code in the $\textrm{main}()$ function will change:
```cpp
int main() {
// ... reading the graph ...
mt.assign(k, -1);
vector<bool> used1(n, false);
for (int v = 0; v < n; ++v) {
for (int to : g[v]) {
if (mt[to] == -1) {
mt[to] = v;
used1[v] = true;
break;
}
}
}
for (int v = 0; v < n; ++v) {
if (used1[v])
continue;
used.assign(n, false);
try_kuhn(v);
}
for (int i = 0; i < k; ++i)
if (mt[i] != -1)
printf("%d %d\n", mt[i] + 1, i + 1);
}
```
**Another good heuristic** is as follows. At each step, it will search for the vertex of the smallest degree (but not isolated), select any edge from it and add it to the matching,
then remove both these vertices with all incident edges from the graph. Such greed works very well on random graphs; in many cases it even builds the maximum matching (although
there is a test case against it, on which it will find a matching that is much smaller than the maximum).
## Notes
* Kuhn's algorithm is a subroutine in the **Hungarian algorithm**, also known as the **Kuhn-Munkres algorithm**.
* Kuhn's algorithm runs in $O(nm)$ time. It is generally simple to implement, however, more efficient algorithms exist for the maximum bipartite matching problem - such as the
**Hopcroft-Karp-Karzanov algorithm**, which runs in $O(\sqrt{n}m)$ time.
* The [minimum vertex cover problem](https://en.wikipedia.org/wiki/Vertex_cover) is NP-hard for general graphs. However, [Kőnig's theorem](https://en.wikipedia.org/wiki/K%C5%91nig%27s_theorem_(graph_theory)) gives that, for bipartite graphs, the cardinality of the maximum matching equals the cardinality of the minimum vertex cover. Hence, we can use maximum bipartite matching algorithms to solve the minimum vertex cover problem in polynomial time for bipartite graphs.
|
---
title
kuhn_matching
---
# Kuhn's Algorithm for Maximum Bipartite Matching
## Problem
You are given a bipartite graph $G$ containing $n$ vertices and $m$ edges. Find the maximum matching, i.e., select as many edges as possible so
that no selected edge shares a vertex with any other selected edge.
## Algorithm Description
### Required Definitions
* A **matching** $M$ is a set of pairwise non-adjacent edges of a graph (in other words, no more than one edge from the set should be incident to any vertex of the graph $M$).
The **cardinality** of a matching is the number of edges in it.
All those vertices that have an adjacent edge from the matching (i.e., which have degree exactly one in the subgraph formed by $M$) are called **saturated**
by this matching.
* A **maximal matching** is a matching $M$ of a graph $G$ that is not a subset of any other matching.
* A **maximum matching** (also known as maximum-cardinality matching) is a matching that contains the largest possible number of edges. Every maximum matching is a maximal matching.
* A **path** of length $k$ here means a *simple* path (i.e. not containing repeated vertices or edges) containing $k$ edges, unless specified otherwise.
* An **alternating path** (in a bipartite graph, with respect to some matching) is a path in which the edges alternately belong / do not belong to the matching.
* An **augmenting path** (in a bipartite graph, with respect to some matching) is an alternating path whose initial and final vertices are unsaturated, i.e.,
they do not belong in the matching.
* The **symmetric difference** (also known as the **disjunctive union**) of sets $A$ and $B$, represented by $A \oplus B$, is the set of all elements that belong to exactly one of $A$ or $B$, but not to both.
That is, $A \oplus B = (A - B) \cup (B - A) = (A \cup B) - (A \cap B)$.
### Berge's lemma
This lemma was proven by the French mathematician **Claude Berge** in 1957, although it already was observed by the Danish mathematician **Julius Petersen** in 1891 and
the Hungarian mathematician **Denés Kőnig** in 1931.
#### Formulation
A matching $M$ is maximum $\Leftrightarrow$ there is no augmenting path relative to the matching $M$.
#### Proof
Both sides of the bi-implication will be proven by contradiction.
1. A matching $M$ is maximum $\Rightarrow$ there is no augmenting path relative to the matching $M$.
Let there be an augmenting path $P$ relative to the given maximum matching $M$. This augmenting path $P$ will necessarily be of odd length, having one more edge not in $M$ than the number of edges it has that are also in $M$.
We create a new matching $M'$ by including all edges in the original matching $M$ except those also in the $P$, and the edges in $P$ that are not in $M$.
This is a valid matching because the initial and final vertices of $P$ are unsaturated by $M$, and the rest of the vertices are saturated only by the matching $P \cap M$.
This new matching $M'$ will have one more edge than $M$, and so $M$ could not have been maximum.
Formally, given an augmenting path $P$ w.r.t. some maximum matching $M$, the matching $M' = P \oplus M$ is such that $|M'| = |M| + 1$, a contradiction.
2. A matching $M$ is maximum $\Leftarrow$ there is no augmenting path relative to the matching $M$.
Let there be a matching $M'$ of greater cardinality than $M$. We consider the symmetric difference $Q = M \oplus M'$. The subgraph $Q$ is no longer necessarily a matching.
Any vertex in $Q$ has a maximum degree of $2$, which means that all connected components in it are one of the three -
* an isolated vertex
* a (simple) path whose edges are alternately from $M$ and $M'$
* a cycle of even length whose edges are alternately from $M$ and $M'$
Since $M'$ has a cardinality greater than $M$, $Q$ has more edges from $M'$ than $M$. By the Pigeonhole principle, at least one connected component will be a path having
more edges from $M'$ than $M$. Because any such path is alternating, it will have initial and final vertices unsaturated by $M$, making it an augmenting path for $M$,
which contradicts the premise.   $\blacksquare$
### Kuhn's algorithm
Kuhn's algorithm is a direct application of Berge's lemma. It is essentially described as follows:
First, we take an empty matching. Then, while the algorithm is able to find an augmenting path, we update the matching by alternating it along this path and repeat the process of finding the augmenting path. As soon as it is not possible to find such a path, we stop the process - the current matching is the maximum.
It remains to detail the way to find augmenting paths. Kuhn's algorithm simply searches for any of these paths using [depth-first](depth-first-search.md) or [breadth-first](breadth-first-search.md) traversal. The algorithm
looks through all the vertices of the graph in turn, starting each traversal from it, trying to find an augmenting path starting at this vertex.
The algorithm is more convenient to describe if we assume that the input graph is already split into two parts (although, in fact, the algorithm can be implemented in such a way
that the input graph is not explicitly split into two parts).
The algorithm looks at all the vertices $v$ of the first part of the graph: $v = 1 \ldots n_1$. If the current vertex $v$ is already saturated with the current matching
(i.e., some edge adjacent to it has already been selected), then skip this vertex. Otherwise, the algorithm tries to saturate this vertex, for which it starts
a search for an augmenting path starting from this vertex.
The search for an augmenting path is carried out using a special depth-first or breadth-first traversal (usually depth-first traversal is used for ease of implementation).
Initially, the depth-first traversal is at the current unsaturated vertex $v$ of the first part. Let's look through all edges from this vertex. Let the current edge be an edge
$(v, to)$. If the vertex $to$ is not yet saturated with matching, then we have succeeded in finding an augmenting path: it consists of a single edge $(v, to)$;
in this case, we simply include this edge in the matching and stop searching for the augmenting path from the vertex $v$. Otherwise, if $to$ is already saturated with some edge
$(to, p)$,
then will go along this edge: thus we will try to find an augmenting path passing through the edges $(v, to),(to, p), \ldots$.
To do this, simply go to the vertex $p$ in our traversal - now we try to find an augmenting path from this vertex.
So, this traversal, launched from the vertex $v$, will either find an augmenting path, and thereby saturate the vertex $v$, or it will not find such an augmenting path (and, therefore, this vertex $v$ cannot be saturated).
After all the vertices $v = 1 \ldots n_1$ have been scanned, the current matching will be maximum.
### Running time
Kuhn's algorithm can be thought of as a series of $n$ depth/breadth-first traversal runs on the entire graph. Therefore, the whole algorithm is executed in time $O(nm)$, which
in the worst case is $O(n^3)$.
However, this estimate can be improved slightly. It turns out that for Kuhn's algorithm, it is important which part of the graph is chosen as the first and which as the second.
Indeed, in the implementation described above, the depth/breadth-first traversal starts only from the vertices of the first part, so the entire algorithm is executed in
time $O(n_1m)$, where $n_1$ is the number of vertices of the first part. In the worst case, this is $O(n_1 ^ 2 n_2)$ (where $n_2$ is the number of vertices of the second part).
This shows that it is more profitable when the first part contains fewer vertices than the second. On very unbalanced graphs (when $n_1$ and $n_2$ are very different),
this translates into a significant difference in runtimes.
## Implementation
### Standard implementation
Let us present here an implementation of the above algorithm based on depth-first traversal and accepting a bipartite graph in the form of a graph explicitly split into two parts.
This implementation is very concise, and perhaps it should be remembered in this form.
Here $n$ is the number of vertices in the first part, $k$ - in the second part, $g[v]$ is the list of edges from the top of the first part (i.e. the list of numbers of the
vertices to which these edges lead from $v$). The vertices in both parts are numbered independently, i.e. vertices in the first part are numbered $1 \ldots n$, and those in the
second are numbered $1 \ldots k$.
Then there are two auxiliary arrays: $\rm mt$ and $\rm used$. The first - $\rm mt$ - contains information about the current matching. For convenience of programming,
this information is contained only for the vertices of the second part: $\textrm{mt[} i \rm]$ - this is the number of the vertex of the first part connected by an edge with the vertex $i$ of
the second part (or $-1$, if no matching edge comes out of it). The second array is $\rm used$: the usual array of "visits" to the vertices in the depth-first traversal
(it is needed just so that the depth-first traversal does not enter the same vertex twice).
A function $\textrm{try_kuhn}$ is a depth-first traversal. It returns $\rm true$ if it was able to find an augmenting path from the vertex $v$, and it is considered that this
function has already performed the alternation of matching along the found chain.
Inside the function, all the edges outgoing from the vertex $v$ of the first part are scanned, and then the following is checked: if this edge leads to an unsaturated vertex
$to$, or if this vertex $to$ is saturated, but it is possible to find an increasing chain by recursively starting from $\textrm{mt[}to \rm ]$, then we say that we have found an
augmenting path, and before returning from the function with the result $\rm true$, we alternate the current edge: we redirect the edge adjacent to $to$ to the vertex $v$.
The main program first indicates that the current matching is empty (the list $\rm mt$ is filled with numbers $-1$). Then the vertex $v$ of the first part is searched by $\textrm{try_kuhn}$,
and a depth-first traversal is started from it, having previously zeroed the array $\rm used$.
It is worth noting that the size of the matching is easy to get as the number of calls $\textrm{try_kuhn}$ in the main program that returned the result $\rm true$. The desired
maximum matching itself is contained in the array $\rm mt$.
```cpp
int n, k;
vector<vector<int>> g;
vector<int> mt;
vector<bool> used;
bool try_kuhn(int v) {
if (used[v])
return false;
used[v] = true;
for (int to : g[v]) {
if (mt[to] == -1 || try_kuhn(mt[to])) {
mt[to] = v;
return true;
}
}
return false;
}
int main() {
//... reading the graph ...
mt.assign(k, -1);
for (int v = 0; v < n; ++v) {
used.assign(n, false);
try_kuhn(v);
}
for (int i = 0; i < k; ++i)
if (mt[i] != -1)
printf("%d %d\n", mt[i] + 1, i + 1);
}
```
We repeat once again that Kuhn's algorithm is easy to implement in such a way that it works on graphs that are known to be bipartite, but their explicit splitting into two parts
has not been given. In this case, it will be necessary to abandon the convenient division into two parts, and store all the information for all vertices of the graph. For this,
an array of lists $g$ is now specified not only for the vertices of the first part, but for all the vertices of the graph (of course, now the vertices of both parts are numbered
in a common numbering - from $1$ to $n$). Arrays $\rm mt$ and are $\rm used$ are now also defined for the vertices of both parts, and, accordingly, they need to be kept in this state.
### Improved implementation
Let us modify the algorithm as follows. Before the main loop of the algorithm, we will find an **arbitrary matching** by some simple algorithm (a simple **heuristic algorithm**),
and only then we will execute a loop with calls to the $\textrm{try_kuhn}()$ function, which will improve this matching. As a result, the algorithm will work noticeably faster on
random graphs - because in most graphs, you can easily find a matching of a sufficiently large size using heuristics, and then improve the found matching to the maximum using
the usual Kuhn's algorithm. Thus, we will save on launching a depth-first traversal from those vertices that we have already included using the heuristic into the current matching.
For example, you can simply iterate over all the vertices of the first part, and for each of them, find an arbitrary edge that can be added to the matching, and add it.
Even such a simple heuristic can speed up Kuhn's algorithm several times.
Please note that the main loop will have to be slightly modified. Since when calling the function $\textrm{try_kuhn}$ in the main loop, it is assumed that the current vertex is
not yet included in the matching, you need to add an appropriate check.
In the implementation, only the code in the $\textrm{main}()$ function will change:
```cpp
int main() {
// ... reading the graph ...
mt.assign(k, -1);
vector<bool> used1(n, false);
for (int v = 0; v < n; ++v) {
for (int to : g[v]) {
if (mt[to] == -1) {
mt[to] = v;
used1[v] = true;
break;
}
}
}
for (int v = 0; v < n; ++v) {
if (used1[v])
continue;
used.assign(n, false);
try_kuhn(v);
}
for (int i = 0; i < k; ++i)
if (mt[i] != -1)
printf("%d %d\n", mt[i] + 1, i + 1);
}
```
**Another good heuristic** is as follows. At each step, it will search for the vertex of the smallest degree (but not isolated), select any edge from it and add it to the matching,
then remove both these vertices with all incident edges from the graph. Such greed works very well on random graphs; in many cases it even builds the maximum matching (although
there is a test case against it, on which it will find a matching that is much smaller than the maximum).
## Notes
* Kuhn's algorithm is a subroutine in the **Hungarian algorithm**, also known as the **Kuhn-Munkres algorithm**.
* Kuhn's algorithm runs in $O(nm)$ time. It is generally simple to implement, however, more efficient algorithms exist for the maximum bipartite matching problem - such as the
**Hopcroft-Karp-Karzanov algorithm**, which runs in $O(\sqrt{n}m)$ time.
* The [minimum vertex cover problem](https://en.wikipedia.org/wiki/Vertex_cover) is NP-hard for general graphs. However, [Kőnig's theorem](https://en.wikipedia.org/wiki/K%C5%91nig%27s_theorem_(graph_theory)) gives that, for bipartite graphs, the cardinality of the maximum matching equals the cardinality of the minimum vertex cover. Hence, we can use maximum bipartite matching algorithms to solve the minimum vertex cover problem in polynomial time for bipartite graphs.
## Practice Problems
* [Kattis - Gopher II](https://open.kattis.com/problems/gopher2)
* [Kattis - Borders](https://open.kattis.com/problems/borders)
|
Kuhn's Algorithm for Maximum Bipartite Matching
|
---
title
strong_connected_components
---
# Finding strongly connected components / Building condensation graph
## Definitions
You are given a directed graph $G$ with vertices $V$ and edges $E$. It is possible that there are loops and multiple edges. Let's denote $n$ as number of vertices and $m$ as number of edges in $G$.
**Strongly connected component** is a maximal subset of vertices $C$ such that any two vertices of this subset are reachable from each other, i.e. for any $u, v \in C$:
$$u \mapsto v, v \mapsto u$$
where $\mapsto$ means reachability, i.e. existence of the path from first vertex to the second.
It is obvious, that strongly connected components do not intersect each other, i.e. this is a partition of all graph vertices. Thus we can give a definition of condensation graph $G^{SCC}$ as a graph containing every strongly connected component as one vertex. Each vertex of the condensation graph corresponds to the strongly connected component of graph $G$. There is an oriented edge between two vertices $C_i$ and $C_j$ of the condensation graph if and only if there are two vertices $u \in C_i, v \in C_j$ such that there is an edge in initial graph, i.e. $(u, v) \in E$.
The most important property of the condensation graph is that it is **acyclic**. Indeed, suppose that there is an edge between $C$ and $C'$, let's prove that there is no edge from $C'$ to $C$. Suppose that $C' \mapsto C$. Then there are two vertices $u' \in C$ and $v' \in C'$ such that $v' \mapsto u'$. But since $u$ and $u'$ are in the same strongly connected component then there is a path between them; the same for $v$ and $v'$. As a result, if we join these paths we have that $v \mapsto u$ and at the same time $u \mapsto v$. Therefore $u$ and $v$ should be at the same strongly connected component, so this is contradiction. This completes the proof.
The algorithm described in the next section extracts all strongly connected components in a given graph. It is quite easy to build a condensation graph then.
## Description of the algorithm
Described algorithm was independently suggested by Kosaraju and Sharir at 1979. This is an easy-to-implement algorithm based on two series of [depth first search](depth-first-search.md), and working for $O(n + m)$ time.
**On the first step** of the algorithm we are doing sequence of depth first searches, visiting the entire graph. We start at each vertex of the graph and run a depth first search from every non-visited vertex. For each vertex we are keeping track of **exit time** $tout[v]$. These exit times have a key role in an algorithm and this role is expressed in next theorem.
First, let's make notations: let's define exit time $tout[C]$ from the strongly connected component $C$ as maximum of values $tout[v]$ by all $v \in C$. Besides, during the proof of the theorem we will mention entry times $tin[v]$ in each vertex and in the same way consider $tin[C]$ for each strongly connected component $C$ as minimum of values $tin[v]$ by all $v \in C$.
**Theorem**. Let $C$ and $C'$ are two different strongly connected components and there is an edge $(C, C')$ in a condensation graph between these two vertices. Then $tout[C] > tout[C']$.
There are two main different cases at the proof depending on which component will be visited by depth first search first, i.e. depending on difference between $tin[C]$ and $tin[C']$:
- The component $C$ was reached first. It means that depth first search comes at some vertex $v$ of component $C$ at some moment, but all other vertices of components $C$ and $C'$ were not visited yet. By condition there is an edge $(C, C')$ in a condensation graph, so not only the entire component $C$ is reachable from $v$ but the whole component $C'$ is reachable as well. It means that depth first search that is running from vertex $v$ will visit all vertices of components $C$ and $C'$, so they will be descendants for $v$ in a depth first search tree, i.e. for each vertex $u \in C \cup C', u \ne v$ we have that $tout[v] > tout[u]$, as we claimed.
- Assume that component $C'$ was visited first. Similarly, depth first search comes at some vertex $v$ of component $C'$ at some moment, but all other vertices of components $C$ and $C'$ were not visited yet. But by condition there is an edge $(C, C')$ in the condensation graph, so, because of acyclic property of condensation graph, there is no back path from $C'$ to $C$, i.e. depth first search from vertex $v$ will not reach vertices of $C$. It means that vertices of $C$ will be visited by depth first search later, so $tout[C] > tout[C']$. This completes the proof.
Proved theorem is **the base of algorithm** for finding strongly connected components. It follows that any edge $(C, C')$ in condensation graph comes from a component with a larger value of $tout$ to component with a smaller value.
If we sort all vertices $v \in V$ in decreasing order of their exit time $tout[v]$ then the first vertex $u$ is going to be a vertex belonging to "root" strongly connected component, i.e. a vertex that has no incoming edges in the condensation graph. Now we want to run such search from this vertex $u$ so that it will visit all vertices in this strongly connected component, but not others; doing so, we can gradually select all strongly connected components: let's remove all vertices corresponding to the first selected component, and then let's find a vertex with the largest value of $tout$, and run this search from it, and so on.
Let's consider transposed graph $G^T$, i.e. graph received from $G$ by reversing the direction of each edge.
Obviously, this graph will have the same strongly connected components as the initial graph.
Moreover, the condensation graph $G^{SCC}$ will also get transposed.
It means that there will be no edges from our "root" component to other components.
Thus, for visiting the whole "root" strongly connected component, containing vertex $v$, is enough to run search from vertex $v$ in graph $G^T$. This search will visit all vertices of this strongly connected component and only them. As was mentioned before, we can remove these vertices from the graph then, and find the next vertex with a maximal value of $tout[v]$ and run search in transposed graph from it, and so on.
Thus, we built next **algorithm** for selecting strongly connected components:
1st step. Run sequence of depth first search of graph $G$ which will return vertices with increasing exit time $tout$, i.e. some list $order$.
2nd step. Build transposed graph $G^T$. Run a series of depth (breadth) first searches in the order determined by list $order$ (to be exact in reverse order, i.e. in decreasing order of exit times). Every set of vertices, reached after the next search, will be the next strongly connected component.
Algorithm asymptotic is $O(n + m)$, because it is just two depth (breadth) first searches.
Finally, it is appropriate to mention [topological sort](topological-sort.md) here. First of all, step 1 of the algorithm represents reversed topological sort of graph $G$ (actually this is exactly what vertices' sort by exit time means). Secondly, the algorithm's scheme generates strongly connected components by decreasing order of their exit times, thus it generates components - vertices of condensation graph - in topological sort order.
## Implementation
```cpp
vector<vector<int>> adj, adj_rev;
vector<bool> used;
vector<int> order, component;
void dfs1(int v) {
used[v] = true;
for (auto u : adj[v])
if (!used[u])
dfs1(u);
order.push_back(v);
}
void dfs2(int v) {
used[v] = true;
component.push_back(v);
for (auto u : adj_rev[v])
if (!used[u])
dfs2(u);
}
int main() {
int n;
// ... read n ...
for (;;) {
int a, b;
// ... read next directed edge (a,b) ...
adj[a].push_back(b);
adj_rev[b].push_back(a);
}
used.assign(n, false);
for (int i = 0; i < n; i++)
if (!used[i])
dfs1(i);
used.assign(n, false);
reverse(order.begin(), order.end());
for (auto v : order)
if (!used[v]) {
dfs2 (v);
// ... processing next component ...
component.clear();
}
}
```
Here, $g$ is graph, $gr$ is transposed graph. Function $dfs1$ implements depth first search on graph $G$, function $dfs2$ - on transposed graph $G^T$. Function $dfs1$ fills the list $order$ with vertices in increasing order of their exit times (actually, it is making a topological sort). Function $dfs2$ stores all reached vertices in list $component$, that is going to store next strongly connected component after each run.
### Condensation Graph Implementation
```cpp
// continuing from previous code
vector<int> roots(n, 0);
vector<int> root_nodes;
vector<vector<int>> adj_scc(n);
for (auto v : order)
if (!used[v]) {
dfs2(v);
int root = component.front();
for (auto u : component) roots[u] = root;
root_nodes.push_back(root);
component.clear();
}
for (int v = 0; v < n; v++)
for (auto u : adj[v]) {
int root_v = roots[v],
root_u = roots[u];
if (root_u != root_v)
adj_scc[root_v].push_back(root_u);
}
```
Here, we have selected the root of each component as the first node in its list. This node will represent its entire SCC in the condensation graph. `roots[v]` indicates the root node for the SCC to which node `v` belongs. `root_nodes` is the list of all root nodes (one per component) in the condensation graph.
`adj_scc` is the adjacency list of the `root_nodes`. We can now traverse on `adj_scc` as our condensation graph, using only those nodes which belong to `root_nodes`.
## Literature
* Thomas Cormen, Charles Leiserson, Ronald Rivest, Clifford Stein. Introduction to Algorithms [2005].
* M. Sharir. A strong-connectivity algorithm and its applications in data-flow analysis [1979].
|
---
title
strong_connected_components
---
# Finding strongly connected components / Building condensation graph
## Definitions
You are given a directed graph $G$ with vertices $V$ and edges $E$. It is possible that there are loops and multiple edges. Let's denote $n$ as number of vertices and $m$ as number of edges in $G$.
**Strongly connected component** is a maximal subset of vertices $C$ such that any two vertices of this subset are reachable from each other, i.e. for any $u, v \in C$:
$$u \mapsto v, v \mapsto u$$
where $\mapsto$ means reachability, i.e. existence of the path from first vertex to the second.
It is obvious, that strongly connected components do not intersect each other, i.e. this is a partition of all graph vertices. Thus we can give a definition of condensation graph $G^{SCC}$ as a graph containing every strongly connected component as one vertex. Each vertex of the condensation graph corresponds to the strongly connected component of graph $G$. There is an oriented edge between two vertices $C_i$ and $C_j$ of the condensation graph if and only if there are two vertices $u \in C_i, v \in C_j$ such that there is an edge in initial graph, i.e. $(u, v) \in E$.
The most important property of the condensation graph is that it is **acyclic**. Indeed, suppose that there is an edge between $C$ and $C'$, let's prove that there is no edge from $C'$ to $C$. Suppose that $C' \mapsto C$. Then there are two vertices $u' \in C$ and $v' \in C'$ such that $v' \mapsto u'$. But since $u$ and $u'$ are in the same strongly connected component then there is a path between them; the same for $v$ and $v'$. As a result, if we join these paths we have that $v \mapsto u$ and at the same time $u \mapsto v$. Therefore $u$ and $v$ should be at the same strongly connected component, so this is contradiction. This completes the proof.
The algorithm described in the next section extracts all strongly connected components in a given graph. It is quite easy to build a condensation graph then.
## Description of the algorithm
Described algorithm was independently suggested by Kosaraju and Sharir at 1979. This is an easy-to-implement algorithm based on two series of [depth first search](depth-first-search.md), and working for $O(n + m)$ time.
**On the first step** of the algorithm we are doing sequence of depth first searches, visiting the entire graph. We start at each vertex of the graph and run a depth first search from every non-visited vertex. For each vertex we are keeping track of **exit time** $tout[v]$. These exit times have a key role in an algorithm and this role is expressed in next theorem.
First, let's make notations: let's define exit time $tout[C]$ from the strongly connected component $C$ as maximum of values $tout[v]$ by all $v \in C$. Besides, during the proof of the theorem we will mention entry times $tin[v]$ in each vertex and in the same way consider $tin[C]$ for each strongly connected component $C$ as minimum of values $tin[v]$ by all $v \in C$.
**Theorem**. Let $C$ and $C'$ are two different strongly connected components and there is an edge $(C, C')$ in a condensation graph between these two vertices. Then $tout[C] > tout[C']$.
There are two main different cases at the proof depending on which component will be visited by depth first search first, i.e. depending on difference between $tin[C]$ and $tin[C']$:
- The component $C$ was reached first. It means that depth first search comes at some vertex $v$ of component $C$ at some moment, but all other vertices of components $C$ and $C'$ were not visited yet. By condition there is an edge $(C, C')$ in a condensation graph, so not only the entire component $C$ is reachable from $v$ but the whole component $C'$ is reachable as well. It means that depth first search that is running from vertex $v$ will visit all vertices of components $C$ and $C'$, so they will be descendants for $v$ in a depth first search tree, i.e. for each vertex $u \in C \cup C', u \ne v$ we have that $tout[v] > tout[u]$, as we claimed.
- Assume that component $C'$ was visited first. Similarly, depth first search comes at some vertex $v$ of component $C'$ at some moment, but all other vertices of components $C$ and $C'$ were not visited yet. But by condition there is an edge $(C, C')$ in the condensation graph, so, because of acyclic property of condensation graph, there is no back path from $C'$ to $C$, i.e. depth first search from vertex $v$ will not reach vertices of $C$. It means that vertices of $C$ will be visited by depth first search later, so $tout[C] > tout[C']$. This completes the proof.
Proved theorem is **the base of algorithm** for finding strongly connected components. It follows that any edge $(C, C')$ in condensation graph comes from a component with a larger value of $tout$ to component with a smaller value.
If we sort all vertices $v \in V$ in decreasing order of their exit time $tout[v]$ then the first vertex $u$ is going to be a vertex belonging to "root" strongly connected component, i.e. a vertex that has no incoming edges in the condensation graph. Now we want to run such search from this vertex $u$ so that it will visit all vertices in this strongly connected component, but not others; doing so, we can gradually select all strongly connected components: let's remove all vertices corresponding to the first selected component, and then let's find a vertex with the largest value of $tout$, and run this search from it, and so on.
Let's consider transposed graph $G^T$, i.e. graph received from $G$ by reversing the direction of each edge.
Obviously, this graph will have the same strongly connected components as the initial graph.
Moreover, the condensation graph $G^{SCC}$ will also get transposed.
It means that there will be no edges from our "root" component to other components.
Thus, for visiting the whole "root" strongly connected component, containing vertex $v$, is enough to run search from vertex $v$ in graph $G^T$. This search will visit all vertices of this strongly connected component and only them. As was mentioned before, we can remove these vertices from the graph then, and find the next vertex with a maximal value of $tout[v]$ and run search in transposed graph from it, and so on.
Thus, we built next **algorithm** for selecting strongly connected components:
1st step. Run sequence of depth first search of graph $G$ which will return vertices with increasing exit time $tout$, i.e. some list $order$.
2nd step. Build transposed graph $G^T$. Run a series of depth (breadth) first searches in the order determined by list $order$ (to be exact in reverse order, i.e. in decreasing order of exit times). Every set of vertices, reached after the next search, will be the next strongly connected component.
Algorithm asymptotic is $O(n + m)$, because it is just two depth (breadth) first searches.
Finally, it is appropriate to mention [topological sort](topological-sort.md) here. First of all, step 1 of the algorithm represents reversed topological sort of graph $G$ (actually this is exactly what vertices' sort by exit time means). Secondly, the algorithm's scheme generates strongly connected components by decreasing order of their exit times, thus it generates components - vertices of condensation graph - in topological sort order.
## Implementation
```cpp
vector<vector<int>> adj, adj_rev;
vector<bool> used;
vector<int> order, component;
void dfs1(int v) {
used[v] = true;
for (auto u : adj[v])
if (!used[u])
dfs1(u);
order.push_back(v);
}
void dfs2(int v) {
used[v] = true;
component.push_back(v);
for (auto u : adj_rev[v])
if (!used[u])
dfs2(u);
}
int main() {
int n;
// ... read n ...
for (;;) {
int a, b;
// ... read next directed edge (a,b) ...
adj[a].push_back(b);
adj_rev[b].push_back(a);
}
used.assign(n, false);
for (int i = 0; i < n; i++)
if (!used[i])
dfs1(i);
used.assign(n, false);
reverse(order.begin(), order.end());
for (auto v : order)
if (!used[v]) {
dfs2 (v);
// ... processing next component ...
component.clear();
}
}
```
Here, $g$ is graph, $gr$ is transposed graph. Function $dfs1$ implements depth first search on graph $G$, function $dfs2$ - on transposed graph $G^T$. Function $dfs1$ fills the list $order$ with vertices in increasing order of their exit times (actually, it is making a topological sort). Function $dfs2$ stores all reached vertices in list $component$, that is going to store next strongly connected component after each run.
### Condensation Graph Implementation
```cpp
// continuing from previous code
vector<int> roots(n, 0);
vector<int> root_nodes;
vector<vector<int>> adj_scc(n);
for (auto v : order)
if (!used[v]) {
dfs2(v);
int root = component.front();
for (auto u : component) roots[u] = root;
root_nodes.push_back(root);
component.clear();
}
for (int v = 0; v < n; v++)
for (auto u : adj[v]) {
int root_v = roots[v],
root_u = roots[u];
if (root_u != root_v)
adj_scc[root_v].push_back(root_u);
}
```
Here, we have selected the root of each component as the first node in its list. This node will represent its entire SCC in the condensation graph. `roots[v]` indicates the root node for the SCC to which node `v` belongs. `root_nodes` is the list of all root nodes (one per component) in the condensation graph.
`adj_scc` is the adjacency list of the `root_nodes`. We can now traverse on `adj_scc` as our condensation graph, using only those nodes which belong to `root_nodes`.
## Literature
* Thomas Cormen, Charles Leiserson, Ronald Rivest, Clifford Stein. Introduction to Algorithms [2005].
* M. Sharir. A strong-connectivity algorithm and its applications in data-flow analysis [1979].
## Practice Problems
* [SPOJ - Good Travels](http://www.spoj.com/problems/GOODA/)
* [SPOJ - Lego](http://www.spoj.com/problems/LEGO/)
* [Codechef - Chef and Round Run](https://www.codechef.com/AUG16/problems/CHEFRRUN)
* [Dev Skills - A Song of Fire and Ice](https://devskill.com/CodingProblems/ViewProblem/79)
* [UVA - 11838 - Come and Go](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2938)
* [UVA 247 - Calling Circles](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=183)
* [UVA 13057 - Prove Them All](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=4955)
* [UVA 12645 - Water Supply](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=4393)
* [UVA 11770 - Lighting Away](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2870)
* [UVA 12926 - Trouble in Terrorist Town](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=862&page=show_problem&problem=4805)
* [UVA 11324 - The Largest Clique](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2299)
* [UVA 11709 - Trust groups](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2756)
* [UVA 12745 - Wishmaster](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=4598)
* [SPOJ - True Friends](http://www.spoj.com/problems/TFRIENDS/)
* [SPOJ - Capital City](http://www.spoj.com/problems/CAPCITY/)
* [Codeforces - Scheme](http://codeforces.com/contest/22/problem/E)
* [SPOJ - Ada and Panels](http://www.spoj.com/problems/ADAPANEL/)
* [CSES - Flight Routes Check](https://cses.fi/problemset/task/1682)
* [CSES - Planets and Kingdoms](https://cses.fi/problemset/task/1683)
* [CSES -Coin Collector](https://cses.fi/problemset/task/1686)
* [Codeforces - Checkposts](https://codeforces.com/problemset/problem/427/C)
|
Finding strongly connected components / Building condensation graph
|
---
title
- Original
---
# Maximum flow - MPM algorithm
MPM (Malhotra, Pramodh-Kumar and Maheshwari) algorithm solves the maximum flow problem in $O(V^3)$. This algorithm is similar to [Dinic's algorithm](dinic.md).
## Algorithm
Like Dinic's algorithm, MPM runs in phases, during each phase we find the blocking flow in the layered network of the residual network of $G$.
The main difference from Dinic's is how we find the blocking flow.
Consider the layered network $L$.
For each node we define its' _inner potential_ and _outer potential_ as:
$$\begin{align}
p_{in}(v) &= \sum\limits_{(u, v)\in L}(c(u, v) - f(u, v)) \\\\
p_{out}(v) &= \sum\limits_{(v, u)\in L}(c(v, u) - f(v, u))
\end{align}$$
Also we set $p_{in}(s) = p_{out}(t) = \infty$.
Given $p_{in}$ and $p_{out}$ we define the _potential_ as $p(v) = min(p_{in}(v), p_{out}(v))$.
We call a node $r$ a _reference node_ if $p(r) = min\{p(v)\}$.
Consider a reference node $r$.
We claim that the flow can be increased by $p(r)$ in such a way that $p(r)$ becomes $0$.
It is true because $L$ is acyclic, so we can push the flow out of $r$ by outgoing edges and it will reach $t$ because each node has enough outer potential to push the flow out when it reaches it.
Similarly, we can pull the flow from $s$.
The construction of the blocked flow is based on this fact.
On each iteration we find a reference node and push the flow from $s$ to $t$ through $r$.
This process can be simulated by BFS.
All completely saturated arcs can be deleted from $L$ as they won't be used later in this phase anyway.
Likewise, all the nodes different from $s$ and $t$ without outgoing or incoming arcs can be deleted.
Each phase works in $O(V^2)$ because there are at most $V$ iterations (because at least the chosen reference node is deleted), and on each iteration we delete all the edges we passed through except at most $V$.
Summing, we get $O(V^2 + E) = O(V^2)$.
Since there are less than $V$ phases (see the proof [here](dinic.md)), MPM works in $O(V^3)$ total.
## Implementation
```{.cpp file=mpm}
struct MPM{
struct FlowEdge{
int v, u;
long long cap, flow;
FlowEdge(){}
FlowEdge(int _v, int _u, long long _cap, long long _flow)
: v(_v), u(_u), cap(_cap), flow(_flow){}
FlowEdge(int _v, int _u, long long _cap)
: v(_v), u(_u), cap(_cap), flow(0ll){}
};
const long long flow_inf = 1e18;
vector<FlowEdge> edges;
vector<char> alive;
vector<long long> pin, pout;
vector<list<int> > in, out;
vector<vector<int> > adj;
vector<long long> ex;
int n, m = 0;
int s, t;
vector<int> level;
vector<int> q;
int qh, qt;
void resize(int _n){
n = _n;
ex.resize(n);
q.resize(n);
pin.resize(n);
pout.resize(n);
adj.resize(n);
level.resize(n);
in.resize(n);
out.resize(n);
}
MPM(){}
MPM(int _n, int _s, int _t){resize(_n); s = _s; t = _t;}
void add_edge(int v, int u, long long cap){
edges.push_back(FlowEdge(v, u, cap));
edges.push_back(FlowEdge(u, v, 0));
adj[v].push_back(m);
adj[u].push_back(m + 1);
m += 2;
}
bool bfs(){
while(qh < qt){
int v = q[qh++];
for(int id : adj[v]){
if(edges[id].cap - edges[id].flow < 1)continue;
if(level[edges[id].u] != -1)continue;
level[edges[id].u] = level[v] + 1;
q[qt++] = edges[id].u;
}
}
return level[t] != -1;
}
long long pot(int v){
return min(pin[v], pout[v]);
}
void remove_node(int v){
for(int i : in[v]){
int u = edges[i].v;
auto it = find(out[u].begin(), out[u].end(), i);
out[u].erase(it);
pout[u] -= edges[i].cap - edges[i].flow;
}
for(int i : out[v]){
int u = edges[i].u;
auto it = find(in[u].begin(), in[u].end(), i);
in[u].erase(it);
pin[u] -= edges[i].cap - edges[i].flow;
}
}
void push(int from, int to, long long f, bool forw){
qh = qt = 0;
ex.assign(n, 0);
ex[from] = f;
q[qt++] = from;
while(qh < qt){
int v = q[qh++];
if(v == to)
break;
long long must = ex[v];
auto it = forw ? out[v].begin() : in[v].begin();
while(true){
int u = forw ? edges[*it].u : edges[*it].v;
long long pushed = min(must, edges[*it].cap - edges[*it].flow);
if(pushed == 0)break;
if(forw){
pout[v] -= pushed;
pin[u] -= pushed;
}
else{
pin[v] -= pushed;
pout[u] -= pushed;
}
if(ex[u] == 0)
q[qt++] = u;
ex[u] += pushed;
edges[*it].flow += pushed;
edges[(*it)^1].flow -= pushed;
must -= pushed;
if(edges[*it].cap - edges[*it].flow == 0){
auto jt = it;
++jt;
if(forw){
in[u].erase(find(in[u].begin(), in[u].end(), *it));
out[v].erase(it);
}
else{
out[u].erase(find(out[u].begin(), out[u].end(), *it));
in[v].erase(it);
}
it = jt;
}
else break;
if(!must)break;
}
}
}
long long flow(){
long long ans = 0;
while(true){
pin.assign(n, 0);
pout.assign(n, 0);
level.assign(n, -1);
alive.assign(n, true);
level[s] = 0;
qh = 0; qt = 1;
q[0] = s;
if(!bfs())
break;
for(int i = 0; i < n; i++){
out[i].clear();
in[i].clear();
}
for(int i = 0; i < m; i++){
if(edges[i].cap - edges[i].flow == 0)
continue;
int v = edges[i].v, u = edges[i].u;
if(level[v] + 1 == level[u] && (level[u] < level[t] || u == t)){
in[u].push_back(i);
out[v].push_back(i);
pin[u] += edges[i].cap - edges[i].flow;
pout[v] += edges[i].cap - edges[i].flow;
}
}
pin[s] = pout[t] = flow_inf;
while(true){
int v = -1;
for(int i = 0; i < n; i++){
if(!alive[i])continue;
if(v == -1 || pot(i) < pot(v))
v = i;
}
if(v == -1)
break;
if(pot(v) == 0){
alive[v] = false;
remove_node(v);
continue;
}
long long f = pot(v);
ans += f;
push(v, s, f, false);
push(v, t, f, true);
alive[v] = false;
remove_node(v);
}
}
return ans;
}
};
```
|
---
title
- Original
---
# Maximum flow - MPM algorithm
MPM (Malhotra, Pramodh-Kumar and Maheshwari) algorithm solves the maximum flow problem in $O(V^3)$. This algorithm is similar to [Dinic's algorithm](dinic.md).
## Algorithm
Like Dinic's algorithm, MPM runs in phases, during each phase we find the blocking flow in the layered network of the residual network of $G$.
The main difference from Dinic's is how we find the blocking flow.
Consider the layered network $L$.
For each node we define its' _inner potential_ and _outer potential_ as:
$$\begin{align}
p_{in}(v) &= \sum\limits_{(u, v)\in L}(c(u, v) - f(u, v)) \\\\
p_{out}(v) &= \sum\limits_{(v, u)\in L}(c(v, u) - f(v, u))
\end{align}$$
Also we set $p_{in}(s) = p_{out}(t) = \infty$.
Given $p_{in}$ and $p_{out}$ we define the _potential_ as $p(v) = min(p_{in}(v), p_{out}(v))$.
We call a node $r$ a _reference node_ if $p(r) = min\{p(v)\}$.
Consider a reference node $r$.
We claim that the flow can be increased by $p(r)$ in such a way that $p(r)$ becomes $0$.
It is true because $L$ is acyclic, so we can push the flow out of $r$ by outgoing edges and it will reach $t$ because each node has enough outer potential to push the flow out when it reaches it.
Similarly, we can pull the flow from $s$.
The construction of the blocked flow is based on this fact.
On each iteration we find a reference node and push the flow from $s$ to $t$ through $r$.
This process can be simulated by BFS.
All completely saturated arcs can be deleted from $L$ as they won't be used later in this phase anyway.
Likewise, all the nodes different from $s$ and $t$ without outgoing or incoming arcs can be deleted.
Each phase works in $O(V^2)$ because there are at most $V$ iterations (because at least the chosen reference node is deleted), and on each iteration we delete all the edges we passed through except at most $V$.
Summing, we get $O(V^2 + E) = O(V^2)$.
Since there are less than $V$ phases (see the proof [here](dinic.md)), MPM works in $O(V^3)$ total.
## Implementation
```{.cpp file=mpm}
struct MPM{
struct FlowEdge{
int v, u;
long long cap, flow;
FlowEdge(){}
FlowEdge(int _v, int _u, long long _cap, long long _flow)
: v(_v), u(_u), cap(_cap), flow(_flow){}
FlowEdge(int _v, int _u, long long _cap)
: v(_v), u(_u), cap(_cap), flow(0ll){}
};
const long long flow_inf = 1e18;
vector<FlowEdge> edges;
vector<char> alive;
vector<long long> pin, pout;
vector<list<int> > in, out;
vector<vector<int> > adj;
vector<long long> ex;
int n, m = 0;
int s, t;
vector<int> level;
vector<int> q;
int qh, qt;
void resize(int _n){
n = _n;
ex.resize(n);
q.resize(n);
pin.resize(n);
pout.resize(n);
adj.resize(n);
level.resize(n);
in.resize(n);
out.resize(n);
}
MPM(){}
MPM(int _n, int _s, int _t){resize(_n); s = _s; t = _t;}
void add_edge(int v, int u, long long cap){
edges.push_back(FlowEdge(v, u, cap));
edges.push_back(FlowEdge(u, v, 0));
adj[v].push_back(m);
adj[u].push_back(m + 1);
m += 2;
}
bool bfs(){
while(qh < qt){
int v = q[qh++];
for(int id : adj[v]){
if(edges[id].cap - edges[id].flow < 1)continue;
if(level[edges[id].u] != -1)continue;
level[edges[id].u] = level[v] + 1;
q[qt++] = edges[id].u;
}
}
return level[t] != -1;
}
long long pot(int v){
return min(pin[v], pout[v]);
}
void remove_node(int v){
for(int i : in[v]){
int u = edges[i].v;
auto it = find(out[u].begin(), out[u].end(), i);
out[u].erase(it);
pout[u] -= edges[i].cap - edges[i].flow;
}
for(int i : out[v]){
int u = edges[i].u;
auto it = find(in[u].begin(), in[u].end(), i);
in[u].erase(it);
pin[u] -= edges[i].cap - edges[i].flow;
}
}
void push(int from, int to, long long f, bool forw){
qh = qt = 0;
ex.assign(n, 0);
ex[from] = f;
q[qt++] = from;
while(qh < qt){
int v = q[qh++];
if(v == to)
break;
long long must = ex[v];
auto it = forw ? out[v].begin() : in[v].begin();
while(true){
int u = forw ? edges[*it].u : edges[*it].v;
long long pushed = min(must, edges[*it].cap - edges[*it].flow);
if(pushed == 0)break;
if(forw){
pout[v] -= pushed;
pin[u] -= pushed;
}
else{
pin[v] -= pushed;
pout[u] -= pushed;
}
if(ex[u] == 0)
q[qt++] = u;
ex[u] += pushed;
edges[*it].flow += pushed;
edges[(*it)^1].flow -= pushed;
must -= pushed;
if(edges[*it].cap - edges[*it].flow == 0){
auto jt = it;
++jt;
if(forw){
in[u].erase(find(in[u].begin(), in[u].end(), *it));
out[v].erase(it);
}
else{
out[u].erase(find(out[u].begin(), out[u].end(), *it));
in[v].erase(it);
}
it = jt;
}
else break;
if(!must)break;
}
}
}
long long flow(){
long long ans = 0;
while(true){
pin.assign(n, 0);
pout.assign(n, 0);
level.assign(n, -1);
alive.assign(n, true);
level[s] = 0;
qh = 0; qt = 1;
q[0] = s;
if(!bfs())
break;
for(int i = 0; i < n; i++){
out[i].clear();
in[i].clear();
}
for(int i = 0; i < m; i++){
if(edges[i].cap - edges[i].flow == 0)
continue;
int v = edges[i].v, u = edges[i].u;
if(level[v] + 1 == level[u] && (level[u] < level[t] || u == t)){
in[u].push_back(i);
out[v].push_back(i);
pin[u] += edges[i].cap - edges[i].flow;
pout[v] += edges[i].cap - edges[i].flow;
}
}
pin[s] = pout[t] = flow_inf;
while(true){
int v = -1;
for(int i = 0; i < n; i++){
if(!alive[i])continue;
if(v == -1 || pot(i) < pot(v))
v = i;
}
if(v == -1)
break;
if(pot(v) == 0){
alive[v] = false;
remove_node(v);
continue;
}
long long f = pot(v);
ans += f;
push(v, s, f, false);
push(v, t, f, true);
alive[v] = false;
remove_node(v);
}
}
return ans;
}
};
```
|
Maximum flow - MPM algorithm
|
---
title
topological_sort
---
# Topological Sorting
You are given a directed graph with $n$ vertices and $m$ edges.
You have to find an **order of the vertices**, so that every edge leads from the vertex with a smaller index to a vertex with a larger one.
In other words, you want to find a permutation of the vertices (**topological order**) which corresponds to the order defined by all edges of the graph.
Here is one given graph together with its topological order:
<center>


</center>
Topological order can be **non-unique** (for example, if there exist three vertices $a$, $b$, $c$ for which there exist paths from $a$ to $b$ and from $a$ to $c$ but not paths from $b$ to $c$ or from $c$ to $b$).
The example graph also has multiple topological orders, a second topological order is the following:
<center>

</center>
A Topological order may **not exist** at all.
It only exists, if the directed graph contains no cycles.
Otherwise because there is a contradiction: if there is a cycle containing the vertices $a$ and $b$, then $a$ needs to have a smaller index than $b$ (since you can reach $b$ from $a$) and also a bigger one (as you can reach $a$ from $b$).
The algorithm described in this article also shows by construction, that every acyclic directed graph contains at least one topological order.
A common problem in which topological sorting occurs is the following. There are $n$ variables with unknown values. For some variables we know that one of them is less than the other. You have to check whether these constraints are contradictory, and if not, output the variables in ascending order (if several answers are possible, output any of them). It is easy to notice that this is exactly the problem of finding topological order of a graph with $n$ vertices.
## The Algorithm
To solve this problem we will use [depth-first search](depth-first-search.md).
Let's assume that the graph is acyclic. What does the depth-first search do?
When starting from some vertex $v$, DFS tries to traverse along all edges outgoing from $v$.
It stops at the edges for which the ends have been already been visited previously, and traverses along the rest of the edges and continues recursively at their ends.
Thus, by the time of the function call $\text{dfs}(v)$ has finished, all vertices that are reachable from $v$ have been either directly (via one edge) or indirectly visited by the search.
Let's append the vertex $v$ to a list, when we finish $\text{dfs}(v)$. Since all reachable vertices have already been visited, they will already be in the list when we append $v$.
Let's do this for every vertex in the graph, with one or multiple depth-first search runs.
For every directed edge $v \rightarrow u$ in the graph, $u$ will appear earlier in this list than $v$, because $u$ is reachable from $v$.
So if we just label the vertices in this list with $n-1, n-2, \dots, 1, 0$, we have found a topological order of the graph.
In other words, the list represents the reversed topological order.
These explanations can also be presented in terms of exit times of the DFS algorithm.
The exit time for vertex $v$ is the time at which the function call $\text{dfs}(v)$ finished (the times can be numbered from $0$ to $n-1$).
It is easy to understand that exit time of any vertex $v$ is always greater than the exit time of any vertex reachable from it (since they were visited either before the call $\text{dfs}(v)$ or during it). Thus, the desired topological ordering are the vertices in descending order of their exit times.
## Implementation
Here is an implementation which assumes that the graph is acyclic, i.e. the desired topological ordering exists. If necessary, you can easily check that the graph is acyclic, as described in the article on [depth-first search](depth-first-search.md).
```cpp
int n; // number of vertices
vector<vector<int>> adj; // adjacency list of graph
vector<bool> visited;
vector<int> ans;
void dfs(int v) {
visited[v] = true;
for (int u : adj[v]) {
if (!visited[u])
dfs(u);
}
ans.push_back(v);
}
void topological_sort() {
visited.assign(n, false);
ans.clear();
for (int i = 0; i < n; ++i) {
if (!visited[i])
dfs(i);
}
reverse(ans.begin(), ans.end());
}
```
The main function of the solution is `topological_sort`, which initializes DFS variables, launches DFS and receives the answer in the vector `ans`.
|
---
title
topological_sort
---
# Topological Sorting
You are given a directed graph with $n$ vertices and $m$ edges.
You have to find an **order of the vertices**, so that every edge leads from the vertex with a smaller index to a vertex with a larger one.
In other words, you want to find a permutation of the vertices (**topological order**) which corresponds to the order defined by all edges of the graph.
Here is one given graph together with its topological order:
<center>


</center>
Topological order can be **non-unique** (for example, if there exist three vertices $a$, $b$, $c$ for which there exist paths from $a$ to $b$ and from $a$ to $c$ but not paths from $b$ to $c$ or from $c$ to $b$).
The example graph also has multiple topological orders, a second topological order is the following:
<center>

</center>
A Topological order may **not exist** at all.
It only exists, if the directed graph contains no cycles.
Otherwise because there is a contradiction: if there is a cycle containing the vertices $a$ and $b$, then $a$ needs to have a smaller index than $b$ (since you can reach $b$ from $a$) and also a bigger one (as you can reach $a$ from $b$).
The algorithm described in this article also shows by construction, that every acyclic directed graph contains at least one topological order.
A common problem in which topological sorting occurs is the following. There are $n$ variables with unknown values. For some variables we know that one of them is less than the other. You have to check whether these constraints are contradictory, and if not, output the variables in ascending order (if several answers are possible, output any of them). It is easy to notice that this is exactly the problem of finding topological order of a graph with $n$ vertices.
## The Algorithm
To solve this problem we will use [depth-first search](depth-first-search.md).
Let's assume that the graph is acyclic. What does the depth-first search do?
When starting from some vertex $v$, DFS tries to traverse along all edges outgoing from $v$.
It stops at the edges for which the ends have been already been visited previously, and traverses along the rest of the edges and continues recursively at their ends.
Thus, by the time of the function call $\text{dfs}(v)$ has finished, all vertices that are reachable from $v$ have been either directly (via one edge) or indirectly visited by the search.
Let's append the vertex $v$ to a list, when we finish $\text{dfs}(v)$. Since all reachable vertices have already been visited, they will already be in the list when we append $v$.
Let's do this for every vertex in the graph, with one or multiple depth-first search runs.
For every directed edge $v \rightarrow u$ in the graph, $u$ will appear earlier in this list than $v$, because $u$ is reachable from $v$.
So if we just label the vertices in this list with $n-1, n-2, \dots, 1, 0$, we have found a topological order of the graph.
In other words, the list represents the reversed topological order.
These explanations can also be presented in terms of exit times of the DFS algorithm.
The exit time for vertex $v$ is the time at which the function call $\text{dfs}(v)$ finished (the times can be numbered from $0$ to $n-1$).
It is easy to understand that exit time of any vertex $v$ is always greater than the exit time of any vertex reachable from it (since they were visited either before the call $\text{dfs}(v)$ or during it). Thus, the desired topological ordering are the vertices in descending order of their exit times.
## Implementation
Here is an implementation which assumes that the graph is acyclic, i.e. the desired topological ordering exists. If necessary, you can easily check that the graph is acyclic, as described in the article on [depth-first search](depth-first-search.md).
```cpp
int n; // number of vertices
vector<vector<int>> adj; // adjacency list of graph
vector<bool> visited;
vector<int> ans;
void dfs(int v) {
visited[v] = true;
for (int u : adj[v]) {
if (!visited[u])
dfs(u);
}
ans.push_back(v);
}
void topological_sort() {
visited.assign(n, false);
ans.clear();
for (int i = 0; i < n; ++i) {
if (!visited[i])
dfs(i);
}
reverse(ans.begin(), ans.end());
}
```
The main function of the solution is `topological_sort`, which initializes DFS variables, launches DFS and receives the answer in the vector `ans`.
## Practice Problems
- [SPOJ TOPOSORT - Topological Sorting [difficulty: easy]](http://www.spoj.com/problems/TOPOSORT/)
- [UVA 10305 - Ordering Tasks [difficulty: easy]](https://onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1246)
- [UVA 124 - Following Orders [difficulty: easy]](https://onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=60)
- [UVA 200 - Rare Order [difficulty: easy]](https://onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=136)
- [Codeforces 510C - Fox and Names [difficulty: easy]](http://codeforces.com/problemset/problem/510/C)
- [SPOJ RPLA - Answer the boss!](https://www.spoj.com/problems/RPLA/)
- [CSES - Course Schedule](https://cses.fi/problemset/task/1679)
- [CSES - Longest Flight Route](https://cses.fi/problemset/task/1680)
- [CSES - Game Routes](https://cses.fi/problemset/task/1681)
|
Topological Sorting
|
---
title
prufer_code_cayley_formula
---
# Prüfer code
In this article we will look at the so-called **Prüfer code** (or Prüfer sequence), which is a way of encoding a labeled tree into a sequence of numbers in a unique way.
With the help of the Prüfer code we will prove **Cayley's formula** (which specified the number of spanning trees in a complete graph).
Also we show the solution to the problem of counting the number of ways of adding edges to a graph to make it connected.
**Note**, we will not consider trees consisting of a single vertex - this is a special case in which multiple statements clash.
## Prüfer code
The Prüfer code is a way of encoding a labeled tree with $n$ vertices using a sequence of $n - 2$ integers in the interval $[0; n-1]$.
This encoding also acts as a **bijection** between all spanning trees of a complete graph and the numerical sequences.
Although using the Prüfer code for storing and operating on tree is impractical due the specification of the representation, the Prüfer codes are used frequently: mostly in solving combinatorial problems.
The inventor - Heinz Prüfer - proposed this code in 1918 as a proof for Cayley's formula.
### Building the Prüfer code for a given tree
The Prüfer code is constructed as follows.
We will repeat the following procedure $n - 2$ times:
we select the leaf of the tree with the smallest number, remove it from the tree, and write down the number of the vertex that was connected to it.
After $n - 2$ iterations there will only remain $2$ vertices, and the algorithm ends.
Thus the Prüfer code for a given tree is a sequence of $n - 2$ numbers, where each number is the number of the connected vertex, i.e. this number is in the interval $[0, n-1]$.
The algorithm for computing the Prüfer code can be implemented easily with $O(n \log n)$ time complexity, simply by using a data structure to extract the minimum (for instance `set` or `priority_queue` in C++), which contains a list of all the current leafs.
```{.cpp file=pruefer_code_slow}
vector<vector<int>> adj;
vector<int> pruefer_code() {
int n = adj.size();
set<int> leafs;
vector<int> degree(n);
vector<bool> killed(n, false);
for (int i = 0; i < n; i++) {
degree[i] = adj[i].size();
if (degree[i] == 1)
leafs.insert(i);
}
vector<int> code(n - 2);
for (int i = 0; i < n - 2; i++) {
int leaf = *leafs.begin();
leafs.erase(leafs.begin());
killed[leaf] = true;
int v;
for (int u : adj[leaf]) {
if (!killed[u])
v = u;
}
code[i] = v;
if (--degree[v] == 1)
leafs.insert(v);
}
return code;
}
```
However the construction can also be implemented in linear time.
Such an approach is described in the next section.
### Building the Prüfer code for a given tree in linear time
The essence of the algorithm is to use a **moving pointer**, which will always point to the current leaf vertex that we want to remove.
At first glance this seems impossible, because during the process of constructing the Prüfer code the leaf number can increase and decrease.
However after a closer look, this is actually not true.
The number of leafs will not increase. Either the number decreases by one (we remove one leaf vertex and don't gain a new one), or it stay the same (we remove one leaf vertex and gain another one).
In the first case there is no other way than searching for the next smallest leaf vertex.
In the second case, however, we can decide in $O(1)$ time, if we can continue using the vertex that became a new leaf vertex, or if we have to search for the next smallest leaf vertex.
And in quite a lot of times we can continue with the new leaf vertex.
To do this we will use a variable $\text{ptr}$, which will indicate that in the set of vertices between $0$ and $\text{ptr}$ is at most one leaf vertex, namely the current one.
All other vertices in that range are either already removed from the tree, or have still more than one adjacent vertices.
At the same time we say, that we haven't removed any leaf vertices bigger than $\text{ptr}$ yet.
This variable is already very helpful in the first case.
After removing the current leaf node, we know that there cannot be a leaf node between $0$ and $\text{ptr}$, therefore we can start the search for the next one directly at $\text{ptr} + 1$, and we don't have to start the search back at vertex $0$.
And in the second case, we can further distinguish two cases:
Either the newly gained leaf vertex is smaller than $\text{ptr}$, then this must be the next leaf vertex, since we know that there are no other vertices smaller than $\text{ptr}$.
Or the newly gained leaf vertex is bigger.
But then we also know that it has to be bigger than $\text{ptr}$, and can start the search again at $\text{ptr} + 1$.
Even though we might have to perform multiple linear searches for the next leaf vertex, the pointer $\text{ptr}$ only increases and therefore the time complexity in total is $O(n)$.
```{.cpp file=pruefer_code_fast}
vector<vector<int>> adj;
vector<int> parent;
void dfs(int v) {
for (int u : adj[v]) {
if (u != parent[v]) {
parent[u] = v;
dfs(u);
}
}
}
vector<int> pruefer_code() {
int n = adj.size();
parent.resize(n);
parent[n-1] = -1;
dfs(n-1);
int ptr = -1;
vector<int> degree(n);
for (int i = 0; i < n; i++) {
degree[i] = adj[i].size();
if (degree[i] == 1 && ptr == -1)
ptr = i;
}
vector<int> code(n - 2);
int leaf = ptr;
for (int i = 0; i < n - 2; i++) {
int next = parent[leaf];
code[i] = next;
if (--degree[next] == 1 && next < ptr) {
leaf = next;
} else {
ptr++;
while (degree[ptr] != 1)
ptr++;
leaf = ptr;
}
}
return code;
}
```
In the code we first find for each its ancestor `parent[i]`, i.e. the ancestor that this vertex will have once we remove it from the tree.
We can find this ancestor by rooting the tree at the vertex $n-1$.
This is possible because the vertex $n-1$ will never be removed from the tree.
We also compute the degree for each vertex.
`ptr` is the pointer that indicates the minimum size of the remaining leaf vertices (except the current one `leaf`).
We will either assign the current leaf vertex with `next`, if this one is also a leaf vertex and it is smaller than `ptr`, or we start a linear search for the smallest leaf vertex by increasing the pointer.
It can be easily seen, that this code has the complexity $O(n)$.
### Some properties of the Prüfer code
- After constructing the Prüfer code two vertices will remain.
One of them is the highest vertex $n-1$, but nothing else can be said about the other one.
- Each vertex appears in the Prüfer code exactly a fixed number of times - its degree minus one.
This can be easily checked, since the degree will get smaller every time we record its label in the code, and we remove it once the degree is $1$.
For the two remaining vertices this fact is also true.
### Restoring the tree using the Prüfer code
To restore the tree it suffice to only focus on the property discussed in the last section.
We already know the degree of all the vertices in the desired tree.
Therefore we can find all leaf vertices, and also the first leaf that was removed in the first step (it has to be the smallest leaf).
This leaf vertex was connected to the vertex corresponding to the number in the first cell of the Prüfer code.
Thus we found the first edge removed by when then the Prüfer code was generated.
We can add this edge to the answer and reduce the degrees at both ends of the edge.
We will repeat this operation until we have used all numbers of the Prüfer code:
we look for the minimum vertex with degree equal to $1$, connect it with the next vertex from the Prüfer code, and reduce the degree.
In the end we only have two vertices left with degree equal to $1$.
These are the vertices that didn't got removed by the Prüfer code process.
We connect them to get the last edge of the tree.
One of them will always be the vertex $n-1$.
This algorithm can be **implemented** easily in $O(n \log n)$: we use a data structure that supports extracting the minimum (for example `set<>` or `priority_queue<>` in C++) to store all the leaf vertices.
The following implementation returns the list of edges corresponding to the tree.
```{.cpp file=pruefer_decode_slow}
vector<pair<int, int>> pruefer_decode(vector<int> const& code) {
int n = code.size() + 2;
vector<int> degree(n, 1);
for (int i : code)
degree[i]++;
set<int> leaves;
for (int i = 0; i < n; i++) {
if (degree[i] == 1)
leaves.insert(i);
}
vector<pair<int, int>> edges;
for (int v : code) {
int leaf = *leaves.begin();
leaves.erase(leaves.begin());
edges.emplace_back(leaf, v);
if (--degree[v] == 1)
leaves.insert(v);
}
edges.emplace_back(*leaves.begin(), n-1);
return edges;
}
```
### Restoring the tree using the Prüfer code in linear time
To obtain the tree in linear time we can apply the same technique used to obtain the Prüfer code in linear time.
We don't need a data structure to extract the minimum.
Instead we can notice that, after processing the current edge, only one vertex becomes a leaf.
Therefore we can either continue with this vertex, or we find a smaller one with a linear search by moving a pointer.
```{.cpp file=pruefer_decode_fast}
vector<pair<int, int>> pruefer_decode(vector<int> const& code) {
int n = code.size() + 2;
vector<int> degree(n, 1);
for (int i : code)
degree[i]++;
int ptr = 0;
while (degree[ptr] != 1)
ptr++;
int leaf = ptr;
vector<pair<int, int>> edges;
for (int v : code) {
edges.emplace_back(leaf, v);
if (--degree[v] == 1 && v < ptr) {
leaf = v;
} else {
ptr++;
while (degree[ptr] != 1)
ptr++;
leaf = ptr;
}
}
edges.emplace_back(leaf, n-1);
return edges;
}
```
### Bijection between trees and Prüfer codes
For each tree there exists a Prüfer code corresponding to it.
And for each Prüfer code we can restore the original tree.
It follows that also every Prüfer code (i.e. a sequence of $n-2$ numbers in the range $[0; n - 1]$) corresponds to a tree.
Therefore all trees and all Prüfer codes form a bijection (a **one-to-one correspondence**).
## Cayley's formula
Cayley's formula states that the **number of spanning trees in a complete labeled graph** with $n$ vertices is equal to:
$$n^{n-2}$$
There are multiple proofs for this formula.
Using the Prüfer code concept this statement comes without any surprise.
In fact any Prüfer code with $n-2$ numbers from the interval $[0; n-1]$ corresponds to some tree with $n$ vertices.
So we have $n^{n-2}$ different such Prüfer codes.
Since each such tree is a spanning tree of a complete graph with $n$ vertices, the number of such spanning trees is also $n^{n-2}$.
## Number of ways to make a graph connected
The concept of Prüfer codes are even more powerful.
It allows to create a lot more general formulas than Cayley's formula.
In this problem we are given a graph with $n$ vertices and $m$ edges.
The graph currently has $k$ components.
We want to compute the number of ways of adding $k-1$ edges so that the graph becomes connected (obviously $k-1$ is the minimum number necessary to make the graph connected).
Let us derive a formula for solving this problem.
We use $s_1, \dots, s_k$ for the sizes of the connected components in the graph.
We cannot add edges within a connected component.
Therefore it turns out that this problem is very similar to the search for the number of spanning trees of a complete graph with $k$ vertices.
The only difference is that each vertex has actually the size $s_i$: each edge connecting the vertex $i$, actually multiplies the answer by $s_i$.
Thus in order to calculate the number of possible ways it is important to count how often each of the $k$ vertices is used in the connecting tree.
To obtain a formula for the problem it is necessary to sum the answer over all possible degrees.
Let $d_1, \dots, d_k$ be the degrees of the vertices in the tree after connecting the vertices.
The sum of the degrees is twice the number of edges:
$$\sum_{i=1}^k d_i = 2k - 2$$
If the vertex $i$ has degree $d_i$, then it appears $d_i - 1$ times in the Prüfer code.
The Prüfer code for a tree with $k$ vertices has length $k-2$.
So the number of ways to choose a code with $k-2$ numbers where the number $i$ appears exactly $d_i - 1$ times is equal to the **multinomial coefficient**
$$\binom{k-2}{d_1-1, d_2-1, \dots, d_k-1} = \frac{(k-2)!}{(d_1-1)! (d_2-1)! \cdots (d_k-1)!}.$$
The fact that each edge adjacent to the vertex $i$ multiplies the answer by $s_i$ we receive the answer, assuming that the degrees of the vertices are $d_1, \dots, d_k$:
$$s_1^{d_1} \cdot s_2^{d_2} \cdots s_k^{d_k} \cdot \binom{k-2}{d_1-1, d_2-1, \dots, d_k-1}$$
To get the final answer we need to sum this for all possible ways to choose the degrees:
$$\sum_{\substack{d_i \ge 1 \\\\ \sum_{i=1}^k d_i = 2k -2}} s_1^{d_1} \cdot s_2^{d_2} \cdots s_k^{d_k} \cdot \binom{k-2}{d_1-1, d_2-1, \dots, d_k-1}$$
Currently this looks like a really horrible answer, however we can use the **multinomial theorem**, which says:
$$(x_1 + \dots + x_m)^p = \sum_{\substack{c_i \ge 0 \\\\ \sum_{i=1}^m c_i = p}} x_1^{c_1} \cdot x_2^{c_2} \cdots x_m^{c_m} \cdot \binom{p}{c_1, c_2, \dots c_m}$$
This look already pretty similar.
To use it we only need to substitute with $e_i = d_i - 1$:
$$\sum_{\substack{e_i \ge 0 \\\\ \sum_{i=1}^k e_i = k - 2}} s_1^{e_1+1} \cdot s_2^{e_2+1} \cdots s_k^{e_k+1} \cdot \binom{k-2}{e_1, e_2, \dots, e_k}$$
After applying the multinomial theorem we get the **answer to the problem**:
$$s_1 \cdot s_2 \cdots s_k \cdot (s_1 + s_2 + \dots + s_k)^{k-2} = s_1 \cdot s_2 \cdots s_k \cdot n^{k-2}$$
By accident this formula also holds for $k = 1$.
|
---
title
prufer_code_cayley_formula
---
# Prüfer code
In this article we will look at the so-called **Prüfer code** (or Prüfer sequence), which is a way of encoding a labeled tree into a sequence of numbers in a unique way.
With the help of the Prüfer code we will prove **Cayley's formula** (which specified the number of spanning trees in a complete graph).
Also we show the solution to the problem of counting the number of ways of adding edges to a graph to make it connected.
**Note**, we will not consider trees consisting of a single vertex - this is a special case in which multiple statements clash.
## Prüfer code
The Prüfer code is a way of encoding a labeled tree with $n$ vertices using a sequence of $n - 2$ integers in the interval $[0; n-1]$.
This encoding also acts as a **bijection** between all spanning trees of a complete graph and the numerical sequences.
Although using the Prüfer code for storing and operating on tree is impractical due the specification of the representation, the Prüfer codes are used frequently: mostly in solving combinatorial problems.
The inventor - Heinz Prüfer - proposed this code in 1918 as a proof for Cayley's formula.
### Building the Prüfer code for a given tree
The Prüfer code is constructed as follows.
We will repeat the following procedure $n - 2$ times:
we select the leaf of the tree with the smallest number, remove it from the tree, and write down the number of the vertex that was connected to it.
After $n - 2$ iterations there will only remain $2$ vertices, and the algorithm ends.
Thus the Prüfer code for a given tree is a sequence of $n - 2$ numbers, where each number is the number of the connected vertex, i.e. this number is in the interval $[0, n-1]$.
The algorithm for computing the Prüfer code can be implemented easily with $O(n \log n)$ time complexity, simply by using a data structure to extract the minimum (for instance `set` or `priority_queue` in C++), which contains a list of all the current leafs.
```{.cpp file=pruefer_code_slow}
vector<vector<int>> adj;
vector<int> pruefer_code() {
int n = adj.size();
set<int> leafs;
vector<int> degree(n);
vector<bool> killed(n, false);
for (int i = 0; i < n; i++) {
degree[i] = adj[i].size();
if (degree[i] == 1)
leafs.insert(i);
}
vector<int> code(n - 2);
for (int i = 0; i < n - 2; i++) {
int leaf = *leafs.begin();
leafs.erase(leafs.begin());
killed[leaf] = true;
int v;
for (int u : adj[leaf]) {
if (!killed[u])
v = u;
}
code[i] = v;
if (--degree[v] == 1)
leafs.insert(v);
}
return code;
}
```
However the construction can also be implemented in linear time.
Such an approach is described in the next section.
### Building the Prüfer code for a given tree in linear time
The essence of the algorithm is to use a **moving pointer**, which will always point to the current leaf vertex that we want to remove.
At first glance this seems impossible, because during the process of constructing the Prüfer code the leaf number can increase and decrease.
However after a closer look, this is actually not true.
The number of leafs will not increase. Either the number decreases by one (we remove one leaf vertex and don't gain a new one), or it stay the same (we remove one leaf vertex and gain another one).
In the first case there is no other way than searching for the next smallest leaf vertex.
In the second case, however, we can decide in $O(1)$ time, if we can continue using the vertex that became a new leaf vertex, or if we have to search for the next smallest leaf vertex.
And in quite a lot of times we can continue with the new leaf vertex.
To do this we will use a variable $\text{ptr}$, which will indicate that in the set of vertices between $0$ and $\text{ptr}$ is at most one leaf vertex, namely the current one.
All other vertices in that range are either already removed from the tree, or have still more than one adjacent vertices.
At the same time we say, that we haven't removed any leaf vertices bigger than $\text{ptr}$ yet.
This variable is already very helpful in the first case.
After removing the current leaf node, we know that there cannot be a leaf node between $0$ and $\text{ptr}$, therefore we can start the search for the next one directly at $\text{ptr} + 1$, and we don't have to start the search back at vertex $0$.
And in the second case, we can further distinguish two cases:
Either the newly gained leaf vertex is smaller than $\text{ptr}$, then this must be the next leaf vertex, since we know that there are no other vertices smaller than $\text{ptr}$.
Or the newly gained leaf vertex is bigger.
But then we also know that it has to be bigger than $\text{ptr}$, and can start the search again at $\text{ptr} + 1$.
Even though we might have to perform multiple linear searches for the next leaf vertex, the pointer $\text{ptr}$ only increases and therefore the time complexity in total is $O(n)$.
```{.cpp file=pruefer_code_fast}
vector<vector<int>> adj;
vector<int> parent;
void dfs(int v) {
for (int u : adj[v]) {
if (u != parent[v]) {
parent[u] = v;
dfs(u);
}
}
}
vector<int> pruefer_code() {
int n = adj.size();
parent.resize(n);
parent[n-1] = -1;
dfs(n-1);
int ptr = -1;
vector<int> degree(n);
for (int i = 0; i < n; i++) {
degree[i] = adj[i].size();
if (degree[i] == 1 && ptr == -1)
ptr = i;
}
vector<int> code(n - 2);
int leaf = ptr;
for (int i = 0; i < n - 2; i++) {
int next = parent[leaf];
code[i] = next;
if (--degree[next] == 1 && next < ptr) {
leaf = next;
} else {
ptr++;
while (degree[ptr] != 1)
ptr++;
leaf = ptr;
}
}
return code;
}
```
In the code we first find for each its ancestor `parent[i]`, i.e. the ancestor that this vertex will have once we remove it from the tree.
We can find this ancestor by rooting the tree at the vertex $n-1$.
This is possible because the vertex $n-1$ will never be removed from the tree.
We also compute the degree for each vertex.
`ptr` is the pointer that indicates the minimum size of the remaining leaf vertices (except the current one `leaf`).
We will either assign the current leaf vertex with `next`, if this one is also a leaf vertex and it is smaller than `ptr`, or we start a linear search for the smallest leaf vertex by increasing the pointer.
It can be easily seen, that this code has the complexity $O(n)$.
### Some properties of the Prüfer code
- After constructing the Prüfer code two vertices will remain.
One of them is the highest vertex $n-1$, but nothing else can be said about the other one.
- Each vertex appears in the Prüfer code exactly a fixed number of times - its degree minus one.
This can be easily checked, since the degree will get smaller every time we record its label in the code, and we remove it once the degree is $1$.
For the two remaining vertices this fact is also true.
### Restoring the tree using the Prüfer code
To restore the tree it suffice to only focus on the property discussed in the last section.
We already know the degree of all the vertices in the desired tree.
Therefore we can find all leaf vertices, and also the first leaf that was removed in the first step (it has to be the smallest leaf).
This leaf vertex was connected to the vertex corresponding to the number in the first cell of the Prüfer code.
Thus we found the first edge removed by when then the Prüfer code was generated.
We can add this edge to the answer and reduce the degrees at both ends of the edge.
We will repeat this operation until we have used all numbers of the Prüfer code:
we look for the minimum vertex with degree equal to $1$, connect it with the next vertex from the Prüfer code, and reduce the degree.
In the end we only have two vertices left with degree equal to $1$.
These are the vertices that didn't got removed by the Prüfer code process.
We connect them to get the last edge of the tree.
One of them will always be the vertex $n-1$.
This algorithm can be **implemented** easily in $O(n \log n)$: we use a data structure that supports extracting the minimum (for example `set<>` or `priority_queue<>` in C++) to store all the leaf vertices.
The following implementation returns the list of edges corresponding to the tree.
```{.cpp file=pruefer_decode_slow}
vector<pair<int, int>> pruefer_decode(vector<int> const& code) {
int n = code.size() + 2;
vector<int> degree(n, 1);
for (int i : code)
degree[i]++;
set<int> leaves;
for (int i = 0; i < n; i++) {
if (degree[i] == 1)
leaves.insert(i);
}
vector<pair<int, int>> edges;
for (int v : code) {
int leaf = *leaves.begin();
leaves.erase(leaves.begin());
edges.emplace_back(leaf, v);
if (--degree[v] == 1)
leaves.insert(v);
}
edges.emplace_back(*leaves.begin(), n-1);
return edges;
}
```
### Restoring the tree using the Prüfer code in linear time
To obtain the tree in linear time we can apply the same technique used to obtain the Prüfer code in linear time.
We don't need a data structure to extract the minimum.
Instead we can notice that, after processing the current edge, only one vertex becomes a leaf.
Therefore we can either continue with this vertex, or we find a smaller one with a linear search by moving a pointer.
```{.cpp file=pruefer_decode_fast}
vector<pair<int, int>> pruefer_decode(vector<int> const& code) {
int n = code.size() + 2;
vector<int> degree(n, 1);
for (int i : code)
degree[i]++;
int ptr = 0;
while (degree[ptr] != 1)
ptr++;
int leaf = ptr;
vector<pair<int, int>> edges;
for (int v : code) {
edges.emplace_back(leaf, v);
if (--degree[v] == 1 && v < ptr) {
leaf = v;
} else {
ptr++;
while (degree[ptr] != 1)
ptr++;
leaf = ptr;
}
}
edges.emplace_back(leaf, n-1);
return edges;
}
```
### Bijection between trees and Prüfer codes
For each tree there exists a Prüfer code corresponding to it.
And for each Prüfer code we can restore the original tree.
It follows that also every Prüfer code (i.e. a sequence of $n-2$ numbers in the range $[0; n - 1]$) corresponds to a tree.
Therefore all trees and all Prüfer codes form a bijection (a **one-to-one correspondence**).
## Cayley's formula
Cayley's formula states that the **number of spanning trees in a complete labeled graph** with $n$ vertices is equal to:
$$n^{n-2}$$
There are multiple proofs for this formula.
Using the Prüfer code concept this statement comes without any surprise.
In fact any Prüfer code with $n-2$ numbers from the interval $[0; n-1]$ corresponds to some tree with $n$ vertices.
So we have $n^{n-2}$ different such Prüfer codes.
Since each such tree is a spanning tree of a complete graph with $n$ vertices, the number of such spanning trees is also $n^{n-2}$.
## Number of ways to make a graph connected
The concept of Prüfer codes are even more powerful.
It allows to create a lot more general formulas than Cayley's formula.
In this problem we are given a graph with $n$ vertices and $m$ edges.
The graph currently has $k$ components.
We want to compute the number of ways of adding $k-1$ edges so that the graph becomes connected (obviously $k-1$ is the minimum number necessary to make the graph connected).
Let us derive a formula for solving this problem.
We use $s_1, \dots, s_k$ for the sizes of the connected components in the graph.
We cannot add edges within a connected component.
Therefore it turns out that this problem is very similar to the search for the number of spanning trees of a complete graph with $k$ vertices.
The only difference is that each vertex has actually the size $s_i$: each edge connecting the vertex $i$, actually multiplies the answer by $s_i$.
Thus in order to calculate the number of possible ways it is important to count how often each of the $k$ vertices is used in the connecting tree.
To obtain a formula for the problem it is necessary to sum the answer over all possible degrees.
Let $d_1, \dots, d_k$ be the degrees of the vertices in the tree after connecting the vertices.
The sum of the degrees is twice the number of edges:
$$\sum_{i=1}^k d_i = 2k - 2$$
If the vertex $i$ has degree $d_i$, then it appears $d_i - 1$ times in the Prüfer code.
The Prüfer code for a tree with $k$ vertices has length $k-2$.
So the number of ways to choose a code with $k-2$ numbers where the number $i$ appears exactly $d_i - 1$ times is equal to the **multinomial coefficient**
$$\binom{k-2}{d_1-1, d_2-1, \dots, d_k-1} = \frac{(k-2)!}{(d_1-1)! (d_2-1)! \cdots (d_k-1)!}.$$
The fact that each edge adjacent to the vertex $i$ multiplies the answer by $s_i$ we receive the answer, assuming that the degrees of the vertices are $d_1, \dots, d_k$:
$$s_1^{d_1} \cdot s_2^{d_2} \cdots s_k^{d_k} \cdot \binom{k-2}{d_1-1, d_2-1, \dots, d_k-1}$$
To get the final answer we need to sum this for all possible ways to choose the degrees:
$$\sum_{\substack{d_i \ge 1 \\\\ \sum_{i=1}^k d_i = 2k -2}} s_1^{d_1} \cdot s_2^{d_2} \cdots s_k^{d_k} \cdot \binom{k-2}{d_1-1, d_2-1, \dots, d_k-1}$$
Currently this looks like a really horrible answer, however we can use the **multinomial theorem**, which says:
$$(x_1 + \dots + x_m)^p = \sum_{\substack{c_i \ge 0 \\\\ \sum_{i=1}^m c_i = p}} x_1^{c_1} \cdot x_2^{c_2} \cdots x_m^{c_m} \cdot \binom{p}{c_1, c_2, \dots c_m}$$
This look already pretty similar.
To use it we only need to substitute with $e_i = d_i - 1$:
$$\sum_{\substack{e_i \ge 0 \\\\ \sum_{i=1}^k e_i = k - 2}} s_1^{e_1+1} \cdot s_2^{e_2+1} \cdots s_k^{e_k+1} \cdot \binom{k-2}{e_1, e_2, \dots, e_k}$$
After applying the multinomial theorem we get the **answer to the problem**:
$$s_1 \cdot s_2 \cdots s_k \cdot (s_1 + s_2 + \dots + s_k)^{k-2} = s_1 \cdot s_2 \cdots s_k \cdot n^{k-2}$$
By accident this formula also holds for $k = 1$.
## Practice problems
- [UVA #10843 - Anne's game](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=20&page=show_problem&problem=1784)
- [Timus #1069 - Prufer Code](http://acm.timus.ru/problem.aspx?space=1&num=1069)
- [Codeforces - Clues](http://codeforces.com/contest/156/problem/D)
- [Topcoder - TheCitiesAndRoadsDivTwo](https://community.topcoder.com/stat?c=problem_statement&pm=10774&rd=14146)
|
Prüfer code
|
---
title
- rib_connectivity
- vertex_connectivity
---
# Edge connectivity / Vertex connectivity
## Definition
Given an undirected graph $G$ with $n$ vertices and $m$ edges.
Both the edge connectivity and the vertex connectivity are characteristics describing the graph.
### Edge connectivity
The **edge connectivity** $\lambda$ of the graph $G$ is the minimum number of edges that need to be deleted, such that the graph $G$ gets disconnected.
For example an already disconnected graph has an edge connectivity of $0$, a connected graph with at least one bridge has an edge connectivity of $1$, and a connected graph with no bridges has an edge connectivity of at least $2$.
We say that a set $S$ of edges **separates** the vertices $s$ and $t$, if, after removing all edges in $S$ from the graph $G$, the vertices $s$ and $t$ end up in different connected components.
It is clear, that the edge connectivity of a graph is equal to the minimum size of such a set separating two vertices $s$ and $t$, taken among all possible pairs $(s, t)$.
### Vertex connectivity
The **vertex connectivity** $\kappa$ of the graph $G$ is the minimum number of vertices that need to be deleted, such that the graph $G$ gets disconnected.
For example an already disconnected graph has the vertex connectivity $0$, and a connected graph with an articulation point has the vertex connectivity $1$.
We define that a complete graph has the vertex connectivity $n-1$.
For all other graphs the vertex connectivity doesn't exceed $n-2$, because you can find a pair of vertices which are not connected by an edge, and remove all other $n-2$ vertices.
We say that a set $T$ of vertices **separates** the vertices $s$ and $t$, if, after removing all vertices in $T$ from the graph $G$, the vertices end up in different connected components.
It is clear, that the vertex connectivity of a graph is equal to the minimal size of such a set separating two vertices $s$ and $t$, taken among all possible pairs $(s, t)$.
## Properties
### The Whitney inequalities
The **Whitney inequalities** (1932) gives a relation between the edge connectivity $\lambda$, the vertex connectivity $\kappa$ and the smallest degree of the vertices $\delta$:
$$\kappa \le \lambda \le \delta$$
Intuitively if we have a set of edges of size $\lambda$, which make the graph disconnected, we can choose one of each end point, and create a set of vertices, that also disconnect the graph.
And this set has size $\le \lambda$.
And if we pick the vertex and the minimal degree $\delta$, and remove all edges connected to it, then we also end up with a disconnected graph.
Therefore the second inequality $\lambda \le \delta$.
It is interesting to note, that the Whitney inequalities cannot be improved:
i.e. for any triple of numbers satisfying this inequality there exists at least one corresponding graph.
One such graph can be constructed in the following way:
The graph will consists of $2(\delta + 1)$ vertices, the first $\delta + 1$ vertices form a clique (all pairs of vertices are connected via an edge), and the second $\delta + 1$ vertices form a second clique.
In addition we connect the two cliques with $\lambda$ edges, such that it uses $\lambda$ different vertices in the first clique, and only $\kappa$ vertices in the second clique.
The resulting graph will have the three characteristics.
### The Ford-Fulkerson theorem
The **Ford-Fulkerson theorem** implies, that the biggest number of edge-disjoint paths connecting two vertices, is equal to the smallest number of edges separating these vertices.
## Computing the values
### Edge connectivity using maximum flow
This method is based on the Ford-Fulkerson theorem.
We iterate over all pairs of vertices $(s, t)$ and between each pair we find the largest number of disjoint paths between them.
This value can be found using a maximum flow algorithm:
we use $s$ as the source, $t$ as the sink, and assign each edge a capacity of $1$.
Then the maximum flow is the number of disjoint paths.
The complexity for the algorithm using [Edmonds-Karp](../graph/edmonds_karp.md) is $O(V^2 V E^2) = O(V^3 E^2)$.
But we should note, that this includes a hidden factor, since it is practically impossible to create a graph such that the maximum flow algorithm will be slow for all sources and sinks.
Especially the algorithm will run pretty fast for random graphs.
### Special algorithm for edge connectivity
The task of finding the edge connectivity if equal to the task of finding the **global minimum cut**.
Special algorithms have been developed for this task.
One of them is the Stoer-Wagner algorithm, which works in $O(V^3)$ or $O(V E)$ time.
### Vertex connectivity
Again we iterate over all pairs of vertices $s$ and $t$, and for each pair we find the minimum number of vertices that separates $s$ and $t$.
By doing this, we can apply the same maximum flow approach as described in the previous sections.
We split each vertex $x$ with $x \neq s$ and $x \neq t$ into two vertices $x_1$ and $x_2$.
We connect these to vertices with a directed edge $(x_1, x_2)$ with the capacity $1$, and replace all edges $(u, v)$ by the two directed edges $(u_2, v_1)$ and $(v_2, u_1)$, both with the capacity of 1.
The by the construction the value of the maximum flow will be equal to the minimum number of vertices that are needed to separate $s$ and $t$.
This approach has the same complexity as the flow approach for finding the edge connectivity.
|
---
title
- rib_connectivity
- vertex_connectivity
---
# Edge connectivity / Vertex connectivity
## Definition
Given an undirected graph $G$ with $n$ vertices and $m$ edges.
Both the edge connectivity and the vertex connectivity are characteristics describing the graph.
### Edge connectivity
The **edge connectivity** $\lambda$ of the graph $G$ is the minimum number of edges that need to be deleted, such that the graph $G$ gets disconnected.
For example an already disconnected graph has an edge connectivity of $0$, a connected graph with at least one bridge has an edge connectivity of $1$, and a connected graph with no bridges has an edge connectivity of at least $2$.
We say that a set $S$ of edges **separates** the vertices $s$ and $t$, if, after removing all edges in $S$ from the graph $G$, the vertices $s$ and $t$ end up in different connected components.
It is clear, that the edge connectivity of a graph is equal to the minimum size of such a set separating two vertices $s$ and $t$, taken among all possible pairs $(s, t)$.
### Vertex connectivity
The **vertex connectivity** $\kappa$ of the graph $G$ is the minimum number of vertices that need to be deleted, such that the graph $G$ gets disconnected.
For example an already disconnected graph has the vertex connectivity $0$, and a connected graph with an articulation point has the vertex connectivity $1$.
We define that a complete graph has the vertex connectivity $n-1$.
For all other graphs the vertex connectivity doesn't exceed $n-2$, because you can find a pair of vertices which are not connected by an edge, and remove all other $n-2$ vertices.
We say that a set $T$ of vertices **separates** the vertices $s$ and $t$, if, after removing all vertices in $T$ from the graph $G$, the vertices end up in different connected components.
It is clear, that the vertex connectivity of a graph is equal to the minimal size of such a set separating two vertices $s$ and $t$, taken among all possible pairs $(s, t)$.
## Properties
### The Whitney inequalities
The **Whitney inequalities** (1932) gives a relation between the edge connectivity $\lambda$, the vertex connectivity $\kappa$ and the smallest degree of the vertices $\delta$:
$$\kappa \le \lambda \le \delta$$
Intuitively if we have a set of edges of size $\lambda$, which make the graph disconnected, we can choose one of each end point, and create a set of vertices, that also disconnect the graph.
And this set has size $\le \lambda$.
And if we pick the vertex and the minimal degree $\delta$, and remove all edges connected to it, then we also end up with a disconnected graph.
Therefore the second inequality $\lambda \le \delta$.
It is interesting to note, that the Whitney inequalities cannot be improved:
i.e. for any triple of numbers satisfying this inequality there exists at least one corresponding graph.
One such graph can be constructed in the following way:
The graph will consists of $2(\delta + 1)$ vertices, the first $\delta + 1$ vertices form a clique (all pairs of vertices are connected via an edge), and the second $\delta + 1$ vertices form a second clique.
In addition we connect the two cliques with $\lambda$ edges, such that it uses $\lambda$ different vertices in the first clique, and only $\kappa$ vertices in the second clique.
The resulting graph will have the three characteristics.
### The Ford-Fulkerson theorem
The **Ford-Fulkerson theorem** implies, that the biggest number of edge-disjoint paths connecting two vertices, is equal to the smallest number of edges separating these vertices.
## Computing the values
### Edge connectivity using maximum flow
This method is based on the Ford-Fulkerson theorem.
We iterate over all pairs of vertices $(s, t)$ and between each pair we find the largest number of disjoint paths between them.
This value can be found using a maximum flow algorithm:
we use $s$ as the source, $t$ as the sink, and assign each edge a capacity of $1$.
Then the maximum flow is the number of disjoint paths.
The complexity for the algorithm using [Edmonds-Karp](../graph/edmonds_karp.md) is $O(V^2 V E^2) = O(V^3 E^2)$.
But we should note, that this includes a hidden factor, since it is practically impossible to create a graph such that the maximum flow algorithm will be slow for all sources and sinks.
Especially the algorithm will run pretty fast for random graphs.
### Special algorithm for edge connectivity
The task of finding the edge connectivity if equal to the task of finding the **global minimum cut**.
Special algorithms have been developed for this task.
One of them is the Stoer-Wagner algorithm, which works in $O(V^3)$ or $O(V E)$ time.
### Vertex connectivity
Again we iterate over all pairs of vertices $s$ and $t$, and for each pair we find the minimum number of vertices that separates $s$ and $t$.
By doing this, we can apply the same maximum flow approach as described in the previous sections.
We split each vertex $x$ with $x \neq s$ and $x \neq t$ into two vertices $x_1$ and $x_2$.
We connect these to vertices with a directed edge $(x_1, x_2)$ with the capacity $1$, and replace all edges $(u, v)$ by the two directed edges $(u_2, v_1)$ and $(v_2, u_1)$, both with the capacity of 1.
The by the construction the value of the maximum flow will be equal to the minimum number of vertices that are needed to separate $s$ and $t$.
This approach has the same complexity as the flow approach for finding the edge connectivity.
|
Edge connectivity / Vertex connectivity
|
---
title
dinic
---
# Maximum flow - Dinic's algorithm
Dinic's algorithm solves the maximum flow problem in $O(V^2E)$. The maximum flow problem is defined in this article [Maximum flow - Ford-Fulkerson and Edmonds-Karp](edmonds_karp.md). This algorithm was discovered by Yefim Dinitz in 1970.
## Definitions
A **residual network** $G^R$ of network $G$ is a network which contains two edges for each edge $(v, u)\in G$:<br>
- $(v, u)$ with capacity $c_{vu}^R = c_{vu} - f_{vu}$
- $(u, v)$ with capacity $c_{uv}^R = f_{vu}$
A **blocking flow** of some network is such a flow that every path from $s$ to $t$ contains at least one edge which is saturated by this flow. Note that a blocking flow is not necessarily maximal.
A **layered network** of a network $G$ is a network built in the following way. Firstly, for each vertex $v$ we calculate $level[v]$ - the shortest path (unweighted) from $s$ to this vertex using only edges with positive capacity. Then we keep only those edges $(v, u)$ for which $level[v] + 1 = level[u]$. Obviously, this network is acyclic.
## Algorithm
The algorithm consists of several phases. On each phase we construct the layered network of the residual network of $G$. Then we find an arbitrary blocking flow in the layered network and add it to the current flow.
## Proof of correctness
Let's show that if the algorithm terminates, it finds the maximum flow.
If the algorithm terminated, it couldn't find a blocking flow in the layered network. It means that the layered network doesn't have any path from $s$ to $t$. It means that the residual network doesn't have any path from $s$ to $t$. It means that the flow is maximum.
## Number of phases
The algorithm terminates in less than $V$ phases. To prove this, we must firstly prove two lemmas.
**Lemma 1.** The distances from $s$ to each vertex don't decrease after each iteration, i. e. $level_{i+1}[v] \ge level_i[v]$.
**Proof.** Fix a phase $i$ and a vertex $v$. Consider any shortest path $P$ from $s$ to $v$ in $G_{i+1}^R$. The length of $P$ equals $level_{i+1}[v]$. Note that $G_{i+1}^R$ can only contain edges from $G_i^R$ and back edges for edges from $G_i^R$. If $P$ has no back edges for $G_i^R$, then $level_{i+1}[v] \ge level_i[v]$ because $P$ is also a path in $G_i^R$. Now, suppose that $P$ has at least one back edge. Let the first such edge be $(u, w)$.Then $level_{i+1}[u] \ge level_i[u]$ (because of the first case). The edge $(u, w)$ doesn't belong to $G_i^R$, so the edge $(w, u)$ was affected by the blocking flow on the previous iteration. It means that $level_i[u] = level_i[w] + 1$. Also, $level_{i+1}[w] = level_{i+1}[u] + 1$. From these two equations and $level_{i+1}[u] \ge level_i[u]$ we obtain $level_{i+1}[w] \ge level_i[w] + 2$. Now we can use the same idea for the rest of the path.
**Lemma 2.** $level_{i+1}[t] > level_i[t]$
**Proof.** From the previous lemma, $level_{i+1}[t] \ge level_i[t]$. Suppose that $level_{i+1}[t] = level_i[t]$. Note that $G_{i+1}^R$ can only contain edges from $G_i^R$ and back edges for edges from $G_i^R$. It means that there is a shortest path in $G_i^R$ which wasn't blocked by the blocking flow. It's a contradiction.
From these two lemmas we conclude that there are less than $V$ phases because $level[t]$ increases, but it can't be greater than $V - 1$.
## Finding blocking flow
In order to find the blocking flow on each iteration, we may simply try pushing flow with DFS from $s$ to $t$ in the layered network while it can be pushed. In order to do it more quickly, we must remove the edges which can't be used to push anymore. To do this we can keep a pointer in each vertex which points to the next edge which can be used.
A single DFS run takes $O(k+V)$ time, where $k$ is the number of pointer advances on this run. Summed up over all runs, number of pointer advances can not exceed $E$. On the other hand, total number of runs won't exceed $E$, as every run saturates at least one edge. In this way, total running time of finding a blocking flow is $O(VE)$.
## Complexity
There are less than $V$ phases, so the total complexity is $O(V^2E)$.
## Unit networks
A **unit network** is a network in which for any vertex except $s$ and $t$ **either incoming or outgoing edge is unique and has unit capacity**. That's exactly the case with the network we build to solve the maximum matching problem with flows.
On unit networks Dinic's algorithm works in $O(E\sqrt{V})$. Let's prove this.
Firstly, each phase now works in $O(E)$ because each edge will be considered at most once.
Secondly, suppose there have already been $\sqrt{V}$ phases. Then all the augmenting paths with the length $\le\sqrt{V}$ have been found. Let $f$ be the current flow, $f'$ be the maximum flow. Consider their difference $f' - f$. It is a flow in $G^R$ of value $|f'| - |f|$ and on each edge it is either $0$ or $1$. It can be decomposed into $|f'| - |f|$ paths from $s$ to $t$ and possibly cycles. As the network is unit, they can't have common vertices, so the total number of vertices is $\ge (|f'| - |f|)\sqrt{V}$, but it is also $\le V$, so in another $\sqrt{V}$ iterations we will definitely find the maximum flow.
### Unit capacities networks
In a more generic settings when all edges have unit capacities, _but the number of incoming and outgoing edges is unbounded_, the paths can't have common edges rather than common vertices. In a similar way it allows to prove the bound of $\sqrt E$ on the number of iterations, hence the running time of Dinic algorithm on such networks is at most $O(E \sqrt E)$.
Finally, it is also possible to prove that the number of phases on unit capacity networks doesn't exceed $O(V^{2/3})$, providing an alternative estimate of $O(EV^{2/3})$ on the networks with particularly large number of edges.
## Implementation
```{.cpp file=dinic}
struct FlowEdge {
int v, u;
long long cap, flow = 0;
FlowEdge(int v, int u, long long cap) : v(v), u(u), cap(cap) {}
};
struct Dinic {
const long long flow_inf = 1e18;
vector<FlowEdge> edges;
vector<vector<int>> adj;
int n, m = 0;
int s, t;
vector<int> level, ptr;
queue<int> q;
Dinic(int n, int s, int t) : n(n), s(s), t(t) {
adj.resize(n);
level.resize(n);
ptr.resize(n);
}
void add_edge(int v, int u, long long cap) {
edges.emplace_back(v, u, cap);
edges.emplace_back(u, v, 0);
adj[v].push_back(m);
adj[u].push_back(m + 1);
m += 2;
}
bool bfs() {
while (!q.empty()) {
int v = q.front();
q.pop();
for (int id : adj[v]) {
if (edges[id].cap - edges[id].flow < 1)
continue;
if (level[edges[id].u] != -1)
continue;
level[edges[id].u] = level[v] + 1;
q.push(edges[id].u);
}
}
return level[t] != -1;
}
long long dfs(int v, long long pushed) {
if (pushed == 0)
return 0;
if (v == t)
return pushed;
for (int& cid = ptr[v]; cid < (int)adj[v].size(); cid++) {
int id = adj[v][cid];
int u = edges[id].u;
if (level[v] + 1 != level[u] || edges[id].cap - edges[id].flow < 1)
continue;
long long tr = dfs(u, min(pushed, edges[id].cap - edges[id].flow));
if (tr == 0)
continue;
edges[id].flow += tr;
edges[id ^ 1].flow -= tr;
return tr;
}
return 0;
}
long long flow() {
long long f = 0;
while (true) {
fill(level.begin(), level.end(), -1);
level[s] = 0;
q.push(s);
if (!bfs())
break;
fill(ptr.begin(), ptr.end(), 0);
while (long long pushed = dfs(s, flow_inf)) {
f += pushed;
}
}
return f;
}
};
```
|
---
title
dinic
---
# Maximum flow - Dinic's algorithm
Dinic's algorithm solves the maximum flow problem in $O(V^2E)$. The maximum flow problem is defined in this article [Maximum flow - Ford-Fulkerson and Edmonds-Karp](edmonds_karp.md). This algorithm was discovered by Yefim Dinitz in 1970.
## Definitions
A **residual network** $G^R$ of network $G$ is a network which contains two edges for each edge $(v, u)\in G$:<br>
- $(v, u)$ with capacity $c_{vu}^R = c_{vu} - f_{vu}$
- $(u, v)$ with capacity $c_{uv}^R = f_{vu}$
A **blocking flow** of some network is such a flow that every path from $s$ to $t$ contains at least one edge which is saturated by this flow. Note that a blocking flow is not necessarily maximal.
A **layered network** of a network $G$ is a network built in the following way. Firstly, for each vertex $v$ we calculate $level[v]$ - the shortest path (unweighted) from $s$ to this vertex using only edges with positive capacity. Then we keep only those edges $(v, u)$ for which $level[v] + 1 = level[u]$. Obviously, this network is acyclic.
## Algorithm
The algorithm consists of several phases. On each phase we construct the layered network of the residual network of $G$. Then we find an arbitrary blocking flow in the layered network and add it to the current flow.
## Proof of correctness
Let's show that if the algorithm terminates, it finds the maximum flow.
If the algorithm terminated, it couldn't find a blocking flow in the layered network. It means that the layered network doesn't have any path from $s$ to $t$. It means that the residual network doesn't have any path from $s$ to $t$. It means that the flow is maximum.
## Number of phases
The algorithm terminates in less than $V$ phases. To prove this, we must firstly prove two lemmas.
**Lemma 1.** The distances from $s$ to each vertex don't decrease after each iteration, i. e. $level_{i+1}[v] \ge level_i[v]$.
**Proof.** Fix a phase $i$ and a vertex $v$. Consider any shortest path $P$ from $s$ to $v$ in $G_{i+1}^R$. The length of $P$ equals $level_{i+1}[v]$. Note that $G_{i+1}^R$ can only contain edges from $G_i^R$ and back edges for edges from $G_i^R$. If $P$ has no back edges for $G_i^R$, then $level_{i+1}[v] \ge level_i[v]$ because $P$ is also a path in $G_i^R$. Now, suppose that $P$ has at least one back edge. Let the first such edge be $(u, w)$.Then $level_{i+1}[u] \ge level_i[u]$ (because of the first case). The edge $(u, w)$ doesn't belong to $G_i^R$, so the edge $(w, u)$ was affected by the blocking flow on the previous iteration. It means that $level_i[u] = level_i[w] + 1$. Also, $level_{i+1}[w] = level_{i+1}[u] + 1$. From these two equations and $level_{i+1}[u] \ge level_i[u]$ we obtain $level_{i+1}[w] \ge level_i[w] + 2$. Now we can use the same idea for the rest of the path.
**Lemma 2.** $level_{i+1}[t] > level_i[t]$
**Proof.** From the previous lemma, $level_{i+1}[t] \ge level_i[t]$. Suppose that $level_{i+1}[t] = level_i[t]$. Note that $G_{i+1}^R$ can only contain edges from $G_i^R$ and back edges for edges from $G_i^R$. It means that there is a shortest path in $G_i^R$ which wasn't blocked by the blocking flow. It's a contradiction.
From these two lemmas we conclude that there are less than $V$ phases because $level[t]$ increases, but it can't be greater than $V - 1$.
## Finding blocking flow
In order to find the blocking flow on each iteration, we may simply try pushing flow with DFS from $s$ to $t$ in the layered network while it can be pushed. In order to do it more quickly, we must remove the edges which can't be used to push anymore. To do this we can keep a pointer in each vertex which points to the next edge which can be used.
A single DFS run takes $O(k+V)$ time, where $k$ is the number of pointer advances on this run. Summed up over all runs, number of pointer advances can not exceed $E$. On the other hand, total number of runs won't exceed $E$, as every run saturates at least one edge. In this way, total running time of finding a blocking flow is $O(VE)$.
## Complexity
There are less than $V$ phases, so the total complexity is $O(V^2E)$.
## Unit networks
A **unit network** is a network in which for any vertex except $s$ and $t$ **either incoming or outgoing edge is unique and has unit capacity**. That's exactly the case with the network we build to solve the maximum matching problem with flows.
On unit networks Dinic's algorithm works in $O(E\sqrt{V})$. Let's prove this.
Firstly, each phase now works in $O(E)$ because each edge will be considered at most once.
Secondly, suppose there have already been $\sqrt{V}$ phases. Then all the augmenting paths with the length $\le\sqrt{V}$ have been found. Let $f$ be the current flow, $f'$ be the maximum flow. Consider their difference $f' - f$. It is a flow in $G^R$ of value $|f'| - |f|$ and on each edge it is either $0$ or $1$. It can be decomposed into $|f'| - |f|$ paths from $s$ to $t$ and possibly cycles. As the network is unit, they can't have common vertices, so the total number of vertices is $\ge (|f'| - |f|)\sqrt{V}$, but it is also $\le V$, so in another $\sqrt{V}$ iterations we will definitely find the maximum flow.
### Unit capacities networks
In a more generic settings when all edges have unit capacities, _but the number of incoming and outgoing edges is unbounded_, the paths can't have common edges rather than common vertices. In a similar way it allows to prove the bound of $\sqrt E$ on the number of iterations, hence the running time of Dinic algorithm on such networks is at most $O(E \sqrt E)$.
Finally, it is also possible to prove that the number of phases on unit capacity networks doesn't exceed $O(V^{2/3})$, providing an alternative estimate of $O(EV^{2/3})$ on the networks with particularly large number of edges.
## Implementation
```{.cpp file=dinic}
struct FlowEdge {
int v, u;
long long cap, flow = 0;
FlowEdge(int v, int u, long long cap) : v(v), u(u), cap(cap) {}
};
struct Dinic {
const long long flow_inf = 1e18;
vector<FlowEdge> edges;
vector<vector<int>> adj;
int n, m = 0;
int s, t;
vector<int> level, ptr;
queue<int> q;
Dinic(int n, int s, int t) : n(n), s(s), t(t) {
adj.resize(n);
level.resize(n);
ptr.resize(n);
}
void add_edge(int v, int u, long long cap) {
edges.emplace_back(v, u, cap);
edges.emplace_back(u, v, 0);
adj[v].push_back(m);
adj[u].push_back(m + 1);
m += 2;
}
bool bfs() {
while (!q.empty()) {
int v = q.front();
q.pop();
for (int id : adj[v]) {
if (edges[id].cap - edges[id].flow < 1)
continue;
if (level[edges[id].u] != -1)
continue;
level[edges[id].u] = level[v] + 1;
q.push(edges[id].u);
}
}
return level[t] != -1;
}
long long dfs(int v, long long pushed) {
if (pushed == 0)
return 0;
if (v == t)
return pushed;
for (int& cid = ptr[v]; cid < (int)adj[v].size(); cid++) {
int id = adj[v][cid];
int u = edges[id].u;
if (level[v] + 1 != level[u] || edges[id].cap - edges[id].flow < 1)
continue;
long long tr = dfs(u, min(pushed, edges[id].cap - edges[id].flow));
if (tr == 0)
continue;
edges[id].flow += tr;
edges[id ^ 1].flow -= tr;
return tr;
}
return 0;
}
long long flow() {
long long f = 0;
while (true) {
fill(level.begin(), level.end(), -1);
level[s] = 0;
q.push(s);
if (!bfs())
break;
fill(ptr.begin(), ptr.end(), 0);
while (long long pushed = dfs(s, flow_inf)) {
f += pushed;
}
}
return f;
}
};
```
|
Maximum flow - Dinic's algorithm
|
---
title: Finding the Eulerian path in O(M)
title
euler_path
---
# Finding the Eulerian path in $O(M)$
A Eulerian path is a path in a graph that passes through all of its edges exactly once.
A Eulerian cycle is a Eulerian path that is a cycle.
The problem is to find the Eulerian path in an **undirected multigraph with loops**.
## Algorithm
First we can check if there is an Eulerian path.
We can use the following theorem. An Eulerian cycle exists if and only if the degrees of all vertices are even.
And an Eulerian path exists if and only if the number of vertices with odd degrees is two (or zero, in the case of the existence of a Eulerian cycle).
In addition, of course, the graph must be sufficiently connected (i.e., if you remove all isolated vertices from it, you should get a connected graph).
To find the Eulerian path / Eulerian cycle we can use the following strategy:
We find all simple cycles and combine them into one - this will be the Eulerian cycle.
If the graph is such that the Eulerian path is not a cycle, then add the missing edge, find the Eulerian cycle, then remove the extra edge.
Looking for all cycles and combining them can be done with a simple recursive procedure:
```nohighlight
procedure FindEulerPath(V)
1. iterate through all the edges outgoing from vertex V;
remove this edge from the graph,
and call FindEulerPath from the second end of this edge;
2. add vertex V to the answer.
```
The complexity of this algorithm is obviously linear with respect to the number of edges.
But we can write the same algorithm in the non-recursive version:
```nohighlight
stack St;
put start vertex in St;
until St is empty
let V be the value at the top of St;
if degree(V) = 0, then
add V to the answer;
remove V from the top of St;
otherwise
find any edge coming out of V;
remove it from the graph;
put the second end of this edge in St;
```
It is easy to check the equivalence of these two forms of the algorithm. However, the second form is obviously faster, and the code will be much more efficient.
## The Domino problem
We give here a classical Eulerian cycle problem - the Domino problem.
There are $N$ dominoes, as it is known, on both ends of the Domino one number is written(usually from 1 to 6, but in our case it is not important). You want to put all the dominoes in a row so that the numbers on any two adjacent dominoes, written on their common side, coincide. Dominoes are allowed to turn.
Reformulate the problem. Let the numbers written on the bottoms be the vertices of the graph, and the dominoes be the edges of this graph (each Domino with numbers $(a,b)$ are the edges $(a,b)$ and $(b, a)$). Then our problem is reduced to the problem of finding the Eulerian path in this graph.
## Implementation
The program below searches for and outputs a Eulerian loop or path in a graph, or outputs $-1$ if it does not exist.
First, the program checks the degree of vertices: if there are no vertices with an odd degree, then the graph has an Euler cycle, if there are $2$ vertices with an odd degree, then in the graph there is only an Euler path (but no Euler cycle), if there are more than $2$ such vertices, then in the graph there is no Euler cycle or Euler path.
To find the Euler path (not a cycle), let's do this: if $V1$ and $V2$ are two vertices of odd degree, then just add an edge $(V1, V2)$, in the resulting graph we find the Euler cycle (it will obviously exist), and then remove the "fictitious" edge $(V1, V2)$ from the answer.
We will look for the Euler cycle exactly as described above (non-recursive version), and at the same time at the end of this algorithm we will check whether the graph was connected or not (if the graph was not connected, then at the end of the algorithm some edges will remain in the graph, and in this case we need to print $-1$).
Finally, the program takes into account that there can be isolated vertices in the graph.
Notice that we use an adjacency matrix in this problem.
Also this implementation handles finding the next with brute-force, which requires to iterate over the complete row in the matrix over and over.
A better way would be to store the graph as an adjacency list, and remove edges in $O(1)$ and mark the reversed edges in separate list.
This way we can archive a $O(N)$ algorithm.
```cpp
int main() {
int n;
vector<vector<int>> g(n, vector<int>(n));
// reading the graph in the adjacency matrix
vector<int> deg(n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j)
deg[i] += g[i][j];
}
int first = 0;
while (first < n && !deg[first])
++first;
if (first == n) {
cout << -1;
return 0;
}
int v1 = -1, v2 = -1;
bool bad = false;
for (int i = 0; i < n; ++i) {
if (deg[i] & 1) {
if (v1 == -1)
v1 = i;
else if (v2 == -1)
v2 = i;
else
bad = true;
}
}
if (v1 != -1)
++g[v1][v2], ++g[v2][v1];
stack<int> st;
st.push(first);
vector<int> res;
while (!st.empty()) {
int v = st.top();
int i;
for (i = 0; i < n; ++i)
if (g[v][i])
break;
if (i == n) {
res.push_back(v);
st.pop();
} else {
--g[v][i];
--g[i][v];
st.push(i);
}
}
if (v1 != -1) {
for (size_t i = 0; i + 1 < res.size(); ++i) {
if ((res[i] == v1 && res[i + 1] == v2) ||
(res[i] == v2 && res[i + 1] == v1)) {
vector<int> res2;
for (size_t j = i + 1; j < res.size(); ++j)
res2.push_back(res[j]);
for (size_t j = 1; j <= i; ++j)
res2.push_back(res[j]);
res = res2;
break;
}
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (g[i][j])
bad = true;
}
}
if (bad) {
cout << -1;
} else {
for (int x : res)
cout << x << " ";
}
}
```
#
|
---
title: Finding the Eulerian path in O(M)
title
euler_path
---
# Finding the Eulerian path in $O(M)$
A Eulerian path is a path in a graph that passes through all of its edges exactly once.
A Eulerian cycle is a Eulerian path that is a cycle.
The problem is to find the Eulerian path in an **undirected multigraph with loops**.
## Algorithm
First we can check if there is an Eulerian path.
We can use the following theorem. An Eulerian cycle exists if and only if the degrees of all vertices are even.
And an Eulerian path exists if and only if the number of vertices with odd degrees is two (or zero, in the case of the existence of a Eulerian cycle).
In addition, of course, the graph must be sufficiently connected (i.e., if you remove all isolated vertices from it, you should get a connected graph).
To find the Eulerian path / Eulerian cycle we can use the following strategy:
We find all simple cycles and combine them into one - this will be the Eulerian cycle.
If the graph is such that the Eulerian path is not a cycle, then add the missing edge, find the Eulerian cycle, then remove the extra edge.
Looking for all cycles and combining them can be done with a simple recursive procedure:
```nohighlight
procedure FindEulerPath(V)
1. iterate through all the edges outgoing from vertex V;
remove this edge from the graph,
and call FindEulerPath from the second end of this edge;
2. add vertex V to the answer.
```
The complexity of this algorithm is obviously linear with respect to the number of edges.
But we can write the same algorithm in the non-recursive version:
```nohighlight
stack St;
put start vertex in St;
until St is empty
let V be the value at the top of St;
if degree(V) = 0, then
add V to the answer;
remove V from the top of St;
otherwise
find any edge coming out of V;
remove it from the graph;
put the second end of this edge in St;
```
It is easy to check the equivalence of these two forms of the algorithm. However, the second form is obviously faster, and the code will be much more efficient.
## The Domino problem
We give here a classical Eulerian cycle problem - the Domino problem.
There are $N$ dominoes, as it is known, on both ends of the Domino one number is written(usually from 1 to 6, but in our case it is not important). You want to put all the dominoes in a row so that the numbers on any two adjacent dominoes, written on their common side, coincide. Dominoes are allowed to turn.
Reformulate the problem. Let the numbers written on the bottoms be the vertices of the graph, and the dominoes be the edges of this graph (each Domino with numbers $(a,b)$ are the edges $(a,b)$ and $(b, a)$). Then our problem is reduced to the problem of finding the Eulerian path in this graph.
## Implementation
The program below searches for and outputs a Eulerian loop or path in a graph, or outputs $-1$ if it does not exist.
First, the program checks the degree of vertices: if there are no vertices with an odd degree, then the graph has an Euler cycle, if there are $2$ vertices with an odd degree, then in the graph there is only an Euler path (but no Euler cycle), if there are more than $2$ such vertices, then in the graph there is no Euler cycle or Euler path.
To find the Euler path (not a cycle), let's do this: if $V1$ and $V2$ are two vertices of odd degree, then just add an edge $(V1, V2)$, in the resulting graph we find the Euler cycle (it will obviously exist), and then remove the "fictitious" edge $(V1, V2)$ from the answer.
We will look for the Euler cycle exactly as described above (non-recursive version), and at the same time at the end of this algorithm we will check whether the graph was connected or not (if the graph was not connected, then at the end of the algorithm some edges will remain in the graph, and in this case we need to print $-1$).
Finally, the program takes into account that there can be isolated vertices in the graph.
Notice that we use an adjacency matrix in this problem.
Also this implementation handles finding the next with brute-force, which requires to iterate over the complete row in the matrix over and over.
A better way would be to store the graph as an adjacency list, and remove edges in $O(1)$ and mark the reversed edges in separate list.
This way we can archive a $O(N)$ algorithm.
```cpp
int main() {
int n;
vector<vector<int>> g(n, vector<int>(n));
// reading the graph in the adjacency matrix
vector<int> deg(n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j)
deg[i] += g[i][j];
}
int first = 0;
while (first < n && !deg[first])
++first;
if (first == n) {
cout << -1;
return 0;
}
int v1 = -1, v2 = -1;
bool bad = false;
for (int i = 0; i < n; ++i) {
if (deg[i] & 1) {
if (v1 == -1)
v1 = i;
else if (v2 == -1)
v2 = i;
else
bad = true;
}
}
if (v1 != -1)
++g[v1][v2], ++g[v2][v1];
stack<int> st;
st.push(first);
vector<int> res;
while (!st.empty()) {
int v = st.top();
int i;
for (i = 0; i < n; ++i)
if (g[v][i])
break;
if (i == n) {
res.push_back(v);
st.pop();
} else {
--g[v][i];
--g[i][v];
st.push(i);
}
}
if (v1 != -1) {
for (size_t i = 0; i + 1 < res.size(); ++i) {
if ((res[i] == v1 && res[i + 1] == v2) ||
(res[i] == v2 && res[i + 1] == v1)) {
vector<int> res2;
for (size_t j = i + 1; j < res.size(); ++j)
res2.push_back(res[j]);
for (size_t j = 1; j <= i; ++j)
res2.push_back(res[j]);
res = res2;
break;
}
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (g[i][j])
bad = true;
}
}
if (bad) {
cout << -1;
} else {
for (int x : res)
cout << x << " ";
}
}
```
### Practice problems:
- [CSES : Mail Delivery](https://cses.fi/problemset/task/1691)
- [CSES : Teleporters Path](https://cses.fi/problemset/task/1693)
|
Finding the Eulerian path in $O(M)$
|
---
title
bridge_searching_online
---
# Finding Bridges Online
We are given an undirected graph.
A bridge is an edge whose removal makes the graph disconnected (or, more precisely, increases the number of connected components).
Our task is to find all the bridges in the given graph.
Informally this task can be put as follows:
we have to find all the "important" roads on the given road map, i.e. such roads that the removal of any of them will lead to some cities being unreachable from others.
There is already the article [Finding Bridges in $O(N+M)$](bridge-searching.md) which solves this task with a [Depth First Search](depth-first-search.md) traversal.
This algorithm will be much more complicated, but it has one big advantage:
the algorithm described in this article works online, which means that the input graph doesn't have to be known in advance.
The edges are added once at a time, and after each addition the algorithm recounts all the bridges in the current graph.
In other words the algorithm is designed to work efficiently on a dynamic, changing graph.
More rigorously the statement of the problem is as follows:
Initially the graph is empty and consists of $n$ vertices.
Then we receive pairs of vertices $(a, b)$, which denote an edge added to the graph.
After each received edge, i.e. after adding each edge, output the current number of bridges in the graph.
It is also possible to maintain a list of all bridges as well as explicitly support the 2-edge-connected components.
The algorithm described below works in $O(n \log n + m)$ time, where $m$ is the number of edges.
The algorithm is based on the data structure [Disjoint Set Union](../data_structures/disjoint_set_union.md).
However the implementation in this article takes $O(n \log n + m \log n)$ time, because it uses the simplified version of the DSU without Union by Rank.
## Algorithm
First let's define a $k$-edge-connected component:
it is a connected component that remains connected whenever you remove fewer than $k$ edges.
It is very easy to see, that the bridges partition the graph into 2-edge-connected components.
If we compress each of those 2-edge-connected components into vertices and only leave the bridges as edges in the compressed graph, then we obtain an acyclic graph, i.e. a forest.
The algorithm described below maintains this forest explicitly as well as the 2-edge-connected components.
It is clear that initially, when the graph is empty, it contains $n$ 2-edge-connected components, which by themselves are not connect.
When adding the next edge $(a, b)$ there can occur three situations:
* Both vertices $a$ and $b$ are in the same 2-edge-connected component - then this edge is not a bridge, and does not change anything in the forest structure, so we can just skip this edge.
Thus, in this case the number of bridges does not change.
* The vertices $a$ and $b$ are in completely different connected components, i.e. each one is part of a different tree.
In this case, the edge $(a, b)$ becomes a new bridge, and these two trees are combined into one (and all the old bridges remain).
Thus, in this case the number of bridges increases by one.
* The vertices $a$ and $b$ are in one connected component, but in different 2-edge-connected components.
In this case, this edge forms a cycle along with some of the old bridges.
All these bridges end being bridges, and the resulting cycle must be compressed into a new 2-edge-connected component.
Thus, in this case the number of bridges decreases by two or more.
Consequently the whole task is reduced to the effective implementation of all these operations over the forest of 2-edge-connected components.
## Data Structures for storing the forest
The only data structure that we need is [Disjoint Set Union](../data_structures/disjoint_set_union.md).
In fact we will make two copies of this structure:
one will be to maintain the connected components, the other to maintain the 2-edge-connected components.
And in addition we store the structure of the trees in the forest of 2-edge-connected components via pointers:
Each 2-edge-connected component will store the index `par[]` of its ancestor in the tree.
We will now consistently disassemble every operation that we need to learn to implement:
* Check whether the two vertices lie in the same connected / 2-edge-connected component.
It is done with the usual DSU algorithm, we just find and compare the representatives of the DSUs.
* Joining two trees for some edge $(a, b)$.
Since it could turn out that neither the vertex $a$ nor the vertex $b$ are the roots of their trees, the only way to connect these two trees is to re-root one of them.
For example you can re-root the tree of vertex $a$, and then attach it to another tree by setting the ancestor of $a$ to $b$.
However the question about the effectiveness of the re-rooting operation arises:
in order to re-root the tree with the root $r$ to the vertex $v$, it is necessary to necessary to visit all vertices on the path between $v$ and $r$ and redirect the pointers `par[]` in the opposite direction, and also change the references to the ancestors in the DSU that is responsible for the connected components.
Thus, the cost of re-rooting is $O(h)$, where $h$ is the height of the tree.
You can make an even worse estimate by saying that the cost is $O(\text{size})$ where $\text{size}$ is the number of vertices in the tree.
The final complexity will not differ.
We now apply a standard technique: we re-root the tree that contains fewer vertices.
Then it is intuitively clear that the worst case is when two trees of approximately equal sizes are combined, but then the result is a tree of twice the size.
This does not allow this situation to happen many times.
In general the total cost can be written in the form of a recurrence:
\[ T(n) = \max_{k = 1 \ldots n-1} \left\{ T(k) + T(n - k) + O(\min(k, n - k))\right\} \]
$T(n)$ is the number of operations necessary to obtain a tree with $n$ vertices by means of re-rooting and unifying trees.
A tree of size $n$ can be created by combining two smaller trees of size $k$ and $n - k$.
This recurrence is has the solution $T(n) = O (n \log n)$.
Thus, the total time spent on all re-rooting operations will be $O(n \log n)$ if we always re-root the smaller of the two trees.
We will have to maintain the size of each connected component, but the data structure DSU makes this possible without difficulty.
* Searching for the cycle formed by adding a new edge $(a, b)$.
Since $a$ and $b$ are already connected in the tree we need to find the [Lowest Common Ancestor](lca.md) of the vertices $a$ and $b$.
The cycle will consist of the paths from $b$ to the LCA, from the LCA to $b$ and the edge $a$ to $b$.
After finding the cycle we compress all vertices of the detected cycle into one vertex.
This means that we already have a complexity proportional to the cycle length, which means that we also can use any LCA algorithm proportional to the length, and don't have to use any fast one.
Since all information about the structure of the tree is available is the ancestor array `par[]`, the only reasonable LCA algorithm is the following:
mark the vertices $a$ and $b$ as visited, then we go to their ancestors `par[a]` and `par[b]` and mark them, then advance to their ancestors and so on, until we reach an already marked vertex.
This vertex is the LCA that we are looking for, and we can find the vertices on the cycle by traversing the path from $a$ and $b$ to the LCA again.
It is obvious that the complexity of this algorithm is proportional to the length of the desired cycle.
* Compression of the cycle by adding a new edge $(a, b)$ in a tree.
We need to create a new 2-edge-connected component, which will consist of all vertices of the detected cycle (also the detected cycle itself could consist of some 2-edge-connected components, but this does not change anything).
In addition it is necessary to compress them in such a way that the structure of the tree is not disturbed, and all pointers `par[]` and two DSUs are still correct.
The easiest way to achieve this is to compress all the vertices of the cycle to their LCA.
In fact the LCA is the highest of the vertices, i.e. its ancestor pointer `par[]` remains unchanged.
For all the other vertices of the loop the ancestors do not need to be updated, since these vertices simply cease to exists.
But in the DSU of the 2-edge-connected components all these vertices will simply point to the LCA.
We will implement the DSU of the 2-edge-connected components without the Union by rank optimization, therefore we will get the complexity $O(\log n)$ on average per query.
To achieve the complexity $O(1)$ on average per query, we need to combine the vertices of the cycle according to Union by rank, and then assign `par[]` accordingly.
## Implementation
Here is the final implementation of the whole algorithm.
As mentioned before, for the sake of simplicity the DSU of the 2-edge-connected components is written without Union by rank, therefore the resulting complexity will be $O(\log n)$ on average.
Also in this implementation the bridges themselves are not stored, only their count `bridges`.
However it will not be difficult to create a `set` of all bridges.
Initially you call the function `init()`, which initializes the two DSUs (creating a separate set for each vertex, and setting the size equal to one), and sets the ancestors `par`.
The main function is `add_edge(a, b)`, which processes and adds a new edge.
```cpp
vector<int> par, dsu_2ecc, dsu_cc, dsu_cc_size;
int bridges;
int lca_iteration;
vector<int> last_visit;
void init(int n) {
par.resize(n);
dsu_2ecc.resize(n);
dsu_cc.resize(n);
dsu_cc_size.resize(n);
lca_iteration = 0;
last_visit.assign(n, 0);
for (int i=0; i<n; ++i) {
dsu_2ecc[i] = i;
dsu_cc[i] = i;
dsu_cc_size[i] = 1;
par[i] = -1;
}
bridges = 0;
}
int find_2ecc(int v) {
if (v == -1)
return -1;
return dsu_2ecc[v] == v ? v : dsu_2ecc[v] = find_2ecc(dsu_2ecc[v]);
}
int find_cc(int v) {
v = find_2ecc(v);
return dsu_cc[v] == v ? v : dsu_cc[v] = find_cc(dsu_cc[v]);
}
void make_root(int v) {
v = find_2ecc(v);
int root = v;
int child = -1;
while (v != -1) {
int p = find_2ecc(par[v]);
par[v] = child;
dsu_cc[v] = root;
child = v;
v = p;
}
dsu_cc_size[root] = dsu_cc_size[child];
}
void merge_path (int a, int b) {
++lca_iteration;
vector<int> path_a, path_b;
int lca = -1;
while (lca == -1) {
if (a != -1) {
a = find_2ecc(a);
path_a.push_back(a);
if (last_visit[a] == lca_iteration){
lca = a;
break;
}
last_visit[a] = lca_iteration;
a = par[a];
}
if (b != -1) {
b = find_2ecc(b);
path_b.push_back(b);
if (last_visit[b] == lca_iteration){
lca = b;
break;
}
last_visit[b] = lca_iteration;
b = par[b];
}
}
for (int v : path_a) {
dsu_2ecc[v] = lca;
if (v == lca)
break;
--bridges;
}
for (int v : path_b) {
dsu_2ecc[v] = lca;
if (v == lca)
break;
--bridges;
}
}
void add_edge(int a, int b) {
a = find_2ecc(a);
b = find_2ecc(b);
if (a == b)
return;
int ca = find_cc(a);
int cb = find_cc(b);
if (ca != cb) {
++bridges;
if (dsu_cc_size[ca] > dsu_cc_size[cb]) {
swap(a, b);
swap(ca, cb);
}
make_root(a);
par[a] = dsu_cc[a] = b;
dsu_cc_size[cb] += dsu_cc_size[a];
} else {
merge_path(a, b);
}
}
```
The DSU for the 2-edge-connected components is stored in the vector `dsu_2ecc`, and the function returning the representative is `find_2ecc(v)`.
This function is used many times in the rest of the code, since after the compression of several vertices into one all these vertices cease to exist, and instead only the leader has the correct ancestor `par` in the forest of 2-edge-connected components.
The DSU for the connected components is stored in the vector `dsu_cc`, and there is also an additional vector `dsu_cc_size` to store the component sizes.
The function `find_cc(v)` returns the leader of the connectivity component (which is actually the root of the tree).
The re-rooting of a tree `make_root(v)` works as described above:
if traverses from the vertex $v$ via the ancestors to the root vertex, each time redirecting the ancestor `par` in the opposite direction.
The link to the representative of the connected component `dsu_cc` is also updated, so that it points to the new root vertex.
After re-rooting we have to assign the new root the correct size of the connected component.
Also we have to be careful that we call `find_2ecc()` to get the representatives of the 2-edge-connected component, rather than some other vertex that have already been compressed.
The cycle finding and compression function `merge_path(a, b)` is also implemented as described above.
It searches for the LCA of $a$ and $b$ be rising these nodes in parallel, until we meet a vertex for the second time.
For efficiency purposes we choose a unique identifier for each LCA finding call, and mark the traversed vertices with it.
This works in $O(1)$, while other approaches like using $set$ perform worse.
The passed paths are stored in the vectors `path_a` and `path_b`, and we use them to walk through them a second time up to the LCA, thereby obtaining all vertices of the cycle.
All the vertices of the cycle get compressed by attaching them to the LCA, hence the average complexity is $O(\log n)$ (since we don't use Union by rank).
All the edges we pass have been bridges, so we subtract 1 for each edge in the cycle.
Finally the query function `add_edge(a, b)` determines the connected components in which the vertices $a$ and $b$ lie.
If they lie in different connectivity components, then a smaller tree is re-rooted and then attached to the larger tree.
Otherwise if the vertices $a$ and $b$ lie in one tree, but in different 2-edge-connected components, then the function `merge_path(a, b)` is called, which will detect the cycle and compress it into one 2-edge-connected component.
|
---
title
bridge_searching_online
---
# Finding Bridges Online
We are given an undirected graph.
A bridge is an edge whose removal makes the graph disconnected (or, more precisely, increases the number of connected components).
Our task is to find all the bridges in the given graph.
Informally this task can be put as follows:
we have to find all the "important" roads on the given road map, i.e. such roads that the removal of any of them will lead to some cities being unreachable from others.
There is already the article [Finding Bridges in $O(N+M)$](bridge-searching.md) which solves this task with a [Depth First Search](depth-first-search.md) traversal.
This algorithm will be much more complicated, but it has one big advantage:
the algorithm described in this article works online, which means that the input graph doesn't have to be known in advance.
The edges are added once at a time, and after each addition the algorithm recounts all the bridges in the current graph.
In other words the algorithm is designed to work efficiently on a dynamic, changing graph.
More rigorously the statement of the problem is as follows:
Initially the graph is empty and consists of $n$ vertices.
Then we receive pairs of vertices $(a, b)$, which denote an edge added to the graph.
After each received edge, i.e. after adding each edge, output the current number of bridges in the graph.
It is also possible to maintain a list of all bridges as well as explicitly support the 2-edge-connected components.
The algorithm described below works in $O(n \log n + m)$ time, where $m$ is the number of edges.
The algorithm is based on the data structure [Disjoint Set Union](../data_structures/disjoint_set_union.md).
However the implementation in this article takes $O(n \log n + m \log n)$ time, because it uses the simplified version of the DSU without Union by Rank.
## Algorithm
First let's define a $k$-edge-connected component:
it is a connected component that remains connected whenever you remove fewer than $k$ edges.
It is very easy to see, that the bridges partition the graph into 2-edge-connected components.
If we compress each of those 2-edge-connected components into vertices and only leave the bridges as edges in the compressed graph, then we obtain an acyclic graph, i.e. a forest.
The algorithm described below maintains this forest explicitly as well as the 2-edge-connected components.
It is clear that initially, when the graph is empty, it contains $n$ 2-edge-connected components, which by themselves are not connect.
When adding the next edge $(a, b)$ there can occur three situations:
* Both vertices $a$ and $b$ are in the same 2-edge-connected component - then this edge is not a bridge, and does not change anything in the forest structure, so we can just skip this edge.
Thus, in this case the number of bridges does not change.
* The vertices $a$ and $b$ are in completely different connected components, i.e. each one is part of a different tree.
In this case, the edge $(a, b)$ becomes a new bridge, and these two trees are combined into one (and all the old bridges remain).
Thus, in this case the number of bridges increases by one.
* The vertices $a$ and $b$ are in one connected component, but in different 2-edge-connected components.
In this case, this edge forms a cycle along with some of the old bridges.
All these bridges end being bridges, and the resulting cycle must be compressed into a new 2-edge-connected component.
Thus, in this case the number of bridges decreases by two or more.
Consequently the whole task is reduced to the effective implementation of all these operations over the forest of 2-edge-connected components.
## Data Structures for storing the forest
The only data structure that we need is [Disjoint Set Union](../data_structures/disjoint_set_union.md).
In fact we will make two copies of this structure:
one will be to maintain the connected components, the other to maintain the 2-edge-connected components.
And in addition we store the structure of the trees in the forest of 2-edge-connected components via pointers:
Each 2-edge-connected component will store the index `par[]` of its ancestor in the tree.
We will now consistently disassemble every operation that we need to learn to implement:
* Check whether the two vertices lie in the same connected / 2-edge-connected component.
It is done with the usual DSU algorithm, we just find and compare the representatives of the DSUs.
* Joining two trees for some edge $(a, b)$.
Since it could turn out that neither the vertex $a$ nor the vertex $b$ are the roots of their trees, the only way to connect these two trees is to re-root one of them.
For example you can re-root the tree of vertex $a$, and then attach it to another tree by setting the ancestor of $a$ to $b$.
However the question about the effectiveness of the re-rooting operation arises:
in order to re-root the tree with the root $r$ to the vertex $v$, it is necessary to necessary to visit all vertices on the path between $v$ and $r$ and redirect the pointers `par[]` in the opposite direction, and also change the references to the ancestors in the DSU that is responsible for the connected components.
Thus, the cost of re-rooting is $O(h)$, where $h$ is the height of the tree.
You can make an even worse estimate by saying that the cost is $O(\text{size})$ where $\text{size}$ is the number of vertices in the tree.
The final complexity will not differ.
We now apply a standard technique: we re-root the tree that contains fewer vertices.
Then it is intuitively clear that the worst case is when two trees of approximately equal sizes are combined, but then the result is a tree of twice the size.
This does not allow this situation to happen many times.
In general the total cost can be written in the form of a recurrence:
\[ T(n) = \max_{k = 1 \ldots n-1} \left\{ T(k) + T(n - k) + O(\min(k, n - k))\right\} \]
$T(n)$ is the number of operations necessary to obtain a tree with $n$ vertices by means of re-rooting and unifying trees.
A tree of size $n$ can be created by combining two smaller trees of size $k$ and $n - k$.
This recurrence is has the solution $T(n) = O (n \log n)$.
Thus, the total time spent on all re-rooting operations will be $O(n \log n)$ if we always re-root the smaller of the two trees.
We will have to maintain the size of each connected component, but the data structure DSU makes this possible without difficulty.
* Searching for the cycle formed by adding a new edge $(a, b)$.
Since $a$ and $b$ are already connected in the tree we need to find the [Lowest Common Ancestor](lca.md) of the vertices $a$ and $b$.
The cycle will consist of the paths from $b$ to the LCA, from the LCA to $b$ and the edge $a$ to $b$.
After finding the cycle we compress all vertices of the detected cycle into one vertex.
This means that we already have a complexity proportional to the cycle length, which means that we also can use any LCA algorithm proportional to the length, and don't have to use any fast one.
Since all information about the structure of the tree is available is the ancestor array `par[]`, the only reasonable LCA algorithm is the following:
mark the vertices $a$ and $b$ as visited, then we go to their ancestors `par[a]` and `par[b]` and mark them, then advance to their ancestors and so on, until we reach an already marked vertex.
This vertex is the LCA that we are looking for, and we can find the vertices on the cycle by traversing the path from $a$ and $b$ to the LCA again.
It is obvious that the complexity of this algorithm is proportional to the length of the desired cycle.
* Compression of the cycle by adding a new edge $(a, b)$ in a tree.
We need to create a new 2-edge-connected component, which will consist of all vertices of the detected cycle (also the detected cycle itself could consist of some 2-edge-connected components, but this does not change anything).
In addition it is necessary to compress them in such a way that the structure of the tree is not disturbed, and all pointers `par[]` and two DSUs are still correct.
The easiest way to achieve this is to compress all the vertices of the cycle to their LCA.
In fact the LCA is the highest of the vertices, i.e. its ancestor pointer `par[]` remains unchanged.
For all the other vertices of the loop the ancestors do not need to be updated, since these vertices simply cease to exists.
But in the DSU of the 2-edge-connected components all these vertices will simply point to the LCA.
We will implement the DSU of the 2-edge-connected components without the Union by rank optimization, therefore we will get the complexity $O(\log n)$ on average per query.
To achieve the complexity $O(1)$ on average per query, we need to combine the vertices of the cycle according to Union by rank, and then assign `par[]` accordingly.
## Implementation
Here is the final implementation of the whole algorithm.
As mentioned before, for the sake of simplicity the DSU of the 2-edge-connected components is written without Union by rank, therefore the resulting complexity will be $O(\log n)$ on average.
Also in this implementation the bridges themselves are not stored, only their count `bridges`.
However it will not be difficult to create a `set` of all bridges.
Initially you call the function `init()`, which initializes the two DSUs (creating a separate set for each vertex, and setting the size equal to one), and sets the ancestors `par`.
The main function is `add_edge(a, b)`, which processes and adds a new edge.
```cpp
vector<int> par, dsu_2ecc, dsu_cc, dsu_cc_size;
int bridges;
int lca_iteration;
vector<int> last_visit;
void init(int n) {
par.resize(n);
dsu_2ecc.resize(n);
dsu_cc.resize(n);
dsu_cc_size.resize(n);
lca_iteration = 0;
last_visit.assign(n, 0);
for (int i=0; i<n; ++i) {
dsu_2ecc[i] = i;
dsu_cc[i] = i;
dsu_cc_size[i] = 1;
par[i] = -1;
}
bridges = 0;
}
int find_2ecc(int v) {
if (v == -1)
return -1;
return dsu_2ecc[v] == v ? v : dsu_2ecc[v] = find_2ecc(dsu_2ecc[v]);
}
int find_cc(int v) {
v = find_2ecc(v);
return dsu_cc[v] == v ? v : dsu_cc[v] = find_cc(dsu_cc[v]);
}
void make_root(int v) {
v = find_2ecc(v);
int root = v;
int child = -1;
while (v != -1) {
int p = find_2ecc(par[v]);
par[v] = child;
dsu_cc[v] = root;
child = v;
v = p;
}
dsu_cc_size[root] = dsu_cc_size[child];
}
void merge_path (int a, int b) {
++lca_iteration;
vector<int> path_a, path_b;
int lca = -1;
while (lca == -1) {
if (a != -1) {
a = find_2ecc(a);
path_a.push_back(a);
if (last_visit[a] == lca_iteration){
lca = a;
break;
}
last_visit[a] = lca_iteration;
a = par[a];
}
if (b != -1) {
b = find_2ecc(b);
path_b.push_back(b);
if (last_visit[b] == lca_iteration){
lca = b;
break;
}
last_visit[b] = lca_iteration;
b = par[b];
}
}
for (int v : path_a) {
dsu_2ecc[v] = lca;
if (v == lca)
break;
--bridges;
}
for (int v : path_b) {
dsu_2ecc[v] = lca;
if (v == lca)
break;
--bridges;
}
}
void add_edge(int a, int b) {
a = find_2ecc(a);
b = find_2ecc(b);
if (a == b)
return;
int ca = find_cc(a);
int cb = find_cc(b);
if (ca != cb) {
++bridges;
if (dsu_cc_size[ca] > dsu_cc_size[cb]) {
swap(a, b);
swap(ca, cb);
}
make_root(a);
par[a] = dsu_cc[a] = b;
dsu_cc_size[cb] += dsu_cc_size[a];
} else {
merge_path(a, b);
}
}
```
The DSU for the 2-edge-connected components is stored in the vector `dsu_2ecc`, and the function returning the representative is `find_2ecc(v)`.
This function is used many times in the rest of the code, since after the compression of several vertices into one all these vertices cease to exist, and instead only the leader has the correct ancestor `par` in the forest of 2-edge-connected components.
The DSU for the connected components is stored in the vector `dsu_cc`, and there is also an additional vector `dsu_cc_size` to store the component sizes.
The function `find_cc(v)` returns the leader of the connectivity component (which is actually the root of the tree).
The re-rooting of a tree `make_root(v)` works as described above:
if traverses from the vertex $v$ via the ancestors to the root vertex, each time redirecting the ancestor `par` in the opposite direction.
The link to the representative of the connected component `dsu_cc` is also updated, so that it points to the new root vertex.
After re-rooting we have to assign the new root the correct size of the connected component.
Also we have to be careful that we call `find_2ecc()` to get the representatives of the 2-edge-connected component, rather than some other vertex that have already been compressed.
The cycle finding and compression function `merge_path(a, b)` is also implemented as described above.
It searches for the LCA of $a$ and $b$ be rising these nodes in parallel, until we meet a vertex for the second time.
For efficiency purposes we choose a unique identifier for each LCA finding call, and mark the traversed vertices with it.
This works in $O(1)$, while other approaches like using $set$ perform worse.
The passed paths are stored in the vectors `path_a` and `path_b`, and we use them to walk through them a second time up to the LCA, thereby obtaining all vertices of the cycle.
All the vertices of the cycle get compressed by attaching them to the LCA, hence the average complexity is $O(\log n)$ (since we don't use Union by rank).
All the edges we pass have been bridges, so we subtract 1 for each edge in the cycle.
Finally the query function `add_edge(a, b)` determines the connected components in which the vertices $a$ and $b$ lie.
If they lie in different connectivity components, then a smaller tree is re-rooted and then attached to the larger tree.
Otherwise if the vertices $a$ and $b$ lie in one tree, but in different 2-edge-connected components, then the function `merge_path(a, b)` is called, which will detect the cycle and compress it into one 2-edge-connected component.
|
Finding Bridges Online
|
---
title
negative_cycle
---
# Finding a negative cycle in the graph
You are given a directed weighted graph $G$ with $N$ vertices and $M$ edges. Find any cycle of negative weight in it, if such a cycle exists.
In another formulation of the problem you have to find all pairs of vertices which have a path of arbitrarily small weight between them.
It is convenient to use different algorithms to solve these two variations of the problem, so we'll discuss both of them here.
## Using Bellman-Ford algorithm
Bellman-Ford algorithm allows you to check whether there exists a cycle of negative weight in the graph, and if it does, find one of these cycles.
The details of the algorithm are described in the article on the [Bellman-Ford](bellman_ford.md) algorithm.
Here we'll describe only its application to this problem.
Do $N$ iterations of Bellman-Ford algorithm. If there were no changes on the last iteration, there is no cycle of negative weight in the graph. Otherwise take a vertex the distance to which has changed, and go from it via its ancestors until a cycle is found. This cycle will be the desired cycle of negative weight.
### Implementation
```cpp
struct Edge {
int a, b, cost;
};
int n, m;
vector<Edge> edges;
const int INF = 1000000000;
void solve()
{
vector<int> d(n);
vector<int> p(n, -1);
int x;
for (int i = 0; i < n; ++i) {
x = -1;
for (Edge e : edges) {
if (d[e.a] + e.cost < d[e.b]) {
d[e.b] = d[e.a] + e.cost;
p[e.b] = e.a;
x = e.b;
}
}
}
if (x == -1) {
cout << "No negative cycle found.";
} else {
for (int i = 0; i < n; ++i)
x = p[x];
vector<int> cycle;
for (int v = x;; v = p[v]) {
cycle.push_back(v);
if (v == x && cycle.size() > 1)
break;
}
reverse(cycle.begin(), cycle.end());
cout << "Negative cycle: ";
for (int v : cycle)
cout << v << ' ';
cout << endl;
}
}
```
## Using Floyd-Warshall algorithm
The Floyd-Warshall algorithm allows to solve the second variation of the problem - finding all pairs of vertices $(i, j)$ which don't have a shortest path between them (i.e. a path of arbitrarily small weight exists).
Again, the details can be found in the [Floyd-Warshall](all-pair-shortest-path-floyd-warshall.md) article, and here we describe only its application.
Run Floyd-Warshall algorithm on the graph.
Initially $d[v][v] = 0$ for each $v$.
But after running the algorithm $d[v][v]$ will be smaller than $0$ if there exists a negative length path from $v$ to $v$.
We can use this to also find all pairs of vertices that don't have a shortest path between them.
We iterate over all pairs of vertices $(i, j)$ and for each pair we check whether they have a shortest path between them.
To do this try all possibilities for an intermediate vertex $t$.
$(i, j)$ doesn't have a shortest path, if one of the intermediate vertices $t$ has $d[t][t] < 0$ (i.e. $t$ is part of a cycle of negative weight), $t$ can be reached from $i$ and $j$ can be reached from $t$.
Then the path from $i$ to $j$ can have arbitrarily small weight.
We will denote this with `-INF`.
### Implementation
```cpp
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
for (int t = 0; t < n; ++t) {
if (d[i][t] < INF && d[t][t] < 0 && d[t][j] < INF)
d[i][j] = - INF;
}
}
}
```
|
---
title
negative_cycle
---
# Finding a negative cycle in the graph
You are given a directed weighted graph $G$ with $N$ vertices and $M$ edges. Find any cycle of negative weight in it, if such a cycle exists.
In another formulation of the problem you have to find all pairs of vertices which have a path of arbitrarily small weight between them.
It is convenient to use different algorithms to solve these two variations of the problem, so we'll discuss both of them here.
## Using Bellman-Ford algorithm
Bellman-Ford algorithm allows you to check whether there exists a cycle of negative weight in the graph, and if it does, find one of these cycles.
The details of the algorithm are described in the article on the [Bellman-Ford](bellman_ford.md) algorithm.
Here we'll describe only its application to this problem.
Do $N$ iterations of Bellman-Ford algorithm. If there were no changes on the last iteration, there is no cycle of negative weight in the graph. Otherwise take a vertex the distance to which has changed, and go from it via its ancestors until a cycle is found. This cycle will be the desired cycle of negative weight.
### Implementation
```cpp
struct Edge {
int a, b, cost;
};
int n, m;
vector<Edge> edges;
const int INF = 1000000000;
void solve()
{
vector<int> d(n);
vector<int> p(n, -1);
int x;
for (int i = 0; i < n; ++i) {
x = -1;
for (Edge e : edges) {
if (d[e.a] + e.cost < d[e.b]) {
d[e.b] = d[e.a] + e.cost;
p[e.b] = e.a;
x = e.b;
}
}
}
if (x == -1) {
cout << "No negative cycle found.";
} else {
for (int i = 0; i < n; ++i)
x = p[x];
vector<int> cycle;
for (int v = x;; v = p[v]) {
cycle.push_back(v);
if (v == x && cycle.size() > 1)
break;
}
reverse(cycle.begin(), cycle.end());
cout << "Negative cycle: ";
for (int v : cycle)
cout << v << ' ';
cout << endl;
}
}
```
## Using Floyd-Warshall algorithm
The Floyd-Warshall algorithm allows to solve the second variation of the problem - finding all pairs of vertices $(i, j)$ which don't have a shortest path between them (i.e. a path of arbitrarily small weight exists).
Again, the details can be found in the [Floyd-Warshall](all-pair-shortest-path-floyd-warshall.md) article, and here we describe only its application.
Run Floyd-Warshall algorithm on the graph.
Initially $d[v][v] = 0$ for each $v$.
But after running the algorithm $d[v][v]$ will be smaller than $0$ if there exists a negative length path from $v$ to $v$.
We can use this to also find all pairs of vertices that don't have a shortest path between them.
We iterate over all pairs of vertices $(i, j)$ and for each pair we check whether they have a shortest path between them.
To do this try all possibilities for an intermediate vertex $t$.
$(i, j)$ doesn't have a shortest path, if one of the intermediate vertices $t$ has $d[t][t] < 0$ (i.e. $t$ is part of a cycle of negative weight), $t$ can be reached from $i$ and $j$ can be reached from $t$.
Then the path from $i$ to $j$ can have arbitrarily small weight.
We will denote this with `-INF`.
### Implementation
```cpp
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
for (int t = 0; t < n; ++t) {
if (d[i][t] < INF && d[t][t] < 0 && d[t][j] < INF)
d[i][j] = - INF;
}
}
}
```
## Practice Problems
- [UVA: Wormholes](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=499)
- [SPOJ: Alice in Amsterdam, I mean Wonderland](http://www.spoj.com/problems/UCV2013B/)
- [SPOJ: Johnsons Algorithm](http://www.spoj.com/problems/JHNSN/)
|
Finding a negative cycle in the graph
|
---
title
dfs
---
# Depth First Search
Depth First Search is one of the main graph algorithms.
Depth First Search finds the lexicographical first path in the graph from a source vertex $u$ to each vertex.
Depth First Search will also find the shortest paths in a tree (because there only exists one simple path), but on general graphs this is not the case.
The algorithm works in $O(m + n)$ time where $n$ is the number of vertices and $m$ is the number of edges.
## Description of the algorithm
The idea behind DFS is to go as deep into the graph as possible, and backtrack once you are at a vertex without any unvisited adjacent vertices.
It is very easy to describe / implement the algorithm recursively:
We start the search at one vertex.
After visiting a vertex, we further perform a DFS for each adjacent vertex that we haven't visited before.
This way we visit all vertices that are reachable from the starting vertex.
For more details check out the implementation.
## Applications of Depth First Search
* Find any path in the graph from source vertex $u$ to all vertices.
* Find lexicographical first path in the graph from source $u$ to all vertices.
* Check if a vertex in a tree is an ancestor of some other vertex:
At the beginning and end of each search call we remember the entry and exit "time" of each vertex.
Now you can find the answer for any pair of vertices $(i, j)$ in $O(1)$:
vertex $i$ is an ancestor of vertex $j$ if and only if $\text{entry}[i] < \text{entry}[j]$ and $\text{exit}[i] > \text{exit}[j]$.
* Find the lowest common ancestor (LCA) of two vertices.
* Topological sorting:
Run a series of depth first searches so as to visit each vertex exactly once in $O(n + m)$ time.
The required topological ordering will be the vertices sorted in descending order of exit time.
* Check whether a given graph is acyclic and find cycles in a graph. (As mentioned above by counting back edges in every connected components).
* Find strongly connected components in a directed graph:
First do a topological sorting of the graph.
Then transpose the graph and run another series of depth first searches in the order defined by the topological sort. For each DFS call the component created by it is a strongly connected component.
* Find bridges in an undirected graph:
First convert the given graph into a directed graph by running a series of depth first searches and making each edge directed as we go through it, in the direction we went. Second, find the strongly connected components in this directed graph. Bridges are the edges whose ends belong to different strongly connected components.
## Classification of edges of a graph
We can classify the edges using the entry and exit time of the end nodes $u$ and $v$ of the edges $(u,v)$.
These classifications are often used for problems like [finding bridges](bridge-searching.md) and [finding articulation points](cutpoints.md).
We perform a DFS and classify the encountered edges using the following rules:
If $v$ is not visited:
* Tree Edge - If $v$ is visited after $u$ then edge $(u,v)$ is called a tree edge. In other words, if $v$ is visited for the first time and $u$ is currently being visited then $(u,v)$ is called tree edge.
These edges form a DFS tree and hence the name tree edges.
If $v$ is visited before $u$:
* Back edges - If $v$ is an ancestor of $u$, then the edge $(u,v)$ is a back edge. $v$ is an ancestor exactly if we already entered $v$, but not exited it yet. Back edges complete a cycle as there is a path from ancestor $v$ to descendant $u$ (in the recursion of DFS) and an edge from descendant $u$ to ancestor $v$ (back edge), thus a cycle is formed. Cycles can be detected using back edges.
* Forward Edges - If $v$ is a descendant of $u$, then edge $(u, v)$ is a forward edge. In other words, if we already visited and exited $v$ and $\text{entry}[u] < \text{entry}[v]$ then the edge $(u,v)$ forms a forward edge.
* Cross Edges: if $v$ is neither an ancestor or descendant of $u$, then edge $(u, v)$ is a cross edge. In other words, if we already visited and exited $v$ and $\text{entry}[u] > \text{entry}[v]$ then $(u,v)$ is a cross edge.
Note: Forward edges and cross edges only exist in directed graphs.
## Implementation
```cpp
vector<vector<int>> adj; // graph represented as an adjacency list
int n; // number of vertices
vector<bool> visited;
void dfs(int v) {
visited[v] = true;
for (int u : adj[v]) {
if (!visited[u])
dfs(u);
}
}
```
This is the most simple implementation of Depth First Search.
As described in the applications it might be useful to also compute the entry and exit times and vertex color.
We will color all vertices with the color 0, if we haven't visited them, with the color 1 if we visited them, and with the color 2, if we already exited the vertex.
Here is a generic implementation that additionally computes those:
```cpp
vector<vector<int>> adj; // graph represented as an adjacency list
int n; // number of vertices
vector<int> color;
vector<int> time_in, time_out;
int dfs_timer = 0;
void dfs(int v) {
time_in[v] = dfs_timer++;
color[v] = 1;
for (int u : adj[v])
if (color[u] == 0)
dfs(u);
color[v] = 2;
time_out[v] = dfs_timer++;
}
```
|
---
title
dfs
---
# Depth First Search
Depth First Search is one of the main graph algorithms.
Depth First Search finds the lexicographical first path in the graph from a source vertex $u$ to each vertex.
Depth First Search will also find the shortest paths in a tree (because there only exists one simple path), but on general graphs this is not the case.
The algorithm works in $O(m + n)$ time where $n$ is the number of vertices and $m$ is the number of edges.
## Description of the algorithm
The idea behind DFS is to go as deep into the graph as possible, and backtrack once you are at a vertex without any unvisited adjacent vertices.
It is very easy to describe / implement the algorithm recursively:
We start the search at one vertex.
After visiting a vertex, we further perform a DFS for each adjacent vertex that we haven't visited before.
This way we visit all vertices that are reachable from the starting vertex.
For more details check out the implementation.
## Applications of Depth First Search
* Find any path in the graph from source vertex $u$ to all vertices.
* Find lexicographical first path in the graph from source $u$ to all vertices.
* Check if a vertex in a tree is an ancestor of some other vertex:
At the beginning and end of each search call we remember the entry and exit "time" of each vertex.
Now you can find the answer for any pair of vertices $(i, j)$ in $O(1)$:
vertex $i$ is an ancestor of vertex $j$ if and only if $\text{entry}[i] < \text{entry}[j]$ and $\text{exit}[i] > \text{exit}[j]$.
* Find the lowest common ancestor (LCA) of two vertices.
* Topological sorting:
Run a series of depth first searches so as to visit each vertex exactly once in $O(n + m)$ time.
The required topological ordering will be the vertices sorted in descending order of exit time.
* Check whether a given graph is acyclic and find cycles in a graph. (As mentioned above by counting back edges in every connected components).
* Find strongly connected components in a directed graph:
First do a topological sorting of the graph.
Then transpose the graph and run another series of depth first searches in the order defined by the topological sort. For each DFS call the component created by it is a strongly connected component.
* Find bridges in an undirected graph:
First convert the given graph into a directed graph by running a series of depth first searches and making each edge directed as we go through it, in the direction we went. Second, find the strongly connected components in this directed graph. Bridges are the edges whose ends belong to different strongly connected components.
## Classification of edges of a graph
We can classify the edges using the entry and exit time of the end nodes $u$ and $v$ of the edges $(u,v)$.
These classifications are often used for problems like [finding bridges](bridge-searching.md) and [finding articulation points](cutpoints.md).
We perform a DFS and classify the encountered edges using the following rules:
If $v$ is not visited:
* Tree Edge - If $v$ is visited after $u$ then edge $(u,v)$ is called a tree edge. In other words, if $v$ is visited for the first time and $u$ is currently being visited then $(u,v)$ is called tree edge.
These edges form a DFS tree and hence the name tree edges.
If $v$ is visited before $u$:
* Back edges - If $v$ is an ancestor of $u$, then the edge $(u,v)$ is a back edge. $v$ is an ancestor exactly if we already entered $v$, but not exited it yet. Back edges complete a cycle as there is a path from ancestor $v$ to descendant $u$ (in the recursion of DFS) and an edge from descendant $u$ to ancestor $v$ (back edge), thus a cycle is formed. Cycles can be detected using back edges.
* Forward Edges - If $v$ is a descendant of $u$, then edge $(u, v)$ is a forward edge. In other words, if we already visited and exited $v$ and $\text{entry}[u] < \text{entry}[v]$ then the edge $(u,v)$ forms a forward edge.
* Cross Edges: if $v$ is neither an ancestor or descendant of $u$, then edge $(u, v)$ is a cross edge. In other words, if we already visited and exited $v$ and $\text{entry}[u] > \text{entry}[v]$ then $(u,v)$ is a cross edge.
Note: Forward edges and cross edges only exist in directed graphs.
## Implementation
```cpp
vector<vector<int>> adj; // graph represented as an adjacency list
int n; // number of vertices
vector<bool> visited;
void dfs(int v) {
visited[v] = true;
for (int u : adj[v]) {
if (!visited[u])
dfs(u);
}
}
```
This is the most simple implementation of Depth First Search.
As described in the applications it might be useful to also compute the entry and exit times and vertex color.
We will color all vertices with the color 0, if we haven't visited them, with the color 1 if we visited them, and with the color 2, if we already exited the vertex.
Here is a generic implementation that additionally computes those:
```cpp
vector<vector<int>> adj; // graph represented as an adjacency list
int n; // number of vertices
vector<int> color;
vector<int> time_in, time_out;
int dfs_timer = 0;
void dfs(int v) {
time_in[v] = dfs_timer++;
color[v] = 1;
for (int u : adj[v])
if (color[u] == 0)
dfs(u);
color[v] = 2;
time_out[v] = dfs_timer++;
}
```
## Practice Problems
* [SPOJ: ABCPATH](http://www.spoj.com/problems/ABCPATH/)
* [SPOJ: EAGLE1](http://www.spoj.com/problems/EAGLE1/)
* [Codeforces: Kefa and Park](http://codeforces.com/problemset/problem/580/C)
* [Timus:Werewolf](http://acm.timus.ru/problem.aspx?space=1&num=1242)
* [Timus:Penguin Avia](http://acm.timus.ru/problem.aspx?space=1&num=1709)
* [Timus:Two Teams](http://acm.timus.ru/problem.aspx?space=1&num=1106)
* [SPOJ - Ada and Island](http://www.spoj.com/problems/ADASEA/)
* [UVA 657 - The die is cast](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=598)
* [SPOJ - Sheep](http://www.spoj.com/problems/KOZE/)
* [SPOJ - Path of the Rightenous Man](http://www.spoj.com/problems/RIOI_2_3/)
* [SPOJ - Validate the Maze](http://www.spoj.com/problems/MAKEMAZE/)
* [SPOJ - Ghosts having Fun](http://www.spoj.com/problems/GHOSTS/)
* [Codeforces - Underground Lab](http://codeforces.com/contest/781/problem/C)
* [DevSkill - Maze Tester (archived)](http://web.archive.org/web/20200319103915/https://www.devskill.com/CodingProblems/ViewProblem/3)
* [DevSkill - Tourist (archived)](http://web.archive.org/web/20190426175135/https://devskill.com/CodingProblems/ViewProblem/17)
* [Codeforces - Anton and Tree](http://codeforces.com/contest/734/problem/E)
* [Codeforces - Transformation: From A to B](http://codeforces.com/contest/727/problem/A)
* [Codeforces - One Way Reform](http://codeforces.com/contest/723/problem/E)
* [Codeforces - Centroids](http://codeforces.com/contest/709/problem/E)
* [Codeforces - Generate a String](http://codeforces.com/contest/710/problem/E)
* [Codeforces - Broken Tree](http://codeforces.com/contest/758/problem/E)
* [Codeforces - Dasha and Puzzle](http://codeforces.com/contest/761/problem/E)
* [Codeforces - Making genome In Berland](http://codeforces.com/contest/638/problem/B)
* [Codeforces - Road Improvement](http://codeforces.com/contest/638/problem/C)
* [Codeforces - Garland](http://codeforces.com/contest/767/problem/C)
* [Codeforces - Labeling Cities](http://codeforces.com/contest/794/problem/D)
* [Codeforces - Send the Fool Futher!](http://codeforces.com/contest/802/problem/K)
* [Codeforces - The tag Game](http://codeforces.com/contest/813/problem/C)
* [Codeforces - Leha and Another game about graphs](http://codeforces.com/contest/841/problem/D)
* [Codeforces - Shortest path problem](http://codeforces.com/contest/845/problem/G)
* [Codeforces - Upgrading Tree](http://codeforces.com/contest/844/problem/E)
* [Codeforces - From Y to Y](http://codeforces.com/contest/849/problem/C)
* [Codeforces - Chemistry in Berland](http://codeforces.com/contest/846/problem/E)
* [Codeforces - Wizards Tour](http://codeforces.com/contest/861/problem/F)
* [Codeforces - Ring Road](http://codeforces.com/contest/24/problem/A)
* [Codeforces - Mail Stamps](http://codeforces.com/contest/29/problem/C)
* [Codeforces - Ant on the Tree](http://codeforces.com/contest/29/problem/D)
* [SPOJ - Cactus](http://www.spoj.com/problems/CAC/)
* [SPOJ - Mixing Chemicals](http://www.spoj.com/problems/AMR10J/)
|
Depth First Search
|
---
title
mst_prim
---
# Minimum spanning tree - Prim's algorithm
Given a weighted, undirected graph $G$ with $n$ vertices and $m$ edges.
You want to find a spanning tree of this graph which connects all vertices and has the least weight (i.e. the sum of weights of edges is minimal).
A spanning tree is a set of edges such that any vertex can reach any other by exactly one simple path.
The spanning tree with the least weight is called a minimum spanning tree.
In the left image you can see a weighted undirected graph, and in the right image you can see the corresponding minimum spanning tree.
<center> </center>
It is easy to see that any spanning tree will necessarily contain $n-1$ edges.
This problem appears quite naturally in a lot of problems.
For instance in the following problem:
there are $n$ cities and for each pair of cities we are given the cost to build a road between them (or we know that is physically impossible to build a road between them).
We have to build roads, such that we can get from each city to every other city, and the cost for building all roads is minimal.
## Prim's Algorithm
This algorithm was originally discovered by the Czech mathematician Vojtěch Jarník in 1930.
However this algorithm is mostly known as Prim's algorithm after the American mathematician Robert Clay Prim, who rediscovered and republished it in 1957.
Additionally Edsger Dijkstra published this algorithm in 1959.
### Algorithm description
Here we describe the algorithm in its simplest form.
The minimum spanning tree is built gradually by adding edges one at a time.
At first the spanning tree consists only of a single vertex (chosen arbitrarily).
Then the minimum weight edge outgoing from this vertex is selected and added to the spanning tree.
After that the spanning tree already consists of two vertices.
Now select and add the edge with the minimum weight that has one end in an already selected vertex (i.e. a vertex that is already part of the spanning tree), and the other end in an unselected vertex.
And so on, i.e. every time we select and add the edge with minimal weight that connects one selected vertex with one unselected vertex.
The process is repeated until the spanning tree contains all vertices (or equivalently until we have $n - 1$ edges).
In the end the constructed spanning tree will be minimal.
If the graph was originally not connected, then there doesn't exist a spanning tree, so the number of selected edges will be less than $n - 1$.
### Proof
Let the graph $G$ be connected, i.e. the answer exists.
We denote by $T$ the resulting graph found by Prim's algorithm, and by $S$ the minimum spanning tree.
Obviously $T$ is indeed a spanning tree and a subgraph of $G$.
We only need to show that the weights of $S$ and $T$ coincide.
Consider the first time in the algorithm when we add an edge to $T$ that is not part of $S$.
Let us denote this edge with $e$, its ends by $a$ and $b$, and the set of already selected vertices as $V$ ($a \in V$ and $b \notin V$, or vice versa).
In the minimal spanning tree $S$ the vertices $a$ and $b$ are connected by some path $P$.
On this path we can find an edge $f$ such that one end of $f$ lies in $V$ and the other end doesn't.
Since the algorithm chose $e$ instead of $f$, it means that the weight of $f$ is greater or equal to the weight of $e$.
We add the edge $e$ to the minimum spanning tree $S$ and remove the edge $f$.
By adding $e$ we created a cycle, and since $f$ was also part of the only cycle, by removing it the resulting graph is again free of cycles.
And because we only removed an edge from a cycle, the resulting graph is still connected.
The resulting spanning tree cannot have a larger total weight, since the weight of $e$ was not larger than the weight of $f$, and it also cannot have a smaller weight since $S$ was a minimum spanning tree.
This means that by replacing the edge $f$ with $e$ we generated a different minimum spanning tree.
And $e$ has to have the same weight as $f$.
Thus all the edges we pick in Prim's algorithm have the same weights as the edges of any minimum spanning tree, which means that Prim's algorithm really generates a minimum spanning tree.
## Implementation
The complexity of the algorithm depends on how we search for the next minimal edge among the appropriate edges.
There are multiple approaches leading to different complexities and different implementations.
### Trivial implementations: $O(n m)$ and $O(n^2 + m \log n)$
If we search the edge by iterating over all possible edges, then it takes $O(m)$ time to find the edge with the minimal weight.
The total complexity will be $O(n m)$.
In the worst case this is $O(n^3)$, really slow.
This algorithm can be improved if we only look at one edge from each already selected vertex.
For example we can sort the edges from each vertex in ascending order of their weights, and store a pointer to the first valid edge (i.e. an edge that goes to an non-selected vertex).
Then after finding and selecting the minimal edge, we update the pointers.
This give a complexity of $O(n^2 + m)$, and for sorting the edges an additional $O(m \log n)$, which gives the complexity $O(n^2 \log n)$ in the worst case.
Below we consider two slightly different algorithms, one for dense and one for sparse graphs, both with a better complexity.
### Dense graphs: $O(n^2)$
We approach this problem from a different angle:
for every not yet selected vertex we will store the minimum edge to an already selected vertex.
Then during a step we only have to look at these minimum weight edges, which will have a complexity of $O(n)$.
After adding an edge some minimum edge pointers have to be recalculated.
Note that the weights only can decrease, i.e. the minimal weight edge of every not yet selected vertex might stay the same, or it will be updated by an edge to the newly selected vertex.
Therefore this phase can also be done in $O(n)$.
Thus we received a version of Prim's algorithm with the complexity $O(n^2)$.
In particular this implementation is very convenient for the Euclidean Minimum Spanning Tree problem:
we have $n$ points on a plane and the distance between each pair of points is the Euclidean distance between them, and we want to find a minimum spanning tree for this complete graph.
This task can be solved by the described algorithm in $O(n^2)$ time and $O(n)$ memory, which is not possible with [Kruskal's algorithm](mst_kruskal.md).
```cpp
int n;
vector<vector<int>> adj; // adjacency matrix of graph
const int INF = 1000000000; // weight INF means there is no edge
struct Edge {
int w = INF, to = -1;
};
void prim() {
int total_weight = 0;
vector<bool> selected(n, false);
vector<Edge> min_e(n);
min_e[0].w = 0;
for (int i=0; i<n; ++i) {
int v = -1;
for (int j = 0; j < n; ++j) {
if (!selected[j] && (v == -1 || min_e[j].w < min_e[v].w))
v = j;
}
if (min_e[v].w == INF) {
cout << "No MST!" << endl;
exit(0);
}
selected[v] = true;
total_weight += min_e[v].w;
if (min_e[v].to != -1)
cout << v << " " << min_e[v].to << endl;
for (int to = 0; to < n; ++to) {
if (adj[v][to] < min_e[to].w)
min_e[to] = {adj[v][to], v};
}
}
cout << total_weight << endl;
}
```
The adjacency matrix `adj[][]` of size $n \times n$ stores the weights of the edges, and it uses the weight `INF` if there doesn't exist an edge between two vertices.
The algorithm uses two arrays: the flag `selected[]`, which indicates which vertices we already have selected, and the array `min_e[]` which stores the edge with minimal weight to an selected vertex for each not-yet-selected vertex (it stores the weight and the end vertex).
The algorithm does $n$ steps, in each iteration the vertex with the smallest edge weight is selected, and the `min_e[]` of all other vertices gets updated.
### Sparse graphs: $O(m \log n)$
In the above described algorithm it is possible to interpret the operations of finding the minimum and modifying some values as set operations.
These two classical operations are supported by many data structure, for example by `set` in C++ (which are implemented via red-black trees).
The main algorithm remains the same, but now we can find the minimum edge in $O(\log n)$ time.
On the other hand recomputing the pointers will now take $O(n \log n)$ time, which is worse than in the previous algorithm.
But when we consider that we only need to update $O(m)$ times in total, and perform $O(n)$ searches for the minimal edge, then the total complexity will be $O(m \log n)$.
For sparse graphs this is better than the above algorithm, but for dense graphs this will be slower.
```cpp
const int INF = 1000000000;
struct Edge {
int w = INF, to = -1;
bool operator<(Edge const& other) const {
return make_pair(w, to) < make_pair(other.w, other.to);
}
};
int n;
vector<vector<Edge>> adj;
void prim() {
int total_weight = 0;
vector<Edge> min_e(n);
min_e[0].w = 0;
set<Edge> q;
q.insert({0, 0});
vector<bool> selected(n, false);
for (int i = 0; i < n; ++i) {
if (q.empty()) {
cout << "No MST!" << endl;
exit(0);
}
int v = q.begin()->to;
selected[v] = true;
total_weight += q.begin()->w;
q.erase(q.begin());
if (min_e[v].to != -1)
cout << v << " " << min_e[v].to << endl;
for (Edge e : adj[v]) {
if (!selected[e.to] && e.w < min_e[e.to].w) {
q.erase({min_e[e.to].w, e.to});
min_e[e.to] = {e.w, v};
q.insert({e.w, e.to});
}
}
}
cout << total_weight << endl;
}
```
Here the graph is represented via a adjacency list `adj[]`, where `adj[v]` contains all edges (in form of weight and target pairs) for the vertex `v`.
`min_e[v]` will store the weight of the smallest edge from vertex `v` to an already selected vertex (again in the form of a weight and target pair).
In addition the queue `q` is filled with all not yet selected vertices in the order of increasing weights `min_e`.
The algorithm does `n` steps, on each of which it selects the vertex `v` with the smallest weight `min_e` (by extracting it from the beginning of the queue), and then looks through all the edges from this vertex and updates the values in `min_e` (during an update we also need to also remove the old edge from the queue `q` and put in the new edge).
|
---
title
mst_prim
---
# Minimum spanning tree - Prim's algorithm
Given a weighted, undirected graph $G$ with $n$ vertices and $m$ edges.
You want to find a spanning tree of this graph which connects all vertices and has the least weight (i.e. the sum of weights of edges is minimal).
A spanning tree is a set of edges such that any vertex can reach any other by exactly one simple path.
The spanning tree with the least weight is called a minimum spanning tree.
In the left image you can see a weighted undirected graph, and in the right image you can see the corresponding minimum spanning tree.
<center> </center>
It is easy to see that any spanning tree will necessarily contain $n-1$ edges.
This problem appears quite naturally in a lot of problems.
For instance in the following problem:
there are $n$ cities and for each pair of cities we are given the cost to build a road between them (or we know that is physically impossible to build a road between them).
We have to build roads, such that we can get from each city to every other city, and the cost for building all roads is minimal.
## Prim's Algorithm
This algorithm was originally discovered by the Czech mathematician Vojtěch Jarník in 1930.
However this algorithm is mostly known as Prim's algorithm after the American mathematician Robert Clay Prim, who rediscovered and republished it in 1957.
Additionally Edsger Dijkstra published this algorithm in 1959.
### Algorithm description
Here we describe the algorithm in its simplest form.
The minimum spanning tree is built gradually by adding edges one at a time.
At first the spanning tree consists only of a single vertex (chosen arbitrarily).
Then the minimum weight edge outgoing from this vertex is selected and added to the spanning tree.
After that the spanning tree already consists of two vertices.
Now select and add the edge with the minimum weight that has one end in an already selected vertex (i.e. a vertex that is already part of the spanning tree), and the other end in an unselected vertex.
And so on, i.e. every time we select and add the edge with minimal weight that connects one selected vertex with one unselected vertex.
The process is repeated until the spanning tree contains all vertices (or equivalently until we have $n - 1$ edges).
In the end the constructed spanning tree will be minimal.
If the graph was originally not connected, then there doesn't exist a spanning tree, so the number of selected edges will be less than $n - 1$.
### Proof
Let the graph $G$ be connected, i.e. the answer exists.
We denote by $T$ the resulting graph found by Prim's algorithm, and by $S$ the minimum spanning tree.
Obviously $T$ is indeed a spanning tree and a subgraph of $G$.
We only need to show that the weights of $S$ and $T$ coincide.
Consider the first time in the algorithm when we add an edge to $T$ that is not part of $S$.
Let us denote this edge with $e$, its ends by $a$ and $b$, and the set of already selected vertices as $V$ ($a \in V$ and $b \notin V$, or vice versa).
In the minimal spanning tree $S$ the vertices $a$ and $b$ are connected by some path $P$.
On this path we can find an edge $f$ such that one end of $f$ lies in $V$ and the other end doesn't.
Since the algorithm chose $e$ instead of $f$, it means that the weight of $f$ is greater or equal to the weight of $e$.
We add the edge $e$ to the minimum spanning tree $S$ and remove the edge $f$.
By adding $e$ we created a cycle, and since $f$ was also part of the only cycle, by removing it the resulting graph is again free of cycles.
And because we only removed an edge from a cycle, the resulting graph is still connected.
The resulting spanning tree cannot have a larger total weight, since the weight of $e$ was not larger than the weight of $f$, and it also cannot have a smaller weight since $S$ was a minimum spanning tree.
This means that by replacing the edge $f$ with $e$ we generated a different minimum spanning tree.
And $e$ has to have the same weight as $f$.
Thus all the edges we pick in Prim's algorithm have the same weights as the edges of any minimum spanning tree, which means that Prim's algorithm really generates a minimum spanning tree.
## Implementation
The complexity of the algorithm depends on how we search for the next minimal edge among the appropriate edges.
There are multiple approaches leading to different complexities and different implementations.
### Trivial implementations: $O(n m)$ and $O(n^2 + m \log n)$
If we search the edge by iterating over all possible edges, then it takes $O(m)$ time to find the edge with the minimal weight.
The total complexity will be $O(n m)$.
In the worst case this is $O(n^3)$, really slow.
This algorithm can be improved if we only look at one edge from each already selected vertex.
For example we can sort the edges from each vertex in ascending order of their weights, and store a pointer to the first valid edge (i.e. an edge that goes to an non-selected vertex).
Then after finding and selecting the minimal edge, we update the pointers.
This give a complexity of $O(n^2 + m)$, and for sorting the edges an additional $O(m \log n)$, which gives the complexity $O(n^2 \log n)$ in the worst case.
Below we consider two slightly different algorithms, one for dense and one for sparse graphs, both with a better complexity.
### Dense graphs: $O(n^2)$
We approach this problem from a different angle:
for every not yet selected vertex we will store the minimum edge to an already selected vertex.
Then during a step we only have to look at these minimum weight edges, which will have a complexity of $O(n)$.
After adding an edge some minimum edge pointers have to be recalculated.
Note that the weights only can decrease, i.e. the minimal weight edge of every not yet selected vertex might stay the same, or it will be updated by an edge to the newly selected vertex.
Therefore this phase can also be done in $O(n)$.
Thus we received a version of Prim's algorithm with the complexity $O(n^2)$.
In particular this implementation is very convenient for the Euclidean Minimum Spanning Tree problem:
we have $n$ points on a plane and the distance between each pair of points is the Euclidean distance between them, and we want to find a minimum spanning tree for this complete graph.
This task can be solved by the described algorithm in $O(n^2)$ time and $O(n)$ memory, which is not possible with [Kruskal's algorithm](mst_kruskal.md).
```cpp
int n;
vector<vector<int>> adj; // adjacency matrix of graph
const int INF = 1000000000; // weight INF means there is no edge
struct Edge {
int w = INF, to = -1;
};
void prim() {
int total_weight = 0;
vector<bool> selected(n, false);
vector<Edge> min_e(n);
min_e[0].w = 0;
for (int i=0; i<n; ++i) {
int v = -1;
for (int j = 0; j < n; ++j) {
if (!selected[j] && (v == -1 || min_e[j].w < min_e[v].w))
v = j;
}
if (min_e[v].w == INF) {
cout << "No MST!" << endl;
exit(0);
}
selected[v] = true;
total_weight += min_e[v].w;
if (min_e[v].to != -1)
cout << v << " " << min_e[v].to << endl;
for (int to = 0; to < n; ++to) {
if (adj[v][to] < min_e[to].w)
min_e[to] = {adj[v][to], v};
}
}
cout << total_weight << endl;
}
```
The adjacency matrix `adj[][]` of size $n \times n$ stores the weights of the edges, and it uses the weight `INF` if there doesn't exist an edge between two vertices.
The algorithm uses two arrays: the flag `selected[]`, which indicates which vertices we already have selected, and the array `min_e[]` which stores the edge with minimal weight to an selected vertex for each not-yet-selected vertex (it stores the weight and the end vertex).
The algorithm does $n$ steps, in each iteration the vertex with the smallest edge weight is selected, and the `min_e[]` of all other vertices gets updated.
### Sparse graphs: $O(m \log n)$
In the above described algorithm it is possible to interpret the operations of finding the minimum and modifying some values as set operations.
These two classical operations are supported by many data structure, for example by `set` in C++ (which are implemented via red-black trees).
The main algorithm remains the same, but now we can find the minimum edge in $O(\log n)$ time.
On the other hand recomputing the pointers will now take $O(n \log n)$ time, which is worse than in the previous algorithm.
But when we consider that we only need to update $O(m)$ times in total, and perform $O(n)$ searches for the minimal edge, then the total complexity will be $O(m \log n)$.
For sparse graphs this is better than the above algorithm, but for dense graphs this will be slower.
```cpp
const int INF = 1000000000;
struct Edge {
int w = INF, to = -1;
bool operator<(Edge const& other) const {
return make_pair(w, to) < make_pair(other.w, other.to);
}
};
int n;
vector<vector<Edge>> adj;
void prim() {
int total_weight = 0;
vector<Edge> min_e(n);
min_e[0].w = 0;
set<Edge> q;
q.insert({0, 0});
vector<bool> selected(n, false);
for (int i = 0; i < n; ++i) {
if (q.empty()) {
cout << "No MST!" << endl;
exit(0);
}
int v = q.begin()->to;
selected[v] = true;
total_weight += q.begin()->w;
q.erase(q.begin());
if (min_e[v].to != -1)
cout << v << " " << min_e[v].to << endl;
for (Edge e : adj[v]) {
if (!selected[e.to] && e.w < min_e[e.to].w) {
q.erase({min_e[e.to].w, e.to});
min_e[e.to] = {e.w, v};
q.insert({e.w, e.to});
}
}
}
cout << total_weight << endl;
}
```
Here the graph is represented via a adjacency list `adj[]`, where `adj[v]` contains all edges (in form of weight and target pairs) for the vertex `v`.
`min_e[v]` will store the weight of the smallest edge from vertex `v` to an already selected vertex (again in the form of a weight and target pair).
In addition the queue `q` is filled with all not yet selected vertices in the order of increasing weights `min_e`.
The algorithm does `n` steps, on each of which it selects the vertex `v` with the smallest weight `min_e` (by extracting it from the beginning of the queue), and then looks through all the edges from this vertex and updates the values in `min_e` (during an update we also need to also remove the old edge from the queue `q` and put in the new edge).
|
Minimum spanning tree - Prim's algorithm
|
---
title
levit_algorithm
---
# D´Esopo-Pape algorithm
Given a graph with $n$ vertices and $m$ edges with weights $w_i$ and a starting vertex $v_0$.
The task is to find the shortest path from the vertex $v_0$ to every other vertex.
The algorithm from D´Esopo-Pape will work faster than [Dijkstra's algorithm](dijkstra.md) and the [Bellman-Ford algorithm](bellman_ford.md) in most cases, and will also work for negative edges.
However not for negative cycles.
## Description
Let the array $d$ contain the shortest path lengths, i.e. $d_i$ is the current length of the shortest path from the vertex $v_0$ to the vertex $i$.
Initially this array is filled with infinity for every vertex, except $d_{v_0} = 0$.
After the algorithm finishes, this array will contain the shortest distances.
Let the array $p$ contain the current ancestors, i.e. $p_i$ is the direct ancestor of the vertex $i$ on the current shortest path from $v_0$ to $i$.
Just like the array $d$, the array $p$ changes gradually during the algorithm and at the end takes its final values.
Now to the algorithm.
At each step three sets of vertices are maintained:
- $M_0$ - vertices, for which the distance has already been calculated (although it might not be the final distance)
- $M_1$ - vertices, for which the distance currently is calculated
- $M_2$ - vertices, for which the distance has not yet been calculated
The vertices in the set $M_1$ are stored in a bidirectional queue (deque).
At each step of the algorithm we take a vertex from the set $M_1$ (from the front of the queue).
Let $u$ be the selected vertex.
We put this vertex $u$ into the set $M_0$.
Then we iterate over all edges coming out of this vertex.
Let $v$ be the second end of the current edge, and $w$ its weight.
- If $v$ belongs to $M_2$, then $v$ is inserted into the set $M_1$ by inserting it at the back of the queue.
$d_v$ is set to $d_u + w$.
- If $v$ belongs to $M_1$, then we try to improve the value of $d_v$: $d_v = \min(d_v, d_u + w)$.
Since $v$ is already in $M_1$, we don't need to insert it into $M_1$ and the queue.
- If $v$ belongs to $M_0$, and if $d_v$ can be improved $d_v > d_u + w$, then we improve $d_v$ and insert the vertex $v$ back to the set $M_1$, placing it at the beginning of the queue.
And of course, with each update in the array $d$ we also have to update the corresponding element in the array $p$.
## Implementation
We will use an array $m$ to store in which set each vertex is currently.
```{.cpp file=desopo_pape}
struct Edge {
int to, w;
};
int n;
vector<vector<Edge>> adj;
const int INF = 1e9;
void shortest_paths(int v0, vector<int>& d, vector<int>& p) {
d.assign(n, INF);
d[v0] = 0;
vector<int> m(n, 2);
deque<int> q;
q.push_back(v0);
p.assign(n, -1);
while (!q.empty()) {
int u = q.front();
q.pop_front();
m[u] = 0;
for (Edge e : adj[u]) {
if (d[e.to] > d[u] + e.w) {
d[e.to] = d[u] + e.w;
p[e.to] = u;
if (m[e.to] == 2) {
m[e.to] = 1;
q.push_back(e.to);
} else if (m[e.to] == 0) {
m[e.to] = 1;
q.push_front(e.to);
}
}
}
}
}
```
## Complexity
The algorithm usually performs quite fast - in most cases, even faster than Dijkstra's algorithm.
However there exist cases for which the algorithm takes exponential time, making it unsuitable in the worst-case. See discussions on [Stack Overflow](https://stackoverflow.com/a/67642821) and [Codeforces](https://codeforces.com/blog/entry/3793) for reference.
|
---
title
levit_algorithm
---
# D´Esopo-Pape algorithm
Given a graph with $n$ vertices and $m$ edges with weights $w_i$ and a starting vertex $v_0$.
The task is to find the shortest path from the vertex $v_0$ to every other vertex.
The algorithm from D´Esopo-Pape will work faster than [Dijkstra's algorithm](dijkstra.md) and the [Bellman-Ford algorithm](bellman_ford.md) in most cases, and will also work for negative edges.
However not for negative cycles.
## Description
Let the array $d$ contain the shortest path lengths, i.e. $d_i$ is the current length of the shortest path from the vertex $v_0$ to the vertex $i$.
Initially this array is filled with infinity for every vertex, except $d_{v_0} = 0$.
After the algorithm finishes, this array will contain the shortest distances.
Let the array $p$ contain the current ancestors, i.e. $p_i$ is the direct ancestor of the vertex $i$ on the current shortest path from $v_0$ to $i$.
Just like the array $d$, the array $p$ changes gradually during the algorithm and at the end takes its final values.
Now to the algorithm.
At each step three sets of vertices are maintained:
- $M_0$ - vertices, for which the distance has already been calculated (although it might not be the final distance)
- $M_1$ - vertices, for which the distance currently is calculated
- $M_2$ - vertices, for which the distance has not yet been calculated
The vertices in the set $M_1$ are stored in a bidirectional queue (deque).
At each step of the algorithm we take a vertex from the set $M_1$ (from the front of the queue).
Let $u$ be the selected vertex.
We put this vertex $u$ into the set $M_0$.
Then we iterate over all edges coming out of this vertex.
Let $v$ be the second end of the current edge, and $w$ its weight.
- If $v$ belongs to $M_2$, then $v$ is inserted into the set $M_1$ by inserting it at the back of the queue.
$d_v$ is set to $d_u + w$.
- If $v$ belongs to $M_1$, then we try to improve the value of $d_v$: $d_v = \min(d_v, d_u + w)$.
Since $v$ is already in $M_1$, we don't need to insert it into $M_1$ and the queue.
- If $v$ belongs to $M_0$, and if $d_v$ can be improved $d_v > d_u + w$, then we improve $d_v$ and insert the vertex $v$ back to the set $M_1$, placing it at the beginning of the queue.
And of course, with each update in the array $d$ we also have to update the corresponding element in the array $p$.
## Implementation
We will use an array $m$ to store in which set each vertex is currently.
```{.cpp file=desopo_pape}
struct Edge {
int to, w;
};
int n;
vector<vector<Edge>> adj;
const int INF = 1e9;
void shortest_paths(int v0, vector<int>& d, vector<int>& p) {
d.assign(n, INF);
d[v0] = 0;
vector<int> m(n, 2);
deque<int> q;
q.push_back(v0);
p.assign(n, -1);
while (!q.empty()) {
int u = q.front();
q.pop_front();
m[u] = 0;
for (Edge e : adj[u]) {
if (d[e.to] > d[u] + e.w) {
d[e.to] = d[u] + e.w;
p[e.to] = u;
if (m[e.to] == 2) {
m[e.to] = 1;
q.push_back(e.to);
} else if (m[e.to] == 0) {
m[e.to] = 1;
q.push_front(e.to);
}
}
}
}
}
```
## Complexity
The algorithm usually performs quite fast - in most cases, even faster than Dijkstra's algorithm.
However there exist cases for which the algorithm takes exponential time, making it unsuitable in the worst-case. See discussions on [Stack Overflow](https://stackoverflow.com/a/67642821) and [Codeforces](https://codeforces.com/blog/entry/3793) for reference.
|
D´Esopo-Pape algorithm
|
---
title
- Original
---
# Second Best Minimum Spanning Tree
A Minimum Spanning Tree $T$ is a tree for the given graph $G$ which spans over all vertices of the given graph and has the minimum weight sum of all the edges, from all the possible spanning trees.
A second best MST $T'$ is a spanning tree, that has the second minimum weight sum of all the edges, from all the possible spanning trees of the graph $G$.
## Observation
Let $T$ be the Minimum Spanning Tree of a graph $G$.
It can be observed, that the second best Minimum Spanning Tree differs from $T$ by only one edge replacement. (For a proof of this statement refer to problem 23-1 [here](http://www-bcf.usc.edu/~shanghua/teaching/Spring2010/public_html/files/HW2_Solutions_A.pdf)).
So we need to find an edge $e_{new}$ which is in not in $T$, and replace it with an edge in $T$ (let it be $e_{old}$) such that the new graph $T' = (T \cup \{e_{new}\}) \setminus \{e_{old}\}$ is a spanning tree and the weight difference ($e_{new} - e_{old}$) is minimum.
## Using Kruskal's Algorithm
We can use Kruskal's algorithm to find the MST first, and then just try to remove a single edge from it and replace it with another.
1. Sort the edges in $O(E \log E)$, then find a MST using Kruskal in $O(E)$.
2. For each edge in the MST (we will have $V-1$ edges in it) temporarily exclude it from the edge list so that it cannot be chosen.
3. Then, again try to find a MST in $O(E)$ using the remaining edges.
4. Do this for all the edges in MST, and take the best of all.
Note: we don’t need to sort the edges again in for Step 3.
So, the overall time complexity will be $O(E \log V + E + V E)$ = $O(V E)$.
## Modeling into a Lowest Common Ancestor (LCA) problem
In the previous approach we tried all possibilities of removing one edge of the MST.
Here we will do the exact opposite.
We try to add every edge that is not already in the MST.
1. Sort the edges in $O(E \log E)$, then find a MST using Kruskal in $O(E)$.
2. For each edge $e$ not already in the MST, temporarily add it to the MST, creating a cycle. The cycle will pass through the LCA.
3. Find the edge $k$ with maximal weight in the cycle that is not equal to $e$, by following the parents of the nodes of edge $e$, up to the LCA.
4. Remove $k$ temporarily, creating a new spanning tree.
5. Compute the weight difference $\delta = weight(e) - weight(k)$, and remember it together with the changed edge.
6. Repeat step 2 for all other edges, and return the spanning tree with the smallest weight difference to the MST.
The time complexity of the algorithm depends on how we compute the $k$s, which are the maximum weight edges in step 2 of this algorithm.
One way to compute them efficiently in $O(E \log V)$ is to transform the problem into a Lowest Common Ancestor (LCA) problem.
We will preprocess the LCA by rooting the MST and will also compute the maximum edge weights for each node on the paths to their ancestors.
This can be done using [Binary Lifting](lca_binary_lifting.md) for LCA.
The final time complexity of this approach is $O(E \log V)$.
For example:
<center>  <br>
*In the image left is the MST and right is the second best MST.*
</center>
In the given graph suppose we root the MST at the blue vertex on the top, and then run our algorithm by start picking the edges not in MST.
Let the edge picked first be the edge $(u, v)$ with weight 36.
Adding this edge to the tree forms a cycle 36 - 7 - 2 - 34.
Now we will find the maximum weight edge in this cycle by finding the $\text{LCA}(u, v) = p$.
We compute the maximum weight edge on the paths from $u$ to $p$ and from $v$ to $p$.
Note: the $\text{LCA}(u, v)$ can also be equal to $u$ or $v$ in some case.
In this example we will get the edge with weight 34 as maximum edge weight in the cycle.
By removing the edge we get a new spanning tree, that has a weight difference of only 2.
After doing this also with all other edges that are not part of the initial MST, we can see that this spanning tree was also the second best spanning tree overall.
Choosing the edge with weight 14 will increase the weight of the tree by 7, choosing the edge with weight 27 increases it by 14, choosing the edge with weight 28 increases it by 21, and choosing the edge with weight 39 will increase the tree by 5.
## Implementation
```cpp
struct edge {
int s, e, w, id;
bool operator<(const struct edge& other) { return w < other.w; }
};
typedef struct edge Edge;
const int N = 2e5 + 5;
long long res = 0, ans = 1e18;
int n, m, a, b, w, id, l = 21;
vector<Edge> edges;
vector<int> h(N, 0), parent(N, -1), size(N, 0), present(N, 0);
vector<vector<pair<int, int>>> adj(N), dp(N, vector<pair<int, int>>(l));
vector<vector<int>> up(N, vector<int>(l, -1));
pair<int, int> combine(pair<int, int> a, pair<int, int> b) {
vector<int> v = {a.first, a.second, b.first, b.second};
int topTwo = -3, topOne = -2;
for (int c : v) {
if (c > topOne) {
topTwo = topOne;
topOne = c;
} else if (c > topTwo && c < topOne) {
topTwo = c;
}
}
return {topOne, topTwo};
}
void dfs(int u, int par, int d) {
h[u] = 1 + h[par];
up[u][0] = par;
dp[u][0] = {d, -1};
for (auto v : adj[u]) {
if (v.first != par) {
dfs(v.first, u, v.second);
}
}
}
pair<int, int> lca(int u, int v) {
pair<int, int> ans = {-2, -3};
if (h[u] < h[v]) {
swap(u, v);
}
for (int i = l - 1; i >= 0; i--) {
if (h[u] - h[v] >= (1 << i)) {
ans = combine(ans, dp[u][i]);
u = up[u][i];
}
}
if (u == v) {
return ans;
}
for (int i = l - 1; i >= 0; i--) {
if (up[u][i] != -1 && up[v][i] != -1 && up[u][i] != up[v][i]) {
ans = combine(ans, combine(dp[u][i], dp[v][i]));
u = up[u][i];
v = up[v][i];
}
}
ans = combine(ans, combine(dp[u][0], dp[v][0]));
return ans;
}
int main(void) {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
parent[i] = i;
size[i] = 1;
}
for (int i = 1; i <= m; i++) {
cin >> a >> b >> w; // 1-indexed
edges.push_back({a, b, w, i - 1});
}
sort(edges.begin(), edges.end());
for (int i = 0; i <= m - 1; i++) {
a = edges[i].s;
b = edges[i].e;
w = edges[i].w;
id = edges[i].id;
if (unite_set(a, b)) {
adj[a].emplace_back(b, w);
adj[b].emplace_back(a, w);
present[id] = 1;
res += w;
}
}
dfs(1, 0, 0);
for (int i = 1; i <= l - 1; i++) {
for (int j = 1; j <= n; ++j) {
if (up[j][i - 1] != -1) {
int v = up[j][i - 1];
up[j][i] = up[v][i - 1];
dp[j][i] = combine(dp[j][i - 1], dp[v][i - 1]);
}
}
}
for (int i = 0; i <= m - 1; i++) {
id = edges[i].id;
w = edges[i].w;
if (!present[id]) {
auto rem = lca(edges[i].s, edges[i].e);
if (rem.first != w) {
if (ans > res + w - rem.first) {
ans = res + w - rem.first;
}
} else if (rem.second != -1) {
if (ans > res + w - rem.second) {
ans = res + w - rem.second;
}
}
}
}
cout << ans << "\n";
return 0;
}
```
## References
1. Competitive Programming-3, by Steven Halim
2. [web.mit.edu](http://web.mit.edu/6.263/www/quiz1-f05-sol.pdf)
|
---
title
- Original
---
# Second Best Minimum Spanning Tree
A Minimum Spanning Tree $T$ is a tree for the given graph $G$ which spans over all vertices of the given graph and has the minimum weight sum of all the edges, from all the possible spanning trees.
A second best MST $T'$ is a spanning tree, that has the second minimum weight sum of all the edges, from all the possible spanning trees of the graph $G$.
## Observation
Let $T$ be the Minimum Spanning Tree of a graph $G$.
It can be observed, that the second best Minimum Spanning Tree differs from $T$ by only one edge replacement. (For a proof of this statement refer to problem 23-1 [here](http://www-bcf.usc.edu/~shanghua/teaching/Spring2010/public_html/files/HW2_Solutions_A.pdf)).
So we need to find an edge $e_{new}$ which is in not in $T$, and replace it with an edge in $T$ (let it be $e_{old}$) such that the new graph $T' = (T \cup \{e_{new}\}) \setminus \{e_{old}\}$ is a spanning tree and the weight difference ($e_{new} - e_{old}$) is minimum.
## Using Kruskal's Algorithm
We can use Kruskal's algorithm to find the MST first, and then just try to remove a single edge from it and replace it with another.
1. Sort the edges in $O(E \log E)$, then find a MST using Kruskal in $O(E)$.
2. For each edge in the MST (we will have $V-1$ edges in it) temporarily exclude it from the edge list so that it cannot be chosen.
3. Then, again try to find a MST in $O(E)$ using the remaining edges.
4. Do this for all the edges in MST, and take the best of all.
Note: we don’t need to sort the edges again in for Step 3.
So, the overall time complexity will be $O(E \log V + E + V E)$ = $O(V E)$.
## Modeling into a Lowest Common Ancestor (LCA) problem
In the previous approach we tried all possibilities of removing one edge of the MST.
Here we will do the exact opposite.
We try to add every edge that is not already in the MST.
1. Sort the edges in $O(E \log E)$, then find a MST using Kruskal in $O(E)$.
2. For each edge $e$ not already in the MST, temporarily add it to the MST, creating a cycle. The cycle will pass through the LCA.
3. Find the edge $k$ with maximal weight in the cycle that is not equal to $e$, by following the parents of the nodes of edge $e$, up to the LCA.
4. Remove $k$ temporarily, creating a new spanning tree.
5. Compute the weight difference $\delta = weight(e) - weight(k)$, and remember it together with the changed edge.
6. Repeat step 2 for all other edges, and return the spanning tree with the smallest weight difference to the MST.
The time complexity of the algorithm depends on how we compute the $k$s, which are the maximum weight edges in step 2 of this algorithm.
One way to compute them efficiently in $O(E \log V)$ is to transform the problem into a Lowest Common Ancestor (LCA) problem.
We will preprocess the LCA by rooting the MST and will also compute the maximum edge weights for each node on the paths to their ancestors.
This can be done using [Binary Lifting](lca_binary_lifting.md) for LCA.
The final time complexity of this approach is $O(E \log V)$.
For example:
<center>  <br>
*In the image left is the MST and right is the second best MST.*
</center>
In the given graph suppose we root the MST at the blue vertex on the top, and then run our algorithm by start picking the edges not in MST.
Let the edge picked first be the edge $(u, v)$ with weight 36.
Adding this edge to the tree forms a cycle 36 - 7 - 2 - 34.
Now we will find the maximum weight edge in this cycle by finding the $\text{LCA}(u, v) = p$.
We compute the maximum weight edge on the paths from $u$ to $p$ and from $v$ to $p$.
Note: the $\text{LCA}(u, v)$ can also be equal to $u$ or $v$ in some case.
In this example we will get the edge with weight 34 as maximum edge weight in the cycle.
By removing the edge we get a new spanning tree, that has a weight difference of only 2.
After doing this also with all other edges that are not part of the initial MST, we can see that this spanning tree was also the second best spanning tree overall.
Choosing the edge with weight 14 will increase the weight of the tree by 7, choosing the edge with weight 27 increases it by 14, choosing the edge with weight 28 increases it by 21, and choosing the edge with weight 39 will increase the tree by 5.
## Implementation
```cpp
struct edge {
int s, e, w, id;
bool operator<(const struct edge& other) { return w < other.w; }
};
typedef struct edge Edge;
const int N = 2e5 + 5;
long long res = 0, ans = 1e18;
int n, m, a, b, w, id, l = 21;
vector<Edge> edges;
vector<int> h(N, 0), parent(N, -1), size(N, 0), present(N, 0);
vector<vector<pair<int, int>>> adj(N), dp(N, vector<pair<int, int>>(l));
vector<vector<int>> up(N, vector<int>(l, -1));
pair<int, int> combine(pair<int, int> a, pair<int, int> b) {
vector<int> v = {a.first, a.second, b.first, b.second};
int topTwo = -3, topOne = -2;
for (int c : v) {
if (c > topOne) {
topTwo = topOne;
topOne = c;
} else if (c > topTwo && c < topOne) {
topTwo = c;
}
}
return {topOne, topTwo};
}
void dfs(int u, int par, int d) {
h[u] = 1 + h[par];
up[u][0] = par;
dp[u][0] = {d, -1};
for (auto v : adj[u]) {
if (v.first != par) {
dfs(v.first, u, v.second);
}
}
}
pair<int, int> lca(int u, int v) {
pair<int, int> ans = {-2, -3};
if (h[u] < h[v]) {
swap(u, v);
}
for (int i = l - 1; i >= 0; i--) {
if (h[u] - h[v] >= (1 << i)) {
ans = combine(ans, dp[u][i]);
u = up[u][i];
}
}
if (u == v) {
return ans;
}
for (int i = l - 1; i >= 0; i--) {
if (up[u][i] != -1 && up[v][i] != -1 && up[u][i] != up[v][i]) {
ans = combine(ans, combine(dp[u][i], dp[v][i]));
u = up[u][i];
v = up[v][i];
}
}
ans = combine(ans, combine(dp[u][0], dp[v][0]));
return ans;
}
int main(void) {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
parent[i] = i;
size[i] = 1;
}
for (int i = 1; i <= m; i++) {
cin >> a >> b >> w; // 1-indexed
edges.push_back({a, b, w, i - 1});
}
sort(edges.begin(), edges.end());
for (int i = 0; i <= m - 1; i++) {
a = edges[i].s;
b = edges[i].e;
w = edges[i].w;
id = edges[i].id;
if (unite_set(a, b)) {
adj[a].emplace_back(b, w);
adj[b].emplace_back(a, w);
present[id] = 1;
res += w;
}
}
dfs(1, 0, 0);
for (int i = 1; i <= l - 1; i++) {
for (int j = 1; j <= n; ++j) {
if (up[j][i - 1] != -1) {
int v = up[j][i - 1];
up[j][i] = up[v][i - 1];
dp[j][i] = combine(dp[j][i - 1], dp[v][i - 1]);
}
}
}
for (int i = 0; i <= m - 1; i++) {
id = edges[i].id;
w = edges[i].w;
if (!present[id]) {
auto rem = lca(edges[i].s, edges[i].e);
if (rem.first != w) {
if (ans > res + w - rem.first) {
ans = res + w - rem.first;
}
} else if (rem.second != -1) {
if (ans > res + w - rem.second) {
ans = res + w - rem.second;
}
}
}
}
cout << ans << "\n";
return 0;
}
```
## References
1. Competitive Programming-3, by Steven Halim
2. [web.mit.edu](http://web.mit.edu/6.263/www/quiz1-f05-sol.pdf)
## Problems
* [Codeforces - Minimum spanning tree for each edge](https://codeforces.com/problemset/problem/609/E)
|
Second Best Minimum Spanning Tree
|
---
title
assignment_mincostflow
---
# Solving assignment problem using min-cost-flow
The **assignment problem** has two equivalent statements:
- Given a square matrix $A[1..N, 1..N]$, you need to select $N$ elements in it so that exactly one element is selected in each row and column, and the sum of the values of these elements is the smallest.
- There are $N$ orders and $N$ machines. The cost of manufacturing on each machine is known for each order. Only one order can be performed on each machine. It is required to assign all orders to the machines so that the total cost is minimized.
Here we will consider the solution of the problem based on the algorithm for finding the [minimum cost flow (min-cost-flow)](min_cost_flow.md), solving the assignment problem in $\mathcal{O}(N^3)$.
## Description
Let's build a bipartite network: there is a source $S$, a drain $T$, in the first part there are $N$ vertices (corresponding to rows of the matrix, or orders), in the second there are also $N$ vertices (corresponding to the columns of the matrix, or machines). Between each vertex $i$ of the first set and each vertex $j$ of the second set, we draw an edge with bandwidth 1 and cost $A_{ij}$. From the source $S$ we draw edges to all vertices $i$ of the first set with bandwidth 1 and cost 0. We draw an edge with bandwidth 1 and cost 0 from each vertex of the second set $j$ to the drain $T$.
We find in the resulting network the maximum flow of the minimum cost. Obviously, the value of the flow will be $N$. Further, for each vertex $i$ of the first segment there is exactly one vertex $j$ of the second segment, such that the flow $F_{ij}$ = 1. Finally, this is a one-to-one correspondence between the vertices of the first segment and the vertices of the second part, which is the solution to the problem (since the found flow has a minimal cost, then the sum of the costs of the selected edges will be the lowest possible, which is the optimality criterion).
The complexity of this solution of the assignment problem depends on the algorithm by which the search for the maximum flow of the minimum cost is performed. The complexity will be $\mathcal{O}(N^3)$ using [Dijkstra](dijkstra.md) or $\mathcal{O}(N^4)$ using [Bellman-Ford](bellman_ford.md). This is due to the fact that the flow is of size $O(N)$ and each iteration of Dijkstra algorithm can be performed in $O(N^2)$, while it is $O(N^3)$ for Bellman-Ford.
## Implementation
The implementation given here is long, it can probably be significantly reduced.
It uses the [SPFA algorithm](bellman_ford.md) for finding shortest paths.
```cpp
const int INF = 1000 * 1000 * 1000;
vector<int> assignment(vector<vector<int>> a) {
int n = a.size();
int m = n * 2 + 2;
vector<vector<int>> f(m, vector<int>(m));
int s = m - 2, t = m - 1;
int cost = 0;
while (true) {
vector<int> dist(m, INF);
vector<int> p(m);
vector<bool> inq(m, false);
queue<int> q;
dist[s] = 0;
p[s] = -1;
q.push(s);
while (!q.empty()) {
int v = q.front();
q.pop();
inq[v] = false;
if (v == s) {
for (int i = 0; i < n; ++i) {
if (f[s][i] == 0) {
dist[i] = 0;
p[i] = s;
inq[i] = true;
q.push(i);
}
}
} else {
if (v < n) {
for (int j = n; j < n + n; ++j) {
if (f[v][j] < 1 && dist[j] > dist[v] + a[v][j - n]) {
dist[j] = dist[v] + a[v][j - n];
p[j] = v;
if (!inq[j]) {
q.push(j);
inq[j] = true;
}
}
}
} else {
for (int j = 0; j < n; ++j) {
if (f[v][j] < 0 && dist[j] > dist[v] - a[j][v - n]) {
dist[j] = dist[v] - a[j][v - n];
p[j] = v;
if (!inq[j]) {
q.push(j);
inq[j] = true;
}
}
}
}
}
}
int curcost = INF;
for (int i = n; i < n + n; ++i) {
if (f[i][t] == 0 && dist[i] < curcost) {
curcost = dist[i];
p[t] = i;
}
}
if (curcost == INF)
break;
cost += curcost;
for (int cur = t; cur != -1; cur = p[cur]) {
int prev = p[cur];
if (prev != -1)
f[cur][prev] = -(f[prev][cur] = 1);
}
}
vector<int> answer(n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (f[i][j + n] == 1)
answer[i] = j;
}
}
return answer;
}
```
|
---
title
assignment_mincostflow
---
# Solving assignment problem using min-cost-flow
The **assignment problem** has two equivalent statements:
- Given a square matrix $A[1..N, 1..N]$, you need to select $N$ elements in it so that exactly one element is selected in each row and column, and the sum of the values of these elements is the smallest.
- There are $N$ orders and $N$ machines. The cost of manufacturing on each machine is known for each order. Only one order can be performed on each machine. It is required to assign all orders to the machines so that the total cost is minimized.
Here we will consider the solution of the problem based on the algorithm for finding the [minimum cost flow (min-cost-flow)](min_cost_flow.md), solving the assignment problem in $\mathcal{O}(N^3)$.
## Description
Let's build a bipartite network: there is a source $S$, a drain $T$, in the first part there are $N$ vertices (corresponding to rows of the matrix, or orders), in the second there are also $N$ vertices (corresponding to the columns of the matrix, or machines). Between each vertex $i$ of the first set and each vertex $j$ of the second set, we draw an edge with bandwidth 1 and cost $A_{ij}$. From the source $S$ we draw edges to all vertices $i$ of the first set with bandwidth 1 and cost 0. We draw an edge with bandwidth 1 and cost 0 from each vertex of the second set $j$ to the drain $T$.
We find in the resulting network the maximum flow of the minimum cost. Obviously, the value of the flow will be $N$. Further, for each vertex $i$ of the first segment there is exactly one vertex $j$ of the second segment, such that the flow $F_{ij}$ = 1. Finally, this is a one-to-one correspondence between the vertices of the first segment and the vertices of the second part, which is the solution to the problem (since the found flow has a minimal cost, then the sum of the costs of the selected edges will be the lowest possible, which is the optimality criterion).
The complexity of this solution of the assignment problem depends on the algorithm by which the search for the maximum flow of the minimum cost is performed. The complexity will be $\mathcal{O}(N^3)$ using [Dijkstra](dijkstra.md) or $\mathcal{O}(N^4)$ using [Bellman-Ford](bellman_ford.md). This is due to the fact that the flow is of size $O(N)$ and each iteration of Dijkstra algorithm can be performed in $O(N^2)$, while it is $O(N^3)$ for Bellman-Ford.
## Implementation
The implementation given here is long, it can probably be significantly reduced.
It uses the [SPFA algorithm](bellman_ford.md) for finding shortest paths.
```cpp
const int INF = 1000 * 1000 * 1000;
vector<int> assignment(vector<vector<int>> a) {
int n = a.size();
int m = n * 2 + 2;
vector<vector<int>> f(m, vector<int>(m));
int s = m - 2, t = m - 1;
int cost = 0;
while (true) {
vector<int> dist(m, INF);
vector<int> p(m);
vector<bool> inq(m, false);
queue<int> q;
dist[s] = 0;
p[s] = -1;
q.push(s);
while (!q.empty()) {
int v = q.front();
q.pop();
inq[v] = false;
if (v == s) {
for (int i = 0; i < n; ++i) {
if (f[s][i] == 0) {
dist[i] = 0;
p[i] = s;
inq[i] = true;
q.push(i);
}
}
} else {
if (v < n) {
for (int j = n; j < n + n; ++j) {
if (f[v][j] < 1 && dist[j] > dist[v] + a[v][j - n]) {
dist[j] = dist[v] + a[v][j - n];
p[j] = v;
if (!inq[j]) {
q.push(j);
inq[j] = true;
}
}
}
} else {
for (int j = 0; j < n; ++j) {
if (f[v][j] < 0 && dist[j] > dist[v] - a[j][v - n]) {
dist[j] = dist[v] - a[j][v - n];
p[j] = v;
if (!inq[j]) {
q.push(j);
inq[j] = true;
}
}
}
}
}
}
int curcost = INF;
for (int i = n; i < n + n; ++i) {
if (f[i][t] == 0 && dist[i] < curcost) {
curcost = dist[i];
p[t] = i;
}
}
if (curcost == INF)
break;
cost += curcost;
for (int cur = t; cur != -1; cur = p[cur]) {
int prev = p[cur];
if (prev != -1)
f[cur][prev] = -(f[prev][cur] = 1);
}
}
vector<int> answer(n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (f[i][j + n] == 1)
answer[i] = j;
}
}
return answer;
}
```
|
Solving assignment problem using min-cost-flow
|
---
title
connected_components
---
# Search for connected components in a graph
Given an undirected graph $G$ with $n$ nodes and $m$ edges. We are required to find in it all the connected components, i.e, several groups of vertices such that within a group each vertex can be reached from another and no path exists between different groups.
## An algorithm for solving the problem
* To solve the problem, we can use Depth First Search or Breadth First Search.
* In fact, we will be doing a series of rounds of DFS: The first round will start from first node and all the nodes in the first connected component will be traversed (found). Then we find the first unvisited node of the remaining nodes, and run Depth First Search on it, thus finding a second connected component. And so on, until all the nodes are visited.
* The total asymptotic running time of this algorithm is $O(n + m)$ : In fact, this algorithm will not run on the same vertex twice, which means that each edge will be seen exactly two times (at one end and at the other end).
## Implementation
``` cpp
int n;
vector<vector<int>> adj;
vector<bool> used;
vector<int> comp;
void dfs(int v) {
used[v] = true ;
comp.push_back(v);
for (int u : adj[v]) {
if (!used[u])
dfs(u);
}
}
void find_comps() {
fill(used.begin(), used.end(), 0);
for (int v = 0; v < n; ++v) {
if (!used[v]) {
comp.clear();
dfs(v);
cout << "Component:" ;
for (int u : comp)
cout << ' ' << u;
cout << endl ;
}
}
}
```
* The most important function that is used is `find_comps()` which finds and displays connected components of the graph.
* The graph is stored in adjacency list representation, i.e `adj[v]` contains a list of vertices that have edges from the vertex `v`.
* Vector `comp` contains a list of nodes in the current connected component.
## Iterative implementation of the code
Deeply recursive functions are in general bad.
Every single recursive call will require a little bit of memory in the stack, and per default programs only have a limited amount of stack space.
So when you do a recursive DFS over a connected graph with millions of nodes, you might run into stack overflows.
It is always possible to translate a recursive program into an iterative program, by manually maintaining a stack data structure.
Since this data structure is allocated on the heap, no stack overflow will occur.
```cpp
int n;
vector<vector<int>> adj;
vector<bool> used;
vector<int> comp;
void dfs(int v) {
stack<int> st;
st.push(v);
while (!st.empty()) {
int curr = st.top();
st.pop();
if (!used[curr]) {
used[curr] = true;
comp.push_back(curr);
for (int i = adj[curr].size() - 1; i >= 0; i--) {
st.push(adj[curr][i]);
}
}
}
}
void find_comps() {
fill(used.begin(), used.end(), 0);
for (int v = 0; v < n ; ++v) {
if (!used[v]) {
comp.clear();
dfs(v);
cout << "Component:" ;
for (int u : comp)
cout << ' ' << u;
cout << endl ;
}
}
}
```
|
---
title
connected_components
---
# Search for connected components in a graph
Given an undirected graph $G$ with $n$ nodes and $m$ edges. We are required to find in it all the connected components, i.e, several groups of vertices such that within a group each vertex can be reached from another and no path exists between different groups.
## An algorithm for solving the problem
* To solve the problem, we can use Depth First Search or Breadth First Search.
* In fact, we will be doing a series of rounds of DFS: The first round will start from first node and all the nodes in the first connected component will be traversed (found). Then we find the first unvisited node of the remaining nodes, and run Depth First Search on it, thus finding a second connected component. And so on, until all the nodes are visited.
* The total asymptotic running time of this algorithm is $O(n + m)$ : In fact, this algorithm will not run on the same vertex twice, which means that each edge will be seen exactly two times (at one end and at the other end).
## Implementation
``` cpp
int n;
vector<vector<int>> adj;
vector<bool> used;
vector<int> comp;
void dfs(int v) {
used[v] = true ;
comp.push_back(v);
for (int u : adj[v]) {
if (!used[u])
dfs(u);
}
}
void find_comps() {
fill(used.begin(), used.end(), 0);
for (int v = 0; v < n; ++v) {
if (!used[v]) {
comp.clear();
dfs(v);
cout << "Component:" ;
for (int u : comp)
cout << ' ' << u;
cout << endl ;
}
}
}
```
* The most important function that is used is `find_comps()` which finds and displays connected components of the graph.
* The graph is stored in adjacency list representation, i.e `adj[v]` contains a list of vertices that have edges from the vertex `v`.
* Vector `comp` contains a list of nodes in the current connected component.
## Iterative implementation of the code
Deeply recursive functions are in general bad.
Every single recursive call will require a little bit of memory in the stack, and per default programs only have a limited amount of stack space.
So when you do a recursive DFS over a connected graph with millions of nodes, you might run into stack overflows.
It is always possible to translate a recursive program into an iterative program, by manually maintaining a stack data structure.
Since this data structure is allocated on the heap, no stack overflow will occur.
```cpp
int n;
vector<vector<int>> adj;
vector<bool> used;
vector<int> comp;
void dfs(int v) {
stack<int> st;
st.push(v);
while (!st.empty()) {
int curr = st.top();
st.pop();
if (!used[curr]) {
used[curr] = true;
comp.push_back(curr);
for (int i = adj[curr].size() - 1; i >= 0; i--) {
st.push(adj[curr][i]);
}
}
}
}
void find_comps() {
fill(used.begin(), used.end(), 0);
for (int v = 0; v < n ; ++v) {
if (!used[v]) {
comp.clear();
dfs(v);
cout << "Component:" ;
for (int u : comp)
cout << ' ' << u;
cout << endl ;
}
}
}
```
## Practice Problems
- [SPOJ: CCOMPS](http://www.spoj.com/problems/CCOMPS/)
- [SPOJ: CT23E](http://www.spoj.com/problems/CT23E/)
- [CODECHEF: GERALD07](https://www.codechef.com/MARCH14/problems/GERALD07)
- [CSES : Building Roads](https://cses.fi/problemset/task/1666)
|
Search for connected components in a graph
|
---
title
rmq_linear
---
# Solve RMQ (Range Minimum Query) by finding LCA (Lowest Common Ancestor)
Given an array `A[0..N-1]`.
For each query of the form `[L, R]` we want to find the minimum in the array `A` starting from position `L` and ending with position `R`.
We will assume that the array `A` doesn't change in the process, i.e. this article describes a solution to the static RMQ problem
Here is a description of an asymptotically optimal solution.
It stands apart from other solutions for the RMQ problem, since it is very different from them:
it reduces the RMQ problem to the LCA problem, and then uses the [Farach-Colton and Bender algorithm](lca_farachcoltonbender.md), which reduces the LCA problem back to a specialized RMQ problem and solves that.
## Algorithm
We construct a **Cartesian tree** from the array `A`.
A Cartesian tree of an array `A` is a binary tree with the min-heap property (the value of parent node has to be smaller or equal than the value of its children) such that the in-order traversal of the tree visits the nodes in the same order as they are in the array `A`.
In other words, a Cartesian tree is a recursive data structure.
The array `A` will be partitioned into 3 parts: the prefix of the array up to the minimum, the minimum, and the remaining suffix.
The root of the tree will be a node corresponding to the minimum element of the array `A`, the left subtree will be the Cartesian tree of the prefix, and the right subtree will be a Cartesian tree of the suffix.
In the following image you can see one array of length 10 and the corresponding Cartesian tree.
<center></center>
The range minimum query `[l, r]` is equivalent to the lowest common ancestor query `[l', r']`, where `l'` is the node corresponding to the element `A[l]` and `r'` the node corresponding to the element `A[r]`.
Indeed the node corresponding to the smallest element in the range has to be an ancestor of all nodes in the range, therefor also from `l'` and `r'`.
This automatically follows from the min-heap property.
And is also has to be the lowest ancestor, because otherwise `l'` and `r'` would be both in the left or in the right subtree, which generates a contradiction since in such a case the minimum wouldn't even be in the range.
In the following image you can see the LCA queries for the RMQ queries `[1, 3]` and `[5, 9]`.
In the first query the LCA of the nodes `A[1]` and `A[3]` is the node corresponding to `A[2]` which has the value 2, and in the second query the LCA of `A[5]` and `A[9]` is the node corresponding to `A[8]` which has the value 3.
<center></center>
Such a tree can be built in $O(N)$ time and the Farach-Colton and Benders algorithm can preprocess the tree in $O(N)$ and find the LCA in $O(1)$.
## Construction of a Cartesian tree
We will build the Cartesian tree by adding the elements one after another.
In each step we maintain a valid Cartesian tree of all the processed elements.
It is easy to see, that adding an element `s[i]` can only change the nodes in the most right path - starting at the root and repeatedly taking the right child - of the tree.
The subtree of the node with the smallest, but greater or equal than `s[i]`, value becomes the left subtree of `s[i]`, and the tree with root `s[i]` will become the new right subtree of the node with the biggest, but smaller than `s[i]` value.
This can be implemented by using a stack to store the indices of the most right nodes.
```cpp
vector<int> parent(n, -1);
stack<int> s;
for (int i = 0; i < n; i++) {
int last = -1;
while (!s.empty() && A[s.top()] >= A[i]) {
last = s.top();
s.pop();
}
if (!s.empty())
parent[i] = s.top();
if (last >= 0)
parent[last] = i;
s.push(i);
}
```
|
---
title
rmq_linear
---
# Solve RMQ (Range Minimum Query) by finding LCA (Lowest Common Ancestor)
Given an array `A[0..N-1]`.
For each query of the form `[L, R]` we want to find the minimum in the array `A` starting from position `L` and ending with position `R`.
We will assume that the array `A` doesn't change in the process, i.e. this article describes a solution to the static RMQ problem
Here is a description of an asymptotically optimal solution.
It stands apart from other solutions for the RMQ problem, since it is very different from them:
it reduces the RMQ problem to the LCA problem, and then uses the [Farach-Colton and Bender algorithm](lca_farachcoltonbender.md), which reduces the LCA problem back to a specialized RMQ problem and solves that.
## Algorithm
We construct a **Cartesian tree** from the array `A`.
A Cartesian tree of an array `A` is a binary tree with the min-heap property (the value of parent node has to be smaller or equal than the value of its children) such that the in-order traversal of the tree visits the nodes in the same order as they are in the array `A`.
In other words, a Cartesian tree is a recursive data structure.
The array `A` will be partitioned into 3 parts: the prefix of the array up to the minimum, the minimum, and the remaining suffix.
The root of the tree will be a node corresponding to the minimum element of the array `A`, the left subtree will be the Cartesian tree of the prefix, and the right subtree will be a Cartesian tree of the suffix.
In the following image you can see one array of length 10 and the corresponding Cartesian tree.
<center></center>
The range minimum query `[l, r]` is equivalent to the lowest common ancestor query `[l', r']`, where `l'` is the node corresponding to the element `A[l]` and `r'` the node corresponding to the element `A[r]`.
Indeed the node corresponding to the smallest element in the range has to be an ancestor of all nodes in the range, therefor also from `l'` and `r'`.
This automatically follows from the min-heap property.
And is also has to be the lowest ancestor, because otherwise `l'` and `r'` would be both in the left or in the right subtree, which generates a contradiction since in such a case the minimum wouldn't even be in the range.
In the following image you can see the LCA queries for the RMQ queries `[1, 3]` and `[5, 9]`.
In the first query the LCA of the nodes `A[1]` and `A[3]` is the node corresponding to `A[2]` which has the value 2, and in the second query the LCA of `A[5]` and `A[9]` is the node corresponding to `A[8]` which has the value 3.
<center></center>
Such a tree can be built in $O(N)$ time and the Farach-Colton and Benders algorithm can preprocess the tree in $O(N)$ and find the LCA in $O(1)$.
## Construction of a Cartesian tree
We will build the Cartesian tree by adding the elements one after another.
In each step we maintain a valid Cartesian tree of all the processed elements.
It is easy to see, that adding an element `s[i]` can only change the nodes in the most right path - starting at the root and repeatedly taking the right child - of the tree.
The subtree of the node with the smallest, but greater or equal than `s[i]`, value becomes the left subtree of `s[i]`, and the tree with root `s[i]` will become the new right subtree of the node with the biggest, but smaller than `s[i]` value.
This can be implemented by using a stack to store the indices of the most right nodes.
```cpp
vector<int> parent(n, -1);
stack<int> s;
for (int i = 0; i < n; i++) {
int last = -1;
while (!s.empty() && A[s.top()] >= A[i]) {
last = s.top();
s.pop();
}
if (!s.empty())
parent[i] = s.top();
if (last >= 0)
parent[last] = i;
s.push(i);
}
```
|
Solve RMQ (Range Minimum Query) by finding LCA (Lowest Common Ancestor)
|
---
title
lca_linear_offline
---
# Lowest Common Ancestor - Tarjan's off-line algorithm
We have a tree $G$ with $n$ nodes and we have $m$ queries of the form $(u, v)$.
For each query $(u, v)$ we want to find the lowest common ancestor of the vertices $u$ and $v$, i.e. the node that is an ancestor of both $u$ and $v$ and has the greatest depth in the tree.
The node $v$ is also an ancestor of $v$, so the LCA can also be one of the two nodes.
In this article we will solve the problem off-line, i.e. we assume that all queries are known in advance, and we therefore answer the queries in any order we like.
The following algorithm allows to answer all $m$ queries in $O(n + m)$ total time, i.e. for sufficiently large $m$ in $O(1)$ for each query.
## Algorithm
The algorithm is named after Robert Tarjan, who discovered it in 1979 and also made many other contributions to the [Disjoint Set Union](../data_structures/disjoint_set_union.md) data structure, which will be heavily used in this algorithm.
The algorithm answers all queries with one [DFS](depth-first-search.md) traversal of the tree.
Namely a query $(u, v)$ is answered at node $u$, if node $v$ has already been visited previously, or vice versa.
So let's assume we are currently at node $v$, we have already made recursive DFS calls, and also already visited the second node $u$ from the query $(u, v)$.
Let's learn how to find the LCA of these two nodes.
Note that $\text{LCA}(u, v)$ is either the node $v$ or one of its ancestors.
So we need to find the lowest node among the ancestors of $v$ (including $v$), for which the node $u$ is a descendant.
Also note that for a fixed $v$ the visited nodes of the tree split into a set of disjoint sets.
Each ancestor $p$ of node $v$ has his own set containing this node and all subtrees with roots in those of its children who are not part of the path from $v$ to the root of the tree.
The set which contains the node $u$ determines the $\text{LCA}(u, v)$:
the LCA is the representative of the set, namely the node on lies on the path between $v$ and the root of the tree.
We only need to learn to efficiently maintain all these sets.
For this purpose we apply the data structure DSU.
To be able to apply Union by rank, we store the real representative (the value on the path between $v$ and the root of the tree) of each set in the array `ancestor`.
Let's discuss the implementation of the DFS.
Let's assume we are currently visiting the node $v$.
We place the node in a new set in the DSU, `ancestor[v] = v`.
As usual we process all children of $v$.
For this we must first recursively call DFS from that node, and then add this node with all its subtree to the set of $v$.
This can be done with the function `union_sets` and the following assignment `ancestor[find_set(v)] = v` (this is necessary, because `union_sets` might change the representative of the set).
Finally after processing all children we can answer all queries of the form $(u, v)$ for which $u$ has been already visited.
The answer to the query, i.e. the LCA of $u$ and $v$, will be the node `ancestor[find_set(u)]`.
It is easy to see that a query will only be answered once.
Let's us determine the time complexity of this algorithm.
Firstly we have $O(n)$ because of the DFS.
Secondly we have the function calls of `union_sets` which happen $n$ times, resulting also in $O(n)$.
And thirdly we have the calls of `find_set` for every query, which gives $O(m)$.
So in total the time complexity is $O(n + m)$, which means that for sufficiently large $m$ this corresponds to $O(1)$ for answering one query.
## Implementation
Here is an implementation of this algorithm.
The implementation of DSU has been not included, as it can be used without any modifications.
```cpp
vector<vector<int>> adj;
vector<vector<int>> queries;
vector<int> ancestor;
vector<bool> visited;
void dfs(int v)
{
visited[v] = true;
ancestor[v] = v;
for (int u : adj[v]) {
if (!visited[u]) {
dfs(u);
union_sets(v, u);
ancestor[find_set(v)] = v;
}
}
for (int other_node : queries[v]) {
if (visited[other_node])
cout << "LCA of " << v << " and " << other_node
<< " is " << ancestor[find_set(other_node)] << ".\n";
}
}
void compute_LCAs() {
// initialize n, adj and DSU
// for (each query (u, v)) {
// queries[u].push_back(v);
// queries[v].push_back(u);
// }
ancestor.resize(n);
visited.assign(n, false);
dfs(0);
}
```
|
---
title
lca_linear_offline
---
# Lowest Common Ancestor - Tarjan's off-line algorithm
We have a tree $G$ with $n$ nodes and we have $m$ queries of the form $(u, v)$.
For each query $(u, v)$ we want to find the lowest common ancestor of the vertices $u$ and $v$, i.e. the node that is an ancestor of both $u$ and $v$ and has the greatest depth in the tree.
The node $v$ is also an ancestor of $v$, so the LCA can also be one of the two nodes.
In this article we will solve the problem off-line, i.e. we assume that all queries are known in advance, and we therefore answer the queries in any order we like.
The following algorithm allows to answer all $m$ queries in $O(n + m)$ total time, i.e. for sufficiently large $m$ in $O(1)$ for each query.
## Algorithm
The algorithm is named after Robert Tarjan, who discovered it in 1979 and also made many other contributions to the [Disjoint Set Union](../data_structures/disjoint_set_union.md) data structure, which will be heavily used in this algorithm.
The algorithm answers all queries with one [DFS](depth-first-search.md) traversal of the tree.
Namely a query $(u, v)$ is answered at node $u$, if node $v$ has already been visited previously, or vice versa.
So let's assume we are currently at node $v$, we have already made recursive DFS calls, and also already visited the second node $u$ from the query $(u, v)$.
Let's learn how to find the LCA of these two nodes.
Note that $\text{LCA}(u, v)$ is either the node $v$ or one of its ancestors.
So we need to find the lowest node among the ancestors of $v$ (including $v$), for which the node $u$ is a descendant.
Also note that for a fixed $v$ the visited nodes of the tree split into a set of disjoint sets.
Each ancestor $p$ of node $v$ has his own set containing this node and all subtrees with roots in those of its children who are not part of the path from $v$ to the root of the tree.
The set which contains the node $u$ determines the $\text{LCA}(u, v)$:
the LCA is the representative of the set, namely the node on lies on the path between $v$ and the root of the tree.
We only need to learn to efficiently maintain all these sets.
For this purpose we apply the data structure DSU.
To be able to apply Union by rank, we store the real representative (the value on the path between $v$ and the root of the tree) of each set in the array `ancestor`.
Let's discuss the implementation of the DFS.
Let's assume we are currently visiting the node $v$.
We place the node in a new set in the DSU, `ancestor[v] = v`.
As usual we process all children of $v$.
For this we must first recursively call DFS from that node, and then add this node with all its subtree to the set of $v$.
This can be done with the function `union_sets` and the following assignment `ancestor[find_set(v)] = v` (this is necessary, because `union_sets` might change the representative of the set).
Finally after processing all children we can answer all queries of the form $(u, v)$ for which $u$ has been already visited.
The answer to the query, i.e. the LCA of $u$ and $v$, will be the node `ancestor[find_set(u)]`.
It is easy to see that a query will only be answered once.
Let's us determine the time complexity of this algorithm.
Firstly we have $O(n)$ because of the DFS.
Secondly we have the function calls of `union_sets` which happen $n$ times, resulting also in $O(n)$.
And thirdly we have the calls of `find_set` for every query, which gives $O(m)$.
So in total the time complexity is $O(n + m)$, which means that for sufficiently large $m$ this corresponds to $O(1)$ for answering one query.
## Implementation
Here is an implementation of this algorithm.
The implementation of DSU has been not included, as it can be used without any modifications.
```cpp
vector<vector<int>> adj;
vector<vector<int>> queries;
vector<int> ancestor;
vector<bool> visited;
void dfs(int v)
{
visited[v] = true;
ancestor[v] = v;
for (int u : adj[v]) {
if (!visited[u]) {
dfs(u);
union_sets(v, u);
ancestor[find_set(v)] = v;
}
}
for (int other_node : queries[v]) {
if (visited[other_node])
cout << "LCA of " << v << " and " << other_node
<< " is " << ancestor[find_set(other_node)] << ".\n";
}
}
void compute_LCAs() {
// initialize n, adj and DSU
// for (each query (u, v)) {
// queries[u].push_back(v);
// queries[v].push_back(u);
// }
ancestor.resize(n);
visited.assign(n, false);
dfs(0);
}
```
|
Lowest Common Ancestor - Tarjan's off-line algorithm
|
---
title
dijkstra_sparse
---
# Dijkstra on sparse graphs
For the statement of the problem, the algorithm with implementation and proof can be found on the article [Dijkstra's algorithm](dijkstra.md).
## Algorithm
We recall in the derivation of the complexity of Dijkstra's algorithm we used two factors:
the time of finding the unmarked vertex with the smallest distance $d[v]$, and the time of the relaxation, i.e. the time of changing the values $d[\text{to}]$.
In the simplest implementation these operations require $O(n)$ and $O(1)$ time.
Therefore, since we perform the first operation $O(n)$ times, and the second one $O(m)$ times, we obtained the complexity $O(n^2 + m)$.
It is clear, that this complexity is optimal for a dense graph, i.e. when $m \approx n^2$.
However in sparse graphs, when $m$ is much smaller than the maximal number of edges $n^2$, the complexity gets less optimal because of the first term.
Thus it is necessary to improve the execution time of the first operation (and of course without greatly affecting the second operation by much).
To accomplish that we can use a variation of multiple auxiliary data structures.
The most efficient is the **Fibonacci heap**, which allows the first operation to run in $O(\log n)$, and the second operation in $O(1)$.
Therefore we will get the complexity $O(n \log n + m)$ for Dijkstra's algorithm, which is also the theoretical minimum for the shortest path search problem.
Therefore this algorithm works optimal, and Fibonacci heaps are the optimal data structure.
There doesn't exist any data structure, that can perform both operations in $O(1)$, because this would also allow to sort a list of random numbers in linear time, which is impossible.
Interestingly there exists an algorithm by Thorup that finds the shortest path in $O(m)$ time, however only works for integer weights, and uses a completely different idea.
So this doesn't lead to any contradictions.
Fibonacci heaps provide the optimal complexity for this task.
However they are quite complex to implement, and also have a quite large hidden constant.
As a compromise you can use data structures, that perform both types of operations (extracting a minimum and updating an item) in $O(\log n)$.
Then the complexity of Dijkstra's algorithm is $O(n \log n + m \log n) = O(m \log n)$.
C++ provides two such data structures: `set` and `priority_queue`.
The first is based on red-black trees, and the second one on heaps.
Therefore `priority_queue` has a smaller hidden constant, but also has a drawback:
it doesn't support the operation of removing an element.
Because of this we need to do a "workaround", that actually leads to a slightly worse factor $\log m$ instead of $\log n$ (although in terms of complexity they are identical).
## Implementation
### set
Let us start with the container `set`.
Since we need to store vertices ordered by their values $d[]$, it is convenient to store actual pairs: the distance and the index of the vertex.
As a result in a `set` pairs are automatically sorted by their distances.
```{.cpp file=dijkstra_sparse_set}
const int INF = 1000000000;
vector<vector<pair<int, int>>> adj;
void dijkstra(int s, vector<int> & d, vector<int> & p) {
int n = adj.size();
d.assign(n, INF);
p.assign(n, -1);
d[s] = 0;
set<pair<int, int>> q;
q.insert({0, s});
while (!q.empty()) {
int v = q.begin()->second;
q.erase(q.begin());
for (auto edge : adj[v]) {
int to = edge.first;
int len = edge.second;
if (d[v] + len < d[to]) {
q.erase({d[to], to});
d[to] = d[v] + len;
p[to] = v;
q.insert({d[to], to});
}
}
}
}
```
We don't need the array $u[]$ from the normal Dijkstra's algorithm implementation any more.
We will use the `set` to store that information, and also find the vertex with the shortest distance with it.
It kinda acts like a queue.
The main loops executes until there are no more vertices in the set/queue.
A vertex with the smallest distance gets extracted, and for each successful relaxation we first remove the old pair, and then after the relaxation add the new pair into the queue.
### priority_queue
The main difference to the implementation with `set` is that in many languages, including C++, we cannot remove elements from the `priority_queue` (although heaps can support that operation in theory).
Therefore we have to use a workaround:
We simply don't delete the old pair from the queue.
As a result a vertex can appear multiple times with different distance in the queue at the same time.
Among these pairs we are only interested in the pairs where the first element is equal to the corresponding value in $d[]$, all the other pairs are old.
Therefore we need to make a small modification:
at the beginning of each iteration, after extracting the next pair, we check if it is an important pair or if it is already an old and handled pair.
This check is important, otherwise the complexity can increase up to $O(n m)$.
By default a `priority_queue` sorts elements in descending order.
To make it sort the elements in ascending order, we can either store the negated distances in it, or pass it a different sorting function.
We will do the second option.
```{.cpp file=dijkstra_sparse_pq}
const int INF = 1000000000;
vector<vector<pair<int, int>>> adj;
void dijkstra(int s, vector<int> & d, vector<int> & p) {
int n = adj.size();
d.assign(n, INF);
p.assign(n, -1);
d[s] = 0;
using pii = pair<int, int>;
priority_queue<pii, vector<pii>, greater<pii>> q;
q.push({0, s});
while (!q.empty()) {
int v = q.top().second;
int d_v = q.top().first;
q.pop();
if (d_v != d[v])
continue;
for (auto edge : adj[v]) {
int to = edge.first;
int len = edge.second;
if (d[v] + len < d[to]) {
d[to] = d[v] + len;
p[to] = v;
q.push({d[to], to});
}
}
}
}
```
In practice the `priority_queue` version is a little bit faster than the version with `set`.
Interestingly, a [2007 technical report](https://www3.cs.stonybrook.edu/~rezaul/papers/TR-07-54.pdf) concluded the variant of the algorithm not using decrease-key operations ran faster than the decrease-key variant, with a greater performance gap for sparse graphs.
### Getting rid of pairs
You can improve the performance a little bit more if you don't store pairs in the containers, but only the vertex indices.
In this case we must overload the comparison operator:
it must compare two vertices using the distances stored in $d[]$.
As a result of the relaxation, the distance of some vertices will change.
However the data structure will not resort itself automatically.
In fact changing distances of vertices in the queue, might destroy the data structure.
As before, we need to remove the vertex before we relax it, and then insert it again afterwards.
Since we only can remove from `set`, this optimization is only applicable for the `set` method, and doesn't work with `priority_queue` implementation.
In practice this significantly increases the performance, especially when larger data types are used to store distances, like `long long` or `double`.
|
---
title
dijkstra_sparse
---
# Dijkstra on sparse graphs
For the statement of the problem, the algorithm with implementation and proof can be found on the article [Dijkstra's algorithm](dijkstra.md).
## Algorithm
We recall in the derivation of the complexity of Dijkstra's algorithm we used two factors:
the time of finding the unmarked vertex with the smallest distance $d[v]$, and the time of the relaxation, i.e. the time of changing the values $d[\text{to}]$.
In the simplest implementation these operations require $O(n)$ and $O(1)$ time.
Therefore, since we perform the first operation $O(n)$ times, and the second one $O(m)$ times, we obtained the complexity $O(n^2 + m)$.
It is clear, that this complexity is optimal for a dense graph, i.e. when $m \approx n^2$.
However in sparse graphs, when $m$ is much smaller than the maximal number of edges $n^2$, the complexity gets less optimal because of the first term.
Thus it is necessary to improve the execution time of the first operation (and of course without greatly affecting the second operation by much).
To accomplish that we can use a variation of multiple auxiliary data structures.
The most efficient is the **Fibonacci heap**, which allows the first operation to run in $O(\log n)$, and the second operation in $O(1)$.
Therefore we will get the complexity $O(n \log n + m)$ for Dijkstra's algorithm, which is also the theoretical minimum for the shortest path search problem.
Therefore this algorithm works optimal, and Fibonacci heaps are the optimal data structure.
There doesn't exist any data structure, that can perform both operations in $O(1)$, because this would also allow to sort a list of random numbers in linear time, which is impossible.
Interestingly there exists an algorithm by Thorup that finds the shortest path in $O(m)$ time, however only works for integer weights, and uses a completely different idea.
So this doesn't lead to any contradictions.
Fibonacci heaps provide the optimal complexity for this task.
However they are quite complex to implement, and also have a quite large hidden constant.
As a compromise you can use data structures, that perform both types of operations (extracting a minimum and updating an item) in $O(\log n)$.
Then the complexity of Dijkstra's algorithm is $O(n \log n + m \log n) = O(m \log n)$.
C++ provides two such data structures: `set` and `priority_queue`.
The first is based on red-black trees, and the second one on heaps.
Therefore `priority_queue` has a smaller hidden constant, but also has a drawback:
it doesn't support the operation of removing an element.
Because of this we need to do a "workaround", that actually leads to a slightly worse factor $\log m$ instead of $\log n$ (although in terms of complexity they are identical).
## Implementation
### set
Let us start with the container `set`.
Since we need to store vertices ordered by their values $d[]$, it is convenient to store actual pairs: the distance and the index of the vertex.
As a result in a `set` pairs are automatically sorted by their distances.
```{.cpp file=dijkstra_sparse_set}
const int INF = 1000000000;
vector<vector<pair<int, int>>> adj;
void dijkstra(int s, vector<int> & d, vector<int> & p) {
int n = adj.size();
d.assign(n, INF);
p.assign(n, -1);
d[s] = 0;
set<pair<int, int>> q;
q.insert({0, s});
while (!q.empty()) {
int v = q.begin()->second;
q.erase(q.begin());
for (auto edge : adj[v]) {
int to = edge.first;
int len = edge.second;
if (d[v] + len < d[to]) {
q.erase({d[to], to});
d[to] = d[v] + len;
p[to] = v;
q.insert({d[to], to});
}
}
}
}
```
We don't need the array $u[]$ from the normal Dijkstra's algorithm implementation any more.
We will use the `set` to store that information, and also find the vertex with the shortest distance with it.
It kinda acts like a queue.
The main loops executes until there are no more vertices in the set/queue.
A vertex with the smallest distance gets extracted, and for each successful relaxation we first remove the old pair, and then after the relaxation add the new pair into the queue.
### priority_queue
The main difference to the implementation with `set` is that in many languages, including C++, we cannot remove elements from the `priority_queue` (although heaps can support that operation in theory).
Therefore we have to use a workaround:
We simply don't delete the old pair from the queue.
As a result a vertex can appear multiple times with different distance in the queue at the same time.
Among these pairs we are only interested in the pairs where the first element is equal to the corresponding value in $d[]$, all the other pairs are old.
Therefore we need to make a small modification:
at the beginning of each iteration, after extracting the next pair, we check if it is an important pair or if it is already an old and handled pair.
This check is important, otherwise the complexity can increase up to $O(n m)$.
By default a `priority_queue` sorts elements in descending order.
To make it sort the elements in ascending order, we can either store the negated distances in it, or pass it a different sorting function.
We will do the second option.
```{.cpp file=dijkstra_sparse_pq}
const int INF = 1000000000;
vector<vector<pair<int, int>>> adj;
void dijkstra(int s, vector<int> & d, vector<int> & p) {
int n = adj.size();
d.assign(n, INF);
p.assign(n, -1);
d[s] = 0;
using pii = pair<int, int>;
priority_queue<pii, vector<pii>, greater<pii>> q;
q.push({0, s});
while (!q.empty()) {
int v = q.top().second;
int d_v = q.top().first;
q.pop();
if (d_v != d[v])
continue;
for (auto edge : adj[v]) {
int to = edge.first;
int len = edge.second;
if (d[v] + len < d[to]) {
d[to] = d[v] + len;
p[to] = v;
q.push({d[to], to});
}
}
}
}
```
In practice the `priority_queue` version is a little bit faster than the version with `set`.
Interestingly, a [2007 technical report](https://www3.cs.stonybrook.edu/~rezaul/papers/TR-07-54.pdf) concluded the variant of the algorithm not using decrease-key operations ran faster than the decrease-key variant, with a greater performance gap for sparse graphs.
### Getting rid of pairs
You can improve the performance a little bit more if you don't store pairs in the containers, but only the vertex indices.
In this case we must overload the comparison operator:
it must compare two vertices using the distances stored in $d[]$.
As a result of the relaxation, the distance of some vertices will change.
However the data structure will not resort itself automatically.
In fact changing distances of vertices in the queue, might destroy the data structure.
As before, we need to remove the vertex before we relax it, and then insert it again afterwards.
Since we only can remove from `set`, this optimization is only applicable for the `set` method, and doesn't work with `priority_queue` implementation.
In practice this significantly increases the performance, especially when larger data types are used to store distances, like `long long` or `double`.
|
Dijkstra on sparse graphs
|
---
title
edmonds_karp
---
# Maximum flow - Ford-Fulkerson and Edmonds-Karp
The Edmonds-Karp algorithm is an implementation of the Ford-Fulkerson method for computing a maximal flow in a flow network.
## Flow network
First let's define what a **flow network**, a **flow**, and a **maximum flow** is.
A **network** is a directed graph $G$ with vertices $V$ and edges $E$ combined with a function $c$, which assigns each edge $e \in E$ a non-negative integer value, the **capacity** of $e$.
Such a network is called a **flow network**, if we additionally label two vertices, one as **source** and one as **sink**.
A **flow** in a flow network is function $f$, that again assigns each edge $e$ a non-negative integer value, namely the flow.
The function has to fulfill the following two conditions:
The flow of an edge cannot exceed the capacity.
$$f(e) \le c(e)$$
And the sum of the incoming flow of a vertex $u$ has to be equal to the sum of the outgoing flow of $u$ except in the source and sink vertices.
$$\sum_{(v, u) \in E} f((v, u)) = \sum_{(u, v) \in E} f((u, v))$$
The source vertex $s$ only has an outgoing flow, and the sink vertex $t$ has only incoming flow.
It is easy to see that the following equation holds:
$$\sum_{(s, u) \in E} f((s, u)) = \sum_{(u, t) \in E} f((u, t))$$
A good analogy for a flow network is the following visualization:
We represent edges as water pipes, the capacity of an edge is the maximal amount of water that can flow through the pipe per second, and the flow of an edge is the amount of water that currently flows through the pipe per second.
This motivates the first flow condition. There cannot flow more water through a pipe than its capacity.
The vertices act as junctions, where water comes out of some pipes, and then, these vertices distribute the water in some way to other pipes.
This also motivates the second flow condition.
All the incoming water has to be distributed to the other pipes in each junction.
It cannot magically disappear or appear.
The source $s$ is origin of all the water, and the water can only drain in the sink $t$.
The following image shows a flow network.
The first value of each edge represents the flow, which is initially 0, and the second value represents the capacity.
<center></center>
The value of the flow of a network is the sum of all the flows that get produced in the source $s$, or equivalently to the sum of all the flows that are consumed by the sink $t$.
A **maximal flow** is a flow with the maximal possible value.
Finding this maximal flow of a flow network is the problem that we want to solve.
In the visualization with water pipes, the problem can be formulated in the following way:
how much water can we push through the pipes from the source to the sink?
The following image shows the maximal flow in the flow network.
<center></center>
## Ford-Fulkerson method
Let's define one more thing.
A **residual capacity** of a directed edge is the capacity minus the flow.
It should be noted that if there is a flow along some directed edge $(u, v)$, then the reversed edge has capacity 0 and we can define the flow of it as $f((v, u)) = -f((u, v))$.
This also defines the residual capacity for all the reversed edges.
We can create a **residual network** from all these edges, which is just a network with the same vertices and edges, but we use the residual capacities as capacities.
The Ford-Fulkerson method works as follows.
First, we set the flow of each edge to zero.
Then we look for an **augmenting path** from $s$ to $t$.
An augmenting path is a simple path in the residual graph, i.e. along the edges whose residual capacity is positive.
If such a path is found, then we can increase the flow along these edges.
We keep on searching for augmenting paths and increasing the flow.
Once an augmenting path doesn't exist anymore, the flow is maximal.
Let us specify in more detail, what increasing the flow along an augmenting path means.
Let $C$ be the smallest residual capacity of the edges in the path.
Then we increase the flow in the following way:
we update $f((u, v)) ~\text{+=}~ C$ and $f((v, u)) ~\text{-=}~ C$ for every edge $(u, v)$ in the path.
Here is an example to demonstrate the method.
We use the same flow network as above.
Initially we start with a flow of 0.
<center></center>
We can find the path $s - A - B - t$ with the residual capacities 7, 5, and 8.
Their minimum is 5, therefore we can increase the flow along this path by 5.
This gives a flow of 5 for the network.
<center> </center>
Again we look for an augmenting path, this time we find $s - D - A - C - t$ with the residual capacities 4, 3, 3, and 5.
Therefore we can increase the flow by 3 and we get a flow of 8 for the network.
<center> </center>
This time we find the path $s - D - C - B - t$ with the residual capacities 1, 2, 3, and 3, and hence, we increase the flow by 1.
<center> </center>
This time we find the augmenting path $s - A - D - C - t$ with the residual capacities 2, 3, 1, and 2.
We can increase the flow by 1.
But this path is very interesting.
It includes the reversed edge $(A, D)$.
In the original flow network, we are not allowed to send any flow from $A$ to $D$.
But because we already have a flow of 3 from $D$ to $A$, this is possible.
The intuition of it is the following:
Instead of sending a flow of 3 from $D$ to $A$, we only send 2 and compensate this by sending an additional flow of 1 from $s$ to $A$, which allows us to send an additional flow of 1 along the path $D - C - t$.
<center> </center>
Now, it is impossible to find an augmenting path between $s$ and $t$, therefore this flow of $10$ is the maximal possible.
We have found the maximal flow.
It should be noted, that the Ford-Fulkerson method doesn't specify a method of finding the augmenting path.
Possible approaches are using [DFS](depth-first-search.md) or [BFS](breadth-first-search.md) which both work in $O(E)$.
If all the capacities of the network are integers, then for each augmenting path the flow of the network increases by at least 1 (for more details see [Integral flow theorem](#integral-theorem)).
Therefore, the complexity of Ford-Fulkerson is $O(E F)$, where $F$ is the maximal flow of the network.
In the case of rational capacities, the algorithm will also terminate, but the complexity is not bounded.
In the case of irrational capacities, the algorithm might never terminate, and might not even converge to the maximal flow.
## Edmonds-Karp algorithm
Edmonds-Karp algorithm is just an implementation of the Ford-Fulkerson method that uses [BFS](breadth-first-search.md) for finding augmenting paths.
The algorithm was first published by Yefim Dinitz in 1970, and later independently published by Jack Edmonds and Richard Karp in 1972.
The complexity can be given independently of the maximal flow.
The algorithm runs in $O(V E^2)$ time, even for irrational capacities.
The intuition is, that every time we find an augmenting path one of the edges becomes saturated, and the distance from the edge to $s$ will be longer if it appears later again in an augmenting path.
The length of the simple paths is bounded by $V$.
### Implementation
The matrix `capacity` stores the capacity for every pair of vertices.
`adj` is the adjacency list of the **undirected graph**, since we have also to use the reversed of directed edges when we are looking for augmenting paths.
The function `maxflow` will return the value of the maximal flow.
During the algorithm, the matrix `capacity` will actually store the residual capacity of the network.
The value of the flow in each edge will actually not be stored, but it is easy to extend the implementation - by using an additional matrix - to also store the flow and return it.
```{.cpp file=edmondskarp}
int n;
vector<vector<int>> capacity;
vector<vector<int>> adj;
int bfs(int s, int t, vector<int>& parent) {
fill(parent.begin(), parent.end(), -1);
parent[s] = -2;
queue<pair<int, int>> q;
q.push({s, INF});
while (!q.empty()) {
int cur = q.front().first;
int flow = q.front().second;
q.pop();
for (int next : adj[cur]) {
if (parent[next] == -1 && capacity[cur][next]) {
parent[next] = cur;
int new_flow = min(flow, capacity[cur][next]);
if (next == t)
return new_flow;
q.push({next, new_flow});
}
}
}
return 0;
}
int maxflow(int s, int t) {
int flow = 0;
vector<int> parent(n);
int new_flow;
while (new_flow = bfs(s, t, parent)) {
flow += new_flow;
int cur = t;
while (cur != s) {
int prev = parent[cur];
capacity[prev][cur] -= new_flow;
capacity[cur][prev] += new_flow;
cur = prev;
}
}
return flow;
}
```
## Integral flow theorem ## { #integral-theorem}
The theorem simply says, that if every capacity in the network is an integer, then the flow in each edge will be an integer in the maximal flow.
## Max-flow min-cut theorem
A **$s$-$t$-cut** is a partition of the vertices of a flow network into two sets, such that a set includes the source $s$ and the other one includes the sink $t$.
The capacity of a $s$-$t$-cut is defined as the sum of capacities of the edges from the source side to the sink side.
Obviously, we cannot send more flow from $s$ to $t$ than the capacity of any $s$-$t$-cut.
Therefore, the maximum flow is bounded by the minimum cut capacity.
The max-flow min-cut theorem goes even further.
It says that the capacity of the maximum flow has to be equal to the capacity of the minimum cut.
In the following image, you can see the minimum cut of the flow network we used earlier.
It shows that the capacity of the cut $\{s, A, D\}$ and $\{B, C, t\}$ is $5 + 3 + 2 = 10$, which is equal to the maximum flow that we found.
Other cuts will have a bigger capacity, like the capacity between $\{s, A\}$ and $\{B, C, D, t\}$ is $4 + 3 + 5 = 12$.
<center></center>
A minimum cut can be found after performing a maximum flow computation using the Ford-Fulkerson method.
One possible minimum cut is the following:
the set of all the vertices that can be reached from $s$ in the residual graph (using edges with positive residual capacity), and the set of all the other vertices.
This partition can be easily found using [DFS](depth-first-search.md) starting at $s$.
|
---
title
edmonds_karp
---
# Maximum flow - Ford-Fulkerson and Edmonds-Karp
The Edmonds-Karp algorithm is an implementation of the Ford-Fulkerson method for computing a maximal flow in a flow network.
## Flow network
First let's define what a **flow network**, a **flow**, and a **maximum flow** is.
A **network** is a directed graph $G$ with vertices $V$ and edges $E$ combined with a function $c$, which assigns each edge $e \in E$ a non-negative integer value, the **capacity** of $e$.
Such a network is called a **flow network**, if we additionally label two vertices, one as **source** and one as **sink**.
A **flow** in a flow network is function $f$, that again assigns each edge $e$ a non-negative integer value, namely the flow.
The function has to fulfill the following two conditions:
The flow of an edge cannot exceed the capacity.
$$f(e) \le c(e)$$
And the sum of the incoming flow of a vertex $u$ has to be equal to the sum of the outgoing flow of $u$ except in the source and sink vertices.
$$\sum_{(v, u) \in E} f((v, u)) = \sum_{(u, v) \in E} f((u, v))$$
The source vertex $s$ only has an outgoing flow, and the sink vertex $t$ has only incoming flow.
It is easy to see that the following equation holds:
$$\sum_{(s, u) \in E} f((s, u)) = \sum_{(u, t) \in E} f((u, t))$$
A good analogy for a flow network is the following visualization:
We represent edges as water pipes, the capacity of an edge is the maximal amount of water that can flow through the pipe per second, and the flow of an edge is the amount of water that currently flows through the pipe per second.
This motivates the first flow condition. There cannot flow more water through a pipe than its capacity.
The vertices act as junctions, where water comes out of some pipes, and then, these vertices distribute the water in some way to other pipes.
This also motivates the second flow condition.
All the incoming water has to be distributed to the other pipes in each junction.
It cannot magically disappear or appear.
The source $s$ is origin of all the water, and the water can only drain in the sink $t$.
The following image shows a flow network.
The first value of each edge represents the flow, which is initially 0, and the second value represents the capacity.
<center></center>
The value of the flow of a network is the sum of all the flows that get produced in the source $s$, or equivalently to the sum of all the flows that are consumed by the sink $t$.
A **maximal flow** is a flow with the maximal possible value.
Finding this maximal flow of a flow network is the problem that we want to solve.
In the visualization with water pipes, the problem can be formulated in the following way:
how much water can we push through the pipes from the source to the sink?
The following image shows the maximal flow in the flow network.
<center></center>
## Ford-Fulkerson method
Let's define one more thing.
A **residual capacity** of a directed edge is the capacity minus the flow.
It should be noted that if there is a flow along some directed edge $(u, v)$, then the reversed edge has capacity 0 and we can define the flow of it as $f((v, u)) = -f((u, v))$.
This also defines the residual capacity for all the reversed edges.
We can create a **residual network** from all these edges, which is just a network with the same vertices and edges, but we use the residual capacities as capacities.
The Ford-Fulkerson method works as follows.
First, we set the flow of each edge to zero.
Then we look for an **augmenting path** from $s$ to $t$.
An augmenting path is a simple path in the residual graph, i.e. along the edges whose residual capacity is positive.
If such a path is found, then we can increase the flow along these edges.
We keep on searching for augmenting paths and increasing the flow.
Once an augmenting path doesn't exist anymore, the flow is maximal.
Let us specify in more detail, what increasing the flow along an augmenting path means.
Let $C$ be the smallest residual capacity of the edges in the path.
Then we increase the flow in the following way:
we update $f((u, v)) ~\text{+=}~ C$ and $f((v, u)) ~\text{-=}~ C$ for every edge $(u, v)$ in the path.
Here is an example to demonstrate the method.
We use the same flow network as above.
Initially we start with a flow of 0.
<center></center>
We can find the path $s - A - B - t$ with the residual capacities 7, 5, and 8.
Their minimum is 5, therefore we can increase the flow along this path by 5.
This gives a flow of 5 for the network.
<center> </center>
Again we look for an augmenting path, this time we find $s - D - A - C - t$ with the residual capacities 4, 3, 3, and 5.
Therefore we can increase the flow by 3 and we get a flow of 8 for the network.
<center> </center>
This time we find the path $s - D - C - B - t$ with the residual capacities 1, 2, 3, and 3, and hence, we increase the flow by 1.
<center> </center>
This time we find the augmenting path $s - A - D - C - t$ with the residual capacities 2, 3, 1, and 2.
We can increase the flow by 1.
But this path is very interesting.
It includes the reversed edge $(A, D)$.
In the original flow network, we are not allowed to send any flow from $A$ to $D$.
But because we already have a flow of 3 from $D$ to $A$, this is possible.
The intuition of it is the following:
Instead of sending a flow of 3 from $D$ to $A$, we only send 2 and compensate this by sending an additional flow of 1 from $s$ to $A$, which allows us to send an additional flow of 1 along the path $D - C - t$.
<center> </center>
Now, it is impossible to find an augmenting path between $s$ and $t$, therefore this flow of $10$ is the maximal possible.
We have found the maximal flow.
It should be noted, that the Ford-Fulkerson method doesn't specify a method of finding the augmenting path.
Possible approaches are using [DFS](depth-first-search.md) or [BFS](breadth-first-search.md) which both work in $O(E)$.
If all the capacities of the network are integers, then for each augmenting path the flow of the network increases by at least 1 (for more details see [Integral flow theorem](#integral-theorem)).
Therefore, the complexity of Ford-Fulkerson is $O(E F)$, where $F$ is the maximal flow of the network.
In the case of rational capacities, the algorithm will also terminate, but the complexity is not bounded.
In the case of irrational capacities, the algorithm might never terminate, and might not even converge to the maximal flow.
## Edmonds-Karp algorithm
Edmonds-Karp algorithm is just an implementation of the Ford-Fulkerson method that uses [BFS](breadth-first-search.md) for finding augmenting paths.
The algorithm was first published by Yefim Dinitz in 1970, and later independently published by Jack Edmonds and Richard Karp in 1972.
The complexity can be given independently of the maximal flow.
The algorithm runs in $O(V E^2)$ time, even for irrational capacities.
The intuition is, that every time we find an augmenting path one of the edges becomes saturated, and the distance from the edge to $s$ will be longer if it appears later again in an augmenting path.
The length of the simple paths is bounded by $V$.
### Implementation
The matrix `capacity` stores the capacity for every pair of vertices.
`adj` is the adjacency list of the **undirected graph**, since we have also to use the reversed of directed edges when we are looking for augmenting paths.
The function `maxflow` will return the value of the maximal flow.
During the algorithm, the matrix `capacity` will actually store the residual capacity of the network.
The value of the flow in each edge will actually not be stored, but it is easy to extend the implementation - by using an additional matrix - to also store the flow and return it.
```{.cpp file=edmondskarp}
int n;
vector<vector<int>> capacity;
vector<vector<int>> adj;
int bfs(int s, int t, vector<int>& parent) {
fill(parent.begin(), parent.end(), -1);
parent[s] = -2;
queue<pair<int, int>> q;
q.push({s, INF});
while (!q.empty()) {
int cur = q.front().first;
int flow = q.front().second;
q.pop();
for (int next : adj[cur]) {
if (parent[next] == -1 && capacity[cur][next]) {
parent[next] = cur;
int new_flow = min(flow, capacity[cur][next]);
if (next == t)
return new_flow;
q.push({next, new_flow});
}
}
}
return 0;
}
int maxflow(int s, int t) {
int flow = 0;
vector<int> parent(n);
int new_flow;
while (new_flow = bfs(s, t, parent)) {
flow += new_flow;
int cur = t;
while (cur != s) {
int prev = parent[cur];
capacity[prev][cur] -= new_flow;
capacity[cur][prev] += new_flow;
cur = prev;
}
}
return flow;
}
```
## Integral flow theorem ## { #integral-theorem}
The theorem simply says, that if every capacity in the network is an integer, then the flow in each edge will be an integer in the maximal flow.
## Max-flow min-cut theorem
A **$s$-$t$-cut** is a partition of the vertices of a flow network into two sets, such that a set includes the source $s$ and the other one includes the sink $t$.
The capacity of a $s$-$t$-cut is defined as the sum of capacities of the edges from the source side to the sink side.
Obviously, we cannot send more flow from $s$ to $t$ than the capacity of any $s$-$t$-cut.
Therefore, the maximum flow is bounded by the minimum cut capacity.
The max-flow min-cut theorem goes even further.
It says that the capacity of the maximum flow has to be equal to the capacity of the minimum cut.
In the following image, you can see the minimum cut of the flow network we used earlier.
It shows that the capacity of the cut $\{s, A, D\}$ and $\{B, C, t\}$ is $5 + 3 + 2 = 10$, which is equal to the maximum flow that we found.
Other cuts will have a bigger capacity, like the capacity between $\{s, A\}$ and $\{B, C, D, t\}$ is $4 + 3 + 5 = 12$.
<center></center>
A minimum cut can be found after performing a maximum flow computation using the Ford-Fulkerson method.
One possible minimum cut is the following:
the set of all the vertices that can be reached from $s$ in the residual graph (using edges with positive residual capacity), and the set of all the other vertices.
This partition can be easily found using [DFS](depth-first-search.md) starting at $s$.
## Practice Problems
- [Codeforces - Array and Operations](https://codeforces.com/contest/498/problem/c)
- [Codeforces - Red-Blue Graph](https://codeforces.com/contest/1288/problem/f)
- [CSES - Download Speed](https://cses.fi/problemset/task/1694)
- [CSES - Police Chase](https://cses.fi/problemset/task/1695)
- [CSES - School Dance](https://cses.fi/problemset/task/1696)
|
Maximum flow - Ford-Fulkerson and Edmonds-Karp
|
---
title
bfs
---
# Breadth-first search
Breadth first search is one of the basic and essential searching algorithms on graphs.
As a result of how the algorithm works, the path found by breadth first search to any node is the shortest path to that node, i.e the path that contains the smallest number of edges in unweighted graphs.
The algorithm works in $O(n + m)$ time, where $n$ is number of vertices and $m$ is the number of edges.
## Description of the algorithm
The algorithm takes as input an unweighted graph and the id of the source vertex $s$. The input graph can be directed or undirected,
it does not matter to the algorithm.
The algorithm can be understood as a fire spreading on the graph: at the zeroth step only the source $s$ is on fire. At each step, the fire burning at each vertex spreads to all of its neighbors. In one iteration of the algorithm, the "ring of
fire" is expanded in width by one unit (hence the name of the algorithm).
More precisely, the algorithm can be stated as follows: Create a queue $q$ which will contain the vertices to be processed and a
Boolean array $used[]$ which indicates for each vertex, if it has been lit (or visited) or not.
Initially, push the source $s$ to the queue and set $used[s] = true$, and for all other vertices $v$ set $used[v] = false$.
Then, loop until the queue is empty and in each iteration, pop a vertex from the front of the queue. Iterate through all the edges going out
of this vertex and if some of these edges go to vertices that are not already lit, set them on fire and place them in the queue.
As a result, when the queue is empty, the "ring of fire" contains all vertices reachable from the source $s$, with each vertex reached in the shortest possible way.
You can also calculate the lengths of the shortest paths (which just requires maintaining an array of path lengths $d[]$) as well as save information to restore all of these shortest paths (for this, it is necessary to maintain an array of "parents" $p[]$, which stores for each vertex the vertex from which we reached it).
## Implementation
We write code for the described algorithm in C++ and Java.
=== "C++"
```cpp
vector<vector<int>> adj; // adjacency list representation
int n; // number of nodes
int s; // source vertex
queue<int> q;
vector<bool> used(n);
vector<int> d(n), p(n);
q.push(s);
used[s] = true;
p[s] = -1;
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : adj[v]) {
if (!used[u]) {
used[u] = true;
q.push(u);
d[u] = d[v] + 1;
p[u] = v;
}
}
}
```
=== "Java"
```java
ArrayList<ArrayList<Integer>> adj = new ArrayList<>(); // adjacency list representation
int n; // number of nodes
int s; // source vertex
LinkedList<Integer> q = new LinkedList<Integer>();
boolean used[] = new boolean[n];
int d[] = new int[n];
int p[] = new int[n];
q.push(s);
used[s] = true;
p[s] = -1;
while (!q.isEmpty()) {
int v = q.pop();
for (int u : adj.get(v)) {
if (!used[u]) {
used[u] = true;
q.push(u);
d[u] = d[v] + 1;
p[u] = v;
}
}
}
```
If we have to restore and display the shortest path from the source to some vertex $u$, it can be done in the following manner:
=== "C++"
```cpp
if (!used[u]) {
cout << "No path!";
} else {
vector<int> path;
for (int v = u; v != -1; v = p[v])
path.push_back(v);
reverse(path.begin(), path.end());
cout << "Path: ";
for (int v : path)
cout << v << " ";
}
```
=== "Java"
```java
if (!used[u]) {
System.out.println("No path!");
} else {
ArrayList<Integer> path = new ArrayList<Integer>();
for (int v = u; v != -1; v = p[v])
path.add(v);
Collections.reverse(path);
for(int v : path)
System.out.println(v);
}
```
## Applications of BFS
* Find the shortest path from a source to other vertices in an unweighted graph.
* Find all connected components in an undirected graph in $O(n + m)$ time:
To do this, we just run BFS starting from each vertex, except for vertices which have already been visited from previous runs.
Thus, we perform normal BFS from each of the vertices, but do not reset the array $used[]$ each and every time we get a new connected component, and the total running time will still be $O(n + m)$ (performing multiple BFS on the graph without zeroing the array $used []$ is called a series of breadth first searches).
* Finding a solution to a problem or a game with the least number of moves, if each state of the game can be represented by a vertex of the graph, and the transitions from one state to the other are the edges of the graph.
* Finding the shortest path in a graph with weights 0 or 1:
This requires just a little modification to normal breadth-first search: Instead of maintaining array $used[]$, we will now check if the distance to vertex is shorter than current found distance, then if the current edge is of zero weight, we add it to the front of the queue else we add it to the back of the queue.This modification is explained in more detail in the article [0-1 BFS](01_bfs.md).
* Finding the shortest cycle in a directed unweighted graph:
Start a breadth-first search from each vertex.
As soon as we try to go from the current vertex back to the source vertex, we have found the shortest cycle containing the source vertex.
At this point we can stop the BFS, and start a new BFS from the next vertex.
From all such cycles (at most one from each BFS) choose the shortest.
* Find all the edges that lie on any shortest path between a given pair of vertices $(a, b)$.
To do this, run two breadth first searches:
one from $a$ and one from $b$.
Let $d_a []$ be the array containing shortest distances obtained from the first BFS (from $a$) and $d_b []$ be the array containing shortest distances obtained from the second BFS from $b$.
Now for every edge $(u, v)$ it is easy to check whether that edge lies on any shortest path between $a$ and $b$:
the criterion is the condition $d_a [u] + 1 + d_b [v] = d_a [b]$.
* Find all the vertices on any shortest path between a given pair of vertices $(a, b)$.
To accomplish that, run two breadth first searches:
one from $a$ and one from $b$.
Let $d_a []$ be the array containing shortest distances obtained from the first BFS (from $a$) and $d_b []$ be the array containing shortest distances obtained from the second BFS (from $b$).
Now for each vertex it is easy to check whether it lies on any shortest path between $a$ and $b$:
the criterion is the condition $d_a [v] + d_b [v] = d_a [b]$.
* Find the shortest path of even length from a source vertex $s$ to a target vertex $t$ in an unweighted graph:
For this, we must construct an auxiliary graph, whose vertices are the state $(v, c)$, where $v$ - the current node, $c = 0$ or $c = 1$ - the current parity.
Any edge $(u, v)$ of the original graph in this new column will turn into two edges $((u, 0), (v, 1))$ and $((u, 1), (v, 0))$.
After that we run a BFS to find the shortest path from the starting vertex $(s, 0)$ to the end vertex $(t, 0)$.
|
---
title
bfs
---
# Breadth-first search
Breadth first search is one of the basic and essential searching algorithms on graphs.
As a result of how the algorithm works, the path found by breadth first search to any node is the shortest path to that node, i.e the path that contains the smallest number of edges in unweighted graphs.
The algorithm works in $O(n + m)$ time, where $n$ is number of vertices and $m$ is the number of edges.
## Description of the algorithm
The algorithm takes as input an unweighted graph and the id of the source vertex $s$. The input graph can be directed or undirected,
it does not matter to the algorithm.
The algorithm can be understood as a fire spreading on the graph: at the zeroth step only the source $s$ is on fire. At each step, the fire burning at each vertex spreads to all of its neighbors. In one iteration of the algorithm, the "ring of
fire" is expanded in width by one unit (hence the name of the algorithm).
More precisely, the algorithm can be stated as follows: Create a queue $q$ which will contain the vertices to be processed and a
Boolean array $used[]$ which indicates for each vertex, if it has been lit (or visited) or not.
Initially, push the source $s$ to the queue and set $used[s] = true$, and for all other vertices $v$ set $used[v] = false$.
Then, loop until the queue is empty and in each iteration, pop a vertex from the front of the queue. Iterate through all the edges going out
of this vertex and if some of these edges go to vertices that are not already lit, set them on fire and place them in the queue.
As a result, when the queue is empty, the "ring of fire" contains all vertices reachable from the source $s$, with each vertex reached in the shortest possible way.
You can also calculate the lengths of the shortest paths (which just requires maintaining an array of path lengths $d[]$) as well as save information to restore all of these shortest paths (for this, it is necessary to maintain an array of "parents" $p[]$, which stores for each vertex the vertex from which we reached it).
## Implementation
We write code for the described algorithm in C++ and Java.
=== "C++"
```cpp
vector<vector<int>> adj; // adjacency list representation
int n; // number of nodes
int s; // source vertex
queue<int> q;
vector<bool> used(n);
vector<int> d(n), p(n);
q.push(s);
used[s] = true;
p[s] = -1;
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : adj[v]) {
if (!used[u]) {
used[u] = true;
q.push(u);
d[u] = d[v] + 1;
p[u] = v;
}
}
}
```
=== "Java"
```java
ArrayList<ArrayList<Integer>> adj = new ArrayList<>(); // adjacency list representation
int n; // number of nodes
int s; // source vertex
LinkedList<Integer> q = new LinkedList<Integer>();
boolean used[] = new boolean[n];
int d[] = new int[n];
int p[] = new int[n];
q.push(s);
used[s] = true;
p[s] = -1;
while (!q.isEmpty()) {
int v = q.pop();
for (int u : adj.get(v)) {
if (!used[u]) {
used[u] = true;
q.push(u);
d[u] = d[v] + 1;
p[u] = v;
}
}
}
```
If we have to restore and display the shortest path from the source to some vertex $u$, it can be done in the following manner:
=== "C++"
```cpp
if (!used[u]) {
cout << "No path!";
} else {
vector<int> path;
for (int v = u; v != -1; v = p[v])
path.push_back(v);
reverse(path.begin(), path.end());
cout << "Path: ";
for (int v : path)
cout << v << " ";
}
```
=== "Java"
```java
if (!used[u]) {
System.out.println("No path!");
} else {
ArrayList<Integer> path = new ArrayList<Integer>();
for (int v = u; v != -1; v = p[v])
path.add(v);
Collections.reverse(path);
for(int v : path)
System.out.println(v);
}
```
## Applications of BFS
* Find the shortest path from a source to other vertices in an unweighted graph.
* Find all connected components in an undirected graph in $O(n + m)$ time:
To do this, we just run BFS starting from each vertex, except for vertices which have already been visited from previous runs.
Thus, we perform normal BFS from each of the vertices, but do not reset the array $used[]$ each and every time we get a new connected component, and the total running time will still be $O(n + m)$ (performing multiple BFS on the graph without zeroing the array $used []$ is called a series of breadth first searches).
* Finding a solution to a problem or a game with the least number of moves, if each state of the game can be represented by a vertex of the graph, and the transitions from one state to the other are the edges of the graph.
* Finding the shortest path in a graph with weights 0 or 1:
This requires just a little modification to normal breadth-first search: Instead of maintaining array $used[]$, we will now check if the distance to vertex is shorter than current found distance, then if the current edge is of zero weight, we add it to the front of the queue else we add it to the back of the queue.This modification is explained in more detail in the article [0-1 BFS](01_bfs.md).
* Finding the shortest cycle in a directed unweighted graph:
Start a breadth-first search from each vertex.
As soon as we try to go from the current vertex back to the source vertex, we have found the shortest cycle containing the source vertex.
At this point we can stop the BFS, and start a new BFS from the next vertex.
From all such cycles (at most one from each BFS) choose the shortest.
* Find all the edges that lie on any shortest path between a given pair of vertices $(a, b)$.
To do this, run two breadth first searches:
one from $a$ and one from $b$.
Let $d_a []$ be the array containing shortest distances obtained from the first BFS (from $a$) and $d_b []$ be the array containing shortest distances obtained from the second BFS from $b$.
Now for every edge $(u, v)$ it is easy to check whether that edge lies on any shortest path between $a$ and $b$:
the criterion is the condition $d_a [u] + 1 + d_b [v] = d_a [b]$.
* Find all the vertices on any shortest path between a given pair of vertices $(a, b)$.
To accomplish that, run two breadth first searches:
one from $a$ and one from $b$.
Let $d_a []$ be the array containing shortest distances obtained from the first BFS (from $a$) and $d_b []$ be the array containing shortest distances obtained from the second BFS (from $b$).
Now for each vertex it is easy to check whether it lies on any shortest path between $a$ and $b$:
the criterion is the condition $d_a [v] + d_b [v] = d_a [b]$.
* Find the shortest path of even length from a source vertex $s$ to a target vertex $t$ in an unweighted graph:
For this, we must construct an auxiliary graph, whose vertices are the state $(v, c)$, where $v$ - the current node, $c = 0$ or $c = 1$ - the current parity.
Any edge $(u, v)$ of the original graph in this new column will turn into two edges $((u, 0), (v, 1))$ and $((u, 1), (v, 0))$.
After that we run a BFS to find the shortest path from the starting vertex $(s, 0)$ to the end vertex $(t, 0)$.
## Practice Problems
* [SPOJ: AKBAR](http://spoj.com/problems/AKBAR)
* [SPOJ: NAKANJ](http://www.spoj.com/problems/NAKANJ/)
* [SPOJ: WATER](http://www.spoj.com/problems/WATER)
* [SPOJ: MICE AND MAZE](http://www.spoj.com/problems/MICEMAZE/)
* [Timus: Caravans](http://acm.timus.ru/problem.aspx?space=1&num=2034)
* [DevSkill - Holloween Party (archived)](http://web.archive.org/web/20200930162803/http://www.devskill.com/CodingProblems/ViewProblem/60)
* [DevSkill - Ohani And The Link Cut Tree (archived)](http://web.archive.org/web/20170216192002/http://devskill.com:80/CodingProblems/ViewProblem/150)
* [SPOJ - Spiky Mazes](http://www.spoj.com/problems/SPIKES/)
* [SPOJ - Four Chips (hard)](http://www.spoj.com/problems/ADV04F1/)
* [SPOJ - Inversion Sort](http://www.spoj.com/problems/INVESORT/)
* [Codeforces - Shortest Path](http://codeforces.com/contest/59/problem/E)
* [SPOJ - Yet Another Multiple Problem](http://www.spoj.com/problems/MULTII/)
* [UVA 11392 - Binary 3xType Multiple](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2387)
* [UVA 10968 - KuPellaKeS](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1909)
* [Codeforces - Police Stations](http://codeforces.com/contest/796/problem/D)
* [Codeforces - Okabe and City](http://codeforces.com/contest/821/problem/D)
* [SPOJ - Find the Treasure](http://www.spoj.com/problems/DIGOKEYS/)
* [Codeforces - Bear and Forgotten Tree 2](http://codeforces.com/contest/653/problem/E)
* [Codeforces - Cycle in Maze](http://codeforces.com/contest/769/problem/C)
* [UVA - 11312 - Flipping Frustration](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2287)
* [SPOJ - Ada and Cycle](http://www.spoj.com/problems/ADACYCLE/)
* [CSES - Labyrinth](https://cses.fi/problemset/task/1193)
* [CSES - Message Route](https://cses.fi/problemset/task/1667/)
* [CSES - Monsters](https://cses.fi/problemset/task/1194)
|
Breadth-first search
|
---
title: Lowest Common Ancestor - O(sqrt(N)) and O(log N) with O(N) preprocessing
title
lca
---
# Lowest Common Ancestor - $O(\sqrt{N})$ and $O(\log N)$ with $O(N)$ preprocessing
Given a tree $G$. Given queries of the form $(v_1, v_2)$, for each query you need to find the lowest common ancestor (or least common ancestor), i.e. a vertex $v$ that lies on the path from the root to $v_1$ and the path from the root to $v_2$, and the vertex should be the lowest. In other words, the desired vertex $v$ is the most bottom ancestor of $v_1$ and $v_2$. It is obvious that their lowest common ancestor lies on a shortest path from $v_1$ and $v_2$. Also, if $v_1$ is the ancestor of $v_2$, $v_1$ is their lowest common ancestor.
### The Idea of the Algorithm
Before answering the queries, we need to **preprocess** the tree.
We make a [DFS](depth-first-search.md) traversal starting at the root and we build a list $\text{euler}$ which stores the order of the vertices that we visit (a vertex is added to the list when we first visit it, and after the return of the DFS traversals to its children).
This is also called an Euler tour of the tree.
It is clear that the size of this list will be $O(N)$.
We also need to build an array $\text{first}[0..N-1]$ which stores for each vertex $i$ its first occurrence in $\text{euler}$.
That is, the first position in $\text{euler}$ such that $\text{euler}[\text{first}[i]] = i$.
Also by using the DFS we can find the height of each node (distance from root to it) and store it in the array $\text{height}[0..N-1]$.
So how can we answer queries using the Euler tour and the additional two arrays?
Suppose the query is a pair of $v_1$ and $v_2$.
Consider the vertices that we visit in the Euler tour between the first visit of $v_1$ and the first visit of $v_2$.
It is easy to see, that the $\text{LCA}(v_1, v_2)$ is the vertex with the lowest height on this path.
We already noticed, that the LCA has to be part of the shortest path between $v_1$ and $v_2$.
Clearly it also has to be the vertex with the smallest height.
And in the Euler tour we essentially use the shortest path, except that we additionally visit all subtrees that we find on the path.
But all vertices in these subtrees are lower in the tree than the LCA and therefore have a larger height.
So the $\text{LCA}(v_1, v_2)$ can be uniquely determined by finding the vertex with the smallest height in the Euler tour between $\text{first}(v_1)$ and $\text{first}(v_2)$.
Let's illustrate this idea.
Consider the following graph and the Euler tour with the corresponding heights:
<center></center>
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\text{Vertices:} & 1 & 2 & 5 & 2 & 6 & 2 & 1 & 3 & 1 & 4 & 7 & 4 & 1 \\ \hline
\text{Heights:} & 1 & 2 & 3 & 2 & 3 & 2 & 1 & 2 & 1 & 2 & 3 & 2 & 1 \\ \hline
\end{array}$$
The tour starting at vertex $6$ and ending at $4$ we visit the vertices $[6, 2, 1, 3, 1, 4]$.
Among those vertices the vertex $1$ has the lowest height, therefore $\text{LCA(6, 4) = 1}$.
To recap:
to answer a query we just need **to find the vertex with smallest height** in the array $\text{euler}$ in the range from $\text{first}[v_1]$ to $\text{first}[v_2]$.
Thus, **the LCA problem is reduced to the RMQ problem** (finding the minimum in an range problem).
Using [Sqrt-Decomposition](../data_structures/sqrt_decomposition.md), it is possible to obtain a solution answering each query in $O(\sqrt{N})$ with preprocessing in $O(N)$ time.
Using a [Segment Tree](../data_structures/segment_tree.md) you can answer each query in $O(\log N)$ with preprocessing in $O(N)$ time.
Since there will almost never be any update to the stored values, a [Sparse Table](../data_structures/sparse-table.md) might be a better choice, allowing $O(1)$ query answering with $O(N\log N)$ build time.
### Implementation
In the following implementation of the LCA algorithm a Segment Tree is used.
```{.cpp file=lca}
struct LCA {
vector<int> height, euler, first, segtree;
vector<bool> visited;
int n;
LCA(vector<vector<int>> &adj, int root = 0) {
n = adj.size();
height.resize(n);
first.resize(n);
euler.reserve(n * 2);
visited.assign(n, false);
dfs(adj, root);
int m = euler.size();
segtree.resize(m * 4);
build(1, 0, m - 1);
}
void dfs(vector<vector<int>> &adj, int node, int h = 0) {
visited[node] = true;
height[node] = h;
first[node] = euler.size();
euler.push_back(node);
for (auto to : adj[node]) {
if (!visited[to]) {
dfs(adj, to, h + 1);
euler.push_back(node);
}
}
}
void build(int node, int b, int e) {
if (b == e) {
segtree[node] = euler[b];
} else {
int mid = (b + e) / 2;
build(node << 1, b, mid);
build(node << 1 | 1, mid + 1, e);
int l = segtree[node << 1], r = segtree[node << 1 | 1];
segtree[node] = (height[l] < height[r]) ? l : r;
}
}
int query(int node, int b, int e, int L, int R) {
if (b > R || e < L)
return -1;
if (b >= L && e <= R)
return segtree[node];
int mid = (b + e) >> 1;
int left = query(node << 1, b, mid, L, R);
int right = query(node << 1 | 1, mid + 1, e, L, R);
if (left == -1) return right;
if (right == -1) return left;
return height[left] < height[right] ? left : right;
}
int lca(int u, int v) {
int left = first[u], right = first[v];
if (left > right)
swap(left, right);
return query(1, 0, euler.size() - 1, left, right);
}
};
```
|
---
title: Lowest Common Ancestor - O(sqrt(N)) and O(log N) with O(N) preprocessing
title
lca
---
# Lowest Common Ancestor - $O(\sqrt{N})$ and $O(\log N)$ with $O(N)$ preprocessing
Given a tree $G$. Given queries of the form $(v_1, v_2)$, for each query you need to find the lowest common ancestor (or least common ancestor), i.e. a vertex $v$ that lies on the path from the root to $v_1$ and the path from the root to $v_2$, and the vertex should be the lowest. In other words, the desired vertex $v$ is the most bottom ancestor of $v_1$ and $v_2$. It is obvious that their lowest common ancestor lies on a shortest path from $v_1$ and $v_2$. Also, if $v_1$ is the ancestor of $v_2$, $v_1$ is their lowest common ancestor.
### The Idea of the Algorithm
Before answering the queries, we need to **preprocess** the tree.
We make a [DFS](depth-first-search.md) traversal starting at the root and we build a list $\text{euler}$ which stores the order of the vertices that we visit (a vertex is added to the list when we first visit it, and after the return of the DFS traversals to its children).
This is also called an Euler tour of the tree.
It is clear that the size of this list will be $O(N)$.
We also need to build an array $\text{first}[0..N-1]$ which stores for each vertex $i$ its first occurrence in $\text{euler}$.
That is, the first position in $\text{euler}$ such that $\text{euler}[\text{first}[i]] = i$.
Also by using the DFS we can find the height of each node (distance from root to it) and store it in the array $\text{height}[0..N-1]$.
So how can we answer queries using the Euler tour and the additional two arrays?
Suppose the query is a pair of $v_1$ and $v_2$.
Consider the vertices that we visit in the Euler tour between the first visit of $v_1$ and the first visit of $v_2$.
It is easy to see, that the $\text{LCA}(v_1, v_2)$ is the vertex with the lowest height on this path.
We already noticed, that the LCA has to be part of the shortest path between $v_1$ and $v_2$.
Clearly it also has to be the vertex with the smallest height.
And in the Euler tour we essentially use the shortest path, except that we additionally visit all subtrees that we find on the path.
But all vertices in these subtrees are lower in the tree than the LCA and therefore have a larger height.
So the $\text{LCA}(v_1, v_2)$ can be uniquely determined by finding the vertex with the smallest height in the Euler tour between $\text{first}(v_1)$ and $\text{first}(v_2)$.
Let's illustrate this idea.
Consider the following graph and the Euler tour with the corresponding heights:
<center></center>
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\text{Vertices:} & 1 & 2 & 5 & 2 & 6 & 2 & 1 & 3 & 1 & 4 & 7 & 4 & 1 \\ \hline
\text{Heights:} & 1 & 2 & 3 & 2 & 3 & 2 & 1 & 2 & 1 & 2 & 3 & 2 & 1 \\ \hline
\end{array}$$
The tour starting at vertex $6$ and ending at $4$ we visit the vertices $[6, 2, 1, 3, 1, 4]$.
Among those vertices the vertex $1$ has the lowest height, therefore $\text{LCA(6, 4) = 1}$.
To recap:
to answer a query we just need **to find the vertex with smallest height** in the array $\text{euler}$ in the range from $\text{first}[v_1]$ to $\text{first}[v_2]$.
Thus, **the LCA problem is reduced to the RMQ problem** (finding the minimum in an range problem).
Using [Sqrt-Decomposition](../data_structures/sqrt_decomposition.md), it is possible to obtain a solution answering each query in $O(\sqrt{N})$ with preprocessing in $O(N)$ time.
Using a [Segment Tree](../data_structures/segment_tree.md) you can answer each query in $O(\log N)$ with preprocessing in $O(N)$ time.
Since there will almost never be any update to the stored values, a [Sparse Table](../data_structures/sparse-table.md) might be a better choice, allowing $O(1)$ query answering with $O(N\log N)$ build time.
### Implementation
In the following implementation of the LCA algorithm a Segment Tree is used.
```{.cpp file=lca}
struct LCA {
vector<int> height, euler, first, segtree;
vector<bool> visited;
int n;
LCA(vector<vector<int>> &adj, int root = 0) {
n = adj.size();
height.resize(n);
first.resize(n);
euler.reserve(n * 2);
visited.assign(n, false);
dfs(adj, root);
int m = euler.size();
segtree.resize(m * 4);
build(1, 0, m - 1);
}
void dfs(vector<vector<int>> &adj, int node, int h = 0) {
visited[node] = true;
height[node] = h;
first[node] = euler.size();
euler.push_back(node);
for (auto to : adj[node]) {
if (!visited[to]) {
dfs(adj, to, h + 1);
euler.push_back(node);
}
}
}
void build(int node, int b, int e) {
if (b == e) {
segtree[node] = euler[b];
} else {
int mid = (b + e) / 2;
build(node << 1, b, mid);
build(node << 1 | 1, mid + 1, e);
int l = segtree[node << 1], r = segtree[node << 1 | 1];
segtree[node] = (height[l] < height[r]) ? l : r;
}
}
int query(int node, int b, int e, int L, int R) {
if (b > R || e < L)
return -1;
if (b >= L && e <= R)
return segtree[node];
int mid = (b + e) >> 1;
int left = query(node << 1, b, mid, L, R);
int right = query(node << 1 | 1, mid + 1, e, L, R);
if (left == -1) return right;
if (right == -1) return left;
return height[left] < height[right] ? left : right;
}
int lca(int u, int v) {
int left = first[u], right = first[v];
if (left > right)
swap(left, right);
return query(1, 0, euler.size() - 1, left, right);
}
};
```
## Practice Problems
- [SPOJ: LCA](http://www.spoj.com/problems/LCA/)
- [SPOJ: DISQUERY](http://www.spoj.com/problems/DISQUERY/)
- [TIMUS: 1471. Distance in the Tree](http://acm.timus.ru/problem.aspx?space=1&num=1471)
- [CODEFORCES: Design Tutorial: Inverse the Problem](http://codeforces.com/problemset/problem/472/D)
- [CODECHEF: Lowest Common Ancestor](https://www.codechef.com/problems/TALCA)
* [SPOJ - Lowest Common Ancestor](http://www.spoj.com/problems/LCASQ/)
* [SPOJ - Ada and Orange Tree](http://www.spoj.com/problems/ADAORANG/)
* [DevSkill - Motoku (archived)](http://web.archive.org/web/20200922005503/https://devskill.com/CodingProblems/ViewProblem/141)
* [UVA 12655 - Trucks](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=4384)
* [Codechef - Pishty and Tree](https://www.codechef.com/problems/PSHTTR)
* [UVA - 12533 - Joining Couples](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=441&page=show_problem&problem=3978)
* [Codechef - So close yet So Far](https://www.codechef.com/problems/CLOSEFAR)
* [Codeforces - Drivers Dissatisfaction](http://codeforces.com/contest/733/problem/F)
* [UVA 11354 - Bond](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2339)
* [SPOJ - Querry on a tree II](http://www.spoj.com/problems/QTREE2/)
* [Codeforces - Best Edge Weight](http://codeforces.com/contest/828/problem/F)
* [Codeforces - Misha, Grisha and Underground](http://codeforces.com/contest/832/problem/D)
* [SPOJ - Nlogonian Tickets](http://www.spoj.com/problems/NTICKETS/)
* [Codeforces - Rowena Rawenclaws Diadem](http://codeforces.com/contest/855/problem/D)
|
Lowest Common Ancestor - $O(\sqrt{N})$ and $O(\log N)$ with $O(N)$ preprocessing
|
---
title: Finding articulation points in a graph in O(N+M)
title
cutpoints
---
# Finding articulation points in a graph in $O(N+M)$
We are given an undirected graph. An articulation point (or cut vertex) is defined as a vertex which, when removed along with associated edges, makes the graph disconnected (or more precisely, increases the number of connected components in the graph). The task is to find all articulation points in the given graph.
The algorithm described here is based on [depth first search](depth-first-search.md) and has $O(N+M)$ complexity, where $N$ is the number of vertices and $M$ is the number of edges in the graph.
## Algorithm
Pick an arbitrary vertex of the graph $root$ and run [depth first search](depth-first-search.md) from it. Note the following fact (which is easy to prove):
- Let's say we are in the DFS, looking through the edges starting from vertex $v\ne root$.
If the current edge $(v, to)$ is such that none of the vertices $to$ or its descendants in the DFS traversal tree has a back-edge to any of ancestors of $v$, then $v$ is an articulation point. Otherwise, $v$ is not an articulation point.
- Let's consider the remaining case of $v=root$.
This vertex will be the point of articulation if and only if this vertex has more than one child in the DFS tree.
Now we have to learn to check this fact for each vertex efficiently. We'll use "time of entry into node" computed by the depth first search.
So, let $tin[v]$ denote entry time for node $v$. We introduce an array $low[v]$ which will let us check the fact for each vertex $v$. $low[v]$ is the minimum of $tin[v]$, the entry times $tin[p]$ for each node $p$ that is connected to node $v$ via a back-edge $(v, p)$ and the values of $low[to]$ for each vertex $to$ which is a direct descendant of $v$ in the DFS tree:
$$low[v] = \min \begin{cases} tin[v] \\ tin[p] &\text{ for all }p\text{ for which }(v, p)\text{ is a back edge} \\ low[to]& \text{ for all }to\text{ for which }(v, to)\text{ is a tree edge} \end{cases}$$
Now, there is a back edge from vertex $v$ or one of its descendants to one of its ancestors if and only if vertex $v$ has a child $to$ for which $low[to] < tin[v]$. If $low[to] = tin[v]$, the back edge comes directly to $v$, otherwise it comes to one of the ancestors of $v$.
Thus, the vertex $v$ in the DFS tree is an articulation point if and only if $low[to] \geq tin[v]$.
## Implementation
The implementation needs to distinguish three cases: when we go down the edge in DFS tree, when we find a back edge to an ancestor of the vertex and when we return to a parent of the vertex. These are the cases:
- $visited[to] = false$ - the edge is part of DFS tree;
- $visited[to] = true$ && $to \neq parent$ - the edge is back edge to one of the ancestors;
- $to = parent$ - the edge leads back to parent in DFS tree.
To implement this, we need a depth first search function which accepts the parent vertex of the current node.
```cpp
int n; // number of nodes
vector<vector<int>> adj; // adjacency list of graph
vector<bool> visited;
vector<int> tin, low;
int timer;
void dfs(int v, int p = -1) {
visited[v] = true;
tin[v] = low[v] = timer++;
int children=0;
for (int to : adj[v]) {
if (to == p) continue;
if (visited[to]) {
low[v] = min(low[v], tin[to]);
} else {
dfs(to, v);
low[v] = min(low[v], low[to]);
if (low[to] >= tin[v] && p!=-1)
IS_CUTPOINT(v);
++children;
}
}
if(p == -1 && children > 1)
IS_CUTPOINT(v);
}
void find_cutpoints() {
timer = 0;
visited.assign(n, false);
tin.assign(n, -1);
low.assign(n, -1);
for (int i = 0; i < n; ++i) {
if (!visited[i])
dfs (i);
}
}
```
Main function is `find_cutpoints`; it performs necessary initialization and starts depth first search in each connected component of the graph.
Function `IS_CUTPOINT(a)` is some function that will process the fact that vertex $a$ is an articulation point, for example, print it (Caution that this can be called multiple times for a vertex).
|
---
title: Finding articulation points in a graph in O(N+M)
title
cutpoints
---
# Finding articulation points in a graph in $O(N+M)$
We are given an undirected graph. An articulation point (or cut vertex) is defined as a vertex which, when removed along with associated edges, makes the graph disconnected (or more precisely, increases the number of connected components in the graph). The task is to find all articulation points in the given graph.
The algorithm described here is based on [depth first search](depth-first-search.md) and has $O(N+M)$ complexity, where $N$ is the number of vertices and $M$ is the number of edges in the graph.
## Algorithm
Pick an arbitrary vertex of the graph $root$ and run [depth first search](depth-first-search.md) from it. Note the following fact (which is easy to prove):
- Let's say we are in the DFS, looking through the edges starting from vertex $v\ne root$.
If the current edge $(v, to)$ is such that none of the vertices $to$ or its descendants in the DFS traversal tree has a back-edge to any of ancestors of $v$, then $v$ is an articulation point. Otherwise, $v$ is not an articulation point.
- Let's consider the remaining case of $v=root$.
This vertex will be the point of articulation if and only if this vertex has more than one child in the DFS tree.
Now we have to learn to check this fact for each vertex efficiently. We'll use "time of entry into node" computed by the depth first search.
So, let $tin[v]$ denote entry time for node $v$. We introduce an array $low[v]$ which will let us check the fact for each vertex $v$. $low[v]$ is the minimum of $tin[v]$, the entry times $tin[p]$ for each node $p$ that is connected to node $v$ via a back-edge $(v, p)$ and the values of $low[to]$ for each vertex $to$ which is a direct descendant of $v$ in the DFS tree:
$$low[v] = \min \begin{cases} tin[v] \\ tin[p] &\text{ for all }p\text{ for which }(v, p)\text{ is a back edge} \\ low[to]& \text{ for all }to\text{ for which }(v, to)\text{ is a tree edge} \end{cases}$$
Now, there is a back edge from vertex $v$ or one of its descendants to one of its ancestors if and only if vertex $v$ has a child $to$ for which $low[to] < tin[v]$. If $low[to] = tin[v]$, the back edge comes directly to $v$, otherwise it comes to one of the ancestors of $v$.
Thus, the vertex $v$ in the DFS tree is an articulation point if and only if $low[to] \geq tin[v]$.
## Implementation
The implementation needs to distinguish three cases: when we go down the edge in DFS tree, when we find a back edge to an ancestor of the vertex and when we return to a parent of the vertex. These are the cases:
- $visited[to] = false$ - the edge is part of DFS tree;
- $visited[to] = true$ && $to \neq parent$ - the edge is back edge to one of the ancestors;
- $to = parent$ - the edge leads back to parent in DFS tree.
To implement this, we need a depth first search function which accepts the parent vertex of the current node.
```cpp
int n; // number of nodes
vector<vector<int>> adj; // adjacency list of graph
vector<bool> visited;
vector<int> tin, low;
int timer;
void dfs(int v, int p = -1) {
visited[v] = true;
tin[v] = low[v] = timer++;
int children=0;
for (int to : adj[v]) {
if (to == p) continue;
if (visited[to]) {
low[v] = min(low[v], tin[to]);
} else {
dfs(to, v);
low[v] = min(low[v], low[to]);
if (low[to] >= tin[v] && p!=-1)
IS_CUTPOINT(v);
++children;
}
}
if(p == -1 && children > 1)
IS_CUTPOINT(v);
}
void find_cutpoints() {
timer = 0;
visited.assign(n, false);
tin.assign(n, -1);
low.assign(n, -1);
for (int i = 0; i < n; ++i) {
if (!visited[i])
dfs (i);
}
}
```
Main function is `find_cutpoints`; it performs necessary initialization and starts depth first search in each connected component of the graph.
Function `IS_CUTPOINT(a)` is some function that will process the fact that vertex $a$ is an articulation point, for example, print it (Caution that this can be called multiple times for a vertex).
## Practice Problems
- [UVA #10199 "Tourist Guide"](http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=13&page=show_problem&problem=1140) [difficulty: low]
- [UVA #315 "Network"](http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=5&page=show_problem&problem=251) [difficulty: low]
- [SPOJ - Submerging Islands](http://www.spoj.com/problems/SUBMERGE/)
- [Codeforces - Cutting Figure](https://codeforces.com/problemset/problem/193/A)
|
Finding articulation points in a graph in $O(N+M)$
|
---
title
preflow_push_faster
---
# Maximum flow - Push-relabel method improved
We will modify the [push-relabel method](push-relabel.md) to achieve a better runtime.
## Description
The modification is extremely simple:
In the previous article we chosen a vertex with excess without any particular rule.
But it turns out, that if we always choose the vertices with the **greatest height**, and apply push and relabel operations on them, then the complexity will become better.
Moreover, to select the vertices with the greatest height we actually don't need any data structures, we simply store the vertices with the greatest height in a list, and recalculate the list once all of them are processed (then vertices with already lower height will be added to the list), or whenever a new vertex with excess and a greater height appears (after relabeling a vertex).
Despite the simplicity, this modification reduces the complexity by a lot.
To be precise, the complexity of the resulting algorithm is $O(V E + V^2 \sqrt{E})$, which in the worst case is $O(V^3)$.
This modification was proposed by Cheriyan and Maheshwari in 1989.
## Implementation
```{.cpp file=push_relabel_faster}
const int inf = 1000000000;
int n;
vector<vector<int>> capacity, flow;
vector<int> height, excess;
void push(int u, int v)
{
int d = min(excess[u], capacity[u][v] - flow[u][v]);
flow[u][v] += d;
flow[v][u] -= d;
excess[u] -= d;
excess[v] += d;
}
void relabel(int u)
{
int d = inf;
for (int i = 0; i < n; i++) {
if (capacity[u][i] - flow[u][i] > 0)
d = min(d, height[i]);
}
if (d < inf)
height[u] = d + 1;
}
vector<int> find_max_height_vertices(int s, int t) {
vector<int> max_height;
for (int i = 0; i < n; i++) {
if (i != s && i != t && excess[i] > 0) {
if (!max_height.empty() && height[i] > height[max_height[0]])
max_height.clear();
if (max_height.empty() || height[i] == height[max_height[0]])
max_height.push_back(i);
}
}
return max_height;
}
int max_flow(int s, int t)
{
height.assign(n, 0);
height[s] = n;
flow.assign(n, vector<int>(n, 0));
excess.assign(n, 0);
excess[s] = inf;
for (int i = 0; i < n; i++) {
if (i != s)
push(s, i);
}
vector<int> current;
while (!(current = find_max_height_vertices(s, t)).empty()) {
for (int i : current) {
bool pushed = false;
for (int j = 0; j < n && excess[i]; j++) {
if (capacity[i][j] - flow[i][j] > 0 && height[i] == height[j] + 1) {
push(i, j);
pushed = true;
}
}
if (!pushed) {
relabel(i);
break;
}
}
}
int max_flow = 0;
for (int i = 0; i < n; i++)
max_flow += flow[i][t];
return max_flow;
}
```
|
---
title
preflow_push_faster
---
# Maximum flow - Push-relabel method improved
We will modify the [push-relabel method](push-relabel.md) to achieve a better runtime.
## Description
The modification is extremely simple:
In the previous article we chosen a vertex with excess without any particular rule.
But it turns out, that if we always choose the vertices with the **greatest height**, and apply push and relabel operations on them, then the complexity will become better.
Moreover, to select the vertices with the greatest height we actually don't need any data structures, we simply store the vertices with the greatest height in a list, and recalculate the list once all of them are processed (then vertices with already lower height will be added to the list), or whenever a new vertex with excess and a greater height appears (after relabeling a vertex).
Despite the simplicity, this modification reduces the complexity by a lot.
To be precise, the complexity of the resulting algorithm is $O(V E + V^2 \sqrt{E})$, which in the worst case is $O(V^3)$.
This modification was proposed by Cheriyan and Maheshwari in 1989.
## Implementation
```{.cpp file=push_relabel_faster}
const int inf = 1000000000;
int n;
vector<vector<int>> capacity, flow;
vector<int> height, excess;
void push(int u, int v)
{
int d = min(excess[u], capacity[u][v] - flow[u][v]);
flow[u][v] += d;
flow[v][u] -= d;
excess[u] -= d;
excess[v] += d;
}
void relabel(int u)
{
int d = inf;
for (int i = 0; i < n; i++) {
if (capacity[u][i] - flow[u][i] > 0)
d = min(d, height[i]);
}
if (d < inf)
height[u] = d + 1;
}
vector<int> find_max_height_vertices(int s, int t) {
vector<int> max_height;
for (int i = 0; i < n; i++) {
if (i != s && i != t && excess[i] > 0) {
if (!max_height.empty() && height[i] > height[max_height[0]])
max_height.clear();
if (max_height.empty() || height[i] == height[max_height[0]])
max_height.push_back(i);
}
}
return max_height;
}
int max_flow(int s, int t)
{
height.assign(n, 0);
height[s] = n;
flow.assign(n, vector<int>(n, 0));
excess.assign(n, 0);
excess[s] = inf;
for (int i = 0; i < n; i++) {
if (i != s)
push(s, i);
}
vector<int> current;
while (!(current = find_max_height_vertices(s, t)).empty()) {
for (int i : current) {
bool pushed = false;
for (int j = 0; j < n && excess[i]; j++) {
if (capacity[i][j] - flow[i][j] > 0 && height[i] == height[j] + 1) {
push(i, j);
pushed = true;
}
}
if (!pushed) {
relabel(i);
break;
}
}
}
int max_flow = 0;
for (int i = 0; i < n; i++)
max_flow += flow[i][t];
return max_flow;
}
```
|
Maximum flow - Push-relabel method improved
|
---
title
ford_bellman
---
# Bellman-Ford Algorithm
**Single source shortest path with negative weight edges**
Suppose that we are given a weighted directed graph $G$ with $n$ vertices and $m$ edges, and some specified vertex $v$. You want to find the length of shortest paths from vertex $v$ to every other vertex.
Unlike the Dijkstra algorithm, this algorithm can also be applied to graphs containing negative weight edges . However, if the graph contains a negative cycle, then, clearly, the shortest path to some vertices may not exist (due to the fact that the weight of the shortest path must be equal to minus infinity); however, this algorithm can be modified to signal the presence of a cycle of negative weight, or even deduce this cycle.
The algorithm bears the name of two American scientists: Richard Bellman and Lester Ford. Ford actually invented this algorithm in 1956 during the study of another mathematical problem, which eventually reduced to a subproblem of finding the shortest paths in the graph, and Ford gave an outline of the algorithm to solve this problem. Bellman in 1958 published an article devoted specifically to the problem of finding the shortest path, and in this article he clearly formulated the algorithm in the form in which it is known to us now.
## Description of the algorithm
Let us assume that the graph contains no negative weight cycle. The case of presence of a negative weight cycle will be discussed below in a separate section.
We will create an array of distances $d[0 \ldots n-1]$, which after execution of the algorithm will contain the answer to the problem. In the beginning we fill it as follows: $d[v] = 0$, and all other elements $d[ ]$ equal to infinity $\infty$.
The algorithm consists of several phases. Each phase scans through all edges of the graph, and the algorithm tries to produce **relaxation** along each edge $(a,b)$ having weight $c$. Relaxation along the edges is an attempt to improve the value $d[b]$ using value $d[a] + c$. In fact, it means that we are trying to improve the answer for this vertex using edge $(a,b)$ and current response for vertex $a$.
It is claimed that $n-1$ phases of the algorithm are sufficient to correctly calculate the lengths of all shortest paths in the graph (again, we believe that the cycles of negative weight do not exist). For unreachable vertices the distance $d[ ]$ will remain equal to infinity $\infty$.
## Implementation
Unlike many other graph algorithms, for Bellman-Ford algorithm, it is more convenient to represent the graph using a single list of all edges (instead of $n$ lists of edges - edges from each vertex). We start the implementation with a structure $\rm edge$ for representing the edges. The input to the algorithm are numbers $n$, $m$, list $e$ of edges and the starting vertex $v$. All the vertices are numbered $0$ to $n - 1$.
### The simplest implementation
The constant $\rm INF$ denotes the number "infinity" — it should be selected in such a way that it is greater than all possible path lengths.
```cpp
struct Edge {
int a, b, cost;
};
int n, m, v;
vector<Edge> edges;
const int INF = 1000000000;
void solve()
{
vector<int> d(n, INF);
d[v] = 0;
for (int i = 0; i < n - 1; ++i)
for (Edge e : edges)
if (d[e.a] < INF)
d[e.b] = min(d[e.b], d[e.a] + e.cost);
// display d, for example, on the screen
}
```
The check `if (d[e.a] < INF)` is needed only if the graph contains negative weight edges: no such verification would result in relaxation from the vertices to which paths have not yet found, and incorrect distance, of the type $\infty - 1$, $\infty - 2$ etc. would appear.
### A better implementation
This algorithm can be somewhat speeded up: often we already get the answer in a few phases and no useful work is done in remaining phases, just a waste visiting all edges. So, let's keep the flag, to tell whether something changed in the current phase or not, and if any phase, nothing changed, the algorithm can be stopped. (This optimization does not improve the asymptotic behavior, i.e., some graphs will still need all $n-1$ phases, but significantly accelerates the behavior of the algorithm "on an average", i.e., on random graphs.)
With this optimization, it is generally unnecessary to restrict manually the number of phases of the algorithm to $n-1$ — the algorithm will stop after the desired number of phases.
```cpp
void solve()
{
vector<int> d(n, INF);
d[v] = 0;
for (;;) {
bool any = false;
for (Edge e : edges)
if (d[e.a] < INF)
if (d[e.b] > d[e.a] + e.cost) {
d[e.b] = d[e.a] + e.cost;
any = true;
}
if (!any)
break;
}
// display d, for example, on the screen
}
```
### Retrieving Path
Let us now consider how to modify the algorithm so that it not only finds the length of shortest paths, but also allows to reconstruct the shortest paths.
For that, let's create another array $p[0 \ldots n-1]$, where for each vertex we store its "predecessor", i.e. the penultimate vertex in the shortest path leading to it. In fact, the shortest path to any vertex $a$ is a shortest path to some vertex $p[a]$, to which we added $a$ at the end of the path.
Note that the algorithm works on the same logic: it assumes that the shortest distance to one vertex is already calculated, and, tries to improve the shortest distance to other vertices from that vertex. Therefore, at the time of improvement we just need to remember $p[ ]$, i.e, the vertex from which this improvement has occurred.
Following is an implementation of the Bellman-Ford with the retrieval of shortest path to a given node $t$:
```cpp
void solve()
{
vector<int> d(n, INF);
d[v] = 0;
vector<int> p(n, -1);
for (;;) {
bool any = false;
for (Edge e : edges)
if (d[e.a] < INF)
if (d[e.b] > d[e.a] + e.cost) {
d[e.b] = d[e.a] + e.cost;
p[e.b] = e.a;
any = true;
}
if (!any)
break;
}
if (d[t] == INF)
cout << "No path from " << v << " to " << t << ".";
else {
vector<int> path;
for (int cur = t; cur != -1; cur = p[cur])
path.push_back(cur);
reverse(path.begin(), path.end());
cout << "Path from " << v << " to " << t << ": ";
for (int u : path)
cout << u << ' ';
}
}
```
Here starting from the vertex $t$, we go through the predecessors till we reach starting vertex with no predecessor, and store all the vertices in the path in the list $\rm path$. This list is a shortest path from $v$ to $t$, but in reverse order, so we call $\rm reverse()$ function over $\rm path$ and then output the path.
## The proof of the algorithm
First, note that for all unreachable vertices $u$ the algorithm will work correctly, the label $d[u]$ will remain equal to infinity (because the algorithm Bellman-Ford will find some way to all reachable vertices from the start vertex $v$, and relaxation for all other remaining vertices will never happen).
Let us now prove the following assertion: After the execution of $i_{th}$ phase, the Bellman-Ford algorithm correctly finds all shortest paths whose number of edges does not exceed $i$.
In other words, for any vertex $a$ let us denote the $k$ number of edges in the shortest path to it (if there are several such paths, you can take any). According to this statement, the algorithm guarantees that after $k_{th}$ phase the shortest path for vertex $a$ will be found.
**Proof**:
Consider an arbitrary vertex $a$ to which there is a path from the starting vertex $v$, and consider a shortest path to it $(p_0=v, p_1, \ldots, p_k=a)$. Before the first phase, the shortest path to the vertex $p_0 = v$ was found correctly. During the first phase, the edge $(p_0,p_1)$ has been checked by the algorithm, and therefore, the distance to the vertex $p_1$ was correctly calculated after the first phase. Repeating this statement $k$ times, we see that after $k_{th}$ phase the distance to the vertex $p_k = a$ gets calculated correctly, which we wanted to prove.
The last thing to notice is that any shortest path cannot have more than $n - 1$ edges. Therefore, the algorithm sufficiently goes up to the $(n-1)_{th}$ phase. After that, it is guaranteed that no relaxation will improve the distance to some vertex.
## The case of a negative cycle
Everywhere above we considered that there is no negative cycle in the graph (precisely, we are interested in a negative cycle that is reachable from the starting vertex $v$, and, for an unreachable cycles nothing in the above algorithm changes). In the presence of a negative cycle(s), there are further complications associated with the fact that distances to all vertices in this cycle, as well as the distances to the vertices reachable from this cycle is not defined — they should be equal to minus infinity $(- \infty)$.
It is easy to see that the Bellman-Ford algorithm can endlessly do the relaxation among all vertices of this cycle and the vertices reachable from it. Therefore, if you do not limit the number of phases to $n - 1$, the algorithm will run indefinitely, constantly improving the distance from these vertices.
Hence we obtain the **criterion for presence of a cycle of negative weights reachable for source vertex $v$**: after $(n-1)_{th}$ phase, if we run algorithm for one more phase, and it performs at least one more relaxation, then the graph contains a negative weight cycle that is reachable from $v$; otherwise, such a cycle does not exist.
Moreover, if such a cycle is found, the Bellman-Ford algorithm can be modified so that it retrieves this cycle as a sequence of vertices contained in it. For this, it is sufficient to remember the last vertex $x$ for which there was a relaxation in $n_{th}$ phase. This vertex will either lie in a negative weight cycle, or is reachable from it. To get the vertices that are guaranteed to lie in a negative cycle, starting from the vertex $x$, pass through to the predecessors $n$ times. Hence we will get the vertex $y$, namely the vertex in the cycle earliest reachable from source. We have to go from this vertex, through the predecessors, until we get back to the same vertex $y$ (and it will happen, because relaxation in a negative weight cycle occur in a circular manner).
### Implementation:
```cpp
void solve()
{
vector<int> d(n, INF);
d[v] = 0;
vector<int> p(n, -1);
int x;
for (int i = 0; i < n; ++i) {
x = -1;
for (Edge e : edges)
if (d[e.a] < INF)
if (d[e.b] > d[e.a] + e.cost) {
d[e.b] = max(-INF, d[e.a] + e.cost);
p[e.b] = e.a;
x = e.b;
}
}
if (x == -1)
cout << "No negative cycle from " << v;
else {
int y = x;
for (int i = 0; i < n; ++i)
y = p[y];
vector<int> path;
for (int cur = y;; cur = p[cur]) {
path.push_back(cur);
if (cur == y && path.size() > 1)
break;
}
reverse(path.begin(), path.end());
cout << "Negative cycle: ";
for (int u : path)
cout << u << ' ';
}
}
```
Due to the presence of a negative cycle, for $n$ iterations of the algorithm, the distances may go far in the negative range (to negative numbers of the order of $-n m W$, where $W$ is the maximum absolute value of any weight in the graph). Hence in the code, we adopted additional measures against the integer overflow as follows:
```cpp
d[e.b] = max(-INF, d[e.a] + e.cost);
```
The above implementation looks for a negative cycle reachable from some starting vertex $v$; however, the algorithm can be modified to just looking for any negative cycle in the graph. For this we need to put all the distance $d[i]$ to zero and not infinity — as if we are looking for the shortest path from all vertices simultaneously; the validity of the detection of a negative cycle is not affected.
For more on this topic — see separate article, [Finding a negative cycle in the graph](finding-negative-cycle-in-graph.md).
## Shortest Path Faster Algorithm (SPFA)
SPFA is a improvement of the Bellman-Ford algorithm which takes advantage of the fact that not all attempts at relaxation will work.
The main idea is to create a queue containing only the vertices that were relaxed but that still could further relax their neighbors.
And whenever you can relax some neighbor, you should put him in the queue. This algorithm can also be used to detect negative cycles as the Bellman-Ford.
The worst case of this algorithm is equal to the $O(n m)$ of the Bellman-Ford, but in practice it works much faster and some [people claim that it works even in $O(m)$ on average](https://en.wikipedia.org/wiki/Shortest_Path_Faster_Algorithm#Average-case_performance). However be careful, because this algorithm is deterministic and it is easy to create counterexamples that make the algorithm run in $O(n m)$.
There are some care to be taken in the implementation, such as the fact that the algorithm continues forever if there is a negative cycle.
To avoid this, it is possible to create a counter that stores how many times a vertex has been relaxed and stop the algorithm as soon as some vertex got relaxed for the $n$-th time.
Note, also there is no reason to put a vertex in the queue if it is already in.
```{.cpp file=spfa}
const int INF = 1000000000;
vector<vector<pair<int, int>>> adj;
bool spfa(int s, vector<int>& d) {
int n = adj.size();
d.assign(n, INF);
vector<int> cnt(n, 0);
vector<bool> inqueue(n, false);
queue<int> q;
d[s] = 0;
q.push(s);
inqueue[s] = true;
while (!q.empty()) {
int v = q.front();
q.pop();
inqueue[v] = false;
for (auto edge : adj[v]) {
int to = edge.first;
int len = edge.second;
if (d[v] + len < d[to]) {
d[to] = d[v] + len;
if (!inqueue[to]) {
q.push(to);
inqueue[to] = true;
cnt[to]++;
if (cnt[to] > n)
return false; // negative cycle
}
}
}
}
return true;
}
```
## Related problems in online judges
A list of tasks that can be solved using the Bellman-Ford algorithm:
* [E-OLYMP #1453 "Ford-Bellman" [difficulty: low]](https://www.e-olymp.com/en/problems/1453)
* [UVA #423 "MPI Maelstrom" [difficulty: low]](http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=364)
* [UVA #534 "Frogger" [difficulty: medium]](http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=7&page=show_problem&problem=475)
* [UVA #10099 "The Tourist Guide" [difficulty: medium]](http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=12&page=show_problem&problem=1040)
* [UVA #515 "King" [difficulty: medium]](http://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=456)
* [UVA 12519 - The Farnsworth Parabox](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=3964)
See also the problem list in the article [Finding the negative cycle in a graph](finding-negative-cycle-in-graph.md).
* [CSES - High Score](https://cses.fi/problemset/task/1673)
* [CSES - Cycle Finding](https://cses.fi/problemset/task/1197)
|
---
title
ford_bellman
---
# Bellman-Ford Algorithm
**Single source shortest path with negative weight edges**
Suppose that we are given a weighted directed graph $G$ with $n$ vertices and $m$ edges, and some specified vertex $v$. You want to find the length of shortest paths from vertex $v$ to every other vertex.
Unlike the Dijkstra algorithm, this algorithm can also be applied to graphs containing negative weight edges . However, if the graph contains a negative cycle, then, clearly, the shortest path to some vertices may not exist (due to the fact that the weight of the shortest path must be equal to minus infinity); however, this algorithm can be modified to signal the presence of a cycle of negative weight, or even deduce this cycle.
The algorithm bears the name of two American scientists: Richard Bellman and Lester Ford. Ford actually invented this algorithm in 1956 during the study of another mathematical problem, which eventually reduced to a subproblem of finding the shortest paths in the graph, and Ford gave an outline of the algorithm to solve this problem. Bellman in 1958 published an article devoted specifically to the problem of finding the shortest path, and in this article he clearly formulated the algorithm in the form in which it is known to us now.
## Description of the algorithm
Let us assume that the graph contains no negative weight cycle. The case of presence of a negative weight cycle will be discussed below in a separate section.
We will create an array of distances $d[0 \ldots n-1]$, which after execution of the algorithm will contain the answer to the problem. In the beginning we fill it as follows: $d[v] = 0$, and all other elements $d[ ]$ equal to infinity $\infty$.
The algorithm consists of several phases. Each phase scans through all edges of the graph, and the algorithm tries to produce **relaxation** along each edge $(a,b)$ having weight $c$. Relaxation along the edges is an attempt to improve the value $d[b]$ using value $d[a] + c$. In fact, it means that we are trying to improve the answer for this vertex using edge $(a,b)$ and current response for vertex $a$.
It is claimed that $n-1$ phases of the algorithm are sufficient to correctly calculate the lengths of all shortest paths in the graph (again, we believe that the cycles of negative weight do not exist). For unreachable vertices the distance $d[ ]$ will remain equal to infinity $\infty$.
## Implementation
Unlike many other graph algorithms, for Bellman-Ford algorithm, it is more convenient to represent the graph using a single list of all edges (instead of $n$ lists of edges - edges from each vertex). We start the implementation with a structure $\rm edge$ for representing the edges. The input to the algorithm are numbers $n$, $m$, list $e$ of edges and the starting vertex $v$. All the vertices are numbered $0$ to $n - 1$.
### The simplest implementation
The constant $\rm INF$ denotes the number "infinity" — it should be selected in such a way that it is greater than all possible path lengths.
```cpp
struct Edge {
int a, b, cost;
};
int n, m, v;
vector<Edge> edges;
const int INF = 1000000000;
void solve()
{
vector<int> d(n, INF);
d[v] = 0;
for (int i = 0; i < n - 1; ++i)
for (Edge e : edges)
if (d[e.a] < INF)
d[e.b] = min(d[e.b], d[e.a] + e.cost);
// display d, for example, on the screen
}
```
The check `if (d[e.a] < INF)` is needed only if the graph contains negative weight edges: no such verification would result in relaxation from the vertices to which paths have not yet found, and incorrect distance, of the type $\infty - 1$, $\infty - 2$ etc. would appear.
### A better implementation
This algorithm can be somewhat speeded up: often we already get the answer in a few phases and no useful work is done in remaining phases, just a waste visiting all edges. So, let's keep the flag, to tell whether something changed in the current phase or not, and if any phase, nothing changed, the algorithm can be stopped. (This optimization does not improve the asymptotic behavior, i.e., some graphs will still need all $n-1$ phases, but significantly accelerates the behavior of the algorithm "on an average", i.e., on random graphs.)
With this optimization, it is generally unnecessary to restrict manually the number of phases of the algorithm to $n-1$ — the algorithm will stop after the desired number of phases.
```cpp
void solve()
{
vector<int> d(n, INF);
d[v] = 0;
for (;;) {
bool any = false;
for (Edge e : edges)
if (d[e.a] < INF)
if (d[e.b] > d[e.a] + e.cost) {
d[e.b] = d[e.a] + e.cost;
any = true;
}
if (!any)
break;
}
// display d, for example, on the screen
}
```
### Retrieving Path
Let us now consider how to modify the algorithm so that it not only finds the length of shortest paths, but also allows to reconstruct the shortest paths.
For that, let's create another array $p[0 \ldots n-1]$, where for each vertex we store its "predecessor", i.e. the penultimate vertex in the shortest path leading to it. In fact, the shortest path to any vertex $a$ is a shortest path to some vertex $p[a]$, to which we added $a$ at the end of the path.
Note that the algorithm works on the same logic: it assumes that the shortest distance to one vertex is already calculated, and, tries to improve the shortest distance to other vertices from that vertex. Therefore, at the time of improvement we just need to remember $p[ ]$, i.e, the vertex from which this improvement has occurred.
Following is an implementation of the Bellman-Ford with the retrieval of shortest path to a given node $t$:
```cpp
void solve()
{
vector<int> d(n, INF);
d[v] = 0;
vector<int> p(n, -1);
for (;;) {
bool any = false;
for (Edge e : edges)
if (d[e.a] < INF)
if (d[e.b] > d[e.a] + e.cost) {
d[e.b] = d[e.a] + e.cost;
p[e.b] = e.a;
any = true;
}
if (!any)
break;
}
if (d[t] == INF)
cout << "No path from " << v << " to " << t << ".";
else {
vector<int> path;
for (int cur = t; cur != -1; cur = p[cur])
path.push_back(cur);
reverse(path.begin(), path.end());
cout << "Path from " << v << " to " << t << ": ";
for (int u : path)
cout << u << ' ';
}
}
```
Here starting from the vertex $t$, we go through the predecessors till we reach starting vertex with no predecessor, and store all the vertices in the path in the list $\rm path$. This list is a shortest path from $v$ to $t$, but in reverse order, so we call $\rm reverse()$ function over $\rm path$ and then output the path.
## The proof of the algorithm
First, note that for all unreachable vertices $u$ the algorithm will work correctly, the label $d[u]$ will remain equal to infinity (because the algorithm Bellman-Ford will find some way to all reachable vertices from the start vertex $v$, and relaxation for all other remaining vertices will never happen).
Let us now prove the following assertion: After the execution of $i_{th}$ phase, the Bellman-Ford algorithm correctly finds all shortest paths whose number of edges does not exceed $i$.
In other words, for any vertex $a$ let us denote the $k$ number of edges in the shortest path to it (if there are several such paths, you can take any). According to this statement, the algorithm guarantees that after $k_{th}$ phase the shortest path for vertex $a$ will be found.
**Proof**:
Consider an arbitrary vertex $a$ to which there is a path from the starting vertex $v$, and consider a shortest path to it $(p_0=v, p_1, \ldots, p_k=a)$. Before the first phase, the shortest path to the vertex $p_0 = v$ was found correctly. During the first phase, the edge $(p_0,p_1)$ has been checked by the algorithm, and therefore, the distance to the vertex $p_1$ was correctly calculated after the first phase. Repeating this statement $k$ times, we see that after $k_{th}$ phase the distance to the vertex $p_k = a$ gets calculated correctly, which we wanted to prove.
The last thing to notice is that any shortest path cannot have more than $n - 1$ edges. Therefore, the algorithm sufficiently goes up to the $(n-1)_{th}$ phase. After that, it is guaranteed that no relaxation will improve the distance to some vertex.
## The case of a negative cycle
Everywhere above we considered that there is no negative cycle in the graph (precisely, we are interested in a negative cycle that is reachable from the starting vertex $v$, and, for an unreachable cycles nothing in the above algorithm changes). In the presence of a negative cycle(s), there are further complications associated with the fact that distances to all vertices in this cycle, as well as the distances to the vertices reachable from this cycle is not defined — they should be equal to minus infinity $(- \infty)$.
It is easy to see that the Bellman-Ford algorithm can endlessly do the relaxation among all vertices of this cycle and the vertices reachable from it. Therefore, if you do not limit the number of phases to $n - 1$, the algorithm will run indefinitely, constantly improving the distance from these vertices.
Hence we obtain the **criterion for presence of a cycle of negative weights reachable for source vertex $v$**: after $(n-1)_{th}$ phase, if we run algorithm for one more phase, and it performs at least one more relaxation, then the graph contains a negative weight cycle that is reachable from $v$; otherwise, such a cycle does not exist.
Moreover, if such a cycle is found, the Bellman-Ford algorithm can be modified so that it retrieves this cycle as a sequence of vertices contained in it. For this, it is sufficient to remember the last vertex $x$ for which there was a relaxation in $n_{th}$ phase. This vertex will either lie in a negative weight cycle, or is reachable from it. To get the vertices that are guaranteed to lie in a negative cycle, starting from the vertex $x$, pass through to the predecessors $n$ times. Hence we will get the vertex $y$, namely the vertex in the cycle earliest reachable from source. We have to go from this vertex, through the predecessors, until we get back to the same vertex $y$ (and it will happen, because relaxation in a negative weight cycle occur in a circular manner).
### Implementation:
```cpp
void solve()
{
vector<int> d(n, INF);
d[v] = 0;
vector<int> p(n, -1);
int x;
for (int i = 0; i < n; ++i) {
x = -1;
for (Edge e : edges)
if (d[e.a] < INF)
if (d[e.b] > d[e.a] + e.cost) {
d[e.b] = max(-INF, d[e.a] + e.cost);
p[e.b] = e.a;
x = e.b;
}
}
if (x == -1)
cout << "No negative cycle from " << v;
else {
int y = x;
for (int i = 0; i < n; ++i)
y = p[y];
vector<int> path;
for (int cur = y;; cur = p[cur]) {
path.push_back(cur);
if (cur == y && path.size() > 1)
break;
}
reverse(path.begin(), path.end());
cout << "Negative cycle: ";
for (int u : path)
cout << u << ' ';
}
}
```
Due to the presence of a negative cycle, for $n$ iterations of the algorithm, the distances may go far in the negative range (to negative numbers of the order of $-n m W$, where $W$ is the maximum absolute value of any weight in the graph). Hence in the code, we adopted additional measures against the integer overflow as follows:
```cpp
d[e.b] = max(-INF, d[e.a] + e.cost);
```
The above implementation looks for a negative cycle reachable from some starting vertex $v$; however, the algorithm can be modified to just looking for any negative cycle in the graph. For this we need to put all the distance $d[i]$ to zero and not infinity — as if we are looking for the shortest path from all vertices simultaneously; the validity of the detection of a negative cycle is not affected.
For more on this topic — see separate article, [Finding a negative cycle in the graph](finding-negative-cycle-in-graph.md).
## Shortest Path Faster Algorithm (SPFA)
SPFA is a improvement of the Bellman-Ford algorithm which takes advantage of the fact that not all attempts at relaxation will work.
The main idea is to create a queue containing only the vertices that were relaxed but that still could further relax their neighbors.
And whenever you can relax some neighbor, you should put him in the queue. This algorithm can also be used to detect negative cycles as the Bellman-Ford.
The worst case of this algorithm is equal to the $O(n m)$ of the Bellman-Ford, but in practice it works much faster and some [people claim that it works even in $O(m)$ on average](https://en.wikipedia.org/wiki/Shortest_Path_Faster_Algorithm#Average-case_performance). However be careful, because this algorithm is deterministic and it is easy to create counterexamples that make the algorithm run in $O(n m)$.
There are some care to be taken in the implementation, such as the fact that the algorithm continues forever if there is a negative cycle.
To avoid this, it is possible to create a counter that stores how many times a vertex has been relaxed and stop the algorithm as soon as some vertex got relaxed for the $n$-th time.
Note, also there is no reason to put a vertex in the queue if it is already in.
```{.cpp file=spfa}
const int INF = 1000000000;
vector<vector<pair<int, int>>> adj;
bool spfa(int s, vector<int>& d) {
int n = adj.size();
d.assign(n, INF);
vector<int> cnt(n, 0);
vector<bool> inqueue(n, false);
queue<int> q;
d[s] = 0;
q.push(s);
inqueue[s] = true;
while (!q.empty()) {
int v = q.front();
q.pop();
inqueue[v] = false;
for (auto edge : adj[v]) {
int to = edge.first;
int len = edge.second;
if (d[v] + len < d[to]) {
d[to] = d[v] + len;
if (!inqueue[to]) {
q.push(to);
inqueue[to] = true;
cnt[to]++;
if (cnt[to] > n)
return false; // negative cycle
}
}
}
}
return true;
}
```
## Related problems in online judges
A list of tasks that can be solved using the Bellman-Ford algorithm:
* [E-OLYMP #1453 "Ford-Bellman" [difficulty: low]](https://www.e-olymp.com/en/problems/1453)
* [UVA #423 "MPI Maelstrom" [difficulty: low]](http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=364)
* [UVA #534 "Frogger" [difficulty: medium]](http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=7&page=show_problem&problem=475)
* [UVA #10099 "The Tourist Guide" [difficulty: medium]](http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=12&page=show_problem&problem=1040)
* [UVA #515 "King" [difficulty: medium]](http://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=456)
* [UVA 12519 - The Farnsworth Parabox](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=3964)
See also the problem list in the article [Finding the negative cycle in a graph](finding-negative-cycle-in-graph.md).
* [CSES - High Score](https://cses.fi/problemset/task/1673)
* [CSES - Cycle Finding](https://cses.fi/problemset/task/1197)
|
Bellman-Ford Algorithm
|
---
title
- Original
---
# 0-1 BFS
It is well-known, that you can find the shortest paths between a single source and all other vertices in $O(|E|)$ using [Breadth First Search](breadth-first-search.md) in an **unweighted graph**, i.e. the distance is the minimal number of edges that you need to traverse from the source to another vertex.
We can interpret such a graph also as a weighted graph, where every edge has the weight $1$.
If not all edges in graph have the same weight, that we need a more general algorithm, like [Dijkstra](dijkstra.md) which runs in $O(|V|^2 + |E|)$ or $O(|E| \log |V|)$ time.
However if the weights are more constrained, we can often do better.
In this article we demonstrate how we can use BFS to solve the SSSP (single-source shortest path) problem in $O(|E|)$, if the weight of each edge is either $0$ or $1$.
## Algorithm
We can develop the algorithm by closely studying Dijkstra's algorithm and thinking about the consequences that our special graph implies.
The general form of Dijkstra's algorithm is (here a `set` is used for the priority queue):
```cpp
d.assign(n, INF);
d[s] = 0;
set<pair<int, int>> q;
q.insert({0, s});
while (!q.empty()) {
int v = q.begin()->second;
q.erase(q.begin());
for (auto edge : adj[v]) {
int u = edge.first;
int w = edge.second;
if (d[v] + w < d[u]) {
q.erase({d[u], u});
d[u] = d[v] + w;
q.insert({d[u], u});
}
}
}
```
We can notice that the difference between the distances between the source `s` and two other vertices in the queue differs by at most one.
Especially, we know that $d[v] \le d[u] \le d[v] + 1$ for each $u \in Q$.
The reason for this is, that we only add vertices with equal distance or with distance plus one to the queue during each iteration.
Assuming there exists a $u$ in the queue with $d[u] - d[v] > 1$, then $u$ must have been insert in the queue via a different vertex $t$ with $d[t] \ge d[u] - 1 > d[v]$.
However this is impossible, since Dijkstra's algorithm iterates over the vertices in increasing order.
This means, that the order of the queue looks like this:
$$Q = \underbrace{v}_{d[v]}, \dots, \underbrace{u}_{d[v]}, \underbrace{m}_{d[v]+1} \dots \underbrace{n}_{d[v]+1}$$
This structure is so simple, that we don't need an actual priority queue, i.e. using a balanced binary tree would be an overkill.
We can simply use a normal queue, and append new vertices at the beginning if the corresponding edge has weight $0$, i.e. if $d[u] = d[v]$, or at the end if the edge has weight $1$, i.e. if $d[u] = d[v] + 1$.
This way the queue still remains sorted at all time.
```cpp
vector<int> d(n, INF);
d[s] = 0;
deque<int> q;
q.push_front(s);
while (!q.empty()) {
int v = q.front();
q.pop_front();
for (auto edge : adj[v]) {
int u = edge.first;
int w = edge.second;
if (d[v] + w < d[u]) {
d[u] = d[v] + w;
if (w == 1)
q.push_back(u);
else
q.push_front(u);
}
}
}
```
## Dial's algorithm
We can extend this even further if we allow the weights of the edges to be even bigger.
If every edge in the graph has a weight $\le k$, then the distances of vertices in the queue will differ by at most $k$ from the distance of $v$ to the source.
So we can keep $k + 1$ buckets for the vertices in the queue, and whenever the bucket corresponding to the smallest distance gets empty, we make a cyclic shift to get the bucket with the next higher distance.
This extension is called **Dial's algorithm**.
|
---
title
- Original
---
# 0-1 BFS
It is well-known, that you can find the shortest paths between a single source and all other vertices in $O(|E|)$ using [Breadth First Search](breadth-first-search.md) in an **unweighted graph**, i.e. the distance is the minimal number of edges that you need to traverse from the source to another vertex.
We can interpret such a graph also as a weighted graph, where every edge has the weight $1$.
If not all edges in graph have the same weight, that we need a more general algorithm, like [Dijkstra](dijkstra.md) which runs in $O(|V|^2 + |E|)$ or $O(|E| \log |V|)$ time.
However if the weights are more constrained, we can often do better.
In this article we demonstrate how we can use BFS to solve the SSSP (single-source shortest path) problem in $O(|E|)$, if the weight of each edge is either $0$ or $1$.
## Algorithm
We can develop the algorithm by closely studying Dijkstra's algorithm and thinking about the consequences that our special graph implies.
The general form of Dijkstra's algorithm is (here a `set` is used for the priority queue):
```cpp
d.assign(n, INF);
d[s] = 0;
set<pair<int, int>> q;
q.insert({0, s});
while (!q.empty()) {
int v = q.begin()->second;
q.erase(q.begin());
for (auto edge : adj[v]) {
int u = edge.first;
int w = edge.second;
if (d[v] + w < d[u]) {
q.erase({d[u], u});
d[u] = d[v] + w;
q.insert({d[u], u});
}
}
}
```
We can notice that the difference between the distances between the source `s` and two other vertices in the queue differs by at most one.
Especially, we know that $d[v] \le d[u] \le d[v] + 1$ for each $u \in Q$.
The reason for this is, that we only add vertices with equal distance or with distance plus one to the queue during each iteration.
Assuming there exists a $u$ in the queue with $d[u] - d[v] > 1$, then $u$ must have been insert in the queue via a different vertex $t$ with $d[t] \ge d[u] - 1 > d[v]$.
However this is impossible, since Dijkstra's algorithm iterates over the vertices in increasing order.
This means, that the order of the queue looks like this:
$$Q = \underbrace{v}_{d[v]}, \dots, \underbrace{u}_{d[v]}, \underbrace{m}_{d[v]+1} \dots \underbrace{n}_{d[v]+1}$$
This structure is so simple, that we don't need an actual priority queue, i.e. using a balanced binary tree would be an overkill.
We can simply use a normal queue, and append new vertices at the beginning if the corresponding edge has weight $0$, i.e. if $d[u] = d[v]$, or at the end if the edge has weight $1$, i.e. if $d[u] = d[v] + 1$.
This way the queue still remains sorted at all time.
```cpp
vector<int> d(n, INF);
d[s] = 0;
deque<int> q;
q.push_front(s);
while (!q.empty()) {
int v = q.front();
q.pop_front();
for (auto edge : adj[v]) {
int u = edge.first;
int w = edge.second;
if (d[v] + w < d[u]) {
d[u] = d[v] + w;
if (w == 1)
q.push_back(u);
else
q.push_front(u);
}
}
}
```
## Dial's algorithm
We can extend this even further if we allow the weights of the edges to be even bigger.
If every edge in the graph has a weight $\le k$, then the distances of vertices in the queue will differ by at most $k$ from the distance of $v$ to the source.
So we can keep $k + 1$ buckets for the vertices in the queue, and whenever the bucket corresponding to the smallest distance gets empty, we make a cyclic shift to get the bucket with the next higher distance.
This extension is called **Dial's algorithm**.
## Practice problems
- [CodeChef - Chef and Reversing](https://www.codechef.com/problems/REVERSE)
- [Labyrinth](https://codeforces.com/contest/1063/problem/B)
- [KATHTHI](http://www.spoj.com/problems/KATHTHI/)
- [DoNotTurn](https://community.topcoder.com/stat?c=problem_statement&pm=10337)
- [Ocean Currents](https://onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=2620)
- [Olya and Energy Drinks](https://codeforces.com/problemset/problem/877/D)
- [Three States](https://codeforces.com/problemset/problem/590/C)
- [Colliding Traffic](https://onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2621)
- [CHamber of Secrets](https://codeforces.com/problemset/problem/173/B)
- [Spiral Maximum](https://codeforces.com/problemset/problem/173/C)
- [Minimum Cost to Make at Least One Valid Path in a Grid](https://leetcode.com/problems/minimum-cost-to-make-at-least-one-valid-path-in-a-grid)
|
0-1 BFS
|
---
title
heavy_light
---
# Heavy-light decomposition
**Heavy-light decomposition** is a fairly general technique that allows us to effectively solve many problems that come down to **queries on a tree** .
## Description
Let there be a tree $G$ of $n$ vertices, with an arbitrary root.
The essence of this tree decomposition is to **split the tree into several paths** so that we can reach the root vertex from any $v$ by traversing at most $\log n$ paths. In addition, none of these paths should intersect with another.
It is clear that if we find such a decomposition for any tree, it will allow us to reduce certain single queries of the form *“calculate something on the path from $a$ to $b$”* to several queries of the type *”calculate something on the segment $[l, r]$ of the $k^{th}$ path”*.
### Construction algorithm
We calculate for each vertex $v$ the size of its subtree $s(v)$, i.e. the number of vertices in the subtree of the vertex $v$ including itself.
Next, consider all the edges leading to the children of a vertex $v$. We call an edge **heavy** if it leads to a vertex $c$ such that:
$$
s(c) \ge \frac{s(v)}{2} \iff \text{edge }(v, c)\text{ is heavy}
$$
All other edges are labeled **light**.
It is obvious that at most one heavy edge can emanate from one vertex downward, because otherwise the vertex $v$ would have at least two children of size $\ge \frac{s(v)}{2}$, and therefore the size of subtree of $v$ would be too big, $s(v) \ge 1 + 2 \frac{s(v)}{2} > s(v)$, which leads to a contradiction.
Now we will decompose the tree into disjoint paths. Consider all the vertices from which no heavy edges come down. We will go up from each such vertex until we reach the root of the tree or go through a light edge. As a result, we will get several paths which are made up of zero or more heavy edges plus one light edge. The path which has an end at the root is an exception to this and will not have a light edge. Let these be called **heavy paths** - these are the desired paths of heavy-light decomposition.
### Proof of correctness
First, we note that the heavy paths obtained by the algorithm will be **disjoint** . In fact, if two such paths have a common edge, it would imply that there are two heavy edges coming out of one vertex, which is impossible.
Secondly, we will show that going down from the root of the tree to an arbitrary vertex, we will **change no more than $\log n$ heavy paths along the way** . Moving down a light edge reduces the size of the current subtree to half or lower:
$$
s(c) < \frac{s(v)}{2} \iff \text{edge }(v, c)\text{ is light}
$$
Thus, we can go through at most $\log n$ light edges before subtree size reduces to one.
Since we can move from one heavy path to another only through a light edge (each heavy path, except the one starting at the root, has one light edge), we cannot change heavy paths more than $\log n$ times along the path from the root to any vertex, as required.
The following image illustrates the decomposition of a sample tree. The heavy edges are thicker than the light edges. The heavy paths are marked by dotted boundaries.
<center></center>
## Sample problems
When solving problems, it is sometimes more convenient to consider the heavy-light decomposition as a set of **vertex disjoint** paths (rather than edge disjoint paths). To do this, it suffices to exclude the last edge from each heavy path if it is a light edge, then no properties are violated, but now each vertex belongs to exactly one heavy path.
Below we will look at some typical tasks that can be solved with the help of heavy-light decomposition.
Separately, it is worth paying attention to the problem of the **sum of numbers on the path**, since this is an example of a problem that can be solved by simpler techniques.
### Maximum value on the path between two vertices
Given a tree, each vertex is assigned a value. There are queries of the form $(a, b)$, where $a$ and $b$ are two vertices in the tree, and it is required to find the maximum value on the path between the vertices $a$ and $b$.
We construct in advance a heavy-light decomposition of the tree. Over each heavy path we will construct a [segment tree](../data_structures/segment_tree.md), which will allow us to search for a vertex with the maximum assigned value in the specified segment of the specified heavy path in $\mathcal{O}(\log n)$. Although the number of heavy paths in heavy-light decomposition can reach $n - 1$, the total size of all paths is bounded by $\mathcal{O}(n)$, therefore the total size of the segment trees will also be linear.
In order to answer a query $(a, b)$, we find the [lowest common ancestor](https://en.wikipedia.org/wiki/Lowest_common_ancestor) of $a$ and $b$ as $l$, by any preferred method. Now the task has been reduced to two queries $(a, l)$ and $(b, l)$, for each of which we can do the following: find the heavy path that the lower vertex lies in, make a query on this path, move to the top of this path, again determine which heavy path we are on and make a query on it, and so on, until we get to the path containing $l$.
One should be careful with the case when, for example, $a$ and $l$ are on the same heavy path - then the maximum query on this path should be done not on any prefix, but on the internal section between $a$ and $l$.
Responding to the subqueries $(a, l)$ and $(b, l)$ each requires going through $\mathcal{O}(\log n)$ heavy paths and for each path a maximum query is made on some section of the path, which again requires $\mathcal{O}(\log n)$ operations in the segment tree.
Hence, one query $(a, b)$ takes $\mathcal{O}(\log^2 n)$ time.
If you additionally calculate and store maximums of all prefixes for each heavy path, then you get a $\mathcal{O}(\log n)$ solution because all maximum queries are on prefixes except at most once when we reach the ancestor $l$.
### Sum of the numbers on the path between two vertices
Given a tree, each vertex is assigned a value. There are queries of the form $(a, b)$, where $a$ and $b$ are two vertices in the tree, and it is required to find the sum of the values on the path between the vertices $a$ and $b$. A variant of this task is possible where additionally there are update operations that change the number assigned to one or more vertices.
This task can be solved similar to the previous problem of maximums with the help of heavy-light decomposition by building segment trees on heavy paths. Prefix sums can be used instead if there are no updates. However, this problem can be solved by simpler techniques too.
If there are no updates, then it is possible to find out the sum on the path between two vertices in parallel with the LCA search of two vertices by [binary lifting](lca_binary_lifting.md) — for this, along with the $2^k$-th ancestors of each vertex it is also necessary to store the sum on the paths up to those ancestors during the preprocessing.
There is a fundamentally different approach to this problem - to consider the [Euler tour](https://en.wikipedia.org/wiki/Euler_tour_technique) of the tree, and build a segment tree on it. This algorithm is considered in an [article about a similar problem](tree_painting.md). Again, if there are no updates, storing prefix sums is enough and a segment tree is not required.
Both of these methods provide relatively simple solutions taking $\mathcal{O}(\log n)$ for one query.
### Repainting the edges of the path between two vertices
Given a tree, each edge is initially painted white. There are updates of the form $(a, b, c)$, where $a$ and $b$ are two vertices and $c$ is a color, which instructs that all the edges on the path from $a$ to $b$ must be repainted with color $c$. After all repaintings, it is required to report how many edges of each color were obtained.
Similar to the above problems, the solution is to simply apply heavy-light decomposition and make a [segment tree](../data_structures/segment_tree.md) over each heavy path.
Each repainting on the path $(a, b)$ will turn into two updates $(a, l)$ and $(b, l)$, where $l$ is the lowest common ancestor of the vertices $a$ and $b$.
$\mathcal{O}(\log n)$ per path for $\mathcal{O}(\log n)$ paths leads to a complexity of $\mathcal{O}(\log^2 n)$ per update.
## Implementation
Certain parts of the above discussed approach can be modified to make implementation easier without losing efficiency.
* The definition of **heavy edge** can be changed to **the edge leading to the child with largest subtree**, with ties broken arbitrarily. This may result is some light edges being converted to heavy, which means some heavy paths will combine to form a single path, but all heavy paths will remain disjoint. It is also still guaranteed that going down a light edge reduces subtree size to half or less.
* Instead of a building segment tree over every heavy path, a single segment tree can be used with disjoint segments allocated to each heavy path.
* It has been mentioned that answering queries requires calculation of the LCA. While LCA can be calculated separately, it is also possible to integrate LCA calculation in the process of answering queries.
To perform heavy-light decomposition:
```cpp
vector<int> parent, depth, heavy, head, pos;
int cur_pos;
int dfs(int v, vector<vector<int>> const& adj) {
int size = 1;
int max_c_size = 0;
for (int c : adj[v]) {
if (c != parent[v]) {
parent[c] = v, depth[c] = depth[v] + 1;
int c_size = dfs(c, adj);
size += c_size;
if (c_size > max_c_size)
max_c_size = c_size, heavy[v] = c;
}
}
return size;
}
void decompose(int v, int h, vector<vector<int>> const& adj) {
head[v] = h, pos[v] = cur_pos++;
if (heavy[v] != -1)
decompose(heavy[v], h, adj);
for (int c : adj[v]) {
if (c != parent[v] && c != heavy[v])
decompose(c, c, adj);
}
}
void init(vector<vector<int>> const& adj) {
int n = adj.size();
parent = vector<int>(n);
depth = vector<int>(n);
heavy = vector<int>(n, -1);
head = vector<int>(n);
pos = vector<int>(n);
cur_pos = 0;
dfs(0, adj);
decompose(0, 0, adj);
}
```
The adjacency list of the tree must be passed to the `init` function, and decomposition is performed assuming vertex `0` as root.
The `dfs` function is used to calculate `heavy[v]`, the child at the other end of the heavy edge from `v`, for every vertex `v`. Additionally `dfs` also stores the parent and depth of each vertex, which will be useful later during queries.
The `decompose` function assigns for each vertex `v` the values `head[v]` and `pos[v]`, which are respectively the head of the heavy path `v` belongs to and the position of `v` on the single segment tree that covers all vertices.
To answer queries on paths, for example the maximum query discussed, we can do something like this:
```cpp
int query(int a, int b) {
int res = 0;
for (; head[a] != head[b]; b = parent[head[b]]) {
if (depth[head[a]] > depth[head[b]])
swap(a, b);
int cur_heavy_path_max = segment_tree_query(pos[head[b]], pos[b]);
res = max(res, cur_heavy_path_max);
}
if (depth[a] > depth[b])
swap(a, b);
int last_heavy_path_max = segment_tree_query(pos[a], pos[b]);
res = max(res, last_heavy_path_max);
return res;
}
```
|
---
title
heavy_light
---
# Heavy-light decomposition
**Heavy-light decomposition** is a fairly general technique that allows us to effectively solve many problems that come down to **queries on a tree** .
## Description
Let there be a tree $G$ of $n$ vertices, with an arbitrary root.
The essence of this tree decomposition is to **split the tree into several paths** so that we can reach the root vertex from any $v$ by traversing at most $\log n$ paths. In addition, none of these paths should intersect with another.
It is clear that if we find such a decomposition for any tree, it will allow us to reduce certain single queries of the form *“calculate something on the path from $a$ to $b$”* to several queries of the type *”calculate something on the segment $[l, r]$ of the $k^{th}$ path”*.
### Construction algorithm
We calculate for each vertex $v$ the size of its subtree $s(v)$, i.e. the number of vertices in the subtree of the vertex $v$ including itself.
Next, consider all the edges leading to the children of a vertex $v$. We call an edge **heavy** if it leads to a vertex $c$ such that:
$$
s(c) \ge \frac{s(v)}{2} \iff \text{edge }(v, c)\text{ is heavy}
$$
All other edges are labeled **light**.
It is obvious that at most one heavy edge can emanate from one vertex downward, because otherwise the vertex $v$ would have at least two children of size $\ge \frac{s(v)}{2}$, and therefore the size of subtree of $v$ would be too big, $s(v) \ge 1 + 2 \frac{s(v)}{2} > s(v)$, which leads to a contradiction.
Now we will decompose the tree into disjoint paths. Consider all the vertices from which no heavy edges come down. We will go up from each such vertex until we reach the root of the tree or go through a light edge. As a result, we will get several paths which are made up of zero or more heavy edges plus one light edge. The path which has an end at the root is an exception to this and will not have a light edge. Let these be called **heavy paths** - these are the desired paths of heavy-light decomposition.
### Proof of correctness
First, we note that the heavy paths obtained by the algorithm will be **disjoint** . In fact, if two such paths have a common edge, it would imply that there are two heavy edges coming out of one vertex, which is impossible.
Secondly, we will show that going down from the root of the tree to an arbitrary vertex, we will **change no more than $\log n$ heavy paths along the way** . Moving down a light edge reduces the size of the current subtree to half or lower:
$$
s(c) < \frac{s(v)}{2} \iff \text{edge }(v, c)\text{ is light}
$$
Thus, we can go through at most $\log n$ light edges before subtree size reduces to one.
Since we can move from one heavy path to another only through a light edge (each heavy path, except the one starting at the root, has one light edge), we cannot change heavy paths more than $\log n$ times along the path from the root to any vertex, as required.
The following image illustrates the decomposition of a sample tree. The heavy edges are thicker than the light edges. The heavy paths are marked by dotted boundaries.
<center></center>
## Sample problems
When solving problems, it is sometimes more convenient to consider the heavy-light decomposition as a set of **vertex disjoint** paths (rather than edge disjoint paths). To do this, it suffices to exclude the last edge from each heavy path if it is a light edge, then no properties are violated, but now each vertex belongs to exactly one heavy path.
Below we will look at some typical tasks that can be solved with the help of heavy-light decomposition.
Separately, it is worth paying attention to the problem of the **sum of numbers on the path**, since this is an example of a problem that can be solved by simpler techniques.
### Maximum value on the path between two vertices
Given a tree, each vertex is assigned a value. There are queries of the form $(a, b)$, where $a$ and $b$ are two vertices in the tree, and it is required to find the maximum value on the path between the vertices $a$ and $b$.
We construct in advance a heavy-light decomposition of the tree. Over each heavy path we will construct a [segment tree](../data_structures/segment_tree.md), which will allow us to search for a vertex with the maximum assigned value in the specified segment of the specified heavy path in $\mathcal{O}(\log n)$. Although the number of heavy paths in heavy-light decomposition can reach $n - 1$, the total size of all paths is bounded by $\mathcal{O}(n)$, therefore the total size of the segment trees will also be linear.
In order to answer a query $(a, b)$, we find the [lowest common ancestor](https://en.wikipedia.org/wiki/Lowest_common_ancestor) of $a$ and $b$ as $l$, by any preferred method. Now the task has been reduced to two queries $(a, l)$ and $(b, l)$, for each of which we can do the following: find the heavy path that the lower vertex lies in, make a query on this path, move to the top of this path, again determine which heavy path we are on and make a query on it, and so on, until we get to the path containing $l$.
One should be careful with the case when, for example, $a$ and $l$ are on the same heavy path - then the maximum query on this path should be done not on any prefix, but on the internal section between $a$ and $l$.
Responding to the subqueries $(a, l)$ and $(b, l)$ each requires going through $\mathcal{O}(\log n)$ heavy paths and for each path a maximum query is made on some section of the path, which again requires $\mathcal{O}(\log n)$ operations in the segment tree.
Hence, one query $(a, b)$ takes $\mathcal{O}(\log^2 n)$ time.
If you additionally calculate and store maximums of all prefixes for each heavy path, then you get a $\mathcal{O}(\log n)$ solution because all maximum queries are on prefixes except at most once when we reach the ancestor $l$.
### Sum of the numbers on the path between two vertices
Given a tree, each vertex is assigned a value. There are queries of the form $(a, b)$, where $a$ and $b$ are two vertices in the tree, and it is required to find the sum of the values on the path between the vertices $a$ and $b$. A variant of this task is possible where additionally there are update operations that change the number assigned to one or more vertices.
This task can be solved similar to the previous problem of maximums with the help of heavy-light decomposition by building segment trees on heavy paths. Prefix sums can be used instead if there are no updates. However, this problem can be solved by simpler techniques too.
If there are no updates, then it is possible to find out the sum on the path between two vertices in parallel with the LCA search of two vertices by [binary lifting](lca_binary_lifting.md) — for this, along with the $2^k$-th ancestors of each vertex it is also necessary to store the sum on the paths up to those ancestors during the preprocessing.
There is a fundamentally different approach to this problem - to consider the [Euler tour](https://en.wikipedia.org/wiki/Euler_tour_technique) of the tree, and build a segment tree on it. This algorithm is considered in an [article about a similar problem](tree_painting.md). Again, if there are no updates, storing prefix sums is enough and a segment tree is not required.
Both of these methods provide relatively simple solutions taking $\mathcal{O}(\log n)$ for one query.
### Repainting the edges of the path between two vertices
Given a tree, each edge is initially painted white. There are updates of the form $(a, b, c)$, where $a$ and $b$ are two vertices and $c$ is a color, which instructs that all the edges on the path from $a$ to $b$ must be repainted with color $c$. After all repaintings, it is required to report how many edges of each color were obtained.
Similar to the above problems, the solution is to simply apply heavy-light decomposition and make a [segment tree](../data_structures/segment_tree.md) over each heavy path.
Each repainting on the path $(a, b)$ will turn into two updates $(a, l)$ and $(b, l)$, where $l$ is the lowest common ancestor of the vertices $a$ and $b$.
$\mathcal{O}(\log n)$ per path for $\mathcal{O}(\log n)$ paths leads to a complexity of $\mathcal{O}(\log^2 n)$ per update.
## Implementation
Certain parts of the above discussed approach can be modified to make implementation easier without losing efficiency.
* The definition of **heavy edge** can be changed to **the edge leading to the child with largest subtree**, with ties broken arbitrarily. This may result is some light edges being converted to heavy, which means some heavy paths will combine to form a single path, but all heavy paths will remain disjoint. It is also still guaranteed that going down a light edge reduces subtree size to half or less.
* Instead of a building segment tree over every heavy path, a single segment tree can be used with disjoint segments allocated to each heavy path.
* It has been mentioned that answering queries requires calculation of the LCA. While LCA can be calculated separately, it is also possible to integrate LCA calculation in the process of answering queries.
To perform heavy-light decomposition:
```cpp
vector<int> parent, depth, heavy, head, pos;
int cur_pos;
int dfs(int v, vector<vector<int>> const& adj) {
int size = 1;
int max_c_size = 0;
for (int c : adj[v]) {
if (c != parent[v]) {
parent[c] = v, depth[c] = depth[v] + 1;
int c_size = dfs(c, adj);
size += c_size;
if (c_size > max_c_size)
max_c_size = c_size, heavy[v] = c;
}
}
return size;
}
void decompose(int v, int h, vector<vector<int>> const& adj) {
head[v] = h, pos[v] = cur_pos++;
if (heavy[v] != -1)
decompose(heavy[v], h, adj);
for (int c : adj[v]) {
if (c != parent[v] && c != heavy[v])
decompose(c, c, adj);
}
}
void init(vector<vector<int>> const& adj) {
int n = adj.size();
parent = vector<int>(n);
depth = vector<int>(n);
heavy = vector<int>(n, -1);
head = vector<int>(n);
pos = vector<int>(n);
cur_pos = 0;
dfs(0, adj);
decompose(0, 0, adj);
}
```
The adjacency list of the tree must be passed to the `init` function, and decomposition is performed assuming vertex `0` as root.
The `dfs` function is used to calculate `heavy[v]`, the child at the other end of the heavy edge from `v`, for every vertex `v`. Additionally `dfs` also stores the parent and depth of each vertex, which will be useful later during queries.
The `decompose` function assigns for each vertex `v` the values `head[v]` and `pos[v]`, which are respectively the head of the heavy path `v` belongs to and the position of `v` on the single segment tree that covers all vertices.
To answer queries on paths, for example the maximum query discussed, we can do something like this:
```cpp
int query(int a, int b) {
int res = 0;
for (; head[a] != head[b]; b = parent[head[b]]) {
if (depth[head[a]] > depth[head[b]])
swap(a, b);
int cur_heavy_path_max = segment_tree_query(pos[head[b]], pos[b]);
res = max(res, cur_heavy_path_max);
}
if (depth[a] > depth[b])
swap(a, b);
int last_heavy_path_max = segment_tree_query(pos[a], pos[b]);
res = max(res, last_heavy_path_max);
return res;
}
```
## Practice problems
- [SPOJ - QTREE - Query on a tree](https://www.spoj.com/problems/QTREE/)
|
Heavy-light decomposition
|
---
title
lca_simpler
---
# Lowest Common Ancestor - Binary Lifting
Let $G$ be a tree.
For every query of the form `(u, v)` we want to find the lowest common ancestor of the nodes `u` and `v`, i.e. we want to find a node `w` that lies on the path from `u` to the root node, that lies on the path from `v` to the root node, and if there are multiple nodes we pick the one that is farthest away from the root node.
In other words the desired node `w` is the lowest ancestor of `u` and `v`.
In particular if `u` is an ancestor of `v`, then `u` is their lowest common ancestor.
The algorithm described in this article will need $O(N \log N)$ for preprocessing the tree, and then $O(\log N)$ for each LCA query.
## Algorithm
For each node we will precompute its ancestor above him, its ancestor two nodes above, its ancestor four above, etc.
Let's store them in the array `up`, i.e. `up[i][j]` is the `2^j`-th ancestor above the node `i` with `i=1...N`, `j=0...ceil(log(N))`.
These information allow us to jump from any node to any ancestor above it in $O(\log N)$ time.
We can compute this array using a [DFS](depth-first-search.md) traversal of the tree.
For each node we will also remember the time of the first visit of this node (i.e. the time when the DFS discovers the node), and the time when we left it (i.e. after we visited all children and exit the DFS function).
We can use this information to determine in constant time if a node is an ancestor of another node.
Suppose now we received a query `(u, v)`.
We can immediately check whether one node is the ancestor of the other.
In this case this node is already the LCA.
If `u` is not the ancestor of `v`, and `v` not the ancestor of `u`, we climb the ancestors of `u` until we find the highest (i.e. closest to the root) node, which is not an ancestor of `v` (i.e. a node `x`, such that `x` is not an ancestor of `v`, but `up[x][0]` is).
We can find this node `x` in $O(\log N)$ time using the array `up`.
We will describe this process in more detail.
Let `L = ceil(log(N))`.
Suppose first that `i = L`.
If `up[u][i]` is not an ancestor of `v`, then we can assign `u = up[u][i]` and decrement `i`.
If `up[u][i]` is an ancestor, then we just decrement `i`.
Clearly after doing this for all non-negative `i` the node `u` will be the desired node - i.e. `u` is still not an ancestor of `v`, but `up[u][0]` is.
Now, obviously, the answer to LCA will be `up[u][0]` - i.e., the smallest node among the ancestors of the node `u`, which is also an ancestor of `v`.
So answering a LCA query will iterate `i` from `ceil(log(N))` to `0` and checks in each iteration if one node is the ancestor of the other.
Consequently each query can be answered in $O(\log N)$.
## Implementation
```cpp
int n, l;
vector<vector<int>> adj;
int timer;
vector<int> tin, tout;
vector<vector<int>> up;
void dfs(int v, int p)
{
tin[v] = ++timer;
up[v][0] = p;
for (int i = 1; i <= l; ++i)
up[v][i] = up[up[v][i-1]][i-1];
for (int u : adj[v]) {
if (u != p)
dfs(u, v);
}
tout[v] = ++timer;
}
bool is_ancestor(int u, int v)
{
return tin[u] <= tin[v] && tout[u] >= tout[v];
}
int lca(int u, int v)
{
if (is_ancestor(u, v))
return u;
if (is_ancestor(v, u))
return v;
for (int i = l; i >= 0; --i) {
if (!is_ancestor(up[u][i], v))
u = up[u][i];
}
return up[u][0];
}
void preprocess(int root) {
tin.resize(n);
tout.resize(n);
timer = 0;
l = ceil(log2(n));
up.assign(n, vector<int>(l + 1));
dfs(root, root);
}
```
|
---
title
lca_simpler
---
# Lowest Common Ancestor - Binary Lifting
Let $G$ be a tree.
For every query of the form `(u, v)` we want to find the lowest common ancestor of the nodes `u` and `v`, i.e. we want to find a node `w` that lies on the path from `u` to the root node, that lies on the path from `v` to the root node, and if there are multiple nodes we pick the one that is farthest away from the root node.
In other words the desired node `w` is the lowest ancestor of `u` and `v`.
In particular if `u` is an ancestor of `v`, then `u` is their lowest common ancestor.
The algorithm described in this article will need $O(N \log N)$ for preprocessing the tree, and then $O(\log N)$ for each LCA query.
## Algorithm
For each node we will precompute its ancestor above him, its ancestor two nodes above, its ancestor four above, etc.
Let's store them in the array `up`, i.e. `up[i][j]` is the `2^j`-th ancestor above the node `i` with `i=1...N`, `j=0...ceil(log(N))`.
These information allow us to jump from any node to any ancestor above it in $O(\log N)$ time.
We can compute this array using a [DFS](depth-first-search.md) traversal of the tree.
For each node we will also remember the time of the first visit of this node (i.e. the time when the DFS discovers the node), and the time when we left it (i.e. after we visited all children and exit the DFS function).
We can use this information to determine in constant time if a node is an ancestor of another node.
Suppose now we received a query `(u, v)`.
We can immediately check whether one node is the ancestor of the other.
In this case this node is already the LCA.
If `u` is not the ancestor of `v`, and `v` not the ancestor of `u`, we climb the ancestors of `u` until we find the highest (i.e. closest to the root) node, which is not an ancestor of `v` (i.e. a node `x`, such that `x` is not an ancestor of `v`, but `up[x][0]` is).
We can find this node `x` in $O(\log N)$ time using the array `up`.
We will describe this process in more detail.
Let `L = ceil(log(N))`.
Suppose first that `i = L`.
If `up[u][i]` is not an ancestor of `v`, then we can assign `u = up[u][i]` and decrement `i`.
If `up[u][i]` is an ancestor, then we just decrement `i`.
Clearly after doing this for all non-negative `i` the node `u` will be the desired node - i.e. `u` is still not an ancestor of `v`, but `up[u][0]` is.
Now, obviously, the answer to LCA will be `up[u][0]` - i.e., the smallest node among the ancestors of the node `u`, which is also an ancestor of `v`.
So answering a LCA query will iterate `i` from `ceil(log(N))` to `0` and checks in each iteration if one node is the ancestor of the other.
Consequently each query can be answered in $O(\log N)$.
## Implementation
```cpp
int n, l;
vector<vector<int>> adj;
int timer;
vector<int> tin, tout;
vector<vector<int>> up;
void dfs(int v, int p)
{
tin[v] = ++timer;
up[v][0] = p;
for (int i = 1; i <= l; ++i)
up[v][i] = up[up[v][i-1]][i-1];
for (int u : adj[v]) {
if (u != p)
dfs(u, v);
}
tout[v] = ++timer;
}
bool is_ancestor(int u, int v)
{
return tin[u] <= tin[v] && tout[u] >= tout[v];
}
int lca(int u, int v)
{
if (is_ancestor(u, v))
return u;
if (is_ancestor(v, u))
return v;
for (int i = l; i >= 0; --i) {
if (!is_ancestor(up[u][i], v))
u = up[u][i];
}
return up[u][0];
}
void preprocess(int root) {
tin.resize(n);
tout.resize(n);
timer = 0;
l = ceil(log2(n));
up.assign(n, vector<int>(l + 1));
dfs(root, root);
}
```
## Practice Problems
* [Codechef - Longest Good Segment](https://www.codechef.com/problems/LGSEG)
* [HackerEarth - Optimal Connectivity](https://www.hackerearth.com/practice/algorithms/graphs/graph-representation/practice-problems/algorithm/optimal-connectivity-c6ae79ca/)
|
Lowest Common Ancestor - Binary Lifting
|
---
title
min_cost_flow
---
# Minimum-cost flow - Successive shortest path algorithm
Given a network $G$ consisting of $n$ vertices and $m$ edges.
For each edge (generally speaking, oriented edges, but see below), the capacity (a non-negative integer) and the cost per unit of flow along this edge (some integer) are given.
Also the source $s$ and the sink $t$ are marked.
For a given value $K$, we have to find a flow of this quantity, and among all flows of this quantity we have to choose the flow with the lowest cost.
This task is called **minimum-cost flow problem**.
Sometimes the task is given a little differently:
you want to find the maximum flow, and among all maximal flows we want to find the one with the least cost.
This is called the **minimum-cost maximum-flow problem**.
Both these problems can be solved effectively with the algorithm of successive shortest paths.
## Algorithm
This algorithm is very similar to the [Edmonds-Karp](edmonds_karp.md) for computing the maximum flow.
### Simplest case
First we only consider the simplest case, where the graph is oriented, and there is at most one edge between any pair of vertices (e.g. if $(i, j)$ is an edge in the graph, then $(j, i)$ cannot be part in it as well).
Let $U_{i j}$ be the capacity of an edge $(i, j)$ if this edge exists.
And let $C_{i j}$ be the cost per unit of flow along this edge $(i, j)$.
And finally let $F_{i, j}$ be the flow along the edge $(i, j)$.
Initially all flow values are zero.
We **modify** the network as follows:
for each edge $(i, j)$ we add the **reverse edge** $(j, i)$ to the network with the capacity $U_{j i} = 0$ and the cost $C_{j i} = -C_{i j}$.
Since, according to our restrictions, the edge $(j, i)$ was not in the network before, we still have a network that is not a multigraph (graph with multiple edges).
In addition we will always keep the condition $F_{j i} = -F_{i j}$ true during the steps of the algorithm.
We define the **residual network** for some fixed flow $F$ as follow (just like in the Ford-Fulkerson algorithm):
the residual network contains only unsaturated edges (i.e. edges in which $F_{i j} < U_{i j}$), and the residual capacity of each such edge is $R_{i j} = U_{i j} - F_{i j}$.
Now we can talk about the **algorithms** to compute the minimum-cost flow.
At each iteration of the algorithm we find the shortest path in the residual graph from $s$ to $t$.
In contrary to Edmonds-Karp we look for the shortest path in terms of the cost of the path, instead of the number of edges.
If there doesn't exists a path anymore, then the algorithm terminates, and the stream $F$ is the desired one.
If a path was found, we increase the flow along it as much as possible (i.e. we find the minimal residual capacity $R$ of the path, and increase the flow by it, and reduce the back edges by the same amount).
If at some point the flow reaches the value $K$, then we stop the algorithm (note that in the last iteration of the algorithm it is necessary to increase the flow by only such an amount so that the final flow value doesn't surpass $K$).
It is not difficult to see, that if we set $K$ to infinity, then the algorithm will find the minimum-cost maximum-flow.
So both variations of the problem can be solved by the same algorithm.
### Undirected graphs / multigraphs
The case of an undirected graph or a multigraph doesn't differ conceptually from the algorithm above.
The algorithm will also work on these graphs.
However it becomes a little more difficult to implement it.
An **undirected edge** $(i, j)$ is actually the same as two oriented edges $(i, j)$ and $(j, i)$ with the same capacity and values.
Since the above-described minimum-cost flow algorithm generates a back edge for each directed edge, so it splits the undirected edge into $4$ directed edges, and we actually get a **multigraph**.
How do we deal with **multiple edges**?
First the flow for each of the multiple edges must be kept separately.
Secondly, when searching for the shortest path, it is necessary to take into account that it is important which of the multiple edges is used in the path.
Thus instead of the usual ancestor array we additionally must store the edge number from which we came from along with the ancestor.
Thirdly, as the flow increases along a certain edge, it is necessary to reduce the flow along the back edge.
Since we have multiple edges, we have to store the edge number for the reversed edge for each edge.
There are no other obstructions with undirected graphs or multigraphs.
### Complexity
The algorithm here is generally exponential in the size of the input. To be more specific, in the worst case it may push only as much as $1$ unit of flow on each iteration, taking $O(F)$ iterations to find a minimum-cost flow of size $F$, making a total runtime to be $O(F \cdot T)$, where $T$ is the time required to find the shortest path from source to sink.
If [Bellman-Ford](bellman_ford.md) algorithm is used for this, it makes the running time $O(F mn)$. It is also possible to modify [Dijkstra's algorithm](dijkstra.md), so that it needs $O(nm)$ pre-processing as an initial step and then works in $O(m \log n)$ per iteration, making the overall running time to be $O(mn + F m \log n)$. [Here](http://web.archive.org/web/20211009144446/https://min-25.hatenablog.com/entry/2018/03/19/235802) is a generator of a graph, on which such algorithm would require $O(2^{n/2} n^2 \log n)$ time.
The modified Dijkstra's algorithm uses so-called potentials from [Johnson's algorithm](https://en.wikipedia.org/wiki/Johnson%27s_algorithm). It is possible to combine the ideas of this algorithm and Dinic's algorithm to reduce the number of iterations from $F$ to $\min(F, nC)$, where $C$ is the maximum cost found among edges. You may read further about potentials and their combination with Dinic algorithm [here](https://codeforces.com/blog/entry/105658).
## Implementation
Here is an implementation using the [SPFA algorithm](bellman_ford.md) for the simplest case.
```{.cpp file=min_cost_flow_successive_shortest_path}
struct Edge
{
int from, to, capacity, cost;
};
vector<vector<int>> adj, cost, capacity;
const int INF = 1e9;
void shortest_paths(int n, int v0, vector<int>& d, vector<int>& p) {
d.assign(n, INF);
d[v0] = 0;
vector<bool> inq(n, false);
queue<int> q;
q.push(v0);
p.assign(n, -1);
while (!q.empty()) {
int u = q.front();
q.pop();
inq[u] = false;
for (int v : adj[u]) {
if (capacity[u][v] > 0 && d[v] > d[u] + cost[u][v]) {
d[v] = d[u] + cost[u][v];
p[v] = u;
if (!inq[v]) {
inq[v] = true;
q.push(v);
}
}
}
}
}
int min_cost_flow(int N, vector<Edge> edges, int K, int s, int t) {
adj.assign(N, vector<int>());
cost.assign(N, vector<int>(N, 0));
capacity.assign(N, vector<int>(N, 0));
for (Edge e : edges) {
adj[e.from].push_back(e.to);
adj[e.to].push_back(e.from);
cost[e.from][e.to] = e.cost;
cost[e.to][e.from] = -e.cost;
capacity[e.from][e.to] = e.capacity;
}
int flow = 0;
int cost = 0;
vector<int> d, p;
while (flow < K) {
shortest_paths(N, s, d, p);
if (d[t] == INF)
break;
// find max flow on that path
int f = K - flow;
int cur = t;
while (cur != s) {
f = min(f, capacity[p[cur]][cur]);
cur = p[cur];
}
// apply flow
flow += f;
cost += f * d[t];
cur = t;
while (cur != s) {
capacity[p[cur]][cur] -= f;
capacity[cur][p[cur]] += f;
cur = p[cur];
}
}
if (flow < K)
return -1;
else
return cost;
}
```
|
---
title
min_cost_flow
---
# Minimum-cost flow - Successive shortest path algorithm
Given a network $G$ consisting of $n$ vertices and $m$ edges.
For each edge (generally speaking, oriented edges, but see below), the capacity (a non-negative integer) and the cost per unit of flow along this edge (some integer) are given.
Also the source $s$ and the sink $t$ are marked.
For a given value $K$, we have to find a flow of this quantity, and among all flows of this quantity we have to choose the flow with the lowest cost.
This task is called **minimum-cost flow problem**.
Sometimes the task is given a little differently:
you want to find the maximum flow, and among all maximal flows we want to find the one with the least cost.
This is called the **minimum-cost maximum-flow problem**.
Both these problems can be solved effectively with the algorithm of successive shortest paths.
## Algorithm
This algorithm is very similar to the [Edmonds-Karp](edmonds_karp.md) for computing the maximum flow.
### Simplest case
First we only consider the simplest case, where the graph is oriented, and there is at most one edge between any pair of vertices (e.g. if $(i, j)$ is an edge in the graph, then $(j, i)$ cannot be part in it as well).
Let $U_{i j}$ be the capacity of an edge $(i, j)$ if this edge exists.
And let $C_{i j}$ be the cost per unit of flow along this edge $(i, j)$.
And finally let $F_{i, j}$ be the flow along the edge $(i, j)$.
Initially all flow values are zero.
We **modify** the network as follows:
for each edge $(i, j)$ we add the **reverse edge** $(j, i)$ to the network with the capacity $U_{j i} = 0$ and the cost $C_{j i} = -C_{i j}$.
Since, according to our restrictions, the edge $(j, i)$ was not in the network before, we still have a network that is not a multigraph (graph with multiple edges).
In addition we will always keep the condition $F_{j i} = -F_{i j}$ true during the steps of the algorithm.
We define the **residual network** for some fixed flow $F$ as follow (just like in the Ford-Fulkerson algorithm):
the residual network contains only unsaturated edges (i.e. edges in which $F_{i j} < U_{i j}$), and the residual capacity of each such edge is $R_{i j} = U_{i j} - F_{i j}$.
Now we can talk about the **algorithms** to compute the minimum-cost flow.
At each iteration of the algorithm we find the shortest path in the residual graph from $s$ to $t$.
In contrary to Edmonds-Karp we look for the shortest path in terms of the cost of the path, instead of the number of edges.
If there doesn't exists a path anymore, then the algorithm terminates, and the stream $F$ is the desired one.
If a path was found, we increase the flow along it as much as possible (i.e. we find the minimal residual capacity $R$ of the path, and increase the flow by it, and reduce the back edges by the same amount).
If at some point the flow reaches the value $K$, then we stop the algorithm (note that in the last iteration of the algorithm it is necessary to increase the flow by only such an amount so that the final flow value doesn't surpass $K$).
It is not difficult to see, that if we set $K$ to infinity, then the algorithm will find the minimum-cost maximum-flow.
So both variations of the problem can be solved by the same algorithm.
### Undirected graphs / multigraphs
The case of an undirected graph or a multigraph doesn't differ conceptually from the algorithm above.
The algorithm will also work on these graphs.
However it becomes a little more difficult to implement it.
An **undirected edge** $(i, j)$ is actually the same as two oriented edges $(i, j)$ and $(j, i)$ with the same capacity and values.
Since the above-described minimum-cost flow algorithm generates a back edge for each directed edge, so it splits the undirected edge into $4$ directed edges, and we actually get a **multigraph**.
How do we deal with **multiple edges**?
First the flow for each of the multiple edges must be kept separately.
Secondly, when searching for the shortest path, it is necessary to take into account that it is important which of the multiple edges is used in the path.
Thus instead of the usual ancestor array we additionally must store the edge number from which we came from along with the ancestor.
Thirdly, as the flow increases along a certain edge, it is necessary to reduce the flow along the back edge.
Since we have multiple edges, we have to store the edge number for the reversed edge for each edge.
There are no other obstructions with undirected graphs or multigraphs.
### Complexity
The algorithm here is generally exponential in the size of the input. To be more specific, in the worst case it may push only as much as $1$ unit of flow on each iteration, taking $O(F)$ iterations to find a minimum-cost flow of size $F$, making a total runtime to be $O(F \cdot T)$, where $T$ is the time required to find the shortest path from source to sink.
If [Bellman-Ford](bellman_ford.md) algorithm is used for this, it makes the running time $O(F mn)$. It is also possible to modify [Dijkstra's algorithm](dijkstra.md), so that it needs $O(nm)$ pre-processing as an initial step and then works in $O(m \log n)$ per iteration, making the overall running time to be $O(mn + F m \log n)$. [Here](http://web.archive.org/web/20211009144446/https://min-25.hatenablog.com/entry/2018/03/19/235802) is a generator of a graph, on which such algorithm would require $O(2^{n/2} n^2 \log n)$ time.
The modified Dijkstra's algorithm uses so-called potentials from [Johnson's algorithm](https://en.wikipedia.org/wiki/Johnson%27s_algorithm). It is possible to combine the ideas of this algorithm and Dinic's algorithm to reduce the number of iterations from $F$ to $\min(F, nC)$, where $C$ is the maximum cost found among edges. You may read further about potentials and their combination with Dinic algorithm [here](https://codeforces.com/blog/entry/105658).
## Implementation
Here is an implementation using the [SPFA algorithm](bellman_ford.md) for the simplest case.
```{.cpp file=min_cost_flow_successive_shortest_path}
struct Edge
{
int from, to, capacity, cost;
};
vector<vector<int>> adj, cost, capacity;
const int INF = 1e9;
void shortest_paths(int n, int v0, vector<int>& d, vector<int>& p) {
d.assign(n, INF);
d[v0] = 0;
vector<bool> inq(n, false);
queue<int> q;
q.push(v0);
p.assign(n, -1);
while (!q.empty()) {
int u = q.front();
q.pop();
inq[u] = false;
for (int v : adj[u]) {
if (capacity[u][v] > 0 && d[v] > d[u] + cost[u][v]) {
d[v] = d[u] + cost[u][v];
p[v] = u;
if (!inq[v]) {
inq[v] = true;
q.push(v);
}
}
}
}
}
int min_cost_flow(int N, vector<Edge> edges, int K, int s, int t) {
adj.assign(N, vector<int>());
cost.assign(N, vector<int>(N, 0));
capacity.assign(N, vector<int>(N, 0));
for (Edge e : edges) {
adj[e.from].push_back(e.to);
adj[e.to].push_back(e.from);
cost[e.from][e.to] = e.cost;
cost[e.to][e.from] = -e.cost;
capacity[e.from][e.to] = e.capacity;
}
int flow = 0;
int cost = 0;
vector<int> d, p;
while (flow < K) {
shortest_paths(N, s, d, p);
if (d[t] == INF)
break;
// find max flow on that path
int f = K - flow;
int cur = t;
while (cur != s) {
f = min(f, capacity[p[cur]][cur]);
cur = p[cur];
}
// apply flow
flow += f;
cost += f * d[t];
cur = t;
while (cur != s) {
capacity[p[cur]][cur] -= f;
capacity[cur][p[cur]] += f;
cur = p[cur];
}
}
if (flow < K)
return -1;
else
return cost;
}
```
|
Minimum-cost flow - Successive shortest path algorithm
|
---
title
bipartite_checking
---
# Check whether a graph is bipartite
A bipartite graph is a graph whose vertices can be divided into two disjoint sets so that every edge connects two vertices from different sets (i.e. there are no edges which connect vertices from the same set). These sets are usually called sides.
You are given an undirected graph. Check whether it is bipartite, and if it is, output its sides.
## Algorithm
There exists a theorem which claims that a graph is bipartite if and only if all its cycles have even length. However, in practice it's more convenient to use a different formulation of the definition: a graph is bipartite if and only if it is two-colorable.
Let's use a series of [breadth-first searches](breadth-first-search.md), starting from each vertex which hasn't been visited yet. In each search, assign the vertex from which we start to side 1. Each time we visit a yet unvisited neighbor of a vertex assigned to one side, we assign it to the other side. When we try to go to a neighbor of a vertex assigned to one side which has already been visited, we check that it has been assigned to the other side; if it has been assigned to the same side, we conclude that the graph is not bipartite. Once we've visited all vertices and successfully assigned them to sides, we know that the graph is bipartite and we have constructed its partitioning.
## Implementation
```cpp
int n;
vector<vector<int>> adj;
vector<int> side(n, -1);
bool is_bipartite = true;
queue<int> q;
for (int st = 0; st < n; ++st) {
if (side[st] == -1) {
q.push(st);
side[st] = 0;
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : adj[v]) {
if (side[u] == -1) {
side[u] = side[v] ^ 1;
q.push(u);
} else {
is_bipartite &= side[u] != side[v];
}
}
}
}
}
cout << (is_bipartite ? "YES" : "NO") << endl;
```
#
|
---
title
bipartite_checking
---
# Check whether a graph is bipartite
A bipartite graph is a graph whose vertices can be divided into two disjoint sets so that every edge connects two vertices from different sets (i.e. there are no edges which connect vertices from the same set). These sets are usually called sides.
You are given an undirected graph. Check whether it is bipartite, and if it is, output its sides.
## Algorithm
There exists a theorem which claims that a graph is bipartite if and only if all its cycles have even length. However, in practice it's more convenient to use a different formulation of the definition: a graph is bipartite if and only if it is two-colorable.
Let's use a series of [breadth-first searches](breadth-first-search.md), starting from each vertex which hasn't been visited yet. In each search, assign the vertex from which we start to side 1. Each time we visit a yet unvisited neighbor of a vertex assigned to one side, we assign it to the other side. When we try to go to a neighbor of a vertex assigned to one side which has already been visited, we check that it has been assigned to the other side; if it has been assigned to the same side, we conclude that the graph is not bipartite. Once we've visited all vertices and successfully assigned them to sides, we know that the graph is bipartite and we have constructed its partitioning.
## Implementation
```cpp
int n;
vector<vector<int>> adj;
vector<int> side(n, -1);
bool is_bipartite = true;
queue<int> q;
for (int st = 0; st < n; ++st) {
if (side[st] == -1) {
q.push(st);
side[st] = 0;
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : adj[v]) {
if (side[u] == -1) {
side[u] = side[v] ^ 1;
q.push(u);
} else {
is_bipartite &= side[u] != side[v];
}
}
}
}
}
cout << (is_bipartite ? "YES" : "NO") << endl;
```
### Practice problems:
- [SPOJ - BUGLIFE](http://www.spoj.com/problems/BUGLIFE/)
- [Codeforces - Graph Without Long Directed Paths](https://codeforces.com/contest/1144/problem/F)
- [Codeforces - String Coloring (easy version)](https://codeforces.com/contest/1296/problem/E1)
- [CSES : Building Teams](https://cses.fi/problemset/task/1668)
|
Check whether a graph is bipartite
|
---
title
2_sat
---
# 2-SAT
SAT (Boolean satisfiability problem) is the problem of assigning Boolean values to variables to satisfy a given Boolean formula.
The Boolean formula will usually be given in CNF (conjunctive normal form), which is a conjunction of multiple clauses, where each clause is a disjunction of literals (variables or negation of variables).
2-SAT (2-satisfiability) is a restriction of the SAT problem, in 2-SAT every clause has exactly two literals.
Here is an example of such a 2-SAT problem.
Find an assignment of $a, b, c$ such that the following formula is true:
$$(a \lor \lnot b) \land (\lnot a \lor b) \land (\lnot a \lor \lnot b) \land (a \lor \lnot c)$$
SAT is NP-complete, there is no known efficient solution known for it.
However 2SAT can be solved efficiently in $O(n + m)$ where $n$ is the number of variables and $m$ is the number of clauses.
## Algorithm:
First we need to convert the problem to a different form, the so-called implicative normal form.
Note that the expression $a \lor b$ is equivalent to $\lnot a \Rightarrow b \land \lnot b \Rightarrow a$ (if one of the two variables is false, then the other one must be true).
We now construct a directed graph of these implications:
for each variable $x$ there will be two vertices $v_x$ and $v_{\lnot x}$.
The edges will correspond to the implications.
Let's look at the example in 2-CNF form:
$$(a \lor \lnot b) \land (\lnot a \lor b) \land (\lnot a \lor \lnot b) \land (a \lor \lnot c)$$
The oriented graph will contain the following vertices and edges:
$$\begin{array}{cccc}
\lnot a \Rightarrow \lnot b & a \Rightarrow b & a \Rightarrow \lnot b & \lnot a \Rightarrow \lnot c\\
b \Rightarrow a & \lnot b \Rightarrow \lnot a & b \Rightarrow \lnot a & c \Rightarrow a
\end{array}$$
You can see the implication graph in the following image:
<center></center>
It is worth paying attention to the property of the implication graph:
if there is an edge $a \Rightarrow b$, then there also is an edge $\lnot b \Rightarrow \lnot a$.
Also note, that if $x$ is reachable from $\lnot x$, and $\lnot x$ is reachable from $x$, then the problem has no solution.
Whatever value we choose for the variable $x$, it will always end in a contradiction - if $x$ will be assigned $\text{true}$ then the implication tell us that $\lnot x$ should also be $\text{true}$ and visa versa.
It turns out, that this condition is not only necessary, but also sufficient.
We will prove this in a few paragraphs below.
First recall, if a vertex is reachable from a second one, and the second one is reachable from the first one, then these two vertices are in the same strongly connected component.
Therefore we can formulate the criterion for the existence of a solution as follows:
In order for this 2-SAT problem to have a solution, it is necessary and sufficient that for any variable $x$ the vertices $x$ and $\lnot x$ are in different strongly connected components of the strong connection of the implication graph.
This criterion can be verified in $O(n + m)$ time by finding all strongly connected components.
The following image shows all strongly connected components for the example.
As we can check easily, neither of the four components contain a vertex $x$ and its negation $\lnot x$, therefore the example has a solution.
We will learn in the next paragraphs how to compute a valid assignment, but just for demonstration purposes the solution $a = \text{false}$, $b = \text{false}$, $c = \text{false}$ is given.
<center></center>
Now we construct the algorithm for finding the solution of the 2-SAT problem on the assumption that the solution exists.
Note that, in spite of the fact that the solution exists, it can happen that $\lnot x$ is reachable from $x$ in the implication graph, or that (but not simultaneously) $x$ is reachable from $\lnot x$.
In that case the choice of either $\text{true}$ or $\text{false}$ for $x$ will lead to a contradiction, while the choice of the other one will not.
Let's learn how to choose a value, such that we don't generate a contradiction.
Let us sort the strongly connected components in topological order (i.e. $\text{comp}[v] \le \text{comp}[u]$ if there is a path from $v$ to $u$) and let $\text{comp}[v]$ denote the index of strongly connected component to which the vertex $v$ belongs.
Then, if $\text{comp}[x] < \text{comp}[\lnot x]$ we assign $x$ with $\text{false}$ and $\text{true}$ otherwise.
Let us prove that with this assignment of the variables we do not arrive at a contradiction.
Suppose $x$ is assigned with $\text{true}$.
The other case can be proven in a similar way.
First we prove that the vertex $x$ cannot reach the vertex $\lnot x$.
Because we assigned $\text{true}$ it has to hold that the index of strongly connected component of $x$ is greater than the index of the component of $\lnot x$.
This means that $\lnot x$ is located on the left of the component containing $x$, and the later vertex cannot reach the first.
Secondly we prove that there doesn't exist a variable $y$, such that the vertices $y$ and $\lnot y$ are both reachable from $x$ in the implication graph.
This would cause a contradiction, because $x = \text{true}$ implies that $y = \text{true}$ and $\lnot y = \text{true}$.
Let us prove this by contradiction.
Suppose that $y$ and $\lnot y$ are both reachable from $x$, then by the property of the implication graph $\lnot x$ is reachable from both $y$ and $\lnot y$.
By transitivity this results that $\lnot x$ is reachable by $x$, which contradicts the assumption.
So we have constructed an algorithm that finds the required values of variables under the assumption that for any variable $x$ the vertices $x$ and $\lnot x$ are in different strongly connected components.
Above showed the correctness of this algorithm.
Consequently we simultaneously proved the above criterion for the existence of a solution.
## Implementation:
Now we can implement the entire algorithm.
First we construct the graph of implications and find all strongly connected components.
This can be accomplished with Kosaraju's algorithm in $O(n + m)$ time.
In the second traversal of the graph Kosaraju's algorithm visits the strongly connected components in topological order, therefore it is easy to compute $\text{comp}[v]$ for each vertex $v$.
Afterwards we can choose the assignment of $x$ by comparing $\text{comp}[x]$ and $\text{comp}[\lnot x]$.
If $\text{comp}[x] = \text{comp}[\lnot x]$ we return $\text{false}$ to indicate that there doesn't exist a valid assignment that satisfies the 2-SAT problem.
Below is the implementation of the solution of the 2-SAT problem for the already constructed graph of implication $adj$ and the transpose graph $adj^{\intercal}$ (in which the direction of each edge is reversed).
In the graph the vertices with indices $2k$ and $2k+1$ are the two vertices corresponding to variable $k$ with $2k+1$ corresponding to the negated variable.
```{.cpp file=2sat}
int n;
vector<vector<int>> adj, adj_t;
vector<bool> used;
vector<int> order, comp;
vector<bool> assignment;
void dfs1(int v) {
used[v] = true;
for (int u : adj[v]) {
if (!used[u])
dfs1(u);
}
order.push_back(v);
}
void dfs2(int v, int cl) {
comp[v] = cl;
for (int u : adj_t[v]) {
if (comp[u] == -1)
dfs2(u, cl);
}
}
bool solve_2SAT() {
order.clear();
used.assign(n, false);
for (int i = 0; i < n; ++i) {
if (!used[i])
dfs1(i);
}
comp.assign(n, -1);
for (int i = 0, j = 0; i < n; ++i) {
int v = order[n - i - 1];
if (comp[v] == -1)
dfs2(v, j++);
}
assignment.assign(n / 2, false);
for (int i = 0; i < n; i += 2) {
if (comp[i] == comp[i + 1])
return false;
assignment[i / 2] = comp[i] > comp[i + 1];
}
return true;
}
void add_disjunction(int a, bool na, int b, bool nb) {
// na and nb signify whether a and b are to be negated
a = 2*a ^ na;
b = 2*b ^ nb;
int neg_a = a ^ 1;
int neg_b = b ^ 1;
adj[neg_a].push_back(b);
adj[neg_b].push_back(a);
adj_t[b].push_back(neg_a);
adj_t[a].push_back(neg_b);
}
```
|
---
title
2_sat
---
# 2-SAT
SAT (Boolean satisfiability problem) is the problem of assigning Boolean values to variables to satisfy a given Boolean formula.
The Boolean formula will usually be given in CNF (conjunctive normal form), which is a conjunction of multiple clauses, where each clause is a disjunction of literals (variables or negation of variables).
2-SAT (2-satisfiability) is a restriction of the SAT problem, in 2-SAT every clause has exactly two literals.
Here is an example of such a 2-SAT problem.
Find an assignment of $a, b, c$ such that the following formula is true:
$$(a \lor \lnot b) \land (\lnot a \lor b) \land (\lnot a \lor \lnot b) \land (a \lor \lnot c)$$
SAT is NP-complete, there is no known efficient solution known for it.
However 2SAT can be solved efficiently in $O(n + m)$ where $n$ is the number of variables and $m$ is the number of clauses.
## Algorithm:
First we need to convert the problem to a different form, the so-called implicative normal form.
Note that the expression $a \lor b$ is equivalent to $\lnot a \Rightarrow b \land \lnot b \Rightarrow a$ (if one of the two variables is false, then the other one must be true).
We now construct a directed graph of these implications:
for each variable $x$ there will be two vertices $v_x$ and $v_{\lnot x}$.
The edges will correspond to the implications.
Let's look at the example in 2-CNF form:
$$(a \lor \lnot b) \land (\lnot a \lor b) \land (\lnot a \lor \lnot b) \land (a \lor \lnot c)$$
The oriented graph will contain the following vertices and edges:
$$\begin{array}{cccc}
\lnot a \Rightarrow \lnot b & a \Rightarrow b & a \Rightarrow \lnot b & \lnot a \Rightarrow \lnot c\\
b \Rightarrow a & \lnot b \Rightarrow \lnot a & b \Rightarrow \lnot a & c \Rightarrow a
\end{array}$$
You can see the implication graph in the following image:
<center></center>
It is worth paying attention to the property of the implication graph:
if there is an edge $a \Rightarrow b$, then there also is an edge $\lnot b \Rightarrow \lnot a$.
Also note, that if $x$ is reachable from $\lnot x$, and $\lnot x$ is reachable from $x$, then the problem has no solution.
Whatever value we choose for the variable $x$, it will always end in a contradiction - if $x$ will be assigned $\text{true}$ then the implication tell us that $\lnot x$ should also be $\text{true}$ and visa versa.
It turns out, that this condition is not only necessary, but also sufficient.
We will prove this in a few paragraphs below.
First recall, if a vertex is reachable from a second one, and the second one is reachable from the first one, then these two vertices are in the same strongly connected component.
Therefore we can formulate the criterion for the existence of a solution as follows:
In order for this 2-SAT problem to have a solution, it is necessary and sufficient that for any variable $x$ the vertices $x$ and $\lnot x$ are in different strongly connected components of the strong connection of the implication graph.
This criterion can be verified in $O(n + m)$ time by finding all strongly connected components.
The following image shows all strongly connected components for the example.
As we can check easily, neither of the four components contain a vertex $x$ and its negation $\lnot x$, therefore the example has a solution.
We will learn in the next paragraphs how to compute a valid assignment, but just for demonstration purposes the solution $a = \text{false}$, $b = \text{false}$, $c = \text{false}$ is given.
<center></center>
Now we construct the algorithm for finding the solution of the 2-SAT problem on the assumption that the solution exists.
Note that, in spite of the fact that the solution exists, it can happen that $\lnot x$ is reachable from $x$ in the implication graph, or that (but not simultaneously) $x$ is reachable from $\lnot x$.
In that case the choice of either $\text{true}$ or $\text{false}$ for $x$ will lead to a contradiction, while the choice of the other one will not.
Let's learn how to choose a value, such that we don't generate a contradiction.
Let us sort the strongly connected components in topological order (i.e. $\text{comp}[v] \le \text{comp}[u]$ if there is a path from $v$ to $u$) and let $\text{comp}[v]$ denote the index of strongly connected component to which the vertex $v$ belongs.
Then, if $\text{comp}[x] < \text{comp}[\lnot x]$ we assign $x$ with $\text{false}$ and $\text{true}$ otherwise.
Let us prove that with this assignment of the variables we do not arrive at a contradiction.
Suppose $x$ is assigned with $\text{true}$.
The other case can be proven in a similar way.
First we prove that the vertex $x$ cannot reach the vertex $\lnot x$.
Because we assigned $\text{true}$ it has to hold that the index of strongly connected component of $x$ is greater than the index of the component of $\lnot x$.
This means that $\lnot x$ is located on the left of the component containing $x$, and the later vertex cannot reach the first.
Secondly we prove that there doesn't exist a variable $y$, such that the vertices $y$ and $\lnot y$ are both reachable from $x$ in the implication graph.
This would cause a contradiction, because $x = \text{true}$ implies that $y = \text{true}$ and $\lnot y = \text{true}$.
Let us prove this by contradiction.
Suppose that $y$ and $\lnot y$ are both reachable from $x$, then by the property of the implication graph $\lnot x$ is reachable from both $y$ and $\lnot y$.
By transitivity this results that $\lnot x$ is reachable by $x$, which contradicts the assumption.
So we have constructed an algorithm that finds the required values of variables under the assumption that for any variable $x$ the vertices $x$ and $\lnot x$ are in different strongly connected components.
Above showed the correctness of this algorithm.
Consequently we simultaneously proved the above criterion for the existence of a solution.
## Implementation:
Now we can implement the entire algorithm.
First we construct the graph of implications and find all strongly connected components.
This can be accomplished with Kosaraju's algorithm in $O(n + m)$ time.
In the second traversal of the graph Kosaraju's algorithm visits the strongly connected components in topological order, therefore it is easy to compute $\text{comp}[v]$ for each vertex $v$.
Afterwards we can choose the assignment of $x$ by comparing $\text{comp}[x]$ and $\text{comp}[\lnot x]$.
If $\text{comp}[x] = \text{comp}[\lnot x]$ we return $\text{false}$ to indicate that there doesn't exist a valid assignment that satisfies the 2-SAT problem.
Below is the implementation of the solution of the 2-SAT problem for the already constructed graph of implication $adj$ and the transpose graph $adj^{\intercal}$ (in which the direction of each edge is reversed).
In the graph the vertices with indices $2k$ and $2k+1$ are the two vertices corresponding to variable $k$ with $2k+1$ corresponding to the negated variable.
```{.cpp file=2sat}
int n;
vector<vector<int>> adj, adj_t;
vector<bool> used;
vector<int> order, comp;
vector<bool> assignment;
void dfs1(int v) {
used[v] = true;
for (int u : adj[v]) {
if (!used[u])
dfs1(u);
}
order.push_back(v);
}
void dfs2(int v, int cl) {
comp[v] = cl;
for (int u : adj_t[v]) {
if (comp[u] == -1)
dfs2(u, cl);
}
}
bool solve_2SAT() {
order.clear();
used.assign(n, false);
for (int i = 0; i < n; ++i) {
if (!used[i])
dfs1(i);
}
comp.assign(n, -1);
for (int i = 0, j = 0; i < n; ++i) {
int v = order[n - i - 1];
if (comp[v] == -1)
dfs2(v, j++);
}
assignment.assign(n / 2, false);
for (int i = 0; i < n; i += 2) {
if (comp[i] == comp[i + 1])
return false;
assignment[i / 2] = comp[i] > comp[i + 1];
}
return true;
}
void add_disjunction(int a, bool na, int b, bool nb) {
// na and nb signify whether a and b are to be negated
a = 2*a ^ na;
b = 2*b ^ nb;
int neg_a = a ^ 1;
int neg_b = b ^ 1;
adj[neg_a].push_back(b);
adj[neg_b].push_back(a);
adj_t[b].push_back(neg_a);
adj_t[a].push_back(neg_b);
}
```
## Practice Problems
* [Codeforces: The Door Problem](http://codeforces.com/contest/776/problem/D)
* [Kattis: Illumination](https://open.kattis.com/problems/illumination)
* [UVA: Rectangles](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=3081)
* [Codeforces : Radio Stations](https://codeforces.com/problemset/problem/1215/F)
* [CSES : Giant Pizza](https://cses.fi/problemset/task/1684)
|
2-SAT
|
---
title
kirchhoff_theorem
---
# Kirchhoff's theorem. Finding the number of spanning trees
Problem: You are given a connected undirected graph (with possible multiple edges) represented using an adjacency matrix. Find the number of different spanning trees of this graph.
The following formula was proven by Kirchhoff in 1847.
## Kirchhoff's matrix tree theorem
Let $A$ be the adjacency matrix of the graph: $A_{u,v}$ is the number of edges between $u$ and $v$.
Let $D$ be the degree matrix of the graph: a diagonal matrix with $D_{u,u}$ being the degree of vertex $u$ (including multiple edges and loops - edges which connect vertex $u$ with itself).
The Laplacian matrix of the graph is defined as $L = D - A$.
According to Kirchhoff's theorem, all cofactors of this matrix are equal to each other, and they are equal to the number of spanning trees of the graph.
The $(i,j)$ cofactor of a matrix is the product of $(-1)^{i + j}$ with the determinant of the matrix that you get after removing the $i$-th row and $j$-th column.
So you can, for example, delete the last row and last column of the matrix $L$, and the absolute value of the determinant of the resulting matrix will give you the number of spanning trees.
The determinant of the matrix can be found in $O(N^3)$ by using the [Gaussian method](../linear_algebra/determinant-gauss.md).
The proof of this theorem is quite difficult and is not presented here; for an outline of the proof and variations of the theorem for graphs without multiple edges and for directed graphs refer to [Wikipedia](https://en.wikipedia.org/wiki/Kirchhoff%27s_theorem).
## Relation to Kirchhoff's circuit laws
Kirchhoff's matrix tree theorem and Kirchhoff's laws for electrical circuit are related in a beautiful way. It is possible to show (using Ohm's law and Kirchhoff's first law) that resistance $R_{ij}$ between two points of the circuit $i$ and $j$ is
$$R_{ij} = \frac{ \left| L^{(i,j)} \right| }{ | L^j | }.$$
Here the matrix $L$ is obtained from the matrix of inverse resistances $A$ ($A_{i,j}$ is inverse of the resistance of the conductor between points $i$ and $j$) using the procedure described in Kirchhoff's matrix tree theorem.
$T^j$ is the matrix with row and column $j$ removed, $T^{(i,j)}$ is the matrix with two rows and two columns $i$ and $j$ removed.
Kirchhoff's theorem gives this formula geometric meaning.
|
---
title
kirchhoff_theorem
---
# Kirchhoff's theorem. Finding the number of spanning trees
Problem: You are given a connected undirected graph (with possible multiple edges) represented using an adjacency matrix. Find the number of different spanning trees of this graph.
The following formula was proven by Kirchhoff in 1847.
## Kirchhoff's matrix tree theorem
Let $A$ be the adjacency matrix of the graph: $A_{u,v}$ is the number of edges between $u$ and $v$.
Let $D$ be the degree matrix of the graph: a diagonal matrix with $D_{u,u}$ being the degree of vertex $u$ (including multiple edges and loops - edges which connect vertex $u$ with itself).
The Laplacian matrix of the graph is defined as $L = D - A$.
According to Kirchhoff's theorem, all cofactors of this matrix are equal to each other, and they are equal to the number of spanning trees of the graph.
The $(i,j)$ cofactor of a matrix is the product of $(-1)^{i + j}$ with the determinant of the matrix that you get after removing the $i$-th row and $j$-th column.
So you can, for example, delete the last row and last column of the matrix $L$, and the absolute value of the determinant of the resulting matrix will give you the number of spanning trees.
The determinant of the matrix can be found in $O(N^3)$ by using the [Gaussian method](../linear_algebra/determinant-gauss.md).
The proof of this theorem is quite difficult and is not presented here; for an outline of the proof and variations of the theorem for graphs without multiple edges and for directed graphs refer to [Wikipedia](https://en.wikipedia.org/wiki/Kirchhoff%27s_theorem).
## Relation to Kirchhoff's circuit laws
Kirchhoff's matrix tree theorem and Kirchhoff's laws for electrical circuit are related in a beautiful way. It is possible to show (using Ohm's law and Kirchhoff's first law) that resistance $R_{ij}$ between two points of the circuit $i$ and $j$ is
$$R_{ij} = \frac{ \left| L^{(i,j)} \right| }{ | L^j | }.$$
Here the matrix $L$ is obtained from the matrix of inverse resistances $A$ ($A_{i,j}$ is inverse of the resistance of the conductor between points $i$ and $j$) using the procedure described in Kirchhoff's matrix tree theorem.
$T^j$ is the matrix with row and column $j$ removed, $T^{(i,j)}$ is the matrix with two rows and two columns $i$ and $j$ removed.
Kirchhoff's theorem gives this formula geometric meaning.
## Practice Problems
- [CODECHEF: Roads in Stars](https://www.codechef.com/problems/STARROAD)
- [SPOJ: Maze](http://www.spoj.com/problems/KPMAZE/)
- [CODECHEF: Complement Spanning Trees](https://www.codechef.com/problems/CSTREE)
|
Kirchhoff's theorem. Finding the number of spanning trees
|
---
title
- Original
---
# Strong Orientation
A **strong orientation** of an undirected graph is an assignment of a direction to each edge that makes it a [strongly connected graph](strongly-connected-components.md).
That is, after the *orientation* we should be able to visit any vertex from any vertex by following the directed edges.
## Solution
Of course, this cannot be done to *every* graph.
Consider a [bridge](bridge-searching.md) in a graph.
We have to assign a direction to it and by doing so we make this bridge "crossable" in only one direction. That means we can't go from one of the bridge's ends to the other, so we can't make the graph strongly connected.
Now consider a [DFS](depth-first-search.md) through a bridgeless connected graph.
Clearly, we will visit each vertex.
And since there are no bridges, we can remove any DFS tree edge and still be able to go
from below the edge to above the edge by using a path that contains at least one back edge.
From this follows that from any vertex we can go to the root of the DFS tree.
Also, from the root of the DFS tree we can visit any vertex we choose.
We found a strong orientation!
In other words, to strongly orient a bridgeless connected graph,
run a DFS on it and let the DFS tree edges point away from the DFS root and
all other edges from the descendant to the ancestor in the DFS tree.
The result that bridgeless connected graphs are exactly the graphs that have strong orientations is called **Robbins' theorem**.
## Problem extension
Let's consider the problem of finding a graph orientation so that the number of SCCs is minimal.
Of course, each graph component can be considered separately.
Now, since only bridgeless graphs are strongly orientable, let's remove all bridges temporarily.
We end up with some number of bridgeless components
(exactly *how many components there were at the beginning* + *how many bridges there were*)
and we know that we can strongly orient each of them.
We were only allowed to orient edges, not remove them, but it turns out we can orient the bridges arbitrarily.
Of course, the easiest way to orient them is to run the algorithm described above without modifications on each original connected component.
### Implementation
Here, the input is *n* — the number of vertices, *m* — the number of edges, then *m* lines describing the edges.
The output is the minimal number of SCCs on the first line and on the second line
a string of *m* characters,
either `>` — telling us that the corresponding edge from the input
is oriented from the left to the right vertex (as in the input),
or `<` — the opposite.
This is a bridge search algorithm modified to also orient the edges,
you can as well orient the edges as a first step and count the SCCs on the oriented graph as a second.
```cpp
vector<vector<pair<int, int>>> adj; // adjacency list - vertex and edge pairs
vector<pair<int, int>> edges;
vector<int> tin, low;
int bridge_cnt;
string orient;
vector<bool> edge_used;
void find_bridges(int v) {
static int time = 0;
low[v] = tin[v] = time++;
for (auto p : adj[v]) {
if (edge_used[p.second]) continue;
edge_used[p.second] = true;
orient[p.second] = v == edges[p.second].first ? '>' : '<';
int nv = p.first;
if (tin[nv] == -1) { // if nv is not visited yet
find_bridges(nv);
low[v] = min(low[v], low[nv]);
if (low[nv] > tin[v]) {
// a bridge between v and nv
bridge_cnt++;
}
} else {
low[v] = min(low[v], low[nv]);
}
}
}
int main() {
int n, m;
scanf("%d %d", &n, &m);
adj.resize(n);
tin.resize(n, -1);
low.resize(n, -1);
orient.resize(m);
edges.resize(m);
edge_used.resize(m);
for (int i = 0; i < m; i++) {
int a, b;
scanf("%d %d", &a, &b);
a--; b--;
adj[a].push_back({b, i});
adj[b].push_back({a, i});
edges[i] = {a, b};
}
int comp_cnt = 0;
for (int v = 0; v < n; v++) {
if (tin[v] == -1) {
comp_cnt++;
find_bridges(v);
}
}
printf("%d\n%s\n", comp_cnt + bridge_cnt, orient.c_str());
}
```
|
---
title
- Original
---
# Strong Orientation
A **strong orientation** of an undirected graph is an assignment of a direction to each edge that makes it a [strongly connected graph](strongly-connected-components.md).
That is, after the *orientation* we should be able to visit any vertex from any vertex by following the directed edges.
## Solution
Of course, this cannot be done to *every* graph.
Consider a [bridge](bridge-searching.md) in a graph.
We have to assign a direction to it and by doing so we make this bridge "crossable" in only one direction. That means we can't go from one of the bridge's ends to the other, so we can't make the graph strongly connected.
Now consider a [DFS](depth-first-search.md) through a bridgeless connected graph.
Clearly, we will visit each vertex.
And since there are no bridges, we can remove any DFS tree edge and still be able to go
from below the edge to above the edge by using a path that contains at least one back edge.
From this follows that from any vertex we can go to the root of the DFS tree.
Also, from the root of the DFS tree we can visit any vertex we choose.
We found a strong orientation!
In other words, to strongly orient a bridgeless connected graph,
run a DFS on it and let the DFS tree edges point away from the DFS root and
all other edges from the descendant to the ancestor in the DFS tree.
The result that bridgeless connected graphs are exactly the graphs that have strong orientations is called **Robbins' theorem**.
## Problem extension
Let's consider the problem of finding a graph orientation so that the number of SCCs is minimal.
Of course, each graph component can be considered separately.
Now, since only bridgeless graphs are strongly orientable, let's remove all bridges temporarily.
We end up with some number of bridgeless components
(exactly *how many components there were at the beginning* + *how many bridges there were*)
and we know that we can strongly orient each of them.
We were only allowed to orient edges, not remove them, but it turns out we can orient the bridges arbitrarily.
Of course, the easiest way to orient them is to run the algorithm described above without modifications on each original connected component.
### Implementation
Here, the input is *n* — the number of vertices, *m* — the number of edges, then *m* lines describing the edges.
The output is the minimal number of SCCs on the first line and on the second line
a string of *m* characters,
either `>` — telling us that the corresponding edge from the input
is oriented from the left to the right vertex (as in the input),
or `<` — the opposite.
This is a bridge search algorithm modified to also orient the edges,
you can as well orient the edges as a first step and count the SCCs on the oriented graph as a second.
```cpp
vector<vector<pair<int, int>>> adj; // adjacency list - vertex and edge pairs
vector<pair<int, int>> edges;
vector<int> tin, low;
int bridge_cnt;
string orient;
vector<bool> edge_used;
void find_bridges(int v) {
static int time = 0;
low[v] = tin[v] = time++;
for (auto p : adj[v]) {
if (edge_used[p.second]) continue;
edge_used[p.second] = true;
orient[p.second] = v == edges[p.second].first ? '>' : '<';
int nv = p.first;
if (tin[nv] == -1) { // if nv is not visited yet
find_bridges(nv);
low[v] = min(low[v], low[nv]);
if (low[nv] > tin[v]) {
// a bridge between v and nv
bridge_cnt++;
}
} else {
low[v] = min(low[v], low[nv]);
}
}
}
int main() {
int n, m;
scanf("%d %d", &n, &m);
adj.resize(n);
tin.resize(n, -1);
low.resize(n, -1);
orient.resize(m);
edges.resize(m);
edge_used.resize(m);
for (int i = 0; i < m; i++) {
int a, b;
scanf("%d %d", &a, &b);
a--; b--;
adj[a].push_back({b, i});
adj[b].push_back({a, i});
edges[i] = {a, b};
}
int comp_cnt = 0;
for (int v = 0; v < n; v++) {
if (tin[v] == -1) {
comp_cnt++;
find_bridges(v);
}
}
printf("%d\n%s\n", comp_cnt + bridge_cnt, orient.c_str());
}
```
## Practice Problems
* [26th Polish OI - Osiedla](https://szkopul.edu.pl/problemset/problem/nldsb4EW1YuZykBlf4lcZL1Y/site/)
|
Strong Orientation
|
---
title
mst_kruskal
---
# Minimum spanning tree - Kruskal's algorithm
Given a weighted undirected graph.
We want to find a subtree of this graph which connects all vertices (i.e. it is a spanning tree) and has the least weight (i.e. the sum of weights of all the edges is minimum) of all possible spanning trees.
This spanning tree is called a minimum spanning tree.
In the left image you can see a weighted undirected graph, and in the right image you can see the corresponding minimum spanning tree.
 
This article will discuss few important facts associated with minimum spanning trees, and then will give the simplest implementation of Kruskal's algorithm for finding minimum spanning tree.
## Properties of the minimum spanning tree
* A minimum spanning tree of a graph is unique, if the weight of all the edges are distinct. Otherwise, there may be multiple minimum spanning trees.
(Specific algorithms typically output one of the possible minimum spanning trees).
* Minimum spanning tree is also the tree with minimum product of weights of edges.
(It can be easily proved by replacing the weights of all edges with their logarithms)
* In a minimum spanning tree of a graph, the maximum weight of an edge is the minimum possible from all possible spanning trees of that graph.
(This follows from the validity of Kruskal's algorithm).
* The maximum spanning tree (spanning tree with the sum of weights of edges being maximum) of a graph can be obtained similarly to that of the minimum spanning tree, by changing the signs of the weights of all the edges to their opposite and then applying any of the minimum spanning tree algorithm.
## Kruskal's algorithm
This algorithm was described by Joseph Bernard Kruskal, Jr. in 1956.
Kruskal's algorithm initially places all the nodes of the original graph isolated from each other, to form a forest of single node trees, and then gradually merges these trees, combining at each iteration any two of all the trees with some edge of the original graph. Before the execution of the algorithm, all edges are sorted by weight (in non-decreasing order). Then begins the process of unification: pick all edges from the first to the last (in sorted order), and if the ends of the currently picked edge belong to different subtrees, these subtrees are combined, and the edge is added to the answer. After iterating through all the edges, all the vertices will belong to the same sub-tree, and we will get the answer.
## The simplest implementation
The following code directly implements the algorithm described above, and is having $O(M \log M + N^2)$ time complexity.
Sorting edges requires $O(M \log N)$ (which is the same as $O(M \log M)$) operations.
Information regarding the subtree to which a vertex belongs is maintained with the help of an array `tree_id[]` - for each vertex `v`, `tree_id[v]` stores the number of the tree , to which `v` belongs.
For each edge, whether it belongs to the ends of different trees, can be determined in $O(1)$.
Finally, the union of the two trees is carried out in $O(N)$ by a simple pass through `tree_id[]` array.
Given that the total number of merge operations is $N-1$, we obtain the asymptotic behavior of $O(M \log N + N^2)$.
```cpp
struct Edge {
int u, v, weight;
bool operator<(Edge const& other) {
return weight < other.weight;
}
};
int n;
vector<Edge> edges;
int cost = 0;
vector<int> tree_id(n);
vector<Edge> result;
for (int i = 0; i < n; i++)
tree_id[i] = i;
sort(edges.begin(), edges.end());
for (Edge e : edges) {
if (tree_id[e.u] != tree_id[e.v]) {
cost += e.weight;
result.push_back(e);
int old_id = tree_id[e.u], new_id = tree_id[e.v];
for (int i = 0; i < n; i++) {
if (tree_id[i] == old_id)
tree_id[i] = new_id;
}
}
}
```
## Proof of correctness
Why does Kruskal's algorithm give us the correct result?
If the original graph was connected, then also the resulting graph will be connected.
Because otherwise there would be two components that could be connected with at least one edge. Though this is impossible, because Kruskal would have chosen one of these edges, since the ids of the components are different.
Also the resulting graph doesn't contain any cycles, since we forbid this explicitly in the algorithm.
Therefore the algorithm generates a spanning tree.
So why does this algorithm give us a minimum spanning tree?
We can show the proposal "if $F$ is a set of edges chosen by the algorithm at any stage in the algorithm, then there exists a MST that contains all edges of $F$" using induction.
The proposal is obviously true at the beginning, the empty set is a subset of any MST.
Now let's assume $F$ is some edge set at any stage of the algorithm, $T$ is a MST containing $F$ and $e$ is the new edge we want to add using Kruskal.
If $e$ generates a cycle, then we don't add it, and so the proposal is still true after this step.
In case that $T$ already contains $e$, the proposal is also true after this step.
In case $T$ doesn't contain the edge $e$, then $T + e$ will contain a cycle $C$.
This cycle will contain at least one edge $f$, that is not in $F$.
The set of edges $T - f + e$ will also be a spanning tree.
Notice that the weight of $f$ cannot be smaller than the weight of $e$, because otherwise Kruskal would have chosen $f$ earlier.
It also cannot have a bigger weight, since that would make the total weight of $T - f + e$ smaller than the total weight of $T$, which is impossible since $T$ is already a MST.
This means that the weight of $e$ has to be the same as the weight of $f$.
Therefore $T - f + e$ is also a MST, and it contains all edges from $F + e$.
So also here the proposal is still fulfilled after the step.
This proves the proposal.
Which means that after iterating over all edges the resulting edge set will be connected, and will be contained in a MST, which means that it has to be a MST already.
## Improved implementation
We can use the [**Disjoint Set Union** (DSU)](../data_structures/disjoint_set_union.md) data structure to write a faster implementation of the Kruskal's algorithm with the time complexity of about $O(M \log N)$. [This article](mst_kruskal_with_dsu.md) details such an approach.
|
---
title
mst_kruskal
---
# Minimum spanning tree - Kruskal's algorithm
Given a weighted undirected graph.
We want to find a subtree of this graph which connects all vertices (i.e. it is a spanning tree) and has the least weight (i.e. the sum of weights of all the edges is minimum) of all possible spanning trees.
This spanning tree is called a minimum spanning tree.
In the left image you can see a weighted undirected graph, and in the right image you can see the corresponding minimum spanning tree.
 
This article will discuss few important facts associated with minimum spanning trees, and then will give the simplest implementation of Kruskal's algorithm for finding minimum spanning tree.
## Properties of the minimum spanning tree
* A minimum spanning tree of a graph is unique, if the weight of all the edges are distinct. Otherwise, there may be multiple minimum spanning trees.
(Specific algorithms typically output one of the possible minimum spanning trees).
* Minimum spanning tree is also the tree with minimum product of weights of edges.
(It can be easily proved by replacing the weights of all edges with their logarithms)
* In a minimum spanning tree of a graph, the maximum weight of an edge is the minimum possible from all possible spanning trees of that graph.
(This follows from the validity of Kruskal's algorithm).
* The maximum spanning tree (spanning tree with the sum of weights of edges being maximum) of a graph can be obtained similarly to that of the minimum spanning tree, by changing the signs of the weights of all the edges to their opposite and then applying any of the minimum spanning tree algorithm.
## Kruskal's algorithm
This algorithm was described by Joseph Bernard Kruskal, Jr. in 1956.
Kruskal's algorithm initially places all the nodes of the original graph isolated from each other, to form a forest of single node trees, and then gradually merges these trees, combining at each iteration any two of all the trees with some edge of the original graph. Before the execution of the algorithm, all edges are sorted by weight (in non-decreasing order). Then begins the process of unification: pick all edges from the first to the last (in sorted order), and if the ends of the currently picked edge belong to different subtrees, these subtrees are combined, and the edge is added to the answer. After iterating through all the edges, all the vertices will belong to the same sub-tree, and we will get the answer.
## The simplest implementation
The following code directly implements the algorithm described above, and is having $O(M \log M + N^2)$ time complexity.
Sorting edges requires $O(M \log N)$ (which is the same as $O(M \log M)$) operations.
Information regarding the subtree to which a vertex belongs is maintained with the help of an array `tree_id[]` - for each vertex `v`, `tree_id[v]` stores the number of the tree , to which `v` belongs.
For each edge, whether it belongs to the ends of different trees, can be determined in $O(1)$.
Finally, the union of the two trees is carried out in $O(N)$ by a simple pass through `tree_id[]` array.
Given that the total number of merge operations is $N-1$, we obtain the asymptotic behavior of $O(M \log N + N^2)$.
```cpp
struct Edge {
int u, v, weight;
bool operator<(Edge const& other) {
return weight < other.weight;
}
};
int n;
vector<Edge> edges;
int cost = 0;
vector<int> tree_id(n);
vector<Edge> result;
for (int i = 0; i < n; i++)
tree_id[i] = i;
sort(edges.begin(), edges.end());
for (Edge e : edges) {
if (tree_id[e.u] != tree_id[e.v]) {
cost += e.weight;
result.push_back(e);
int old_id = tree_id[e.u], new_id = tree_id[e.v];
for (int i = 0; i < n; i++) {
if (tree_id[i] == old_id)
tree_id[i] = new_id;
}
}
}
```
## Proof of correctness
Why does Kruskal's algorithm give us the correct result?
If the original graph was connected, then also the resulting graph will be connected.
Because otherwise there would be two components that could be connected with at least one edge. Though this is impossible, because Kruskal would have chosen one of these edges, since the ids of the components are different.
Also the resulting graph doesn't contain any cycles, since we forbid this explicitly in the algorithm.
Therefore the algorithm generates a spanning tree.
So why does this algorithm give us a minimum spanning tree?
We can show the proposal "if $F$ is a set of edges chosen by the algorithm at any stage in the algorithm, then there exists a MST that contains all edges of $F$" using induction.
The proposal is obviously true at the beginning, the empty set is a subset of any MST.
Now let's assume $F$ is some edge set at any stage of the algorithm, $T$ is a MST containing $F$ and $e$ is the new edge we want to add using Kruskal.
If $e$ generates a cycle, then we don't add it, and so the proposal is still true after this step.
In case that $T$ already contains $e$, the proposal is also true after this step.
In case $T$ doesn't contain the edge $e$, then $T + e$ will contain a cycle $C$.
This cycle will contain at least one edge $f$, that is not in $F$.
The set of edges $T - f + e$ will also be a spanning tree.
Notice that the weight of $f$ cannot be smaller than the weight of $e$, because otherwise Kruskal would have chosen $f$ earlier.
It also cannot have a bigger weight, since that would make the total weight of $T - f + e$ smaller than the total weight of $T$, which is impossible since $T$ is already a MST.
This means that the weight of $e$ has to be the same as the weight of $f$.
Therefore $T - f + e$ is also a MST, and it contains all edges from $F + e$.
So also here the proposal is still fulfilled after the step.
This proves the proposal.
Which means that after iterating over all edges the resulting edge set will be connected, and will be contained in a MST, which means that it has to be a MST already.
## Improved implementation
We can use the [**Disjoint Set Union** (DSU)](../data_structures/disjoint_set_union.md) data structure to write a faster implementation of the Kruskal's algorithm with the time complexity of about $O(M \log N)$. [This article](mst_kruskal_with_dsu.md) details such an approach.
## Practice Problems
* [SPOJ - Koicost](http://www.spoj.com/problems/KOICOST/)
* [SPOJ - MaryBMW](http://www.spoj.com/problems/MARYBMW/)
* [Codechef - Fullmetal Alchemist](https://www.codechef.com/ICL2016/problems/ICL16A)
* [Codeforces - Edges in MST](http://codeforces.com/contest/160/problem/D)
* [UVA 12176 - Bring Your Own Horse](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=3328)
* [UVA 10600 - ACM Contest and Blackout](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1541)
* [UVA 10724 - Road Construction](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=1665)
* [Hackerrank - Roads in HackerLand](https://www.hackerrank.com/contests/june-world-codesprint/challenges/johnland/problem)
* [UVA 11710 - Expensive subway](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2757)
* [Codechef - Chefland and Electricity](https://www.codechef.com/problems/CHEFELEC)
* [UVA 10307 - Killing Aliens in Borg Maze](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1248)
* [Codeforces - Flea](http://codeforces.com/problemset/problem/32/C)
* [Codeforces - Igon in Museum](http://codeforces.com/problemset/problem/598/D)
* [Codeforces - Hongcow Builds a Nation](http://codeforces.com/problemset/problem/744/A)
* [UVA - 908 - Re-connecting Computer Sites](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=849)
* [UVA 1208 - Oreon](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=3649)
* [UVA 1235 - Anti Brute Force Lock](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=3676)
* [UVA 10034 - Freckles](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=975)
* [UVA 11228 - Transportation system](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=2169)
* [UVA 11631 - Dark roads](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2678)
* [UVA 11733 - Airports](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2833)
* [UVA 11747 - Heavy Cycle Edges](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2847)
* [SPOJ - Blinet](http://www.spoj.com/problems/BLINNET/)
* [SPOJ - Help the Old King](http://www.spoj.com/problems/IITKWPCG/)
* [Codeforces - Hierarchy](http://codeforces.com/contest/17/problem/B)
* [SPOJ - Modems](https://www.spoj.com/problems/EC_MODE/)
* [CSES - Road Reparation](https://cses.fi/problemset/task/1675)
* [CSES - Road Construction](https://cses.fi/problemset/task/1676)
|
Minimum spanning tree - Kruskal's algorithm
|
---
title
preflow_push
---
# Maximum flow - Push-relabel algorithm
The push-relabel algorithm (or also known as preflow-push algorithm) is an algorithm for computing the maximum flow of a flow network.
The exact definition of the problem that we want to solve can be found in the article [Maximum flow - Ford-Fulkerson and Edmonds-Karp](edmonds_karp.md).
In this article we will consider solving the problem by pushing a preflow through the network, which will run in $O(V^4)$, or more precisely in $O(V^2 E)$, time.
The algorithm was designed by Andrew Goldberg and Robert Tarjan in 1985.
## Definitions
During the algorithm we will have to handle a **preflow** - i.e. a function $f$ that is similar to the flow function, but does not necessarily satisfies the flow conservation constraint.
For it only the constraints
$$0 \le f(e) \le c(e)$$
and
$$\sum_{(v, u) \in E} f((v, u)) \ge \sum_{(u, v) \in E} f((u, v))$$
have to hold.
So it is possible for some vertex to receive more flow than it distributes.
We say that this vertex has some excess flow, and define the amount of it with the **excess** function $x(u) =\sum_{(v, u) \in E} f((v, u)) - \sum_{(u, v) \in E} f((u, v))$.
In the same way as with the flow function, we can define the residual capacities and the residual graph with the preflow function.
The algorithm will start off with an initial preflow (some vertices having excess), and during the execution the preflow will be handled and modified.
Giving away some details already, the algorithm will pick a vertex with excess, and push the excess to neighboring vertices.
It will repeat this until all vertices, except the source and the sink, are free from excess.
It is easy to see, that a preflow without excess is a valid flow.
This makes the algorithm terminate with an actual flow.
There are still two problem, we have to deal with.
First, how do we guarantee that this actually terminates?
And secondly, how do we guarantee that this will actually give us a maximum flow, and not just any random flow?
To solve these problems we need the help of another function, namely the **labeling** functions $h$, often also called **height** function, which assigns each vertex an integer.
We call a labeling is valid, if $h(s) = |V|$, $h(t) = 0$, and $h(u) \le h(v) + 1$ if there is an edge $(u, v)$ in the residual graph - i.e. the edge $(u, v)$ has a positive capacity in the residual graph.
In other words, if it is possible to increase the flow from $u$ to $v$, then the height of $v$ can be at most one smaller than the height of $u$, but it can be equal or even higher.
It is important to note, that if there exists a valid labeling function, then there doesn't exist an augmenting path from $s$ to $t$ in the residual graph.
Because such a path will have a length of at most $|V| - 1$ edges, and each edge can decrease the height only by at most by one, which is impossible if the first height is $h(s) = |V|$ and the last height is $h(t) = 0$.
Using this labeling function we can state the strategy of the push-relabel algorithm:
We start with a valid preflow and a valid labeling function.
In each step we push some excess between vertices, and update the labels of vertices.
We have to make sure, that after each step the preflow and the labeling are still valid.
If then the algorithm determines, the preflow is a valid flow.
And because we also have a valid labeling, there doesn't exists a path between $s$ and $t$ in the residual graph, which means that the flow is actually a maximum flow.
If we compare the Ford-Fulkerson algorithm with the push-relabel algorithm it seems like the algorithms are the duals of each other.
The Ford-Fulkerson algorithm keeps a valid flow at all time and improves it until there doesn't exists an augmenting path any more, while in the push-relabel algorithm there doesn't exists an augmenting path at any time, and we will improve the preflow until it is a valid flow.
## Algorithm
First we have to initialize the graph with a valid preflow and labeling function.
Using the empty preflow - like it is done in the Ford-Fulkerson algorithm - is not possible, because then there will be an augmenting path and this implies that there doesn't exists a valid labeling.
Therefore we will initialize each edges outgoing from $s$ with its maximal capacity: $f((s, u)) = c((s, u))$.
And all other edges with zero.
In this case there exists a valid labeling, namely $h(s) = |V|$ for the source vertex and $h(u) = 0$ for all other.
Now let's describe the two operations in more detail.
With the `push` operation we try to push as much excess flow from one vertex $u$ to a neighboring vertex $v$.
We have one rule: we are only allowed to push flow from $u$ to $v$ if $h(u) = h(v) + 1$.
In layman's terms, the excess flow has to flow downwards, but not too steeply.
Of course we only can push $\min(x(u), c((u, v)) - f((u, v)))$ flow.
If a vertex has excess, but it is not possible to push the excess to any adjacent vertex, then we need to increase the height of this vertex.
We call this operation `relabel`.
We will increase it by as much as it is possible, while still maintaining validity of the labeling.
To recap, the algorithm in a nutshell is:
We initialize a valid preflow and a valid labeling.
While we can perform push or relabel operations, we perform them.
Afterwards the preflow is actually a flow and we return it.
## Complexity
It is easy to show, that the maximal label of a vertex is $2|V| - 1$.
At this point all remaining excess can and will be pushed back to the source.
This gives at most $O(V^2)$ relabel operations.
It can also be showed, that there will be at most $O(V E)$ saturating pushes (a push where the total capacity of the edge is used) and at most $O(V^2 E)$ non-saturating pushes (a push where the capacity of an edge is not fully used) performed.
If we pick a data structure that allows us to find the next vertex with excess in $O(1)$ time, then the total complexity of the algorithm is $O(V^2 E)$.
## Implementation
```{.cpp file=push_relabel}
const int inf = 1000000000;
int n;
vector<vector<int>> capacity, flow;
vector<int> height, excess, seen;
queue<int> excess_vertices;
void push(int u, int v)
{
int d = min(excess[u], capacity[u][v] - flow[u][v]);
flow[u][v] += d;
flow[v][u] -= d;
excess[u] -= d;
excess[v] += d;
if (d && excess[v] == d)
excess_vertices.push(v);
}
void relabel(int u)
{
int d = inf;
for (int i = 0; i < n; i++) {
if (capacity[u][i] - flow[u][i] > 0)
d = min(d, height[i]);
}
if (d < inf)
height[u] = d + 1;
}
void discharge(int u)
{
while (excess[u] > 0) {
if (seen[u] < n) {
int v = seen[u];
if (capacity[u][v] - flow[u][v] > 0 && height[u] > height[v])
push(u, v);
else
seen[u]++;
} else {
relabel(u);
seen[u] = 0;
}
}
}
int max_flow(int s, int t)
{
height.assign(n, 0);
height[s] = n;
flow.assign(n, vector<int>(n, 0));
excess.assign(n, 0);
excess[s] = inf;
for (int i = 0; i < n; i++) {
if (i != s)
push(s, i);
}
seen.assign(n, 0);
while (!excess_vertices.empty()) {
int u = excess_vertices.front();
excess_vertices.pop();
if (u != s && u != t)
discharge(u);
}
int max_flow = 0;
for (int i = 0; i < n; i++)
max_flow += flow[i][t];
return max_flow;
}
```
Here we use the queue `excess_vertices` to store all vertices that currently have excess.
In that way we can pick the next vertex for a push or a relabel operation in constant time.
And to make sure that we don't spend too much time finding the adjacent vertex to whom we can push, we use a data structure called **current-arc**.
Basically we will iterate over the edges in a circular order and always store the last edge that we used.
This way, for a certain labeling value, we will switch the current edge only $O(n)$ time.
And since the relabeling already takes $O(n)$ time, we don't make the complexity worse.
|
---
title
preflow_push
---
# Maximum flow - Push-relabel algorithm
The push-relabel algorithm (or also known as preflow-push algorithm) is an algorithm for computing the maximum flow of a flow network.
The exact definition of the problem that we want to solve can be found in the article [Maximum flow - Ford-Fulkerson and Edmonds-Karp](edmonds_karp.md).
In this article we will consider solving the problem by pushing a preflow through the network, which will run in $O(V^4)$, or more precisely in $O(V^2 E)$, time.
The algorithm was designed by Andrew Goldberg and Robert Tarjan in 1985.
## Definitions
During the algorithm we will have to handle a **preflow** - i.e. a function $f$ that is similar to the flow function, but does not necessarily satisfies the flow conservation constraint.
For it only the constraints
$$0 \le f(e) \le c(e)$$
and
$$\sum_{(v, u) \in E} f((v, u)) \ge \sum_{(u, v) \in E} f((u, v))$$
have to hold.
So it is possible for some vertex to receive more flow than it distributes.
We say that this vertex has some excess flow, and define the amount of it with the **excess** function $x(u) =\sum_{(v, u) \in E} f((v, u)) - \sum_{(u, v) \in E} f((u, v))$.
In the same way as with the flow function, we can define the residual capacities and the residual graph with the preflow function.
The algorithm will start off with an initial preflow (some vertices having excess), and during the execution the preflow will be handled and modified.
Giving away some details already, the algorithm will pick a vertex with excess, and push the excess to neighboring vertices.
It will repeat this until all vertices, except the source and the sink, are free from excess.
It is easy to see, that a preflow without excess is a valid flow.
This makes the algorithm terminate with an actual flow.
There are still two problem, we have to deal with.
First, how do we guarantee that this actually terminates?
And secondly, how do we guarantee that this will actually give us a maximum flow, and not just any random flow?
To solve these problems we need the help of another function, namely the **labeling** functions $h$, often also called **height** function, which assigns each vertex an integer.
We call a labeling is valid, if $h(s) = |V|$, $h(t) = 0$, and $h(u) \le h(v) + 1$ if there is an edge $(u, v)$ in the residual graph - i.e. the edge $(u, v)$ has a positive capacity in the residual graph.
In other words, if it is possible to increase the flow from $u$ to $v$, then the height of $v$ can be at most one smaller than the height of $u$, but it can be equal or even higher.
It is important to note, that if there exists a valid labeling function, then there doesn't exist an augmenting path from $s$ to $t$ in the residual graph.
Because such a path will have a length of at most $|V| - 1$ edges, and each edge can decrease the height only by at most by one, which is impossible if the first height is $h(s) = |V|$ and the last height is $h(t) = 0$.
Using this labeling function we can state the strategy of the push-relabel algorithm:
We start with a valid preflow and a valid labeling function.
In each step we push some excess between vertices, and update the labels of vertices.
We have to make sure, that after each step the preflow and the labeling are still valid.
If then the algorithm determines, the preflow is a valid flow.
And because we also have a valid labeling, there doesn't exists a path between $s$ and $t$ in the residual graph, which means that the flow is actually a maximum flow.
If we compare the Ford-Fulkerson algorithm with the push-relabel algorithm it seems like the algorithms are the duals of each other.
The Ford-Fulkerson algorithm keeps a valid flow at all time and improves it until there doesn't exists an augmenting path any more, while in the push-relabel algorithm there doesn't exists an augmenting path at any time, and we will improve the preflow until it is a valid flow.
## Algorithm
First we have to initialize the graph with a valid preflow and labeling function.
Using the empty preflow - like it is done in the Ford-Fulkerson algorithm - is not possible, because then there will be an augmenting path and this implies that there doesn't exists a valid labeling.
Therefore we will initialize each edges outgoing from $s$ with its maximal capacity: $f((s, u)) = c((s, u))$.
And all other edges with zero.
In this case there exists a valid labeling, namely $h(s) = |V|$ for the source vertex and $h(u) = 0$ for all other.
Now let's describe the two operations in more detail.
With the `push` operation we try to push as much excess flow from one vertex $u$ to a neighboring vertex $v$.
We have one rule: we are only allowed to push flow from $u$ to $v$ if $h(u) = h(v) + 1$.
In layman's terms, the excess flow has to flow downwards, but not too steeply.
Of course we only can push $\min(x(u), c((u, v)) - f((u, v)))$ flow.
If a vertex has excess, but it is not possible to push the excess to any adjacent vertex, then we need to increase the height of this vertex.
We call this operation `relabel`.
We will increase it by as much as it is possible, while still maintaining validity of the labeling.
To recap, the algorithm in a nutshell is:
We initialize a valid preflow and a valid labeling.
While we can perform push or relabel operations, we perform them.
Afterwards the preflow is actually a flow and we return it.
## Complexity
It is easy to show, that the maximal label of a vertex is $2|V| - 1$.
At this point all remaining excess can and will be pushed back to the source.
This gives at most $O(V^2)$ relabel operations.
It can also be showed, that there will be at most $O(V E)$ saturating pushes (a push where the total capacity of the edge is used) and at most $O(V^2 E)$ non-saturating pushes (a push where the capacity of an edge is not fully used) performed.
If we pick a data structure that allows us to find the next vertex with excess in $O(1)$ time, then the total complexity of the algorithm is $O(V^2 E)$.
## Implementation
```{.cpp file=push_relabel}
const int inf = 1000000000;
int n;
vector<vector<int>> capacity, flow;
vector<int> height, excess, seen;
queue<int> excess_vertices;
void push(int u, int v)
{
int d = min(excess[u], capacity[u][v] - flow[u][v]);
flow[u][v] += d;
flow[v][u] -= d;
excess[u] -= d;
excess[v] += d;
if (d && excess[v] == d)
excess_vertices.push(v);
}
void relabel(int u)
{
int d = inf;
for (int i = 0; i < n; i++) {
if (capacity[u][i] - flow[u][i] > 0)
d = min(d, height[i]);
}
if (d < inf)
height[u] = d + 1;
}
void discharge(int u)
{
while (excess[u] > 0) {
if (seen[u] < n) {
int v = seen[u];
if (capacity[u][v] - flow[u][v] > 0 && height[u] > height[v])
push(u, v);
else
seen[u]++;
} else {
relabel(u);
seen[u] = 0;
}
}
}
int max_flow(int s, int t)
{
height.assign(n, 0);
height[s] = n;
flow.assign(n, vector<int>(n, 0));
excess.assign(n, 0);
excess[s] = inf;
for (int i = 0; i < n; i++) {
if (i != s)
push(s, i);
}
seen.assign(n, 0);
while (!excess_vertices.empty()) {
int u = excess_vertices.front();
excess_vertices.pop();
if (u != s && u != t)
discharge(u);
}
int max_flow = 0;
for (int i = 0; i < n; i++)
max_flow += flow[i][t];
return max_flow;
}
```
Here we use the queue `excess_vertices` to store all vertices that currently have excess.
In that way we can pick the next vertex for a push or a relabel operation in constant time.
And to make sure that we don't spend too much time finding the adjacent vertex to whom we can push, we use a data structure called **current-arc**.
Basically we will iterate over the edges in a circular order and always store the last edge that we used.
This way, for a certain labeling value, we will switch the current edge only $O(n)$ time.
And since the relabeling already takes $O(n)$ time, we don't make the complexity worse.
|
Maximum flow - Push-relabel algorithm
|
---
title: Checking a graph for acyclicity and finding a cycle in O(M)
title
finding_cycle
---
# Checking a graph for acyclicity and finding a cycle in $O(M)$
Consider a directed or undirected graph without loops and multiple edges. We have to check whether it is acyclic, and if it is not, then find any cycle.
We can solve this problem by using [Depth First Search](depth-first-search.md) in $O(M)$ where $M$ is number of edges.
## Algorithm
We will run a series of DFS in the graph. Initially all vertices are colored white (0). From each unvisited (white) vertex, start the DFS, mark it gray (1) while entering and mark it black (2) on exit. If DFS moves to a gray vertex, then we have found a cycle (if the graph is undirected, the edge to parent is not considered).
The cycle itself can be reconstructed using parent array.
## Implementation
Here is an implementation for directed graph.
```cpp
int n;
vector<vector<int>> adj;
vector<char> color;
vector<int> parent;
int cycle_start, cycle_end;
bool dfs(int v) {
color[v] = 1;
for (int u : adj[v]) {
if (color[u] == 0) {
parent[u] = v;
if (dfs(u))
return true;
} else if (color[u] == 1) {
cycle_end = v;
cycle_start = u;
return true;
}
}
color[v] = 2;
return false;
}
void find_cycle() {
color.assign(n, 0);
parent.assign(n, -1);
cycle_start = -1;
for (int v = 0; v < n; v++) {
if (color[v] == 0 && dfs(v))
break;
}
if (cycle_start == -1) {
cout << "Acyclic" << endl;
} else {
vector<int> cycle;
cycle.push_back(cycle_start);
for (int v = cycle_end; v != cycle_start; v = parent[v])
cycle.push_back(v);
cycle.push_back(cycle_start);
reverse(cycle.begin(), cycle.end());
cout << "Cycle found: ";
for (int v : cycle)
cout << v << " ";
cout << endl;
}
}
```
Here is an implementation for undirected graph.
Note that in the undirected version, if a vertex `v` gets colored black, it will never be visited again by the DFS.
This is because we already explored all connected edges of `v` when we first visited it.
The connected component containing `v` (after removing the edge between `v` and its parent) must be a tree, if the DFS has completed processing `v` without finding a cycle.
So we don't even need to distinguish between gray and black states.
Thus we can turn the char vector `color` into a boolean vector `visited`.
```cpp
int n;
vector<vector<int>> adj;
vector<bool> visited;
vector<int> parent;
int cycle_start, cycle_end;
bool dfs(int v, int par) { // passing vertex and its parent vertex
visited[v] = true;
for (int u : adj[v]) {
if(u == par) continue; // skipping edge to parent vertex
if (visited[u]) {
cycle_end = v;
cycle_start = u;
return true;
}
parent[u] = v;
if (dfs(u, parent[u]))
return true;
}
return false;
}
void find_cycle() {
visited.assign(n, false);
parent.assign(n, -1);
cycle_start = -1;
for (int v = 0; v < n; v++) {
if (!visited[v] && dfs(v, parent[v]))
break;
}
if (cycle_start == -1) {
cout << "Acyclic" << endl;
} else {
vector<int> cycle;
cycle.push_back(cycle_start);
for (int v = cycle_end; v != cycle_start; v = parent[v])
cycle.push_back(v);
cycle.push_back(cycle_start);
cout << "Cycle found: ";
for (int v : cycle)
cout << v << " ";
cout << endl;
}
}
```
#
|
---
title: Checking a graph for acyclicity and finding a cycle in O(M)
title
finding_cycle
---
# Checking a graph for acyclicity and finding a cycle in $O(M)$
Consider a directed or undirected graph without loops and multiple edges. We have to check whether it is acyclic, and if it is not, then find any cycle.
We can solve this problem by using [Depth First Search](depth-first-search.md) in $O(M)$ where $M$ is number of edges.
## Algorithm
We will run a series of DFS in the graph. Initially all vertices are colored white (0). From each unvisited (white) vertex, start the DFS, mark it gray (1) while entering and mark it black (2) on exit. If DFS moves to a gray vertex, then we have found a cycle (if the graph is undirected, the edge to parent is not considered).
The cycle itself can be reconstructed using parent array.
## Implementation
Here is an implementation for directed graph.
```cpp
int n;
vector<vector<int>> adj;
vector<char> color;
vector<int> parent;
int cycle_start, cycle_end;
bool dfs(int v) {
color[v] = 1;
for (int u : adj[v]) {
if (color[u] == 0) {
parent[u] = v;
if (dfs(u))
return true;
} else if (color[u] == 1) {
cycle_end = v;
cycle_start = u;
return true;
}
}
color[v] = 2;
return false;
}
void find_cycle() {
color.assign(n, 0);
parent.assign(n, -1);
cycle_start = -1;
for (int v = 0; v < n; v++) {
if (color[v] == 0 && dfs(v))
break;
}
if (cycle_start == -1) {
cout << "Acyclic" << endl;
} else {
vector<int> cycle;
cycle.push_back(cycle_start);
for (int v = cycle_end; v != cycle_start; v = parent[v])
cycle.push_back(v);
cycle.push_back(cycle_start);
reverse(cycle.begin(), cycle.end());
cout << "Cycle found: ";
for (int v : cycle)
cout << v << " ";
cout << endl;
}
}
```
Here is an implementation for undirected graph.
Note that in the undirected version, if a vertex `v` gets colored black, it will never be visited again by the DFS.
This is because we already explored all connected edges of `v` when we first visited it.
The connected component containing `v` (after removing the edge between `v` and its parent) must be a tree, if the DFS has completed processing `v` without finding a cycle.
So we don't even need to distinguish between gray and black states.
Thus we can turn the char vector `color` into a boolean vector `visited`.
```cpp
int n;
vector<vector<int>> adj;
vector<bool> visited;
vector<int> parent;
int cycle_start, cycle_end;
bool dfs(int v, int par) { // passing vertex and its parent vertex
visited[v] = true;
for (int u : adj[v]) {
if(u == par) continue; // skipping edge to parent vertex
if (visited[u]) {
cycle_end = v;
cycle_start = u;
return true;
}
parent[u] = v;
if (dfs(u, parent[u]))
return true;
}
return false;
}
void find_cycle() {
visited.assign(n, false);
parent.assign(n, -1);
cycle_start = -1;
for (int v = 0; v < n; v++) {
if (!visited[v] && dfs(v, parent[v]))
break;
}
if (cycle_start == -1) {
cout << "Acyclic" << endl;
} else {
vector<int> cycle;
cycle.push_back(cycle_start);
for (int v = cycle_end; v != cycle_start; v = parent[v])
cycle.push_back(v);
cycle.push_back(cycle_start);
cout << "Cycle found: ";
for (int v : cycle)
cout << v << " ";
cout << endl;
}
}
```
### Practice problems:
- [CSES : Round Trip](https://cses.fi/problemset/task/1669)
- [CSES : Round Trip II](https://cses.fi/problemset/task/1678/)
|
Checking a graph for acyclicity and finding a cycle in $O(M)$
|
---
title: Finding bridges in a graph in O(N+M)
title
bridge_searching
---
# Finding bridges in a graph in $O(N+M)$
We are given an undirected graph. A bridge is defined as an edge which, when removed, makes the graph disconnected (or more precisely, increases the number of connected components in the graph). The task is to find all bridges in the given graph.
Informally, the problem is formulated as follows: given a map of cities connected with roads, find all "important" roads, i.e. roads which, when removed, cause disappearance of a path between some pair of cities.
The algorithm described here is based on [depth first search](depth-first-search.md) and has $O(N+M)$ complexity, where $N$ is the number of vertices and $M$ is the number of edges in the graph.
Note that there is also the article [Finding Bridges Online](bridge-searching-online.md) - unlike the offline algorithm described here, the online algorithm is able to maintain the list of all bridges in a changing graph (assuming that the only type of change is addition of new edges).
## Algorithm
Pick an arbitrary vertex of the graph $root$ and run [depth first search](depth-first-search.md) from it. Note the following fact (which is easy to prove):
- Let's say we are in the DFS, looking through the edges starting from vertex $v$. The current edge $(v, to)$ is a bridge if and only if none of the vertices $to$ and its descendants in the DFS traversal tree has a back-edge to vertex $v$ or any of its ancestors. Indeed, this condition means that there is no other way from $v$ to $to$ except for edge $(v, to)$.
Now we have to learn to check this fact for each vertex efficiently. We'll use "time of entry into node" computed by the depth first search.
So, let $tin[v]$ denote entry time for node $v$. We introduce an array $low$ which will let us check the fact for each vertex $v$. $low[v]$ is the minimum of $tin[v]$, the entry times $tin[p]$ for each node $p$ that is connected to node $v$ via a back-edge $(v, p)$ and the values of $low[to]$ for each vertex $to$ which is a direct descendant of $v$ in the DFS tree:
$$low[v] = \min \begin{cases} tin[v] \\ tin[p]& \text{ for all }p\text{ for which }(v, p)\text{ is a back edge} \\ low[to]& \text{ for all }to\text{ for which }(v, to)\text{ is a tree edge} \end{cases}$$
Now, there is a back edge from vertex $v$ or one of its descendants to one of its ancestors if and only if vertex $v$ has a child $to$ for which $low[to] \leq tin[v]$. If $low[to] = tin[v]$, the back edge comes directly to $v$, otherwise it comes to one of the ancestors of $v$.
Thus, the current edge $(v, to)$ in the DFS tree is a bridge if and only if $low[to] > tin[v]$.
## Implementation
The implementation needs to distinguish three cases: when we go down the edge in DFS tree, when we find a back edge to an ancestor of the vertex and when we return to a parent of the vertex. These are the cases:
- $visited[to] = false$ - the edge is part of DFS tree;
- $visited[to] = true$ && $to \neq parent$ - the edge is back edge to one of the ancestors;
- $to = parent$ - the edge leads back to parent in DFS tree.
To implement this, we need a depth first search function which accepts the parent vertex of the current node.
```cpp
int n; // number of nodes
vector<vector<int>> adj; // adjacency list of graph
vector<bool> visited;
vector<int> tin, low;
int timer;
void dfs(int v, int p = -1) {
visited[v] = true;
tin[v] = low[v] = timer++;
for (int to : adj[v]) {
if (to == p) continue;
if (visited[to]) {
low[v] = min(low[v], tin[to]);
} else {
dfs(to, v);
low[v] = min(low[v], low[to]);
if (low[to] > tin[v])
IS_BRIDGE(v, to);
}
}
}
void find_bridges() {
timer = 0;
visited.assign(n, false);
tin.assign(n, -1);
low.assign(n, -1);
for (int i = 0; i < n; ++i) {
if (!visited[i])
dfs(i);
}
}
```
Main function is `find_bridges`; it performs necessary initialization and starts depth first search in each connected component of the graph.
Function `IS_BRIDGE(a, b)` is some function that will process the fact that edge $(a, b)$ is a bridge, for example, print it.
Note that this implementation malfunctions if the graph has multiple edges, since it ignores them. Of course, multiple edges will never be a part of the answer, so `IS_BRIDGE` can check additionally that the reported bridge is not a multiple edge. Alternatively it's possible to pass to `dfs` the index of the edge used to enter the vertex instead of the parent vertex (and store the indices of all vertices).
|
---
title: Finding bridges in a graph in O(N+M)
title
bridge_searching
---
# Finding bridges in a graph in $O(N+M)$
We are given an undirected graph. A bridge is defined as an edge which, when removed, makes the graph disconnected (or more precisely, increases the number of connected components in the graph). The task is to find all bridges in the given graph.
Informally, the problem is formulated as follows: given a map of cities connected with roads, find all "important" roads, i.e. roads which, when removed, cause disappearance of a path between some pair of cities.
The algorithm described here is based on [depth first search](depth-first-search.md) and has $O(N+M)$ complexity, where $N$ is the number of vertices and $M$ is the number of edges in the graph.
Note that there is also the article [Finding Bridges Online](bridge-searching-online.md) - unlike the offline algorithm described here, the online algorithm is able to maintain the list of all bridges in a changing graph (assuming that the only type of change is addition of new edges).
## Algorithm
Pick an arbitrary vertex of the graph $root$ and run [depth first search](depth-first-search.md) from it. Note the following fact (which is easy to prove):
- Let's say we are in the DFS, looking through the edges starting from vertex $v$. The current edge $(v, to)$ is a bridge if and only if none of the vertices $to$ and its descendants in the DFS traversal tree has a back-edge to vertex $v$ or any of its ancestors. Indeed, this condition means that there is no other way from $v$ to $to$ except for edge $(v, to)$.
Now we have to learn to check this fact for each vertex efficiently. We'll use "time of entry into node" computed by the depth first search.
So, let $tin[v]$ denote entry time for node $v$. We introduce an array $low$ which will let us check the fact for each vertex $v$. $low[v]$ is the minimum of $tin[v]$, the entry times $tin[p]$ for each node $p$ that is connected to node $v$ via a back-edge $(v, p)$ and the values of $low[to]$ for each vertex $to$ which is a direct descendant of $v$ in the DFS tree:
$$low[v] = \min \begin{cases} tin[v] \\ tin[p]& \text{ for all }p\text{ for which }(v, p)\text{ is a back edge} \\ low[to]& \text{ for all }to\text{ for which }(v, to)\text{ is a tree edge} \end{cases}$$
Now, there is a back edge from vertex $v$ or one of its descendants to one of its ancestors if and only if vertex $v$ has a child $to$ for which $low[to] \leq tin[v]$. If $low[to] = tin[v]$, the back edge comes directly to $v$, otherwise it comes to one of the ancestors of $v$.
Thus, the current edge $(v, to)$ in the DFS tree is a bridge if and only if $low[to] > tin[v]$.
## Implementation
The implementation needs to distinguish three cases: when we go down the edge in DFS tree, when we find a back edge to an ancestor of the vertex and when we return to a parent of the vertex. These are the cases:
- $visited[to] = false$ - the edge is part of DFS tree;
- $visited[to] = true$ && $to \neq parent$ - the edge is back edge to one of the ancestors;
- $to = parent$ - the edge leads back to parent in DFS tree.
To implement this, we need a depth first search function which accepts the parent vertex of the current node.
```cpp
int n; // number of nodes
vector<vector<int>> adj; // adjacency list of graph
vector<bool> visited;
vector<int> tin, low;
int timer;
void dfs(int v, int p = -1) {
visited[v] = true;
tin[v] = low[v] = timer++;
for (int to : adj[v]) {
if (to == p) continue;
if (visited[to]) {
low[v] = min(low[v], tin[to]);
} else {
dfs(to, v);
low[v] = min(low[v], low[to]);
if (low[to] > tin[v])
IS_BRIDGE(v, to);
}
}
}
void find_bridges() {
timer = 0;
visited.assign(n, false);
tin.assign(n, -1);
low.assign(n, -1);
for (int i = 0; i < n; ++i) {
if (!visited[i])
dfs(i);
}
}
```
Main function is `find_bridges`; it performs necessary initialization and starts depth first search in each connected component of the graph.
Function `IS_BRIDGE(a, b)` is some function that will process the fact that edge $(a, b)$ is a bridge, for example, print it.
Note that this implementation malfunctions if the graph has multiple edges, since it ignores them. Of course, multiple edges will never be a part of the answer, so `IS_BRIDGE` can check additionally that the reported bridge is not a multiple edge. Alternatively it's possible to pass to `dfs` the index of the edge used to enter the vertex instead of the parent vertex (and store the indices of all vertices).
## Practice Problems
- [UVA #796 "Critical Links"](http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=737) [difficulty: low]
- [UVA #610 "Street Directions"](http://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=551) [difficulty: medium]
- [Case of the Computer Network (Codeforces Round #310 Div. 1 E)](http://codeforces.com/problemset/problem/555/E) [difficulty: hard]
* [UVA 12363 - Hedge Mazes](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=3785)
* [UVA 315 - Network](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=251)
* [GYM - Computer Network (J)](http://codeforces.com/gym/100114)
* [SPOJ - King Graffs Defense](http://www.spoj.com/problems/GRAFFDEF/)
* [SPOJ - Critical Edges](http://www.spoj.com/problems/EC_P/)
* [Codeforces - Break Up](http://codeforces.com/contest/700/problem/C)
* [Codeforces - Tourist Reform](http://codeforces.com/contest/732/problem/F)
|
Finding bridges in a graph in $O(N+M)$
|
---
title
mst_kruskal_with_dsu
---
# Minimum spanning tree - Kruskal with Disjoint Set Union
For an explanation of the MST problem and the Kruskal algorithm, first see the [main article on Kruskal's algorithm](mst_kruskal.md).
In this article we will consider the data structure ["Disjoint Set Union"](../data_structures/disjoint_set_union.md) for implementing Kruskal's algorithm, which will allow the algorithm to achieve the time complexity of $O(M \log N)$.
## Description
Just as in the simple version of the Kruskal algorithm, we sort all the edges of the graph in non-decreasing order of weights.
Then put each vertex in its own tree (i.e. its set) via calls to the `make_set` function - it will take a total of $O(N)$.
We iterate through all the edges (in sorted order) and for each edge determine whether the ends belong to different trees (with two `find_set` calls in $O(1)$ each).
Finally, we need to perform the union of the two trees (sets), for which the DSU `union_sets` function will be called - also in $O(1)$.
So we get the total time complexity of $O(M \log N + N + M)$ = $O(M \log N)$.
## Implementation
Here is an implementation of Kruskal's algorithm with Union by Rank.
```cpp
vector<int> parent, rank;
void make_set(int v) {
parent[v] = v;
rank[v] = 0;
}
int find_set(int v) {
if (v == parent[v])
return v;
return parent[v] = find_set(parent[v]);
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (rank[a] < rank[b])
swap(a, b);
parent[b] = a;
if (rank[a] == rank[b])
rank[a]++;
}
}
struct Edge {
int u, v, weight;
bool operator<(Edge const& other) {
return weight < other.weight;
}
};
int n;
vector<Edge> edges;
int cost = 0;
vector<Edge> result;
parent.resize(n);
rank.resize(n);
for (int i = 0; i < n; i++)
make_set(i);
sort(edges.begin(), edges.end());
for (Edge e : edges) {
if (find_set(e.u) != find_set(e.v)) {
cost += e.weight;
result.push_back(e);
union_sets(e.u, e.v);
}
}
```
Notice: since the MST will contain exactly $N-1$ edges, we can stop the for loop once we found that many.
|
---
title
mst_kruskal_with_dsu
---
# Minimum spanning tree - Kruskal with Disjoint Set Union
For an explanation of the MST problem and the Kruskal algorithm, first see the [main article on Kruskal's algorithm](mst_kruskal.md).
In this article we will consider the data structure ["Disjoint Set Union"](../data_structures/disjoint_set_union.md) for implementing Kruskal's algorithm, which will allow the algorithm to achieve the time complexity of $O(M \log N)$.
## Description
Just as in the simple version of the Kruskal algorithm, we sort all the edges of the graph in non-decreasing order of weights.
Then put each vertex in its own tree (i.e. its set) via calls to the `make_set` function - it will take a total of $O(N)$.
We iterate through all the edges (in sorted order) and for each edge determine whether the ends belong to different trees (with two `find_set` calls in $O(1)$ each).
Finally, we need to perform the union of the two trees (sets), for which the DSU `union_sets` function will be called - also in $O(1)$.
So we get the total time complexity of $O(M \log N + N + M)$ = $O(M \log N)$.
## Implementation
Here is an implementation of Kruskal's algorithm with Union by Rank.
```cpp
vector<int> parent, rank;
void make_set(int v) {
parent[v] = v;
rank[v] = 0;
}
int find_set(int v) {
if (v == parent[v])
return v;
return parent[v] = find_set(parent[v]);
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (rank[a] < rank[b])
swap(a, b);
parent[b] = a;
if (rank[a] == rank[b])
rank[a]++;
}
}
struct Edge {
int u, v, weight;
bool operator<(Edge const& other) {
return weight < other.weight;
}
};
int n;
vector<Edge> edges;
int cost = 0;
vector<Edge> result;
parent.resize(n);
rank.resize(n);
for (int i = 0; i < n; i++)
make_set(i);
sort(edges.begin(), edges.end());
for (Edge e : edges) {
if (find_set(e.u) != find_set(e.v)) {
cost += e.weight;
result.push_back(e);
union_sets(e.u, e.v);
}
}
```
Notice: since the MST will contain exactly $N-1$ edges, we can stop the for loop once we found that many.
## Practice Problems
See [main article on Kruskal's algorithm](mst_kruskal.md) for the list of practice problems on this topic.
|
Minimum spanning tree - Kruskal with Disjoint Set Union
|
---
title
lca_linear
---
# Lowest Common Ancestor - Farach-Colton and Bender Algorithm
Let $G$ be a tree.
For every query of the form $(u, v)$ we want to find the lowest common ancestor of the nodes $u$ and $v$, i.e. we want to find a node $w$ that lies on the path from $u$ to the root node, that lies on the path from $v$ to the root node, and if there are multiple nodes we pick the one that is farthest away from the root node.
In other words the desired node $w$ is the lowest ancestor of $u$ and $v$.
In particular if $u$ is an ancestor of $v$, then $u$ is their lowest common ancestor.
The algorithm which will be described in this article was developed by Farach-Colton and Bender.
It is asymptotically optimal.
## Algorithm
We use the classical reduction of the LCA problem to the RMQ problem.
We traverse all nodes of the tree with [DFS](depth-first-search.md) and keep an array with all visited nodes and the heights of these nodes.
The LCA of two nodes $u$ and $v$ is the node between the occurrences of $u$ and $v$ in the tour, that has the smallest height.
In the following picture you can see a possible Euler-Tour of a graph and in the list below you can see the visited nodes and their heights.
<center></center>
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\text{Nodes:} & 1 & 2 & 5 & 2 & 6 & 2 & 1 & 3 & 1 & 4 & 7 & 4 & 1 \\ \hline
\text{Heights:} & 1 & 2 & 3 & 2 & 3 & 2 & 1 & 2 & 1 & 2 & 3 & 2 & 1 \\ \hline
\end{array}$$
You can read more about this reduction in the article [Lowest Common Ancestor](lca.md).
In that article the minimum of a range was either found by sqrt-decomposition in $O(\sqrt{N})$ or in $O(\log N)$ using a Segment tree.
In this article we look at how we can solve the given range minimum queries in $O(1)$ time, while still only taking $O(N)$ time for preprocessing.
Note that the reduced RMQ problem is very specific:
any two adjacent elements in the array differ exactly by one (since the elements of the array are nothing more than the heights of the nodes visited in order of traversal, and we either go to a descendant, in which case the next element is one bigger, or go back to the ancestor, in which case the next element is one lower).
The Farach-Colton and Bender algorithm describes a solution for exactly this specialized RMQ problem.
Let's denote with $A$ the array on which we want to perform the range minimum queries.
And $N$ will be the size of $A$.
There is an easy data structure that we can use for solving the RMQ problem with $O(N \log N)$ preprocessing and $O(1)$ for each query: the [Sparse Table](../data_structures/sparse-table.md).
We create a table $T$ where each element $T[i][j]$ is equal to the minimum of $A$ in the interval $[i, i + 2^j - 1]$.
Obviously $0 \leq j \leq \lceil \log N \rceil$, and therefore the size of the Sparse Table will be $O(N \log N)$.
You can build the table easily in $O(N \log N)$ by noting that $T[i][j] = \min(T[i][j-1], T[i+2^{j-1}][j-1])$.
How can we answer a query RMQ in $O(1)$ using this data structure?
Let the received query be $[l, r]$, then the answer is $\min(T[l][\text{sz}], T[r-2^{\text{sz}}+1][\text{sz}])$, where $\text{sz}$ is the biggest exponent such that $2^{\text{sz}}$ is not bigger than the range length $r-l+1$.
Indeed we can take the range $[l, r]$ and cover it two segments of length $2^{\text{sz}}$ - one starting in $l$ and the other ending in $r$.
These segments overlap, but this doesn't interfere with our computation.
To really achieve the time complexity of $O(1)$ per query, we need to know the values of $\text{sz}$ for all possible lengths from $1$ to $N$.
But this can be easily precomputed.
Now we want to improve the complexity of the preprocessing down to $O(N)$.
We divide the array $A$ into blocks of size $K = 0.5 \log N$ with $\log$ being the logarithm to base 2.
For each block we calculate the minimum element and store them in an array $B$.
$B$ has the size $\frac{N}{K}$.
We construct a sparse table from the array $B$.
The size and the time complexity of it will be:
$$\frac{N}{K}\log\left(\frac{N}{K}\right) = \frac{2N}{\log(N)} \log\left(\frac{2N}{\log(N)}\right) =$$
$$= \frac{2N}{\log(N)} \left(1 + \log\left(\frac{N}{\log(N)}\right)\right) \leq \frac{2N}{\log(N)} + 2N = O(N)$$
Now we only have to learn how to quickly answer range minimum queries within each block.
In fact if the received range minimum query is $[l, r]$ and $l$ and $r$ are in different blocks then the answer is the minimum of the following three values:
the minimum of the suffix of block of $l$ starting at $l$, the minimum of the prefix of block of $r$ ending at $r$, and the minimum of the blocks between those.
The minimum of the blocks in between can be answered in $O(1)$ using the Sparse Table.
So this leaves us only the range minimum queries inside blocks.
Here we will exploit the property of the array.
Remember that the values in the array - which are just height values in the tree - will always differ by one.
If we remove the first element of a block, and subtract it from every other item in the block, every block can be identified by a sequence of length $K - 1$ consisting of the number $+1$ and $-1$.
Because these blocks are so small, there are only a few different sequences that can occur.
The number of possible sequences is:
$$2^{K-1} = 2^{0.5 \log(N) - 1} = 0.5 \left(2^{\log(N)}\right)^{0.5} = 0.5 \sqrt{N}$$
Thus the number of different blocks is $O(\sqrt{N})$, and therefore we can precompute the results of range minimum queries inside all different blocks in $O(\sqrt{N} K^2) = O(\sqrt{N} \log^2(N)) = O(N)$ time.
For the implementation we can characterize a block by a bitmask of length $K-1$ (which will fit in a standard int) and store the index of the minimum in an array $\text{block}[\text{mask}][l][r]$ of size $O(\sqrt{N} \log^2(N))$.
So we learned how to precompute range minimum queries within each block, as well as range minimum queries over a range of blocks, all in $O(N)$.
With these precomputations we can answer each query in $O(1)$, by using at most four precomputed values: the minimum of the block containing `l`, the minimum of the block containing `r`, and the two minima of the overlapping segments of the blocks between them.
## Implementation
```cpp
int n;
vector<vector<int>> adj;
int block_size, block_cnt;
vector<int> first_visit;
vector<int> euler_tour;
vector<int> height;
vector<int> log_2;
vector<vector<int>> st;
vector<vector<vector<int>>> blocks;
vector<int> block_mask;
void dfs(int v, int p, int h) {
first_visit[v] = euler_tour.size();
euler_tour.push_back(v);
height[v] = h;
for (int u : adj[v]) {
if (u == p)
continue;
dfs(u, v, h + 1);
euler_tour.push_back(v);
}
}
int min_by_h(int i, int j) {
return height[euler_tour[i]] < height[euler_tour[j]] ? i : j;
}
void precompute_lca(int root) {
// get euler tour & indices of first occurrences
first_visit.assign(n, -1);
height.assign(n, 0);
euler_tour.reserve(2 * n);
dfs(root, -1, 0);
// precompute all log values
int m = euler_tour.size();
log_2.reserve(m + 1);
log_2.push_back(-1);
for (int i = 1; i <= m; i++)
log_2.push_back(log_2[i / 2] + 1);
block_size = max(1, log_2[m] / 2);
block_cnt = (m + block_size - 1) / block_size;
// precompute minimum of each block and build sparse table
st.assign(block_cnt, vector<int>(log_2[block_cnt] + 1));
for (int i = 0, j = 0, b = 0; i < m; i++, j++) {
if (j == block_size)
j = 0, b++;
if (j == 0 || min_by_h(i, st[b][0]) == i)
st[b][0] = i;
}
for (int l = 1; l <= log_2[block_cnt]; l++) {
for (int i = 0; i < block_cnt; i++) {
int ni = i + (1 << (l - 1));
if (ni >= block_cnt)
st[i][l] = st[i][l-1];
else
st[i][l] = min_by_h(st[i][l-1], st[ni][l-1]);
}
}
// precompute mask for each block
block_mask.assign(block_cnt, 0);
for (int i = 0, j = 0, b = 0; i < m; i++, j++) {
if (j == block_size)
j = 0, b++;
if (j > 0 && (i >= m || min_by_h(i - 1, i) == i - 1))
block_mask[b] += 1 << (j - 1);
}
// precompute RMQ for each unique block
int possibilities = 1 << (block_size - 1);
blocks.resize(possibilities);
for (int b = 0; b < block_cnt; b++) {
int mask = block_mask[b];
if (!blocks[mask].empty())
continue;
blocks[mask].assign(block_size, vector<int>(block_size));
for (int l = 0; l < block_size; l++) {
blocks[mask][l][l] = l;
for (int r = l + 1; r < block_size; r++) {
blocks[mask][l][r] = blocks[mask][l][r - 1];
if (b * block_size + r < m)
blocks[mask][l][r] = min_by_h(b * block_size + blocks[mask][l][r],
b * block_size + r) - b * block_size;
}
}
}
}
int lca_in_block(int b, int l, int r) {
return blocks[block_mask[b]][l][r] + b * block_size;
}
int lca(int v, int u) {
int l = first_visit[v];
int r = first_visit[u];
if (l > r)
swap(l, r);
int bl = l / block_size;
int br = r / block_size;
if (bl == br)
return euler_tour[lca_in_block(bl, l % block_size, r % block_size)];
int ans1 = lca_in_block(bl, l % block_size, block_size - 1);
int ans2 = lca_in_block(br, 0, r % block_size);
int ans = min_by_h(ans1, ans2);
if (bl + 1 < br) {
int l = log_2[br - bl - 1];
int ans3 = st[bl+1][l];
int ans4 = st[br - (1 << l)][l];
ans = min_by_h(ans, min_by_h(ans3, ans4));
}
return euler_tour[ans];
}
```
|
---
title
lca_linear
---
# Lowest Common Ancestor - Farach-Colton and Bender Algorithm
Let $G$ be a tree.
For every query of the form $(u, v)$ we want to find the lowest common ancestor of the nodes $u$ and $v$, i.e. we want to find a node $w$ that lies on the path from $u$ to the root node, that lies on the path from $v$ to the root node, and if there are multiple nodes we pick the one that is farthest away from the root node.
In other words the desired node $w$ is the lowest ancestor of $u$ and $v$.
In particular if $u$ is an ancestor of $v$, then $u$ is their lowest common ancestor.
The algorithm which will be described in this article was developed by Farach-Colton and Bender.
It is asymptotically optimal.
## Algorithm
We use the classical reduction of the LCA problem to the RMQ problem.
We traverse all nodes of the tree with [DFS](depth-first-search.md) and keep an array with all visited nodes and the heights of these nodes.
The LCA of two nodes $u$ and $v$ is the node between the occurrences of $u$ and $v$ in the tour, that has the smallest height.
In the following picture you can see a possible Euler-Tour of a graph and in the list below you can see the visited nodes and their heights.
<center></center>
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\text{Nodes:} & 1 & 2 & 5 & 2 & 6 & 2 & 1 & 3 & 1 & 4 & 7 & 4 & 1 \\ \hline
\text{Heights:} & 1 & 2 & 3 & 2 & 3 & 2 & 1 & 2 & 1 & 2 & 3 & 2 & 1 \\ \hline
\end{array}$$
You can read more about this reduction in the article [Lowest Common Ancestor](lca.md).
In that article the minimum of a range was either found by sqrt-decomposition in $O(\sqrt{N})$ or in $O(\log N)$ using a Segment tree.
In this article we look at how we can solve the given range minimum queries in $O(1)$ time, while still only taking $O(N)$ time for preprocessing.
Note that the reduced RMQ problem is very specific:
any two adjacent elements in the array differ exactly by one (since the elements of the array are nothing more than the heights of the nodes visited in order of traversal, and we either go to a descendant, in which case the next element is one bigger, or go back to the ancestor, in which case the next element is one lower).
The Farach-Colton and Bender algorithm describes a solution for exactly this specialized RMQ problem.
Let's denote with $A$ the array on which we want to perform the range minimum queries.
And $N$ will be the size of $A$.
There is an easy data structure that we can use for solving the RMQ problem with $O(N \log N)$ preprocessing and $O(1)$ for each query: the [Sparse Table](../data_structures/sparse-table.md).
We create a table $T$ where each element $T[i][j]$ is equal to the minimum of $A$ in the interval $[i, i + 2^j - 1]$.
Obviously $0 \leq j \leq \lceil \log N \rceil$, and therefore the size of the Sparse Table will be $O(N \log N)$.
You can build the table easily in $O(N \log N)$ by noting that $T[i][j] = \min(T[i][j-1], T[i+2^{j-1}][j-1])$.
How can we answer a query RMQ in $O(1)$ using this data structure?
Let the received query be $[l, r]$, then the answer is $\min(T[l][\text{sz}], T[r-2^{\text{sz}}+1][\text{sz}])$, where $\text{sz}$ is the biggest exponent such that $2^{\text{sz}}$ is not bigger than the range length $r-l+1$.
Indeed we can take the range $[l, r]$ and cover it two segments of length $2^{\text{sz}}$ - one starting in $l$ and the other ending in $r$.
These segments overlap, but this doesn't interfere with our computation.
To really achieve the time complexity of $O(1)$ per query, we need to know the values of $\text{sz}$ for all possible lengths from $1$ to $N$.
But this can be easily precomputed.
Now we want to improve the complexity of the preprocessing down to $O(N)$.
We divide the array $A$ into blocks of size $K = 0.5 \log N$ with $\log$ being the logarithm to base 2.
For each block we calculate the minimum element and store them in an array $B$.
$B$ has the size $\frac{N}{K}$.
We construct a sparse table from the array $B$.
The size and the time complexity of it will be:
$$\frac{N}{K}\log\left(\frac{N}{K}\right) = \frac{2N}{\log(N)} \log\left(\frac{2N}{\log(N)}\right) =$$
$$= \frac{2N}{\log(N)} \left(1 + \log\left(\frac{N}{\log(N)}\right)\right) \leq \frac{2N}{\log(N)} + 2N = O(N)$$
Now we only have to learn how to quickly answer range minimum queries within each block.
In fact if the received range minimum query is $[l, r]$ and $l$ and $r$ are in different blocks then the answer is the minimum of the following three values:
the minimum of the suffix of block of $l$ starting at $l$, the minimum of the prefix of block of $r$ ending at $r$, and the minimum of the blocks between those.
The minimum of the blocks in between can be answered in $O(1)$ using the Sparse Table.
So this leaves us only the range minimum queries inside blocks.
Here we will exploit the property of the array.
Remember that the values in the array - which are just height values in the tree - will always differ by one.
If we remove the first element of a block, and subtract it from every other item in the block, every block can be identified by a sequence of length $K - 1$ consisting of the number $+1$ and $-1$.
Because these blocks are so small, there are only a few different sequences that can occur.
The number of possible sequences is:
$$2^{K-1} = 2^{0.5 \log(N) - 1} = 0.5 \left(2^{\log(N)}\right)^{0.5} = 0.5 \sqrt{N}$$
Thus the number of different blocks is $O(\sqrt{N})$, and therefore we can precompute the results of range minimum queries inside all different blocks in $O(\sqrt{N} K^2) = O(\sqrt{N} \log^2(N)) = O(N)$ time.
For the implementation we can characterize a block by a bitmask of length $K-1$ (which will fit in a standard int) and store the index of the minimum in an array $\text{block}[\text{mask}][l][r]$ of size $O(\sqrt{N} \log^2(N))$.
So we learned how to precompute range minimum queries within each block, as well as range minimum queries over a range of blocks, all in $O(N)$.
With these precomputations we can answer each query in $O(1)$, by using at most four precomputed values: the minimum of the block containing `l`, the minimum of the block containing `r`, and the two minima of the overlapping segments of the blocks between them.
## Implementation
```cpp
int n;
vector<vector<int>> adj;
int block_size, block_cnt;
vector<int> first_visit;
vector<int> euler_tour;
vector<int> height;
vector<int> log_2;
vector<vector<int>> st;
vector<vector<vector<int>>> blocks;
vector<int> block_mask;
void dfs(int v, int p, int h) {
first_visit[v] = euler_tour.size();
euler_tour.push_back(v);
height[v] = h;
for (int u : adj[v]) {
if (u == p)
continue;
dfs(u, v, h + 1);
euler_tour.push_back(v);
}
}
int min_by_h(int i, int j) {
return height[euler_tour[i]] < height[euler_tour[j]] ? i : j;
}
void precompute_lca(int root) {
// get euler tour & indices of first occurrences
first_visit.assign(n, -1);
height.assign(n, 0);
euler_tour.reserve(2 * n);
dfs(root, -1, 0);
// precompute all log values
int m = euler_tour.size();
log_2.reserve(m + 1);
log_2.push_back(-1);
for (int i = 1; i <= m; i++)
log_2.push_back(log_2[i / 2] + 1);
block_size = max(1, log_2[m] / 2);
block_cnt = (m + block_size - 1) / block_size;
// precompute minimum of each block and build sparse table
st.assign(block_cnt, vector<int>(log_2[block_cnt] + 1));
for (int i = 0, j = 0, b = 0; i < m; i++, j++) {
if (j == block_size)
j = 0, b++;
if (j == 0 || min_by_h(i, st[b][0]) == i)
st[b][0] = i;
}
for (int l = 1; l <= log_2[block_cnt]; l++) {
for (int i = 0; i < block_cnt; i++) {
int ni = i + (1 << (l - 1));
if (ni >= block_cnt)
st[i][l] = st[i][l-1];
else
st[i][l] = min_by_h(st[i][l-1], st[ni][l-1]);
}
}
// precompute mask for each block
block_mask.assign(block_cnt, 0);
for (int i = 0, j = 0, b = 0; i < m; i++, j++) {
if (j == block_size)
j = 0, b++;
if (j > 0 && (i >= m || min_by_h(i - 1, i) == i - 1))
block_mask[b] += 1 << (j - 1);
}
// precompute RMQ for each unique block
int possibilities = 1 << (block_size - 1);
blocks.resize(possibilities);
for (int b = 0; b < block_cnt; b++) {
int mask = block_mask[b];
if (!blocks[mask].empty())
continue;
blocks[mask].assign(block_size, vector<int>(block_size));
for (int l = 0; l < block_size; l++) {
blocks[mask][l][l] = l;
for (int r = l + 1; r < block_size; r++) {
blocks[mask][l][r] = blocks[mask][l][r - 1];
if (b * block_size + r < m)
blocks[mask][l][r] = min_by_h(b * block_size + blocks[mask][l][r],
b * block_size + r) - b * block_size;
}
}
}
}
int lca_in_block(int b, int l, int r) {
return blocks[block_mask[b]][l][r] + b * block_size;
}
int lca(int v, int u) {
int l = first_visit[v];
int r = first_visit[u];
if (l > r)
swap(l, r);
int bl = l / block_size;
int br = r / block_size;
if (bl == br)
return euler_tour[lca_in_block(bl, l % block_size, r % block_size)];
int ans1 = lca_in_block(bl, l % block_size, block_size - 1);
int ans2 = lca_in_block(br, 0, r % block_size);
int ans = min_by_h(ans1, ans2);
if (bl + 1 < br) {
int l = log_2[br - bl - 1];
int ans3 = st[bl+1][l];
int ans4 = st[br - (1 << l)][l];
ans = min_by_h(ans, min_by_h(ans3, ans4));
}
return euler_tour[ans];
}
```
|
Lowest Common Ancestor - Farach-Colton and Bender Algorithm
|
---
title
floyd_warshall_algorithm
---
# Floyd-Warshall Algorithm
Given a directed or an undirected weighted graph $G$ with $n$ vertices.
The task is to find the length of the shortest path $d_{ij}$ between each pair of vertices $i$ and $j$.
The graph may have negative weight edges, but no negative weight cycles.
If there is such a negative cycle, you can just traverse this cycle over and over, in each iteration making the cost of the path smaller.
So you can make certain paths arbitrarily small, or in other words that shortest path is undefined.
That automatically means that an undirected graph cannot have any negative weight edges, as such an edge forms already a negative cycle as you can move back and forth along that edge as long as you like.
This algorithm can also be used to detect the presence of negative cycles.
The graph has a negative cycle if at the end of the algorithm, the distance from a vertex $v$ to itself is negative.
This algorithm has been simultaneously published in articles by Robert Floyd and Stephen Warshall in 1962.
However, in 1959, Bernard Roy published essentially the same algorithm, but its publication went unnoticed.
## Description of the algorithm
The key idea of the algorithm is to partition the process of finding the shortest path between any two vertices to several incremental phases.
Let us number the vertices starting from 1 to $n$.
The matrix of distances is $d[ ][ ]$.
Before $k$-th phase ($k = 1 \dots n$), $d[i][j]$ for any vertices $i$ and $j$ stores the length of the shortest path between the vertex $i$ and vertex $j$, which contains only the vertices $\{1, 2, ..., k-1\}$ as internal vertices in the path.
In other words, before $k$-th phase the value of $d[i][j]$ is equal to the length of the shortest path from vertex $i$ to the vertex $j$, if this path is allowed to enter only the vertex with numbers smaller than $k$ (the beginning and end of the path are not restricted by this property).
It is easy to make sure that this property holds for the first phase. For $k = 0$, we can fill matrix with $d[i][j] = w_{i j}$ if there exists an edge between $i$ and $j$ with weight $w_{i j}$ and $d[i][j] = \infty$ if there doesn't exist an edge.
In practice $\infty$ will be some high value.
As we shall see later, this is a requirement for the algorithm.
Suppose now that we are in the $k$-th phase, and we want to compute the matrix $d[ ][ ]$ so that it meets the requirements for the $(k + 1)$-th phase.
We have to fix the distances for some vertices pairs $(i, j)$.
There are two fundamentally different cases:
* The shortest way from the vertex $i$ to the vertex $j$ with internal vertices from the set $\{1, 2, \dots, k\}$ coincides with the shortest path with internal vertices from the set $\{1, 2, \dots, k-1\}$.
In this case, $d[i][j]$ will not change during the transition.
* The shortest path with internal vertices from $\{1, 2, \dots, k\}$ is shorter.
This means that the new, shorter path passes through the vertex $k$.
This means that we can split the shortest path between $i$ and $j$ into two paths:
the path between $i$ and $k$, and the path between $k$ and $j$.
It is clear that both this paths only use internal vertices of $\{1, 2, \dots, k-1\}$ and are the shortest such paths in that respect.
Therefore we already have computed the lengths of those paths before, and we can compute the length of the shortest path between $i$ and $j$ as $d[i][k] + d[k][j]$.
Combining these two cases we find that we can recalculate the length of all pairs $(i, j)$ in the $k$-th phase in the following way:
$$d_{\text{new}}[i][j] = min(d[i][j], d[i][k] + d[k][j])$$
Thus, all the work that is required in the $k$-th phase is to iterate over all pairs of vertices and recalculate the length of the shortest path between them.
As a result, after the $n$-th phase, the value $d[i][j]$ in the distance matrix is the length of the shortest path between $i$ and $j$, or is $\infty$ if the path between the vertices $i$ and $j$ does not exist.
A last remark - we don't need to create a separate distance matrix $d_{\text{new}}[ ][ ]$ for temporarily storing the shortest paths of the $k$-th phase, i.e. all changes can be made directly in the matrix $d[ ][ ]$ at any phase.
In fact at any $k$-th phase we are at most improving the distance of any path in the distance matrix, hence we cannot worsen the length of the shortest path for any pair of the vertices that are to be processed in the $(k+1)$-th phase or later.
The time complexity of this algorithm is obviously $O(n^3)$.
## Implementation
Let $d[][]$ is a 2D array of size $n \times n$, which is filled according to the $0$-th phase as explained earlier.
Also we will set $d[i][i] = 0$ for any $i$ at the $0$-th phase.
Then the algorithm is implemented as follows:
```cpp
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
```
It is assumed that if there is no edge between any two vertices $i$ and $j$, then the matrix at $d[i][j]$ contains a large number (large enough so that it is greater than the length of any path in this graph).
Then this edge will always be unprofitable to take, and the algorithm will work correctly.
However if there are negative weight edges in the graph, special measures have to be taken.
Otherwise the resulting values in matrix may be of the form $\infty - 1$, $\infty - 2$, etc., which, of course, still indicates that between the respective vertices doesn't exist a path.
Therefore, if the graph has negative weight edges, it is better to write the Floyd-Warshall algorithm in the following way, so that it does not perform transitions using paths that don't exist.
```cpp
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (d[i][k] < INF && d[k][j] < INF)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
```
## Retrieving the sequence of vertices in the shortest path
It is easy to maintain additional information with which it will be possible to retrieve the shortest path between any two given vertices in the form of a sequence of vertices.
For this, in addition to the distance matrix $d[ ][ ]$, a matrix of ancestors $p[ ][ ]$ must be maintained, which will contain the number of the phase where the shortest distance between two vertices was last modified.
It is clear that the number of the phase is nothing more than a vertex in the middle of the desired shortest path.
Now we just need to find the shortest path between vertices $i$ and $p[i][j]$, and between $p[i][j]$ and $j$.
This leads to a simple recursive reconstruction algorithm of the shortest path.
## The case of real weights
If the weights of the edges are not integer but real, it is necessary to take the errors, which occur when working with float types, into account.
The Floyd-Warshall algorithm has the unpleasant effect, that the errors accumulate very quickly.
In fact if there is an error in the first phase of $\delta$, this error may propagate to the second iteration as $2 \delta$, to the third iteration as $4 \delta$, and so on.
To avoid this the algorithm can be modified to take the error (EPS = $\delta$) into account by using following comparison:
```cpp
if (d[i][k] + d[k][j] < d[i][j] - EPS)
d[i][j] = d[i][k] + d[k][j];
```
## The case of negative cycles
Formally the Floyd-Warshall algorithm does not apply to graphs containing negative weight cycle(s).
But for all pairs of vertices $i$ and $j$ for which there doesn't exist a path starting at $i$, visiting a negative cycle, and end at $j$, the algorithm will still work correctly.
For the pair of vertices for which the answer does not exist (due to the presence of a negative cycle in the path between them), the Floyd algorithm will store any number (perhaps highly negative, but not necessarily) in the distance matrix.
However it is possible to improve the Floyd-Warshall algorithm, so that it carefully treats such pairs of vertices, and outputs them, for example as $-\text{INF}$.
This can be done in the following way:
let us run the usual Floyd-Warshall algorithm for a given graph.
Then a shortest path between vertices $i$ and $j$ does not exist, if and only if, there is a vertex $t$ that is reachable from $i$ and also from $j$, for which $d[t][t] < 0$.
In addition, when using the Floyd-Warshall algorithm for graphs with negative cycles, we should keep in mind that situations may arise in which distances can get exponentially fast into the negative.
Therefore integer overflow must be handled by limiting the minimal distance by some value (e.g. $-\text{INF}$).
To learn more about finding negative cycles in a graph, see the separate article [Finding a negative cycle in the graph](finding-negative-cycle-in-graph.md).
|
---
title
floyd_warshall_algorithm
---
# Floyd-Warshall Algorithm
Given a directed or an undirected weighted graph $G$ with $n$ vertices.
The task is to find the length of the shortest path $d_{ij}$ between each pair of vertices $i$ and $j$.
The graph may have negative weight edges, but no negative weight cycles.
If there is such a negative cycle, you can just traverse this cycle over and over, in each iteration making the cost of the path smaller.
So you can make certain paths arbitrarily small, or in other words that shortest path is undefined.
That automatically means that an undirected graph cannot have any negative weight edges, as such an edge forms already a negative cycle as you can move back and forth along that edge as long as you like.
This algorithm can also be used to detect the presence of negative cycles.
The graph has a negative cycle if at the end of the algorithm, the distance from a vertex $v$ to itself is negative.
This algorithm has been simultaneously published in articles by Robert Floyd and Stephen Warshall in 1962.
However, in 1959, Bernard Roy published essentially the same algorithm, but its publication went unnoticed.
## Description of the algorithm
The key idea of the algorithm is to partition the process of finding the shortest path between any two vertices to several incremental phases.
Let us number the vertices starting from 1 to $n$.
The matrix of distances is $d[ ][ ]$.
Before $k$-th phase ($k = 1 \dots n$), $d[i][j]$ for any vertices $i$ and $j$ stores the length of the shortest path between the vertex $i$ and vertex $j$, which contains only the vertices $\{1, 2, ..., k-1\}$ as internal vertices in the path.
In other words, before $k$-th phase the value of $d[i][j]$ is equal to the length of the shortest path from vertex $i$ to the vertex $j$, if this path is allowed to enter only the vertex with numbers smaller than $k$ (the beginning and end of the path are not restricted by this property).
It is easy to make sure that this property holds for the first phase. For $k = 0$, we can fill matrix with $d[i][j] = w_{i j}$ if there exists an edge between $i$ and $j$ with weight $w_{i j}$ and $d[i][j] = \infty$ if there doesn't exist an edge.
In practice $\infty$ will be some high value.
As we shall see later, this is a requirement for the algorithm.
Suppose now that we are in the $k$-th phase, and we want to compute the matrix $d[ ][ ]$ so that it meets the requirements for the $(k + 1)$-th phase.
We have to fix the distances for some vertices pairs $(i, j)$.
There are two fundamentally different cases:
* The shortest way from the vertex $i$ to the vertex $j$ with internal vertices from the set $\{1, 2, \dots, k\}$ coincides with the shortest path with internal vertices from the set $\{1, 2, \dots, k-1\}$.
In this case, $d[i][j]$ will not change during the transition.
* The shortest path with internal vertices from $\{1, 2, \dots, k\}$ is shorter.
This means that the new, shorter path passes through the vertex $k$.
This means that we can split the shortest path between $i$ and $j$ into two paths:
the path between $i$ and $k$, and the path between $k$ and $j$.
It is clear that both this paths only use internal vertices of $\{1, 2, \dots, k-1\}$ and are the shortest such paths in that respect.
Therefore we already have computed the lengths of those paths before, and we can compute the length of the shortest path between $i$ and $j$ as $d[i][k] + d[k][j]$.
Combining these two cases we find that we can recalculate the length of all pairs $(i, j)$ in the $k$-th phase in the following way:
$$d_{\text{new}}[i][j] = min(d[i][j], d[i][k] + d[k][j])$$
Thus, all the work that is required in the $k$-th phase is to iterate over all pairs of vertices and recalculate the length of the shortest path between them.
As a result, after the $n$-th phase, the value $d[i][j]$ in the distance matrix is the length of the shortest path between $i$ and $j$, or is $\infty$ if the path between the vertices $i$ and $j$ does not exist.
A last remark - we don't need to create a separate distance matrix $d_{\text{new}}[ ][ ]$ for temporarily storing the shortest paths of the $k$-th phase, i.e. all changes can be made directly in the matrix $d[ ][ ]$ at any phase.
In fact at any $k$-th phase we are at most improving the distance of any path in the distance matrix, hence we cannot worsen the length of the shortest path for any pair of the vertices that are to be processed in the $(k+1)$-th phase or later.
The time complexity of this algorithm is obviously $O(n^3)$.
## Implementation
Let $d[][]$ is a 2D array of size $n \times n$, which is filled according to the $0$-th phase as explained earlier.
Also we will set $d[i][i] = 0$ for any $i$ at the $0$-th phase.
Then the algorithm is implemented as follows:
```cpp
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
```
It is assumed that if there is no edge between any two vertices $i$ and $j$, then the matrix at $d[i][j]$ contains a large number (large enough so that it is greater than the length of any path in this graph).
Then this edge will always be unprofitable to take, and the algorithm will work correctly.
However if there are negative weight edges in the graph, special measures have to be taken.
Otherwise the resulting values in matrix may be of the form $\infty - 1$, $\infty - 2$, etc., which, of course, still indicates that between the respective vertices doesn't exist a path.
Therefore, if the graph has negative weight edges, it is better to write the Floyd-Warshall algorithm in the following way, so that it does not perform transitions using paths that don't exist.
```cpp
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (d[i][k] < INF && d[k][j] < INF)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
```
## Retrieving the sequence of vertices in the shortest path
It is easy to maintain additional information with which it will be possible to retrieve the shortest path between any two given vertices in the form of a sequence of vertices.
For this, in addition to the distance matrix $d[ ][ ]$, a matrix of ancestors $p[ ][ ]$ must be maintained, which will contain the number of the phase where the shortest distance between two vertices was last modified.
It is clear that the number of the phase is nothing more than a vertex in the middle of the desired shortest path.
Now we just need to find the shortest path between vertices $i$ and $p[i][j]$, and between $p[i][j]$ and $j$.
This leads to a simple recursive reconstruction algorithm of the shortest path.
## The case of real weights
If the weights of the edges are not integer but real, it is necessary to take the errors, which occur when working with float types, into account.
The Floyd-Warshall algorithm has the unpleasant effect, that the errors accumulate very quickly.
In fact if there is an error in the first phase of $\delta$, this error may propagate to the second iteration as $2 \delta$, to the third iteration as $4 \delta$, and so on.
To avoid this the algorithm can be modified to take the error (EPS = $\delta$) into account by using following comparison:
```cpp
if (d[i][k] + d[k][j] < d[i][j] - EPS)
d[i][j] = d[i][k] + d[k][j];
```
## The case of negative cycles
Formally the Floyd-Warshall algorithm does not apply to graphs containing negative weight cycle(s).
But for all pairs of vertices $i$ and $j$ for which there doesn't exist a path starting at $i$, visiting a negative cycle, and end at $j$, the algorithm will still work correctly.
For the pair of vertices for which the answer does not exist (due to the presence of a negative cycle in the path between them), the Floyd algorithm will store any number (perhaps highly negative, but not necessarily) in the distance matrix.
However it is possible to improve the Floyd-Warshall algorithm, so that it carefully treats such pairs of vertices, and outputs them, for example as $-\text{INF}$.
This can be done in the following way:
let us run the usual Floyd-Warshall algorithm for a given graph.
Then a shortest path between vertices $i$ and $j$ does not exist, if and only if, there is a vertex $t$ that is reachable from $i$ and also from $j$, for which $d[t][t] < 0$.
In addition, when using the Floyd-Warshall algorithm for graphs with negative cycles, we should keep in mind that situations may arise in which distances can get exponentially fast into the negative.
Therefore integer overflow must be handled by limiting the minimal distance by some value (e.g. $-\text{INF}$).
To learn more about finding negative cycles in a graph, see the separate article [Finding a negative cycle in the graph](finding-negative-cycle-in-graph.md).
## Practice Problems
- [UVA: Page Hopping](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=762)
- [SPOJ: Possible Friends](http://www.spoj.com/problems/SOCIALNE/)
- [CODEFORCES: Greg and Graph](http://codeforces.com/problemset/problem/295/B)
- [SPOJ: CHICAGO - 106 miles to Chicago](http://www.spoj.com/problems/CHICAGO/)
* [UVA 10724 - Road Construction](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=1665)
* [UVA 117 - The Postal Worker Rings Once](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=53)
* [Codeforces - Traveling Graph](http://codeforces.com/problemset/problem/21/D)
* [UVA - 1198 - The Geodetic Set Problem](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=3639)
* [UVA - 10048 - Audiophobia](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=989)
* [UVA - 125 - Numbering Paths](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=61)
* [LOJ - Travel Company](http://lightoj.com/volume_showproblem.php?problem=1221)
* [UVA 423 - MPI Maelstrom](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=364)
* [UVA 1416 - Warfare And Logistics](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=4162)
* [UVA 1233 - USHER](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=3674)
* [UVA 10793 - The Orc Attack](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1734)
* [UVA 10099 The Tourist Guide](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1040)
* [UVA 869 - Airline Comparison](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=810)
* [UVA 13211 - Geonosis](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=5134)
* [SPOJ - Defend the Rohan](http://www.spoj.com/problems/ROHAAN/)
* [Codeforces - Roads in Berland](http://codeforces.com/contest/25/problem/C)
* [Codeforces - String Problem](http://codeforces.com/contest/33/problem/B)
* [GYM - Manic Moving (C)](http://codeforces.com/gym/101223)
* [SPOJ - Arbitrage](http://www.spoj.com/problems/ARBITRAG/)
* [UVA - 12179 - Randomly-priced Tickets](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=3331)
* [LOJ - 1086 - Jogging Trails](http://lightoj.com/volume_showproblem.php?problem=1086)
* [SPOJ - Ingredients](http://www.spoj.com/problems/INGRED/)
* [CSES - Shortest Routes II](https://cses.fi/problemset/task/1672)
|
Floyd-Warshall Algorithm
|
---
title
assignment_mincostflow
---
# Solving assignment problem using min-cost-flow
The **assignment problem** has two equivalent statements:
- Given a square matrix $A[1..N, 1..N]$, you need to select $N$ elements in it so that exactly one element is selected in each row and column, and the sum of the values of these elements is the smallest.
- There are $N$ orders and $N$ machines. The cost of manufacturing on each machine is known for each order. Only one order can be performed on each machine. It is required to assign all orders to the machines so that the total cost is minimized.
Here we will consider the solution of the problem based on the algorithm for finding the [minimum cost flow (min-cost-flow)](min_cost_flow.md), solving the assignment problem in $\mathcal{O}(N^3)$.
## Description
Let's build a bipartite network: there is a source $S$, a drain $T$, in the first part there are $N$ vertices (corresponding to rows of the matrix, or orders), in the second there are also $N$ vertices (corresponding to the columns of the matrix, or machines). Between each vertex $i$ of the first set and each vertex $j$ of the second set, we draw an edge with bandwidth 1 and cost $A_{ij}$. From the source $S$ we draw edges to all vertices $i$ of the first set with bandwidth 1 and cost 0. We draw an edge with bandwidth 1 and cost 0 from each vertex of the second set $j$ to the drain $T$.
We find in the resulting network the maximum flow of the minimum cost. Obviously, the value of the flow will be $N$. Further, for each vertex $i$ of the first segment there is exactly one vertex $j$ of the second segment, such that the flow $F_{ij}$ = 1. Finally, this is a one-to-one correspondence between the vertices of the first segment and the vertices of the second part, which is the solution to the problem (since the found flow has a minimal cost, then the sum of the costs of the selected edges will be the lowest possible, which is the optimality criterion).
The complexity of this solution of the assignment problem depends on the algorithm by which the search for the maximum flow of the minimum cost is performed. The complexity will be $\mathcal{O}(N^3)$ using [Dijkstra](dijkstra.md) or $\mathcal{O}(N^4)$ using [Bellman-Ford](bellman_ford.md). This is due to the fact that the flow is of size $O(N)$ and each iteration of Dijkstra algorithm can be performed in $O(N^2)$, while it is $O(N^3)$ for Bellman-Ford.
## Implementation
The implementation given here is long, it can probably be significantly reduced.
It uses the [SPFA algorithm](bellman_ford.md) for finding shortest paths.
```cpp
const int INF = 1000 * 1000 * 1000;
vector<int> assignment(vector<vector<int>> a) {
int n = a.size();
int m = n * 2 + 2;
vector<vector<int>> f(m, vector<int>(m));
int s = m - 2, t = m - 1;
int cost = 0;
while (true) {
vector<int> dist(m, INF);
vector<int> p(m);
vector<bool> inq(m, false);
queue<int> q;
dist[s] = 0;
p[s] = -1;
q.push(s);
while (!q.empty()) {
int v = q.front();
q.pop();
inq[v] = false;
if (v == s) {
for (int i = 0; i < n; ++i) {
if (f[s][i] == 0) {
dist[i] = 0;
p[i] = s;
inq[i] = true;
q.push(i);
}
}
} else {
if (v < n) {
for (int j = n; j < n + n; ++j) {
if (f[v][j] < 1 && dist[j] > dist[v] + a[v][j - n]) {
dist[j] = dist[v] + a[v][j - n];
p[j] = v;
if (!inq[j]) {
q.push(j);
inq[j] = true;
}
}
}
} else {
for (int j = 0; j < n; ++j) {
if (f[v][j] < 0 && dist[j] > dist[v] - a[j][v - n]) {
dist[j] = dist[v] - a[j][v - n];
p[j] = v;
if (!inq[j]) {
q.push(j);
inq[j] = true;
}
}
}
}
}
}
int curcost = INF;
for (int i = n; i < n + n; ++i) {
if (f[i][t] == 0 && dist[i] < curcost) {
curcost = dist[i];
p[t] = i;
}
}
if (curcost == INF)
break;
cost += curcost;
for (int cur = t; cur != -1; cur = p[cur]) {
int prev = p[cur];
if (prev != -1)
f[cur][prev] = -(f[prev][cur] = 1);
}
}
vector<int> answer(n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (f[i][j + n] == 1)
answer[i] = j;
}
}
return answer;
}
```
|
---
title
assignment_mincostflow
---
# Solving assignment problem using min-cost-flow
The **assignment problem** has two equivalent statements:
- Given a square matrix $A[1..N, 1..N]$, you need to select $N$ elements in it so that exactly one element is selected in each row and column, and the sum of the values of these elements is the smallest.
- There are $N$ orders and $N$ machines. The cost of manufacturing on each machine is known for each order. Only one order can be performed on each machine. It is required to assign all orders to the machines so that the total cost is minimized.
Here we will consider the solution of the problem based on the algorithm for finding the [minimum cost flow (min-cost-flow)](min_cost_flow.md), solving the assignment problem in $\mathcal{O}(N^3)$.
## Description
Let's build a bipartite network: there is a source $S$, a drain $T$, in the first part there are $N$ vertices (corresponding to rows of the matrix, or orders), in the second there are also $N$ vertices (corresponding to the columns of the matrix, or machines). Between each vertex $i$ of the first set and each vertex $j$ of the second set, we draw an edge with bandwidth 1 and cost $A_{ij}$. From the source $S$ we draw edges to all vertices $i$ of the first set with bandwidth 1 and cost 0. We draw an edge with bandwidth 1 and cost 0 from each vertex of the second set $j$ to the drain $T$.
We find in the resulting network the maximum flow of the minimum cost. Obviously, the value of the flow will be $N$. Further, for each vertex $i$ of the first segment there is exactly one vertex $j$ of the second segment, such that the flow $F_{ij}$ = 1. Finally, this is a one-to-one correspondence between the vertices of the first segment and the vertices of the second part, which is the solution to the problem (since the found flow has a minimal cost, then the sum of the costs of the selected edges will be the lowest possible, which is the optimality criterion).
The complexity of this solution of the assignment problem depends on the algorithm by which the search for the maximum flow of the minimum cost is performed. The complexity will be $\mathcal{O}(N^3)$ using [Dijkstra](dijkstra.md) or $\mathcal{O}(N^4)$ using [Bellman-Ford](bellman_ford.md). This is due to the fact that the flow is of size $O(N)$ and each iteration of Dijkstra algorithm can be performed in $O(N^2)$, while it is $O(N^3)$ for Bellman-Ford.
## Implementation
The implementation given here is long, it can probably be significantly reduced.
It uses the [SPFA algorithm](bellman_ford.md) for finding shortest paths.
```cpp
const int INF = 1000 * 1000 * 1000;
vector<int> assignment(vector<vector<int>> a) {
int n = a.size();
int m = n * 2 + 2;
vector<vector<int>> f(m, vector<int>(m));
int s = m - 2, t = m - 1;
int cost = 0;
while (true) {
vector<int> dist(m, INF);
vector<int> p(m);
vector<bool> inq(m, false);
queue<int> q;
dist[s] = 0;
p[s] = -1;
q.push(s);
while (!q.empty()) {
int v = q.front();
q.pop();
inq[v] = false;
if (v == s) {
for (int i = 0; i < n; ++i) {
if (f[s][i] == 0) {
dist[i] = 0;
p[i] = s;
inq[i] = true;
q.push(i);
}
}
} else {
if (v < n) {
for (int j = n; j < n + n; ++j) {
if (f[v][j] < 1 && dist[j] > dist[v] + a[v][j - n]) {
dist[j] = dist[v] + a[v][j - n];
p[j] = v;
if (!inq[j]) {
q.push(j);
inq[j] = true;
}
}
}
} else {
for (int j = 0; j < n; ++j) {
if (f[v][j] < 0 && dist[j] > dist[v] - a[j][v - n]) {
dist[j] = dist[v] - a[j][v - n];
p[j] = v;
if (!inq[j]) {
q.push(j);
inq[j] = true;
}
}
}
}
}
}
int curcost = INF;
for (int i = n; i < n + n; ++i) {
if (f[i][t] == 0 && dist[i] < curcost) {
curcost = dist[i];
p[t] = i;
}
}
if (curcost == INF)
break;
cost += curcost;
for (int cur = t; cur != -1; cur = p[cur]) {
int prev = p[cur];
if (prev != -1)
f[cur][prev] = -(f[prev][cur] = 1);
}
}
vector<int> answer(n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (f[i][j + n] == 1)
answer[i] = j;
}
}
return answer;
}
```
|
Solving assignment problem using min-cost-flow
|
---
title
bfs
---
# Breadth-first search
Breadth first search is one of the basic and essential searching algorithms on graphs.
As a result of how the algorithm works, the path found by breadth first search to any node is the shortest path to that node, i.e the path that contains the smallest number of edges in unweighted graphs.
The algorithm works in $O(n + m)$ time, where $n$ is number of vertices and $m$ is the number of edges.
## Description of the algorithm
The algorithm takes as input an unweighted graph and the id of the source vertex $s$. The input graph can be directed or undirected,
it does not matter to the algorithm.
The algorithm can be understood as a fire spreading on the graph: at the zeroth step only the source $s$ is on fire. At each step, the fire burning at each vertex spreads to all of its neighbors. In one iteration of the algorithm, the "ring of
fire" is expanded in width by one unit (hence the name of the algorithm).
More precisely, the algorithm can be stated as follows: Create a queue $q$ which will contain the vertices to be processed and a
Boolean array $used[]$ which indicates for each vertex, if it has been lit (or visited) or not.
Initially, push the source $s$ to the queue and set $used[s] = true$, and for all other vertices $v$ set $used[v] = false$.
Then, loop until the queue is empty and in each iteration, pop a vertex from the front of the queue. Iterate through all the edges going out
of this vertex and if some of these edges go to vertices that are not already lit, set them on fire and place them in the queue.
As a result, when the queue is empty, the "ring of fire" contains all vertices reachable from the source $s$, with each vertex reached in the shortest possible way.
You can also calculate the lengths of the shortest paths (which just requires maintaining an array of path lengths $d[]$) as well as save information to restore all of these shortest paths (for this, it is necessary to maintain an array of "parents" $p[]$, which stores for each vertex the vertex from which we reached it).
## Implementation
We write code for the described algorithm in C++ and Java.
=== "C++"
```cpp
vector<vector<int>> adj; // adjacency list representation
int n; // number of nodes
int s; // source vertex
queue<int> q;
vector<bool> used(n);
vector<int> d(n), p(n);
q.push(s);
used[s] = true;
p[s] = -1;
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : adj[v]) {
if (!used[u]) {
used[u] = true;
q.push(u);
d[u] = d[v] + 1;
p[u] = v;
}
}
}
```
=== "Java"
```java
ArrayList<ArrayList<Integer>> adj = new ArrayList<>(); // adjacency list representation
int n; // number of nodes
int s; // source vertex
LinkedList<Integer> q = new LinkedList<Integer>();
boolean used[] = new boolean[n];
int d[] = new int[n];
int p[] = new int[n];
q.push(s);
used[s] = true;
p[s] = -1;
while (!q.isEmpty()) {
int v = q.pop();
for (int u : adj.get(v)) {
if (!used[u]) {
used[u] = true;
q.push(u);
d[u] = d[v] + 1;
p[u] = v;
}
}
}
```
If we have to restore and display the shortest path from the source to some vertex $u$, it can be done in the following manner:
=== "C++"
```cpp
if (!used[u]) {
cout << "No path!";
} else {
vector<int> path;
for (int v = u; v != -1; v = p[v])
path.push_back(v);
reverse(path.begin(), path.end());
cout << "Path: ";
for (int v : path)
cout << v << " ";
}
```
=== "Java"
```java
if (!used[u]) {
System.out.println("No path!");
} else {
ArrayList<Integer> path = new ArrayList<Integer>();
for (int v = u; v != -1; v = p[v])
path.add(v);
Collections.reverse(path);
for(int v : path)
System.out.println(v);
}
```
## Applications of BFS
* Find the shortest path from a source to other vertices in an unweighted graph.
* Find all connected components in an undirected graph in $O(n + m)$ time:
To do this, we just run BFS starting from each vertex, except for vertices which have already been visited from previous runs.
Thus, we perform normal BFS from each of the vertices, but do not reset the array $used[]$ each and every time we get a new connected component, and the total running time will still be $O(n + m)$ (performing multiple BFS on the graph without zeroing the array $used []$ is called a series of breadth first searches).
* Finding a solution to a problem or a game with the least number of moves, if each state of the game can be represented by a vertex of the graph, and the transitions from one state to the other are the edges of the graph.
* Finding the shortest path in a graph with weights 0 or 1:
This requires just a little modification to normal breadth-first search: Instead of maintaining array $used[]$, we will now check if the distance to vertex is shorter than current found distance, then if the current edge is of zero weight, we add it to the front of the queue else we add it to the back of the queue.This modification is explained in more detail in the article [0-1 BFS](01_bfs.md).
* Finding the shortest cycle in a directed unweighted graph:
Start a breadth-first search from each vertex.
As soon as we try to go from the current vertex back to the source vertex, we have found the shortest cycle containing the source vertex.
At this point we can stop the BFS, and start a new BFS from the next vertex.
From all such cycles (at most one from each BFS) choose the shortest.
* Find all the edges that lie on any shortest path between a given pair of vertices $(a, b)$.
To do this, run two breadth first searches:
one from $a$ and one from $b$.
Let $d_a []$ be the array containing shortest distances obtained from the first BFS (from $a$) and $d_b []$ be the array containing shortest distances obtained from the second BFS from $b$.
Now for every edge $(u, v)$ it is easy to check whether that edge lies on any shortest path between $a$ and $b$:
the criterion is the condition $d_a [u] + 1 + d_b [v] = d_a [b]$.
* Find all the vertices on any shortest path between a given pair of vertices $(a, b)$.
To accomplish that, run two breadth first searches:
one from $a$ and one from $b$.
Let $d_a []$ be the array containing shortest distances obtained from the first BFS (from $a$) and $d_b []$ be the array containing shortest distances obtained from the second BFS (from $b$).
Now for each vertex it is easy to check whether it lies on any shortest path between $a$ and $b$:
the criterion is the condition $d_a [v] + d_b [v] = d_a [b]$.
* Find the shortest path of even length from a source vertex $s$ to a target vertex $t$ in an unweighted graph:
For this, we must construct an auxiliary graph, whose vertices are the state $(v, c)$, where $v$ - the current node, $c = 0$ or $c = 1$ - the current parity.
Any edge $(u, v)$ of the original graph in this new column will turn into two edges $((u, 0), (v, 1))$ and $((u, 1), (v, 0))$.
After that we run a BFS to find the shortest path from the starting vertex $(s, 0)$ to the end vertex $(t, 0)$.
|
---
title
bfs
---
# Breadth-first search
Breadth first search is one of the basic and essential searching algorithms on graphs.
As a result of how the algorithm works, the path found by breadth first search to any node is the shortest path to that node, i.e the path that contains the smallest number of edges in unweighted graphs.
The algorithm works in $O(n + m)$ time, where $n$ is number of vertices and $m$ is the number of edges.
## Description of the algorithm
The algorithm takes as input an unweighted graph and the id of the source vertex $s$. The input graph can be directed or undirected,
it does not matter to the algorithm.
The algorithm can be understood as a fire spreading on the graph: at the zeroth step only the source $s$ is on fire. At each step, the fire burning at each vertex spreads to all of its neighbors. In one iteration of the algorithm, the "ring of
fire" is expanded in width by one unit (hence the name of the algorithm).
More precisely, the algorithm can be stated as follows: Create a queue $q$ which will contain the vertices to be processed and a
Boolean array $used[]$ which indicates for each vertex, if it has been lit (or visited) or not.
Initially, push the source $s$ to the queue and set $used[s] = true$, and for all other vertices $v$ set $used[v] = false$.
Then, loop until the queue is empty and in each iteration, pop a vertex from the front of the queue. Iterate through all the edges going out
of this vertex and if some of these edges go to vertices that are not already lit, set them on fire and place them in the queue.
As a result, when the queue is empty, the "ring of fire" contains all vertices reachable from the source $s$, with each vertex reached in the shortest possible way.
You can also calculate the lengths of the shortest paths (which just requires maintaining an array of path lengths $d[]$) as well as save information to restore all of these shortest paths (for this, it is necessary to maintain an array of "parents" $p[]$, which stores for each vertex the vertex from which we reached it).
## Implementation
We write code for the described algorithm in C++ and Java.
=== "C++"
```cpp
vector<vector<int>> adj; // adjacency list representation
int n; // number of nodes
int s; // source vertex
queue<int> q;
vector<bool> used(n);
vector<int> d(n), p(n);
q.push(s);
used[s] = true;
p[s] = -1;
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : adj[v]) {
if (!used[u]) {
used[u] = true;
q.push(u);
d[u] = d[v] + 1;
p[u] = v;
}
}
}
```
=== "Java"
```java
ArrayList<ArrayList<Integer>> adj = new ArrayList<>(); // adjacency list representation
int n; // number of nodes
int s; // source vertex
LinkedList<Integer> q = new LinkedList<Integer>();
boolean used[] = new boolean[n];
int d[] = new int[n];
int p[] = new int[n];
q.push(s);
used[s] = true;
p[s] = -1;
while (!q.isEmpty()) {
int v = q.pop();
for (int u : adj.get(v)) {
if (!used[u]) {
used[u] = true;
q.push(u);
d[u] = d[v] + 1;
p[u] = v;
}
}
}
```
If we have to restore and display the shortest path from the source to some vertex $u$, it can be done in the following manner:
=== "C++"
```cpp
if (!used[u]) {
cout << "No path!";
} else {
vector<int> path;
for (int v = u; v != -1; v = p[v])
path.push_back(v);
reverse(path.begin(), path.end());
cout << "Path: ";
for (int v : path)
cout << v << " ";
}
```
=== "Java"
```java
if (!used[u]) {
System.out.println("No path!");
} else {
ArrayList<Integer> path = new ArrayList<Integer>();
for (int v = u; v != -1; v = p[v])
path.add(v);
Collections.reverse(path);
for(int v : path)
System.out.println(v);
}
```
## Applications of BFS
* Find the shortest path from a source to other vertices in an unweighted graph.
* Find all connected components in an undirected graph in $O(n + m)$ time:
To do this, we just run BFS starting from each vertex, except for vertices which have already been visited from previous runs.
Thus, we perform normal BFS from each of the vertices, but do not reset the array $used[]$ each and every time we get a new connected component, and the total running time will still be $O(n + m)$ (performing multiple BFS on the graph without zeroing the array $used []$ is called a series of breadth first searches).
* Finding a solution to a problem or a game with the least number of moves, if each state of the game can be represented by a vertex of the graph, and the transitions from one state to the other are the edges of the graph.
* Finding the shortest path in a graph with weights 0 or 1:
This requires just a little modification to normal breadth-first search: Instead of maintaining array $used[]$, we will now check if the distance to vertex is shorter than current found distance, then if the current edge is of zero weight, we add it to the front of the queue else we add it to the back of the queue.This modification is explained in more detail in the article [0-1 BFS](01_bfs.md).
* Finding the shortest cycle in a directed unweighted graph:
Start a breadth-first search from each vertex.
As soon as we try to go from the current vertex back to the source vertex, we have found the shortest cycle containing the source vertex.
At this point we can stop the BFS, and start a new BFS from the next vertex.
From all such cycles (at most one from each BFS) choose the shortest.
* Find all the edges that lie on any shortest path between a given pair of vertices $(a, b)$.
To do this, run two breadth first searches:
one from $a$ and one from $b$.
Let $d_a []$ be the array containing shortest distances obtained from the first BFS (from $a$) and $d_b []$ be the array containing shortest distances obtained from the second BFS from $b$.
Now for every edge $(u, v)$ it is easy to check whether that edge lies on any shortest path between $a$ and $b$:
the criterion is the condition $d_a [u] + 1 + d_b [v] = d_a [b]$.
* Find all the vertices on any shortest path between a given pair of vertices $(a, b)$.
To accomplish that, run two breadth first searches:
one from $a$ and one from $b$.
Let $d_a []$ be the array containing shortest distances obtained from the first BFS (from $a$) and $d_b []$ be the array containing shortest distances obtained from the second BFS (from $b$).
Now for each vertex it is easy to check whether it lies on any shortest path between $a$ and $b$:
the criterion is the condition $d_a [v] + d_b [v] = d_a [b]$.
* Find the shortest path of even length from a source vertex $s$ to a target vertex $t$ in an unweighted graph:
For this, we must construct an auxiliary graph, whose vertices are the state $(v, c)$, where $v$ - the current node, $c = 0$ or $c = 1$ - the current parity.
Any edge $(u, v)$ of the original graph in this new column will turn into two edges $((u, 0), (v, 1))$ and $((u, 1), (v, 0))$.
After that we run a BFS to find the shortest path from the starting vertex $(s, 0)$ to the end vertex $(t, 0)$.
## Practice Problems
* [SPOJ: AKBAR](http://spoj.com/problems/AKBAR)
* [SPOJ: NAKANJ](http://www.spoj.com/problems/NAKANJ/)
* [SPOJ: WATER](http://www.spoj.com/problems/WATER)
* [SPOJ: MICE AND MAZE](http://www.spoj.com/problems/MICEMAZE/)
* [Timus: Caravans](http://acm.timus.ru/problem.aspx?space=1&num=2034)
* [DevSkill - Holloween Party (archived)](http://web.archive.org/web/20200930162803/http://www.devskill.com/CodingProblems/ViewProblem/60)
* [DevSkill - Ohani And The Link Cut Tree (archived)](http://web.archive.org/web/20170216192002/http://devskill.com:80/CodingProblems/ViewProblem/150)
* [SPOJ - Spiky Mazes](http://www.spoj.com/problems/SPIKES/)
* [SPOJ - Four Chips (hard)](http://www.spoj.com/problems/ADV04F1/)
* [SPOJ - Inversion Sort](http://www.spoj.com/problems/INVESORT/)
* [Codeforces - Shortest Path](http://codeforces.com/contest/59/problem/E)
* [SPOJ - Yet Another Multiple Problem](http://www.spoj.com/problems/MULTII/)
* [UVA 11392 - Binary 3xType Multiple](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2387)
* [UVA 10968 - KuPellaKeS](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1909)
* [Codeforces - Police Stations](http://codeforces.com/contest/796/problem/D)
* [Codeforces - Okabe and City](http://codeforces.com/contest/821/problem/D)
* [SPOJ - Find the Treasure](http://www.spoj.com/problems/DIGOKEYS/)
* [Codeforces - Bear and Forgotten Tree 2](http://codeforces.com/contest/653/problem/E)
* [Codeforces - Cycle in Maze](http://codeforces.com/contest/769/problem/C)
* [UVA - 11312 - Flipping Frustration](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2287)
* [SPOJ - Ada and Cycle](http://www.spoj.com/problems/ADACYCLE/)
* [CSES - Labyrinth](https://cses.fi/problemset/task/1193)
* [CSES - Message Route](https://cses.fi/problemset/task/1667/)
* [CSES - Monsters](https://cses.fi/problemset/task/1194)
|
Breadth-first search
|
---
title
johnson_problem_2
---
# Scheduling jobs on two machines
This task is about finding an optimal schedule for $n$ jobs on two machines.
Every item must first be processed on the first machine, and afterwards on the second one.
The $i$-th job takes $a_i$ time on the first machine, and $b_i$ time on the second machine.
Each machine can only process one job at a time.
We want to find the optimal order of the jobs, so that the final processing time is the minimum possible.
This solution that is discussed here is called Johnson's rule (named after S. M. Johnson).
It is worth noting, that the task becomes NP-complete, if we have more than two machines.
## Construction of the algorithm
Note first, that we can assume that the order of jobs for the first and the second machine have to coincide.
In fact, since the jobs for the second machine become available after processing them at the first, and if there are several jobs available for the second machine, than the processing time will be equal to the sum of their $b_i$, regardless of their order.
Therefore it is only advantageous to send the jobs to the second machine in the same order as we sent them to the first machine.
Consider the order of the jobs, which coincides with their input order $1, 2, \dots, n$.
We denote by $x_i$ the **idle time** of the second machine immediately before processing $i$.
Our goal is to **minimize the total idle time**:
$$F(x) = \sum x_i ~ \rightarrow \min$$
For the first job we have $x_1 = a_1$.
For the second job, since it gets sent to the machine at the time $a_1 + a_2$, and the second machine gets free at $x_1 + b_1$, we have $x_2 = \max\left((a_1 + a_2) - (x_1 + b_1), 0\right)$.
In general we get the equation:
$$x_k = \max\left(\sum_{i=1}^k a_i - \sum_{i=1}^{k-1} b_i - \sum_{i=1}^{k-1} x_i, 0 \right)$$
We can now calculate the **total idle time** $F(x)$.
It is claimed that it has the form
$$F(x) = \max_{k=1 \dots n} K_i,$$
where
$$K_i = \sum_{i=1}^k a_i - \sum_{i=1}^{k-1} b_i.$$
This can be easily verified using induction.
We now use the **permutation method**:
we will exchange two neighboring jobs $j$ and $j+1$ and see how this will change the total idle time.
By the form of the expression of $K_i$, it is clear that only $K_j$ and $K_{j+1}$ change, we denote their new values with $K_j'$ and $K_{j+1}'$.
If this change from of the jobs $j$ and $j+1$ increased the total idle time, it has to be the case that:
$$\max(K_j, K_{j+1}) \le \max(K_j', K_{j+1}')$$
(Switching two jobs might also have no impact at all.
The above condition is only a sufficient one, but not a necessary one.)
After removing $\sum_{i=1}^{j+1} a_i - \sum_{i=1}^{j-1} b_i$ from both sides of the inequality, we get:
$$\max(-a_{j+1}, -b_j) \le \max(-b_{j+1}, -a_j)$$
And after getting rid of the negative signs:
$$\min(a_j, b_{j+1}) \le \min(b_j, a_{j+1})$$
Thus we obtained a **comparator**:
by sorting the jobs on it, we obtain an optimal order of the jobs, in which no two jobs can be switched with an improvement of the final time.
However you can further **simplify** the sorting, if you look at the comparator from a different angle.
The comparator can be interpreted in the following way:
If we have the four times $(a_j, a_{j+1}, b_j, b_{j+1})$, and the minimum of them is a time corresponding to the first machine, then the corresponding job should be done first.
If the minimum time is a time from the second machine, then it should go later.
Thus we can sort the jobs by $\min(a_i, b_i)$, and if the processing time of the current job on the first machine is less then the processing time on the second machine, then this job must be done before all the remaining jobs, and otherwise after all remaining tasks.
One way or another, it turns out that by Johnson's rule we can solve the problem by sorting the jobs, and thus receive a time complexity of $O(n \log n)$.
## Implementation
Here we implement the second variation of the described algorithm.
```{.cpp file=johnsons_rule}
struct Job {
int a, b, idx;
bool operator<(Job o) const {
return min(a, b) < min(o.a, o.b);
}
};
vector<Job> johnsons_rule(vector<Job> jobs) {
sort(jobs.begin(), jobs.end());
vector<Job> a, b;
for (Job j : jobs) {
if (j.a < j.b)
a.push_back(j);
else
b.push_back(j);
}
a.insert(a.end(), b.rbegin(), b.rend());
return a;
}
pair<int, int> finish_times(vector<Job> const& jobs) {
int t1 = 0, t2 = 0;
for (Job j : jobs) {
t1 += j.a;
t2 = max(t2, t1) + j.b;
}
return make_pair(t1, t2);
}
```
All the information about each job is store in struct.
The first function sorts all jobs and computes the optimal schedule.
The second function computes the finish times of both machines given a schedule.
|
---
title
johnson_problem_2
---
# Scheduling jobs on two machines
This task is about finding an optimal schedule for $n$ jobs on two machines.
Every item must first be processed on the first machine, and afterwards on the second one.
The $i$-th job takes $a_i$ time on the first machine, and $b_i$ time on the second machine.
Each machine can only process one job at a time.
We want to find the optimal order of the jobs, so that the final processing time is the minimum possible.
This solution that is discussed here is called Johnson's rule (named after S. M. Johnson).
It is worth noting, that the task becomes NP-complete, if we have more than two machines.
## Construction of the algorithm
Note first, that we can assume that the order of jobs for the first and the second machine have to coincide.
In fact, since the jobs for the second machine become available after processing them at the first, and if there are several jobs available for the second machine, than the processing time will be equal to the sum of their $b_i$, regardless of their order.
Therefore it is only advantageous to send the jobs to the second machine in the same order as we sent them to the first machine.
Consider the order of the jobs, which coincides with their input order $1, 2, \dots, n$.
We denote by $x_i$ the **idle time** of the second machine immediately before processing $i$.
Our goal is to **minimize the total idle time**:
$$F(x) = \sum x_i ~ \rightarrow \min$$
For the first job we have $x_1 = a_1$.
For the second job, since it gets sent to the machine at the time $a_1 + a_2$, and the second machine gets free at $x_1 + b_1$, we have $x_2 = \max\left((a_1 + a_2) - (x_1 + b_1), 0\right)$.
In general we get the equation:
$$x_k = \max\left(\sum_{i=1}^k a_i - \sum_{i=1}^{k-1} b_i - \sum_{i=1}^{k-1} x_i, 0 \right)$$
We can now calculate the **total idle time** $F(x)$.
It is claimed that it has the form
$$F(x) = \max_{k=1 \dots n} K_i,$$
where
$$K_i = \sum_{i=1}^k a_i - \sum_{i=1}^{k-1} b_i.$$
This can be easily verified using induction.
We now use the **permutation method**:
we will exchange two neighboring jobs $j$ and $j+1$ and see how this will change the total idle time.
By the form of the expression of $K_i$, it is clear that only $K_j$ and $K_{j+1}$ change, we denote their new values with $K_j'$ and $K_{j+1}'$.
If this change from of the jobs $j$ and $j+1$ increased the total idle time, it has to be the case that:
$$\max(K_j, K_{j+1}) \le \max(K_j', K_{j+1}')$$
(Switching two jobs might also have no impact at all.
The above condition is only a sufficient one, but not a necessary one.)
After removing $\sum_{i=1}^{j+1} a_i - \sum_{i=1}^{j-1} b_i$ from both sides of the inequality, we get:
$$\max(-a_{j+1}, -b_j) \le \max(-b_{j+1}, -a_j)$$
And after getting rid of the negative signs:
$$\min(a_j, b_{j+1}) \le \min(b_j, a_{j+1})$$
Thus we obtained a **comparator**:
by sorting the jobs on it, we obtain an optimal order of the jobs, in which no two jobs can be switched with an improvement of the final time.
However you can further **simplify** the sorting, if you look at the comparator from a different angle.
The comparator can be interpreted in the following way:
If we have the four times $(a_j, a_{j+1}, b_j, b_{j+1})$, and the minimum of them is a time corresponding to the first machine, then the corresponding job should be done first.
If the minimum time is a time from the second machine, then it should go later.
Thus we can sort the jobs by $\min(a_i, b_i)$, and if the processing time of the current job on the first machine is less then the processing time on the second machine, then this job must be done before all the remaining jobs, and otherwise after all remaining tasks.
One way or another, it turns out that by Johnson's rule we can solve the problem by sorting the jobs, and thus receive a time complexity of $O(n \log n)$.
## Implementation
Here we implement the second variation of the described algorithm.
```{.cpp file=johnsons_rule}
struct Job {
int a, b, idx;
bool operator<(Job o) const {
return min(a, b) < min(o.a, o.b);
}
};
vector<Job> johnsons_rule(vector<Job> jobs) {
sort(jobs.begin(), jobs.end());
vector<Job> a, b;
for (Job j : jobs) {
if (j.a < j.b)
a.push_back(j);
else
b.push_back(j);
}
a.insert(a.end(), b.rbegin(), b.rend());
return a;
}
pair<int, int> finish_times(vector<Job> const& jobs) {
int t1 = 0, t2 = 0;
for (Job j : jobs) {
t1 += j.a;
t2 = max(t2, t1) + j.b;
}
return make_pair(t1, t2);
}
```
All the information about each job is store in struct.
The first function sorts all jobs and computes the optimal schedule.
The second function computes the finish times of both machines given a schedule.
|
Scheduling jobs on two machines
|
---
title
schedule_with_completion_duration
---
# Optimal schedule of jobs given their deadlines and durations
Suppose, we have a set of jobs, and we are aware of every job’s deadline and its duration. The execution of a job cannot be interrupted prior to its ending. It is required to create such a schedule to accomplish the biggest number of jobs.
## Solving
The algorithm of the solving is **greedy**. Let’s sort all the jobs by their deadlines and look at them in descending order. Also, let’s create a queue $q$, in which we’ll gradually put the jobs and extract one with the least run-time (for instance, we can use set or priority_queue). Initially, $q$ is empty.
Suppose, we’re looking at the $i$-th job. First of all, let’s put it into $q$. Let’s consider the period of time between the deadline of $i$-th job and the deadline of $i-1$-th job. That is the segment of some length $T$. We will extract jobs from $q$ (in their left duration ascending order) and execute them until the whole segment $T$ is filled. Important: if at any moment of time the extracted job can only be partly executed until segment $T$ is filled, then we execute this job partly just as far as possible, i.e., during the $T$-time, and we put the remaining part of a job back into $q$.
On the algorithm’s completion we’ll choose the optimal solution (or, at least, one of several solutions). The running time of algorithm is $O(n \log n)$.
## Implementation
The following function takes a vector of jobs (consisting of a deadline, a duration, and the job's index) and computes a vector containing all indices of the used jobs in the optimal schedule.
Notice that you still need to sort these jobs by their deadline, if you want to write down the plan explicitly.
```{.cpp file=schedule_deadline_duration}
struct Job {
int deadline, duration, idx;
bool operator<(Job o) const {
return deadline < o.deadline;
}
};
vector<int> compute_schedule(vector<Job> jobs) {
sort(jobs.begin(), jobs.end());
set<pair<int,int>> s;
vector<int> schedule;
for (int i = jobs.size()-1; i >= 0; i--) {
int t = jobs[i].deadline - (i ? jobs[i-1].deadline : 0);
s.insert(make_pair(jobs[i].duration, jobs[i].idx));
while (t && !s.empty()) {
auto it = s.begin();
if (it->first <= t) {
t -= it->first;
schedule.push_back(it->second);
} else {
s.insert(make_pair(it->first - t, it->second));
t = 0;
}
s.erase(it);
}
}
return schedule;
}
```
|
---
title
schedule_with_completion_duration
---
# Optimal schedule of jobs given their deadlines and durations
Suppose, we have a set of jobs, and we are aware of every job’s deadline and its duration. The execution of a job cannot be interrupted prior to its ending. It is required to create such a schedule to accomplish the biggest number of jobs.
## Solving
The algorithm of the solving is **greedy**. Let’s sort all the jobs by their deadlines and look at them in descending order. Also, let’s create a queue $q$, in which we’ll gradually put the jobs and extract one with the least run-time (for instance, we can use set or priority_queue). Initially, $q$ is empty.
Suppose, we’re looking at the $i$-th job. First of all, let’s put it into $q$. Let’s consider the period of time between the deadline of $i$-th job and the deadline of $i-1$-th job. That is the segment of some length $T$. We will extract jobs from $q$ (in their left duration ascending order) and execute them until the whole segment $T$ is filled. Important: if at any moment of time the extracted job can only be partly executed until segment $T$ is filled, then we execute this job partly just as far as possible, i.e., during the $T$-time, and we put the remaining part of a job back into $q$.
On the algorithm’s completion we’ll choose the optimal solution (or, at least, one of several solutions). The running time of algorithm is $O(n \log n)$.
## Implementation
The following function takes a vector of jobs (consisting of a deadline, a duration, and the job's index) and computes a vector containing all indices of the used jobs in the optimal schedule.
Notice that you still need to sort these jobs by their deadline, if you want to write down the plan explicitly.
```{.cpp file=schedule_deadline_duration}
struct Job {
int deadline, duration, idx;
bool operator<(Job o) const {
return deadline < o.deadline;
}
};
vector<int> compute_schedule(vector<Job> jobs) {
sort(jobs.begin(), jobs.end());
set<pair<int,int>> s;
vector<int> schedule;
for (int i = jobs.size()-1; i >= 0; i--) {
int t = jobs[i].deadline - (i ? jobs[i-1].deadline : 0);
s.insert(make_pair(jobs[i].duration, jobs[i].idx));
while (t && !s.empty()) {
auto it = s.begin();
if (it->first <= t) {
t -= it->first;
schedule.push_back(it->second);
} else {
s.insert(make_pair(it->first - t, it->second));
t = 0;
}
s.erase(it);
}
}
return schedule;
}
```
|
Optimal schedule of jobs given their deadlines and durations
|
---
title
johnson_problem_1
---
# Scheduling jobs on one machine
This task is about finding an optimal schedule for $n$ jobs on a single machine, if the job $i$ can be processed in $t_i$ time, but for the $t$ seconds waiting before processing the job a penalty of $f_i(t)$ has to be paid.
Thus the task asks to find such an permutation of the jobs, so that the total penalty is minimal.
If we denote by $\pi$ the permutation of the jobs ($\pi_1$ is the first processed item, $\pi_2$ the second, etc.), then the total penalty is equal to:
$$F(\pi) = f_{\pi_1}(0) + f_{\pi_2}(t_{\pi_1}) + f_{\pi_3}(t_{\pi_1} + t_{\pi_2}) + \dots + f_{\pi_n}\left(\sum_{i=1}^{n-1} t_{\pi_i}\right)$$
## Solutions for special cases
### Linear penalty functions
First we will solve the problem in the case that all penalty functions $f_i(t)$ are linear, i.e. they have the form $f_i(t) = c_i \cdot t$, where $c_i$ is a non-negative number.
Note that these functions don't have a constant term.
Otherwise we can sum up all constant term, and resolve the problem without them.
Let us fixate some permutation $\pi$, and take an index $i = 1 \dots n-1$.
Let the permutation $\pi'$ be equal to the permutation $\pi$ with the elements $i$ and $i+1$ switched.
Let's see how much the penalty changed.
$$F(\pi') - F(\pi) =$$
It is easy to see that the changes only occur in the $i$-th and $(i+1)$-th summands:
$$\begin{align}
&= c_{\pi_i'} \cdot \sum_{k = 1}^{i-1} t_{\pi_k'} + c_{\pi_{i+1}'} \cdot \sum_{k = 1}^i t_{\pi_k'} - c_{\pi_i} \cdot \sum_{k = 1}^{i-1} t_{\pi_k} - c_{\pi_{i+1}} \cdot \sum_{k = 1}^i t_{\pi_k} \\
&= c_{\pi_{i+1}} \cdot \sum_{k = 1}^{i-1} t_{\pi_k'} + c_{\pi_i} \cdot \sum_{k = 1}^i t_{\pi_k'} - c_{\pi_i} \cdot \sum_{k = 1}^{i-1} t_{\pi_k} - c_{\pi_{i+1}} \cdot \sum_{k = 1}^i t_{\pi_k} \\
&= c_{\pi_i} \cdot t_{\pi_{i+1}} - c_{\pi_{i+1}} \cdot t_{\pi_i}
\end{align}$$
It is easy to see, that if the schedule $\pi$ is optimal, than any change in it leads to an increased penalty (or to the identical penalty), therefore for the optimal schedule we can write down the following condition:
$$c_{\pi_{i}} \cdot t_{\pi_{i+1}} - c_{\pi_{i+1}} \cdot t_{\pi_i} \ge 0 \quad \forall i = 1 \dots n-1$$
And after rearranging we get:
$$\frac{c_{\pi_i}}{t_{\pi_i}} \ge \frac{c_{\pi_{i+1}}}{t_{\pi_{i+1}}} \quad \forall i = 1 \dots n-1$$
Thus we obtain the **optimal schedule** by simply **sorting** the jobs by the fraction $\frac{c_i}{t_i}$ in non-ascending order.
It should be noted, that we constructed this algorithm by the so-called **permutation method**:
we tried to swap two adjacent elements, calculated how much the penalty changed, and then derived the algorithm for finding the optimal method.
### Exponential penalty function
Let the penalty function look like this:
$$f_i(t) = c_i \cdot e^{\alpha \cdot t},$$
where all numbers $c_i$ are non-negative and the constant $\alpha$ is positive.
By applying the permutation method, it is easy to determine that the jobs must be sorted in non-ascending order of the value:
$$v_i = \frac{1 - e^{\alpha \cdot t_i}}{c_i}$$
### Identical monotone penalty function
In this case we consider the case that all $f_i(t)$ are equal, and this function is monotone increasing.
It is obvious that in this case the optimal permutation is to arrange the jobs by non-descending processing time $t_i$.
## The Livshits-Kladov theorem
The Livshits-Kladov theorem establishes that the permutation method is only applicable for the above mentioned three cases, i.e.:
- Linear case: $f_i(t) = c_i(t) + d_i$, where $c_i$ are non-negative constants,
- Exponential case: $f_i(t) = c_i \cdot e_{\alpha \cdot t} + d_i$, where $c_i$ and $\alpha$ are positive constants,
- Identical case: $f_i(t) = \phi(t)$, where $\phi$ is a monotone increasing function.
In all other cases the method cannot be applied.
The theorem is proven under the assumption that the penalty functions are sufficiently smooth (the third derivatives exists).
In all three case we apply the permutation method, through which the desired optimal schedule can be found by sorting, hence in $O(n \log n)$ time.
|
---
title
johnson_problem_1
---
# Scheduling jobs on one machine
This task is about finding an optimal schedule for $n$ jobs on a single machine, if the job $i$ can be processed in $t_i$ time, but for the $t$ seconds waiting before processing the job a penalty of $f_i(t)$ has to be paid.
Thus the task asks to find such an permutation of the jobs, so that the total penalty is minimal.
If we denote by $\pi$ the permutation of the jobs ($\pi_1$ is the first processed item, $\pi_2$ the second, etc.), then the total penalty is equal to:
$$F(\pi) = f_{\pi_1}(0) + f_{\pi_2}(t_{\pi_1}) + f_{\pi_3}(t_{\pi_1} + t_{\pi_2}) + \dots + f_{\pi_n}\left(\sum_{i=1}^{n-1} t_{\pi_i}\right)$$
## Solutions for special cases
### Linear penalty functions
First we will solve the problem in the case that all penalty functions $f_i(t)$ are linear, i.e. they have the form $f_i(t) = c_i \cdot t$, where $c_i$ is a non-negative number.
Note that these functions don't have a constant term.
Otherwise we can sum up all constant term, and resolve the problem without them.
Let us fixate some permutation $\pi$, and take an index $i = 1 \dots n-1$.
Let the permutation $\pi'$ be equal to the permutation $\pi$ with the elements $i$ and $i+1$ switched.
Let's see how much the penalty changed.
$$F(\pi') - F(\pi) =$$
It is easy to see that the changes only occur in the $i$-th and $(i+1)$-th summands:
$$\begin{align}
&= c_{\pi_i'} \cdot \sum_{k = 1}^{i-1} t_{\pi_k'} + c_{\pi_{i+1}'} \cdot \sum_{k = 1}^i t_{\pi_k'} - c_{\pi_i} \cdot \sum_{k = 1}^{i-1} t_{\pi_k} - c_{\pi_{i+1}} \cdot \sum_{k = 1}^i t_{\pi_k} \\
&= c_{\pi_{i+1}} \cdot \sum_{k = 1}^{i-1} t_{\pi_k'} + c_{\pi_i} \cdot \sum_{k = 1}^i t_{\pi_k'} - c_{\pi_i} \cdot \sum_{k = 1}^{i-1} t_{\pi_k} - c_{\pi_{i+1}} \cdot \sum_{k = 1}^i t_{\pi_k} \\
&= c_{\pi_i} \cdot t_{\pi_{i+1}} - c_{\pi_{i+1}} \cdot t_{\pi_i}
\end{align}$$
It is easy to see, that if the schedule $\pi$ is optimal, than any change in it leads to an increased penalty (or to the identical penalty), therefore for the optimal schedule we can write down the following condition:
$$c_{\pi_{i}} \cdot t_{\pi_{i+1}} - c_{\pi_{i+1}} \cdot t_{\pi_i} \ge 0 \quad \forall i = 1 \dots n-1$$
And after rearranging we get:
$$\frac{c_{\pi_i}}{t_{\pi_i}} \ge \frac{c_{\pi_{i+1}}}{t_{\pi_{i+1}}} \quad \forall i = 1 \dots n-1$$
Thus we obtain the **optimal schedule** by simply **sorting** the jobs by the fraction $\frac{c_i}{t_i}$ in non-ascending order.
It should be noted, that we constructed this algorithm by the so-called **permutation method**:
we tried to swap two adjacent elements, calculated how much the penalty changed, and then derived the algorithm for finding the optimal method.
### Exponential penalty function
Let the penalty function look like this:
$$f_i(t) = c_i \cdot e^{\alpha \cdot t},$$
where all numbers $c_i$ are non-negative and the constant $\alpha$ is positive.
By applying the permutation method, it is easy to determine that the jobs must be sorted in non-ascending order of the value:
$$v_i = \frac{1 - e^{\alpha \cdot t_i}}{c_i}$$
### Identical monotone penalty function
In this case we consider the case that all $f_i(t)$ are equal, and this function is monotone increasing.
It is obvious that in this case the optimal permutation is to arrange the jobs by non-descending processing time $t_i$.
## The Livshits-Kladov theorem
The Livshits-Kladov theorem establishes that the permutation method is only applicable for the above mentioned three cases, i.e.:
- Linear case: $f_i(t) = c_i(t) + d_i$, where $c_i$ are non-negative constants,
- Exponential case: $f_i(t) = c_i \cdot e_{\alpha \cdot t} + d_i$, where $c_i$ and $\alpha$ are positive constants,
- Identical case: $f_i(t) = \phi(t)$, where $\phi$ is a monotone increasing function.
In all other cases the method cannot be applied.
The theorem is proven under the assumption that the penalty functions are sufficiently smooth (the third derivatives exists).
In all three case we apply the permutation method, through which the desired optimal schedule can be found by sorting, hence in $O(n \log n)$ time.
|
Scheduling jobs on one machine
|
---
title
binomial_coeff
---
# Binomial Coefficients
Binomial coefficients $\binom n k$ are the number of ways to select a set of $k$ elements from $n$ different elements without taking into account the order of arrangement of these elements (i.e., the number of unordered sets).
Binomial coefficients are also the coefficients in the expansion of $(a + b) ^ n$ (so-called binomial theorem):
$$ (a+b)^n = \binom n 0 a^n + \binom n 1 a^{n-1} b + \binom n 2 a^{n-2} b^2 + \cdots + \binom n k a^{n-k} b^k + \cdots + \binom n n b^n $$
It is believed that this formula, as well as the triangle which allows efficient calculation of the coefficients, was discovered by Blaise Pascal in the 17th century. Nevertheless, it was known to the Chinese mathematician Yang Hui, who lived in the 13th century. Perhaps it was discovered by a Persian scholar Omar Khayyam. Moreover, Indian mathematician Pingala, who lived earlier in the 3rd. BC, got similar results. The merit of the Newton is that he generalized this formula for exponents that are not natural.
## Calculation
**Analytic formula** for the calculation:
$$ \binom n k = \frac {n!} {k!(n-k)!} $$
This formula can be easily deduced from the problem of ordered arrangement (number of ways to select $k$ different elements from $n$ different elements). First, let's count the number of ordered selections of $k$ elements. There are $n$ ways to select the first element, $n-1$ ways to select the second element, $n-2$ ways to select the third element, and so on. As a result, we get the formula of the number of ordered arrangements: $n (n-1) (n-2) \cdots (n - k + 1) = \frac {n!} {(n-k)!}$. We can easily move to unordered arrangements, noting that each unordered arrangement corresponds to exactly $k!$ ordered arrangements ($k!$ is the number of possible permutations of $k$ elements). We get the final formula by dividing $\frac {n!} {(n-k)!}$ by $k!$.
**Recurrence formula** (which is associated with the famous "Pascal's Triangle"):
$$ \binom n k = \binom {n-1} {k-1} + \binom {n-1} k $$
It is easy to deduce this using the analytic formula.
Note that for $n \lt k$ the value of $\binom n k$ is assumed to be zero.
## Properties
Binomial coefficients have many different properties. Here are the simplest of them:
* Symmetry rule:
\[ \binom n k = \binom n {n-k} \]
* Factoring in:
\[ \binom n k = \frac n k \binom {n-1} {k-1} \]
* Sum over $k$:
\[ \sum_{k = 0}^n \binom n k = 2 ^ n \]
* Sum over $n$:
\[ \sum_{m = 0}^n \binom m k = \binom {n + 1} {k + 1} \]
* Sum over $n$ and $k$:
\[ \sum_{k = 0}^m \binom {n + k} k = \binom {n + m + 1} m \]
* Sum of the squares:
\[ {\binom n 0}^2 + {\binom n 1}^2 + \cdots + {\binom n n}^2 = \binom {2n} n \]
* Weighted sum:
\[ 1 \binom n 1 + 2 \binom n 2 + \cdots + n \binom n n = n 2^{n-1} \]
* Connection with the [Fibonacci numbers](../algebra/fibonacci-numbers.md):
\[ \binom n 0 + \binom {n-1} 1 + \cdots + \binom {n-k} k + \cdots + \binom 0 n = F_{n+1} \]
## Calculation
### Straightforward calculation using analytical formula
The first, straightforward formula is very easy to code, but this method is likely to overflow even for relatively small values of $n$ and $k$ (even if the answer completely fit into some datatype, the calculation of the intermediate factorials can lead to overflow). Therefore, this method often can only be used with [long arithmetic](../algebra/big-integer.md):
```cpp
int C(int n, int k) {
int res = 1;
for (int i = n - k + 1; i <= n; ++i)
res *= i;
for (int i = 2; i <= k; ++i)
res /= i;
return res;
}
```
### Improved implementation
Note that in the above implementation numerator and denominator have the same number of factors ($k$), each of which is greater than or equal to 1. Therefore, we can replace our fraction with a product $k$ fractions, each of which is real-valued. However, on each step after multiplying current answer by each of the next fractions the answer will still be integer (this follows from the property of factoring in).
C++ implementation:
```cpp
int C(int n, int k) {
double res = 1;
for (int i = 1; i <= k; ++i)
res = res * (n - k + i) / i;
return (int)(res + 0.01);
}
```
Here we carefully cast the floating point number to an integer, taking into account that due to the accumulated errors, it may be slightly less than the true value (for example, $2.99999$ instead of $3$).
### Pascal's Triangle
By using the recurrence relation we can construct a table of binomial coefficients (Pascal's triangle) and take the result from it. The advantage of this method is that intermediate results never exceed the answer and calculating each new table element requires only one addition. The flaw is slow execution for large $n$ and $k$ if you just need a single value and not the whole table (because in order to calculate $\binom n k$ you will need to build a table of all $\binom i j, 1 \le i \le n, 1 \le j \le n$, or at least to $1 \le j \le \min (i, 2k)$). The time complexity can be considered to be $\mathcal{O}(n^2)$.
C++ implementation:
```cpp
const int maxn = ...;
int C[maxn + 1][maxn + 1];
C[0][0] = 1;
for (int n = 1; n <= maxn; ++n) {
C[n][0] = C[n][n] = 1;
for (int k = 1; k < n; ++k)
C[n][k] = C[n - 1][k - 1] + C[n - 1][k];
}
```
If the entire table of values is not necessary, storing only two last rows of it is sufficient (current $n$-th row and the previous $n-1$-th).
### Calculation in $O(1)$ {data-toc-label="Calculation in O(1)"}
Finally, in some situations it is beneficial to precompute all the factorials in order to produce any necessary binomial coefficient with only two divisions later. This can be advantageous when using [long arithmetic](../algebra/big-integer.md), when the memory does not allow precomputation of the whole Pascal's triangle.
## Computing binomial coefficients modulo $m$ {data-toc-label="Computing binomial coefficients modulo m"}
Quite often you come across the problem of computing binomial coefficients modulo some $m$.
### Binomial coefficient for small $n$ {data-toc-label="Binomial coefficient for small n"}
The previously discussed approach of Pascal's triangle can be used to calculate all values of $\binom{n}{k} \bmod m$ for reasonably small $n$, since it requires time complexity $\mathcal{O}(n^2)$. This approach can handle any modulo, since only addition operations are used.
### Binomial coefficient modulo large prime
The formula for the binomial coefficients is
$$\binom n k = \frac {n!} {k!(n-k)!},$$
so if we want to compute it modulo some prime $m > n$ we get
$$\binom n k \equiv n! \cdot (k!)^{-1} \cdot ((n-k)!)^{-1} \mod m.$$
First we precompute all factorials modulo $m$ up to $\text{MAXN}!$ in $O(\text{MAXN})$ time.
```cpp
factorial[0] = 1;
for (int i = 1; i <= MAXN; i++) {
factorial[i] = factorial[i - 1] * i % m;
}
```
And afterwards we can compute the binomial coefficient in $O(\log m)$ time.
```cpp
long long binomial_coefficient(int n, int k) {
return factorial[n] * inverse(factorial[k] * factorial[n - k] % m) % m;
}
```
We even can compute the binomial coefficient in $O(1)$ time if we precompute the inverses of all factorials in $O(\text{MAXN} \log m)$ using the regular method for computing the inverse, or even in $O(\text{MAXN})$ time using the congruence $(x!)^{-1} \equiv ((x-1)!)^{-1} \cdot x^{-1}$ and the method for [computing all inverses](../algebra/module-inverse.md#mod-inv-all-num) in $O(n)$.
```cpp
long long binomial_coefficient(int n, int k) {
return factorial[n] * inverse_factorial[k] % m * inverse_factorial[n - k] % m;
}
```
### Binomial coefficient modulo prime power { #mod-prime-pow}
Here we want to compute the binomial coefficient modulo some prime power, i.e. $m = p^b$ for some prime $p$.
If $p > \max(k, n-k)$, then we can use the same method as described in the previous section.
But if $p \le \max(k, n-k)$, then at least one of $k!$ and $(n-k)!$ are not coprime with $m$, and therefore we cannot compute the inverses - they don't exist.
Nevertheless we can compute the binomial coefficient.
The idea is the following:
We compute for each $x!$ the biggest exponent $c$ such that $p^c$ divides $x!$, i.e. $p^c ~|~ x!$.
Let $c(x)$ be that number.
And let $g(x) := \frac{x!}{p^{c(x)}}$.
Then we can write the binomial coefficient as:
$$\binom n k = \frac {g(n) p^{c(n)}} {g(k) p^{c(k)} g(n-k) p^{c(n-k)}} = \frac {g(n)} {g(k) g(n-k)}p^{c(n) - c(k) - c(n-k)}$$
The interesting thing is, that $g(x)$ is now free from the prime divisor $p$.
Therefore $g(x)$ is coprime to m, and we can compute the modular inverses of $g(k)$ and $g(n-k)$.
After precomputing all values for $g$ and $c$, which can be done efficiently using dynamic programming in $\mathcal{O}(n)$, we can compute the binomial coefficient in $O(\log m)$ time.
Or precompute all inverses and all powers of $p$, and then compute the binomial coefficient in $O(1)$.
Notice, if $c(n) - c(k) - c(n-k) \ge b$, than $p^b ~|~ p^{c(n) - c(k) - c(n-k)}$, and the binomial coefficient is $0$.
### Binomial coefficient modulo an arbitrary number
Now we compute the binomial coefficient modulo some arbitrary modulus $m$.
Let the prime factorization of $m$ be $m = p_1^{e_1} p_2^{e_2} \cdots p_h^{e_h}$.
We can compute the binomial coefficient modulo $p_i^{e_i}$ for every $i$.
This gives us $h$ different congruences.
Since all moduli $p_i^{e_i}$ are coprime, we can apply the [Chinese Remainder Theorem](../algebra/chinese-remainder-theorem.md) to compute the binomial coefficient modulo the product of the moduli, which is the desired binomial coefficient modulo $m$.
### Binomial coefficient for large $n$ and small modulo {data-toc-label="Binomial coefficient for large n and small modulo"}
When $n$ is too large, the $\mathcal{O}(n)$ algorithms discussed above become impractical. However, if the modulo $m$ is small there are still ways to calculate $\binom{n}{k} \bmod m$.
When the modulo $m$ is prime, there are 2 options:
* [Lucas's theorem](https://en.wikipedia.org/wiki/Lucas's_theorem) can be applied which breaks the problem of computing $\binom{n}{k} \bmod m$ into $\log_m n$ problems of the form $\binom{x_i}{y_i} \bmod m$ where $x_i, y_i < m$. If each reduced coefficient is calculated using precomputed factorials and inverse factorials, the complexity is $\mathcal{O}(m + \log_m n)$.
* The method of computing [factorial modulo P](../algebra/factorial-modulo.md) can be used to get the required $g$ and $c$ values and use them as described in the section of [modulo prime power](#mod-prime-pow). This takes $\mathcal{O}(m \log_m n)$.
When $m$ is not prime but square-free, the prime factors of $m$ can be obtained and the coefficient modulo each prime factor can be calculated using either of the above methods, and the overall answer can be obtained by the Chinese Remainder Theorem.
When $m$ is not square-free, a [generalization of Lucas's theorem for prime powers](https://web.archive.org/web/20170202003812/http://www.dms.umontreal.ca/~andrew/PDF/BinCoeff.pdf) can be applied instead of Lucas's theorem.
|
---
title
binomial_coeff
---
# Binomial Coefficients
Binomial coefficients $\binom n k$ are the number of ways to select a set of $k$ elements from $n$ different elements without taking into account the order of arrangement of these elements (i.e., the number of unordered sets).
Binomial coefficients are also the coefficients in the expansion of $(a + b) ^ n$ (so-called binomial theorem):
$$ (a+b)^n = \binom n 0 a^n + \binom n 1 a^{n-1} b + \binom n 2 a^{n-2} b^2 + \cdots + \binom n k a^{n-k} b^k + \cdots + \binom n n b^n $$
It is believed that this formula, as well as the triangle which allows efficient calculation of the coefficients, was discovered by Blaise Pascal in the 17th century. Nevertheless, it was known to the Chinese mathematician Yang Hui, who lived in the 13th century. Perhaps it was discovered by a Persian scholar Omar Khayyam. Moreover, Indian mathematician Pingala, who lived earlier in the 3rd. BC, got similar results. The merit of the Newton is that he generalized this formula for exponents that are not natural.
## Calculation
**Analytic formula** for the calculation:
$$ \binom n k = \frac {n!} {k!(n-k)!} $$
This formula can be easily deduced from the problem of ordered arrangement (number of ways to select $k$ different elements from $n$ different elements). First, let's count the number of ordered selections of $k$ elements. There are $n$ ways to select the first element, $n-1$ ways to select the second element, $n-2$ ways to select the third element, and so on. As a result, we get the formula of the number of ordered arrangements: $n (n-1) (n-2) \cdots (n - k + 1) = \frac {n!} {(n-k)!}$. We can easily move to unordered arrangements, noting that each unordered arrangement corresponds to exactly $k!$ ordered arrangements ($k!$ is the number of possible permutations of $k$ elements). We get the final formula by dividing $\frac {n!} {(n-k)!}$ by $k!$.
**Recurrence formula** (which is associated with the famous "Pascal's Triangle"):
$$ \binom n k = \binom {n-1} {k-1} + \binom {n-1} k $$
It is easy to deduce this using the analytic formula.
Note that for $n \lt k$ the value of $\binom n k$ is assumed to be zero.
## Properties
Binomial coefficients have many different properties. Here are the simplest of them:
* Symmetry rule:
\[ \binom n k = \binom n {n-k} \]
* Factoring in:
\[ \binom n k = \frac n k \binom {n-1} {k-1} \]
* Sum over $k$:
\[ \sum_{k = 0}^n \binom n k = 2 ^ n \]
* Sum over $n$:
\[ \sum_{m = 0}^n \binom m k = \binom {n + 1} {k + 1} \]
* Sum over $n$ and $k$:
\[ \sum_{k = 0}^m \binom {n + k} k = \binom {n + m + 1} m \]
* Sum of the squares:
\[ {\binom n 0}^2 + {\binom n 1}^2 + \cdots + {\binom n n}^2 = \binom {2n} n \]
* Weighted sum:
\[ 1 \binom n 1 + 2 \binom n 2 + \cdots + n \binom n n = n 2^{n-1} \]
* Connection with the [Fibonacci numbers](../algebra/fibonacci-numbers.md):
\[ \binom n 0 + \binom {n-1} 1 + \cdots + \binom {n-k} k + \cdots + \binom 0 n = F_{n+1} \]
## Calculation
### Straightforward calculation using analytical formula
The first, straightforward formula is very easy to code, but this method is likely to overflow even for relatively small values of $n$ and $k$ (even if the answer completely fit into some datatype, the calculation of the intermediate factorials can lead to overflow). Therefore, this method often can only be used with [long arithmetic](../algebra/big-integer.md):
```cpp
int C(int n, int k) {
int res = 1;
for (int i = n - k + 1; i <= n; ++i)
res *= i;
for (int i = 2; i <= k; ++i)
res /= i;
return res;
}
```
### Improved implementation
Note that in the above implementation numerator and denominator have the same number of factors ($k$), each of which is greater than or equal to 1. Therefore, we can replace our fraction with a product $k$ fractions, each of which is real-valued. However, on each step after multiplying current answer by each of the next fractions the answer will still be integer (this follows from the property of factoring in).
C++ implementation:
```cpp
int C(int n, int k) {
double res = 1;
for (int i = 1; i <= k; ++i)
res = res * (n - k + i) / i;
return (int)(res + 0.01);
}
```
Here we carefully cast the floating point number to an integer, taking into account that due to the accumulated errors, it may be slightly less than the true value (for example, $2.99999$ instead of $3$).
### Pascal's Triangle
By using the recurrence relation we can construct a table of binomial coefficients (Pascal's triangle) and take the result from it. The advantage of this method is that intermediate results never exceed the answer and calculating each new table element requires only one addition. The flaw is slow execution for large $n$ and $k$ if you just need a single value and not the whole table (because in order to calculate $\binom n k$ you will need to build a table of all $\binom i j, 1 \le i \le n, 1 \le j \le n$, or at least to $1 \le j \le \min (i, 2k)$). The time complexity can be considered to be $\mathcal{O}(n^2)$.
C++ implementation:
```cpp
const int maxn = ...;
int C[maxn + 1][maxn + 1];
C[0][0] = 1;
for (int n = 1; n <= maxn; ++n) {
C[n][0] = C[n][n] = 1;
for (int k = 1; k < n; ++k)
C[n][k] = C[n - 1][k - 1] + C[n - 1][k];
}
```
If the entire table of values is not necessary, storing only two last rows of it is sufficient (current $n$-th row and the previous $n-1$-th).
### Calculation in $O(1)$ {data-toc-label="Calculation in O(1)"}
Finally, in some situations it is beneficial to precompute all the factorials in order to produce any necessary binomial coefficient with only two divisions later. This can be advantageous when using [long arithmetic](../algebra/big-integer.md), when the memory does not allow precomputation of the whole Pascal's triangle.
## Computing binomial coefficients modulo $m$ {data-toc-label="Computing binomial coefficients modulo m"}
Quite often you come across the problem of computing binomial coefficients modulo some $m$.
### Binomial coefficient for small $n$ {data-toc-label="Binomial coefficient for small n"}
The previously discussed approach of Pascal's triangle can be used to calculate all values of $\binom{n}{k} \bmod m$ for reasonably small $n$, since it requires time complexity $\mathcal{O}(n^2)$. This approach can handle any modulo, since only addition operations are used.
### Binomial coefficient modulo large prime
The formula for the binomial coefficients is
$$\binom n k = \frac {n!} {k!(n-k)!},$$
so if we want to compute it modulo some prime $m > n$ we get
$$\binom n k \equiv n! \cdot (k!)^{-1} \cdot ((n-k)!)^{-1} \mod m.$$
First we precompute all factorials modulo $m$ up to $\text{MAXN}!$ in $O(\text{MAXN})$ time.
```cpp
factorial[0] = 1;
for (int i = 1; i <= MAXN; i++) {
factorial[i] = factorial[i - 1] * i % m;
}
```
And afterwards we can compute the binomial coefficient in $O(\log m)$ time.
```cpp
long long binomial_coefficient(int n, int k) {
return factorial[n] * inverse(factorial[k] * factorial[n - k] % m) % m;
}
```
We even can compute the binomial coefficient in $O(1)$ time if we precompute the inverses of all factorials in $O(\text{MAXN} \log m)$ using the regular method for computing the inverse, or even in $O(\text{MAXN})$ time using the congruence $(x!)^{-1} \equiv ((x-1)!)^{-1} \cdot x^{-1}$ and the method for [computing all inverses](../algebra/module-inverse.md#mod-inv-all-num) in $O(n)$.
```cpp
long long binomial_coefficient(int n, int k) {
return factorial[n] * inverse_factorial[k] % m * inverse_factorial[n - k] % m;
}
```
### Binomial coefficient modulo prime power { #mod-prime-pow}
Here we want to compute the binomial coefficient modulo some prime power, i.e. $m = p^b$ for some prime $p$.
If $p > \max(k, n-k)$, then we can use the same method as described in the previous section.
But if $p \le \max(k, n-k)$, then at least one of $k!$ and $(n-k)!$ are not coprime with $m$, and therefore we cannot compute the inverses - they don't exist.
Nevertheless we can compute the binomial coefficient.
The idea is the following:
We compute for each $x!$ the biggest exponent $c$ such that $p^c$ divides $x!$, i.e. $p^c ~|~ x!$.
Let $c(x)$ be that number.
And let $g(x) := \frac{x!}{p^{c(x)}}$.
Then we can write the binomial coefficient as:
$$\binom n k = \frac {g(n) p^{c(n)}} {g(k) p^{c(k)} g(n-k) p^{c(n-k)}} = \frac {g(n)} {g(k) g(n-k)}p^{c(n) - c(k) - c(n-k)}$$
The interesting thing is, that $g(x)$ is now free from the prime divisor $p$.
Therefore $g(x)$ is coprime to m, and we can compute the modular inverses of $g(k)$ and $g(n-k)$.
After precomputing all values for $g$ and $c$, which can be done efficiently using dynamic programming in $\mathcal{O}(n)$, we can compute the binomial coefficient in $O(\log m)$ time.
Or precompute all inverses and all powers of $p$, and then compute the binomial coefficient in $O(1)$.
Notice, if $c(n) - c(k) - c(n-k) \ge b$, than $p^b ~|~ p^{c(n) - c(k) - c(n-k)}$, and the binomial coefficient is $0$.
### Binomial coefficient modulo an arbitrary number
Now we compute the binomial coefficient modulo some arbitrary modulus $m$.
Let the prime factorization of $m$ be $m = p_1^{e_1} p_2^{e_2} \cdots p_h^{e_h}$.
We can compute the binomial coefficient modulo $p_i^{e_i}$ for every $i$.
This gives us $h$ different congruences.
Since all moduli $p_i^{e_i}$ are coprime, we can apply the [Chinese Remainder Theorem](../algebra/chinese-remainder-theorem.md) to compute the binomial coefficient modulo the product of the moduli, which is the desired binomial coefficient modulo $m$.
### Binomial coefficient for large $n$ and small modulo {data-toc-label="Binomial coefficient for large n and small modulo"}
When $n$ is too large, the $\mathcal{O}(n)$ algorithms discussed above become impractical. However, if the modulo $m$ is small there are still ways to calculate $\binom{n}{k} \bmod m$.
When the modulo $m$ is prime, there are 2 options:
* [Lucas's theorem](https://en.wikipedia.org/wiki/Lucas's_theorem) can be applied which breaks the problem of computing $\binom{n}{k} \bmod m$ into $\log_m n$ problems of the form $\binom{x_i}{y_i} \bmod m$ where $x_i, y_i < m$. If each reduced coefficient is calculated using precomputed factorials and inverse factorials, the complexity is $\mathcal{O}(m + \log_m n)$.
* The method of computing [factorial modulo P](../algebra/factorial-modulo.md) can be used to get the required $g$ and $c$ values and use them as described in the section of [modulo prime power](#mod-prime-pow). This takes $\mathcal{O}(m \log_m n)$.
When $m$ is not prime but square-free, the prime factors of $m$ can be obtained and the coefficient modulo each prime factor can be calculated using either of the above methods, and the overall answer can be obtained by the Chinese Remainder Theorem.
When $m$ is not square-free, a [generalization of Lucas's theorem for prime powers](https://web.archive.org/web/20170202003812/http://www.dms.umontreal.ca/~andrew/PDF/BinCoeff.pdf) can be applied instead of Lucas's theorem.
## Practice Problems
* [Codechef - Number of ways](https://www.codechef.com/LTIME24/problems/NWAYS/)
* [Codeforces - Curious Array](http://codeforces.com/problemset/problem/407/C)
* [LightOj - Necklaces](http://www.lightoj.com/volume_showproblem.php?problem=1419)
* [HACKEREARTH: Binomial Coefficient](https://www.hackerearth.com/problem/algorithm/binomial-coefficient-1/description/)
* [SPOJ - Ada and Teams](http://www.spoj.com/problems/ADATEAMS/)
* [DevSkill - Drive In Grid](https://devskill.com/CodingProblems/ViewProblem/61)
* [SPOJ - Greedy Walking](http://www.spoj.com/problems/UCV2013E/)
* [UVa 13214 - The Robot's Grid](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=5137)
* [SPOJ - Good Predictions](http://www.spoj.com/problems/GOODB/)
* [SPOJ - Card Game](http://www.spoj.com/problems/HC12/)
* [SPOJ - Topper Rama Rao](http://www.spoj.com/problems/HLP_RAMS/)
* [UVa 13184 - Counting Edges and Graphs](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=5095)
* [Codeforces - Anton and School 2](http://codeforces.com/contest/785/problem/D)
* [DevSkill - Parandthesis](https://devskill.com/CodingProblems/ViewProblem/255)
* [Codeforces - Bacterial Melee](http://codeforces.com/contest/760/problem/F)
* [Codeforces - Points, Lines and Ready-made Titles](http://codeforces.com/contest/872/problem/E)
* [SPOJ - The Ultimate Riddle](https://www.spoj.com/problems/DCEPC13D/)
* [CodeChef - Long Sandwich](https://www.codechef.com/MAY17/problems/SANDWICH/)
* [Codeforces - Placing Jinas](https://codeforces.com/problemset/problem/1696/E)
## References
* [Blog fishi.devtail.io](https://fishi.devtail.io/weblog/2015/06/25/computing-large-binomial-coefficients-modulo-prime-non-prime/)
* [Question on Mathematics StackExchange](https://math.stackexchange.com/questions/95491/n-choose-k-bmod-m-using-chinese-remainder-theorem)
* [Question on CodeChef Discuss](https://discuss.codechef.com/questions/98129/your-approach-to-solve-sandwich)
|
Binomial Coefficients
|
---
title
inclusion_exclusion_principle
---
# The Inclusion-Exclusion Principle
The inclusion-exclusion principle is an important combinatorial way to compute the size of a set or the probability of complex events. It relates the sizes of individual sets with their union.
## Statement
### The verbal formula
The inclusion-exclusion principle can be expressed as follows:
To compute the size of a union of multiple sets, it is necessary to sum the sizes of these sets **separately**, and then subtract the sizes of all **pairwise** intersections of the sets, then add back the size of the intersections of **triples** of the sets, subtract the size of **quadruples** of the sets, and so on, up to the intersection of **all** sets.
### The formulation in terms of sets
The above definition can be expressed mathematically as follows:
$$\left| \bigcup_{i=1}^n A_i \right| = \sum_{i=1}^n|A_i| - \sum_{1\leq i<j\leq n} |A_i \cap A_j| + \sum _{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k| - \cdots + (-1)^{n-1} | A_1 \cap \cdots \cap A_n |$$
And in a more compact way:
$$\left|\bigcup_{i=1}^n A_i \right| = \sum_{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}} (-1)^{|J|-1}{\Biggl |}\bigcap_{j\in J}A_{j}{\Biggr |}$$
### The formulation using Venn diagrams
Let the diagram show three sets $A$, $B$ and $C$:

Then the area of their union $A \cup B \cup C$ is equal to the sum of the areas $A$, $B$ and $C$ less double-covered areas $A \cap B$, $A \cap C$, $B \cap C$, but with the addition of the area covered by three sets $A \cap B \cap C$:
$$S(A \cup B \cup C) = S(A) + S(B) + S(C) - S(A \cap B) - S(A \cap C) - S(B \cap C) + S(A \cap B \cap C)$$
It can also be generalized for an association of $n$ sets.
### The formulation in terms of probability theory
If $A_i$ $(i = 1,2...n)$ are events and ${\cal P}(A_i)$ the probability of an event from $A_i$ to occur, then the probability of their union (i.e. the probability that at least one of the events occur) is equal to:
$$\begin{eqnarray}
{\cal P} \left( \bigcup_{i=1}^n A_i \right) &=& \sum_{i=1}^n{\cal P}(A_i)\ - \sum_{1\leq i<j\leq n} {\cal P}(A_i \cap A_j)\ + \\
&+& \sum _{1\leq i<j<k\leq n}{\cal P}(A_i \cap A_j \cap A_k) - \cdots + (-1)^{n-1} {\cal P}( A_1 \cap \cdots \cap A_n )
\end{eqnarray}$$
And in a more compact way:
$${\cal P} \left(\bigcup_{i=1}^n A_i \right) = \sum_{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}} (-1)^{|J|-1}\ {\cal P}{\Biggl (}\bigcap_{j\in J}A_{j}{\Biggr )}$$
## Proof
For the proof it is convenient to use the mathematical formulation in terms of set theory:
$$\left|\bigcup_{i=1}^n A_i \right| = \sum_{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}} (-1)^{|J|-1}{\Biggl |}\bigcap_{j\in J}A_{j}{\Biggr |}$$
We want to prove that any element contained in at least one of the sets $A_i$ will occur in the formula only once (note that elements which are not present in any of the sets $A_i$ will never be considered on the right part of the formula).
Consider an element $x$ occurring in $k \geq 1$ sets $A_i$. We will show it is counted only once in the formula. Note that:
* in terms which $|J| = 1$, the item $x$ will be counted **$+\ k$** times;
* in terms which $|J| = 2$, the item $x$ will be counted **$-\ \binom{k}{2}$** times - because it will be counted in those terms that include two of the $k$ sets containing $x$;
* in terms which $|J| = 3$, the item $x$ will be counted **$+\ \binom{k}{3}$** times;
* $\cdots$
* in terms which $|J| = k$, the item $x$ will be counted **$(-1)^{k-1}\cdot \binom{k}{k}$** times;
* in terms which $|J| \gt k$, the item $x$ will be counted **zero** times;
This leads us to the following sum of [binomial coefficients](binomial-coefficients.md):
$$ T = \binom{k}{1} - \binom{k}{2} + \binom{k}{3} - \cdots + (-1)^{i-1}\cdot \binom{k}{i} + \cdots + (-1)^{k-1}\cdot \binom{k}{k}$$
This expression is very similar to the binomial expansion of $(1 - x)^k$:
$$ (1 - x)^k = \binom{k}{0} - \binom{k}{1} \cdot x + \binom{k}{2} \cdot x^2 - \binom{k}{3} \cdot x^3 + \cdots + (-1)^k\cdot \binom{k}{k} \cdot x^k $$
When $x = 1$, $(1 - x)^k$ looks a lot like $T$. However, the expression has an additional $\binom{k}{0} = 1$, and it is multiplied by $-1$. That leads us to $(1 - 1)^k = 1 - T$. Therefore $T = 1 - (1 - 1)^k = 1$, what was required to prove. The element is counted only once.
## Generalization for calculating number of elements in exactly $r$ sets {data-toc-label="Generalization for calculating number of elements in exactly r sets"}
Inclusion-exclusion principle can be rewritten to calculate number of elements which are present in zero sets:
$$\left|\bigcap_{i=1}^n \overline{A_i}\right|=\sum_{m=0}^n (-1)^m \sum_{|X|=m} \left|\bigcap_{i\in X} A_{i}\right|$$
Consider its generalization to calculate number of elements which are present in exactly $r$ sets:
$$\left|\bigcup_{|B|=r}\left[\bigcap_{i \in B} A_i \cap \bigcap_{j \not\in B} \overline{A_j}\right]\right|=\sum_{m=r}^n (-1)^{m-r}\dbinom{m}{r} \sum_{|X|=m} \left|\bigcap_{i \in X} A_{i}\right|$$
To prove this formula, consider some particular $B$. Due to basic inclusion-exclusion principle we can say about it that:
$$\left|\bigcap_{i \in B} A_i \cap \bigcap_{j \not \in B} \overline{A_j}\right|=\sum_{m=r}^{n} (-1)^{m-r} \sum_{\substack{|X|=m \newline B \subset X}}\left|\bigcap_{i\in X} A_{i}\right|$$
The sets on the left side do not intersect for different $B$, thus we can sum them up directly. Also one should note that any set $X$ will always have coefficient $(-1)^{m-r}$ if it occurs and it will occur for exactly $\dbinom{m}{r}$ sets $B$.
## Usage when solving problems
The inclusion-exclusion principle is hard to understand without studying its applications.
First, we will look at three simplest tasks "at paper", illustrating applications of the principle, and then consider more practical problems which are difficult to solve without inclusion-exclusion principle.
Tasks asking to "find the **number** of ways" are worth of note, as they sometimes lead to polynomial solutions, not necessarily exponential.
### A simple task on permutations
Task: count how many permutations of numbers from $0$ to $9$ exist such that the first element is greater than $1$ and the last one is less than $8$.
Let's count the number of "bad" permutations, that is, permutations in which the first element is $\leq 1$ and/or the last is $\geq 8$.
We will denote by $X$ the set of permutations in which the first element is $\leq 1$ and $Y$ the set of permutations in which the last element is $\geq 8$. Then the number of "bad" permutations, as on the inclusion-exclusion formula, will be:
$$ |X \cup Y| = |X| + |Y| - |X \cap Y| $$
After a simple combinatorial calculation, we will get to:
$$ 2 \cdot 9! + 2 \cdot 9! - 2 \cdot 2 \cdot 8! $$
The only thing left is to subtract this number from the total of $10!$ to get the number of "good" permutations.
### A simple task on (0, 1, 2) sequences
Task: count how many sequences of length $n$ exist consisting only of numbers $0,1,2$ such that each number occurs **at least once**.
Again let us turn to the inverse problem, i.e. we calculate the number of sequences which do **not** contain **at least one** of the numbers.
Let's denote by $A_i (i = 0,1,2)$ the set of sequences in which the digit $i$ does **not** occur.
The formula of inclusion-exclusion on the number of "bad" sequences will be:
$$ |A_0 \cup A_1 \cup A_2| = |A_0| + |A_1| + |A_2| - |A_0 \cap A_1| - |A_0 \cap A_2| - |A_1 \cap A_2| + |A_0 \cap A_1 \cap A_2| $$
* The size of each $A_i$ is $2^n$, as each sequence can only contain two of the digits.
* The size of each pairwise intersection $A_i \cap A_j$ is equal to $1$, as there will be only one digit to build the sequence.
* The size of the intersection of all three sets is equal to $0$, as there will be no digits to build the sequence.
As we solved the inverse problem, we subtract it from the total of $3^n$ sequences:
$$3^n - (3 \cdot 2^n - 3 \cdot 1 + 0)$$
<div id="the-number-of-integer-solutions-to-the-equation"></div>
### Number of upper-bound integer sums {: #number-of-upper-bound-integer-sums }
Consider the following equation:
$$x_1 + x_2 + x_3 + x_4 + x_5 + x_6 = 20$$
where $0 \le x_i \le 8 ~ (i = 1,2,\ldots 6)$.
Task: count the number of solutions to the equation.
Forget the restriction on $x_i$ for a moment and just count the number of nonnegative solutions to this equation. This is easily done using [Stars and Bars](stars_and_bars.md):
we want to break a sequence of $20$ units into $6$ groups, which is the same as arranging $5$ _bars_ and $20$ _stars_:
$$N_0 = \binom{25}{5}$$
We will now calculate the number of "bad" solutions with the inclusion-exclusion principle. The "bad" solutions will be those in which one or more $x_i$ are greater than $9$.
Denote by $A_k ~ (k = 1,2\ldots 6)$ the set of solutions where $x_k \ge 9$, and all other $x_i \ge 0 ~ (i \ne k)$ (they may be $\ge 9$ or not). To calculate the size of $A_k$, note that we have essentially the same combinatorial problem that was solved in the two paragraphs above, but now $9$ of the units are excluded from the slots and definitely belong to the first group. Thus:
$$ | A_k | = \binom{16}{5} $$
Similarly, the size of the intersection between two sets $A_k$ and $A_p$ (for $k \ne p$) is equal to:
$$ \left| A_k \cap A_p \right| = \binom{7}{5}$$
The size of each intersection of three sets is zero, since $20$ units will not be enough for three or more variables greater than or equal to $9$.
Combining all this into the formula of inclusions-exceptions and given that we solved the inverse problem, we finally get the answer:
$$\binom{25}{5} - \left(\binom{6}{1} \cdot \binom{16}{5} - \binom{6}{2} \cdot \binom{7}{5}\right) $$
### The number of relative primes in a given interval
Task: given two numbers $n$ and $r$, count the number of integers in the interval $[1;r]$ that are relatively prime to n (their greatest common divisor is $1$).
Let's solve the inverse problem - compute the number of not mutually primes with $n$.
We will denote the prime factors of $n$ as $p_i (i = 1\cdots k)$.
How many numbers in the interval $[1;r]$ are divisible by $p_i$? The answer to this question is:
$$ \left\lfloor \frac{ r }{ p_i } \right\rfloor $$
However, if we simply sum these numbers, some numbers will be summarized several times (those that share multiple $p_i$ as their factors). Therefore, it is necessary to use the inclusion-exclusion principle.
We will iterate over all $2^k$ subsets of $p_i$s, calculate their product and add or subtract the number of multiples of their product.
Here is a C++ implementation:
```cpp
int solve (int n, int r) {
vector<int> p;
for (int i=2; i*i<=n; ++i)
if (n % i == 0) {
p.push_back (i);
while (n % i == 0)
n /= i;
}
if (n > 1)
p.push_back (n);
int sum = 0;
for (int msk=1; msk<(1<<p.size()); ++msk) {
int mult = 1,
bits = 0;
for (int i=0; i<(int)p.size(); ++i)
if (msk & (1<<i)) {
++bits;
mult *= p[i];
}
int cur = r / mult;
if (bits % 2 == 1)
sum += cur;
else
sum -= cur;
}
return r - sum;
}
```
Asymptotics of the solution is $O (\sqrt{n})$.
### The number of integers in a given interval which are multiple of at least one of the given numbers
Given $n$ numbers $a_i$ and number $r$. You want to count the number of integers in the interval $[1; r]$ that are multiple of at least one of the $a_i$.
The solution algorithm is almost identical to the one for previous task — construct the formula of inclusion-exclusion on the numbers $a_i$, i.e. each term in this formula is the number of numbers divisible by a given subset of numbers $a_i$ (in other words, divisible by their [least common multiple](../algebra/euclid-algorithm.md)).
So we will now iterate over all $2^n$ subsets of integers $a_i$ with $O(n \log r)$ operations to find their least common multiple, adding or subtracting the number of multiples of it in the interval. Asymptotics is $O (2^n\cdot n\cdot \log r)$.
### The number of strings that satisfy a given pattern
Consider $n$ patterns of strings of the same length, consisting only of letters ($a...z$) or question marks. You're also given a number $k$. A string matches a pattern if it has the same length as the pattern, and at each position, either the corresponding characters are equal or the character in the pattern is a question mark. The task is to count the number of strings that match exactly $k$ of the patterns (first problem) and at least $k$ of the patterns (second problem).
Notice first that we can easily count the number of strings that satisfy at once all of the specified patterns. To do this, simply "cross" patterns: iterate though the positions ("slots") and look at a position over all patterns. If all patterns have a question mark in this position, the character can be any letter from $a$ to $z$. Otherwise, the character of this position is uniquely defined by the patterns that do not contain a question mark.
Learn now to solve the first version of the problem: when the string must satisfy exactly $k$ of the patterns.
To solve it, iterate and fix a specific subset $X$ from the set of patterns consisting of $k$ patterns. Then we have to count the number of strings that satisfy this set of patterns, and only matches it, that is, they don't match any other pattern. We will use the inclusion-exclusion principle in a slightly different manner: we sum on all supersets $Y$ (subsets from the original set of strings that contain $X$), and either add to the current answer or subtract it from the number of strings:
$$ ans(X) = \sum_{Y \supseteq X} (-1)^{|Y|-k} \cdot f(Y) $$
Where $f(Y)$ is the number of strings that match $Y$ (at least $Y$).
(If you have a hard time figuring out this, you can try drawing Venn Diagrams.)
If we sum up on all $ans(X)$, we will get the final answer:
$$ ans = \sum_{X ~ : ~ |X| = k} ans(X) $$
However, asymptotics of this solution is $O(3^k \cdot k)$. To improve it, notice that different $ans(X)$ computations very often share $Y$ sets.
We will reverse the formula of inclusion-exclusion and sum in terms of $Y$ sets. Now it becomes clear that the same set $Y$ would be taken into account in the computation of $ans(X)$ of $\binom{|Y|}{k}$ sets with the same sign $(-1)^{|Y| - k}$.
$$ ans = \sum_{Y ~ : ~ |Y| \ge k} (-1)^{|Y|-k} \cdot \binom{|Y|}{k} \cdot f(Y) $$
Now our solution has asymptotics $O(2^k \cdot k)$.
We will now solve the second version of the problem: find the number of strings that match **at least** $k$ of the patterns.
Of course, we can just use the solution to the first version of the problem and add the answers for sets with size greater than $k$. However, you may notice that in this problem, a set |Y| is considered in the formula for all sets with size $\ge k$ which are contained in $Y$. That said, we can write the part of the expression that is being multiplied by $f(Y)$ as:
$$ (-1)^{|Y|-k} \cdot \binom{|Y|}{k} + (-1)^{|Y|-k-1} \cdot \binom{|Y|}{k+1} + (-1)^{|Y|-k-2} \cdot \binom{|Y|}{k+2} + \cdots + (-1)^{|Y|-|Y|} \cdot \binom{|Y|}{|Y|} $$
Looking at Graham's (Graham, Knuth, Patashnik. "Concrete mathematics" [1998] ), we see a well-known formula for [binomial coefficients](binomial-coefficients.md):
$$ \sum_{k=0}^m (-1)^k \cdot \binom{n}{k} = (-1)^m \cdot \binom{n-1}{m} $$
Applying it here, we find that the entire sum of binomial coefficients is minimized:
$$ (-1)^{|Y|-k} \cdot \binom{|Y|-1}{|Y|-k} $$
Thus, for this task, we also obtained a solution with the asymptotics $O(2^k \cdot k)$:
$$ ans = \sum_{Y ~ : ~ |Y| \ge k} (-1)^{|Y|-k} \cdot \binom{|Y|-1}{|Y|-k} \cdot f(Y) $$
### The number of ways of going from a cell to another
There is a field $n \times m$, and $k$ of its cells are impassable walls. A robot is initially at the cell $(1,1)$ (bottom left). The robot can only move right or up, and eventually it needs to get into the cell $(n,m)$, avoiding all obstacles. You need to count the number of ways he can do it.
Assume that the sizes $n$ and $m$ are very large (say, $10^9$), and the number $k$ is small (around $100$).
For now, sort the obstacles by their coordinate $x$, and in case of equality — coordinate $y$.
Also just learn how to solve a problem without obstacles: i.e. learn how to count the number of ways to get from one cell to another. In one axis, we need to go through $x$ cells, and on the other, $y$ cells. From simple combinatorics, we get a formula using [binomial coefficients](binomial-coefficients.md):
$$\binom{x+y}{x}$$
Now to count the number of ways to get from one cell to another, avoiding all obstacles, you can use inclusion-exclusion to solve the inverse problem: count the number of ways to walk through the board stepping at a subset of obstacles (and subtract it from the total number of ways).
When iterating over a subset of the obstacles that we'll step, to count the number of ways to do this simply multiply the number of all paths from starting cell to the first of the selected obstacles, a first obstacle to the second, and so on, and then add or subtract this number from the answer, in accordance with the standard formula of inclusion-exclusion.
However, this will again be non-polynomial in complexity $O(2^k \cdot k)$.
Here goes a polynomial solution:
We will use dynamic programming. For convenience, push (1,1) to the beginning and (n,m) at the end of the obstacles array. Let's compute the numbers $d[i]$ — the number of ways to get from the starting point ($0-th$) to $i-th$, without stepping on any other obstacle (except for $i$, of course). We will compute this number for all the obstacle cells, and also for the ending one.
Let's forget for a second the obstacles and just count the number of paths from cell $0$ to $i$. We need to consider some "bad" paths, the ones that pass through the obstacles, and subtract them from the total number of ways of going from $0$ to $i$.
When considering an obstacle $t$ between $0$ and $i$ ($0 < t < i$), on which we can step, we see that the number of paths from $0$ to $i$ that pass through $t$ which have $t$ as the **first obstacle between start and $i$**. We can compute that as: $d[t]$ multiplied by the number of arbitrary paths from $t$ to $i$. We can count the number of "bad" ways summing this for all $t$ between $0$ and $i$.
We can compute $d[i]$ in $O(k)$ for $O(k)$ obstacles, so this solution has complexity $O(k^2)$.
### The number of coprime quadruples
You're given $n$ numbers: $a_1, a_2, \ldots, a_n$. You are required to count the number of ways to choose four numbers so that their combined greatest common divisor is equal to one.
We will solve the inverse problem — compute the number of "bad" quadruples, i.e. quadruples in which all numbers are divisible by a number $d > 1$.
We will use the inclusion-exclusion principle while summing over all possible groups of four numbers divisible by a divisor $d$.
$$ans = \sum_{d \ge 2} (-1)^{deg(d)-1} \cdot f(d)$$
where $deg(d)$ is the number of primes in the factorization of the number $d$ and $f(d)$ the number of quadruples divisible by $d$.
To calculate the function $f(d)$, you just have to count the number of multiples of $d$ (as mentioned on a previous task) and use [binomial coefficients](binomial-coefficients.md) to count the number of ways to choose four of them.
Thus, using the formula of inclusions-exclusions we sum the number of groups of four divisible by a prime number, then subtract the number of quadruples which are divisible by the product of two primes, add quadruples divisible by three primes, etc.
### The number of harmonic triplets
You are given a number $n \le 10^6$. You are required to count the number of triples $2 \le a < b < c \le n$ that satisfy one of the following conditions:
* or ${\rm gcd}(a,b) = {\rm gcd}(a,c) = {\rm gcd}(b,c) = 1$,
* or ${\rm gcd}(a,b) > 1, {\rm gcd}(a,c) > 1, {\rm gcd}(b,c) > 1$.
First, go straight to the inverse problem — i.e. count the number of non-harmonic triples.
Second, note that any non-harmonic triplet is made of a pair of coprimes and a third number that is not coprime with at least one from the pair.
Thus, the number of non-harmonic triples that contain $i$ is equal the number of integers from $2$ to $n$ that are coprimes with $i$ multiplied by the number of integers that are not coprime with $i$.
Either $gcd(a,b) = 1 \wedge gcd(a,c) > 1 \wedge gcd(b,c) > 1$
or $gcd(a,b) = 1 \wedge gcd(a,c) = 1 \wedge gcd(b,c) > 1$
In both of these cases, it will be counted twice. The first case will be counted when $i = a$ and when $i = b$. The second case will be counted when $i = b$ and when $i = c$. Therefore, to compute the number of non-harmonic triples, we sum this calculation through all $i$ from $2$ to $n$ and divide it by $2$.
Now all we have left to solve is to learn to count the number of coprimes to $i$ in the interval $[2;n]$. Although this problem has already been mentioned, the above solution is not suitable here — it would require the factorization of each of the integers from $2$ to $n$, and then iterating through all subsets of these primes.
A faster solution is possible with such modification of the sieve of Eratosthenes:
1. First, we find all numbers in the interval $[2;n]$ such that its simple factorization does not include a prime factor twice. We will also need to know, for these numbers, how many factors it includes.
* To do this we will maintain an array $deg[i]$ to store the number of primes in the factorization of $i$, and an array $good[i]$, to mark either if $i$ contains each factor at most once ($good[i] = 1$) or not ($good[i] = 0$). When iterating from $2$ to $n$, if we reach a number that has $deg$ equal to $0$, then it is a prime and its $deg$ is $1$.
* During the sieve of Eratosthenes, we will iterate $i$ from $2$ to $n$. When processing a prime number we go through all of its multiples and increase their $deg[]$. If one of these multiples is multiple of the square of $i$, then we can put $good$ as false.
2. Second, we need to calculate the answer for all $i$ from $2$ to $n$, i.e., the array $cnt[]$ — the number of integers not coprime with $i$.
* To do this, remember how the formula of inclusion-exclusion works — actually here we implement the same concept, but with inverted logic: we iterate over a component (a product of primes from the factorization) and add or subtract its term on the formula of inclusion-exclusion of each of its multiples.
* So, let's say we are processing a number $i$ such that $good[i] = true$, i.e., it is involved in the formula of inclusion-exclusion. Iterate through all numbers that are multiples of $i$, and either add or subtract $\lfloor N/i \rfloor$ from their $cnt[]$ (the signal depends on $deg[i]$: if $deg[i]$ is odd, then we must add, otherwise subtract).
Here's a C++ implementation:
```cpp
int n;
bool good[MAXN];
int deg[MAXN], cnt[MAXN];
long long solve() {
memset (good, 1, sizeof good);
memset (deg, 0, sizeof deg);
memset (cnt, 0, sizeof cnt);
long long ans_bad = 0;
for (int i=2; i<=n; ++i) {
if (good[i]) {
if (deg[i] == 0) deg[i] = 1;
for (int j=1; i*j<=n; ++j) {
if (j > 1 && deg[i] == 1)
if (j % i == 0)
good[i*j] = false;
else
++deg[i*j];
cnt[i*j] += (n / i) * (deg[i]%2==1 ? +1 : -1);
}
}
ans_bad += (cnt[i] - 1) * 1ll * (n-1 - cnt[i]);
}
return (n-1) * 1ll * (n-2) * (n-3) / 6 - ans_bad / 2;
}
```
The asymptotics of our solution is $O(n \log n)$, as for almost every number up to $n$ we make $n/i$ iterations on the nested loop.
### The number of permutations without fixed points (derangements)
Prove that the number of permutations of length $n$ without fixed points (i.e. no number $i$ is in position $i$ - also called a derangement) is equal to the following number:
$$n! - \binom{n}{1} \cdot (n-1)! + \binom{n}{2} \cdot (n-2)! - \binom{n}{3} \cdot (n-3)! + \cdots \pm \binom{n}{n} \cdot (n-n)! $$
and approximately equal to:
$$ \frac{ n! }{ e } $$
(if you round this expression to the nearest whole number — you get exactly the number of permutations without fixed points)
Denote by $A_k$ the set of permutations of length $n$ with a fixed point at position $k$ ($1 \le k \le n$) (i.e. element $k$ is at position $k$).
We now use the formula of inclusion-exclusion to count the number of permutations with at least one fixed point. For this we need to learn to count sizes of an intersection of sets $A_i$, as follows:
$$\begin{eqnarray}
\left| A_p \right| &=& (n-1)!\ , \\
\left| A_p \cap A_q \right| &=& (n-2)!\ , \\
\left| A_p \cap A_q \cap A_r \right| &=& (n-3)!\ , \\
\cdots ,
\end{eqnarray}$$
because if we know that the number of fixed points is equal $x$, then we know the position of $x$ elements of the permutation, and all other $(n-x)$ elements can be placed anywhere.
Substituting this into the formula of inclusion-exclusion, and given that the number of ways to choose a subset of size $x$ from the set of $n$ elements is equal to $\binom{n}{x}$, we obtain a formula for the number of permutations with at least one fixed point:
$$\binom{n}{1} \cdot (n-1)! - \binom{n}{2} \cdot (n-2)! + \binom{n}{3} \cdot (n-3)! - \cdots \pm \binom{n}{n} \cdot (n-n)! $$
Then the number of permutations without fixed points is equal to:
$$n! - \binom{n}{1} \cdot (n-1)! + \binom{n}{2} \cdot (n-2)! - \binom{n}{3} \cdot (n-3)! + \cdots \pm \binom{n}{n} \cdot (n-n)! $$
Simplifying this expression, we obtain **exact and approximate expressions for the number of permutations without fixed points**:
$$ n! \left( 1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \cdots \pm \frac{1}{n!} \right ) \approx \frac{n!}{e} $$
(because the sum in brackets are the first $n+1$ terms of the expansion in Taylor series $e^{-1}$)
It is worth noting that a similar problem can be solved this way: when you need the fixed points were not among the $m$ first elements of permutations (and not among all, as we just solved). The formula obtained is as the given above accurate formula, but it will go up to the sum of $k$, instead of $n$.
|
---
title
inclusion_exclusion_principle
---
# The Inclusion-Exclusion Principle
The inclusion-exclusion principle is an important combinatorial way to compute the size of a set or the probability of complex events. It relates the sizes of individual sets with their union.
## Statement
### The verbal formula
The inclusion-exclusion principle can be expressed as follows:
To compute the size of a union of multiple sets, it is necessary to sum the sizes of these sets **separately**, and then subtract the sizes of all **pairwise** intersections of the sets, then add back the size of the intersections of **triples** of the sets, subtract the size of **quadruples** of the sets, and so on, up to the intersection of **all** sets.
### The formulation in terms of sets
The above definition can be expressed mathematically as follows:
$$\left| \bigcup_{i=1}^n A_i \right| = \sum_{i=1}^n|A_i| - \sum_{1\leq i<j\leq n} |A_i \cap A_j| + \sum _{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k| - \cdots + (-1)^{n-1} | A_1 \cap \cdots \cap A_n |$$
And in a more compact way:
$$\left|\bigcup_{i=1}^n A_i \right| = \sum_{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}} (-1)^{|J|-1}{\Biggl |}\bigcap_{j\in J}A_{j}{\Biggr |}$$
### The formulation using Venn diagrams
Let the diagram show three sets $A$, $B$ and $C$:

Then the area of their union $A \cup B \cup C$ is equal to the sum of the areas $A$, $B$ and $C$ less double-covered areas $A \cap B$, $A \cap C$, $B \cap C$, but with the addition of the area covered by three sets $A \cap B \cap C$:
$$S(A \cup B \cup C) = S(A) + S(B) + S(C) - S(A \cap B) - S(A \cap C) - S(B \cap C) + S(A \cap B \cap C)$$
It can also be generalized for an association of $n$ sets.
### The formulation in terms of probability theory
If $A_i$ $(i = 1,2...n)$ are events and ${\cal P}(A_i)$ the probability of an event from $A_i$ to occur, then the probability of their union (i.e. the probability that at least one of the events occur) is equal to:
$$\begin{eqnarray}
{\cal P} \left( \bigcup_{i=1}^n A_i \right) &=& \sum_{i=1}^n{\cal P}(A_i)\ - \sum_{1\leq i<j\leq n} {\cal P}(A_i \cap A_j)\ + \\
&+& \sum _{1\leq i<j<k\leq n}{\cal P}(A_i \cap A_j \cap A_k) - \cdots + (-1)^{n-1} {\cal P}( A_1 \cap \cdots \cap A_n )
\end{eqnarray}$$
And in a more compact way:
$${\cal P} \left(\bigcup_{i=1}^n A_i \right) = \sum_{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}} (-1)^{|J|-1}\ {\cal P}{\Biggl (}\bigcap_{j\in J}A_{j}{\Biggr )}$$
## Proof
For the proof it is convenient to use the mathematical formulation in terms of set theory:
$$\left|\bigcup_{i=1}^n A_i \right| = \sum_{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}} (-1)^{|J|-1}{\Biggl |}\bigcap_{j\in J}A_{j}{\Biggr |}$$
We want to prove that any element contained in at least one of the sets $A_i$ will occur in the formula only once (note that elements which are not present in any of the sets $A_i$ will never be considered on the right part of the formula).
Consider an element $x$ occurring in $k \geq 1$ sets $A_i$. We will show it is counted only once in the formula. Note that:
* in terms which $|J| = 1$, the item $x$ will be counted **$+\ k$** times;
* in terms which $|J| = 2$, the item $x$ will be counted **$-\ \binom{k}{2}$** times - because it will be counted in those terms that include two of the $k$ sets containing $x$;
* in terms which $|J| = 3$, the item $x$ will be counted **$+\ \binom{k}{3}$** times;
* $\cdots$
* in terms which $|J| = k$, the item $x$ will be counted **$(-1)^{k-1}\cdot \binom{k}{k}$** times;
* in terms which $|J| \gt k$, the item $x$ will be counted **zero** times;
This leads us to the following sum of [binomial coefficients](binomial-coefficients.md):
$$ T = \binom{k}{1} - \binom{k}{2} + \binom{k}{3} - \cdots + (-1)^{i-1}\cdot \binom{k}{i} + \cdots + (-1)^{k-1}\cdot \binom{k}{k}$$
This expression is very similar to the binomial expansion of $(1 - x)^k$:
$$ (1 - x)^k = \binom{k}{0} - \binom{k}{1} \cdot x + \binom{k}{2} \cdot x^2 - \binom{k}{3} \cdot x^3 + \cdots + (-1)^k\cdot \binom{k}{k} \cdot x^k $$
When $x = 1$, $(1 - x)^k$ looks a lot like $T$. However, the expression has an additional $\binom{k}{0} = 1$, and it is multiplied by $-1$. That leads us to $(1 - 1)^k = 1 - T$. Therefore $T = 1 - (1 - 1)^k = 1$, what was required to prove. The element is counted only once.
## Generalization for calculating number of elements in exactly $r$ sets {data-toc-label="Generalization for calculating number of elements in exactly r sets"}
Inclusion-exclusion principle can be rewritten to calculate number of elements which are present in zero sets:
$$\left|\bigcap_{i=1}^n \overline{A_i}\right|=\sum_{m=0}^n (-1)^m \sum_{|X|=m} \left|\bigcap_{i\in X} A_{i}\right|$$
Consider its generalization to calculate number of elements which are present in exactly $r$ sets:
$$\left|\bigcup_{|B|=r}\left[\bigcap_{i \in B} A_i \cap \bigcap_{j \not\in B} \overline{A_j}\right]\right|=\sum_{m=r}^n (-1)^{m-r}\dbinom{m}{r} \sum_{|X|=m} \left|\bigcap_{i \in X} A_{i}\right|$$
To prove this formula, consider some particular $B$. Due to basic inclusion-exclusion principle we can say about it that:
$$\left|\bigcap_{i \in B} A_i \cap \bigcap_{j \not \in B} \overline{A_j}\right|=\sum_{m=r}^{n} (-1)^{m-r} \sum_{\substack{|X|=m \newline B \subset X}}\left|\bigcap_{i\in X} A_{i}\right|$$
The sets on the left side do not intersect for different $B$, thus we can sum them up directly. Also one should note that any set $X$ will always have coefficient $(-1)^{m-r}$ if it occurs and it will occur for exactly $\dbinom{m}{r}$ sets $B$.
## Usage when solving problems
The inclusion-exclusion principle is hard to understand without studying its applications.
First, we will look at three simplest tasks "at paper", illustrating applications of the principle, and then consider more practical problems which are difficult to solve without inclusion-exclusion principle.
Tasks asking to "find the **number** of ways" are worth of note, as they sometimes lead to polynomial solutions, not necessarily exponential.
### A simple task on permutations
Task: count how many permutations of numbers from $0$ to $9$ exist such that the first element is greater than $1$ and the last one is less than $8$.
Let's count the number of "bad" permutations, that is, permutations in which the first element is $\leq 1$ and/or the last is $\geq 8$.
We will denote by $X$ the set of permutations in which the first element is $\leq 1$ and $Y$ the set of permutations in which the last element is $\geq 8$. Then the number of "bad" permutations, as on the inclusion-exclusion formula, will be:
$$ |X \cup Y| = |X| + |Y| - |X \cap Y| $$
After a simple combinatorial calculation, we will get to:
$$ 2 \cdot 9! + 2 \cdot 9! - 2 \cdot 2 \cdot 8! $$
The only thing left is to subtract this number from the total of $10!$ to get the number of "good" permutations.
### A simple task on (0, 1, 2) sequences
Task: count how many sequences of length $n$ exist consisting only of numbers $0,1,2$ such that each number occurs **at least once**.
Again let us turn to the inverse problem, i.e. we calculate the number of sequences which do **not** contain **at least one** of the numbers.
Let's denote by $A_i (i = 0,1,2)$ the set of sequences in which the digit $i$ does **not** occur.
The formula of inclusion-exclusion on the number of "bad" sequences will be:
$$ |A_0 \cup A_1 \cup A_2| = |A_0| + |A_1| + |A_2| - |A_0 \cap A_1| - |A_0 \cap A_2| - |A_1 \cap A_2| + |A_0 \cap A_1 \cap A_2| $$
* The size of each $A_i$ is $2^n$, as each sequence can only contain two of the digits.
* The size of each pairwise intersection $A_i \cap A_j$ is equal to $1$, as there will be only one digit to build the sequence.
* The size of the intersection of all three sets is equal to $0$, as there will be no digits to build the sequence.
As we solved the inverse problem, we subtract it from the total of $3^n$ sequences:
$$3^n - (3 \cdot 2^n - 3 \cdot 1 + 0)$$
<div id="the-number-of-integer-solutions-to-the-equation"></div>
### Number of upper-bound integer sums {: #number-of-upper-bound-integer-sums }
Consider the following equation:
$$x_1 + x_2 + x_3 + x_4 + x_5 + x_6 = 20$$
where $0 \le x_i \le 8 ~ (i = 1,2,\ldots 6)$.
Task: count the number of solutions to the equation.
Forget the restriction on $x_i$ for a moment and just count the number of nonnegative solutions to this equation. This is easily done using [Stars and Bars](stars_and_bars.md):
we want to break a sequence of $20$ units into $6$ groups, which is the same as arranging $5$ _bars_ and $20$ _stars_:
$$N_0 = \binom{25}{5}$$
We will now calculate the number of "bad" solutions with the inclusion-exclusion principle. The "bad" solutions will be those in which one or more $x_i$ are greater than $9$.
Denote by $A_k ~ (k = 1,2\ldots 6)$ the set of solutions where $x_k \ge 9$, and all other $x_i \ge 0 ~ (i \ne k)$ (they may be $\ge 9$ or not). To calculate the size of $A_k$, note that we have essentially the same combinatorial problem that was solved in the two paragraphs above, but now $9$ of the units are excluded from the slots and definitely belong to the first group. Thus:
$$ | A_k | = \binom{16}{5} $$
Similarly, the size of the intersection between two sets $A_k$ and $A_p$ (for $k \ne p$) is equal to:
$$ \left| A_k \cap A_p \right| = \binom{7}{5}$$
The size of each intersection of three sets is zero, since $20$ units will not be enough for three or more variables greater than or equal to $9$.
Combining all this into the formula of inclusions-exceptions and given that we solved the inverse problem, we finally get the answer:
$$\binom{25}{5} - \left(\binom{6}{1} \cdot \binom{16}{5} - \binom{6}{2} \cdot \binom{7}{5}\right) $$
### The number of relative primes in a given interval
Task: given two numbers $n$ and $r$, count the number of integers in the interval $[1;r]$ that are relatively prime to n (their greatest common divisor is $1$).
Let's solve the inverse problem - compute the number of not mutually primes with $n$.
We will denote the prime factors of $n$ as $p_i (i = 1\cdots k)$.
How many numbers in the interval $[1;r]$ are divisible by $p_i$? The answer to this question is:
$$ \left\lfloor \frac{ r }{ p_i } \right\rfloor $$
However, if we simply sum these numbers, some numbers will be summarized several times (those that share multiple $p_i$ as their factors). Therefore, it is necessary to use the inclusion-exclusion principle.
We will iterate over all $2^k$ subsets of $p_i$s, calculate their product and add or subtract the number of multiples of their product.
Here is a C++ implementation:
```cpp
int solve (int n, int r) {
vector<int> p;
for (int i=2; i*i<=n; ++i)
if (n % i == 0) {
p.push_back (i);
while (n % i == 0)
n /= i;
}
if (n > 1)
p.push_back (n);
int sum = 0;
for (int msk=1; msk<(1<<p.size()); ++msk) {
int mult = 1,
bits = 0;
for (int i=0; i<(int)p.size(); ++i)
if (msk & (1<<i)) {
++bits;
mult *= p[i];
}
int cur = r / mult;
if (bits % 2 == 1)
sum += cur;
else
sum -= cur;
}
return r - sum;
}
```
Asymptotics of the solution is $O (\sqrt{n})$.
### The number of integers in a given interval which are multiple of at least one of the given numbers
Given $n$ numbers $a_i$ and number $r$. You want to count the number of integers in the interval $[1; r]$ that are multiple of at least one of the $a_i$.
The solution algorithm is almost identical to the one for previous task — construct the formula of inclusion-exclusion on the numbers $a_i$, i.e. each term in this formula is the number of numbers divisible by a given subset of numbers $a_i$ (in other words, divisible by their [least common multiple](../algebra/euclid-algorithm.md)).
So we will now iterate over all $2^n$ subsets of integers $a_i$ with $O(n \log r)$ operations to find their least common multiple, adding or subtracting the number of multiples of it in the interval. Asymptotics is $O (2^n\cdot n\cdot \log r)$.
### The number of strings that satisfy a given pattern
Consider $n$ patterns of strings of the same length, consisting only of letters ($a...z$) or question marks. You're also given a number $k$. A string matches a pattern if it has the same length as the pattern, and at each position, either the corresponding characters are equal or the character in the pattern is a question mark. The task is to count the number of strings that match exactly $k$ of the patterns (first problem) and at least $k$ of the patterns (second problem).
Notice first that we can easily count the number of strings that satisfy at once all of the specified patterns. To do this, simply "cross" patterns: iterate though the positions ("slots") and look at a position over all patterns. If all patterns have a question mark in this position, the character can be any letter from $a$ to $z$. Otherwise, the character of this position is uniquely defined by the patterns that do not contain a question mark.
Learn now to solve the first version of the problem: when the string must satisfy exactly $k$ of the patterns.
To solve it, iterate and fix a specific subset $X$ from the set of patterns consisting of $k$ patterns. Then we have to count the number of strings that satisfy this set of patterns, and only matches it, that is, they don't match any other pattern. We will use the inclusion-exclusion principle in a slightly different manner: we sum on all supersets $Y$ (subsets from the original set of strings that contain $X$), and either add to the current answer or subtract it from the number of strings:
$$ ans(X) = \sum_{Y \supseteq X} (-1)^{|Y|-k} \cdot f(Y) $$
Where $f(Y)$ is the number of strings that match $Y$ (at least $Y$).
(If you have a hard time figuring out this, you can try drawing Venn Diagrams.)
If we sum up on all $ans(X)$, we will get the final answer:
$$ ans = \sum_{X ~ : ~ |X| = k} ans(X) $$
However, asymptotics of this solution is $O(3^k \cdot k)$. To improve it, notice that different $ans(X)$ computations very often share $Y$ sets.
We will reverse the formula of inclusion-exclusion and sum in terms of $Y$ sets. Now it becomes clear that the same set $Y$ would be taken into account in the computation of $ans(X)$ of $\binom{|Y|}{k}$ sets with the same sign $(-1)^{|Y| - k}$.
$$ ans = \sum_{Y ~ : ~ |Y| \ge k} (-1)^{|Y|-k} \cdot \binom{|Y|}{k} \cdot f(Y) $$
Now our solution has asymptotics $O(2^k \cdot k)$.
We will now solve the second version of the problem: find the number of strings that match **at least** $k$ of the patterns.
Of course, we can just use the solution to the first version of the problem and add the answers for sets with size greater than $k$. However, you may notice that in this problem, a set |Y| is considered in the formula for all sets with size $\ge k$ which are contained in $Y$. That said, we can write the part of the expression that is being multiplied by $f(Y)$ as:
$$ (-1)^{|Y|-k} \cdot \binom{|Y|}{k} + (-1)^{|Y|-k-1} \cdot \binom{|Y|}{k+1} + (-1)^{|Y|-k-2} \cdot \binom{|Y|}{k+2} + \cdots + (-1)^{|Y|-|Y|} \cdot \binom{|Y|}{|Y|} $$
Looking at Graham's (Graham, Knuth, Patashnik. "Concrete mathematics" [1998] ), we see a well-known formula for [binomial coefficients](binomial-coefficients.md):
$$ \sum_{k=0}^m (-1)^k \cdot \binom{n}{k} = (-1)^m \cdot \binom{n-1}{m} $$
Applying it here, we find that the entire sum of binomial coefficients is minimized:
$$ (-1)^{|Y|-k} \cdot \binom{|Y|-1}{|Y|-k} $$
Thus, for this task, we also obtained a solution with the asymptotics $O(2^k \cdot k)$:
$$ ans = \sum_{Y ~ : ~ |Y| \ge k} (-1)^{|Y|-k} \cdot \binom{|Y|-1}{|Y|-k} \cdot f(Y) $$
### The number of ways of going from a cell to another
There is a field $n \times m$, and $k$ of its cells are impassable walls. A robot is initially at the cell $(1,1)$ (bottom left). The robot can only move right or up, and eventually it needs to get into the cell $(n,m)$, avoiding all obstacles. You need to count the number of ways he can do it.
Assume that the sizes $n$ and $m$ are very large (say, $10^9$), and the number $k$ is small (around $100$).
For now, sort the obstacles by their coordinate $x$, and in case of equality — coordinate $y$.
Also just learn how to solve a problem without obstacles: i.e. learn how to count the number of ways to get from one cell to another. In one axis, we need to go through $x$ cells, and on the other, $y$ cells. From simple combinatorics, we get a formula using [binomial coefficients](binomial-coefficients.md):
$$\binom{x+y}{x}$$
Now to count the number of ways to get from one cell to another, avoiding all obstacles, you can use inclusion-exclusion to solve the inverse problem: count the number of ways to walk through the board stepping at a subset of obstacles (and subtract it from the total number of ways).
When iterating over a subset of the obstacles that we'll step, to count the number of ways to do this simply multiply the number of all paths from starting cell to the first of the selected obstacles, a first obstacle to the second, and so on, and then add or subtract this number from the answer, in accordance with the standard formula of inclusion-exclusion.
However, this will again be non-polynomial in complexity $O(2^k \cdot k)$.
Here goes a polynomial solution:
We will use dynamic programming. For convenience, push (1,1) to the beginning and (n,m) at the end of the obstacles array. Let's compute the numbers $d[i]$ — the number of ways to get from the starting point ($0-th$) to $i-th$, without stepping on any other obstacle (except for $i$, of course). We will compute this number for all the obstacle cells, and also for the ending one.
Let's forget for a second the obstacles and just count the number of paths from cell $0$ to $i$. We need to consider some "bad" paths, the ones that pass through the obstacles, and subtract them from the total number of ways of going from $0$ to $i$.
When considering an obstacle $t$ between $0$ and $i$ ($0 < t < i$), on which we can step, we see that the number of paths from $0$ to $i$ that pass through $t$ which have $t$ as the **first obstacle between start and $i$**. We can compute that as: $d[t]$ multiplied by the number of arbitrary paths from $t$ to $i$. We can count the number of "bad" ways summing this for all $t$ between $0$ and $i$.
We can compute $d[i]$ in $O(k)$ for $O(k)$ obstacles, so this solution has complexity $O(k^2)$.
### The number of coprime quadruples
You're given $n$ numbers: $a_1, a_2, \ldots, a_n$. You are required to count the number of ways to choose four numbers so that their combined greatest common divisor is equal to one.
We will solve the inverse problem — compute the number of "bad" quadruples, i.e. quadruples in which all numbers are divisible by a number $d > 1$.
We will use the inclusion-exclusion principle while summing over all possible groups of four numbers divisible by a divisor $d$.
$$ans = \sum_{d \ge 2} (-1)^{deg(d)-1} \cdot f(d)$$
where $deg(d)$ is the number of primes in the factorization of the number $d$ and $f(d)$ the number of quadruples divisible by $d$.
To calculate the function $f(d)$, you just have to count the number of multiples of $d$ (as mentioned on a previous task) and use [binomial coefficients](binomial-coefficients.md) to count the number of ways to choose four of them.
Thus, using the formula of inclusions-exclusions we sum the number of groups of four divisible by a prime number, then subtract the number of quadruples which are divisible by the product of two primes, add quadruples divisible by three primes, etc.
### The number of harmonic triplets
You are given a number $n \le 10^6$. You are required to count the number of triples $2 \le a < b < c \le n$ that satisfy one of the following conditions:
* or ${\rm gcd}(a,b) = {\rm gcd}(a,c) = {\rm gcd}(b,c) = 1$,
* or ${\rm gcd}(a,b) > 1, {\rm gcd}(a,c) > 1, {\rm gcd}(b,c) > 1$.
First, go straight to the inverse problem — i.e. count the number of non-harmonic triples.
Second, note that any non-harmonic triplet is made of a pair of coprimes and a third number that is not coprime with at least one from the pair.
Thus, the number of non-harmonic triples that contain $i$ is equal the number of integers from $2$ to $n$ that are coprimes with $i$ multiplied by the number of integers that are not coprime with $i$.
Either $gcd(a,b) = 1 \wedge gcd(a,c) > 1 \wedge gcd(b,c) > 1$
or $gcd(a,b) = 1 \wedge gcd(a,c) = 1 \wedge gcd(b,c) > 1$
In both of these cases, it will be counted twice. The first case will be counted when $i = a$ and when $i = b$. The second case will be counted when $i = b$ and when $i = c$. Therefore, to compute the number of non-harmonic triples, we sum this calculation through all $i$ from $2$ to $n$ and divide it by $2$.
Now all we have left to solve is to learn to count the number of coprimes to $i$ in the interval $[2;n]$. Although this problem has already been mentioned, the above solution is not suitable here — it would require the factorization of each of the integers from $2$ to $n$, and then iterating through all subsets of these primes.
A faster solution is possible with such modification of the sieve of Eratosthenes:
1. First, we find all numbers in the interval $[2;n]$ such that its simple factorization does not include a prime factor twice. We will also need to know, for these numbers, how many factors it includes.
* To do this we will maintain an array $deg[i]$ to store the number of primes in the factorization of $i$, and an array $good[i]$, to mark either if $i$ contains each factor at most once ($good[i] = 1$) or not ($good[i] = 0$). When iterating from $2$ to $n$, if we reach a number that has $deg$ equal to $0$, then it is a prime and its $deg$ is $1$.
* During the sieve of Eratosthenes, we will iterate $i$ from $2$ to $n$. When processing a prime number we go through all of its multiples and increase their $deg[]$. If one of these multiples is multiple of the square of $i$, then we can put $good$ as false.
2. Second, we need to calculate the answer for all $i$ from $2$ to $n$, i.e., the array $cnt[]$ — the number of integers not coprime with $i$.
* To do this, remember how the formula of inclusion-exclusion works — actually here we implement the same concept, but with inverted logic: we iterate over a component (a product of primes from the factorization) and add or subtract its term on the formula of inclusion-exclusion of each of its multiples.
* So, let's say we are processing a number $i$ such that $good[i] = true$, i.e., it is involved in the formula of inclusion-exclusion. Iterate through all numbers that are multiples of $i$, and either add or subtract $\lfloor N/i \rfloor$ from their $cnt[]$ (the signal depends on $deg[i]$: if $deg[i]$ is odd, then we must add, otherwise subtract).
Here's a C++ implementation:
```cpp
int n;
bool good[MAXN];
int deg[MAXN], cnt[MAXN];
long long solve() {
memset (good, 1, sizeof good);
memset (deg, 0, sizeof deg);
memset (cnt, 0, sizeof cnt);
long long ans_bad = 0;
for (int i=2; i<=n; ++i) {
if (good[i]) {
if (deg[i] == 0) deg[i] = 1;
for (int j=1; i*j<=n; ++j) {
if (j > 1 && deg[i] == 1)
if (j % i == 0)
good[i*j] = false;
else
++deg[i*j];
cnt[i*j] += (n / i) * (deg[i]%2==1 ? +1 : -1);
}
}
ans_bad += (cnt[i] - 1) * 1ll * (n-1 - cnt[i]);
}
return (n-1) * 1ll * (n-2) * (n-3) / 6 - ans_bad / 2;
}
```
The asymptotics of our solution is $O(n \log n)$, as for almost every number up to $n$ we make $n/i$ iterations on the nested loop.
### The number of permutations without fixed points (derangements)
Prove that the number of permutations of length $n$ without fixed points (i.e. no number $i$ is in position $i$ - also called a derangement) is equal to the following number:
$$n! - \binom{n}{1} \cdot (n-1)! + \binom{n}{2} \cdot (n-2)! - \binom{n}{3} \cdot (n-3)! + \cdots \pm \binom{n}{n} \cdot (n-n)! $$
and approximately equal to:
$$ \frac{ n! }{ e } $$
(if you round this expression to the nearest whole number — you get exactly the number of permutations without fixed points)
Denote by $A_k$ the set of permutations of length $n$ with a fixed point at position $k$ ($1 \le k \le n$) (i.e. element $k$ is at position $k$).
We now use the formula of inclusion-exclusion to count the number of permutations with at least one fixed point. For this we need to learn to count sizes of an intersection of sets $A_i$, as follows:
$$\begin{eqnarray}
\left| A_p \right| &=& (n-1)!\ , \\
\left| A_p \cap A_q \right| &=& (n-2)!\ , \\
\left| A_p \cap A_q \cap A_r \right| &=& (n-3)!\ , \\
\cdots ,
\end{eqnarray}$$
because if we know that the number of fixed points is equal $x$, then we know the position of $x$ elements of the permutation, and all other $(n-x)$ elements can be placed anywhere.
Substituting this into the formula of inclusion-exclusion, and given that the number of ways to choose a subset of size $x$ from the set of $n$ elements is equal to $\binom{n}{x}$, we obtain a formula for the number of permutations with at least one fixed point:
$$\binom{n}{1} \cdot (n-1)! - \binom{n}{2} \cdot (n-2)! + \binom{n}{3} \cdot (n-3)! - \cdots \pm \binom{n}{n} \cdot (n-n)! $$
Then the number of permutations without fixed points is equal to:
$$n! - \binom{n}{1} \cdot (n-1)! + \binom{n}{2} \cdot (n-2)! - \binom{n}{3} \cdot (n-3)! + \cdots \pm \binom{n}{n} \cdot (n-n)! $$
Simplifying this expression, we obtain **exact and approximate expressions for the number of permutations without fixed points**:
$$ n! \left( 1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \cdots \pm \frac{1}{n!} \right ) \approx \frac{n!}{e} $$
(because the sum in brackets are the first $n+1$ terms of the expansion in Taylor series $e^{-1}$)
It is worth noting that a similar problem can be solved this way: when you need the fixed points were not among the $m$ first elements of permutations (and not among all, as we just solved). The formula obtained is as the given above accurate formula, but it will go up to the sum of $k$, instead of $n$.
## Practice Problems
A list of tasks that can be solved using the principle of inclusions-exclusions:
* [UVA #10325 "The Lottery" [difficulty: low]](http://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=1266)
* [UVA #11806 "Cheerleaders" [difficulty: low]](http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2906)
* [TopCoder SRM 477 "CarelessSecretary" [difficulty: low]](http://www.topcoder.com/stat?c=problem_statement&pm=10875)
* [TopCoder TCHS 16 "Divisibility" [difficulty: low]](http://community.topcoder.com/stat?c=problem_statement&pm=6658&rd=10068)
* [SPOJ #6285 NGM2 , "Another Game With Numbers" [difficulty: low]](http://www.spoj.com/problems/NGM2/)
* [TopCoder SRM 382 "CharmingTicketsEasy" [difficulty: medium]](http://community.topcoder.com/stat?c=problem_statement&pm=8470)
* [TopCoder SRM 390 "SetOfPatterns" [difficulty: medium]](http://www.topcoder.com/stat?c=problem_statement&pm=8307)
* [TopCoder SRM 176 "Deranged" [difficulty: medium]](http://community.topcoder.com/stat?c=problem_statement&pm=2013)
* [TopCoder SRM 457 "TheHexagonsDivOne" [difficulty: medium]](http://community.topcoder.com/stat?c=problem_statement&pm=10702&rd=14144&rm=303184&cr=22697599)
* [Test>>>thebest "HarmonicTriples" (in Russian) [difficulty: medium]](http://esci.ru/ttb/statement-62.htm)
* [SPOJ #4191 MSKYCODE "Sky Code" [difficulty: medium]](http://www.spoj.com/problems/MSKYCODE/)
* [SPOJ #4168 SQFREE "Square-free integers" [difficulty: medium]](http://www.spoj.com/problems/SQFREE/)
* [CodeChef "Count Relations" [difficulty: medium]](http://www.codechef.com/JAN11/problems/COUNTREL/)
* [SPOJ - Almost Prime Numbers Again](http://www.spoj.com/problems/KPRIMESB/)
* [SPOJ - Find number of Pair of Friends](http://www.spoj.com/problems/IITKWPCH/)
* [SPOJ - Balanced Cow Subsets](http://www.spoj.com/problems/SUBSET/)
* [SPOJ - EASY MATH [difficulty: medium]](http://www.spoj.com/problems/EASYMATH/)
* [SPOJ - MOMOS - FEASTOFPIGS [difficulty: easy]](https://www.spoj.com/problems/MOMOS/)
* [Atcoder - Grid 2 [difficulty: easy]](https://atcoder.jp/contests/dp/tasks/dp_y/)
* [Codeforces - Count GCD](https://codeforces.com/contest/1750/problem/D)
|
The Inclusion-Exclusion Principle
|
---
title: Generating all K-combinations
title
generating_combinations
---
# Generating all $K$-combinations
In this article we will discuss the problem of generating all $K$-combinations.
Given the natural numbers $N$ and $K$, and considering a set of numbers from $1$ to $N$.
The task is to derive all **subsets of size $K$**.
## Generate next lexicographical $K$-combination {data-toc-label="Generate next lexicographical K-combination"}
First we will generate them in lexicographical order.
The algorithm for this is simple. The first combination will be ${1, 2, ..., K}$. Now let's see how
to find the combination that immediately follows this, lexicographically. To do so, we consider our
current combination, and find the rightmost element that has not yet reached its highest possible value. Once
finding this element, we increment it by $1$, and assign the lowest valid value to all subsequent
elements.
```{.cpp file=next_combination}
bool next_combination(vector<int>& a, int n) {
int k = (int)a.size();
for (int i = k - 1; i >= 0; i--) {
if (a[i] < n - k + i + 1) {
a[i]++;
for (int j = i + 1; j < k; j++)
a[j] = a[j - 1] + 1;
return true;
}
}
return false;
}
```
## Generate all $K$-combinations such that adjacent combinations differ by one element {data-toc-label="Generate all K-combinations such that adjacent combinations differ by one element"}
This time we want to generate all $K$-combinations in such
an order, that adjacent combinations differ exactly by one element.
This can be solved using the [Gray Code](../algebra/gray-code.md):
If we assign a bitmask to each subset, then by generating and iterating over these bitmasks with Gray codes, we can obtain our answer.
The task of generating $K$-combinations can also be solved using Gray Codes in a different way:
Generate Gray Codes for the numbers from $0$ to $2^N - 1$ and leave only those codes containing $K$ $1$s.
The surprising fact is that in the resulting sequence of $K$ set bits, any two neighboring masks (including the
first and last mask - neighboring in a cyclic sense) - will differ exactly by two bits, which is our objective (remove
a number, add a number).
Let us prove this:
For the proof, we recall the fact that the sequence $G(N)$ (representing the $N$<sup>th</sup> Gray Code) can
be obtained as follows:
$$G(N) = 0G(N-1) \cup 1G(N-1)^\text{R}$$
That is, consider the Gray Code sequence for $N-1$, and prefix $0$ before every term. And consider the
reversed Gray Code sequence for $N-1$ and prefix a $1$ before every mask, and
concatenate these two sequences.
Now we may produce our proof.
First, we prove that the first and last masks differ exactly in two bits. To do this, it is sufficient to note
that the first mask of the sequence $G(N)$, will be of the form $N-K$ $0$s, followed by $K$ $1$s. As
the first bit is set as $0$, after which $(N-K-1)$ $0$s follow, after which $K$ set bits follow and the last mask will be of the form $1$, then $(N-K)$ $0$s, then $K-1$ $1$s.
Applying the principle of mathematical induction, and using the formula for $G(N)$, concludes the proof.
Now our task is to show that any two adjacent codes also differ exactly in two bits, we can do this by considering our recursive equation for the generation of Gray Codes. Let us assume the content of the two halves formed by $G(N-1)$ is true. Now we need to prove that the new consecutive pair formed at the junction (by the concatenation of these two halves) is also valid, i.e. they differ by exactly two bits.
This can be done, as we know the last mask of the first half and the first mask of the second half. The last mask of the first half would be $1$, then $(N-K-1)$ $0$s, then $K-1$ $1$s. And the first mask of the second half would be $0$, then $(N-K-2)$ $0$s would follow, and then $K$ $1$s. Thus, comparing the two masks, we find exactly two bits that differ.
The following is a naive implementation working by generating all $2^{n}$ possible subsets, and finding subsets of size
$K$.
```{.cpp file=generate_all_combinations_naive}
int gray_code (int n) {
return n ^ (n >> 1);
}
int count_bits (int n) {
int res = 0;
for (; n; n >>= 1)
res += n & 1;
return res;
}
void all_combinations (int n, int k) {
for (int i = 0; i < (1 << n); i++) {
int cur = gray_code (i);
if (count_bits(cur) == k) {
for (int j = 0; j < n; j++) {
if (cur & (1 << j))
cout << j + 1;
}
cout << "\n";
}
}
}
```
It's worth mentioning that a more efficient implementation exists that only resorts to building valid combinations and thus
works in $O\left(N \cdot \binom{N}{K}\right)$ however it is recursive in nature and for smaller values of $N$ it probably has a larger constant
than the previous solution.
The implementation is derived from the formula:
$$G(N, K) = 0G(N-1, K) \cup 1G(N-1, K-1)^\text{R}$$
This formula is obtained by modifying the general equation to determine the Gray code, and works by selecting the
subsequence from appropriate elements.
Its implementation is as follows:
```{.cpp file=generate_all_combinations_fast}
vector<int> ans;
void gen(int n, int k, int idx, bool rev) {
if (k > n || k < 0)
return;
if (!n) {
for (int i = 0; i < idx; ++i) {
if (ans[i])
cout << i + 1;
}
cout << "\n";
return;
}
ans[idx] = rev;
gen(n - 1, k - rev, idx + 1, false);
ans[idx] = !rev;
gen(n - 1, k - !rev, idx + 1, true);
}
void all_combinations(int n, int k) {
ans.resize(n);
gen(n, k, 0, false);
}
```
|
---
title: Generating all K-combinations
title
generating_combinations
---
# Generating all $K$-combinations
In this article we will discuss the problem of generating all $K$-combinations.
Given the natural numbers $N$ and $K$, and considering a set of numbers from $1$ to $N$.
The task is to derive all **subsets of size $K$**.
## Generate next lexicographical $K$-combination {data-toc-label="Generate next lexicographical K-combination"}
First we will generate them in lexicographical order.
The algorithm for this is simple. The first combination will be ${1, 2, ..., K}$. Now let's see how
to find the combination that immediately follows this, lexicographically. To do so, we consider our
current combination, and find the rightmost element that has not yet reached its highest possible value. Once
finding this element, we increment it by $1$, and assign the lowest valid value to all subsequent
elements.
```{.cpp file=next_combination}
bool next_combination(vector<int>& a, int n) {
int k = (int)a.size();
for (int i = k - 1; i >= 0; i--) {
if (a[i] < n - k + i + 1) {
a[i]++;
for (int j = i + 1; j < k; j++)
a[j] = a[j - 1] + 1;
return true;
}
}
return false;
}
```
## Generate all $K$-combinations such that adjacent combinations differ by one element {data-toc-label="Generate all K-combinations such that adjacent combinations differ by one element"}
This time we want to generate all $K$-combinations in such
an order, that adjacent combinations differ exactly by one element.
This can be solved using the [Gray Code](../algebra/gray-code.md):
If we assign a bitmask to each subset, then by generating and iterating over these bitmasks with Gray codes, we can obtain our answer.
The task of generating $K$-combinations can also be solved using Gray Codes in a different way:
Generate Gray Codes for the numbers from $0$ to $2^N - 1$ and leave only those codes containing $K$ $1$s.
The surprising fact is that in the resulting sequence of $K$ set bits, any two neighboring masks (including the
first and last mask - neighboring in a cyclic sense) - will differ exactly by two bits, which is our objective (remove
a number, add a number).
Let us prove this:
For the proof, we recall the fact that the sequence $G(N)$ (representing the $N$<sup>th</sup> Gray Code) can
be obtained as follows:
$$G(N) = 0G(N-1) \cup 1G(N-1)^\text{R}$$
That is, consider the Gray Code sequence for $N-1$, and prefix $0$ before every term. And consider the
reversed Gray Code sequence for $N-1$ and prefix a $1$ before every mask, and
concatenate these two sequences.
Now we may produce our proof.
First, we prove that the first and last masks differ exactly in two bits. To do this, it is sufficient to note
that the first mask of the sequence $G(N)$, will be of the form $N-K$ $0$s, followed by $K$ $1$s. As
the first bit is set as $0$, after which $(N-K-1)$ $0$s follow, after which $K$ set bits follow and the last mask will be of the form $1$, then $(N-K)$ $0$s, then $K-1$ $1$s.
Applying the principle of mathematical induction, and using the formula for $G(N)$, concludes the proof.
Now our task is to show that any two adjacent codes also differ exactly in two bits, we can do this by considering our recursive equation for the generation of Gray Codes. Let us assume the content of the two halves formed by $G(N-1)$ is true. Now we need to prove that the new consecutive pair formed at the junction (by the concatenation of these two halves) is also valid, i.e. they differ by exactly two bits.
This can be done, as we know the last mask of the first half and the first mask of the second half. The last mask of the first half would be $1$, then $(N-K-1)$ $0$s, then $K-1$ $1$s. And the first mask of the second half would be $0$, then $(N-K-2)$ $0$s would follow, and then $K$ $1$s. Thus, comparing the two masks, we find exactly two bits that differ.
The following is a naive implementation working by generating all $2^{n}$ possible subsets, and finding subsets of size
$K$.
```{.cpp file=generate_all_combinations_naive}
int gray_code (int n) {
return n ^ (n >> 1);
}
int count_bits (int n) {
int res = 0;
for (; n; n >>= 1)
res += n & 1;
return res;
}
void all_combinations (int n, int k) {
for (int i = 0; i < (1 << n); i++) {
int cur = gray_code (i);
if (count_bits(cur) == k) {
for (int j = 0; j < n; j++) {
if (cur & (1 << j))
cout << j + 1;
}
cout << "\n";
}
}
}
```
It's worth mentioning that a more efficient implementation exists that only resorts to building valid combinations and thus
works in $O\left(N \cdot \binom{N}{K}\right)$ however it is recursive in nature and for smaller values of $N$ it probably has a larger constant
than the previous solution.
The implementation is derived from the formula:
$$G(N, K) = 0G(N-1, K) \cup 1G(N-1, K-1)^\text{R}$$
This formula is obtained by modifying the general equation to determine the Gray code, and works by selecting the
subsequence from appropriate elements.
Its implementation is as follows:
```{.cpp file=generate_all_combinations_fast}
vector<int> ans;
void gen(int n, int k, int idx, bool rev) {
if (k > n || k < 0)
return;
if (!n) {
for (int i = 0; i < idx; ++i) {
if (ans[i])
cout << i + 1;
}
cout << "\n";
return;
}
ans[idx] = rev;
gen(n - 1, k - rev, idx + 1, false);
ans[idx] = !rev;
gen(n - 1, k - !rev, idx + 1, true);
}
void all_combinations(int n, int k) {
ans.resize(n);
gen(n, k, 0, false);
}
```
|
Generating all $K$-combinations
|
---
title
bishops_arrangement
---
# Placing Bishops on a Chessboard
Find the number of ways to place $K$ bishops on an $N \times N$ chessboard so that no two bishops attack each other.
## Algorithm
This problem can be solved using dynamic programming.
Let's enumerate the diagonals of the chessboard as follows: black diagonals have odd indices, white diagonals have even indices, and the diagonals are numbered in non-decreasing order of the number of squares in them. Here is an example for a $5 \times 5$ chessboard.
$$\begin{matrix}
\bf{1} & 2 & \bf{5} & 6 & \bf{9} \\\
2 & \bf{5} & 6 & \bf{9} & 8 \\\
\bf{5} & 6 & \bf{9} & 8 & \bf{7} \\\
6 & \bf{9} & 8 & \bf{7} & 4 \\\
\bf{9} & 8 & \bf{7} & 4 & \bf{3} \\\
\end{matrix}$$
Let `D[i][j]` denote the number of ways to place `j` bishops on diagonals with indices up to `i` which have the same color as diagonal `i`.
Then `i = 1...2N-1` and `j = 0...K`.
We can calculate `D[i][j]` using only values of `D[i-2]` (we subtract 2 because we only consider diagonals of the same color as $i$).
There are two ways to get `D[i][j]`.
Either we place all `j` bishops on previous diagonals: then there are `D[i-2][j]` ways to achieve this.
Or we place one bishop on diagonal `i` and `j-1` bishops on previous diagonals.
The number of ways to do this equals the number of squares in diagonal `i` minus `j-1`, because each of `j-1` bishops placed on previous diagonals will block one square on the current diagonal.
The number of squares in diagonal `i` can be calculated as follows:
```cpp
int squares (int i) {
if (i & 1)
return i / 4 * 2 + 1;
else
return (i - 1) / 4 * 2 + 2;
}
```
The base case is simple: `D[i][0] = 1`, `D[1][1] = 1`.
Once we have calculated all values of `D[i][j]`, the answer can be obtained as follows:
consider all possible numbers of bishops placed on black diagonals `i=0...K`, with corresponding numbers of bishops on white diagonals `K-i`.
The bishops placed on black and white diagonals never attack each other, so the placements can be done independently.
The index of the last black diagonal is `2N-1`, the last white one is `2N-2`.
For each `i` we add `D[2N-1][i] * D[2N-2][K-i]` to the answer.
## Implementation
```cpp
int bishop_placements(int N, int K)
{
if (K > 2 * N - 1)
return 0;
vector<vector<int>> D(N * 2, vector<int>(K + 1));
for (int i = 0; i < N * 2; ++i)
D[i][0] = 1;
D[1][1] = 1;
for (int i = 2; i < N * 2; ++i)
for (int j = 1; j <= K; ++j)
D[i][j] = D[i-2][j] + D[i-2][j-1] * (squares(i) - j + 1);
int ans = 0;
for (int i = 0; i <= K; ++i)
ans += D[N*2-1][i] * D[N*2-2][K-i];
return ans;
}
```
|
---
title
bishops_arrangement
---
# Placing Bishops on a Chessboard
Find the number of ways to place $K$ bishops on an $N \times N$ chessboard so that no two bishops attack each other.
## Algorithm
This problem can be solved using dynamic programming.
Let's enumerate the diagonals of the chessboard as follows: black diagonals have odd indices, white diagonals have even indices, and the diagonals are numbered in non-decreasing order of the number of squares in them. Here is an example for a $5 \times 5$ chessboard.
$$\begin{matrix}
\bf{1} & 2 & \bf{5} & 6 & \bf{9} \\\
2 & \bf{5} & 6 & \bf{9} & 8 \\\
\bf{5} & 6 & \bf{9} & 8 & \bf{7} \\\
6 & \bf{9} & 8 & \bf{7} & 4 \\\
\bf{9} & 8 & \bf{7} & 4 & \bf{3} \\\
\end{matrix}$$
Let `D[i][j]` denote the number of ways to place `j` bishops on diagonals with indices up to `i` which have the same color as diagonal `i`.
Then `i = 1...2N-1` and `j = 0...K`.
We can calculate `D[i][j]` using only values of `D[i-2]` (we subtract 2 because we only consider diagonals of the same color as $i$).
There are two ways to get `D[i][j]`.
Either we place all `j` bishops on previous diagonals: then there are `D[i-2][j]` ways to achieve this.
Or we place one bishop on diagonal `i` and `j-1` bishops on previous diagonals.
The number of ways to do this equals the number of squares in diagonal `i` minus `j-1`, because each of `j-1` bishops placed on previous diagonals will block one square on the current diagonal.
The number of squares in diagonal `i` can be calculated as follows:
```cpp
int squares (int i) {
if (i & 1)
return i / 4 * 2 + 1;
else
return (i - 1) / 4 * 2 + 2;
}
```
The base case is simple: `D[i][0] = 1`, `D[1][1] = 1`.
Once we have calculated all values of `D[i][j]`, the answer can be obtained as follows:
consider all possible numbers of bishops placed on black diagonals `i=0...K`, with corresponding numbers of bishops on white diagonals `K-i`.
The bishops placed on black and white diagonals never attack each other, so the placements can be done independently.
The index of the last black diagonal is `2N-1`, the last white one is `2N-2`.
For each `i` we add `D[2N-1][i] * D[2N-2][K-i]` to the answer.
## Implementation
```cpp
int bishop_placements(int N, int K)
{
if (K > 2 * N - 1)
return 0;
vector<vector<int>> D(N * 2, vector<int>(K + 1));
for (int i = 0; i < N * 2; ++i)
D[i][0] = 1;
D[1][1] = 1;
for (int i = 2; i < N * 2; ++i)
for (int j = 1; j <= K; ++j)
D[i][j] = D[i-2][j] + D[i-2][j-1] * (squares(i) - j + 1);
int ans = 0;
for (int i = 0; i <= K; ++i)
ans += D[N*2-1][i] * D[N*2-2][K-i];
return ans;
}
```
|
Placing Bishops on a Chessboard
|
---
title
catalan_numbers
---
# Catalan Numbers
Catalan numbers is a number sequence, which is found useful in a number of combinatorial problems, often involving recursively-defined objects.
This sequence was named after the Belgian mathematician [Catalan](https://en.wikipedia.org/wiki/Eug%C3%A8ne_Charles_Catalan), who lived in the 19th century. (In fact it was known before to Euler, who lived a century before Catalan).
The first few Catalan numbers $C_n$ (starting from zero):
$1, 1, 2, 5, 14, 42, 132, 429, 1430, \ldots$
### Application in some combinatorial problems
The Catalan number $C_n$ is the solution for
- Number of correct bracket sequence consisting of $n$ opening and $n$ closing brackets.
- The number of rooted full binary trees with $n + 1$ leaves (vertices are not numbered). A rooted binary tree is full if every vertex has either two children or no children.
- The number of ways to completely parenthesize $n + 1$ factors.
- The number of triangulations of a convex polygon with $n + 2$ sides (i.e. the number of partitions of polygon into disjoint triangles by using the diagonals).
- The number of ways to connect the $2n$ points on a circle to form $n$ disjoint chords.
- The number of [non-isomorphic](https://en.wikipedia.org/wiki/Graph_isomorphism) full binary trees with $n$ internal nodes (i.e. nodes having at least one son).
- The number of monotonic lattice paths from point $(0, 0)$ to point $(n, n)$ in a square lattice of size $n \times n$, which do not pass above the main diagonal (i.e. connecting $(0, 0)$ to $(n, n)$).
- Number of permutations of length $n$ that can be [stack sorted](https://en.wikipedia.org/wiki/Stack-sortable_permutation) (i.e. it can be shown that the rearrangement is stack sorted if and only if there is no such index $i < j < k$, such that $a_k < a_i < a_j$ ).
- The number of [non-crossing partitions](https://en.wikipedia.org/wiki/Noncrossing_partition) of a set of $n$ elements.
- The number of ways to cover the ladder $1 \ldots n$ using $n$ rectangles (The ladder consists of $n$ columns, where $i^{th}$ column has a height $i$).
## Calculations
There are two formulas for the Catalan numbers: **Recursive and Analytical**. Since, we believe that all the mentioned above problems are equivalent (have the same solution), for the proof of the formulas below we will choose the task which it is easiest to do.
### Recursive formula
$$C_0 = C_1 = 1$$
$$C_n = \sum_{k = 0}^{n-1} C_k C_{n-1-k} , {n} \geq 2$$
The recurrence formula can be easily deduced from the problem of the correct bracket sequence.
The leftmost opening parenthesis $l$ corresponds to certain closing bracket $r$, which divides the sequence into 2 parts which in turn should be a correct sequence of brackets. Thus formula is also divided into 2 parts. If we denote $k = {r - l - 1}$, then for fixed $r$, there will be exactly $C_k C_{n-1-k}$ such bracket sequences. Summing this over all admissible $k's$, we get the recurrence relation on $C_n$.
You can also think it in this manner. By definition, $C_n$ denotes number of correct bracket sequences. Now, the sequence may be divided into 2 parts of length $k$ and ${n - k}$, each of which should be a correct bracket sequence. Example :
$( ) ( ( ) )$ can be divided into $( )$ and $( ( ) )$, but cannot be divided into $( ) ($ and $( ) )$. Again summing over all admissible $k's$, we get the recurrence relation on $C_n$.
#### C++ implementation
```cpp
const int MOD = ....
const int MAX = ....
int catalan[MAX];
void init() {
catalan[0] = catalan[1] = 1;
for (int i=2; i<=n; i++) {
catalan[i] = 0;
for (int j=0; j < i; j++) {
catalan[i] += (catalan[j] * catalan[i-j-1]) % MOD;
if (catalan[i] >= MOD) {
catalan[i] -= MOD;
}
}
}
}
```
### Analytical formula
$$C_n = \frac{1}{n + 1} {\binom{2n}{n}}$$
(here $\binom{n}{k}$ denotes the usual binomial coefficient, i.e. number of ways to select $k$ objects from set of $n$ objects).
The above formula can be easily concluded from the problem of the monotonic paths in square grid. The total number of monotonic paths in the lattice size of $n \times n$ is given by $\binom{2n}{n}$.
Now we count the number of monotonic paths which cross the main diagonal. Consider such paths crossing the main diagonal and find the first edge in it which is above the diagonal. Reflect the path about the diagonal all the way, going after this edge. The result is always a monotonic path in the grid $(n - 1) \times (n + 1)$. On the other hand, any monotonic path in the lattice $(n - 1) \times (n + 1)$ must intersect the diagonal. Hence, we enumerated all monotonic paths crossing the main diagonal in the lattice $n \times n$.
The number of monotonic paths in the lattice $(n - 1) \times (n + 1)$ are $\binom{2n}{n-1}$ . Let us call such paths as "bad" paths. As a result, to obtain the number of monotonic paths which do not cross the main diagonal, we subtract the above "bad" paths, obtaining the formula:
$$C_n = \binom{2n}{n} - \binom{2n}{n-1} = \frac{1}{n + 1} \binom{2n}{n} , {n} \geq 0$$
## Reference
- [Catalan Number by Tom Davis](http://www.geometer.org/mathcircles/catalan.pdf)
|
---
title
catalan_numbers
---
# Catalan Numbers
Catalan numbers is a number sequence, which is found useful in a number of combinatorial problems, often involving recursively-defined objects.
This sequence was named after the Belgian mathematician [Catalan](https://en.wikipedia.org/wiki/Eug%C3%A8ne_Charles_Catalan), who lived in the 19th century. (In fact it was known before to Euler, who lived a century before Catalan).
The first few Catalan numbers $C_n$ (starting from zero):
$1, 1, 2, 5, 14, 42, 132, 429, 1430, \ldots$
### Application in some combinatorial problems
The Catalan number $C_n$ is the solution for
- Number of correct bracket sequence consisting of $n$ opening and $n$ closing brackets.
- The number of rooted full binary trees with $n + 1$ leaves (vertices are not numbered). A rooted binary tree is full if every vertex has either two children or no children.
- The number of ways to completely parenthesize $n + 1$ factors.
- The number of triangulations of a convex polygon with $n + 2$ sides (i.e. the number of partitions of polygon into disjoint triangles by using the diagonals).
- The number of ways to connect the $2n$ points on a circle to form $n$ disjoint chords.
- The number of [non-isomorphic](https://en.wikipedia.org/wiki/Graph_isomorphism) full binary trees with $n$ internal nodes (i.e. nodes having at least one son).
- The number of monotonic lattice paths from point $(0, 0)$ to point $(n, n)$ in a square lattice of size $n \times n$, which do not pass above the main diagonal (i.e. connecting $(0, 0)$ to $(n, n)$).
- Number of permutations of length $n$ that can be [stack sorted](https://en.wikipedia.org/wiki/Stack-sortable_permutation) (i.e. it can be shown that the rearrangement is stack sorted if and only if there is no such index $i < j < k$, such that $a_k < a_i < a_j$ ).
- The number of [non-crossing partitions](https://en.wikipedia.org/wiki/Noncrossing_partition) of a set of $n$ elements.
- The number of ways to cover the ladder $1 \ldots n$ using $n$ rectangles (The ladder consists of $n$ columns, where $i^{th}$ column has a height $i$).
## Calculations
There are two formulas for the Catalan numbers: **Recursive and Analytical**. Since, we believe that all the mentioned above problems are equivalent (have the same solution), for the proof of the formulas below we will choose the task which it is easiest to do.
### Recursive formula
$$C_0 = C_1 = 1$$
$$C_n = \sum_{k = 0}^{n-1} C_k C_{n-1-k} , {n} \geq 2$$
The recurrence formula can be easily deduced from the problem of the correct bracket sequence.
The leftmost opening parenthesis $l$ corresponds to certain closing bracket $r$, which divides the sequence into 2 parts which in turn should be a correct sequence of brackets. Thus formula is also divided into 2 parts. If we denote $k = {r - l - 1}$, then for fixed $r$, there will be exactly $C_k C_{n-1-k}$ such bracket sequences. Summing this over all admissible $k's$, we get the recurrence relation on $C_n$.
You can also think it in this manner. By definition, $C_n$ denotes number of correct bracket sequences. Now, the sequence may be divided into 2 parts of length $k$ and ${n - k}$, each of which should be a correct bracket sequence. Example :
$( ) ( ( ) )$ can be divided into $( )$ and $( ( ) )$, but cannot be divided into $( ) ($ and $( ) )$. Again summing over all admissible $k's$, we get the recurrence relation on $C_n$.
#### C++ implementation
```cpp
const int MOD = ....
const int MAX = ....
int catalan[MAX];
void init() {
catalan[0] = catalan[1] = 1;
for (int i=2; i<=n; i++) {
catalan[i] = 0;
for (int j=0; j < i; j++) {
catalan[i] += (catalan[j] * catalan[i-j-1]) % MOD;
if (catalan[i] >= MOD) {
catalan[i] -= MOD;
}
}
}
}
```
### Analytical formula
$$C_n = \frac{1}{n + 1} {\binom{2n}{n}}$$
(here $\binom{n}{k}$ denotes the usual binomial coefficient, i.e. number of ways to select $k$ objects from set of $n$ objects).
The above formula can be easily concluded from the problem of the monotonic paths in square grid. The total number of monotonic paths in the lattice size of $n \times n$ is given by $\binom{2n}{n}$.
Now we count the number of monotonic paths which cross the main diagonal. Consider such paths crossing the main diagonal and find the first edge in it which is above the diagonal. Reflect the path about the diagonal all the way, going after this edge. The result is always a monotonic path in the grid $(n - 1) \times (n + 1)$. On the other hand, any monotonic path in the lattice $(n - 1) \times (n + 1)$ must intersect the diagonal. Hence, we enumerated all monotonic paths crossing the main diagonal in the lattice $n \times n$.
The number of monotonic paths in the lattice $(n - 1) \times (n + 1)$ are $\binom{2n}{n-1}$ . Let us call such paths as "bad" paths. As a result, to obtain the number of monotonic paths which do not cross the main diagonal, we subtract the above "bad" paths, obtaining the formula:
$$C_n = \binom{2n}{n} - \binom{2n}{n-1} = \frac{1}{n + 1} \binom{2n}{n} , {n} \geq 0$$
## Reference
- [Catalan Number by Tom Davis](http://www.geometer.org/mathcircles/catalan.pdf)
## Practice Problems
- [Codechef - PANSTACK](https://www.codechef.com/APRIL12/problems/PANSTACK/)
- [Spoj - Skyline](http://www.spoj.com/problems/SKYLINE/)
- [UVA - Safe Salutations](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=932)
- [Codeforces - How many trees?](http://codeforces.com/problemset/problem/9/D)
- [SPOJ - FUNPROB](http://www.spoj.com/problems/FUNPROB/)
* [LOJ - 1170 - Counting Perfect BST](http://lightoj.com/volume_showproblem.php?problem=1170)
* [UVA - 12887 - The Soldier's Dilemma](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=4752)
|
Catalan Numbers
|
---
title
burnside_polya
---
# Burnside's lemma / Pólya enumeration theorem
## Burnside's lemma
**Burnside's lemma** was formulated and proven by **Burnside** in 1897, but historically it was already discovered in 1887 by **Frobenius**, and even earlier in 1845 by **Cauchy**.
Therefore it is also sometimes named the **Cauchy-Frobenius lemma**.
Burnside's lemma allows us to count the number of equivalence classes in sets, based on internal symmetry.
### Objects and representations
We have to clearly distinguish between the number of objects and the number of representations.
Different representations can correspond to the same objects, but of course any representation corresponds to exactly one object.
Consequently the set of all representations is divided into equivalence classes.
Our task is to compute the number of objects, or equivalently, the number of equivalence classes.
The following example will make the difference between object and representation clearer.
### Example: coloring of binary trees
Suppose we have the following problem.
We have to count the number of ways to color a rooted binary tree with $n$ vertices with two colors, where at each vertex we do not distinguish between the left and the right children.
Here the set of objects is the set of different colorings of the tree.
We now define the set of representations.
A representation of a coloring is a function $f(v)$, which assigns each vertex a color (here we use the colors $0$ and $1$).
The set of representations is the set containing all possible functions of this kind, and its size is obviously equal to $2^n$.
At the same time we introduce a partition of this set into equivalence classes.
For example, suppose $n = 3$, and the tree consists of the root $1$ and its two children $2$ and $3$.
Then the following functions $f_1$ and $f_2$ are considered equivalent.
$$\begin{array}{ll}
f_1(1) = 0 & f_2(1) = 0\\
f_1(2) = 1 & f_2(2) = 0\\
f_1(3) = 0 & f_2(3) = 1
\end{array}$$
### Invariant permutations
Why do these two function $f_1$ and $f_2$ belong to the same equivalence class?
Intuitively this is understandable - we can rearrange the children of vertex $1$, the vertices $2$ and $3$, and after such a transformation of the function $f_1$ it will coincide with $f_2$.
But formally this means that there exists an **invariant permutation** $\pi$ (i.e. a permutation which does not change the object itself, but only its representation), such that:
$$f_2 \pi \equiv f_1$$
So starting from the definition of objects, we can find all the invariant permutations, i.e. all permutations which do not change the object when applying the permutation to the representation.
Then we can check whether two functions $f_1$ and $f_2$ are equivalent (i.e. if they correspond to the same object) by checking the condition $f_2 \pi \equiv f_1$ for each invariant permutation (or equivalently $f_1 \pi \equiv f_2$).
If at least one permutation is found for which the condition is satisfied, then $f_1$ and $f_2$ are equivalent, otherwise they are not equivalent.
Finding all such invariant permutations with respect to the object definition is a key step for the application of both Burnside's lemma and the Pólya enumeration theorem.
It is clear that these invariant permutations depend on the specific problem, and their finding is a purely heuristic process based on intuitive considerations.
However in most cases it is sufficient to manually find several "basic" permutations, with which all other permutations can be generated (and this part of the work can be shifted to a computer).
It is not difficult to understand that invariant permutations form a **group**, since the product (composition) of invariant permutations is again an invariant permutation.
We denote the **group of invariant permutations** by $G$.
### The statement of the lemma
For the formulation of the lemma we need one more definition from algebra.
A **fixed point** $f$ for a permutation $\pi$ is an element that is invariant under this permutation: $f \equiv f \pi$.
For example in our example the fixed points are those functions $f$, which correspond to colorings that do not change when the permutation $\pi$ is applied to them (i.e. they do not change in the formal sense of the equality of functions).
We denote by $I(\pi)$ the **number of fixed points** for the permutation $\pi$.
Then **Burnside's lemma** goes as follows:
the number of equivalence classes is equal to the sum of the numbers of fixed points with respect to all permutations from the group $G$, divided by the size of this group:
$$|\text{Classes}| = \frac{1}{|G|} \sum_{\pi \in G} I(\pi)$$
Although Burnside's lemma itself is not so convenient to use in practice (it is unclear how to quickly look for the value $I(\pi)$, it most clearly reveals the mathematical essence on which the idea of calculating equivalence classes is based.
### Proof of Burnside's lemma
The proof of Burnside's lemma described here is not important for the practical applications, so it can be skipped on the first reading.
The proof here is the simplest known, and does not use group theory.
The proof was published by Kenneth P. Bogart in 1991.
We need to prove the following statement:
$$|\text{Classes}| \cdot |G| = \sum_{\pi \in G} I(\pi)$$
The value on the right side is nothing more than the number of "invariant pairs" $(f, \pi)$, i.e. pairs such that $f \pi \equiv f$.
It is obvious that we can change the order of summation.
We let the sum iterate over all elements $f$ and sum over the values $J(f)$ - the number of permutations for which $f$ is a fixed point.
$$|\text{Classes}| \cdot |G| = \sum_{f} J(f)$$
To prove this formula we will compose a table with columns labeled with all functions $f_i$ and rows labeled with all permutations $\pi_j$.
And we fill the cells with $f_i \pi_j$.
If we look at the columns in this table as sets, then some of them will coincide, and this means that the corresponding functions $f$ for these columns are also equivalent.
Thus the numbers of different (as sets) columns is equal to the number of classes.
Incidentally, from the standpoint of group theory, the column labeled with $f_i$ is the orbit of this element.
For equivalent elements the orbits coincides, and the number of orbits gives exactly the number of classes.
Thus the columns of the table decompose into equivalence classes.
Let us fix a class, and look at the columns in it.
First, note that these columns can only contain elements $f_i$ of the equivalence class (otherwise some permutation $\pi_j$ moved one of the functions into a different equivalence class, which is impossible since we only look at invariant permutations).
Secondly each element $f_i$ will occur the same number of times in each column (this also follows from the fact that the columns correspond to equivalent elements).
From this we can conclude, that all the columns within the same equivalence class coincide with each other as multisets.
Now fix an arbitrary element $f$.
On the one hand, it occurs in its column exactly $J(f)$ times (by definition).
On the other hand, all columns within the same equivalence class are the same as multisets.
Therefore within each column of a given equivalence class any element $g$ occurs exactly $J(g)$ times.
Thus if we arbitrarily take one column from each equivalence class, and sum the number of elements in them, we obtain on one hand $|\text{Classes}| \cdot |G|$ (simply by multiplying the number of columns by the number of rows), and on the other hand the sum of the quantities $J(f)$ for all $f$ (this follows from all the previous arguments):
$$|\text{Classes}| \cdot |G| = \sum_{f} J(f)$$
## Pólya enumeration theorem
The Pólya enumeration theorem is a generalization of Burnside's lemma, and it also provides a more convenient tool for finding the number of equivalence classes.
It should be noted that this theorem was already discovered before Pólya by Redfield in 1927, but his publication went unnoticed by mathematicians.
Pólya independently came to the same results in 1937, and his publication was more successful.
Here we discuss only a special case of the Pólya enumeration theorem, which will turn out very useful in practice.
The general formula of the theorem will not be discussed.
We denote by $C(\pi)$ the number of cycles in the permutation $\pi$.
Then the following formula (a **special case of the Pólya enumeration theorem**) holds:
$$|\text{Classes}| = \frac{1}{|G|} \sum_{\pi \in G} k^{C(\pi)}$$
$k$ is the number of values that each representation element can take, in the case of the coloring of a binary tree this would be $k = 2$.
### Evidence
This formula is a direct consequence of Burnside's lemma.
To get it, we just need to find an explicit expression for $I(\pi)$, which appears in the lemma.
Recall, that $I(\pi)$ is the number of fixed points in the permutation $\pi$.
Thus we consider a permutation $\pi$ and some element $f$.
During the application of $\pi$, the elements in $f$ move via the cycles in the permutation.
Since the result should obtain $f \equiv f \pi$, the elements touched by one cycle must all be equal.
At the same time different cycles are independent.
Thus for each permutation cycle $\pi$ we can choose one value (among $k$ possible) and thus we get the number of fixed points:
$$I(\pi) = k^{C(\pi)}$$
## Application: Coloring necklaces
The problem "Necklace" is one of the classical combinatorial problems.
The task is to count the number of different necklaces from $n$ beads, each of which can be painted in one of the $k$ colors.
When comparing two necklaces, they can be rotated, but not reversed (i.e. a cyclic shift is permitted).
In this problem we can immediately find the group of invariant permutations:
$$\begin{align}
\pi_0 &= 1 2 3 \dots n\\
\pi_1 &= 2 3 \dots n 1\\
\pi_2 &= 3 \dots n 12\\
&\dots\\
\pi_{n-1} &= n 1 2 3\dots\end{align}$$
Let us find an explicit formula for calculating $C(\pi_i)$.
First we note, that the permutation $\pi_i$ has at the $j$-th position the value $i + j$ (taken modulo $n$).
If we check the cycle structure for $\pi_i$.
We see that $1$ goes to $1 + i$, $1 + i$ goes to $1 + 2i$, which goes to $1 + 3i$, etc., until we come to a number of the form $1 + k n$.
Similar statements can be made for the remaining elements.
Hence we see that all cycles have the same length, namely $\frac{\text{lcm}(i, n)}{i} = \frac{n}{\gcd(i, n)}$.
Thus the number of cycles in $\pi_i$ will be equal to $\gcd(i, n)$.
Substituting these values into the Pólya enumeration theorem, we obtain the solution:
$$\frac{1}{n} \sum_{i=1}^n k^{\gcd(i, n)}$$
You can leave this formula in this form, or you can simplify it even more.
Let transfer the sum so that it iterates over all divisors of $n$.
In the original sum there will be many equivalent terms: if $i$ is not a divisor of $n$, then such a divisor can be found after computing $\gcd(i, n)$.
Therefore for each divisor $d ~|~ n$ its term $k^{\gcd(d, n)} = k^d$ will appear in the sum multiple times, i.e. the answer to the problem can be rewritten as
$$\frac{1}{n} \sum_{d ~|~ n} C_d k^d,$$
where $C_d$ is the number of such numbers $i$ with $\gcd(i, n) = d$.
We can find an explicit expression for this value.
Any such number $i$ has the form $i = d j$ with $\gcd(j, n / d) = 1$ (otherwise $\gcd(i, n) > d$).
So we can count the number of $j$ with this behavior.
[Euler's phi function](../algebra/phi-function.md) gives us the result $C_d = \phi(n / d)$, and therefore we get the answer:
$$\frac{1}{n} \sum_{d ~|~ n} \phi\left(\frac{n}{d}\right) k^d$$
## Application: Coloring a torus
Quite often we cannot obtain an explicit formula for the number of equivalence classes.
In many problems the number of permutations in a group can be too large for manual calculations and it is not possible to compute analytically the number of cycles in them.
In that case we should manually find several "basic" permutations, so that they can generate the entire group $G$.
Next we can write a program that will generate all permutations of the group $G$, count the number of cycles in them, and compute the answer with the formula.
Consider the example of the problem for coloring a torus.
There is a checkered sheet of paper $n \times m$ ($n < m$), some of the cells are black.
Then a cylinder is obtained from this sheet by gluing together the two sides with lengths $m$.
Then a torus is obtained from the cylinder by gluing together the two circles (top and bottom) without twisting.
The task is to compute the number of different colored tori, assuming that we cannot see the glued lines, and the torus can be turned and turned.
We again start with a piece of $n \times m$ paper.
It is easy to see that the following types of transformations preserve the equivalence class:
a cyclic shift of the rows, a cyclic shift of the columns, and a rotation of the sheet by 180 degrees.
It is also easy to see, that these transformations can generate the entire group of invariant transformations.
If we somehow number the cells of the paper, then we can write three permutations $p_1$, $p_2$, $p_3$ corresponding to these types of transformation.
Next it only remains to generate all permutations obtained as a product.
It is obvious that all such permutations have the form $p_1^{i_1} p_2^{i_2} p_3^{i_3}$ where $i_1 = 0 \dots m-1$, $i_2 = 0 \dots n-1$, $i_3 = 0 \dots 1$.
Thus we can write the implementations to this problem.
```{.cpp file=burnside_tori}
using Permutation = vector<int>;
void operator*=(Permutation& p, Permutation const& q) {
Permutation copy = p;
for (int i = 0; i < p.size(); i++)
p[i] = copy[q[i]];
}
int count_cycles(Permutation p) {
int cnt = 0;
for (int i = 0; i < p.size(); i++) {
if (p[i] != -1) {
cnt++;
for (int j = i; p[j] != -1;) {
int next = p[j];
p[j] = -1;
j = next;
}
}
}
return cnt;
}
int solve(int n, int m) {
Permutation p(n*m), p1(n*m), p2(n*m), p3(n*m);
for (int i = 0; i < n*m; i++) {
p[i] = i;
p1[i] = (i % n + 1) % n + i / n * n;
p2[i] = (i / n + 1) % m * n + i % n;
p3[i] = (m - 1 - i / n) * n + (n - 1 - i % n);
}
set<Permutation> s;
for (int i1 = 0; i1 < n; i1++) {
for (int i2 = 0; i2 < m; i2++) {
for (int i3 = 0; i3 < 2; i3++) {
s.insert(p);
p *= p3;
}
p *= p2;
}
p *= p1;
}
int sum = 0;
for (Permutation const& p : s) {
sum += 1 << count_cycles(p);
}
return sum / s.size();
}
```
|
---
title
burnside_polya
---
# Burnside's lemma / Pólya enumeration theorem
## Burnside's lemma
**Burnside's lemma** was formulated and proven by **Burnside** in 1897, but historically it was already discovered in 1887 by **Frobenius**, and even earlier in 1845 by **Cauchy**.
Therefore it is also sometimes named the **Cauchy-Frobenius lemma**.
Burnside's lemma allows us to count the number of equivalence classes in sets, based on internal symmetry.
### Objects and representations
We have to clearly distinguish between the number of objects and the number of representations.
Different representations can correspond to the same objects, but of course any representation corresponds to exactly one object.
Consequently the set of all representations is divided into equivalence classes.
Our task is to compute the number of objects, or equivalently, the number of equivalence classes.
The following example will make the difference between object and representation clearer.
### Example: coloring of binary trees
Suppose we have the following problem.
We have to count the number of ways to color a rooted binary tree with $n$ vertices with two colors, where at each vertex we do not distinguish between the left and the right children.
Here the set of objects is the set of different colorings of the tree.
We now define the set of representations.
A representation of a coloring is a function $f(v)$, which assigns each vertex a color (here we use the colors $0$ and $1$).
The set of representations is the set containing all possible functions of this kind, and its size is obviously equal to $2^n$.
At the same time we introduce a partition of this set into equivalence classes.
For example, suppose $n = 3$, and the tree consists of the root $1$ and its two children $2$ and $3$.
Then the following functions $f_1$ and $f_2$ are considered equivalent.
$$\begin{array}{ll}
f_1(1) = 0 & f_2(1) = 0\\
f_1(2) = 1 & f_2(2) = 0\\
f_1(3) = 0 & f_2(3) = 1
\end{array}$$
### Invariant permutations
Why do these two function $f_1$ and $f_2$ belong to the same equivalence class?
Intuitively this is understandable - we can rearrange the children of vertex $1$, the vertices $2$ and $3$, and after such a transformation of the function $f_1$ it will coincide with $f_2$.
But formally this means that there exists an **invariant permutation** $\pi$ (i.e. a permutation which does not change the object itself, but only its representation), such that:
$$f_2 \pi \equiv f_1$$
So starting from the definition of objects, we can find all the invariant permutations, i.e. all permutations which do not change the object when applying the permutation to the representation.
Then we can check whether two functions $f_1$ and $f_2$ are equivalent (i.e. if they correspond to the same object) by checking the condition $f_2 \pi \equiv f_1$ for each invariant permutation (or equivalently $f_1 \pi \equiv f_2$).
If at least one permutation is found for which the condition is satisfied, then $f_1$ and $f_2$ are equivalent, otherwise they are not equivalent.
Finding all such invariant permutations with respect to the object definition is a key step for the application of both Burnside's lemma and the Pólya enumeration theorem.
It is clear that these invariant permutations depend on the specific problem, and their finding is a purely heuristic process based on intuitive considerations.
However in most cases it is sufficient to manually find several "basic" permutations, with which all other permutations can be generated (and this part of the work can be shifted to a computer).
It is not difficult to understand that invariant permutations form a **group**, since the product (composition) of invariant permutations is again an invariant permutation.
We denote the **group of invariant permutations** by $G$.
### The statement of the lemma
For the formulation of the lemma we need one more definition from algebra.
A **fixed point** $f$ for a permutation $\pi$ is an element that is invariant under this permutation: $f \equiv f \pi$.
For example in our example the fixed points are those functions $f$, which correspond to colorings that do not change when the permutation $\pi$ is applied to them (i.e. they do not change in the formal sense of the equality of functions).
We denote by $I(\pi)$ the **number of fixed points** for the permutation $\pi$.
Then **Burnside's lemma** goes as follows:
the number of equivalence classes is equal to the sum of the numbers of fixed points with respect to all permutations from the group $G$, divided by the size of this group:
$$|\text{Classes}| = \frac{1}{|G|} \sum_{\pi \in G} I(\pi)$$
Although Burnside's lemma itself is not so convenient to use in practice (it is unclear how to quickly look for the value $I(\pi)$, it most clearly reveals the mathematical essence on which the idea of calculating equivalence classes is based.
### Proof of Burnside's lemma
The proof of Burnside's lemma described here is not important for the practical applications, so it can be skipped on the first reading.
The proof here is the simplest known, and does not use group theory.
The proof was published by Kenneth P. Bogart in 1991.
We need to prove the following statement:
$$|\text{Classes}| \cdot |G| = \sum_{\pi \in G} I(\pi)$$
The value on the right side is nothing more than the number of "invariant pairs" $(f, \pi)$, i.e. pairs such that $f \pi \equiv f$.
It is obvious that we can change the order of summation.
We let the sum iterate over all elements $f$ and sum over the values $J(f)$ - the number of permutations for which $f$ is a fixed point.
$$|\text{Classes}| \cdot |G| = \sum_{f} J(f)$$
To prove this formula we will compose a table with columns labeled with all functions $f_i$ and rows labeled with all permutations $\pi_j$.
And we fill the cells with $f_i \pi_j$.
If we look at the columns in this table as sets, then some of them will coincide, and this means that the corresponding functions $f$ for these columns are also equivalent.
Thus the numbers of different (as sets) columns is equal to the number of classes.
Incidentally, from the standpoint of group theory, the column labeled with $f_i$ is the orbit of this element.
For equivalent elements the orbits coincides, and the number of orbits gives exactly the number of classes.
Thus the columns of the table decompose into equivalence classes.
Let us fix a class, and look at the columns in it.
First, note that these columns can only contain elements $f_i$ of the equivalence class (otherwise some permutation $\pi_j$ moved one of the functions into a different equivalence class, which is impossible since we only look at invariant permutations).
Secondly each element $f_i$ will occur the same number of times in each column (this also follows from the fact that the columns correspond to equivalent elements).
From this we can conclude, that all the columns within the same equivalence class coincide with each other as multisets.
Now fix an arbitrary element $f$.
On the one hand, it occurs in its column exactly $J(f)$ times (by definition).
On the other hand, all columns within the same equivalence class are the same as multisets.
Therefore within each column of a given equivalence class any element $g$ occurs exactly $J(g)$ times.
Thus if we arbitrarily take one column from each equivalence class, and sum the number of elements in them, we obtain on one hand $|\text{Classes}| \cdot |G|$ (simply by multiplying the number of columns by the number of rows), and on the other hand the sum of the quantities $J(f)$ for all $f$ (this follows from all the previous arguments):
$$|\text{Classes}| \cdot |G| = \sum_{f} J(f)$$
## Pólya enumeration theorem
The Pólya enumeration theorem is a generalization of Burnside's lemma, and it also provides a more convenient tool for finding the number of equivalence classes.
It should be noted that this theorem was already discovered before Pólya by Redfield in 1927, but his publication went unnoticed by mathematicians.
Pólya independently came to the same results in 1937, and his publication was more successful.
Here we discuss only a special case of the Pólya enumeration theorem, which will turn out very useful in practice.
The general formula of the theorem will not be discussed.
We denote by $C(\pi)$ the number of cycles in the permutation $\pi$.
Then the following formula (a **special case of the Pólya enumeration theorem**) holds:
$$|\text{Classes}| = \frac{1}{|G|} \sum_{\pi \in G} k^{C(\pi)}$$
$k$ is the number of values that each representation element can take, in the case of the coloring of a binary tree this would be $k = 2$.
### Evidence
This formula is a direct consequence of Burnside's lemma.
To get it, we just need to find an explicit expression for $I(\pi)$, which appears in the lemma.
Recall, that $I(\pi)$ is the number of fixed points in the permutation $\pi$.
Thus we consider a permutation $\pi$ and some element $f$.
During the application of $\pi$, the elements in $f$ move via the cycles in the permutation.
Since the result should obtain $f \equiv f \pi$, the elements touched by one cycle must all be equal.
At the same time different cycles are independent.
Thus for each permutation cycle $\pi$ we can choose one value (among $k$ possible) and thus we get the number of fixed points:
$$I(\pi) = k^{C(\pi)}$$
## Application: Coloring necklaces
The problem "Necklace" is one of the classical combinatorial problems.
The task is to count the number of different necklaces from $n$ beads, each of which can be painted in one of the $k$ colors.
When comparing two necklaces, they can be rotated, but not reversed (i.e. a cyclic shift is permitted).
In this problem we can immediately find the group of invariant permutations:
$$\begin{align}
\pi_0 &= 1 2 3 \dots n\\
\pi_1 &= 2 3 \dots n 1\\
\pi_2 &= 3 \dots n 12\\
&\dots\\
\pi_{n-1} &= n 1 2 3\dots\end{align}$$
Let us find an explicit formula for calculating $C(\pi_i)$.
First we note, that the permutation $\pi_i$ has at the $j$-th position the value $i + j$ (taken modulo $n$).
If we check the cycle structure for $\pi_i$.
We see that $1$ goes to $1 + i$, $1 + i$ goes to $1 + 2i$, which goes to $1 + 3i$, etc., until we come to a number of the form $1 + k n$.
Similar statements can be made for the remaining elements.
Hence we see that all cycles have the same length, namely $\frac{\text{lcm}(i, n)}{i} = \frac{n}{\gcd(i, n)}$.
Thus the number of cycles in $\pi_i$ will be equal to $\gcd(i, n)$.
Substituting these values into the Pólya enumeration theorem, we obtain the solution:
$$\frac{1}{n} \sum_{i=1}^n k^{\gcd(i, n)}$$
You can leave this formula in this form, or you can simplify it even more.
Let transfer the sum so that it iterates over all divisors of $n$.
In the original sum there will be many equivalent terms: if $i$ is not a divisor of $n$, then such a divisor can be found after computing $\gcd(i, n)$.
Therefore for each divisor $d ~|~ n$ its term $k^{\gcd(d, n)} = k^d$ will appear in the sum multiple times, i.e. the answer to the problem can be rewritten as
$$\frac{1}{n} \sum_{d ~|~ n} C_d k^d,$$
where $C_d$ is the number of such numbers $i$ with $\gcd(i, n) = d$.
We can find an explicit expression for this value.
Any such number $i$ has the form $i = d j$ with $\gcd(j, n / d) = 1$ (otherwise $\gcd(i, n) > d$).
So we can count the number of $j$ with this behavior.
[Euler's phi function](../algebra/phi-function.md) gives us the result $C_d = \phi(n / d)$, and therefore we get the answer:
$$\frac{1}{n} \sum_{d ~|~ n} \phi\left(\frac{n}{d}\right) k^d$$
## Application: Coloring a torus
Quite often we cannot obtain an explicit formula for the number of equivalence classes.
In many problems the number of permutations in a group can be too large for manual calculations and it is not possible to compute analytically the number of cycles in them.
In that case we should manually find several "basic" permutations, so that they can generate the entire group $G$.
Next we can write a program that will generate all permutations of the group $G$, count the number of cycles in them, and compute the answer with the formula.
Consider the example of the problem for coloring a torus.
There is a checkered sheet of paper $n \times m$ ($n < m$), some of the cells are black.
Then a cylinder is obtained from this sheet by gluing together the two sides with lengths $m$.
Then a torus is obtained from the cylinder by gluing together the two circles (top and bottom) without twisting.
The task is to compute the number of different colored tori, assuming that we cannot see the glued lines, and the torus can be turned and turned.
We again start with a piece of $n \times m$ paper.
It is easy to see that the following types of transformations preserve the equivalence class:
a cyclic shift of the rows, a cyclic shift of the columns, and a rotation of the sheet by 180 degrees.
It is also easy to see, that these transformations can generate the entire group of invariant transformations.
If we somehow number the cells of the paper, then we can write three permutations $p_1$, $p_2$, $p_3$ corresponding to these types of transformation.
Next it only remains to generate all permutations obtained as a product.
It is obvious that all such permutations have the form $p_1^{i_1} p_2^{i_2} p_3^{i_3}$ where $i_1 = 0 \dots m-1$, $i_2 = 0 \dots n-1$, $i_3 = 0 \dots 1$.
Thus we can write the implementations to this problem.
```{.cpp file=burnside_tori}
using Permutation = vector<int>;
void operator*=(Permutation& p, Permutation const& q) {
Permutation copy = p;
for (int i = 0; i < p.size(); i++)
p[i] = copy[q[i]];
}
int count_cycles(Permutation p) {
int cnt = 0;
for (int i = 0; i < p.size(); i++) {
if (p[i] != -1) {
cnt++;
for (int j = i; p[j] != -1;) {
int next = p[j];
p[j] = -1;
j = next;
}
}
}
return cnt;
}
int solve(int n, int m) {
Permutation p(n*m), p1(n*m), p2(n*m), p3(n*m);
for (int i = 0; i < n*m; i++) {
p[i] = i;
p1[i] = (i % n + 1) % n + i / n * n;
p2[i] = (i / n + 1) % m * n + i % n;
p3[i] = (m - 1 - i / n) * n + (n - 1 - i % n);
}
set<Permutation> s;
for (int i1 = 0; i1 < n; i1++) {
for (int i2 = 0; i2 < m; i2++) {
for (int i3 = 0; i3 < 2; i3++) {
s.insert(p);
p *= p3;
}
p *= p2;
}
p *= p1;
}
int sum = 0;
for (Permutation const& p : s) {
sum += 1 << count_cycles(p);
}
return sum / s.size();
}
```
|
Burnside's lemma / Pólya enumeration theorem
|
---
title
counting_connected_graphs
---
# Counting labeled graphs
## Labeled graphs
Let the number of vertices in a graph be $n$.
We have to compute the number $G_n$ of labeled graphs with $n$ vertices (labeled means that the vertices are marked with the numbers from $1$ to $n$).
The edges of the graphs are considered undirected, and loops and multiple edges are forbidden.
We consider the set of all possible edges of the graph.
For each edge $(i, j)$ we can assume that $i < j$ (because the graph is undirected, and there are no loops).
Therefore the set of all edges has the cardinality $\binom{n}{2}$, i.e. $\frac{n(n-1)}{2}$.
Since any labeled graph is uniquely determined by its edges, the number of labeled graphs with $n$ vertices is equal to:
$$G_n = 2^{\frac{n(n-1)}{2}}$$
## Connected labeled graphs
Here, we additionally impose the restriction that the graph has to be connected.
Let's denote the required number of connected graphs with $n$ vertices as $C_n$.
We will first discuss how many **disconnected** graphs exists.
Then the number of connected graphs will be $G_n$ minus the number of disconnected graphs.
Even more, we will count the number of **disconnected, rooted graphs**.A rooted graph is a graph, where we emphasize one vertex by labeling it as root.
Obviously we have $n$ possibilities to root a graph with $n$ labeled vertices, therefore we will need to divide the number of disconnected rooted graphs by $n$ at the end to get the number of disconnected graphs.
The root vertex will appear in a connected component of size $1, \dots n-1$.
There are $k \binom{n}{k} C_k G_{n-k}$ graphs such that the root vertex is in a connected component with $k$ vertices (there are $\binom{n}{k}$ ways to choose $k$ vertices for the component, these are connected in one of $C_k$ ways, the root vertex can be any of the $k$ vertices, and the remainder $n-k$ vertices can be connected/disconnected in any way, which gives a factor of $G_{n-k}$).
Therefore the number of disconnected graphs with $n$ vertices is:
$$\frac{1}{n} \sum_{k=1}^{n-1} k \binom{n}{k} C_k G_{n-k}$$
And finally the number of connected graphs is:
$$C_n = G_n - \frac{1}{n} \sum_{k=1}^{n-1} k \binom{n}{k} C_k G_{n-k}$$
## Labeled graphs with $k$ connected components {data-toc-label="Labeled graphs with k connected components"}
Based on the formula from the previous section, we will learn how to count the number of labeled graphs with $n$ vertices and $k$ connected components.
This number can be computed using dynamic programming.
We will compute $D[i][j]$ - the number of labeled graphs with $i$ vertices and $j$ components - for each $i \le n$ and $j \le k$.
Let's discuss how to compute the next element $D[n][k]$ if we already know the previous values.
We use a common approach, we take the last vertex (index $n$).
This vertex belongs to some component.
If the size of this component be $s$, then there are $\binom{n-1}{s-1}$ ways to choose such a set of vertices, and $C_s$ ways to connect them.After removing this component from the graph we have $n-s$ remaining vertices with $k-1$ connected components.
Therefore we obtain the following recurrence relation:
$$D[n][k] = \sum_{s=1}^{n} \binom{n-1}{s-1} C_s D[n-s][k-1]$$
|
---
title
counting_connected_graphs
---
# Counting labeled graphs
## Labeled graphs
Let the number of vertices in a graph be $n$.
We have to compute the number $G_n$ of labeled graphs with $n$ vertices (labeled means that the vertices are marked with the numbers from $1$ to $n$).
The edges of the graphs are considered undirected, and loops and multiple edges are forbidden.
We consider the set of all possible edges of the graph.
For each edge $(i, j)$ we can assume that $i < j$ (because the graph is undirected, and there are no loops).
Therefore the set of all edges has the cardinality $\binom{n}{2}$, i.e. $\frac{n(n-1)}{2}$.
Since any labeled graph is uniquely determined by its edges, the number of labeled graphs with $n$ vertices is equal to:
$$G_n = 2^{\frac{n(n-1)}{2}}$$
## Connected labeled graphs
Here, we additionally impose the restriction that the graph has to be connected.
Let's denote the required number of connected graphs with $n$ vertices as $C_n$.
We will first discuss how many **disconnected** graphs exists.
Then the number of connected graphs will be $G_n$ minus the number of disconnected graphs.
Even more, we will count the number of **disconnected, rooted graphs**.A rooted graph is a graph, where we emphasize one vertex by labeling it as root.
Obviously we have $n$ possibilities to root a graph with $n$ labeled vertices, therefore we will need to divide the number of disconnected rooted graphs by $n$ at the end to get the number of disconnected graphs.
The root vertex will appear in a connected component of size $1, \dots n-1$.
There are $k \binom{n}{k} C_k G_{n-k}$ graphs such that the root vertex is in a connected component with $k$ vertices (there are $\binom{n}{k}$ ways to choose $k$ vertices for the component, these are connected in one of $C_k$ ways, the root vertex can be any of the $k$ vertices, and the remainder $n-k$ vertices can be connected/disconnected in any way, which gives a factor of $G_{n-k}$).
Therefore the number of disconnected graphs with $n$ vertices is:
$$\frac{1}{n} \sum_{k=1}^{n-1} k \binom{n}{k} C_k G_{n-k}$$
And finally the number of connected graphs is:
$$C_n = G_n - \frac{1}{n} \sum_{k=1}^{n-1} k \binom{n}{k} C_k G_{n-k}$$
## Labeled graphs with $k$ connected components {data-toc-label="Labeled graphs with k connected components"}
Based on the formula from the previous section, we will learn how to count the number of labeled graphs with $n$ vertices and $k$ connected components.
This number can be computed using dynamic programming.
We will compute $D[i][j]$ - the number of labeled graphs with $i$ vertices and $j$ components - for each $i \le n$ and $j \le k$.
Let's discuss how to compute the next element $D[n][k]$ if we already know the previous values.
We use a common approach, we take the last vertex (index $n$).
This vertex belongs to some component.
If the size of this component be $s$, then there are $\binom{n-1}{s-1}$ ways to choose such a set of vertices, and $C_s$ ways to connect them.After removing this component from the graph we have $n-s$ remaining vertices with $k-1$ connected components.
Therefore we obtain the following recurrence relation:
$$D[n][k] = \sum_{s=1}^{n} \binom{n-1}{s-1} C_s D[n-s][k-1]$$
|
Counting labeled graphs
|
---
title
bracket_sequences
---
# Balanced bracket sequences
A **balanced bracket sequence** is a string consisting of only brackets, such that this sequence, when inserted certain numbers and mathematical operations, gives a valid mathematical expression.
Formally you can define balanced bracket sequence with:
- $e$ (the empty string) is a balanced bracket sequence.
- if $s$ is a balanced bracket sequence, then so is $(s)$.
- if $s$ and $t$ are balanced bracket sequences, then so is $s t$.
For instance $(())()$ is a balanced bracket sequence, but $())($ is not.
Of course you can define other bracket sequences also with multiple bracket types in a similar fashion.
In this article we discuss some classic problems involving balanced bracket sequences (for simplicity we will only call them sequences): validation, number of sequences, finding the lexicographical next sequence, generating all sequences of a certain size, finding the index of sequence, and generating the $k$-th sequences.
We will also discuss two variations for the problems, the simpler version when only one type of brackets is allowed, and the harder case when there are multiple types.
## Balance validation
We want to check if a given string is balanced or not.
At first suppose there is only one type of bracket.
For this case there exists a very simple algorithm.
Let $\text{depth}$ be the current number of open brackets.
Initially $\text{depth} = 0$.
We iterate over all character of the string, if the current bracket character is an opening bracket, then we increment $\text{depth}$, otherwise we decrement it.
If at any time the variable $\text{depth}$ gets negative, or at the end it is different from $0$, then the string is not a balanced sequence.
Otherwise it is.
If there are several bracket types involved, then the algorithm needs to be changes.
Instead of a counter $\text{depth}$ we create a stack, in which we will store all opening brackets that we meet.
If the current bracket character is an opening one, we put it onto the stack.
If it is a closing one, then we check if the stack is non-empty, and if the top element of the stack is of the same type as the current closing bracket.
If both conditions are fulfilled, then we remove the opening bracket from the stack.
If at any time one of the conditions is not fulfilled, or at the end the stack is not empty, then the string is not balanced.
Otherwise it is.
## Number of balanced sequences
### Formula
The number of balanced bracket sequences with only one bracket type can be calculated using the [Catalan numbers](catalan-numbers.md).
The number of balanced bracket sequences of length $2n$ ($n$ pairs of brackets) is:
$$\frac{1}{n+1} \binom{2n}{n}$$
If we allow $k$ types of brackets, then each pair be of any of the $k$ types (independently of the others), thus the number of balanced bracket sequences is:
$$\frac{1}{n+1} \binom{2n}{n} k^n$$
### Dynamic programming
On the other hand these numbers can be computed using **dynamic programming**.
Let $d[n]$ be the number of regular bracket sequences with $n$ pairs of bracket.
Note that in the first position there is always an opening bracket.
And somewhere later is the corresponding closing bracket of the pair.
It is clear that inside this pair there is a balanced bracket sequence, and similarly after this pair there is a balanced bracket sequence.
So to compute $d[n]$, we will look at how many balanced sequences of $i$ pairs of brackets are inside this first bracket pair, and how many balanced sequences with $n-1-i$ pairs are after this pair.
Consequently the formula has the form:
$$d[n] = \sum_{i=0}^{n-1} d[i] \cdot d[n-1-i]$$
The initial value for this recurrence is $d[0] = 1$.
## Finding the lexicographical next balanced sequence
Here we only consider the case with one valid bracket type.
Given a balanced sequence, we have to find the next (in lexicographical order) balanced sequence.
It should be obvious, that we have to find the rightmost opening bracket, which we can replace by a closing bracket without violation the condition, that there are more closing brackets than opening brackets up to this position.
After replacing this position, we can fill the remaining part of the string with the lexicographically minimal one: i.e. first with as much opening brackets as possible, and then fill up the remaining positions with closing brackets.
In other words we try to leave a long as possible prefix unchanged, and the suffix gets replaced by the lexicographically minimal one.
To find this position, we can iterate over the character from right to left, and maintain the balance $\text{depth}$ of open and closing brackets.
When we meet an opening brackets, we will decrement $\text{depth}$, and when we meet a closing bracket, we increase it.
If we are at some point meet an opening bracket, and the balance after processing this symbol is positive, then we have found the rightmost position that we can change.
We change the symbol, compute the number of opening and closing brackets that we have to add to the right side, and arrange them in the lexicographically minimal way.
If we find do suitable position, then this sequence is already the maximal possible one, and there is no answer.
```{.cpp file=next_balanced_brackets_sequence}
bool next_balanced_sequence(string & s) {
int n = s.size();
int depth = 0;
for (int i = n - 1; i >= 0; i--) {
if (s[i] == '(')
depth--;
else
depth++;
if (s[i] == '(' && depth > 0) {
depth--;
int open = (n - i - 1 - depth) / 2;
int close = n - i - 1 - open;
string next = s.substr(0, i) + ')' + string(open, '(') + string(close, ')');
s.swap(next);
return true;
}
}
return false;
}
```
This function computes in $O(n)$ time the next balanced bracket sequence, and returns false if there is no next one.
## Finding all balanced sequences
Sometimes it is required to find and output all balanced bracket sequences of a specific length $n$.
To generate then, we can start with the lexicographically smallest sequence $((\dots(())\dots))$, and then continue to find the next lexicographically sequences with the algorithm described in the previous section.
However, if the length of the sequence is not very long (e.g. $n$ smaller than $12$), then we can also generate all permutations conveniently with the C++ STL function `next_permutation`, and check each one for balanceness.
Also they can be generate using the ideas we used for counting all sequences with dynamic programming.
We will discuss the ideas in the next two sections.
## Sequence index
Given a balanced bracket sequence with $n$ pairs of brackets.
We have to find its index in the lexicographically ordered list of all balanced sequences with $n$ bracket pairs.
Let's define an auxiliary array $d[i][j]$, where $i$ is the length of the bracket sequence (semi-balanced, each closing bracket has a corresponding opening bracket, but not every opening bracket has necessarily a corresponding closing one), and $j$ is the current balance (difference between opening and closing brackets).
$d[i][j]$ is the number of such sequences that fit the parameters.
We will calculate these numbers with only one bracket type.
For the start value $i = 0$ the answer is obvious: $d[0][0] = 1$, and $d[0][j] = 0$ for $j > 0$.
Now let $i > 0$, and we look at the last character in the sequence.
If the last character was an opening bracket $($, then the state before was $(i-1, j-1)$, if it was a closing bracket $)$, then the previous state was $(i-1, j+1)$.
Thus we obtain the recursion formula:
$$d[i][j] = d[i-1][j-1] + d[i-1][j+1]$$
$d[i][j] = 0$ holds obviously for negative $j$.
Thus we can compute this array in $O(n^2)$.
Now let us generate the index for a given sequence.
First let there be only one type of brackets.
We will us the counter $\text{depth}$ which tells us how nested we currently are, and iterate over the characters of the sequence.
If the current character $s[i]$ is equal to $($, then we increment $\text{depth}$.
If the current character $s[i]$ is equal to $)$, then we must add $d[2n-i-1][\text{depth}+1]$ to the answer, taking all possible endings starting with a $($ into account (which are lexicographically smaller sequences), and then decrement $\text{depth}$.
New let there be $k$ different bracket types.
Thus, when we look at the current character $s[i]$ before recomputing $\text{depth}$, we have to go through all bracket types that are smaller than the current character, and try to put this bracket into the current position (obtaining a new balance $\text{ndepth} = \text{depth} \pm 1$), and add the number of ways to finish the sequence (length $2n-i-1$, balance $ndepth$) to the answer:
$$d[2n - i - 1][\text{ndepth}] \cdot k^{\frac{2n - i - 1 - ndepth}{2}}$$
This formula can be derived as follows:
First we "forget" that there are multiple bracket types, and just take the answer $d[2n - i - 1][\text{ndepth}]$.
Now we consider how the answer will change is we have $k$ types of brackets.
We have $2n - i - 1$ undefined positions, of which $\text{ndepth}$ are already predetermined because of the opening brackets.
But all the other brackets ($(2n - i - 1 - \text{ndepth})/2$ pairs) can be of any type, therefore we multiply the number by such a power of $k$.
## Finding the $k$-th sequence {data-toc-label="Finding the k-th sequence"}
Let $n$ be the number of bracket pairs in the sequence.
We have to find the $k$-th balanced sequence in lexicographically sorted list of all balanced sequences for a given $k$.
As in the previous section we compute the auxiliary array $d[i][j]$, the number of semi-balanced bracket sequences of length $i$ with balance $j$.
First, we start with only one bracket type.
We will iterate over the characters in the string we want to generate.
As in the previous problem we store a counter $\text{depth}$, the current nesting depth.
In each position we have to decide if we use an opening of a closing bracket.
To have to put an opening bracket character, it $d[2n - i - 1][\text{depth}+1] \ge k$.
We increment the counter $\text{depth}$, and move on to the next character.
Otherwise we decrement $k$ by $d[2n - i - 1][\text{depth}+1]$, put a closing bracket and move on.
```{.cpp file=kth_balances_bracket}
string kth_balanced(int n, int k) {
vector<vector<int>> d(2*n+1, vector<int>(n+1, 0));
d[0][0] = 1;
for (int i = 1; i <= 2*n; i++) {
d[i][0] = d[i-1][1];
for (int j = 1; j < n; j++)
d[i][j] = d[i-1][j-1] + d[i-1][j+1];
d[i][n] = d[i-1][n-1];
}
string ans;
int depth = 0;
for (int i = 0; i < 2*n; i++) {
if (depth + 1 <= n && d[2*n-i-1][depth+1] >= k) {
ans += '(';
depth++;
} else {
ans += ')';
if (depth + 1 <= n)
k -= d[2*n-i-1][depth+1];
depth--;
}
}
return ans;
}
```
Now let there be $k$ types of brackets.
The solution will only differ slightly in that we have to multiply the value $d[2n-i-1][\text{ndepth}]$ by $k^{(2n-i-1-\text{ndepth})/2}$ and take into account that there can be different bracket types for the next character.
Here is an implementation using two types of brackets: round and square:
```{.cpp file=kth_balances_bracket_multiple}
string kth_balanced2(int n, int k) {
vector<vector<int>> d(2*n+1, vector<int>(n+1, 0));
d[0][0] = 1;
for (int i = 1; i <= 2*n; i++) {
d[i][0] = d[i-1][1];
for (int j = 1; j < n; j++)
d[i][j] = d[i-1][j-1] + d[i-1][j+1];
d[i][n] = d[i-1][n-1];
}
string ans;
int shift, depth = 0;
stack<char> st;
for (int i = 0; i < 2*n; i++) {
// '('
shift = ((2*n-i-1-depth-1) / 2);
if (shift >= 0 && depth + 1 <= n) {
int cnt = d[2*n-i-1][depth+1] << shift;
if (cnt >= k) {
ans += '(';
st.push('(');
depth++;
continue;
}
k -= cnt;
}
// ')'
shift = ((2*n-i-1-depth+1) / 2);
if (shift >= 0 && depth && st.top() == '(') {
int cnt = d[2*n-i-1][depth-1] << shift;
if (cnt >= k) {
ans += ')';
st.pop();
depth--;
continue;
}
k -= cnt;
}
// '['
shift = ((2*n-i-1-depth-1) / 2);
if (shift >= 0 && depth + 1 <= n) {
int cnt = d[2*n-i-1][depth+1] << shift;
if (cnt >= k) {
ans += '[';
st.push('[');
depth++;
continue;
}
k -= cnt;
}
// ']'
ans += ']';
st.pop();
depth--;
}
return ans;
}
```
|
---
title
bracket_sequences
---
# Balanced bracket sequences
A **balanced bracket sequence** is a string consisting of only brackets, such that this sequence, when inserted certain numbers and mathematical operations, gives a valid mathematical expression.
Formally you can define balanced bracket sequence with:
- $e$ (the empty string) is a balanced bracket sequence.
- if $s$ is a balanced bracket sequence, then so is $(s)$.
- if $s$ and $t$ are balanced bracket sequences, then so is $s t$.
For instance $(())()$ is a balanced bracket sequence, but $())($ is not.
Of course you can define other bracket sequences also with multiple bracket types in a similar fashion.
In this article we discuss some classic problems involving balanced bracket sequences (for simplicity we will only call them sequences): validation, number of sequences, finding the lexicographical next sequence, generating all sequences of a certain size, finding the index of sequence, and generating the $k$-th sequences.
We will also discuss two variations for the problems, the simpler version when only one type of brackets is allowed, and the harder case when there are multiple types.
## Balance validation
We want to check if a given string is balanced or not.
At first suppose there is only one type of bracket.
For this case there exists a very simple algorithm.
Let $\text{depth}$ be the current number of open brackets.
Initially $\text{depth} = 0$.
We iterate over all character of the string, if the current bracket character is an opening bracket, then we increment $\text{depth}$, otherwise we decrement it.
If at any time the variable $\text{depth}$ gets negative, or at the end it is different from $0$, then the string is not a balanced sequence.
Otherwise it is.
If there are several bracket types involved, then the algorithm needs to be changes.
Instead of a counter $\text{depth}$ we create a stack, in which we will store all opening brackets that we meet.
If the current bracket character is an opening one, we put it onto the stack.
If it is a closing one, then we check if the stack is non-empty, and if the top element of the stack is of the same type as the current closing bracket.
If both conditions are fulfilled, then we remove the opening bracket from the stack.
If at any time one of the conditions is not fulfilled, or at the end the stack is not empty, then the string is not balanced.
Otherwise it is.
## Number of balanced sequences
### Formula
The number of balanced bracket sequences with only one bracket type can be calculated using the [Catalan numbers](catalan-numbers.md).
The number of balanced bracket sequences of length $2n$ ($n$ pairs of brackets) is:
$$\frac{1}{n+1} \binom{2n}{n}$$
If we allow $k$ types of brackets, then each pair be of any of the $k$ types (independently of the others), thus the number of balanced bracket sequences is:
$$\frac{1}{n+1} \binom{2n}{n} k^n$$
### Dynamic programming
On the other hand these numbers can be computed using **dynamic programming**.
Let $d[n]$ be the number of regular bracket sequences with $n$ pairs of bracket.
Note that in the first position there is always an opening bracket.
And somewhere later is the corresponding closing bracket of the pair.
It is clear that inside this pair there is a balanced bracket sequence, and similarly after this pair there is a balanced bracket sequence.
So to compute $d[n]$, we will look at how many balanced sequences of $i$ pairs of brackets are inside this first bracket pair, and how many balanced sequences with $n-1-i$ pairs are after this pair.
Consequently the formula has the form:
$$d[n] = \sum_{i=0}^{n-1} d[i] \cdot d[n-1-i]$$
The initial value for this recurrence is $d[0] = 1$.
## Finding the lexicographical next balanced sequence
Here we only consider the case with one valid bracket type.
Given a balanced sequence, we have to find the next (in lexicographical order) balanced sequence.
It should be obvious, that we have to find the rightmost opening bracket, which we can replace by a closing bracket without violation the condition, that there are more closing brackets than opening brackets up to this position.
After replacing this position, we can fill the remaining part of the string with the lexicographically minimal one: i.e. first with as much opening brackets as possible, and then fill up the remaining positions with closing brackets.
In other words we try to leave a long as possible prefix unchanged, and the suffix gets replaced by the lexicographically minimal one.
To find this position, we can iterate over the character from right to left, and maintain the balance $\text{depth}$ of open and closing brackets.
When we meet an opening brackets, we will decrement $\text{depth}$, and when we meet a closing bracket, we increase it.
If we are at some point meet an opening bracket, and the balance after processing this symbol is positive, then we have found the rightmost position that we can change.
We change the symbol, compute the number of opening and closing brackets that we have to add to the right side, and arrange them in the lexicographically minimal way.
If we find do suitable position, then this sequence is already the maximal possible one, and there is no answer.
```{.cpp file=next_balanced_brackets_sequence}
bool next_balanced_sequence(string & s) {
int n = s.size();
int depth = 0;
for (int i = n - 1; i >= 0; i--) {
if (s[i] == '(')
depth--;
else
depth++;
if (s[i] == '(' && depth > 0) {
depth--;
int open = (n - i - 1 - depth) / 2;
int close = n - i - 1 - open;
string next = s.substr(0, i) + ')' + string(open, '(') + string(close, ')');
s.swap(next);
return true;
}
}
return false;
}
```
This function computes in $O(n)$ time the next balanced bracket sequence, and returns false if there is no next one.
## Finding all balanced sequences
Sometimes it is required to find and output all balanced bracket sequences of a specific length $n$.
To generate then, we can start with the lexicographically smallest sequence $((\dots(())\dots))$, and then continue to find the next lexicographically sequences with the algorithm described in the previous section.
However, if the length of the sequence is not very long (e.g. $n$ smaller than $12$), then we can also generate all permutations conveniently with the C++ STL function `next_permutation`, and check each one for balanceness.
Also they can be generate using the ideas we used for counting all sequences with dynamic programming.
We will discuss the ideas in the next two sections.
## Sequence index
Given a balanced bracket sequence with $n$ pairs of brackets.
We have to find its index in the lexicographically ordered list of all balanced sequences with $n$ bracket pairs.
Let's define an auxiliary array $d[i][j]$, where $i$ is the length of the bracket sequence (semi-balanced, each closing bracket has a corresponding opening bracket, but not every opening bracket has necessarily a corresponding closing one), and $j$ is the current balance (difference between opening and closing brackets).
$d[i][j]$ is the number of such sequences that fit the parameters.
We will calculate these numbers with only one bracket type.
For the start value $i = 0$ the answer is obvious: $d[0][0] = 1$, and $d[0][j] = 0$ for $j > 0$.
Now let $i > 0$, and we look at the last character in the sequence.
If the last character was an opening bracket $($, then the state before was $(i-1, j-1)$, if it was a closing bracket $)$, then the previous state was $(i-1, j+1)$.
Thus we obtain the recursion formula:
$$d[i][j] = d[i-1][j-1] + d[i-1][j+1]$$
$d[i][j] = 0$ holds obviously for negative $j$.
Thus we can compute this array in $O(n^2)$.
Now let us generate the index for a given sequence.
First let there be only one type of brackets.
We will us the counter $\text{depth}$ which tells us how nested we currently are, and iterate over the characters of the sequence.
If the current character $s[i]$ is equal to $($, then we increment $\text{depth}$.
If the current character $s[i]$ is equal to $)$, then we must add $d[2n-i-1][\text{depth}+1]$ to the answer, taking all possible endings starting with a $($ into account (which are lexicographically smaller sequences), and then decrement $\text{depth}$.
New let there be $k$ different bracket types.
Thus, when we look at the current character $s[i]$ before recomputing $\text{depth}$, we have to go through all bracket types that are smaller than the current character, and try to put this bracket into the current position (obtaining a new balance $\text{ndepth} = \text{depth} \pm 1$), and add the number of ways to finish the sequence (length $2n-i-1$, balance $ndepth$) to the answer:
$$d[2n - i - 1][\text{ndepth}] \cdot k^{\frac{2n - i - 1 - ndepth}{2}}$$
This formula can be derived as follows:
First we "forget" that there are multiple bracket types, and just take the answer $d[2n - i - 1][\text{ndepth}]$.
Now we consider how the answer will change is we have $k$ types of brackets.
We have $2n - i - 1$ undefined positions, of which $\text{ndepth}$ are already predetermined because of the opening brackets.
But all the other brackets ($(2n - i - 1 - \text{ndepth})/2$ pairs) can be of any type, therefore we multiply the number by such a power of $k$.
## Finding the $k$-th sequence {data-toc-label="Finding the k-th sequence"}
Let $n$ be the number of bracket pairs in the sequence.
We have to find the $k$-th balanced sequence in lexicographically sorted list of all balanced sequences for a given $k$.
As in the previous section we compute the auxiliary array $d[i][j]$, the number of semi-balanced bracket sequences of length $i$ with balance $j$.
First, we start with only one bracket type.
We will iterate over the characters in the string we want to generate.
As in the previous problem we store a counter $\text{depth}$, the current nesting depth.
In each position we have to decide if we use an opening of a closing bracket.
To have to put an opening bracket character, it $d[2n - i - 1][\text{depth}+1] \ge k$.
We increment the counter $\text{depth}$, and move on to the next character.
Otherwise we decrement $k$ by $d[2n - i - 1][\text{depth}+1]$, put a closing bracket and move on.
```{.cpp file=kth_balances_bracket}
string kth_balanced(int n, int k) {
vector<vector<int>> d(2*n+1, vector<int>(n+1, 0));
d[0][0] = 1;
for (int i = 1; i <= 2*n; i++) {
d[i][0] = d[i-1][1];
for (int j = 1; j < n; j++)
d[i][j] = d[i-1][j-1] + d[i-1][j+1];
d[i][n] = d[i-1][n-1];
}
string ans;
int depth = 0;
for (int i = 0; i < 2*n; i++) {
if (depth + 1 <= n && d[2*n-i-1][depth+1] >= k) {
ans += '(';
depth++;
} else {
ans += ')';
if (depth + 1 <= n)
k -= d[2*n-i-1][depth+1];
depth--;
}
}
return ans;
}
```
Now let there be $k$ types of brackets.
The solution will only differ slightly in that we have to multiply the value $d[2n-i-1][\text{ndepth}]$ by $k^{(2n-i-1-\text{ndepth})/2}$ and take into account that there can be different bracket types for the next character.
Here is an implementation using two types of brackets: round and square:
```{.cpp file=kth_balances_bracket_multiple}
string kth_balanced2(int n, int k) {
vector<vector<int>> d(2*n+1, vector<int>(n+1, 0));
d[0][0] = 1;
for (int i = 1; i <= 2*n; i++) {
d[i][0] = d[i-1][1];
for (int j = 1; j < n; j++)
d[i][j] = d[i-1][j-1] + d[i-1][j+1];
d[i][n] = d[i-1][n-1];
}
string ans;
int shift, depth = 0;
stack<char> st;
for (int i = 0; i < 2*n; i++) {
// '('
shift = ((2*n-i-1-depth-1) / 2);
if (shift >= 0 && depth + 1 <= n) {
int cnt = d[2*n-i-1][depth+1] << shift;
if (cnt >= k) {
ans += '(';
st.push('(');
depth++;
continue;
}
k -= cnt;
}
// ')'
shift = ((2*n-i-1-depth+1) / 2);
if (shift >= 0 && depth && st.top() == '(') {
int cnt = d[2*n-i-1][depth-1] << shift;
if (cnt >= k) {
ans += ')';
st.pop();
depth--;
continue;
}
k -= cnt;
}
// '['
shift = ((2*n-i-1-depth-1) / 2);
if (shift >= 0 && depth + 1 <= n) {
int cnt = d[2*n-i-1][depth+1] << shift;
if (cnt >= k) {
ans += '[';
st.push('[');
depth++;
continue;
}
k -= cnt;
}
// ']'
ans += ']';
st.pop();
depth--;
}
return ans;
}
```
|
Balanced bracket sequences
|
---
title
- Original
---
# Stars and bars
Stars and bars is a mathematical technique for solving certain combinatorial problems.
It occurs whenever you want to count the number of ways to group identical objects.
## Theorem
The number of ways to put $n$ identical objects into $k$ labeled boxes is
$$\binom{n + k - 1}{n}.$$
The proof involves turning the objects into stars and separating the boxes using bars (therefore the name).
E.g. we can represent with $\bigstar | \bigstar \bigstar |~| \bigstar \bigstar$ the following situation:
in the first box is one object, in the second box are two objects, the third one is empty and in the last box are two objects.
This is one way of dividing 5 objects into 4 boxes.
It should be pretty obvious, that every partition can be represented using $n$ stars and $k - 1$ bars and every stars and bars permutation using $n$ stars and $k - 1$ bars represents one partition.
Therefore the number of ways to divide $n$ identical objects into $k$ labeled boxes is the same number as there are permutations of $n$ stars and $k - 1$ bars.
The [Binomial Coefficient](binomial-coefficients.md) gives us the desired formula.
## Number of non-negative integer sums
This problem is a direct application of the theorem.
You want to count the number of solution of the equation
$$x_1 + x_2 + \dots + x_k = n$$
with $x_i \ge 0$.
Again we can represent a solution using stars and bars.
E.g. the solution $1 + 3 + 0 = 4$ for $n = 4$, $k = 3$ can be represented using $\bigstar | \bigstar \bigstar \bigstar |$.
It is easy to see, that this is exactly the stars and bars theorem.
Therefore the solution is $\binom{n + k - 1}{n}$.
## Number of lower-bound integer sums
This can easily be extended to integer sums with different lower bounds.
I.e. we want to count the number of solutions for the equation
$$x_1 + x_2 + \dots + x_k = n$$
with $x_i \ge a_i$.
After substituting $x_i' := x_i - a_i$ we receive the modified equation
$$(x_1' + a_i) + (x_2' + a_i) + \dots + (x_k' + a_k) = n$$
$$\Leftrightarrow ~ ~ x_1' + x_2' + \dots + x_k' = n - a_1 - a_2 - \dots - a_k$$
with $x_i' \ge 0$.
So we have reduced the problem to the simpler case with $x_i' \ge 0$ and again can apply the stars and bars theorem.
## Number of upper-bound integer sums
With some help of the [Inclusion-Exclusion Principle](./inclusion-exclusion.md), you can also restrict the integers with upper bounds.
See the [Number of upper-bound integer sums](./inclusion-exclusion.md#number-of-upper-bound-integer-sums) section in the corresponding article.
|
---
title
- Original
---
# Stars and bars
Stars and bars is a mathematical technique for solving certain combinatorial problems.
It occurs whenever you want to count the number of ways to group identical objects.
## Theorem
The number of ways to put $n$ identical objects into $k$ labeled boxes is
$$\binom{n + k - 1}{n}.$$
The proof involves turning the objects into stars and separating the boxes using bars (therefore the name).
E.g. we can represent with $\bigstar | \bigstar \bigstar |~| \bigstar \bigstar$ the following situation:
in the first box is one object, in the second box are two objects, the third one is empty and in the last box are two objects.
This is one way of dividing 5 objects into 4 boxes.
It should be pretty obvious, that every partition can be represented using $n$ stars and $k - 1$ bars and every stars and bars permutation using $n$ stars and $k - 1$ bars represents one partition.
Therefore the number of ways to divide $n$ identical objects into $k$ labeled boxes is the same number as there are permutations of $n$ stars and $k - 1$ bars.
The [Binomial Coefficient](binomial-coefficients.md) gives us the desired formula.
## Number of non-negative integer sums
This problem is a direct application of the theorem.
You want to count the number of solution of the equation
$$x_1 + x_2 + \dots + x_k = n$$
with $x_i \ge 0$.
Again we can represent a solution using stars and bars.
E.g. the solution $1 + 3 + 0 = 4$ for $n = 4$, $k = 3$ can be represented using $\bigstar | \bigstar \bigstar \bigstar |$.
It is easy to see, that this is exactly the stars and bars theorem.
Therefore the solution is $\binom{n + k - 1}{n}$.
## Number of lower-bound integer sums
This can easily be extended to integer sums with different lower bounds.
I.e. we want to count the number of solutions for the equation
$$x_1 + x_2 + \dots + x_k = n$$
with $x_i \ge a_i$.
After substituting $x_i' := x_i - a_i$ we receive the modified equation
$$(x_1' + a_i) + (x_2' + a_i) + \dots + (x_k' + a_k) = n$$
$$\Leftrightarrow ~ ~ x_1' + x_2' + \dots + x_k' = n - a_1 - a_2 - \dots - a_k$$
with $x_i' \ge 0$.
So we have reduced the problem to the simpler case with $x_i' \ge 0$ and again can apply the stars and bars theorem.
## Number of upper-bound integer sums
With some help of the [Inclusion-Exclusion Principle](./inclusion-exclusion.md), you can also restrict the integers with upper bounds.
See the [Number of upper-bound integer sums](./inclusion-exclusion.md#number-of-upper-bound-integer-sums) section in the corresponding article.
## Practice Problems
* [Codeforces - Array](https://codeforces.com/contest/57/problem/C)
* [Codeforces - Kyoya and Coloured Balls](https://codeforces.com/problemset/problem/553/A)
|
Stars and bars
|
# Garner's algorithm
A consequence of the [Chinese Remainder Theorem](chinese-remainder-theorem.md) is, that we can represent big numbers using an array of small integers.
For example, let $p$ be the product of the first $1000$ primes. $p$ has around $3000$ digits.
Any number $a$ less than $p$ can be represented as an array $a_1, \ldots, a_k$, where $a_i \equiv a \pmod{p_i}$.
But to do this we obviously need to know how to get back the number $a$ from its representation.
One way is discussed in the article about the Chinese Remainder Theorem.
In this article we discuss an alternative, Garner's Algorithm, which can also be used for this purpose.
## Mixed Radix Representation
We can represent the number $a$ in the **mixed radix** representation:
$$a = x_1 + x_2 p_1 + x_3 p_1 p_2 + \ldots + x_k p_1 \cdots p_{k-1} \text{ with }x_i \in [0, p_i)$$
A mixed radix representation is a positional numeral system, that's a generalization of the typical number systems, like the binary numeral system or the decimal numeral system.
For instance the decimal numeral system is a positional numeral system with the radix (or base) 10.
Every a number is represented as a string of digits $d_1 d_2 d_3 \dots d_n$ between $0$ and $9$, and
E.g. the string $415$ represents the number $4 \cdot 10^2 + 1 \cdot 10^1 + 5 \cdot 10^0$.
In general the string of digits $d_1 d_2 d_3 \dots d_n$ represents the number $d_1 b^{n-1} + d_2 b^{n-2} + \cdots + d_n b^0$ in the positional numeral system with radix $b$.
In a mixed radix system, we don't have one radix any more. The base varies from position to position.
## Garner's algorithm
Garner's algorithm computes the digits $x_1, \ldots, x_k$.
Notice, that the digits are relatively small.
The digit $x_i$ is an integer between $0$ and $p_i - 1$.
Let $r_{ij}$ denote the inverse of $p_i$ modulo $p_j$
$$r_{ij} = (p_i)^{-1} \pmod{p_j}$$
which can be found using the algorithm described in [Modular Inverse](module-inverse.md).
Substituting $a$ from the mixed radix representation into the first congruence equation we obtain
$$a_1 \equiv x_1 \pmod{p_1}.$$
Substituting into the second equation yields
$$a_2 \equiv x_1 + x_2 p_1 \pmod{p_2},$$
which can be rewritten by subtracting $x_1$ and dividing by $p_1$ to get
$$\begin{array}{rclr}
a_2 - x_1 &\equiv& x_2 p_1 &\pmod{p_2} \\
(a_2 - x_1) r_{12} &\equiv& x_2 &\pmod{p_2} \\
x_2 &\equiv& (a_2 - x_1) r_{12} &\pmod{p_2}
\end{array}$$
Similarly we get that
$$x_3 \equiv ((a_3 - x_1) r_{13} - x_2) r_{23} \pmod{p_3}.$$
Now, we can clearly see an emerging pattern, which can be expressed by the following code:
```cpp
for (int i = 0; i < k; ++i) {
x[i] = a[i];
for (int j = 0; j < i; ++j) {
x[i] = r[j][i] * (x[i] - x[j]);
x[i] = x[i] % p[i];
if (x[i] < 0)
x[i] += p[i];
}
}
```
So we learned how to calculate digits $x_i$ in $O(k^2)$ time. The number $a$ can now be calculated using the previously mentioned formula
$$a = x_1 + x_2 \cdot p_1 + x_3 \cdot p_1 \cdot p_2 + \ldots + x_k \cdot p_1 \cdots p_{k-1}$$
It is worth noting that in practice, we almost probably need to compute the answer $a$ using [Arbitrary-Precision Arithmetic](big-integer.md), but the digits $x_i$ (because they are small) can usually be calculated using built-in types, and therefore Garner's algorithm is very efficient.
## Implementation of Garner's Algorithm
It is convenient to implement this algorithm using Java, because it has built-in support for large numbers through the `BigInteger` class.
Here we show an implementation that can store big numbers in the form of a set of congruence equations.
It supports addition, subtraction and multiplication.
And with Garner's algorithm we can convert the set of equations into the unique integer.
In this code, we take 100 prime numbers greater than $10^9$, which allows representing numbers as large as $10^{900}$.
```java
final int SZ = 100;
int pr[] = new int[SZ];
int r[][] = new int[SZ][SZ];
void init() {
for (int x = 1000 * 1000 * 1000, i = 0; i < SZ; ++x)
if (BigInteger.valueOf(x).isProbablePrime(100))
pr[i++] = x;
for (int i = 0; i < SZ; ++i)
for (int j = i + 1; j < SZ; ++j)
r[i][j] =
BigInteger.valueOf(pr[i]).modInverse(BigInteger.valueOf(pr[j])).intValue();
}
class Number {
int a[] = new int[SZ];
public Number() {
}
public Number(int n) {
for (int i = 0; i < SZ; ++i)
a[i] = n % pr[i];
}
public Number(BigInteger n) {
for (int i = 0; i < SZ; ++i)
a[i] = n.mod(BigInteger.valueOf(pr[i])).intValue();
}
public Number add(Number n) {
Number result = new Number();
for (int i = 0; i < SZ; ++i)
result.a[i] = (a[i] + n.a[i]) % pr[i];
return result;
}
public Number subtract(Number n) {
Number result = new Number();
for (int i = 0; i < SZ; ++i)
result.a[i] = (a[i] - n.a[i] + pr[i]) % pr[i];
return result;
}
public Number multiply(Number n) {
Number result = new Number();
for (int i = 0; i < SZ; ++i)
result.a[i] = (int)((a[i] * 1l * n.a[i]) % pr[i]);
return result;
}
public BigInteger bigIntegerValue(boolean can_be_negative) {
BigInteger result = BigInteger.ZERO, mult = BigInteger.ONE;
int x[] = new int[SZ];
for (int i = 0; i < SZ; ++i) {
x[i] = a[i];
for (int j = 0; j < i; ++j) {
long cur = (x[i] - x[j]) * 1l * r[j][i];
x[i] = (int)((cur % pr[i] + pr[i]) % pr[i]);
}
result = result.add(mult.multiply(BigInteger.valueOf(x[i])));
mult = mult.multiply(BigInteger.valueOf(pr[i]));
}
if (can_be_negative)
if (result.compareTo(mult.shiftRight(1)) >= 0)
result = result.subtract(mult);
return result;
}
}
```
|
# Garner's algorithm
A consequence of the [Chinese Remainder Theorem](chinese-remainder-theorem.md) is, that we can represent big numbers using an array of small integers.
For example, let $p$ be the product of the first $1000$ primes. $p$ has around $3000$ digits.
Any number $a$ less than $p$ can be represented as an array $a_1, \ldots, a_k$, where $a_i \equiv a \pmod{p_i}$.
But to do this we obviously need to know how to get back the number $a$ from its representation.
One way is discussed in the article about the Chinese Remainder Theorem.
In this article we discuss an alternative, Garner's Algorithm, which can also be used for this purpose.
## Mixed Radix Representation
We can represent the number $a$ in the **mixed radix** representation:
$$a = x_1 + x_2 p_1 + x_3 p_1 p_2 + \ldots + x_k p_1 \cdots p_{k-1} \text{ with }x_i \in [0, p_i)$$
A mixed radix representation is a positional numeral system, that's a generalization of the typical number systems, like the binary numeral system or the decimal numeral system.
For instance the decimal numeral system is a positional numeral system with the radix (or base) 10.
Every a number is represented as a string of digits $d_1 d_2 d_3 \dots d_n$ between $0$ and $9$, and
E.g. the string $415$ represents the number $4 \cdot 10^2 + 1 \cdot 10^1 + 5 \cdot 10^0$.
In general the string of digits $d_1 d_2 d_3 \dots d_n$ represents the number $d_1 b^{n-1} + d_2 b^{n-2} + \cdots + d_n b^0$ in the positional numeral system with radix $b$.
In a mixed radix system, we don't have one radix any more. The base varies from position to position.
## Garner's algorithm
Garner's algorithm computes the digits $x_1, \ldots, x_k$.
Notice, that the digits are relatively small.
The digit $x_i$ is an integer between $0$ and $p_i - 1$.
Let $r_{ij}$ denote the inverse of $p_i$ modulo $p_j$
$$r_{ij} = (p_i)^{-1} \pmod{p_j}$$
which can be found using the algorithm described in [Modular Inverse](module-inverse.md).
Substituting $a$ from the mixed radix representation into the first congruence equation we obtain
$$a_1 \equiv x_1 \pmod{p_1}.$$
Substituting into the second equation yields
$$a_2 \equiv x_1 + x_2 p_1 \pmod{p_2},$$
which can be rewritten by subtracting $x_1$ and dividing by $p_1$ to get
$$\begin{array}{rclr}
a_2 - x_1 &\equiv& x_2 p_1 &\pmod{p_2} \\
(a_2 - x_1) r_{12} &\equiv& x_2 &\pmod{p_2} \\
x_2 &\equiv& (a_2 - x_1) r_{12} &\pmod{p_2}
\end{array}$$
Similarly we get that
$$x_3 \equiv ((a_3 - x_1) r_{13} - x_2) r_{23} \pmod{p_3}.$$
Now, we can clearly see an emerging pattern, which can be expressed by the following code:
```cpp
for (int i = 0; i < k; ++i) {
x[i] = a[i];
for (int j = 0; j < i; ++j) {
x[i] = r[j][i] * (x[i] - x[j]);
x[i] = x[i] % p[i];
if (x[i] < 0)
x[i] += p[i];
}
}
```
So we learned how to calculate digits $x_i$ in $O(k^2)$ time. The number $a$ can now be calculated using the previously mentioned formula
$$a = x_1 + x_2 \cdot p_1 + x_3 \cdot p_1 \cdot p_2 + \ldots + x_k \cdot p_1 \cdots p_{k-1}$$
It is worth noting that in practice, we almost probably need to compute the answer $a$ using [Arbitrary-Precision Arithmetic](big-integer.md), but the digits $x_i$ (because they are small) can usually be calculated using built-in types, and therefore Garner's algorithm is very efficient.
## Implementation of Garner's Algorithm
It is convenient to implement this algorithm using Java, because it has built-in support for large numbers through the `BigInteger` class.
Here we show an implementation that can store big numbers in the form of a set of congruence equations.
It supports addition, subtraction and multiplication.
And with Garner's algorithm we can convert the set of equations into the unique integer.
In this code, we take 100 prime numbers greater than $10^9$, which allows representing numbers as large as $10^{900}$.
```java
final int SZ = 100;
int pr[] = new int[SZ];
int r[][] = new int[SZ][SZ];
void init() {
for (int x = 1000 * 1000 * 1000, i = 0; i < SZ; ++x)
if (BigInteger.valueOf(x).isProbablePrime(100))
pr[i++] = x;
for (int i = 0; i < SZ; ++i)
for (int j = i + 1; j < SZ; ++j)
r[i][j] =
BigInteger.valueOf(pr[i]).modInverse(BigInteger.valueOf(pr[j])).intValue();
}
class Number {
int a[] = new int[SZ];
public Number() {
}
public Number(int n) {
for (int i = 0; i < SZ; ++i)
a[i] = n % pr[i];
}
public Number(BigInteger n) {
for (int i = 0; i < SZ; ++i)
a[i] = n.mod(BigInteger.valueOf(pr[i])).intValue();
}
public Number add(Number n) {
Number result = new Number();
for (int i = 0; i < SZ; ++i)
result.a[i] = (a[i] + n.a[i]) % pr[i];
return result;
}
public Number subtract(Number n) {
Number result = new Number();
for (int i = 0; i < SZ; ++i)
result.a[i] = (a[i] - n.a[i] + pr[i]) % pr[i];
return result;
}
public Number multiply(Number n) {
Number result = new Number();
for (int i = 0; i < SZ; ++i)
result.a[i] = (int)((a[i] * 1l * n.a[i]) % pr[i]);
return result;
}
public BigInteger bigIntegerValue(boolean can_be_negative) {
BigInteger result = BigInteger.ZERO, mult = BigInteger.ONE;
int x[] = new int[SZ];
for (int i = 0; i < SZ; ++i) {
x[i] = a[i];
for (int j = 0; j < i; ++j) {
long cur = (x[i] - x[j]) * 1l * r[j][i];
x[i] = (int)((cur % pr[i] + pr[i]) % pr[i]);
}
result = result.add(mult.multiply(BigInteger.valueOf(x[i])));
mult = mult.multiply(BigInteger.valueOf(pr[i]));
}
if (can_be_negative)
if (result.compareTo(mult.shiftRight(1)) >= 0)
result = result.subtract(mult);
return result;
}
}
```
|
Garner's algorithm
|
---
title
factorial_divisors
---
# Finding Power of Factorial Divisor
You are given two numbers $n$ and $k$. Find the largest power of $k$ $x$ such that $n!$ is divisible by $k^x$.
## Prime $k$ {data-toc-label="Prime k"}
Let's first consider the case of prime $k$. The explicit expression for factorial
$$n! = 1 \cdot 2 \cdot 3 \ldots (n-1) \cdot n$$
Note that every $k$-th element of the product is divisible by $k$, i.e. adds $+1$ to the answer; the number of such elements is $\Bigl\lfloor\dfrac{n}{k}\Bigr\rfloor$.
Next, every $k^2$-th element is divisible by $k^2$, i.e. adds another $+1$ to the answer (the first power of $k$ has already been counted in the previous paragraph). The number of such elements is $\Bigl\lfloor\dfrac{n}{k^2}\Bigr\rfloor$.
And so on, for every $i$ each $k^i$-th element adds another $+1$ to the answer, and there are $\Bigl\lfloor\dfrac{n}{k^i}\Bigr\rfloor$ such elements.
The final answer is
$$\Bigl\lfloor\dfrac{n}{k}\Bigr\rfloor + \Bigl\lfloor\dfrac{n}{k^2}\Bigr\rfloor + \ldots + \Bigl\lfloor\dfrac{n}{k^i}\Bigr\rfloor + \ldots$$
This result is also known as [Legendre's formula](https://en.wikipedia.org/wiki/Legendre%27s_formula).
The sum is of course finite, since only approximately the first $\log_k n$ elements are not zeros. Thus, the runtime of this algorithm is $O(\log_k n)$.
### Implementation
```cpp
int fact_pow (int n, int k) {
int res = 0;
while (n) {
n /= k;
res += n;
}
return res;
}
```
## Composite $k$ {data-toc-label="Composite k"}
The same idea can't be applied directly. Instead we can factor $k$, representing it as $k = k_1^{p_1} \cdot \ldots \cdot k_m^{p_m}$. For each $k_i$, we find the number of times it is present in $n!$ using the algorithm described above - let's call this value $a_i$. The answer for composite $k$ will be
$$\min_ {i=1 \ldots m} \dfrac{a_i}{p_i}$$
|
---
title
factorial_divisors
---
# Finding Power of Factorial Divisor
You are given two numbers $n$ and $k$. Find the largest power of $k$ $x$ such that $n!$ is divisible by $k^x$.
## Prime $k$ {data-toc-label="Prime k"}
Let's first consider the case of prime $k$. The explicit expression for factorial
$$n! = 1 \cdot 2 \cdot 3 \ldots (n-1) \cdot n$$
Note that every $k$-th element of the product is divisible by $k$, i.e. adds $+1$ to the answer; the number of such elements is $\Bigl\lfloor\dfrac{n}{k}\Bigr\rfloor$.
Next, every $k^2$-th element is divisible by $k^2$, i.e. adds another $+1$ to the answer (the first power of $k$ has already been counted in the previous paragraph). The number of such elements is $\Bigl\lfloor\dfrac{n}{k^2}\Bigr\rfloor$.
And so on, for every $i$ each $k^i$-th element adds another $+1$ to the answer, and there are $\Bigl\lfloor\dfrac{n}{k^i}\Bigr\rfloor$ such elements.
The final answer is
$$\Bigl\lfloor\dfrac{n}{k}\Bigr\rfloor + \Bigl\lfloor\dfrac{n}{k^2}\Bigr\rfloor + \ldots + \Bigl\lfloor\dfrac{n}{k^i}\Bigr\rfloor + \ldots$$
This result is also known as [Legendre's formula](https://en.wikipedia.org/wiki/Legendre%27s_formula).
The sum is of course finite, since only approximately the first $\log_k n$ elements are not zeros. Thus, the runtime of this algorithm is $O(\log_k n)$.
### Implementation
```cpp
int fact_pow (int n, int k) {
int res = 0;
while (n) {
n /= k;
res += n;
}
return res;
}
```
## Composite $k$ {data-toc-label="Composite k"}
The same idea can't be applied directly. Instead we can factor $k$, representing it as $k = k_1^{p_1} \cdot \ldots \cdot k_m^{p_m}$. For each $k_i$, we find the number of times it is present in $n!$ using the algorithm described above - let's call this value $a_i$. The answer for composite $k$ will be
$$\min_ {i=1 \ldots m} \dfrac{a_i}{p_i}$$
|
Finding Power of Factorial Divisor
|
---
title
- Original
---
# Operations on polynomials and series
Problems in competitive programming, especially the ones involving enumeration some kind, are often solved by reducing the problem to computing something on polynomials and formal power series.
This includes concepts such as polynomial multiplication, interpolation, and more complicated ones, such as polynomial logarithms and exponents. In this article, a brief overview of such operations and common approaches to them is presented.
## Basic Notion and facts
In this section, we focus more on the definitions and "intuitive" properties of various polynomial operations. The technical details of their implementation and complexities will be covered in later sections.
### Polynomial multiplication
!!! info "Definition"
**Univariate polynomial** is an expression of form $A(x) = a_0 + a_1 x + \dots + a_n x^n$.
The values $a_0, \dots, a_n$ are polynomial coefficients, typically taken from some set of numbers or number-like structures. In this article, we assume that the coefficients are taken from some [field](https://en.wikipedia.org/wiki/Field_(mathematics)), meaning that operations of addition, subtraction, multiplication and division are well-defined for them (except for division by $0$) and they generally behave in a similar way to real numbers.
Typical example of such field is the field of remainders modulo prime number $p$.
For simplicity we will drop the term _univariate_, as this is the only kind of polynomials we consider in this article. We will also write $A$ instead of $A(x)$ wherever possible, which will be understandable from the context. It is assumed that either $a_n \neq 0$ or $A(x)=0$.
!!! info "Definition"
The **product** of two polynomials is defined by expanding it as an arithmetic expression:
$$
A(x) B(x) = \left(\sum\limits_{i=0}^n a_i x^i \right)\left(\sum\limits_{j=0}^m b_j x^j\right) = \sum\limits_{i,j} a_i b_j x^{i+j} = \sum\limits_{k=0}^{n+m} c_k x^k = C(x).
$$
The sequence $c_0, c_1, \dots, c_{n+m}$ of the coefficients of $C(x)$ is called the **convolution** of $a_0, \dots, a_n$ and $b_0, \dots, b_m$.
!!! info "Definition"
The **degree** of a polynomial $A$ with $a_n \neq 0$ is defined as $\deg A = n$.
For consistency, degree of $A(x) = 0$ is defined as $\deg A = -\infty$.
In this notion, $\deg AB = \deg A + \deg B$ for any polynomials $A$ and $B$.
Convolutions are the basis of solving many enumerative problems.
!!! Example
You have $n$ objects of the first kind and $m$ objects of the second kind.
Objects of first kind are valued $a_1, \dots, a_n$, and objects of the second kind are valued $b_1, \dots, b_m$.
You pick a single object of the first kind and a single object of the second kind. How many ways are there to get the total value $k$?
??? hint "Solution"
Consider the product $(x^{a_1} + \dots + x^{a_n})(x^{b_1} + \dots + x^{b_m})$. If you expand it, each monomial will correspond to the pair $(a_i, b_j)$ and contribute to the coefficient near $x^{a_i+b_j}$. In other words, the answer is the coefficient near $x^k$ in the product.
!!! Example
You throw a $6$-sided die $n$ times and sum up the results from all throws. What is the probability of getting sum of $k$?
??? hint "Solution"
The answer is the number of outcomes having the sum $k$, divided by the total number of outcomes, which is $6^n$.
What is the number of outcomes having the sum $k$? For $n=1$, it may be represented by a polynomial $A(x) = x^1+x^2+\dots+x^6$.
For $n=2$, using the same approach as in the example above, we conclude that it is represented by the polynomial $(x^1+x^2+\dots+x^6)^2$.
That being said, the answer to the problem is the $k$-th coefficient of $(x^1+x^2+\dots+x^6)^n$, divided by $6^n$.
The coefficient near $x^k$ in the polynomial $A(x)$ is denoted shortly as $[x^k]A$.
### Formal power series
!!! info "Definition"
A **formal power series** is an infinite sum $A(x) = a_0 + a_1 x + a_2 x^2 + \dots$, considered regardless of its convergence properties.
In other words, when we consider e.g. a sum $1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\dots=2$, we imply that it _converges_ to $2$ when the number of summands approach infinity. However, formal series are only considered in terms of sequences that make them.
!!! info "Definition"
The **product** of formal power series $A(x)$ and $B(x)$, is also defined by expanding it as an arithmetic expression:
$$
A(x) B(x) = \left(\sum\limits_{i=0}^\infty a_i x^i \right)\left(\sum\limits_{j=0}^\infty b_j x^j\right) = \sum\limits_{i,j} a_i b_j x^{i+j} = \sum\limits_{k=0}^{\infty} c_k x^k = C(x),
$$
where the coefficients $c_0, c_1, \dots$ are define as finite sums
$$
c_k = \sum\limits_{i=0}^k a_i b_{k-i}.
$$
The sequence $c_0, c_1, \dots$ is also called a **convolution** of $a_0, a_1, \dots$ and $b_0, b_1, \dots$, generalizing the concept to infinite sequences.
Thus, polynomials may be considered formal power series, but with finite number of coefficients.
Formal power series play a crucial role in enumerative combinatorics, where they're studied as [generating functions](https://en.wikipedia.org/wiki/Generating_function) for various sequences. Detailed explanation of generating functions and the intuition behind them will, unfortunately, be out of scope for this article, therefore the curious reader is referenced e.g. [here](https://codeforces.com/blog/entry/103979) for details about their combinatorial meaning.
However, we will very briefly mention that if $A(x)$ and $B(x)$ are generating functions for sequences that enumerate some objects by number of "atoms" in them (e.g. trees by the number of vertices), then the product $A(x) B(x)$ enumerates objects that can be described as pairs of objects of kinds $A$ and $B$, enumerates by the total number of "atoms" in the pair.
!!! Example
Let $A(x) = \sum\limits_{i=0}^\infty 2^i x^i$ enumerate packs of stones, each stone colored in one of $2$ colors (so, there are $2^i$ such packs of size $i$) and $B(x) = \sum\limits_{j=0}^{\infty} 3^j x^j$ enumerate packs of stones, each stone colored in one of $3$ colors. Then $C(x) = A(x) B(x) = \sum\limits_{k=0}^\infty c_k x^k$ would enumerate objects that may be described as "two packs of stones, first pack only of stones of type $A$, second pack only of stones of type $B$, with total number of stones being $k$" for $c_k$.
In a similar way, there is an intuitive meaning to some other functions over formal power series.
### Long polynomial division
Similar to integers, it is possible to define long division on polynomials.
!!! info "Definition"
For any polynomials $A$ and $B \neq 0$, one may represent $A$ as
$$
A = D \cdot B + R,~ \deg R < \deg B,
$$
where $R$ is called the **remainder** of $A$ modulo $B$ and $D$ is called the **quotient**.
Denoting $\deg A = n$ and $\deg B = m$, naive way to do it is to use long division, during which you multiply $B$ by the monomial $\frac{a_n}{b_m} x^{n - m}$ and subtract it from $A$, until the degree of $A$ is smaller than that of $B$. What remains of $A$ in the end will be the remainder (hence the name), and the polynomials with which you multiplied $B$ in the process, summed together, form the quotient.
!!! info "Definition"
If $A$ and $B$ have the same remainder modulo $C$, they're said to be **equivalent** modulo $C$, which is denoted as
$$
A \equiv B \pmod{C}.
$$
Polynomial long division is useful because of its many important properties:
- $A$ is a multiple of $B$ if and only if $A \equiv 0 \pmod B$.
- It implies that $A \equiv B \pmod C$ if and only if $A-B$ is a multiple of $C$.
- In particular, $A \equiv B \pmod{C \cdot D}$ implies $A \equiv B \pmod{C}$.
- For any linear polynomial $x-r$ it holds that $A(x) \equiv A(r) \pmod{x-r}$.
- It implies that $A$ is a multiple of $x-r$ if and only if $A(r)=0$.
- For modulo being $x^k$, it holds that $A \equiv a_0 + a_1 x + \dots + a_{k-1} x^{k-1} \pmod{x^k}$.
Note that long division can't be properly defined for formal power series. Instead, for any $A(x)$ such that $a_0 \neq 0$, it is possible to define an inverse formal power series $A^{-1}(x)$, such that $A(x) A^{-1}(x) = 1$. This fact, in turn, can be used to compute the result of long division for polynomials.
## Basic implementation
[Here](https://github.com/cp-algorithms/cp-algorithms-aux/blob/master/src/polynomial.cpp) you can find the basic implementation of polynomial algebra.
It supports all trivial operations and some other useful methods. The main class is `poly<T>` for polynomials with coefficients of type `T`.
All arithmetic operation `+`, `-`, `*`, `%` and `/` are supported, `%` and `/` standing for remainder and quotient in Euclidean division.
There is also the class `modular<m>` for performing arithmetic operations on remainders modulo a prime number `m`.
Other useful functions:
- `deriv()`: computes the derivative $P'(x)$ of $P(x)$.
- `integr()`: computes the indefinite integral $Q(x) = \int P(x)$ of $P(x)$ such that $Q(0)=0$.
- `inv(size_t n)`: calculate the first $n$ coefficients of $P^{-1}(x)$ in $O(n \log n)$.
- `log(size_t n)`: calculate the first $n$ coefficients of $\ln P(x)$ in $O(n \log n)$.
- `exp(size_t n)`: calculate the first $n$ coefficients of $\exp P(x)$ in $O(n \log n)$.
- `pow(size_t k, size_t n)`: calculate the first $n$ coefficients for $P^{k}(x)$ in $O(n \log nk)$.
- `deg()`: returns the degree of $P(x)$.
- `lead()`: returns the coefficient of $x^{\deg P(x)}$.
- `resultant(poly<T> a, poly<T> b)`: computes the resultant of $a$ and $b$ in $O(|a| \cdot |b|)$.
- `bpow(T x, size_t n)`: computes $x^n$.
- `bpow(T x, size_t n, T m)`: computes $x^n \pmod{m}$.
- `chirpz(T z, size_t n)`: computes $P(1), P(z), P(z^2), \dots, P(z^{n-1})$ in $O(n \log n)$.
- `vector<T> eval(vector<T> x)`: evaluates $P(x_1), \dots, P(x_n)$ in $O(n \log^2 n)$.
- `poly<T> inter(vector<T> x, vector<T> y)`: interpolates a polynomial by a set of pairs $P(x_i) = y_i$ in $O(n \log^2 n)$.
- And some more, feel free to explore the code!
## Arithmetic
### Multiplication
The very core operation is the multiplication of two polynomials. That is, given the polynomials $A$ and $B$:
$$A = a_0 + a_1 x + \dots + a_n x^n$$
$$B = b_0 + b_1 x + \dots + b_m x^m$$
You have to compute polynomial $C = A \cdot B$, which is defined as
$$\boxed{C = \sum\limits_{i=0}^n \sum\limits_{j=0}^m a_i b_j x^{i+j}} = c_0 + c_1 x + \dots + c_{n+m} x^{n+m}.$$
It can be computed in $O(n \log n)$ via the [Fast Fourier transform](fft.md) and almost all methods here will use it as subroutine.
### Inverse series
If $A(0) \neq 0$ there always exists an infinite formal power series $A^{-1}(x) = q_0+q_1 x + q_2 x^2 + \dots$ such that $A^{-1} A = 1$. It often proves useful to compute first $k$ coefficients of $A^{-1}$ (that is, to compute it modulo $x^k$). There are two major ways to calculate it.
#### Divide and conquer
This algorithm was mentioned in [Schönhage's article](http://algo.inria.fr/seminars/sem00-01/schoenhage.pdf) and is inspired by [Graeffe's method](https://en.wikipedia.org/wiki/Graeffe's_method). It is known that for $B(x)=A(x)A(-x)$ it holds that $B(x)=B(-x)$, that is, $B(x)$ is an even polynomial. It means that it only has non-zero coefficients with even numbers and can be represented as $B(x)=T(x^2)$. Thus, we can do the following transition:
$$A^{-1}(x) \equiv \frac{1}{A(x)} \equiv \frac{A(-x)}{A(x)A(-x)} \equiv \frac{A(-x)}{T(x^2)} \pmod{x^k}$$
Note that $T(x)$ can be computed with a single multiplication, after which we're only interested in the first half of coefficients of its inverse series. This effectively reduces the initial problem of computing $A^{-1} \pmod{x^k}$ to computing $T^{-1} \pmod{x^{\lfloor k / 2 \rfloor}}$.
The complexity of this method can be estimated as
$$T(n) = T(n/2) + O(n \log n) = O(n \log n).$$
#### Sieveking–Kung algorithm
The generic process described here is known as Hensel lifting, as it follows from Hensel's lemma. We'll cover it in more detail further below, but for now let's focus on ad hoc solution. "Lifting" part here means that we start with the approximation $B_0=q_0=a_0^{-1}$, which is $A^{-1} \pmod x$ and then iteratively lift from $\bmod x^a$ to $\bmod x^{2a}$.
Let $B_k \equiv A^{-1} \pmod{x^a}$. The next approximation needs to follow the equation $A B_{k+1} \equiv 1 \pmod{x^{2a}}$ and may be represented as $B_{k+1} = B_k + x^a C$. From this follows the equation
$$A(B_k + x^{a}C) \equiv 1 \pmod{x^{2a}}.$$
Let $A B_k \equiv 1 + x^a D \pmod{x^{2a}}$, then the equation above implies
$$x^a(D+AC) \equiv 0 \pmod{x^{2a}} \implies D \equiv -AC \pmod{x^a} \implies C \equiv -B_k D \pmod{x^a}.$$
From this, one can obtain the final formula, which is
$$x^a C \equiv -B_k x^a D \equiv B_k(1-AB_k) \pmod{x^{2a}} \implies \boxed{B_{k+1} \equiv B_k(2-AB_k) \pmod{x^{2a}}}$$
Thus starting with $B_0 \equiv a_0^{-1} \pmod x$ we will compute the sequence $B_k$ such that $AB_k \equiv 1 \pmod{x^{2^k}}$ with the complexity
$$T(n) = T(n/2) + O(n \log n) = O(n \log n).$$
The algorithm here might seem a bit more complicated than the first one, but it has a very solid and practical reasoning behind it, as well as a great generalization potential if looked from a different perspective, which would be explained further below.
### Euclidean division
Consider two polynomials $A(x)$ and $B(x)$ of degrees $n$ and $m$. As it was said earlier you can rewrite $A(x)$ as
$$A(x) = B(x) D(x) + R(x), \deg R < \deg B.$$
Let $n \geq m$, it would imply that $\deg D = n - m$ and the leading $n-m+1$ coefficients of $A$ don't influence $R$. It means that you can recover $D(x)$ from the largest $n-m+1$ coefficients of $A(x)$ and $B(x)$ if you consider it as a system of equations.
The system of linear equations we're talking about can be written in the following form:
$$\begin{bmatrix} a_n \\ \vdots \\ a_{m+1} \\ a_{m} \end{bmatrix} = \begin{bmatrix}
b_m & \dots & 0 & 0 \\
\vdots & \ddots & \vdots & \vdots \\
\dots & \dots & b_m & 0 \\
\dots & \dots & b_{m-1} & b_m
\end{bmatrix} \begin{bmatrix}d_{n-m} \\ \vdots \\ d_1 \\ d_0\end{bmatrix}$$
From the looks of it, we can conclude that with the introduction of reversed polynomials
$$A^R(x) = x^nA(x^{-1})= a_n + a_{n-1} x + \dots + a_0 x^n$$
$$B^R(x) = x^m B(x^{-1}) = b_m + b_{m-1} x + \dots + b_0 x^m$$
$$D^R(x) = x^{n-m}D(x^{-1}) = d_{n-m} + d_{n-m-1} x + \dots + d_0 x^{n-m}$$
the system may be rewritten as
$$A^R(x) \equiv B^R(x) D^R(x) \pmod{x^{n-m+1}}.$$
From this you can unambiguously recover all coefficients of $D(x)$:
$$\boxed{D^R(x) \equiv A^R(x) (B^R(x))^{-1} \pmod{x^{n-m+1}}}$$
And from this, in turn, you can recover $R(x)$ as $R(x) = A(x) - B(x)D(x)$.
Note that the matrix above is a so-called triangular [Toeplitz matrix](https://en.wikipedia.org/wiki/Toeplitz_matrix) and, as we see here, solving system of linear equations with arbitrary Toeplitz matrix is, in fact, equivalent to polynomial inversion. Moreover, inverse matrix of it would also be triangular Toeplitz matrix and its entries, in terms used above, are the coefficients of $(B^R(x))^{-1} \pmod{x^{n-m+1}}$.
## Calculating functions of polynomial
### Newton's method
Let's generalize the Sieveking–Kung algorithm. Consider equation $F(P) = 0$ where $P(x)$ should be a polynomial and $F(x)$ is some polynomial-valued function defined as
$$F(x) = \sum\limits_{i=0}^\infty \alpha_i (x-\beta)^i,$$
where $\beta$ is some constant. It can be proven that if we introduce a new formal variable $y$, we can express $F(x)$ as
$$F(x) = F(y) + (x-y)F'(y) + (x-y)^2 G(x,y),$$
where $F'(x)$ is the derivative formal power series defined as
$$F'(x) = \sum\limits_{i=0}^\infty (i+1)\alpha_{i+1}(x-\beta)^i,$$
and $G(x, y)$ is some formal power series of $x$ and $y$. With this result we can find the solution iteratively.
Let $F(Q_k) \equiv 0 \pmod{x^{a}}$. We need to find $Q_{k+1} \equiv Q_k + x^a C \pmod{x^{2a}}$ such that $F(Q_{k+1}) \equiv 0 \pmod{x^{2a}}$.
Substituting $x = Q_{k+1}$ and $y=Q_k$ in the formula above, we get
$$F(Q_{k+1}) \equiv F(Q_k) + (Q_{k+1} - Q_k) F'(Q_k) + (Q_{k+1} - Q_k)^2 G(x, y) \pmod x^{2a}.$$
Since $Q_{k+1} - Q_k \equiv 0 \pmod{x^a}$, it also holds that $(Q_{k+1} - Q_k)^2 \equiv 0 \pmod{x^{2a}}$, thus
$$0 \equiv F(Q_{k+1}) \equiv F(Q_k) + (Q_{k+1} - Q_k) F'(Q_k) \pmod{x^{2a}}.$$
The last formula gives us the value of $Q_{k+1}$:
$$\boxed{Q_{k+1} = Q_k - \dfrac{F(Q_k)}{F'(Q_k)} \pmod{x^{2a}}}$$
Thus, knowing how to invert polynomials and how to compute $F(Q_k)$, we can find $n$ coefficients of $P$ with the complexity
$$T(n) = T(n/2) + f(n),$$
where $f(n)$ is the time needed to compute $F(Q_k)$ and $F'(Q_k)^{-1}$ which is usually $O(n \log n)$.
The iterative rule above is known in numerical analysis as [Newton's method](https://en.wikipedia.org/wiki/Newton%27s_method).
#### Hensel's lemma
As was mentioned earlier, formally and generically this result is known as [Hensel's lemma](https://en.wikipedia.org/wiki/Hensel%27s_lemma) and it may in fact used in even broader sense when we work with a series of nested rings. In this particular case we worked with a sequence of polynomial remainders modulo $x$, $x^2$, $x^3$ and so on.
Another example where Hensel's lifting might be helpful are so-called [p-adic numbers](https://en.wikipedia.org/wiki/P-adic_number) where we, in fact, work with the sequence of integer remainders modulo $p$, $p^2$, $p^3$ and so on. For example, Newton's method can be used to find all possible [automorphic numbers](https://en.wikipedia.org/wiki/Automorphic_number) (numbers that end on itself when squared) with a given number base. The problem is left as an exercise to the reader. You might consider [this](https://acm.timus.ru/problem.aspx?space=1&num=1698) problem to check if your solution works for $10$-based numbers.
### Logarithm
For the function $\ln P(x)$ it's known that:
$$
\boxed{(\ln P(x))' = \dfrac{P'(x)}{P(x)}}
$$
Thus we can calculate $n$ coefficients of $\ln P(x)$ in $O(n \log n)$.
### Inverse series
Turns out, we can get the formula for $A^{-1}$ using Newton's method.
For this we take the equation $A=Q^{-1}$, thus:
$$F(Q) = Q^{-1} - A$$
$$F'(Q) = -Q^{-2}$$
$$\boxed{Q_{k+1} \equiv Q_k(2-AQ_k) \pmod{x^{2^{k+1}}}}$$
### Exponent
Let's learn to calculate $e^{P(x)}=Q(x)$. It should hold that $\ln Q = P$, thus:
$$F(Q) = \ln Q - P$$
$$F'(Q) = Q^{-1}$$
$$\boxed{Q_{k+1} \equiv Q_k(1 + P - \ln Q_k) \pmod{x^{2^{k+1}}}}$$
### $k$-th power { data-toc-label="k-th power" }
Now we need to calculate $P^k(x)=Q$. This may be done via the following formula:
$$Q = \exp\left[k \ln P(x)\right]$$
Note though, that you can calculate the logarithms and the exponents correctly only if you can find some initial $Q_0$.
To find it, you should calculate the logarithm or the exponent of the constant coefficient of the polynomial.
But the only reasonable way to do it is if $P(0)=1$ for $Q = \ln P$ so $Q(0)=0$ and if $P(0)=0$ for $Q = e^P$ so $Q(0)=1$.
Thus you can use formula above only if $P(0) = 1$. Otherwise if $P(x) = \alpha x^t T(x)$ where $T(0)=1$ you can write that:
$$\boxed{P^k(x) = \alpha^kx^{kt} \exp[k \ln T(x)]}$$
Note that you also can calculate some $k$-th root of a polynomial if you can calculate $\sqrt[k]{\alpha}$, for example for $\alpha=1$.
## Evaluation and Interpolation
### Chirp-z Transform
For the particular case when you need to evaluate a polynomial in the points $x_r = z^{2r}$ you can do the following:
$$A(z^{2r}) = \sum\limits_{k=0}^n a_k z^{2kr}$$
Let's substitute $2kr = r^2+k^2-(r-k)^2$. Then this sum rewrites as:
$$\boxed{A(z^{2r}) = z^{r^2}\sum\limits_{k=0}^n (a_k z^{k^2}) z^{-(r-k)^2}}$$
Which is up to the factor $z^{r^2}$ equal to the convolution of the sequences $u_k = a_k z^{k^2}$ and $v_k = z^{-k^2}$.
Note that $u_k$ has indexes from $0$ to $n$ here and $v_k$ has indexes from $-n$ to $m$ where $m$ is the maximum power of $z$ which you need.
Now if you need to evaluate a polynomial in the points $x_r = z^{2r+1}$ you can reduce it to the previous task by the transformation $a_k \to a_k z^k$.
It gives us an $O(n \log n)$ algorithm when you need to compute values in powers of $z$, thus you may compute the DFT for non-powers of two.
Another observation is that $kr = \binom{k+r}{2} - \binom{k}{2} - \binom{r}{2}$. Then we have
$$\boxed{A(z^r) = z^{-\binom{r}{2}}\sum\limits_{k=0}^n \left(a_k z^{-\binom{k}{2}}\right)z^{\binom{k+r}{2}}}$$
The coefficient of $x^{n+r}$ of the product of the polynomials $A_0(x) = \sum\limits_{k=0}^n a_{n-k}z^{-\binom{n-k}{2}}x^k$ and $A_1(x) = \sum\limits_{k\geq 0}z^{\binom{k}{2}}x^k$ equals $z^{\binom{r}{2}}A(z^r)$. You can use the formula $z^{\binom{k+1}{2}}=z^{\binom{k}{2}+k}$ to calculate the coefficients of $A_0(x)$ and $A_1(x)$.
### Multi-point Evaluation
Assume you need to calculate $A(x_1), \dots, A(x_n)$. As mentioned earlier, $A(x) \equiv A(x_i) \pmod{x-x_i}$. Thus you may do the following:
1. Compute a segment tree such that in the segment $[l,r)$ stands the product $P_{l, r}(x) = (x-x_l)(x-x_{l+1})\dots(x-x_{r-1})$.
2. Starting with $l=1$ and $r=n+1$ at the root node. Let $m=\lfloor(l+r)/2\rfloor$. Let's move down to $[l,m)$ with the polynomial $A(x) \pmod{P_{l,m}(x)}$.
3. This will recursively compute $A(x_l), \dots, A(x_{m-1})$, now do the same for $[m,r)$ with $A(x) \pmod{P_{m,r}(x)}$.
4. Concatenate the results from the first and second recursive call and return them.
The whole procedure will run in $O(n \log^2 n)$.
### Interpolation
There's a direct formula by Lagrange to interpolate a polynomial, given set of pairs $(x_i, y_i)$:
$$\boxed{A(x) = \sum\limits_{i=1}^n y_i \prod\limits_{j \neq i}\dfrac{x-x_j}{x_i - x_j}}$$
Computing it directly is a hard thing but turns out, we may compute it in $O(n \log^2 n)$ with a divide and conquer approach:
Consider $P(x) = (x-x_1)\dots(x-x_n)$. To know the coefficients of the denominators in $A(x)$ we should compute products like:
$$
P_i = \prod\limits_{j \neq i} (x_i-x_j)
$$
But if you consider the derivative $P'(x)$ you'll find out that $P'(x_i) = P_i$. Thus you can compute $P_i$'s via evaluation in $O(n \log^2 n)$.
Now consider the recursive algorithm done on same segment tree as in the multi-point evaluation. It starts in the leaves with the value $\dfrac{y_i}{P_i}$ in each leaf.
When we return from the recursion we should merge the results from the left and the right vertices as $A_{l,r} = A_{l,m}P_{m,r} + P_{l,m} A_{m,r}$.
In this way when you return back to the root you'll have exactly $A(x)$ in it.
The total procedure also works in $O(n \log^2 n)$.
## GCD and Resultants
Assume you're given polynomials $A(x) = a_0 + a_1 x + \dots + a_n x^n$ and $B(x) = b_0 + b_1 x + \dots + b_m x^m$.
Let $\lambda_0, \dots, \lambda_n$ be the roots of $A(x)$ and let $\mu_0, \dots, \mu_m$ be the roots of $B(x)$ counted with their multiplicities.
You want to know if $A(x)$ and $B(x)$ have any roots in common. There are two interconnected ways to do that.
### Euclidean algorithm
Well, we already have an [article](euclid-algorithm.md) about it. For an arbitrary domain you can write the Euclidean algorithm as easy as:
```cpp
template<typename T>
T gcd(const T &a, const T &b) {
return b == T(0) ? a : gcd(b, a % b);
}
```
It can be proven that for polynomials $A(x)$ and $B(x)$ it will work in $O(nm)$.
### Resultant
Let's calculate the product $A(\mu_0)\cdots A(\mu_m)$. It will be equal to zero if and only if some $\mu_i$ is the root of $A(x)$.
For symmetry we can also multiply it with $b_m^n$ and rewrite the whole product in the following form:
$$\boxed{\mathcal{R}(A, B) = b_m^n\prod\limits_{j=0}^m A(\mu_j) = b_m^n a_m^n \prod\limits_{i=0}^n \prod\limits_{j=0}^m (\mu_j - \lambda_i)= (-1)^{mn}a_n^m \prod\limits_{i=0}^n B(\lambda_i)}$$
The value defined above is called the resultant of the polynomials $A(x)$ and $B(x)$. From the definition you may find the following properties:
1. $\mathcal R(A, B) = (-1)^{nm} \mathcal R(B, A)$.
2. $\mathcal R(A, B)= a_n^m b_m^n$ when $n=0$ or $m=0$.
3. If $b_m=1$ then $\mathcal R(A - CB, B) = \mathcal R(A, B)$ for an arbitrary polynomial $C(x)$ and $n,m \geq 1$.
4. From this follows $\mathcal R(A, B) = b_m^{\deg(A) - \deg(A-CB)}\mathcal R(A - CB, B)$ for arbitrary $A(x)$, $B(x)$, $C(x)$.
Miraculously it means that resultant of two polynomials is actually always from the same ring as their coefficients!
Also these properties allow us to calculate the resultant alongside the Euclidean algorithm, which works in $O(nm)$.
```cpp
template<typename T>
T resultant(poly<T> a, poly<T> b) {
if(b.is_zero()) {
return 0;
} else if(b.deg() == 0) {
return bpow(b.lead(), a.deg());
} else {
int pw = a.deg();
a %= b;
pw -= a.deg();
base mul = bpow(b.lead(), pw) * base((b.deg() & a.deg() & 1) ? -1 : 1);
base ans = resultant(b, a);
return ans * mul;
}
}
```
### Half-GCD algorithm
There is a way to calculate the GCD and resultants in $O(n \log^2 n)$.
The procedure to do so implements a $2 \times 2$ linear transform which maps a pair of polynomials $a(x)$, $b(x)$ into another pair $c(x), d(x)$ such that $\deg d(x) \leq \frac{\deg a(x)}{2}$. If you're careful enough, you can compute the half-GCD of any pair of polynomials with at most $2$ recursive calls to the polynomials which are at least $2$ times smaller.
The specific details of the algorithm are somewhat tedious to explain, however you can find its implementation in the library, as `half_gcd` function.
After half-GCD is implemented, you can repeatedly apply it to polynomials until you're reduced to the pair of $\gcd(a, b)$ and $0$.
|
---
title
- Original
---
# Operations on polynomials and series
Problems in competitive programming, especially the ones involving enumeration some kind, are often solved by reducing the problem to computing something on polynomials and formal power series.
This includes concepts such as polynomial multiplication, interpolation, and more complicated ones, such as polynomial logarithms and exponents. In this article, a brief overview of such operations and common approaches to them is presented.
## Basic Notion and facts
In this section, we focus more on the definitions and "intuitive" properties of various polynomial operations. The technical details of their implementation and complexities will be covered in later sections.
### Polynomial multiplication
!!! info "Definition"
**Univariate polynomial** is an expression of form $A(x) = a_0 + a_1 x + \dots + a_n x^n$.
The values $a_0, \dots, a_n$ are polynomial coefficients, typically taken from some set of numbers or number-like structures. In this article, we assume that the coefficients are taken from some [field](https://en.wikipedia.org/wiki/Field_(mathematics)), meaning that operations of addition, subtraction, multiplication and division are well-defined for them (except for division by $0$) and they generally behave in a similar way to real numbers.
Typical example of such field is the field of remainders modulo prime number $p$.
For simplicity we will drop the term _univariate_, as this is the only kind of polynomials we consider in this article. We will also write $A$ instead of $A(x)$ wherever possible, which will be understandable from the context. It is assumed that either $a_n \neq 0$ or $A(x)=0$.
!!! info "Definition"
The **product** of two polynomials is defined by expanding it as an arithmetic expression:
$$
A(x) B(x) = \left(\sum\limits_{i=0}^n a_i x^i \right)\left(\sum\limits_{j=0}^m b_j x^j\right) = \sum\limits_{i,j} a_i b_j x^{i+j} = \sum\limits_{k=0}^{n+m} c_k x^k = C(x).
$$
The sequence $c_0, c_1, \dots, c_{n+m}$ of the coefficients of $C(x)$ is called the **convolution** of $a_0, \dots, a_n$ and $b_0, \dots, b_m$.
!!! info "Definition"
The **degree** of a polynomial $A$ with $a_n \neq 0$ is defined as $\deg A = n$.
For consistency, degree of $A(x) = 0$ is defined as $\deg A = -\infty$.
In this notion, $\deg AB = \deg A + \deg B$ for any polynomials $A$ and $B$.
Convolutions are the basis of solving many enumerative problems.
!!! Example
You have $n$ objects of the first kind and $m$ objects of the second kind.
Objects of first kind are valued $a_1, \dots, a_n$, and objects of the second kind are valued $b_1, \dots, b_m$.
You pick a single object of the first kind and a single object of the second kind. How many ways are there to get the total value $k$?
??? hint "Solution"
Consider the product $(x^{a_1} + \dots + x^{a_n})(x^{b_1} + \dots + x^{b_m})$. If you expand it, each monomial will correspond to the pair $(a_i, b_j)$ and contribute to the coefficient near $x^{a_i+b_j}$. In other words, the answer is the coefficient near $x^k$ in the product.
!!! Example
You throw a $6$-sided die $n$ times and sum up the results from all throws. What is the probability of getting sum of $k$?
??? hint "Solution"
The answer is the number of outcomes having the sum $k$, divided by the total number of outcomes, which is $6^n$.
What is the number of outcomes having the sum $k$? For $n=1$, it may be represented by a polynomial $A(x) = x^1+x^2+\dots+x^6$.
For $n=2$, using the same approach as in the example above, we conclude that it is represented by the polynomial $(x^1+x^2+\dots+x^6)^2$.
That being said, the answer to the problem is the $k$-th coefficient of $(x^1+x^2+\dots+x^6)^n$, divided by $6^n$.
The coefficient near $x^k$ in the polynomial $A(x)$ is denoted shortly as $[x^k]A$.
### Formal power series
!!! info "Definition"
A **formal power series** is an infinite sum $A(x) = a_0 + a_1 x + a_2 x^2 + \dots$, considered regardless of its convergence properties.
In other words, when we consider e.g. a sum $1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\dots=2$, we imply that it _converges_ to $2$ when the number of summands approach infinity. However, formal series are only considered in terms of sequences that make them.
!!! info "Definition"
The **product** of formal power series $A(x)$ and $B(x)$, is also defined by expanding it as an arithmetic expression:
$$
A(x) B(x) = \left(\sum\limits_{i=0}^\infty a_i x^i \right)\left(\sum\limits_{j=0}^\infty b_j x^j\right) = \sum\limits_{i,j} a_i b_j x^{i+j} = \sum\limits_{k=0}^{\infty} c_k x^k = C(x),
$$
where the coefficients $c_0, c_1, \dots$ are define as finite sums
$$
c_k = \sum\limits_{i=0}^k a_i b_{k-i}.
$$
The sequence $c_0, c_1, \dots$ is also called a **convolution** of $a_0, a_1, \dots$ and $b_0, b_1, \dots$, generalizing the concept to infinite sequences.
Thus, polynomials may be considered formal power series, but with finite number of coefficients.
Formal power series play a crucial role in enumerative combinatorics, where they're studied as [generating functions](https://en.wikipedia.org/wiki/Generating_function) for various sequences. Detailed explanation of generating functions and the intuition behind them will, unfortunately, be out of scope for this article, therefore the curious reader is referenced e.g. [here](https://codeforces.com/blog/entry/103979) for details about their combinatorial meaning.
However, we will very briefly mention that if $A(x)$ and $B(x)$ are generating functions for sequences that enumerate some objects by number of "atoms" in them (e.g. trees by the number of vertices), then the product $A(x) B(x)$ enumerates objects that can be described as pairs of objects of kinds $A$ and $B$, enumerates by the total number of "atoms" in the pair.
!!! Example
Let $A(x) = \sum\limits_{i=0}^\infty 2^i x^i$ enumerate packs of stones, each stone colored in one of $2$ colors (so, there are $2^i$ such packs of size $i$) and $B(x) = \sum\limits_{j=0}^{\infty} 3^j x^j$ enumerate packs of stones, each stone colored in one of $3$ colors. Then $C(x) = A(x) B(x) = \sum\limits_{k=0}^\infty c_k x^k$ would enumerate objects that may be described as "two packs of stones, first pack only of stones of type $A$, second pack only of stones of type $B$, with total number of stones being $k$" for $c_k$.
In a similar way, there is an intuitive meaning to some other functions over formal power series.
### Long polynomial division
Similar to integers, it is possible to define long division on polynomials.
!!! info "Definition"
For any polynomials $A$ and $B \neq 0$, one may represent $A$ as
$$
A = D \cdot B + R,~ \deg R < \deg B,
$$
where $R$ is called the **remainder** of $A$ modulo $B$ and $D$ is called the **quotient**.
Denoting $\deg A = n$ and $\deg B = m$, naive way to do it is to use long division, during which you multiply $B$ by the monomial $\frac{a_n}{b_m} x^{n - m}$ and subtract it from $A$, until the degree of $A$ is smaller than that of $B$. What remains of $A$ in the end will be the remainder (hence the name), and the polynomials with which you multiplied $B$ in the process, summed together, form the quotient.
!!! info "Definition"
If $A$ and $B$ have the same remainder modulo $C$, they're said to be **equivalent** modulo $C$, which is denoted as
$$
A \equiv B \pmod{C}.
$$
Polynomial long division is useful because of its many important properties:
- $A$ is a multiple of $B$ if and only if $A \equiv 0 \pmod B$.
- It implies that $A \equiv B \pmod C$ if and only if $A-B$ is a multiple of $C$.
- In particular, $A \equiv B \pmod{C \cdot D}$ implies $A \equiv B \pmod{C}$.
- For any linear polynomial $x-r$ it holds that $A(x) \equiv A(r) \pmod{x-r}$.
- It implies that $A$ is a multiple of $x-r$ if and only if $A(r)=0$.
- For modulo being $x^k$, it holds that $A \equiv a_0 + a_1 x + \dots + a_{k-1} x^{k-1} \pmod{x^k}$.
Note that long division can't be properly defined for formal power series. Instead, for any $A(x)$ such that $a_0 \neq 0$, it is possible to define an inverse formal power series $A^{-1}(x)$, such that $A(x) A^{-1}(x) = 1$. This fact, in turn, can be used to compute the result of long division for polynomials.
## Basic implementation
[Here](https://github.com/cp-algorithms/cp-algorithms-aux/blob/master/src/polynomial.cpp) you can find the basic implementation of polynomial algebra.
It supports all trivial operations and some other useful methods. The main class is `poly<T>` for polynomials with coefficients of type `T`.
All arithmetic operation `+`, `-`, `*`, `%` and `/` are supported, `%` and `/` standing for remainder and quotient in Euclidean division.
There is also the class `modular<m>` for performing arithmetic operations on remainders modulo a prime number `m`.
Other useful functions:
- `deriv()`: computes the derivative $P'(x)$ of $P(x)$.
- `integr()`: computes the indefinite integral $Q(x) = \int P(x)$ of $P(x)$ such that $Q(0)=0$.
- `inv(size_t n)`: calculate the first $n$ coefficients of $P^{-1}(x)$ in $O(n \log n)$.
- `log(size_t n)`: calculate the first $n$ coefficients of $\ln P(x)$ in $O(n \log n)$.
- `exp(size_t n)`: calculate the first $n$ coefficients of $\exp P(x)$ in $O(n \log n)$.
- `pow(size_t k, size_t n)`: calculate the first $n$ coefficients for $P^{k}(x)$ in $O(n \log nk)$.
- `deg()`: returns the degree of $P(x)$.
- `lead()`: returns the coefficient of $x^{\deg P(x)}$.
- `resultant(poly<T> a, poly<T> b)`: computes the resultant of $a$ and $b$ in $O(|a| \cdot |b|)$.
- `bpow(T x, size_t n)`: computes $x^n$.
- `bpow(T x, size_t n, T m)`: computes $x^n \pmod{m}$.
- `chirpz(T z, size_t n)`: computes $P(1), P(z), P(z^2), \dots, P(z^{n-1})$ in $O(n \log n)$.
- `vector<T> eval(vector<T> x)`: evaluates $P(x_1), \dots, P(x_n)$ in $O(n \log^2 n)$.
- `poly<T> inter(vector<T> x, vector<T> y)`: interpolates a polynomial by a set of pairs $P(x_i) = y_i$ in $O(n \log^2 n)$.
- And some more, feel free to explore the code!
## Arithmetic
### Multiplication
The very core operation is the multiplication of two polynomials. That is, given the polynomials $A$ and $B$:
$$A = a_0 + a_1 x + \dots + a_n x^n$$
$$B = b_0 + b_1 x + \dots + b_m x^m$$
You have to compute polynomial $C = A \cdot B$, which is defined as
$$\boxed{C = \sum\limits_{i=0}^n \sum\limits_{j=0}^m a_i b_j x^{i+j}} = c_0 + c_1 x + \dots + c_{n+m} x^{n+m}.$$
It can be computed in $O(n \log n)$ via the [Fast Fourier transform](fft.md) and almost all methods here will use it as subroutine.
### Inverse series
If $A(0) \neq 0$ there always exists an infinite formal power series $A^{-1}(x) = q_0+q_1 x + q_2 x^2 + \dots$ such that $A^{-1} A = 1$. It often proves useful to compute first $k$ coefficients of $A^{-1}$ (that is, to compute it modulo $x^k$). There are two major ways to calculate it.
#### Divide and conquer
This algorithm was mentioned in [Schönhage's article](http://algo.inria.fr/seminars/sem00-01/schoenhage.pdf) and is inspired by [Graeffe's method](https://en.wikipedia.org/wiki/Graeffe's_method). It is known that for $B(x)=A(x)A(-x)$ it holds that $B(x)=B(-x)$, that is, $B(x)$ is an even polynomial. It means that it only has non-zero coefficients with even numbers and can be represented as $B(x)=T(x^2)$. Thus, we can do the following transition:
$$A^{-1}(x) \equiv \frac{1}{A(x)} \equiv \frac{A(-x)}{A(x)A(-x)} \equiv \frac{A(-x)}{T(x^2)} \pmod{x^k}$$
Note that $T(x)$ can be computed with a single multiplication, after which we're only interested in the first half of coefficients of its inverse series. This effectively reduces the initial problem of computing $A^{-1} \pmod{x^k}$ to computing $T^{-1} \pmod{x^{\lfloor k / 2 \rfloor}}$.
The complexity of this method can be estimated as
$$T(n) = T(n/2) + O(n \log n) = O(n \log n).$$
#### Sieveking–Kung algorithm
The generic process described here is known as Hensel lifting, as it follows from Hensel's lemma. We'll cover it in more detail further below, but for now let's focus on ad hoc solution. "Lifting" part here means that we start with the approximation $B_0=q_0=a_0^{-1}$, which is $A^{-1} \pmod x$ and then iteratively lift from $\bmod x^a$ to $\bmod x^{2a}$.
Let $B_k \equiv A^{-1} \pmod{x^a}$. The next approximation needs to follow the equation $A B_{k+1} \equiv 1 \pmod{x^{2a}}$ and may be represented as $B_{k+1} = B_k + x^a C$. From this follows the equation
$$A(B_k + x^{a}C) \equiv 1 \pmod{x^{2a}}.$$
Let $A B_k \equiv 1 + x^a D \pmod{x^{2a}}$, then the equation above implies
$$x^a(D+AC) \equiv 0 \pmod{x^{2a}} \implies D \equiv -AC \pmod{x^a} \implies C \equiv -B_k D \pmod{x^a}.$$
From this, one can obtain the final formula, which is
$$x^a C \equiv -B_k x^a D \equiv B_k(1-AB_k) \pmod{x^{2a}} \implies \boxed{B_{k+1} \equiv B_k(2-AB_k) \pmod{x^{2a}}}$$
Thus starting with $B_0 \equiv a_0^{-1} \pmod x$ we will compute the sequence $B_k$ such that $AB_k \equiv 1 \pmod{x^{2^k}}$ with the complexity
$$T(n) = T(n/2) + O(n \log n) = O(n \log n).$$
The algorithm here might seem a bit more complicated than the first one, but it has a very solid and practical reasoning behind it, as well as a great generalization potential if looked from a different perspective, which would be explained further below.
### Euclidean division
Consider two polynomials $A(x)$ and $B(x)$ of degrees $n$ and $m$. As it was said earlier you can rewrite $A(x)$ as
$$A(x) = B(x) D(x) + R(x), \deg R < \deg B.$$
Let $n \geq m$, it would imply that $\deg D = n - m$ and the leading $n-m+1$ coefficients of $A$ don't influence $R$. It means that you can recover $D(x)$ from the largest $n-m+1$ coefficients of $A(x)$ and $B(x)$ if you consider it as a system of equations.
The system of linear equations we're talking about can be written in the following form:
$$\begin{bmatrix} a_n \\ \vdots \\ a_{m+1} \\ a_{m} \end{bmatrix} = \begin{bmatrix}
b_m & \dots & 0 & 0 \\
\vdots & \ddots & \vdots & \vdots \\
\dots & \dots & b_m & 0 \\
\dots & \dots & b_{m-1} & b_m
\end{bmatrix} \begin{bmatrix}d_{n-m} \\ \vdots \\ d_1 \\ d_0\end{bmatrix}$$
From the looks of it, we can conclude that with the introduction of reversed polynomials
$$A^R(x) = x^nA(x^{-1})= a_n + a_{n-1} x + \dots + a_0 x^n$$
$$B^R(x) = x^m B(x^{-1}) = b_m + b_{m-1} x + \dots + b_0 x^m$$
$$D^R(x) = x^{n-m}D(x^{-1}) = d_{n-m} + d_{n-m-1} x + \dots + d_0 x^{n-m}$$
the system may be rewritten as
$$A^R(x) \equiv B^R(x) D^R(x) \pmod{x^{n-m+1}}.$$
From this you can unambiguously recover all coefficients of $D(x)$:
$$\boxed{D^R(x) \equiv A^R(x) (B^R(x))^{-1} \pmod{x^{n-m+1}}}$$
And from this, in turn, you can recover $R(x)$ as $R(x) = A(x) - B(x)D(x)$.
Note that the matrix above is a so-called triangular [Toeplitz matrix](https://en.wikipedia.org/wiki/Toeplitz_matrix) and, as we see here, solving system of linear equations with arbitrary Toeplitz matrix is, in fact, equivalent to polynomial inversion. Moreover, inverse matrix of it would also be triangular Toeplitz matrix and its entries, in terms used above, are the coefficients of $(B^R(x))^{-1} \pmod{x^{n-m+1}}$.
## Calculating functions of polynomial
### Newton's method
Let's generalize the Sieveking–Kung algorithm. Consider equation $F(P) = 0$ where $P(x)$ should be a polynomial and $F(x)$ is some polynomial-valued function defined as
$$F(x) = \sum\limits_{i=0}^\infty \alpha_i (x-\beta)^i,$$
where $\beta$ is some constant. It can be proven that if we introduce a new formal variable $y$, we can express $F(x)$ as
$$F(x) = F(y) + (x-y)F'(y) + (x-y)^2 G(x,y),$$
where $F'(x)$ is the derivative formal power series defined as
$$F'(x) = \sum\limits_{i=0}^\infty (i+1)\alpha_{i+1}(x-\beta)^i,$$
and $G(x, y)$ is some formal power series of $x$ and $y$. With this result we can find the solution iteratively.
Let $F(Q_k) \equiv 0 \pmod{x^{a}}$. We need to find $Q_{k+1} \equiv Q_k + x^a C \pmod{x^{2a}}$ such that $F(Q_{k+1}) \equiv 0 \pmod{x^{2a}}$.
Substituting $x = Q_{k+1}$ and $y=Q_k$ in the formula above, we get
$$F(Q_{k+1}) \equiv F(Q_k) + (Q_{k+1} - Q_k) F'(Q_k) + (Q_{k+1} - Q_k)^2 G(x, y) \pmod x^{2a}.$$
Since $Q_{k+1} - Q_k \equiv 0 \pmod{x^a}$, it also holds that $(Q_{k+1} - Q_k)^2 \equiv 0 \pmod{x^{2a}}$, thus
$$0 \equiv F(Q_{k+1}) \equiv F(Q_k) + (Q_{k+1} - Q_k) F'(Q_k) \pmod{x^{2a}}.$$
The last formula gives us the value of $Q_{k+1}$:
$$\boxed{Q_{k+1} = Q_k - \dfrac{F(Q_k)}{F'(Q_k)} \pmod{x^{2a}}}$$
Thus, knowing how to invert polynomials and how to compute $F(Q_k)$, we can find $n$ coefficients of $P$ with the complexity
$$T(n) = T(n/2) + f(n),$$
where $f(n)$ is the time needed to compute $F(Q_k)$ and $F'(Q_k)^{-1}$ which is usually $O(n \log n)$.
The iterative rule above is known in numerical analysis as [Newton's method](https://en.wikipedia.org/wiki/Newton%27s_method).
#### Hensel's lemma
As was mentioned earlier, formally and generically this result is known as [Hensel's lemma](https://en.wikipedia.org/wiki/Hensel%27s_lemma) and it may in fact used in even broader sense when we work with a series of nested rings. In this particular case we worked with a sequence of polynomial remainders modulo $x$, $x^2$, $x^3$ and so on.
Another example where Hensel's lifting might be helpful are so-called [p-adic numbers](https://en.wikipedia.org/wiki/P-adic_number) where we, in fact, work with the sequence of integer remainders modulo $p$, $p^2$, $p^3$ and so on. For example, Newton's method can be used to find all possible [automorphic numbers](https://en.wikipedia.org/wiki/Automorphic_number) (numbers that end on itself when squared) with a given number base. The problem is left as an exercise to the reader. You might consider [this](https://acm.timus.ru/problem.aspx?space=1&num=1698) problem to check if your solution works for $10$-based numbers.
### Logarithm
For the function $\ln P(x)$ it's known that:
$$
\boxed{(\ln P(x))' = \dfrac{P'(x)}{P(x)}}
$$
Thus we can calculate $n$ coefficients of $\ln P(x)$ in $O(n \log n)$.
### Inverse series
Turns out, we can get the formula for $A^{-1}$ using Newton's method.
For this we take the equation $A=Q^{-1}$, thus:
$$F(Q) = Q^{-1} - A$$
$$F'(Q) = -Q^{-2}$$
$$\boxed{Q_{k+1} \equiv Q_k(2-AQ_k) \pmod{x^{2^{k+1}}}}$$
### Exponent
Let's learn to calculate $e^{P(x)}=Q(x)$. It should hold that $\ln Q = P$, thus:
$$F(Q) = \ln Q - P$$
$$F'(Q) = Q^{-1}$$
$$\boxed{Q_{k+1} \equiv Q_k(1 + P - \ln Q_k) \pmod{x^{2^{k+1}}}}$$
### $k$-th power { data-toc-label="k-th power" }
Now we need to calculate $P^k(x)=Q$. This may be done via the following formula:
$$Q = \exp\left[k \ln P(x)\right]$$
Note though, that you can calculate the logarithms and the exponents correctly only if you can find some initial $Q_0$.
To find it, you should calculate the logarithm or the exponent of the constant coefficient of the polynomial.
But the only reasonable way to do it is if $P(0)=1$ for $Q = \ln P$ so $Q(0)=0$ and if $P(0)=0$ for $Q = e^P$ so $Q(0)=1$.
Thus you can use formula above only if $P(0) = 1$. Otherwise if $P(x) = \alpha x^t T(x)$ where $T(0)=1$ you can write that:
$$\boxed{P^k(x) = \alpha^kx^{kt} \exp[k \ln T(x)]}$$
Note that you also can calculate some $k$-th root of a polynomial if you can calculate $\sqrt[k]{\alpha}$, for example for $\alpha=1$.
## Evaluation and Interpolation
### Chirp-z Transform
For the particular case when you need to evaluate a polynomial in the points $x_r = z^{2r}$ you can do the following:
$$A(z^{2r}) = \sum\limits_{k=0}^n a_k z^{2kr}$$
Let's substitute $2kr = r^2+k^2-(r-k)^2$. Then this sum rewrites as:
$$\boxed{A(z^{2r}) = z^{r^2}\sum\limits_{k=0}^n (a_k z^{k^2}) z^{-(r-k)^2}}$$
Which is up to the factor $z^{r^2}$ equal to the convolution of the sequences $u_k = a_k z^{k^2}$ and $v_k = z^{-k^2}$.
Note that $u_k$ has indexes from $0$ to $n$ here and $v_k$ has indexes from $-n$ to $m$ where $m$ is the maximum power of $z$ which you need.
Now if you need to evaluate a polynomial in the points $x_r = z^{2r+1}$ you can reduce it to the previous task by the transformation $a_k \to a_k z^k$.
It gives us an $O(n \log n)$ algorithm when you need to compute values in powers of $z$, thus you may compute the DFT for non-powers of two.
Another observation is that $kr = \binom{k+r}{2} - \binom{k}{2} - \binom{r}{2}$. Then we have
$$\boxed{A(z^r) = z^{-\binom{r}{2}}\sum\limits_{k=0}^n \left(a_k z^{-\binom{k}{2}}\right)z^{\binom{k+r}{2}}}$$
The coefficient of $x^{n+r}$ of the product of the polynomials $A_0(x) = \sum\limits_{k=0}^n a_{n-k}z^{-\binom{n-k}{2}}x^k$ and $A_1(x) = \sum\limits_{k\geq 0}z^{\binom{k}{2}}x^k$ equals $z^{\binom{r}{2}}A(z^r)$. You can use the formula $z^{\binom{k+1}{2}}=z^{\binom{k}{2}+k}$ to calculate the coefficients of $A_0(x)$ and $A_1(x)$.
### Multi-point Evaluation
Assume you need to calculate $A(x_1), \dots, A(x_n)$. As mentioned earlier, $A(x) \equiv A(x_i) \pmod{x-x_i}$. Thus you may do the following:
1. Compute a segment tree such that in the segment $[l,r)$ stands the product $P_{l, r}(x) = (x-x_l)(x-x_{l+1})\dots(x-x_{r-1})$.
2. Starting with $l=1$ and $r=n+1$ at the root node. Let $m=\lfloor(l+r)/2\rfloor$. Let's move down to $[l,m)$ with the polynomial $A(x) \pmod{P_{l,m}(x)}$.
3. This will recursively compute $A(x_l), \dots, A(x_{m-1})$, now do the same for $[m,r)$ with $A(x) \pmod{P_{m,r}(x)}$.
4. Concatenate the results from the first and second recursive call and return them.
The whole procedure will run in $O(n \log^2 n)$.
### Interpolation
There's a direct formula by Lagrange to interpolate a polynomial, given set of pairs $(x_i, y_i)$:
$$\boxed{A(x) = \sum\limits_{i=1}^n y_i \prod\limits_{j \neq i}\dfrac{x-x_j}{x_i - x_j}}$$
Computing it directly is a hard thing but turns out, we may compute it in $O(n \log^2 n)$ with a divide and conquer approach:
Consider $P(x) = (x-x_1)\dots(x-x_n)$. To know the coefficients of the denominators in $A(x)$ we should compute products like:
$$
P_i = \prod\limits_{j \neq i} (x_i-x_j)
$$
But if you consider the derivative $P'(x)$ you'll find out that $P'(x_i) = P_i$. Thus you can compute $P_i$'s via evaluation in $O(n \log^2 n)$.
Now consider the recursive algorithm done on same segment tree as in the multi-point evaluation. It starts in the leaves with the value $\dfrac{y_i}{P_i}$ in each leaf.
When we return from the recursion we should merge the results from the left and the right vertices as $A_{l,r} = A_{l,m}P_{m,r} + P_{l,m} A_{m,r}$.
In this way when you return back to the root you'll have exactly $A(x)$ in it.
The total procedure also works in $O(n \log^2 n)$.
## GCD and Resultants
Assume you're given polynomials $A(x) = a_0 + a_1 x + \dots + a_n x^n$ and $B(x) = b_0 + b_1 x + \dots + b_m x^m$.
Let $\lambda_0, \dots, \lambda_n$ be the roots of $A(x)$ and let $\mu_0, \dots, \mu_m$ be the roots of $B(x)$ counted with their multiplicities.
You want to know if $A(x)$ and $B(x)$ have any roots in common. There are two interconnected ways to do that.
### Euclidean algorithm
Well, we already have an [article](euclid-algorithm.md) about it. For an arbitrary domain you can write the Euclidean algorithm as easy as:
```cpp
template<typename T>
T gcd(const T &a, const T &b) {
return b == T(0) ? a : gcd(b, a % b);
}
```
It can be proven that for polynomials $A(x)$ and $B(x)$ it will work in $O(nm)$.
### Resultant
Let's calculate the product $A(\mu_0)\cdots A(\mu_m)$. It will be equal to zero if and only if some $\mu_i$ is the root of $A(x)$.
For symmetry we can also multiply it with $b_m^n$ and rewrite the whole product in the following form:
$$\boxed{\mathcal{R}(A, B) = b_m^n\prod\limits_{j=0}^m A(\mu_j) = b_m^n a_m^n \prod\limits_{i=0}^n \prod\limits_{j=0}^m (\mu_j - \lambda_i)= (-1)^{mn}a_n^m \prod\limits_{i=0}^n B(\lambda_i)}$$
The value defined above is called the resultant of the polynomials $A(x)$ and $B(x)$. From the definition you may find the following properties:
1. $\mathcal R(A, B) = (-1)^{nm} \mathcal R(B, A)$.
2. $\mathcal R(A, B)= a_n^m b_m^n$ when $n=0$ or $m=0$.
3. If $b_m=1$ then $\mathcal R(A - CB, B) = \mathcal R(A, B)$ for an arbitrary polynomial $C(x)$ and $n,m \geq 1$.
4. From this follows $\mathcal R(A, B) = b_m^{\deg(A) - \deg(A-CB)}\mathcal R(A - CB, B)$ for arbitrary $A(x)$, $B(x)$, $C(x)$.
Miraculously it means that resultant of two polynomials is actually always from the same ring as their coefficients!
Also these properties allow us to calculate the resultant alongside the Euclidean algorithm, which works in $O(nm)$.
```cpp
template<typename T>
T resultant(poly<T> a, poly<T> b) {
if(b.is_zero()) {
return 0;
} else if(b.deg() == 0) {
return bpow(b.lead(), a.deg());
} else {
int pw = a.deg();
a %= b;
pw -= a.deg();
base mul = bpow(b.lead(), pw) * base((b.deg() & a.deg() & 1) ? -1 : 1);
base ans = resultant(b, a);
return ans * mul;
}
}
```
### Half-GCD algorithm
There is a way to calculate the GCD and resultants in $O(n \log^2 n)$.
The procedure to do so implements a $2 \times 2$ linear transform which maps a pair of polynomials $a(x)$, $b(x)$ into another pair $c(x), d(x)$ such that $\deg d(x) \leq \frac{\deg a(x)}{2}$. If you're careful enough, you can compute the half-GCD of any pair of polynomials with at most $2$ recursive calls to the polynomials which are at least $2$ times smaller.
The specific details of the algorithm are somewhat tedious to explain, however you can find its implementation in the library, as `half_gcd` function.
After half-GCD is implemented, you can repeatedly apply it to polynomials until you're reduced to the pair of $\gcd(a, b)$ and $0$.
## Problems
- [CodeChef - RNG](https://www.codechef.com/problems/RNG)
- [CodeForces - Basis Change](https://codeforces.com/gym/102129/problem/D)
- [CodeForces - Permutant](https://codeforces.com/gym/102129/problem/G)
- [CodeForces - Medium Hadron Collider](https://codeforces.com/gym/102129/problem/C)
|
Operations on polynomials and series
|
---
title
eratosthenes_sieve
---
# Sieve of Eratosthenes
Sieve of Eratosthenes is an algorithm for finding all the prime numbers in a segment $[1;n]$ using $O(n \log \log n)$ operations.
The algorithm is very simple:
at the beginning we write down all numbers between 2 and $n$.
We mark all proper multiples of 2 (since 2 is the smallest prime number) as composite.
A proper multiple of a number $x$, is a number greater than $x$ and divisible by $x$.
Then we find the next number that hasn't been marked as composite, in this case it is 3.
Which means 3 is prime, and we mark all proper multiples of 3 as composite.
The next unmarked number is 5, which is the next prime number, and we mark all proper multiples of it.
And we continue this procedure until we processed all numbers in the row.
In the following image you can see a visualization of the algorithm for computing all prime numbers in the range $[1; 16]$. It can be seen, that quite often we mark numbers as composite multiple times.
<center></center>
The idea behind is this:
A number is prime, if none of the smaller prime numbers divides it.
Since we iterate over the prime numbers in order, we already marked all numbers, who are divisible by at least one of the prime numbers, as divisible.
Hence if we reach a cell and it is not marked, then it isn't divisible by any smaller prime number and therefore has to be prime.
## Implementation
```cpp
int n;
vector<bool> is_prime(n+1, true);
is_prime[0] = is_prime[1] = false;
for (int i = 2; i <= n; i++) {
if (is_prime[i] && (long long)i * i <= n) {
for (int j = i * i; j <= n; j += i)
is_prime[j] = false;
}
}
```
This code first marks all numbers except zero and one as potential prime numbers, then it begins the process of sifting composite numbers.
For this it iterates over all numbers from $2$ to $n$.
If the current number $i$ is a prime number, it marks all numbers that are multiples of $i$ as composite numbers, starting from $i^2$.
This is already an optimization over naive way of implementing it, and is allowed as all smaller numbers that are multiples of $i$ necessary also have a prime factor which is less than $i$, so all of them were already sifted earlier.
Since $i^2$ can easily overflow the type `int`, the additional verification is done using type `long long` before the second nested loop.
Using such implementation the algorithm consumes $O(n)$ of the memory (obviously) and performs $O(n \log \log n)$ (see next section).
## Asymptotic analysis
It's simple to prove a running time of $O(n \log n)$ without knowing anything about the distribution of primes - ignoring the `is_prime` check, the inner loop runs (at most) $n/i$ times for $i = 2, 3, 4, \dots$, leading the total number of operations in the inner loop to be a harmonic sum like $n(1/2 + 1/3 + 1/4 + \cdots)$, which is bounded by $O(n \log n)$.
Let's prove that algorithm's running time is $O(n \log \log n)$.
The algorithm will perform $\frac{n}{p}$ operations for every prime $p \le n$ the inner loop.
Hence, we need to evaluate the next expression:
$$\sum_{\substack{p \le n, \\\ p \text{ prime}}} \frac n p = n \cdot \sum_{\substack{p \le n, \\\ p \text{ prime}}} \frac 1 p.$$
Let's recall two known facts.
- The number of prime numbers less than or equal to $n$ is approximately $\frac n {\ln n}$.
- The $k$-th prime number approximately equals $k \ln k$ (that follows immediately from the previous fact).
Thus we can write down the sum in the following way:
$$\sum_{\substack{p \le n, \\\ p \text{ prime}}} \frac 1 p \approx \frac 1 2 + \sum_{k = 2}^{\frac n {\ln n}} \frac 1 {k \ln k}.$$
Here we extracted the first prime number 2 from the sum, because $k = 1$ in approximation $k \ln k$ is $0$ and causes a division by zero.
Now, let's evaluate this sum using the integral of a same function over $k$ from $2$ to $\frac n {\ln n}$ (we can make such approximation because, in fact, the sum is related to the integral as its approximation using the rectangle method):
$$\sum_{k = 2}^{\frac n {\ln n}} \frac 1 {k \ln k} \approx \int_2^{\frac n {\ln n}} \frac 1 {k \ln k} dk.$$
The antiderivative for the integrand is $\ln \ln k$. Using a substitution and removing terms of lower order, we'll get the result:
$$\int_2^{\frac n {\ln n}} \frac 1 {k \ln k} dk = \ln \ln \frac n {\ln n} - \ln \ln 2 = \ln(\ln n - \ln \ln n) - \ln \ln 2 \approx \ln \ln n.$$
Now, returning to the original sum, we'll get its approximate evaluation:
$$\sum_{\substack{p \le n, \\\ p\ is\ prime}} \frac n p \approx n \ln \ln n + o(n).$$
You can find a more strict proof (that gives more precise evaluation which is accurate within constant multipliers) in the book authored by Hardy & Wright "An Introduction to the Theory of Numbers" (p. 349).
## Different optimizations of the Sieve of Eratosthenes
The biggest weakness of the algorithm is, that it "walks" along the memory multiple times, only manipulating single elements.
This is not very cache friendly.
And because of that, the constant which is concealed in $O(n \log \log n)$ is comparably big.
Besides, the consumed memory is a bottleneck for big $n$.
The methods presented below allow us to reduce the quantity of the performed operations, as well as to shorten the consumed memory noticeably.
### Sieving till root
Obviously, to find all the prime numbers until $n$, it will be enough just to perform the sifting only by the prime numbers, which do not exceed the root of $n$.
```cpp
int n;
vector<bool> is_prime(n+1, true);
is_prime[0] = is_prime[1] = false;
for (int i = 2; i * i <= n; i++) {
if (is_prime[i]) {
for (int j = i * i; j <= n; j += i)
is_prime[j] = false;
}
}
```
Such optimization doesn't affect the complexity (indeed, by repeating the proof presented above we'll get the evaluation $n \ln \ln \sqrt n + o(n)$, which is asymptotically the same according to the properties of logarithms), though the number of operations will reduce noticeably.
### Sieving by the odd numbers only
Since all even numbers (except $2$) are composite, we can stop checking even numbers at all. Instead, we need to operate with odd numbers only.
First, it will allow us to half the needed memory. Second, it will reduce the number of operations performing by algorithm approximately in half.
### Memory consumption and speed of operations
We should notice, that these two implementations of the Sieve of Eratosthenes use $n$ bits of memory by using the data structure `vector<bool>`.
`vector<bool>` is not a regular container that stores a series of `bool` (as in most computer architectures a `bool` takes one byte of memory).
It's a memory-optimization specialization of `vector<T>`, that only consumes $\frac{N}{8}$ bytes of memory.
Modern processors architectures work much more efficiently with bytes than with bits as they usually cannot access bits directly.
So underneath the `vector<bool>` stores the bits in a large continuous memory, accesses the memory in blocks of a few bytes, and extracts/sets the bits with bit operations like bit masking and bit shifting.
Because of that there is a certain overhead when you read or write bits with a `vector<bool>`, and quite often using a `vector<char>` (which uses 1 byte for each entry, so 8x the amount of memory) is faster.
However, for the simple implementations of the Sieve of Eratosthenes using a `vector<bool>` is faster.
You are limited by how fast you can load the data into the cache, and therefore using less memory gives a big advantage.
A benchmark ([link](https://gist.github.com/jakobkogler/e6359ea9ced24fe304f1a8af3c9bee0e)) shows, that using a `vector<bool>` is between 1.4x and 1.7x faster than using a `vector<char>`.
The same considerations also apply to `bitset`.
It's also an efficient way of storing bits, similar to `vector<bool>`, so it takes only $\frac{N}{8}$ bytes of memory, but is a bit slower in accessing the elements.
In the benchmark above `bitset` performs a bit worse than `vector<bool>`.
Another drawback from `bitset` is that you need to know the size at compile time.
### Segmented Sieve
It follows from the optimization "sieving till root" that there is no need to keep the whole array `is_prime[1...n]` at all time.
For sieving it is enough to just keep the prime numbers until the root of $n$, i.e. `prime[1... sqrt(n)]`, split the complete range into blocks, and sieve each block separately.
Let $s$ be a constant which determines the size of the block, then we have $\lceil {\frac n s} \rceil$ blocks altogether, and the block $k$ ($k = 0 ... \lfloor {\frac n s} \rfloor$) contains the numbers in a segment $[ks; ks + s - 1]$.
We can work on blocks by turns, i.e. for every block $k$ we will go through all the prime numbers (from $1$ to $\sqrt n$) and perform sieving using them.
It is worth noting, that we have to modify the strategy a little bit when handling the first numbers: first, all the prime numbers from $[1; \sqrt n]$ shouldn't remove themselves; and second, the numbers $0$ and $1$ should be marked as non-prime numbers.
While working on the last block it should not be forgotten that the last needed number $n$ is not necessary located in the end of the block.
As discussed previously, the typical implementation of the Sieve of Eratosthenes is limited by the speed how fast you can load data into the CPU caches.
By splitting the range of potential prime numbers $[1; n]$ into smaller blocks, we never have to keep multiple blocks in memory at the same time, and all operations are much more cache-friendlier.
As we are now no longer limited by the cache speeds, we can replace the `vector<bool>` with a `vector<char>`, and gain some additional performance as the processors can handle read and writes with bytes directly and don't need to rely on bit operations for extracting individual bits.
The benchmark ([link](https://gist.github.com/jakobkogler/e6359ea9ced24fe304f1a8af3c9bee0e)) shows, that using a `vector<char>` is about 3x faster in this situation than using a `vector<bool>`.
A word of caution: those numbers might differ depending on architecture, compiler, and optimization levels.
Here we have an implementation that counts the number of primes smaller than or equal to $n$ using block sieving.
```cpp
int count_primes(int n) {
const int S = 10000;
vector<int> primes;
int nsqrt = sqrt(n);
vector<char> is_prime(nsqrt + 2, true);
for (int i = 2; i <= nsqrt; i++) {
if (is_prime[i]) {
primes.push_back(i);
for (int j = i * i; j <= nsqrt; j += i)
is_prime[j] = false;
}
}
int result = 0;
vector<char> block(S);
for (int k = 0; k * S <= n; k++) {
fill(block.begin(), block.end(), true);
int start = k * S;
for (int p : primes) {
int start_idx = (start + p - 1) / p;
int j = max(start_idx, p) * p - start;
for (; j < S; j += p)
block[j] = false;
}
if (k == 0)
block[0] = block[1] = false;
for (int i = 0; i < S && start + i <= n; i++) {
if (block[i])
result++;
}
}
return result;
}
```
The running time of block sieving is the same as for regular sieve of Eratosthenes (unless the size of the blocks is very small), but the needed memory will shorten to $O(\sqrt{n} + S)$ and we have better caching results.
On the other hand, there will be a division for each pair of a block and prime number from $[1; \sqrt{n}]$, and that will be far worse for smaller block sizes.
Hence, it is necessary to keep balance when selecting the constant $S$.
We achieved the best results for block sizes between $10^4$ and $10^5$.
## Find primes in range
Sometimes we need to find all prime numbers in a range $[L,R]$ of small size (e.g. $R - L + 1 \approx 1e7$), where $R$ can be very large (e.g. $1e12$).
To solve such a problem, we can use the idea of the Segmented sieve.
We pre-generate all prime numbers up to $\sqrt R$, and use those primes to mark all composite numbers in the segment $[L, R]$.
```cpp
vector<char> segmentedSieve(long long L, long long R) {
// generate all primes up to sqrt(R)
long long lim = sqrt(R);
vector<char> mark(lim + 1, false);
vector<long long> primes;
for (long long i = 2; i <= lim; ++i) {
if (!mark[i]) {
primes.emplace_back(i);
for (long long j = i * i; j <= lim; j += i)
mark[j] = true;
}
}
vector<char> isPrime(R - L + 1, true);
for (long long i : primes)
for (long long j = max(i * i, (L + i - 1) / i * i); j <= R; j += i)
isPrime[j - L] = false;
if (L == 1)
isPrime[0] = false;
return isPrime;
}
```
Time complexity of this approach is $O((R - L + 1) \log \log (R) + \sqrt R \log \log \sqrt R)$.
It's also possible that we don't pre-generate all prime numbers:
```cpp
vector<char> segmentedSieveNoPreGen(long long L, long long R) {
vector<char> isPrime(R - L + 1, true);
long long lim = sqrt(R);
for (long long i = 2; i <= lim; ++i)
for (long long j = max(i * i, (L + i - 1) / i * i); j <= R; j += i)
isPrime[j - L] = false;
if (L == 1)
isPrime[0] = false;
return isPrime;
}
```
Obviously, the complexity is worse, which is $O((R - L + 1) \log (R) + \sqrt R)$. However, it still runs very fast in practice.
## Linear time modification
We can modify the algorithm in a such a way, that it only has linear time complexity.
This approach is described in the article [Linear Sieve](prime-sieve-linear.md).
However, this algorithm also has its own weaknesses.
|
---
title
eratosthenes_sieve
---
# Sieve of Eratosthenes
Sieve of Eratosthenes is an algorithm for finding all the prime numbers in a segment $[1;n]$ using $O(n \log \log n)$ operations.
The algorithm is very simple:
at the beginning we write down all numbers between 2 and $n$.
We mark all proper multiples of 2 (since 2 is the smallest prime number) as composite.
A proper multiple of a number $x$, is a number greater than $x$ and divisible by $x$.
Then we find the next number that hasn't been marked as composite, in this case it is 3.
Which means 3 is prime, and we mark all proper multiples of 3 as composite.
The next unmarked number is 5, which is the next prime number, and we mark all proper multiples of it.
And we continue this procedure until we processed all numbers in the row.
In the following image you can see a visualization of the algorithm for computing all prime numbers in the range $[1; 16]$. It can be seen, that quite often we mark numbers as composite multiple times.
<center></center>
The idea behind is this:
A number is prime, if none of the smaller prime numbers divides it.
Since we iterate over the prime numbers in order, we already marked all numbers, who are divisible by at least one of the prime numbers, as divisible.
Hence if we reach a cell and it is not marked, then it isn't divisible by any smaller prime number and therefore has to be prime.
## Implementation
```cpp
int n;
vector<bool> is_prime(n+1, true);
is_prime[0] = is_prime[1] = false;
for (int i = 2; i <= n; i++) {
if (is_prime[i] && (long long)i * i <= n) {
for (int j = i * i; j <= n; j += i)
is_prime[j] = false;
}
}
```
This code first marks all numbers except zero and one as potential prime numbers, then it begins the process of sifting composite numbers.
For this it iterates over all numbers from $2$ to $n$.
If the current number $i$ is a prime number, it marks all numbers that are multiples of $i$ as composite numbers, starting from $i^2$.
This is already an optimization over naive way of implementing it, and is allowed as all smaller numbers that are multiples of $i$ necessary also have a prime factor which is less than $i$, so all of them were already sifted earlier.
Since $i^2$ can easily overflow the type `int`, the additional verification is done using type `long long` before the second nested loop.
Using such implementation the algorithm consumes $O(n)$ of the memory (obviously) and performs $O(n \log \log n)$ (see next section).
## Asymptotic analysis
It's simple to prove a running time of $O(n \log n)$ without knowing anything about the distribution of primes - ignoring the `is_prime` check, the inner loop runs (at most) $n/i$ times for $i = 2, 3, 4, \dots$, leading the total number of operations in the inner loop to be a harmonic sum like $n(1/2 + 1/3 + 1/4 + \cdots)$, which is bounded by $O(n \log n)$.
Let's prove that algorithm's running time is $O(n \log \log n)$.
The algorithm will perform $\frac{n}{p}$ operations for every prime $p \le n$ the inner loop.
Hence, we need to evaluate the next expression:
$$\sum_{\substack{p \le n, \\\ p \text{ prime}}} \frac n p = n \cdot \sum_{\substack{p \le n, \\\ p \text{ prime}}} \frac 1 p.$$
Let's recall two known facts.
- The number of prime numbers less than or equal to $n$ is approximately $\frac n {\ln n}$.
- The $k$-th prime number approximately equals $k \ln k$ (that follows immediately from the previous fact).
Thus we can write down the sum in the following way:
$$\sum_{\substack{p \le n, \\\ p \text{ prime}}} \frac 1 p \approx \frac 1 2 + \sum_{k = 2}^{\frac n {\ln n}} \frac 1 {k \ln k}.$$
Here we extracted the first prime number 2 from the sum, because $k = 1$ in approximation $k \ln k$ is $0$ and causes a division by zero.
Now, let's evaluate this sum using the integral of a same function over $k$ from $2$ to $\frac n {\ln n}$ (we can make such approximation because, in fact, the sum is related to the integral as its approximation using the rectangle method):
$$\sum_{k = 2}^{\frac n {\ln n}} \frac 1 {k \ln k} \approx \int_2^{\frac n {\ln n}} \frac 1 {k \ln k} dk.$$
The antiderivative for the integrand is $\ln \ln k$. Using a substitution and removing terms of lower order, we'll get the result:
$$\int_2^{\frac n {\ln n}} \frac 1 {k \ln k} dk = \ln \ln \frac n {\ln n} - \ln \ln 2 = \ln(\ln n - \ln \ln n) - \ln \ln 2 \approx \ln \ln n.$$
Now, returning to the original sum, we'll get its approximate evaluation:
$$\sum_{\substack{p \le n, \\\ p\ is\ prime}} \frac n p \approx n \ln \ln n + o(n).$$
You can find a more strict proof (that gives more precise evaluation which is accurate within constant multipliers) in the book authored by Hardy & Wright "An Introduction to the Theory of Numbers" (p. 349).
## Different optimizations of the Sieve of Eratosthenes
The biggest weakness of the algorithm is, that it "walks" along the memory multiple times, only manipulating single elements.
This is not very cache friendly.
And because of that, the constant which is concealed in $O(n \log \log n)$ is comparably big.
Besides, the consumed memory is a bottleneck for big $n$.
The methods presented below allow us to reduce the quantity of the performed operations, as well as to shorten the consumed memory noticeably.
### Sieving till root
Obviously, to find all the prime numbers until $n$, it will be enough just to perform the sifting only by the prime numbers, which do not exceed the root of $n$.
```cpp
int n;
vector<bool> is_prime(n+1, true);
is_prime[0] = is_prime[1] = false;
for (int i = 2; i * i <= n; i++) {
if (is_prime[i]) {
for (int j = i * i; j <= n; j += i)
is_prime[j] = false;
}
}
```
Such optimization doesn't affect the complexity (indeed, by repeating the proof presented above we'll get the evaluation $n \ln \ln \sqrt n + o(n)$, which is asymptotically the same according to the properties of logarithms), though the number of operations will reduce noticeably.
### Sieving by the odd numbers only
Since all even numbers (except $2$) are composite, we can stop checking even numbers at all. Instead, we need to operate with odd numbers only.
First, it will allow us to half the needed memory. Second, it will reduce the number of operations performing by algorithm approximately in half.
### Memory consumption and speed of operations
We should notice, that these two implementations of the Sieve of Eratosthenes use $n$ bits of memory by using the data structure `vector<bool>`.
`vector<bool>` is not a regular container that stores a series of `bool` (as in most computer architectures a `bool` takes one byte of memory).
It's a memory-optimization specialization of `vector<T>`, that only consumes $\frac{N}{8}$ bytes of memory.
Modern processors architectures work much more efficiently with bytes than with bits as they usually cannot access bits directly.
So underneath the `vector<bool>` stores the bits in a large continuous memory, accesses the memory in blocks of a few bytes, and extracts/sets the bits with bit operations like bit masking and bit shifting.
Because of that there is a certain overhead when you read or write bits with a `vector<bool>`, and quite often using a `vector<char>` (which uses 1 byte for each entry, so 8x the amount of memory) is faster.
However, for the simple implementations of the Sieve of Eratosthenes using a `vector<bool>` is faster.
You are limited by how fast you can load the data into the cache, and therefore using less memory gives a big advantage.
A benchmark ([link](https://gist.github.com/jakobkogler/e6359ea9ced24fe304f1a8af3c9bee0e)) shows, that using a `vector<bool>` is between 1.4x and 1.7x faster than using a `vector<char>`.
The same considerations also apply to `bitset`.
It's also an efficient way of storing bits, similar to `vector<bool>`, so it takes only $\frac{N}{8}$ bytes of memory, but is a bit slower in accessing the elements.
In the benchmark above `bitset` performs a bit worse than `vector<bool>`.
Another drawback from `bitset` is that you need to know the size at compile time.
### Segmented Sieve
It follows from the optimization "sieving till root" that there is no need to keep the whole array `is_prime[1...n]` at all time.
For sieving it is enough to just keep the prime numbers until the root of $n$, i.e. `prime[1... sqrt(n)]`, split the complete range into blocks, and sieve each block separately.
Let $s$ be a constant which determines the size of the block, then we have $\lceil {\frac n s} \rceil$ blocks altogether, and the block $k$ ($k = 0 ... \lfloor {\frac n s} \rfloor$) contains the numbers in a segment $[ks; ks + s - 1]$.
We can work on blocks by turns, i.e. for every block $k$ we will go through all the prime numbers (from $1$ to $\sqrt n$) and perform sieving using them.
It is worth noting, that we have to modify the strategy a little bit when handling the first numbers: first, all the prime numbers from $[1; \sqrt n]$ shouldn't remove themselves; and second, the numbers $0$ and $1$ should be marked as non-prime numbers.
While working on the last block it should not be forgotten that the last needed number $n$ is not necessary located in the end of the block.
As discussed previously, the typical implementation of the Sieve of Eratosthenes is limited by the speed how fast you can load data into the CPU caches.
By splitting the range of potential prime numbers $[1; n]$ into smaller blocks, we never have to keep multiple blocks in memory at the same time, and all operations are much more cache-friendlier.
As we are now no longer limited by the cache speeds, we can replace the `vector<bool>` with a `vector<char>`, and gain some additional performance as the processors can handle read and writes with bytes directly and don't need to rely on bit operations for extracting individual bits.
The benchmark ([link](https://gist.github.com/jakobkogler/e6359ea9ced24fe304f1a8af3c9bee0e)) shows, that using a `vector<char>` is about 3x faster in this situation than using a `vector<bool>`.
A word of caution: those numbers might differ depending on architecture, compiler, and optimization levels.
Here we have an implementation that counts the number of primes smaller than or equal to $n$ using block sieving.
```cpp
int count_primes(int n) {
const int S = 10000;
vector<int> primes;
int nsqrt = sqrt(n);
vector<char> is_prime(nsqrt + 2, true);
for (int i = 2; i <= nsqrt; i++) {
if (is_prime[i]) {
primes.push_back(i);
for (int j = i * i; j <= nsqrt; j += i)
is_prime[j] = false;
}
}
int result = 0;
vector<char> block(S);
for (int k = 0; k * S <= n; k++) {
fill(block.begin(), block.end(), true);
int start = k * S;
for (int p : primes) {
int start_idx = (start + p - 1) / p;
int j = max(start_idx, p) * p - start;
for (; j < S; j += p)
block[j] = false;
}
if (k == 0)
block[0] = block[1] = false;
for (int i = 0; i < S && start + i <= n; i++) {
if (block[i])
result++;
}
}
return result;
}
```
The running time of block sieving is the same as for regular sieve of Eratosthenes (unless the size of the blocks is very small), but the needed memory will shorten to $O(\sqrt{n} + S)$ and we have better caching results.
On the other hand, there will be a division for each pair of a block and prime number from $[1; \sqrt{n}]$, and that will be far worse for smaller block sizes.
Hence, it is necessary to keep balance when selecting the constant $S$.
We achieved the best results for block sizes between $10^4$ and $10^5$.
## Find primes in range
Sometimes we need to find all prime numbers in a range $[L,R]$ of small size (e.g. $R - L + 1 \approx 1e7$), where $R$ can be very large (e.g. $1e12$).
To solve such a problem, we can use the idea of the Segmented sieve.
We pre-generate all prime numbers up to $\sqrt R$, and use those primes to mark all composite numbers in the segment $[L, R]$.
```cpp
vector<char> segmentedSieve(long long L, long long R) {
// generate all primes up to sqrt(R)
long long lim = sqrt(R);
vector<char> mark(lim + 1, false);
vector<long long> primes;
for (long long i = 2; i <= lim; ++i) {
if (!mark[i]) {
primes.emplace_back(i);
for (long long j = i * i; j <= lim; j += i)
mark[j] = true;
}
}
vector<char> isPrime(R - L + 1, true);
for (long long i : primes)
for (long long j = max(i * i, (L + i - 1) / i * i); j <= R; j += i)
isPrime[j - L] = false;
if (L == 1)
isPrime[0] = false;
return isPrime;
}
```
Time complexity of this approach is $O((R - L + 1) \log \log (R) + \sqrt R \log \log \sqrt R)$.
It's also possible that we don't pre-generate all prime numbers:
```cpp
vector<char> segmentedSieveNoPreGen(long long L, long long R) {
vector<char> isPrime(R - L + 1, true);
long long lim = sqrt(R);
for (long long i = 2; i <= lim; ++i)
for (long long j = max(i * i, (L + i - 1) / i * i); j <= R; j += i)
isPrime[j - L] = false;
if (L == 1)
isPrime[0] = false;
return isPrime;
}
```
Obviously, the complexity is worse, which is $O((R - L + 1) \log (R) + \sqrt R)$. However, it still runs very fast in practice.
## Linear time modification
We can modify the algorithm in a such a way, that it only has linear time complexity.
This approach is described in the article [Linear Sieve](prime-sieve-linear.md).
However, this algorithm also has its own weaknesses.
## Practice Problems
* [Leetcode - Four Divisors](https://leetcode.com/problems/four-divisors/)
* [Leetcode - Count Primes](https://leetcode.com/problems/count-primes/)
* [SPOJ - Printing Some Primes](http://www.spoj.com/problems/TDPRIMES/)
* [SPOJ - A Conjecture of Paul Erdos](http://www.spoj.com/problems/HS08PAUL/)
* [SPOJ - Primal Fear](http://www.spoj.com/problems/VECTAR8/)
* [SPOJ - Primes Triangle (I)](http://www.spoj.com/problems/PTRI/)
* [Codeforces - Almost Prime](http://codeforces.com/contest/26/problem/A)
* [Codeforces - Sherlock And His Girlfriend](http://codeforces.com/contest/776/problem/B)
* [SPOJ - Namit in Trouble](http://www.spoj.com/problems/NGIRL/)
* [SPOJ - Bazinga!](http://www.spoj.com/problems/DCEPC505/)
* [Project Euler - Prime pair connection](https://www.hackerrank.com/contests/projecteuler/challenges/euler134)
* [SPOJ - N-Factorful](http://www.spoj.com/problems/NFACTOR/)
* [SPOJ - Binary Sequence of Prime Numbers](http://www.spoj.com/problems/BSPRIME/)
* [UVA 11353 - A Different Kind of Sorting](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2338)
* [SPOJ - Prime Generator](http://www.spoj.com/problems/PRIME1/)
* [SPOJ - Printing some primes (hard)](http://www.spoj.com/problems/PRIMES2/)
* [Codeforces - Nodbach Problem](https://codeforces.com/problemset/problem/17/A)
* [Codefoces - Colliders](https://codeforces.com/problemset/problem/154/B)
|
Sieve of Eratosthenes
|
---
title
binary_pow
---
# Binary Exponentiation
Binary exponentiation (also known as exponentiation by squaring) is a trick which allows to calculate $a^n$ using only $O(\log n)$ multiplications (instead of $O(n)$ multiplications required by the naive approach).
It also has important applications in many tasks unrelated to arithmetic, since it
can be used with any operations that have the property of **associativity**:
$$(X \cdot Y) \cdot Z = X \cdot (Y \cdot Z)$$
Most obviously this applies to modular multiplication, to multiplication of matrices and
to other problems which we will discuss below.
## Algorithm
Raising $a$ to the power of $n$ is expressed naively as multiplication by $a$ done $n - 1$ times:
$a^{n} = a \cdot a \cdot \ldots \cdot a$. However, this approach is not practical for large $a$ or $n$.
$a^{b+c} = a^b \cdot a^c$ and $a^{2b} = a^b \cdot a^b = (a^b)^2$.
The idea of binary exponentiation is, that we split the work using the binary representation of the exponent.
Let's write $n$ in base 2, for example:
$$3^{13} = 3^{1101_2} = 3^8 \cdot 3^4 \cdot 3^1$$
Since the number $n$ has exactly $\lfloor \log_2 n \rfloor + 1$ digits in base 2, we only need to perform $O(\log n)$ multiplications, if we know the powers $a^1, a^2, a^4, a^8, \dots, a^{2^{\lfloor \log n \rfloor}}$.
So we only need to know a fast way to compute those.
Luckily this is very easy, since an element in the sequence is just the square of the previous element.
$$\begin{align}
3^1 &= 3 \\
3^2 &= \left(3^1\right)^2 = 3^2 = 9 \\
3^4 &= \left(3^2\right)^2 = 9^2 = 81 \\
3^8 &= \left(3^4\right)^2 = 81^2 = 6561
\end{align}$$
So to get the final answer for $3^{13}$, we only need to multiply three of them (skipping $3^2$ because the corresponding bit in $n$ is not set):
$3^{13} = 6561 \cdot 81 \cdot 3 = 1594323$
The final complexity of this algorithm is $O(\log n)$: we have to compute $\log n$ powers of $a$, and then have to do at most $\log n$ multiplications to get the final answer from them.
The following recursive approach expresses the same idea:
$$a^n = \begin{cases}
1 &\text{if } n == 0 \\
\left(a^{\frac{n}{2}}\right)^2 &\text{if } n > 0 \text{ and } n \text{ even}\\
\left(a^{\frac{n - 1}{2}}\right)^2 \cdot a &\text{if } n > 0 \text{ and } n \text{ odd}\\
\end{cases}$$
## Implementation
First the recursive approach, which is a direct translation of the recursive formula:
```cpp
long long binpow(long long a, long long b) {
if (b == 0)
return 1;
long long res = binpow(a, b / 2);
if (b % 2)
return res * res * a;
else
return res * res;
}
```
The second approach accomplishes the same task without recursion.
It computes all the powers in a loop, and multiplies the ones with the corresponding set bit in $n$.
Although the complexity of both approaches is identical, this approach will be faster in practice since we don't have the overhead of the recursive calls.
```cpp
long long binpow(long long a, long long b) {
long long res = 1;
while (b > 0) {
if (b & 1)
res = res * a;
a = a * a;
b >>= 1;
}
return res;
}
```
## Applications
### Effective computation of large exponents modulo a number
**Problem:**
Compute $x^n \bmod m$.
This is a very common operation. For instance it is used in computing the [modular multiplicative inverse](module-inverse.md).
**Solution:**
Since we know that the modulo operator doesn't interfere with multiplications ($a \cdot b \equiv (a \bmod m) \cdot (b \bmod m) \pmod m$), we can directly use the same code, and just replace every multiplication with a modular multiplication:
```cpp
long long binpow(long long a, long long b, long long m) {
a %= m;
long long res = 1;
while (b > 0) {
if (b & 1)
res = res * a % m;
a = a * a % m;
b >>= 1;
}
return res;
}
```
**Note:**
It's possible to speed this algorithm for large $b >> m$.
If $m$ is a prime number $x^n \equiv x^{n \bmod (m-1)} \pmod{m}$ for prime $m$, and $x^n \equiv x^{n \bmod{\phi(m)}} \pmod{m}$ for composite $m$.
This follows directly from Fermat's little theorem and Euler's theorem, see the article about [Modular Inverses](module-inverse.md#fermat-euler) for more details.
### Effective computation of Fibonacci numbers
**Problem:** Compute $n$-th Fibonacci number $F_n$.
**Solution:** For more details, see the [Fibonacci Number article](fibonacci-numbers.md).
We will only go through an overview of the algorithm.
To compute the next Fibonacci number, only the two previous ones are needed, as $F_n = F_{n-1} + F_{n-2}$.
We can build a $2 \times 2$ matrix that describes this transformation:
the transition from $F_i$ and $F_{i+1}$ to $F_{i+1}$ and $F_{i+2}$.
For example, applying this transformation to the pair $F_0$ and $F_1$ would change it into $F_1$ and $F_2$.
Therefore, we can raise this transformation matrix to the $n$-th power to find $F_n$ in time complexity $O(\log n)$.
### Applying a permutation $k$ times { data-toc-label='Applying a permutation <script type="math/tex">k</script> times' }
**Problem:** You are given a sequence of length $n$. Apply to it a given permutation $k$ times.
**Solution:** Simply raise the permutation to $k$-th power using binary exponentiation, and then apply it to the sequence. This will give you a time complexity of $O(n \log k)$.
```cpp
vector<int> applyPermutation(vector<int> sequence, vector<int> permutation) {
vector<int> newSequence(sequence.size());
for(int i = 0; i < sequence.size(); i++) {
newSequence[i] = sequence[permutation[i]];
}
return newSequence;
}
vector<int> permute(vector<int> sequence, vector<int> permutation, long long b) {
while (b > 0) {
if (b & 1) {
sequence = applyPermutation(sequence, permutation);
}
permutation = applyPermutation(permutation, permutation);
b >>= 1;
}
return sequence;
}
```
**Note:** This task can be solved more efficiently in linear time by building the permutation graph and considering each cycle independently. You could then compute $k$ modulo the size of the cycle and find the final position for each number which is part of this cycle.
### Fast application of a set of geometric operations to a set of points
**Problem:** Given $n$ points $p_i$, apply $m$ transformations to each of these points. Each transformation can be a shift, a scaling or a rotation around a given axis by a given angle. There is also a "loop" operation which applies a given list of transformations $k$ times ("loop" operations can be nested). You should apply all transformations faster than $O(n \cdot length)$, where $length$ is the total number of transformations to be applied (after unrolling "loop" operations).
**Solution:** Let's look at how the different types of transformations change the coordinates:
* Shift operation: adds a different constant to each of the coordinates.
* Scaling operation: multiplies each of the coordinates by a different constant.
* Rotation operation: the transformation is more complicated (we won't go in details here), but each of the new coordinates still can be represented as a linear combination of the old ones.
As you can see, each of the transformations can be represented as a linear operation on the coordinates. Thus, a transformation can be written as a $4 \times 4$ matrix of the form:
$$\begin{pmatrix}
a_{11} & a_ {12} & a_ {13} & a_ {14} \\
a_{21} & a_ {22} & a_ {23} & a_ {24} \\
a_{31} & a_ {32} & a_ {33} & a_ {34} \\
a_{41} & a_ {42} & a_ {43} & a_ {44}
\end{pmatrix}$$
that, when multiplied by a vector with the old coordinates and an unit gives a new vector with the new coordinates and an unit:
$$\begin{pmatrix} x & y & z & 1 \end{pmatrix} \cdot
\begin{pmatrix}
a_{11} & a_ {12} & a_ {13} & a_ {14} \\
a_{21} & a_ {22} & a_ {23} & a_ {24} \\
a_{31} & a_ {32} & a_ {33} & a_ {34} \\
a_{41} & a_ {42} & a_ {43} & a_ {44}
\end{pmatrix}
= \begin{pmatrix} x' & y' & z' & 1 \end{pmatrix}$$
(Why introduce a fictitious fourth coordinate, you ask? That is the beauty of [homogeneous coordinates](https://en.wikipedia.org/wiki/Homogeneous_coordinates), which find great application in computer graphics. Without this, it would not be possible to implement affine operations like the shift operation as a single matrix multiplication, as it requires us to _add_ a constant to the coordinates. The affine transformation becomes a linear transformation in the higher dimension!)
Here are some examples of how transformations are represented in matrix form:
* Shift operation: shift $x$ coordinate by $5$, $y$ coordinate by $7$ and $z$ coordinate by $9$.
$$\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
5 & 7 & 9 & 1
\end{pmatrix}$$
* Scaling operation: scale the $x$ coordinate by $10$ and the other two by $5$.
$$\begin{pmatrix}
10 & 0 & 0 & 0 \\
0 & 5 & 0 & 0 \\
0 & 0 & 5 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}$$
* Rotation operation: rotate $\theta$ degrees around the $x$ axis following the right-hand rule (counter-clockwise direction).
$$\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos \theta & -\sin \theta & 0 \\
0 & \sin \theta & \cos \theta & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}$$
Now, once every transformation is described as a matrix, the sequence of transformations can be described as a product of these matrices, and a "loop" of $k$ repetitions can be described as the matrix raised to the power of $k$ (which can be calculated using binary exponentiation in $O(\log{k})$). This way, the matrix which represents all transformations can be calculated first in $O(m \log{k})$, and then it can be applied to each of the $n$ points in $O(n)$ for a total complexity of $O(n + m \log{k})$.
### Number of paths of length $k$ in a graph { data-toc-label='Number of paths of length <script type="math/tex">k</script> in a graph' }
**Problem:** Given a directed unweighted graph of $n$ vertices, find the number of paths of length $k$ from any vertex $u$ to any other vertex $v$.
**Solution:** This problem is considered in more detail in [a separate article](../graph/fixed_length_paths.md). The algorithm consists of raising the adjacency matrix $M$ of the graph (a matrix where $m_{ij} = 1$ if there is an edge from $i$ to $j$, or $0$ otherwise) to the $k$-th power. Now $m_{ij}$ will be the number of paths of length $k$ from $i$ to $j$. The time complexity of this solution is $O(n^3 \log k)$.
**Note:** In that same article, another variation of this problem is considered: when the edges are weighted and it is required to find the minimum weight path containing exactly $k$ edges. As shown in that article, this problem is also solved by exponentiation of the adjacency matrix. The matrix would have the weight of the edge from $i$ to $j$, or $\infty$ if there is no such edge.
Instead of the usual operation of multiplying two matrices, a modified one should be used:
instead of multiplication, both values are added, and instead of a summation, a minimum is taken.
That is: $result_{ij} = \min\limits_{1\ \leq\ k\ \leq\ n}(a_{ik} + b_{kj})$.
### Variation of binary exponentiation: multiplying two numbers modulo $m$ { data-toc-label='Variation of binary exponentiation: multiplying two numbers modulo <script type="math/tex">m</script>' }
**Problem:** Multiply two numbers $a$ and $b$ modulo $m$. $a$ and $b$ fit in the built-in data types, but their product is too big to fit in a 64-bit integer. The idea is to compute $a \cdot b \pmod m$ without using bignum arithmetics.
**Solution:** We simply apply the binary construction algorithm described above, only performing additions instead of multiplications. In other words, we have "expanded" the multiplication of two numbers to $O (\log m)$ operations of addition and multiplication by two (which, in essence, is an addition).
$$a \cdot b = \begin{cases}
0 &\text{if }a = 0 \\
2 \cdot \frac{a}{2} \cdot b &\text{if }a > 0 \text{ and }a \text{ even} \\
2 \cdot \frac{a-1}{2} \cdot b + b &\text{if }a > 0 \text{ and }a \text{ odd}
\end{cases}$$
**Note:** You can solve this task in a different way by using floating-point operations. First compute the expression $\frac{a \cdot b}{m}$ using floating-point numbers and cast it to an unsigned integer $q$. Subtract $q \cdot m$ from $a \cdot b$ using unsigned integer arithmetics and take it modulo $m$ to find the answer. This solution looks rather unreliable, but it is very fast, and very easy to implement. See [here](https://cs.stackexchange.com/questions/77016/modular-multiplication) for more information.
|
---
title
binary_pow
---
# Binary Exponentiation
Binary exponentiation (also known as exponentiation by squaring) is a trick which allows to calculate $a^n$ using only $O(\log n)$ multiplications (instead of $O(n)$ multiplications required by the naive approach).
It also has important applications in many tasks unrelated to arithmetic, since it
can be used with any operations that have the property of **associativity**:
$$(X \cdot Y) \cdot Z = X \cdot (Y \cdot Z)$$
Most obviously this applies to modular multiplication, to multiplication of matrices and
to other problems which we will discuss below.
## Algorithm
Raising $a$ to the power of $n$ is expressed naively as multiplication by $a$ done $n - 1$ times:
$a^{n} = a \cdot a \cdot \ldots \cdot a$. However, this approach is not practical for large $a$ or $n$.
$a^{b+c} = a^b \cdot a^c$ and $a^{2b} = a^b \cdot a^b = (a^b)^2$.
The idea of binary exponentiation is, that we split the work using the binary representation of the exponent.
Let's write $n$ in base 2, for example:
$$3^{13} = 3^{1101_2} = 3^8 \cdot 3^4 \cdot 3^1$$
Since the number $n$ has exactly $\lfloor \log_2 n \rfloor + 1$ digits in base 2, we only need to perform $O(\log n)$ multiplications, if we know the powers $a^1, a^2, a^4, a^8, \dots, a^{2^{\lfloor \log n \rfloor}}$.
So we only need to know a fast way to compute those.
Luckily this is very easy, since an element in the sequence is just the square of the previous element.
$$\begin{align}
3^1 &= 3 \\
3^2 &= \left(3^1\right)^2 = 3^2 = 9 \\
3^4 &= \left(3^2\right)^2 = 9^2 = 81 \\
3^8 &= \left(3^4\right)^2 = 81^2 = 6561
\end{align}$$
So to get the final answer for $3^{13}$, we only need to multiply three of them (skipping $3^2$ because the corresponding bit in $n$ is not set):
$3^{13} = 6561 \cdot 81 \cdot 3 = 1594323$
The final complexity of this algorithm is $O(\log n)$: we have to compute $\log n$ powers of $a$, and then have to do at most $\log n$ multiplications to get the final answer from them.
The following recursive approach expresses the same idea:
$$a^n = \begin{cases}
1 &\text{if } n == 0 \\
\left(a^{\frac{n}{2}}\right)^2 &\text{if } n > 0 \text{ and } n \text{ even}\\
\left(a^{\frac{n - 1}{2}}\right)^2 \cdot a &\text{if } n > 0 \text{ and } n \text{ odd}\\
\end{cases}$$
## Implementation
First the recursive approach, which is a direct translation of the recursive formula:
```cpp
long long binpow(long long a, long long b) {
if (b == 0)
return 1;
long long res = binpow(a, b / 2);
if (b % 2)
return res * res * a;
else
return res * res;
}
```
The second approach accomplishes the same task without recursion.
It computes all the powers in a loop, and multiplies the ones with the corresponding set bit in $n$.
Although the complexity of both approaches is identical, this approach will be faster in practice since we don't have the overhead of the recursive calls.
```cpp
long long binpow(long long a, long long b) {
long long res = 1;
while (b > 0) {
if (b & 1)
res = res * a;
a = a * a;
b >>= 1;
}
return res;
}
```
## Applications
### Effective computation of large exponents modulo a number
**Problem:**
Compute $x^n \bmod m$.
This is a very common operation. For instance it is used in computing the [modular multiplicative inverse](module-inverse.md).
**Solution:**
Since we know that the modulo operator doesn't interfere with multiplications ($a \cdot b \equiv (a \bmod m) \cdot (b \bmod m) \pmod m$), we can directly use the same code, and just replace every multiplication with a modular multiplication:
```cpp
long long binpow(long long a, long long b, long long m) {
a %= m;
long long res = 1;
while (b > 0) {
if (b & 1)
res = res * a % m;
a = a * a % m;
b >>= 1;
}
return res;
}
```
**Note:**
It's possible to speed this algorithm for large $b >> m$.
If $m$ is a prime number $x^n \equiv x^{n \bmod (m-1)} \pmod{m}$ for prime $m$, and $x^n \equiv x^{n \bmod{\phi(m)}} \pmod{m}$ for composite $m$.
This follows directly from Fermat's little theorem and Euler's theorem, see the article about [Modular Inverses](module-inverse.md#fermat-euler) for more details.
### Effective computation of Fibonacci numbers
**Problem:** Compute $n$-th Fibonacci number $F_n$.
**Solution:** For more details, see the [Fibonacci Number article](fibonacci-numbers.md).
We will only go through an overview of the algorithm.
To compute the next Fibonacci number, only the two previous ones are needed, as $F_n = F_{n-1} + F_{n-2}$.
We can build a $2 \times 2$ matrix that describes this transformation:
the transition from $F_i$ and $F_{i+1}$ to $F_{i+1}$ and $F_{i+2}$.
For example, applying this transformation to the pair $F_0$ and $F_1$ would change it into $F_1$ and $F_2$.
Therefore, we can raise this transformation matrix to the $n$-th power to find $F_n$ in time complexity $O(\log n)$.
### Applying a permutation $k$ times { data-toc-label='Applying a permutation <script type="math/tex">k</script> times' }
**Problem:** You are given a sequence of length $n$. Apply to it a given permutation $k$ times.
**Solution:** Simply raise the permutation to $k$-th power using binary exponentiation, and then apply it to the sequence. This will give you a time complexity of $O(n \log k)$.
```cpp
vector<int> applyPermutation(vector<int> sequence, vector<int> permutation) {
vector<int> newSequence(sequence.size());
for(int i = 0; i < sequence.size(); i++) {
newSequence[i] = sequence[permutation[i]];
}
return newSequence;
}
vector<int> permute(vector<int> sequence, vector<int> permutation, long long b) {
while (b > 0) {
if (b & 1) {
sequence = applyPermutation(sequence, permutation);
}
permutation = applyPermutation(permutation, permutation);
b >>= 1;
}
return sequence;
}
```
**Note:** This task can be solved more efficiently in linear time by building the permutation graph and considering each cycle independently. You could then compute $k$ modulo the size of the cycle and find the final position for each number which is part of this cycle.
### Fast application of a set of geometric operations to a set of points
**Problem:** Given $n$ points $p_i$, apply $m$ transformations to each of these points. Each transformation can be a shift, a scaling or a rotation around a given axis by a given angle. There is also a "loop" operation which applies a given list of transformations $k$ times ("loop" operations can be nested). You should apply all transformations faster than $O(n \cdot length)$, where $length$ is the total number of transformations to be applied (after unrolling "loop" operations).
**Solution:** Let's look at how the different types of transformations change the coordinates:
* Shift operation: adds a different constant to each of the coordinates.
* Scaling operation: multiplies each of the coordinates by a different constant.
* Rotation operation: the transformation is more complicated (we won't go in details here), but each of the new coordinates still can be represented as a linear combination of the old ones.
As you can see, each of the transformations can be represented as a linear operation on the coordinates. Thus, a transformation can be written as a $4 \times 4$ matrix of the form:
$$\begin{pmatrix}
a_{11} & a_ {12} & a_ {13} & a_ {14} \\
a_{21} & a_ {22} & a_ {23} & a_ {24} \\
a_{31} & a_ {32} & a_ {33} & a_ {34} \\
a_{41} & a_ {42} & a_ {43} & a_ {44}
\end{pmatrix}$$
that, when multiplied by a vector with the old coordinates and an unit gives a new vector with the new coordinates and an unit:
$$\begin{pmatrix} x & y & z & 1 \end{pmatrix} \cdot
\begin{pmatrix}
a_{11} & a_ {12} & a_ {13} & a_ {14} \\
a_{21} & a_ {22} & a_ {23} & a_ {24} \\
a_{31} & a_ {32} & a_ {33} & a_ {34} \\
a_{41} & a_ {42} & a_ {43} & a_ {44}
\end{pmatrix}
= \begin{pmatrix} x' & y' & z' & 1 \end{pmatrix}$$
(Why introduce a fictitious fourth coordinate, you ask? That is the beauty of [homogeneous coordinates](https://en.wikipedia.org/wiki/Homogeneous_coordinates), which find great application in computer graphics. Without this, it would not be possible to implement affine operations like the shift operation as a single matrix multiplication, as it requires us to _add_ a constant to the coordinates. The affine transformation becomes a linear transformation in the higher dimension!)
Here are some examples of how transformations are represented in matrix form:
* Shift operation: shift $x$ coordinate by $5$, $y$ coordinate by $7$ and $z$ coordinate by $9$.
$$\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
5 & 7 & 9 & 1
\end{pmatrix}$$
* Scaling operation: scale the $x$ coordinate by $10$ and the other two by $5$.
$$\begin{pmatrix}
10 & 0 & 0 & 0 \\
0 & 5 & 0 & 0 \\
0 & 0 & 5 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}$$
* Rotation operation: rotate $\theta$ degrees around the $x$ axis following the right-hand rule (counter-clockwise direction).
$$\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos \theta & -\sin \theta & 0 \\
0 & \sin \theta & \cos \theta & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}$$
Now, once every transformation is described as a matrix, the sequence of transformations can be described as a product of these matrices, and a "loop" of $k$ repetitions can be described as the matrix raised to the power of $k$ (which can be calculated using binary exponentiation in $O(\log{k})$). This way, the matrix which represents all transformations can be calculated first in $O(m \log{k})$, and then it can be applied to each of the $n$ points in $O(n)$ for a total complexity of $O(n + m \log{k})$.
### Number of paths of length $k$ in a graph { data-toc-label='Number of paths of length <script type="math/tex">k</script> in a graph' }
**Problem:** Given a directed unweighted graph of $n$ vertices, find the number of paths of length $k$ from any vertex $u$ to any other vertex $v$.
**Solution:** This problem is considered in more detail in [a separate article](../graph/fixed_length_paths.md). The algorithm consists of raising the adjacency matrix $M$ of the graph (a matrix where $m_{ij} = 1$ if there is an edge from $i$ to $j$, or $0$ otherwise) to the $k$-th power. Now $m_{ij}$ will be the number of paths of length $k$ from $i$ to $j$. The time complexity of this solution is $O(n^3 \log k)$.
**Note:** In that same article, another variation of this problem is considered: when the edges are weighted and it is required to find the minimum weight path containing exactly $k$ edges. As shown in that article, this problem is also solved by exponentiation of the adjacency matrix. The matrix would have the weight of the edge from $i$ to $j$, or $\infty$ if there is no such edge.
Instead of the usual operation of multiplying two matrices, a modified one should be used:
instead of multiplication, both values are added, and instead of a summation, a minimum is taken.
That is: $result_{ij} = \min\limits_{1\ \leq\ k\ \leq\ n}(a_{ik} + b_{kj})$.
### Variation of binary exponentiation: multiplying two numbers modulo $m$ { data-toc-label='Variation of binary exponentiation: multiplying two numbers modulo <script type="math/tex">m</script>' }
**Problem:** Multiply two numbers $a$ and $b$ modulo $m$. $a$ and $b$ fit in the built-in data types, but their product is too big to fit in a 64-bit integer. The idea is to compute $a \cdot b \pmod m$ without using bignum arithmetics.
**Solution:** We simply apply the binary construction algorithm described above, only performing additions instead of multiplications. In other words, we have "expanded" the multiplication of two numbers to $O (\log m)$ operations of addition and multiplication by two (which, in essence, is an addition).
$$a \cdot b = \begin{cases}
0 &\text{if }a = 0 \\
2 \cdot \frac{a}{2} \cdot b &\text{if }a > 0 \text{ and }a \text{ even} \\
2 \cdot \frac{a-1}{2} \cdot b + b &\text{if }a > 0 \text{ and }a \text{ odd}
\end{cases}$$
**Note:** You can solve this task in a different way by using floating-point operations. First compute the expression $\frac{a \cdot b}{m}$ using floating-point numbers and cast it to an unsigned integer $q$. Subtract $q \cdot m$ from $a \cdot b$ using unsigned integer arithmetics and take it modulo $m$ to find the answer. This solution looks rather unreliable, but it is very fast, and very easy to implement. See [here](https://cs.stackexchange.com/questions/77016/modular-multiplication) for more information.
## Practice Problems
* [UVa 1230 - MODEX](http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=24&page=show_problem&problem=3671)
* [UVa 374 - Big Mod](http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=24&page=show_problem&problem=310)
* [UVa 11029 - Leading and Trailing](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=1970)
* [Codeforces - Parking Lot](http://codeforces.com/problemset/problem/630/I)
* [leetcode - Count good numbers](https://leetcode.com/problems/count-good-numbers/)
* [Codechef - Chef and Riffles](https://www.codechef.com/JAN221B/problems/RIFFLES)
* [Codeforces - Decoding Genome](https://codeforces.com/contest/222/problem/E)
* [Codeforces - Neural Network Country](https://codeforces.com/contest/852/problem/B)
* [Codeforces - Magic Gems](https://codeforces.com/problemset/problem/1117/D)
* [SPOJ - The last digit](http://www.spoj.com/problems/LASTDIG/)
* [SPOJ - Locker](http://www.spoj.com/problems/LOCKER/)
* [LA - 3722 Jewel-eating Monsters](https://vjudge.net/problem/UVALive-3722)
* [SPOJ - Just add it](http://www.spoj.com/problems/ZSUM/)
* [Codeforces - Stairs and Lines](https://codeforces.com/contest/498/problem/E)
|
Binary Exponentiation
|
---
title
balanced_ternary
---
# Balanced Ternary

This is a non-standard but still positional **numeral system**. Its feature is that digits can have one of the values `-1`, `0` and `1`.
Nevertheless, its base is still `3` (because there are three possible values). Since it is not convenient to write `-1` as a digit,
we'll use letter `Z` further for this purpose. If you think it is quite a strange system - look at the picture - here is one of the
computers utilizing it.
So here are few first numbers written in balanced ternary:
```nohighlight
0 0
1 1
2 1Z
3 10
4 11
5 1ZZ
6 1Z0
7 1Z1
8 10Z
9 100
```
This system allows you to write negative values without leading minus sign: you can simply invert digits in any positive number.
```nohighlight
-1 Z
-2 Z1
-3 Z0
-4 ZZ
-5 Z11
```
Note that a negative number starts with `Z` and positive with `1`.
## Conversion algorithm
It is easy to represent a given number in **balanced ternary** via temporary representing it in normal ternary number system. When value is
in standard ternary, its digits are either `0` or `1` or `2`. Iterating from the lowest digit we can safely skip any `0`s and `1`s,
however `2` should be turned into `Z` with adding `1` to the next digit. Digits `3` should be turned into `0` on the same terms -
such digits are not present in the number initially but they can be encountered after increasing some `2`s.
**Example 1:** Let us convert `64` to balanced ternary. At first we use normal ternary to rewrite the number:
$$ 64_{10} = 02101_{3} $$
Let us process it from the least significant (rightmost) digit:
- `1`,`0` and `1` are skipped as it is.( Because `0` and `1` are allowed in balanced ternary )
- `2` is turned into `Z` increasing the digit to its left, so we get `1Z101`.
The final result is `1Z101`.
Let us convert it back to the decimal system by adding the weighted positional values:
$$ 1Z101 = 81 \cdot 1 + 27 \cdot (-1) + 9 \cdot 1 + 3 \cdot 0 + 1 \cdot 1 = 64_{10} $$
**Example 2:** Let us convert `237` to balanced ternary. At first we use normal ternary to rewrite the number:
$$ 237_{10} = 22210_{3} $$
Let us process it from the least significant (rightmost) digit:
- `0` and `1` are skipped as it is.( Because `0` and `1` are allowed in balanced ternary )
- `2` is turned into `Z` increasing the digit to its left, so we get `23Z10`.
- `3` is turned into `0` increasing the digit to its left, so we get `30Z10`.
- `3` is turned into `0` increasing the digit to its left( which is by default `0` ), and so we get `100Z10`.
The final result is `100Z10`.
Let us convert it back to the decimal system by adding the weighted positional values:
$$ 100Z10 = 243 \cdot 1 + 81 \cdot 0 + 27 \cdot 0 + 9 \cdot (-1) + 3 \cdot 1 + 1 \cdot 0 = 237_{10} $$
|
---
title
balanced_ternary
---
# Balanced Ternary

This is a non-standard but still positional **numeral system**. Its feature is that digits can have one of the values `-1`, `0` and `1`.
Nevertheless, its base is still `3` (because there are three possible values). Since it is not convenient to write `-1` as a digit,
we'll use letter `Z` further for this purpose. If you think it is quite a strange system - look at the picture - here is one of the
computers utilizing it.
So here are few first numbers written in balanced ternary:
```nohighlight
0 0
1 1
2 1Z
3 10
4 11
5 1ZZ
6 1Z0
7 1Z1
8 10Z
9 100
```
This system allows you to write negative values without leading minus sign: you can simply invert digits in any positive number.
```nohighlight
-1 Z
-2 Z1
-3 Z0
-4 ZZ
-5 Z11
```
Note that a negative number starts with `Z` and positive with `1`.
## Conversion algorithm
It is easy to represent a given number in **balanced ternary** via temporary representing it in normal ternary number system. When value is
in standard ternary, its digits are either `0` or `1` or `2`. Iterating from the lowest digit we can safely skip any `0`s and `1`s,
however `2` should be turned into `Z` with adding `1` to the next digit. Digits `3` should be turned into `0` on the same terms -
such digits are not present in the number initially but they can be encountered after increasing some `2`s.
**Example 1:** Let us convert `64` to balanced ternary. At first we use normal ternary to rewrite the number:
$$ 64_{10} = 02101_{3} $$
Let us process it from the least significant (rightmost) digit:
- `1`,`0` and `1` are skipped as it is.( Because `0` and `1` are allowed in balanced ternary )
- `2` is turned into `Z` increasing the digit to its left, so we get `1Z101`.
The final result is `1Z101`.
Let us convert it back to the decimal system by adding the weighted positional values:
$$ 1Z101 = 81 \cdot 1 + 27 \cdot (-1) + 9 \cdot 1 + 3 \cdot 0 + 1 \cdot 1 = 64_{10} $$
**Example 2:** Let us convert `237` to balanced ternary. At first we use normal ternary to rewrite the number:
$$ 237_{10} = 22210_{3} $$
Let us process it from the least significant (rightmost) digit:
- `0` and `1` are skipped as it is.( Because `0` and `1` are allowed in balanced ternary )
- `2` is turned into `Z` increasing the digit to its left, so we get `23Z10`.
- `3` is turned into `0` increasing the digit to its left, so we get `30Z10`.
- `3` is turned into `0` increasing the digit to its left( which is by default `0` ), and so we get `100Z10`.
The final result is `100Z10`.
Let us convert it back to the decimal system by adding the weighted positional values:
$$ 100Z10 = 243 \cdot 1 + 81 \cdot 0 + 27 \cdot 0 + 9 \cdot (-1) + 3 \cdot 1 + 1 \cdot 0 = 237_{10} $$
## Practice Problems
* [Topcoder SRM 604, Div1-250](http://community.topcoder.com/stat?c=problem_statement&pm=12917&rd=15837)
|
Balanced Ternary
|
---
title
discrete_root
---
# Discrete Root
The problem of finding a discrete root is defined as follows. Given a prime $n$ and two integers $a$ and $k$, find all $x$ for which:
$x^k \equiv a \pmod n$
## The algorithm
We will solve this problem by reducing it to the [discrete logarithm problem](discrete-log.md).
Let's apply the concept of a [primitive root](primitive-root.md) modulo $n$. Let $g$ be a primitive root modulo $n$. Note that since $n$ is prime, it must exist, and it can be found in $O(Ans \cdot \log \phi (n) \cdot \log n) = O(Ans \cdot \log^2 n)$ plus time of factoring $\phi (n)$.
We can easily discard the case where $a = 0$. In this case, obviously there is only one answer: $x = 0$.
Since we know that $n$ is a prime and any number between 1 and $n-1$ can be represented as a power of the primitive root, we can represent the discrete root problem as follows:
$(g^y)^k \equiv a \pmod n$
where
$x \equiv g^y \pmod n$
This, in turn, can be rewritten as
$(g^k)^y \equiv a \pmod n$
Now we have one unknown $y$, which is a discrete logarithm problem. The solution can be found using Shanks' baby-step giant-step algorithm in $O(\sqrt {n} \log n)$ (or we can verify that there are no solutions).
Having found one solution $y_0$, one of solutions of discrete root problem will be $x_0 = g^{y_0} \pmod n$.
## Finding all solutions from one known solution
To solve the given problem in full, we need to find all solutions knowing one of them: $x_0 = g^{y_0} \pmod n$.
Let's recall the fact that a primitive root always has order of $\phi (n)$, i.e. the smallest power of $g$ which gives 1 is $\phi (n)$. Therefore, if we add the term $\phi (n)$ to the exponential, we still get the same value:
$x^k \equiv g^{ y_0 \cdot k + l \cdot \phi (n)} \equiv a \pmod n \forall l \in Z$
Hence, all the solutions are of the form:
$x = g^{y_0 + \frac {l \cdot \phi (n)}{k}} \pmod n \forall l \in Z$.
where $l$ is chosen such that the fraction must be an integer. For this to be true, the numerator has to be divisible by the least common multiple of $\phi (n)$ and $k$. Remember that least common multiple of two numbers $lcm(a, b) = \frac{a \cdot b}{gcd(a, b)}$; we'll get
$x = g^{y_0 + i \frac {\phi (n)}{gcd(k, \phi (n))}} \pmod n \forall i \in Z$.
This is the final formula for all solutions of the discrete root problem.
## Implementation
Here is a full implementation, including procedures for finding the primitive root, discrete log and finding and printing all solutions.
```cpp
int gcd(int a, int b) {
return a ? gcd(b % a, a) : b;
}
int powmod(int a, int b, int p) {
int res = 1;
while (b > 0) {
if (b & 1) {
res = res * a % p;
}
a = a * a % p;
b >>= 1;
}
return res;
}
// Finds the primitive root modulo p
int generator(int p) {
vector<int> fact;
int phi = p-1, n = phi;
for (int i = 2; i * i <= n; ++i) {
if (n % i == 0) {
fact.push_back(i);
while (n % i == 0)
n /= i;
}
}
if (n > 1)
fact.push_back(n);
for (int res = 2; res <= p; ++res) {
bool ok = true;
for (int factor : fact) {
if (powmod(res, phi / factor, p) == 1) {
ok = false;
break;
}
}
if (ok) return res;
}
return -1;
}
// This program finds all numbers x such that x^k = a (mod n)
int main() {
int n, k, a;
scanf("%d %d %d", &n, &k, &a);
if (a == 0) {
puts("1\n0");
return 0;
}
int g = generator(n);
// Baby-step giant-step discrete logarithm algorithm
int sq = (int) sqrt (n + .0) + 1;
vector<pair<int, int>> dec(sq);
for (int i = 1; i <= sq; ++i)
dec[i-1] = {powmod(g, i * sq * k % (n - 1), n), i};
sort(dec.begin(), dec.end());
int any_ans = -1;
for (int i = 0; i < sq; ++i) {
int my = powmod(g, i * k % (n - 1), n) * a % n;
auto it = lower_bound(dec.begin(), dec.end(), make_pair(my, 0));
if (it != dec.end() && it->first == my) {
any_ans = it->second * sq - i;
break;
}
}
if (any_ans == -1) {
puts("0");
return 0;
}
// Print all possible answers
int delta = (n-1) / gcd(k, n-1);
vector<int> ans;
for (int cur = any_ans % delta; cur < n-1; cur += delta)
ans.push_back(powmod(g, cur, n));
sort(ans.begin(), ans.end());
printf("%d\n", ans.size());
for (int answer : ans)
printf("%d ", answer);
}
```
|
---
title
discrete_root
---
# Discrete Root
The problem of finding a discrete root is defined as follows. Given a prime $n$ and two integers $a$ and $k$, find all $x$ for which:
$x^k \equiv a \pmod n$
## The algorithm
We will solve this problem by reducing it to the [discrete logarithm problem](discrete-log.md).
Let's apply the concept of a [primitive root](primitive-root.md) modulo $n$. Let $g$ be a primitive root modulo $n$. Note that since $n$ is prime, it must exist, and it can be found in $O(Ans \cdot \log \phi (n) \cdot \log n) = O(Ans \cdot \log^2 n)$ plus time of factoring $\phi (n)$.
We can easily discard the case where $a = 0$. In this case, obviously there is only one answer: $x = 0$.
Since we know that $n$ is a prime and any number between 1 and $n-1$ can be represented as a power of the primitive root, we can represent the discrete root problem as follows:
$(g^y)^k \equiv a \pmod n$
where
$x \equiv g^y \pmod n$
This, in turn, can be rewritten as
$(g^k)^y \equiv a \pmod n$
Now we have one unknown $y$, which is a discrete logarithm problem. The solution can be found using Shanks' baby-step giant-step algorithm in $O(\sqrt {n} \log n)$ (or we can verify that there are no solutions).
Having found one solution $y_0$, one of solutions of discrete root problem will be $x_0 = g^{y_0} \pmod n$.
## Finding all solutions from one known solution
To solve the given problem in full, we need to find all solutions knowing one of them: $x_0 = g^{y_0} \pmod n$.
Let's recall the fact that a primitive root always has order of $\phi (n)$, i.e. the smallest power of $g$ which gives 1 is $\phi (n)$. Therefore, if we add the term $\phi (n)$ to the exponential, we still get the same value:
$x^k \equiv g^{ y_0 \cdot k + l \cdot \phi (n)} \equiv a \pmod n \forall l \in Z$
Hence, all the solutions are of the form:
$x = g^{y_0 + \frac {l \cdot \phi (n)}{k}} \pmod n \forall l \in Z$.
where $l$ is chosen such that the fraction must be an integer. For this to be true, the numerator has to be divisible by the least common multiple of $\phi (n)$ and $k$. Remember that least common multiple of two numbers $lcm(a, b) = \frac{a \cdot b}{gcd(a, b)}$; we'll get
$x = g^{y_0 + i \frac {\phi (n)}{gcd(k, \phi (n))}} \pmod n \forall i \in Z$.
This is the final formula for all solutions of the discrete root problem.
## Implementation
Here is a full implementation, including procedures for finding the primitive root, discrete log and finding and printing all solutions.
```cpp
int gcd(int a, int b) {
return a ? gcd(b % a, a) : b;
}
int powmod(int a, int b, int p) {
int res = 1;
while (b > 0) {
if (b & 1) {
res = res * a % p;
}
a = a * a % p;
b >>= 1;
}
return res;
}
// Finds the primitive root modulo p
int generator(int p) {
vector<int> fact;
int phi = p-1, n = phi;
for (int i = 2; i * i <= n; ++i) {
if (n % i == 0) {
fact.push_back(i);
while (n % i == 0)
n /= i;
}
}
if (n > 1)
fact.push_back(n);
for (int res = 2; res <= p; ++res) {
bool ok = true;
for (int factor : fact) {
if (powmod(res, phi / factor, p) == 1) {
ok = false;
break;
}
}
if (ok) return res;
}
return -1;
}
// This program finds all numbers x such that x^k = a (mod n)
int main() {
int n, k, a;
scanf("%d %d %d", &n, &k, &a);
if (a == 0) {
puts("1\n0");
return 0;
}
int g = generator(n);
// Baby-step giant-step discrete logarithm algorithm
int sq = (int) sqrt (n + .0) + 1;
vector<pair<int, int>> dec(sq);
for (int i = 1; i <= sq; ++i)
dec[i-1] = {powmod(g, i * sq * k % (n - 1), n), i};
sort(dec.begin(), dec.end());
int any_ans = -1;
for (int i = 0; i < sq; ++i) {
int my = powmod(g, i * k % (n - 1), n) * a % n;
auto it = lower_bound(dec.begin(), dec.end(), make_pair(my, 0));
if (it != dec.end() && it->first == my) {
any_ans = it->second * sq - i;
break;
}
}
if (any_ans == -1) {
puts("0");
return 0;
}
// Print all possible answers
int delta = (n-1) / gcd(k, n-1);
vector<int> ans;
for (int cur = any_ans % delta; cur < n-1; cur += delta)
ans.push_back(powmod(g, cur, n));
sort(ans.begin(), ans.end());
printf("%d\n", ans.size());
for (int answer : ans)
printf("%d ", answer);
}
```
## Practice problems
* [Codeforces - Lunar New Year and a Recursive Sequence](https://codeforces.com/contest/1106/problem/F)
|
Discrete Root
|
---
title
- Original
---
# Integer factorization
In this article we list several algorithms for factorizing integers, each of them can be both fast and also slow (some slower than others) depending on their input.
Notice, if the number that you want to factorize is actually a prime number, most of the algorithms, especially Fermat's factorization algorithm, Pollard's p-1, Pollard's rho algorithm will run very slow.
So it makes sense to perform a probabilistic (or a fast deterministic) [primality test](primality_tests.md) before trying to factorize the number.
## Trial division
This is the most basic algorithm to find a prime factorization.
We divide by each possible divisor $d$.
We can notice, that it is impossible that all prime factors of a composite number $n$ are bigger than $\sqrt{n}$.
Therefore, we only need to test the divisors $2 \le d \le \sqrt{n}$, which gives us the prime factorization in $O(\sqrt{n})$.
(This is [pseudo-polynomial time](https://en.wikipedia.org/wiki/Pseudo-polynomial_time), i.e. polynomial in the value of the input but exponential in the number of bits of the input.)
The smallest divisor has to be a prime number.
We remove the factor from the number, and repeat the process.
If we cannot find any divisor in the range $[2; \sqrt{n}]$, then the number itself has to be prime.
```{.cpp file=factorization_trial_division1}
vector<long long> trial_division1(long long n) {
vector<long long> factorization;
for (long long d = 2; d * d <= n; d++) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
```
### Wheel factorization
This is an optimization of the trial division.
The idea is the following.
Once we know that the number is not divisible by 2, we don't need to check every other even number.
This leaves us with only $50\%$ of the numbers to check.
After checking 2, we can simply start with 3 and skip every other number.
```{.cpp file=factorization_trial_division2}
vector<long long> trial_division2(long long n) {
vector<long long> factorization;
while (n % 2 == 0) {
factorization.push_back(2);
n /= 2;
}
for (long long d = 3; d * d <= n; d += 2) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
```
This method can be extended.
If the number is not divisible by 3, we can also ignore all other multiples of 3 in the future computations.
So we only need to check the numbers $5, 7, 11, 13, 17, 19, 23, \dots$.
We can observe a pattern of these remaining numbers.
We need to check all numbers with $d \bmod 6 = 1$ and $d \bmod 6 = 5$.
So this leaves us with only $33.3\%$ percent of the numbers to check.
We can implement this by checking the primes 2 and 3 first, and then start checking with 5 and alternatively skip 1 or 3 numbers.
We can extend this even further.
Here is an implementation for the prime number 2, 3 and 5.
It's convenient to use an array to store how much we have to skip.
```{.cpp file=factorization_trial_division3}
vector<long long> trial_division3(long long n) {
vector<long long> factorization;
for (int d : {2, 3, 5}) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
static array<int, 8> increments = {4, 2, 4, 2, 4, 6, 2, 6};
int i = 0;
for (long long d = 7; d * d <= n; d += increments[i++]) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
if (i == 8)
i = 0;
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
```
If we extend this further with more primes, we can even reach better percentages.
However, also the skip lists will get a lot bigger.
### Precomputed primes
Extending the wheel factorization with more and more primes will leave exactly the primes to check.
So a good way of checking is just to precompute all prime numbers with the [Sieve of Eratosthenes](sieve-of-eratosthenes.md) until $\sqrt{n}$ and test them individually.
```{.cpp file=factorization_trial_division4}
vector<long long> primes;
vector<long long> trial_division4(long long n) {
vector<long long> factorization;
for (long long d : primes) {
if (d * d > n)
break;
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
```
## Fermat's factorization method
We can write an odd composite number $n = p \cdot q$ as the difference of two squares $n = a^2 - b^2$:
$$n = \left(\frac{p + q}{2}\right)^2 - \left(\frac{p - q}{2}\right)^2$$
Fermat's factorization method tries to exploit the fact, by guessing the first square $a^2$, and check if the remaining part $b^2 = a^2 - n$ is also a square number.
If it is, then we have found the factors $a - b$ and $a + b$ of $n$.
```cpp
int fermat(int n) {
int a = ceil(sqrt(n));
int b2 = a*a - n;
int b = round(sqrt(b2));
while (b * b != b2) {
a = a + 1;
b2 = a*a - n;
b = round(sqrt(b2));
}
return a - b;
}
```
Notice, this factorization method can be very fast, if the difference between the two factors $p$ and $q$ is small.
The algorithm runs in $O(|p - q|)$ time.
However since it is very slow, once the factors are far apart, it is rarely used in practice.
However there are still a huge number of optimizations for this approach.
E.g. by looking at the squares $a^2$ modulo a fixed small number, you can notice that you don't have to look at certain values $a$ since they cannot produce a square number $a^2 - n$.
## Pollard's $p - 1$ method { data-toc-label="Pollard's <script type='math/tex'>p - 1</script> method" }
It is very likely that at least one factor of a number is $B$**-powersmooth** for small $B$.
$B$-powersmooth means that every prime power $d^k$ that divides $p-1$ is at most $B$.
E.g. the prime factorization of $4817191$ is $1303 \cdot 3697$.
And the factors are $31$-powersmooth and $16$-powersmooth respectably, because $1303 - 1 = 2 \cdot 3 \cdot 7 \cdot 31$ and $3697 - 1 = 2^4 \cdot 3 \cdot 7 \cdot 11$.
In 1974 John Pollard invented a method to extracts $B$-powersmooth factors from a composite number.
The idea comes from [Fermat's little theorem](phi-function.md#application).
Let a factorization of $n$ be $n = p \cdot q$.
It says that if $a$ is coprime to $p$, the following statement holds:
$$a^{p - 1} \equiv 1 \pmod{p}$$
This also means that
$$a^{(p - 1)^k} \equiv a^{k \cdot (p - 1)} \equiv 1 \pmod{p}.$$
So for any $M$ with $p - 1 ~|~ M$ we know that $a^M \equiv 1$.
This means that $a^M - 1 = p \cdot r$, and because of that also $p ~|~ \gcd(a^M - 1, n)$.
Therefore, if $p - 1$ for a factor $p$ of $n$ divides $M$, we can extract a factor using [Euclid's algorithm](euclid-algorithm.md).
It is clear, that the smallest $M$ that is a multiple of every $B$-powersmooth number is $\text{lcm}(1,~2~,3~,4~,~\dots,~B)$.
Or alternatively:
$$M = \prod_{\text{prime } q \le B} q^{\lfloor \log_q B \rfloor}$$
Notice, if $p-1$ divides $M$ for all prime factors $p$ of $n$, then $\gcd(a^M - 1, n)$ will just be $n$.
In this case we don't receive a factor.
Therefore we will try to perform the $\gcd$ multiple time, while we compute $M$.
Some composite numbers don't have $B$-powersmooth factors for small $B$.
E.g. the factors of the composite number $100~000~000~000~000~493 = 763~013 \cdot 131~059~365~961$ are $190~753$-powersmooth and $1~092~161~383$-powersmooth.
We would have to choose $B >= 190~753$ to factorize the number.
In the following implementation we start with $B = 10$ and increase $B$ after each each iteration.
```{.cpp file=factorization_p_minus_1}
long long pollards_p_minus_1(long long n) {
int B = 10;
long long g = 1;
while (B <= 1000000 && g < n) {
long long a = 2 + rand() % (n - 3);
g = gcd(a, n);
if (g > 1)
return g;
// compute a^M
for (int p : primes) {
if (p >= B)
continue;
long long p_power = 1;
while (p_power * p <= B)
p_power *= p;
a = power(a, p_power, n);
g = gcd(a - 1, n);
if (g > 1 && g < n)
return g;
}
B *= 2;
}
return 1;
}
```
Notice, this is a probabilistic algorithm.
It can happen that the algorithm doesn't find a factor.
The complexity is $O(B \log B \log^2 n)$ per iteration.
## Pollard's rho algorithm
Another factorization algorithm from John Pollard.
Let the prime factorization of a number be $n = p q$.
The algorithm looks at a pseudo-random sequence $\{x_i\} = \{x_0,~f(x_0),~f(f(x_0)),~\dots\}$ where $f$ is a polynomial function, usually $f(x) = (x^2 + c) \bmod n$ is chosen with $c = 1$.
Actually we are not very interested in the sequence $\{x_i\}$, we are more interested in the sequence $\{x_i \bmod p\}$.
Since $f$ is a polynomial function and all the values are in the range $[0;~p)$ this sequence will begin to cycle sooner or later.
The **birthday paradox** actually suggests, that the expected number of elements is $O(\sqrt{p})$ until the repetition starts.
If $p$ is smaller than $\sqrt{n}$, the repetition will start very likely in $O(\sqrt[4]{n})$.
Here is a visualization of such a sequence $\{x_i \bmod p\}$ with $n = 2206637$, $p = 317$, $x_0 = 2$ and $f(x) = x^2 + 1$.
From the form of the sequence you can see very clearly why the algorithm is called Pollard's $\rho$ algorithm.
<center></center>
There is still one big open question.
We don't know $p$ yet, so how can we argue about the sequence $\{x_i \bmod p\}$?
It's actually quite easy.
There is a cycle in the sequence $\{x_i \bmod p\}_{i \le j}$ if and only if there are two indices $s, t \le j$ such that $x_s \equiv x_t \bmod p$.
This equation can be rewritten as $x_s - x_t \equiv 0 \bmod p$ which is the same as $p ~|~ \gcd(x_s - x_t, n)$.
Therefore, if we find two indices $s$ and $t$ with $g = \gcd(x_s - x_t, n) > 1$, we have found a cycle and also a factor $g$ of $n$.
Notice that it is possible that $g = n$.
In this case we haven't found a proper factor, and we have to repeat the algorithm with different parameter (different starting value $x_0$, different constant $c$ in the polynomial function $f$).
To find the cycle, we can use any common cycle detection algorithm.
### Floyd's cycle-finding algorithm
This algorithm finds a cycle by using two pointers.
These pointers move over the sequence at different speeds.
In each iteration the first pointer advances to the next element, but the second pointer advances two elements.
It's not hard to see, that if there exists a cycle, the second pointer will make at least one full cycle and then meet the first pointer during the next few cycle loops.
If the cycle length is $\lambda$ and the $\mu$ is the first index at which the cycle starts, then the algorithm will run in $O(\lambda + \mu)$ time.
This algorithm is also known as **tortoise and the hare algorithm**, based on the tale in which a tortoise (here a slow pointer) and a hare (here a faster pointer) make a race.
It is actually possible to determine the parameter $\lambda$ and $\mu$ using this algorithm (also in $O(\lambda + \mu)$ time and $O(1)$ space), but here is just the simplified version for finding the cycle at all.
The algorithm and returns true as soon as it detects a cycle.
If the sequence doesn't have a cycle, then the function will never stop.
However this cannot happen during Pollard's rho algorithm.
```text
function floyd(f, x0):
tortoise = x0
hare = f(x0)
while tortoise != hare:
tortoise = f(tortoise)
hare = f(f(hare))
return true
```
### Implementation
First here is a implementation using the **Floyd's cycle-finding algorithm**.
The algorithm runs (usually) in $O(\sqrt[4]{n} \log(n))$ time.
```{.cpp file=pollard_rho}
long long mult(long long a, long long b, long long mod) {
return (__int128)a * b % mod;
}
long long f(long long x, long long c, long long mod) {
return (mult(x, x, mod) + c) % mod;
}
long long rho(long long n, long long x0=2, long long c=1) {
long long x = x0;
long long y = x0;
long long g = 1;
while (g == 1) {
x = f(x, c, n);
y = f(y, c, n);
y = f(y, c, n);
g = gcd(abs(x - y), n);
}
return g;
}
```
The following table shows the values of $x$ and $y$ during the algorithm for $n = 2206637$, $x_0 = 2$ and $c = 1$.
$$
\newcommand\T{\Rule{0pt}{1em}{.3em}}
\begin{array}{|l|l|l|l|l|l|}
\hline
i & x_i \bmod n & x_{2i} \bmod n & x_i \bmod 317 & x_{2i} \bmod 317 & \gcd(x_i - x_{2i}, n) \\
\hline
0 & 2 & 2 & 2 & 2 & - \\
1 & 5 & 26 & 5 & 26 & 1 \\
2 & 26 & 458330 & 26 & 265 & 1 \\
3 & 677 & 1671573 & 43 & 32 & 1 \\
4 & 458330 & 641379 & 265 & 88 & 1 \\
5 & 1166412 & 351937 & 169 & 67 & 1 \\
6 & 1671573 & 1264682 & 32 & 169 & 1 \\
7 & 2193080 & 2088470 & 74 & 74 & 317 \\
\hline
\end{array}$$
The implementation uses a function `mult`, that multiplies two integers $\le 10^{18}$ without overflow by using a GCC's type `__int128` for 128-bit integer.
If GCC is not available, you can using a similar idea as [binary exponentiation](binary-exp.md).
```{.cpp file=pollard_rho_mult2}
long long mult(long long a, long long b, long long mod) {
long long result = 0;
while (b) {
if (b & 1)
result = (result + a) % mod;
a = (a + a) % mod;
b >>= 1;
}
return result;
}
```
Alternatively you can also implement the [Montgomery multiplication](montgomery_multiplication.md).
As already noticed above: if $n$ is composite and the algorithm returns $n$ as factor, you have to repeat the procedure with different parameter $x_0$ and $c$.
E.g. the choice $x_0 = c = 1$ will not factor $25 = 5 \cdot 5$.
The algorithm will just return $25$.
However the choice $x_0 = 1$, $c = 2$ will factor it.
### Brent's algorithm
Brent uses a similar algorithm as Floyd.
It also uses two pointer.
But instead of advancing the pointers by one and two respectably, we advance them in powers of two.
As soon as $2^i$ is greater than $\lambda$ and $\mu$, we will find the cycle.
```text
function floyd(f, x0):
tortoise = x0
hare = f(x0)
l = 1
while tortoise != hare:
tortoise = hare
repeat l times:
hare = f(hare)
if tortoise == hare:
return true
l *= 2
return true
```
Brent's algorithm also runs in linear time, but is usually faster than Floyd's algorithm, since it uses less evaluations of the function $f$.
### Implementation
The straightforward implementation using Brent's algorithms can be speeded up by noticing, that we can omit the terms $x_l - x_k$ if $k < \frac{3 \cdot l}{2}$.
Also, instead of performing the $\gcd$ computation at every step, we multiply the terms and do it every few steps and backtrack if we overshoot.
```{.cpp file=pollard_rho_brent}
long long brent(long long n, long long x0=2, long long c=1) {
long long x = x0;
long long g = 1;
long long q = 1;
long long xs, y;
int m = 128;
int l = 1;
while (g == 1) {
y = x;
for (int i = 1; i < l; i++)
x = f(x, c, n);
int k = 0;
while (k < l && g == 1) {
xs = x;
for (int i = 0; i < m && i < l - k; i++) {
x = f(x, c, n);
q = mult(q, abs(y - x), n);
}
g = gcd(q, n);
k += m;
}
l *= 2;
}
if (g == n) {
do {
xs = f(xs, c, n);
g = gcd(abs(xs - y), n);
} while (g == 1);
}
return g;
}
```
The combination of a trial division for small prime numbers together with Brent's version of Pollard's rho algorithm will make a very powerful factorization algorithm.
|
---
title
- Original
---
# Integer factorization
In this article we list several algorithms for factorizing integers, each of them can be both fast and also slow (some slower than others) depending on their input.
Notice, if the number that you want to factorize is actually a prime number, most of the algorithms, especially Fermat's factorization algorithm, Pollard's p-1, Pollard's rho algorithm will run very slow.
So it makes sense to perform a probabilistic (or a fast deterministic) [primality test](primality_tests.md) before trying to factorize the number.
## Trial division
This is the most basic algorithm to find a prime factorization.
We divide by each possible divisor $d$.
We can notice, that it is impossible that all prime factors of a composite number $n$ are bigger than $\sqrt{n}$.
Therefore, we only need to test the divisors $2 \le d \le \sqrt{n}$, which gives us the prime factorization in $O(\sqrt{n})$.
(This is [pseudo-polynomial time](https://en.wikipedia.org/wiki/Pseudo-polynomial_time), i.e. polynomial in the value of the input but exponential in the number of bits of the input.)
The smallest divisor has to be a prime number.
We remove the factor from the number, and repeat the process.
If we cannot find any divisor in the range $[2; \sqrt{n}]$, then the number itself has to be prime.
```{.cpp file=factorization_trial_division1}
vector<long long> trial_division1(long long n) {
vector<long long> factorization;
for (long long d = 2; d * d <= n; d++) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
```
### Wheel factorization
This is an optimization of the trial division.
The idea is the following.
Once we know that the number is not divisible by 2, we don't need to check every other even number.
This leaves us with only $50\%$ of the numbers to check.
After checking 2, we can simply start with 3 and skip every other number.
```{.cpp file=factorization_trial_division2}
vector<long long> trial_division2(long long n) {
vector<long long> factorization;
while (n % 2 == 0) {
factorization.push_back(2);
n /= 2;
}
for (long long d = 3; d * d <= n; d += 2) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
```
This method can be extended.
If the number is not divisible by 3, we can also ignore all other multiples of 3 in the future computations.
So we only need to check the numbers $5, 7, 11, 13, 17, 19, 23, \dots$.
We can observe a pattern of these remaining numbers.
We need to check all numbers with $d \bmod 6 = 1$ and $d \bmod 6 = 5$.
So this leaves us with only $33.3\%$ percent of the numbers to check.
We can implement this by checking the primes 2 and 3 first, and then start checking with 5 and alternatively skip 1 or 3 numbers.
We can extend this even further.
Here is an implementation for the prime number 2, 3 and 5.
It's convenient to use an array to store how much we have to skip.
```{.cpp file=factorization_trial_division3}
vector<long long> trial_division3(long long n) {
vector<long long> factorization;
for (int d : {2, 3, 5}) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
static array<int, 8> increments = {4, 2, 4, 2, 4, 6, 2, 6};
int i = 0;
for (long long d = 7; d * d <= n; d += increments[i++]) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
if (i == 8)
i = 0;
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
```
If we extend this further with more primes, we can even reach better percentages.
However, also the skip lists will get a lot bigger.
### Precomputed primes
Extending the wheel factorization with more and more primes will leave exactly the primes to check.
So a good way of checking is just to precompute all prime numbers with the [Sieve of Eratosthenes](sieve-of-eratosthenes.md) until $\sqrt{n}$ and test them individually.
```{.cpp file=factorization_trial_division4}
vector<long long> primes;
vector<long long> trial_division4(long long n) {
vector<long long> factorization;
for (long long d : primes) {
if (d * d > n)
break;
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
```
## Fermat's factorization method
We can write an odd composite number $n = p \cdot q$ as the difference of two squares $n = a^2 - b^2$:
$$n = \left(\frac{p + q}{2}\right)^2 - \left(\frac{p - q}{2}\right)^2$$
Fermat's factorization method tries to exploit the fact, by guessing the first square $a^2$, and check if the remaining part $b^2 = a^2 - n$ is also a square number.
If it is, then we have found the factors $a - b$ and $a + b$ of $n$.
```cpp
int fermat(int n) {
int a = ceil(sqrt(n));
int b2 = a*a - n;
int b = round(sqrt(b2));
while (b * b != b2) {
a = a + 1;
b2 = a*a - n;
b = round(sqrt(b2));
}
return a - b;
}
```
Notice, this factorization method can be very fast, if the difference between the two factors $p$ and $q$ is small.
The algorithm runs in $O(|p - q|)$ time.
However since it is very slow, once the factors are far apart, it is rarely used in practice.
However there are still a huge number of optimizations for this approach.
E.g. by looking at the squares $a^2$ modulo a fixed small number, you can notice that you don't have to look at certain values $a$ since they cannot produce a square number $a^2 - n$.
## Pollard's $p - 1$ method { data-toc-label="Pollard's <script type='math/tex'>p - 1</script> method" }
It is very likely that at least one factor of a number is $B$**-powersmooth** for small $B$.
$B$-powersmooth means that every prime power $d^k$ that divides $p-1$ is at most $B$.
E.g. the prime factorization of $4817191$ is $1303 \cdot 3697$.
And the factors are $31$-powersmooth and $16$-powersmooth respectably, because $1303 - 1 = 2 \cdot 3 \cdot 7 \cdot 31$ and $3697 - 1 = 2^4 \cdot 3 \cdot 7 \cdot 11$.
In 1974 John Pollard invented a method to extracts $B$-powersmooth factors from a composite number.
The idea comes from [Fermat's little theorem](phi-function.md#application).
Let a factorization of $n$ be $n = p \cdot q$.
It says that if $a$ is coprime to $p$, the following statement holds:
$$a^{p - 1} \equiv 1 \pmod{p}$$
This also means that
$$a^{(p - 1)^k} \equiv a^{k \cdot (p - 1)} \equiv 1 \pmod{p}.$$
So for any $M$ with $p - 1 ~|~ M$ we know that $a^M \equiv 1$.
This means that $a^M - 1 = p \cdot r$, and because of that also $p ~|~ \gcd(a^M - 1, n)$.
Therefore, if $p - 1$ for a factor $p$ of $n$ divides $M$, we can extract a factor using [Euclid's algorithm](euclid-algorithm.md).
It is clear, that the smallest $M$ that is a multiple of every $B$-powersmooth number is $\text{lcm}(1,~2~,3~,4~,~\dots,~B)$.
Or alternatively:
$$M = \prod_{\text{prime } q \le B} q^{\lfloor \log_q B \rfloor}$$
Notice, if $p-1$ divides $M$ for all prime factors $p$ of $n$, then $\gcd(a^M - 1, n)$ will just be $n$.
In this case we don't receive a factor.
Therefore we will try to perform the $\gcd$ multiple time, while we compute $M$.
Some composite numbers don't have $B$-powersmooth factors for small $B$.
E.g. the factors of the composite number $100~000~000~000~000~493 = 763~013 \cdot 131~059~365~961$ are $190~753$-powersmooth and $1~092~161~383$-powersmooth.
We would have to choose $B >= 190~753$ to factorize the number.
In the following implementation we start with $B = 10$ and increase $B$ after each each iteration.
```{.cpp file=factorization_p_minus_1}
long long pollards_p_minus_1(long long n) {
int B = 10;
long long g = 1;
while (B <= 1000000 && g < n) {
long long a = 2 + rand() % (n - 3);
g = gcd(a, n);
if (g > 1)
return g;
// compute a^M
for (int p : primes) {
if (p >= B)
continue;
long long p_power = 1;
while (p_power * p <= B)
p_power *= p;
a = power(a, p_power, n);
g = gcd(a - 1, n);
if (g > 1 && g < n)
return g;
}
B *= 2;
}
return 1;
}
```
Notice, this is a probabilistic algorithm.
It can happen that the algorithm doesn't find a factor.
The complexity is $O(B \log B \log^2 n)$ per iteration.
## Pollard's rho algorithm
Another factorization algorithm from John Pollard.
Let the prime factorization of a number be $n = p q$.
The algorithm looks at a pseudo-random sequence $\{x_i\} = \{x_0,~f(x_0),~f(f(x_0)),~\dots\}$ where $f$ is a polynomial function, usually $f(x) = (x^2 + c) \bmod n$ is chosen with $c = 1$.
Actually we are not very interested in the sequence $\{x_i\}$, we are more interested in the sequence $\{x_i \bmod p\}$.
Since $f$ is a polynomial function and all the values are in the range $[0;~p)$ this sequence will begin to cycle sooner or later.
The **birthday paradox** actually suggests, that the expected number of elements is $O(\sqrt{p})$ until the repetition starts.
If $p$ is smaller than $\sqrt{n}$, the repetition will start very likely in $O(\sqrt[4]{n})$.
Here is a visualization of such a sequence $\{x_i \bmod p\}$ with $n = 2206637$, $p = 317$, $x_0 = 2$ and $f(x) = x^2 + 1$.
From the form of the sequence you can see very clearly why the algorithm is called Pollard's $\rho$ algorithm.
<center></center>
There is still one big open question.
We don't know $p$ yet, so how can we argue about the sequence $\{x_i \bmod p\}$?
It's actually quite easy.
There is a cycle in the sequence $\{x_i \bmod p\}_{i \le j}$ if and only if there are two indices $s, t \le j$ such that $x_s \equiv x_t \bmod p$.
This equation can be rewritten as $x_s - x_t \equiv 0 \bmod p$ which is the same as $p ~|~ \gcd(x_s - x_t, n)$.
Therefore, if we find two indices $s$ and $t$ with $g = \gcd(x_s - x_t, n) > 1$, we have found a cycle and also a factor $g$ of $n$.
Notice that it is possible that $g = n$.
In this case we haven't found a proper factor, and we have to repeat the algorithm with different parameter (different starting value $x_0$, different constant $c$ in the polynomial function $f$).
To find the cycle, we can use any common cycle detection algorithm.
### Floyd's cycle-finding algorithm
This algorithm finds a cycle by using two pointers.
These pointers move over the sequence at different speeds.
In each iteration the first pointer advances to the next element, but the second pointer advances two elements.
It's not hard to see, that if there exists a cycle, the second pointer will make at least one full cycle and then meet the first pointer during the next few cycle loops.
If the cycle length is $\lambda$ and the $\mu$ is the first index at which the cycle starts, then the algorithm will run in $O(\lambda + \mu)$ time.
This algorithm is also known as **tortoise and the hare algorithm**, based on the tale in which a tortoise (here a slow pointer) and a hare (here a faster pointer) make a race.
It is actually possible to determine the parameter $\lambda$ and $\mu$ using this algorithm (also in $O(\lambda + \mu)$ time and $O(1)$ space), but here is just the simplified version for finding the cycle at all.
The algorithm and returns true as soon as it detects a cycle.
If the sequence doesn't have a cycle, then the function will never stop.
However this cannot happen during Pollard's rho algorithm.
```text
function floyd(f, x0):
tortoise = x0
hare = f(x0)
while tortoise != hare:
tortoise = f(tortoise)
hare = f(f(hare))
return true
```
### Implementation
First here is a implementation using the **Floyd's cycle-finding algorithm**.
The algorithm runs (usually) in $O(\sqrt[4]{n} \log(n))$ time.
```{.cpp file=pollard_rho}
long long mult(long long a, long long b, long long mod) {
return (__int128)a * b % mod;
}
long long f(long long x, long long c, long long mod) {
return (mult(x, x, mod) + c) % mod;
}
long long rho(long long n, long long x0=2, long long c=1) {
long long x = x0;
long long y = x0;
long long g = 1;
while (g == 1) {
x = f(x, c, n);
y = f(y, c, n);
y = f(y, c, n);
g = gcd(abs(x - y), n);
}
return g;
}
```
The following table shows the values of $x$ and $y$ during the algorithm for $n = 2206637$, $x_0 = 2$ and $c = 1$.
$$
\newcommand\T{\Rule{0pt}{1em}{.3em}}
\begin{array}{|l|l|l|l|l|l|}
\hline
i & x_i \bmod n & x_{2i} \bmod n & x_i \bmod 317 & x_{2i} \bmod 317 & \gcd(x_i - x_{2i}, n) \\
\hline
0 & 2 & 2 & 2 & 2 & - \\
1 & 5 & 26 & 5 & 26 & 1 \\
2 & 26 & 458330 & 26 & 265 & 1 \\
3 & 677 & 1671573 & 43 & 32 & 1 \\
4 & 458330 & 641379 & 265 & 88 & 1 \\
5 & 1166412 & 351937 & 169 & 67 & 1 \\
6 & 1671573 & 1264682 & 32 & 169 & 1 \\
7 & 2193080 & 2088470 & 74 & 74 & 317 \\
\hline
\end{array}$$
The implementation uses a function `mult`, that multiplies two integers $\le 10^{18}$ without overflow by using a GCC's type `__int128` for 128-bit integer.
If GCC is not available, you can using a similar idea as [binary exponentiation](binary-exp.md).
```{.cpp file=pollard_rho_mult2}
long long mult(long long a, long long b, long long mod) {
long long result = 0;
while (b) {
if (b & 1)
result = (result + a) % mod;
a = (a + a) % mod;
b >>= 1;
}
return result;
}
```
Alternatively you can also implement the [Montgomery multiplication](montgomery_multiplication.md).
As already noticed above: if $n$ is composite and the algorithm returns $n$ as factor, you have to repeat the procedure with different parameter $x_0$ and $c$.
E.g. the choice $x_0 = c = 1$ will not factor $25 = 5 \cdot 5$.
The algorithm will just return $25$.
However the choice $x_0 = 1$, $c = 2$ will factor it.
### Brent's algorithm
Brent uses a similar algorithm as Floyd.
It also uses two pointer.
But instead of advancing the pointers by one and two respectably, we advance them in powers of two.
As soon as $2^i$ is greater than $\lambda$ and $\mu$, we will find the cycle.
```text
function floyd(f, x0):
tortoise = x0
hare = f(x0)
l = 1
while tortoise != hare:
tortoise = hare
repeat l times:
hare = f(hare)
if tortoise == hare:
return true
l *= 2
return true
```
Brent's algorithm also runs in linear time, but is usually faster than Floyd's algorithm, since it uses less evaluations of the function $f$.
### Implementation
The straightforward implementation using Brent's algorithms can be speeded up by noticing, that we can omit the terms $x_l - x_k$ if $k < \frac{3 \cdot l}{2}$.
Also, instead of performing the $\gcd$ computation at every step, we multiply the terms and do it every few steps and backtrack if we overshoot.
```{.cpp file=pollard_rho_brent}
long long brent(long long n, long long x0=2, long long c=1) {
long long x = x0;
long long g = 1;
long long q = 1;
long long xs, y;
int m = 128;
int l = 1;
while (g == 1) {
y = x;
for (int i = 1; i < l; i++)
x = f(x, c, n);
int k = 0;
while (k < l && g == 1) {
xs = x;
for (int i = 0; i < m && i < l - k; i++) {
x = f(x, c, n);
q = mult(q, abs(y - x), n);
}
g = gcd(q, n);
k += m;
}
l *= 2;
}
if (g == n) {
do {
xs = f(xs, c, n);
g = gcd(abs(xs - y), n);
} while (g == 1);
}
return g;
}
```
The combination of a trial division for small prime numbers together with Brent's version of Pollard's rho algorithm will make a very powerful factorization algorithm.
## Practice Problems
- [SPOJ - FACT0](https://www.spoj.com/problems/FACT0/)
- [SPOJ - FACT1](https://www.spoj.com/problems/FACT1/)
- [SPOJ - FACT2](https://www.spoj.com/problems/FACT2/)
- [GCPC 15 - Divisions](https://codeforces.com/gym/100753)
|
Integer factorization
|
---
title
all_submasks
---
# Submask Enumeration
## Enumerating all submasks of a given mask
Given a bitmask $m$, you want to efficiently iterate through all of its submasks, that is, masks $s$ in which only bits that were included in mask $m$ are set.
Consider the implementation of this algorithm, based on tricks with bit operations:
```cpp
int s = m;
while (s > 0) {
... you can use s ...
s = (s-1) & m;
}
```
or, using a more compact `for` statement:
```cpp
for (int s=m; s; s=(s-1)&m)
... you can use s ...
```
In both variants of the code, the submask equal to zero will not be processed. We can either process it outside the loop, or use a less elegant design, for example:
```cpp
for (int s=m; ; s=(s-1)&m) {
... you can use s ...
if (s==0) break;
}
```
Let us examine why the above code visits all submasks of $m$, without repetition, and in descending order.
Suppose we have a current bitmask $s$, and we want to move on to the next bitmask. By subtracting from the mask $s$ one unit, we will remove the rightmost set bit and all bits to the right of it will become 1. Then we remove all the "extra" one bits that are not included in the mask $m$ and therefore can't be a part of a submask. We do this removal by using the bitwise operation `(s-1) & m`. As a result, we "cut" mask $s-1$ to determine the highest value that it can take, that is, the next submask after $s$ in descending order.
Thus, this algorithm generates all submasks of this mask in descending order, performing only two operations per iteration.
A special case is when $s = 0$. After executing $s-1$ we get a mask where all bits are set (bit representation of -1), and after `(s-1) & m` we will have that $s$ will be equal to $m$. Therefore, with the mask $s = 0$ be careful — if the loop does not end at zero, the algorithm may enter an infinite loop.
## Iterating through all masks with their submasks. Complexity $O(3^n)$
In many problems, especially those that use bitmask dynamic programming, you want to iterate through all bitmasks and for each mask, iterate through all of its submasks:
```cpp
for (int m=0; m<(1<<n); ++m)
for (int s=m; s; s=(s-1)&m)
... s and m ...
```
Let's prove that the inner loop will execute a total of $O(3^n)$ iterations.
**First proof**: Consider the $i$-th bit. There are exactly three options for it:
1. it is not included in the mask $m$ (and therefore not included in submask $s$),
2. it is included in $m$, but not included in $s$, or
3. it is included in both $m$ and $s$.
As there are a total of $n$ bits, there will be $3^n$ different combinations.
**Second proof**: Note that if mask $m$ has $k$ enabled bits, then it will have $2^k$ submasks. As we have a total of $\binom{n}{k}$ masks with $k$ enabled bits (see [binomial coefficients](../combinatorics/binomial-coefficients.md)), then the total number of combinations for all masks will be:
$$\sum_{k=0}^n \binom{n}{k} \cdot 2^k$$
To calculate this number, note that the sum above is equal to the expansion of $(1+2)^n$ using the binomial theorem. Therefore, we have $3^n$ combinations, as we wanted to prove.
|
---
title
all_submasks
---
# Submask Enumeration
## Enumerating all submasks of a given mask
Given a bitmask $m$, you want to efficiently iterate through all of its submasks, that is, masks $s$ in which only bits that were included in mask $m$ are set.
Consider the implementation of this algorithm, based on tricks with bit operations:
```cpp
int s = m;
while (s > 0) {
... you can use s ...
s = (s-1) & m;
}
```
or, using a more compact `for` statement:
```cpp
for (int s=m; s; s=(s-1)&m)
... you can use s ...
```
In both variants of the code, the submask equal to zero will not be processed. We can either process it outside the loop, or use a less elegant design, for example:
```cpp
for (int s=m; ; s=(s-1)&m) {
... you can use s ...
if (s==0) break;
}
```
Let us examine why the above code visits all submasks of $m$, without repetition, and in descending order.
Suppose we have a current bitmask $s$, and we want to move on to the next bitmask. By subtracting from the mask $s$ one unit, we will remove the rightmost set bit and all bits to the right of it will become 1. Then we remove all the "extra" one bits that are not included in the mask $m$ and therefore can't be a part of a submask. We do this removal by using the bitwise operation `(s-1) & m`. As a result, we "cut" mask $s-1$ to determine the highest value that it can take, that is, the next submask after $s$ in descending order.
Thus, this algorithm generates all submasks of this mask in descending order, performing only two operations per iteration.
A special case is when $s = 0$. After executing $s-1$ we get a mask where all bits are set (bit representation of -1), and after `(s-1) & m` we will have that $s$ will be equal to $m$. Therefore, with the mask $s = 0$ be careful — if the loop does not end at zero, the algorithm may enter an infinite loop.
## Iterating through all masks with their submasks. Complexity $O(3^n)$
In many problems, especially those that use bitmask dynamic programming, you want to iterate through all bitmasks and for each mask, iterate through all of its submasks:
```cpp
for (int m=0; m<(1<<n); ++m)
for (int s=m; s; s=(s-1)&m)
... s and m ...
```
Let's prove that the inner loop will execute a total of $O(3^n)$ iterations.
**First proof**: Consider the $i$-th bit. There are exactly three options for it:
1. it is not included in the mask $m$ (and therefore not included in submask $s$),
2. it is included in $m$, but not included in $s$, or
3. it is included in both $m$ and $s$.
As there are a total of $n$ bits, there will be $3^n$ different combinations.
**Second proof**: Note that if mask $m$ has $k$ enabled bits, then it will have $2^k$ submasks. As we have a total of $\binom{n}{k}$ masks with $k$ enabled bits (see [binomial coefficients](../combinatorics/binomial-coefficients.md)), then the total number of combinations for all masks will be:
$$\sum_{k=0}^n \binom{n}{k} \cdot 2^k$$
To calculate this number, note that the sum above is equal to the expansion of $(1+2)^n$ using the binomial theorem. Therefore, we have $3^n$ combinations, as we wanted to prove.
## Practice Problems
* [Atcoder - Close Group](https://atcoder.jp/contests/abc187/tasks/abc187_f)
* [Codeforces - Nuclear Fusion](http://codeforces.com/problemset/problem/71/E)
* [Codeforces - Sandy and Nuts](http://codeforces.com/problemset/problem/599/E)
* [Uva 1439 - Exclusive Access 2](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=4185)
* [UVa 11825 - Hackers' Crackdown](https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2925)
|
Submask Enumeration
|
---
title
- Original
---
<!--?title Continued fractions -->
# Continued fractions
**Continued fraction** is a representation of a real number as a specific convergent sequence of rational numbers. They are useful in competitive programming because they are easy to compute and can be efficiently used to find the best possible rational approximation of the underlying real number (among all numbers whose denominator doesn't exceed a given value).
Besides that, continued fractions are closely related to Euclidean algorithm which makes them useful in a bunch of number-theoretical problems.
## Continued fraction representation
!!! info "Definition"
Let $a_0, a_1, \dots, a_k \in \mathbb Z$ and $a_1, a_2, \dots, a_k \geq 1$. Then the expression
$$r=a_0 + \frac{1}{a_1 + \frac{1}{\dots + \frac{1}{a_k}}},$$
is called the **continued fraction representation** of the rational number $r$ and is denoted shortly as $r=[a_0;a_1,a_2,\dots,a_k]$.
??? example
Let $r = \frac{5}{3}$. There are two ways to represent it as a continued fraction:
$$
\begin{align}
r = [1;1,1,1] &= 1+\frac{1}{1+\frac{1}{1+\frac{1}{1}}},\\
r = [1;1,2] &= 1+\frac{1}{1+\frac{1}{2}}.
\end{align}
$$
It can be proven that any rational number can be represented as a continued fraction in exactly $2$ ways:
$$r = [a_0;a_1,\dots,a_k,1] = [a_0;a_1,\dots,a_k+1].$$
Moreover, the length $k$ of such continued fraction is estimated as $k = O(\log \min(p, q))$ for $r=\frac{p}{q}$.
The reasoning behind this will be clear once we delve into the details of the continued fraction construction.
!!! info "Definition"
Let $a_0,a_1,a_2, \dots$ be an integer sequence such that $a_1, a_2, \dots \geq 1$. Let $r_k = [a_0; a_1, \dots, a_k]$. Then the expression
$$r = a_0 + \frac{1}{a_1 + \frac{1}{a_2+\dots}} = \lim\limits_{k \to \infty} r_k.$$
is called the **continued fraction representation** of the irrational number $r$ and is denoted shortly as $r = [a_0;a_1,a_2,\dots]$.
Note that for $r=[a_0;a_1,\dots]$ and integer $k$, it holds that $r+k = [a_0+k; a_1, \dots]$.
Another important observation is that $\frac{1}{r}=[0;a_0, a_1, \dots]$ when $a_0 > 0$ and $\frac{1}{r} = [a_1; a_2, \dots]$ when $a_0 = 0$.
!!! info "Definition"
In the definition above, rational numbers $r_0, r_1, r_2, \dots$ are called the **convergents** of $r$.
Correspondingly, individual $r_k = [a_0; a_1, \dots, a_k] = \frac{p_k}{q_k}$ is called the $k$-th **convergent** of $r$.
??? example
Consider $r = [1; 1, 1, 1, \dots]$. It can be proven by induction that $r_k = \frac{F_{k+2}}{F_{k+1}}$, where $F_k$ is the Fibonacci sequence defined as $F_0 = 0$, $F_1 = 1$ and $F_{k} = F_{k-1} + F_{k-2}$. From the Binet's formula, it is known that
$$r_k = \frac{\phi^{k+2} - \psi^{k+2}}{\phi^{k+1} - \psi^{k+1}},$$
where $\phi = \frac{1+\sqrt{5}}{2} \approx 1.618$ is the golden ratio and $\psi = \frac{1-\sqrt{5}}{2} = -\frac{1}{\phi} \approx -0.618$. Thus,
$$r = 1+\frac{1}{1+\frac{1}{1+\dots}}=\lim\limits_{k \to \infty} r_k = \phi = \frac{1+\sqrt{5}}{2}.$$
Note that in this specific case, an alternative way to find $r$ would be to solve the equation
$$r = 1+\frac{1}{r} \implies r^2 = r + 1. $$
!!! info "Definition"
Let $r_k = [a_0; a_1, \dots, a_{k-1}, a_k]$. The numbers $[a_0; a_1, \dots, a_{k-1}, t]$ for $1 \leq t \leq a_k$ are called **semiconvergents**.
We will typically refer to (semi)convergents that are greater than $r$ as **upper** (semi)convergents and to those that are less than $r$ as **lower** (semi)convergents.
!!! info "Definition"
Complementary to convergents, we define the **[complete quotients](https://en.wikipedia.org/wiki/Complete_quotient)** as $s_k = [a_k; a_{k+1}, a_{k+2}, \dots]$.
Correspondingly, we will call an individual $s_k$ the $k$-th complete quotient of $r$.
From the definitions above, one can conclude that $s_k \geq 1$ for $k \geq 1$.
Treating $[a_0; a_1, \dots, a_k]$ as a formal algebraic expression and allowing arbitrary real numbers instead of $a_i$, we obtain
$$r = [a_0; a_1, \dots, a_{k-1}, s_k].$$
In particular, $r = [s_0] = s_0$. On the other hand, we can express $s_k$ as
$$s_k = [a_k; s_{k+1}] = a_k + \frac{1}{s_{k+1}},$$
meaning that we can compute $a_k = \lfloor s_k \rfloor$ and $s_{k+1} = (s_k - a_k)^{-1}$ from $s_k$.
The sequence $a_0, a_1, \dots$ is well-defined unless $s_k=a_k$ which only happens when $r$ is a rational number.
Thus the continued fraction representation is uniquely defined for any irrational number $r$.
### Implementation
In the code snippets we will mostly assume finite continued fractions.
From $s_k$, the transition to $s_{k+1}$ looks like
$$s_k =\left\lfloor s_k \right\rfloor + \frac{1}{s_{k+1}}.$$
From this expression, the next complete quotient $s_{k+1}$ is obtained as
$$s_{k+1} = \left(s_k-\left\lfloor s_k\right\rfloor\right)^{-1}.$$
For $s_k=\frac{p}{q}$ it means that
$$
s_{k+1} = \left(\frac{p}{q}-\left\lfloor \frac{p}{q} \right\rfloor\right)^{-1} = \frac{q}{p-q\cdot \lfloor \frac{p}{q} \rfloor} = \frac{q}{p \bmod q}.
$$
Thus, the computation of a continued fraction representation for $r=\frac{p}{q}$ follows the steps of the Euclidean algorithm for $p$ and $q$.
From this also follows that $\gcd(p_k, q_k) = 1$ for $\frac{p_k}{q_k} = [a_0; a_1, \dots, a_k]$. Hence, convergents are always irreducible.
=== "C++"
```cpp
auto fraction(int p, int q) {
vector<int> a;
while(q) {
a.push_back(p / q);
tie(p, q) = make_pair(q, p % q);
}
return a;
}
```
=== "Python"
```py
def fraction(p, q):
a = []
while q:
a.append(p // q)
p, q = q, p % q
return a
```
## Key results
To provide some motivation for further study of continued fraction, we give some key facts now.
??? note "Recurrence"
For the convergents $r_k = \frac{p_k}{q_k}$, the following recurrence stands, allowing their fast computation:
$$\frac{p_k}{q_k}=\frac{a_k p_{k-1} + p_{k-2}}{a_k q_{k-1} + q_{k-2}},$$
where $\frac{p_{-1}}{q_{-1}}=\frac{1}{0}$ and $\frac{p_{-2}}{q_{-2}}=\frac{0}{1}$.
??? note "Deviations"
The deviation of $r_k = \frac{p_k}{q_k}$ from $r$ can be generally estimated as
$$\left|\frac{p_k}{q_k}-r\right| \leq \frac{1}{q_k q_{k+1}} \leq \frac{1}{q_k^2}.$$
Multiplying both sides with $q_k$, we obtain alternate estimation:
$$|p_k - q_k r| \leq \frac{1}{q_{k+1}}.$$
From the recurrence above it follows that $q_k$ grows at least as fast as Fibonacci numbers.
On the picture below you may see the visualization of how convergents $r_k$ approach $r=\frac{1+\sqrt 5}{2}$:

$r=\frac{1+\sqrt 5}{2}$ is depicted by blue dotted line. Odd convergents approach it from above and even convergents approach it from below.
??? note "Lattice hulls"
Consider convex hulls of points above and below the line $y=rx$.
Odd convergents $(q_k;p_k)$ are the vertices of the upper hull, while the even convergents $(q_k;p_k)$ are the vertices of the bottom hull.
All integers vertices on the hulls are obtained as $(q;p)$ such that
$$\frac{p}{q} = \frac{tp_{k-1} + p_{k-2}}{tq_{k-1} + q_{k-2}}$$
for integer $0 \leq t \leq a_k$. In other words, the set of lattice points on the hulls corresponds to the set of semiconvergents.
On the picture below, you may see the convergents and semiconvergents (intermediate gray points) of $r=\frac{9}{7}$.

??? note "Best approximations"
Let $\frac{p}{q}$ be the fraction to minimize $\left|r-\frac{p}{q}\right|$ subject to $q \leq x$ for some $x$.
Then $\frac{p}{q}$ is a semiconvergent of $r$.
The last fact allows to find the best rational approximations of $r$ by checking its semiconvergents.
Below you will find the further explanation and a bit of intuition and interpretation for these facts.
## Convergents
Let's take a closer look at the convergents that were defined earlier. For $r=[a_0, a_1, a_2, \dots]$, its convergents are
\begin{gather}
r_0=[a_0],\\r_1=[a_0, a_1],\\ \dots,\\ r_k=[a_0, a_1, \dots, a_k].
\end{gather}
Convergents are the core concept of continued fractions, so it is important to study their properties.
For the number $r$, its $k$-th convergent $r_k = \frac{p_k}{q_k}$ can be computed as
$$r_k = \frac{P_k(a_0,a_1,\dots,a_k)}{P_{k-1}(a_1,\dots,a_k)} = \frac{a_k p_{k-1} + p_{k-2}}{a_k q_{k-1} + q_{k-2}},$$
where $P_k(a_0,\dots,a_k)$ is [the continuant](https://en.wikipedia.org/wiki/Continuant_(mathematics)), a multivariate polynomial defined as
$$P_k(x_0,x_1,\dots,x_k) = \det \begin{bmatrix}
x_k & 1 & 0 & \dots & 0 \\
-1 & x_{k-1} & 1 & \dots & 0 \\
0 & -1 & x_2 & . & \vdots \\
\vdots & \vdots & . & \ddots & 1 \\
0 & 0 & \dots & -1 & x_0
\end{bmatrix}_{\textstyle .}$$
Thus, $r_k$ is a weighted [mediant](https://en.wikipedia.org/wiki/Mediant_(mathematics)) of $r_{k-1}$ and $r_{k-2}$.
For consistency, two additional convergents $r_{-1} = \frac{1}{0}$ and $r_{-2} = \frac{0}{1}$ are defined.
??? hint "Detailed explanation"
The numerator and the denominator of $r_k$ can be seen as multivariate polynomials of $a_0, a_1, \dots, a_k$:
$$r_k = \frac{P_k(a_0, a_1, \dots, a_k)}{Q_k(a_0,a_1, \dots, a_k)}.$$
From the definition of convergents,
$$r_k = a_0 + \frac{1}{[a_1;a_2,\dots, a_k]}= a_0 + \frac{Q_{k-1}(a_1, \dots, a_k)}{P_{k-1}(a_1, \dots, a_k)} = \frac{a_0 P_{k-1}(a_1, \dots, a_k) + Q_{k-1}(a_1, \dots, a_k)}{P_{k-1}(a_1, \dots, a_k)}.$$
From this follows $Q_k(a_0, \dots, a_k) = P_{k-1}(a_1, \dots, a_k)$. This yields the relation
$$P_k(a_0, \dots, a_k) = a_0 P_{k-1}(a_1, \dots, a_k) + P_{k-2}(a_2, \dots, a_k).$$
Initially, $r_0 = \frac{a_0}{1}$ and $r_1 = \frac{a_0 a_1 + 1}{a_1}$, thus
$$\begin{align}P_0(a_0)&=a_0,\\ P_1(a_0, a_1) &= a_0 a_1 + 1.\end{align}$$
For consistency, it is convenient to define $P_{-1} = 1$ and $P_{-2}=0$ and formally say that $r_{-1} = \frac{1}{0}$ and $r_{-2}=\frac{0}{1}$.
From numerical analysis, it is known that the determinant of an arbitrary tridiagonal matrix
$$T_k = \det \begin{bmatrix}
a_0 & b_0 & 0 & \dots & 0 \\
c_0 & a_1 & b_1 & \dots & 0 \\
0 & c_1 & a_2 & . & \vdots \\
\vdots & \vdots & . & \ddots & c_{k-1} \\
0 & 0 & \dots & b_{k-1} & a_k
\end{bmatrix}$$
can be computed recursively as $T_k = a_k T_{k-1} - b_{k-1} c_{k-1} T_{k-2}$. Comparing it to $P_k$, we get a direct expression
$$P_k = \det \begin{bmatrix}
x_k & 1 & 0 & \dots & 0 \\
-1 & x_{k-1} & 1 & \dots & 0 \\
0 & -1 & x_2 & . & \vdots \\
\vdots & \vdots & . & \ddots & 1 \\
0 & 0 & \dots & -1 & x_0
\end{bmatrix}_{\textstyle .}$$
This polynomial is also known as [the continuant](https://en.wikipedia.org/wiki/Continuant_(mathematics)) due to its close relation with continued fraction. The continuant won't change if the sequence on the main diagonal is reversed. This yields an alternative formula to compute it:
$$P_k(a_0, \dots, a_k) = a_k P_{k-1}(a_0, \dots, a_{k-1}) + P_{k-2}(a_0, \dots, a_{k-2}).$$
### Implementation
We will compute the convergents as a pair of sequences $p_{-2}, p_{-1}, p_0, p_1, \dots, p_k$ and $q_{-2}, q_{-1}, q_0, q_1, \dots, q_k$:
=== "C++"
```cpp
auto convergents(vector<int> a) {
vector<int> p = {0, 1};
vector<int> q = {1, 0};
for(auto it: a) {
p.push_back(p[p.size() - 1] * it + p[p.size() - 2]);
q.push_back(q[q.size() - 1] * it + q[q.size() - 2]);
}
return make_pair(p, q);
}
```
=== "Python"
```py
def convergents(a):
p = [0, 1]
q = [1, 0]
for it in a:
p.append(p[-1]*it + p[-2])
q.append(q[-1]*it + q[-2])
return p, q
```
## Trees of continued fractions
There are two major ways to unite all possible continued fractions into useful tree structures.
### Stern-Brocot tree
[The Stern-Brocot tree](../others/stern_brocot_tree_farey_sequences.md) is a binary search tree that contains all distinct positive rational numbers.
The tree generally looks as follows:
<figure>
<img src="https://upload.wikimedia.org/wikipedia/commons/3/37/SternBrocotTree.svg">
<figcaption>
<a href="https://commons.wikimedia.org/wiki/File:SternBrocotTree.svg">The image</a> by <a href="https://commons.wikimedia.org/wiki/User:Aaron_Rotenberg">Aaron Rotenberg</a> is licensed under <a href="https://creativecommons.org/licenses/by-sa/3.0/deed.en">CC BY-SA 3.0</a>
</figcaption>
</figure>
Fractions $\frac{0}{1}$ and $\frac{1}{0}$ are "virtually" kept on the left and right sides of the tree correspondingly.
Then the fraction in a node is a mediant $\frac{a+c}{b+d}$ of two fractions $\frac{a}{b}$ and $\frac{c}{d}$ above it.
The recurrence $\frac{p_k}{q_k}=\frac{a_k p_{k-1} + p_{k-2}}{a_k q_{k-1} + q_{k-2}}$ means that the continued fraction representation encodes the path to $\frac{p_k}{q_k}$ in the tree. To find $[a_0; a_1, \dots, a_{k}, 1]$, one has to make $a_0$ moves to the right, $a_1$ moves to the left, $a_2$ moves to the right and so on up to $a_k$.
The parent of $[a_0; a_1, \dots, a_k,1]$ then is the fraction obtained by taking one step back in the last used direction.
In other words, it is $[a_0; a_1, \dots, a_k-1,1]$ when $a_k > 1$ and $[a_0; a_1, \dots, a_{k-1}, 1]$ when $a_k = 1$.
Thus the children of $[a_0; a_1, \dots, a_k, 1]$ are $[a_0; a_1, \dots, a_k+1, 1]$ and $[a_0; a_1, \dots, a_k, 1, 1]$.
Let's index the Stern-Brocot tree. The root vertex is assigned an index $1$. Then for a vertex $v$, the index of its left child is assigned by changing the leading bit of $v$ from $1$ to $10$ and for the right child, it's assigned by changing the leading bit from $1$ to $11$:
<figure><img src="https://upload.wikimedia.org/wikipedia/commons/1/18/Stern-brocot-index.svg" width="500px"/></figure>
In this indexing, the continued fraction representation of a rational number specifies the [run-length encoding](https://en.wikipedia.org/wiki/Run-length_encoding) of its binary index.
For $\frac{5}{2} = [2;2] = [2;1,1]$, its index is $1011_2$ and its run-length encoding, considering bits in the ascending order, is $[2;1,1]$.
Another example is $\frac{2}{5} = [0;2,2]=[0;2,1,1]$, which has index $1100_2$ and its run-length encoding is, indeed, $[0;2,2]$.
It is worth noting that the Stern-Brocot tree is, in fact, a [treap](../data_structures/treap.md). That is, it is a binary search tree by $\frac{p}{q}$, but it is a heap by both $p$ and $q$.
!!! example "Comparing continued fractions"
You're given $A=[a_0; a_1, \dots, a_n]$ and $B=[b_0; b_1, \dots, b_m]$. Which fraction is smaller?
??? hint "Solution"
Assume for now that $A$ and $B$ are irrational and their continued fraction representations denote an infinite descent in the Stern-Brocot tree.
As we already mentioned, in this representation $a_0$ denotes the number of right turns in the descent, $a_1$ denotes the number of consequent left turns and so on. Therefore, when we compare $a_k$ and $b_k$, if $a_k = b_k$ we should just move on to comparing $a_{k+1}$ and $b_{k+1}$. Otherwise, if we're at right descents, we should check if $a_k < b_k$ and if we're at left descents, we should check if $a_k > b_k$ to tell whether $A < B$.
In other words, for irrational $A$ and $B$ it would be $A < B$ if and only if $(a_0, -a_1, a_2, -a_3, \dots) < (b_0, -b_1, b_2, -b_3, \dots)$ with lexicographical comparison.
Now, formally using $\infty$ as an element of continued fraction representation it is possible to emulate irrational numbers $A-\varepsilon$ and $A+\varepsilon$, that is, elements that are smaller (greater) than $A$, but greater (smaller) than any other real number. Specifically, for $A=[a_0; a_1, \dots, a_n]$, one of these two elements can be emulated as $[a_0; a_1, \dots, a_n, \infty]$ and the other can be emulated as $[a_0; a_1, \dots, a_n - 1, 1, \infty]$.
Which one corresponds to $A-\varepsilon$ and which one to $A+\varepsilon$ can be determined by the parity of $n$ or by comparing them as irrational numbers.
=== "Python"
```py
# check if a < b assuming that a[-1] = b[-1] = infty and a != b
def less(a, b):
a = [(-1)**i*a[i] for i in range(len(a))]
b = [(-1)**i*b[i] for i in range(len(b))]
return a < b
# [a0; a1, ..., ak] -> [a0, a1, ..., ak-1, 1]
def expand(a):
if a: # empty a = inf
a[-1] -= 1
a.append(1)
return a
# return a-eps, a+eps
def pm_eps(a):
b = expand(a.copy())
a.append(float('inf'))
b.append(float('inf'))
return (a, b) if less(a, b) else (b, a)
```
!!! example "Best inner point"
You're given $\frac{0}{1} \leq \frac{p_0}{q_0} < \frac{p_1}{q_1} \leq \frac{1}{0}$. Find the rational number $\frac{p}{q}$ such that $(q; p)$ is lexicographically smallest and $\frac{p_0}{q_0} < \frac{p}{q} < \frac{p_1}{q_1}$.
??? hint "Solution"
In terms of the Stern-Brocot tree it means that we need to find the LCA of $\frac{p_0}{q_0}$ and $\frac{p_1}{q_1}$. Due to the connection between Stern-Brocot tree and continued fraction, this LCA would roughly correspond to the largest common prefix of continued fraction representations for $\frac{p_0}{q_0}$ and $\frac{p_1}{q_1}$.
So, if $\frac{p_0}{q_0} = [a_0; a_1, \dots, a_{k-1}, a_k, \dots]$ and $\frac{p_1}{q_1} = [a_0; a_1, \dots, a_{k-1}, b_k, \dots]$ are irrational numbers, the LCA is $[a_0; a_1, \dots, \min(a_k, b_k)+1]$.
For rational $r_0$ and $r_1$, one of them could be the LCA itself which would require us to casework it. To simplify the solution for rational $r_0$ and $r_1$, it is possible to use continued fraction representation of $r_0 + \varepsilon$ and $r_1 - \varepsilon$ which was derived in the previous problem.
=== "Python"
```py
# finds lexicographically smallest (q, p)
# such that p0/q0 < p/q < p1/q1
def middle(p0, q0, p1, q1):
a0 = pm_eps(fraction(p0, q0))[1]
a1 = pm_eps(fraction(p1, q1))[0]
a = []
for i in range(min(len(a0), len(a1))):
a.append(min(a0[i], a1[i]))
if a0[i] != a1[i]:
break
a[-1] += 1
p, q = convergents(a)
return p[-1], q[-1]
```
!!! example "[GCJ 2019, Round 2 - New Elements: Part 2](https://codingcompetitions.withgoogle.com/codejam/round/0000000000051679/0000000000146184)"
You're given $N$ positive integer pairs $(C_i, J_i)$. You need to find a positive integer pair $(x, y)$ such that $C_i x + J_i y$ is a strictly increasing sequence.
Among such pairs, find the lexicographically minimum one.
??? hint "Solution"
Rephrasing the statement, $A_i x + B_i y$ must be positive for all $i$, where $A_i = C_i - C_{i-1}$ and $B_i = J_i - J_{i-1}$.
Among such equations we have four significant groups for $A_i x + B_i y > 0$:
1. $A_i, B_i > 0$ can be ignored since we're looking for $x, y > 0$.
2. $A_i, B_i \leq 0$ would provide "IMPOSSIBLE" as an answer.
3. $A_i > 0$, $B_i \leq 0$. Such constraints are equivalent to $\frac{y}{x} < \frac{A_i}{-B_i}$.
4. $A_i \leq 0$, $B_i > 0$. Such constraints are equivalent to $\frac{y}{x} > \frac{-A_i}{B_i}$.
Let $\frac{p_0}{q_0}$ be the largest $\frac{-A_i}{B_i}$ from the fourth group and $\frac{p_1}{q_1}$ be the smallest $\frac{A_i}{-B_i}$ from the third group.
The problem is now, given $\frac{p_0}{q_0} < \frac{p_1}{q_1}$, find a fraction $\frac{p}{q}$ such that $(q;p)$ is lexicographically smallest and $\frac{p_0}{q_0} < \frac{p}{q} < \frac{p_1}{q_1}$.
=== "Python"
```py
def solve():
n = int(input())
C = [0] * n
J = [0] * n
# p0/q0 < y/x < p1/q1
p0, q0 = 0, 1
p1, q1 = 1, 0
fail = False
for i in range(n):
C[i], J[i] = map(int, input().split())
if i > 0:
A = C[i] - C[i-1]
B = J[i] - J[i-1]
if A <= 0 and B <= 0:
fail = True
elif B > 0 and A < 0: # y/x > (-A)/B if B > 0
if (-A)*q0 > p0*B:
p0, q0 = -A, B
elif B < 0 and A > 0: # y/x < A/(-B) if B < 0
if A*q1 < p1*(-B):
p1, q1 = A, -B
if p0*q1 >= p1*q0 or fail:
return 'IMPOSSIBLE'
p, q = middle(p0, q0, p1, q1)
return str(q) + ' ' + str(p)
```
### Calkin-Wilf tree
A somewhat simpler way to organize continued fractions in a binary tree is the [Calkin-Wilf tree](https://en.wikipedia.org/wiki/Calkin–Wilf_tree).
The tree generally looks like this:
<figure>
<img src="https://upload.wikimedia.org/wikipedia/commons/8/82/Calkin–Wilf_tree.svg" width="500px"/>
<figcaption><a href="https://commons.wikimedia.org/wiki/File:Calkin–Wilf_tree.svg">The image</a> by <a href="https://commons.wikimedia.org/wiki/User:Olli_Niemitalo">Olli Niemitalo</a>, <a href="https://commons.wikimedia.org/wiki/User:Proz">Proz</a> is licensed under <a href="https://creativecommons.org/publicdomain/zero/1.0/deed.en">CC0 1.0</a></figcaption>
</figure>
In the root of the tree, the number $\frac{1}{1}$ is located. Then, for the vertex with a number $\frac{p}{q}$, its children are $\frac{p}{p+q}$ and $\frac{p+q}{q}$.
Unlike the Stern-Brocot tree, the Calkin-Wilf tree is not a binary _search_ tree, so it can't be used to perform rational binary search.
In the Calkin-Wilf tree, the direct parent of a fraction $\frac{p}{q}$ is $\frac{p-q}{q}$ when $p>q$ and $\frac{p}{q-p}$ otherwise.
For the Stern-Brocot tree, we used the recurrence for convergents. To draw the connection between the continued fraction and the Calkin-Wilf tree, we should recall the recurrence for complete quotients. If $s_k = \frac{p}{q}$, then $s_{k+1} = \frac{q}{p \mod q} = \frac{q}{p-\lfloor p/q \rfloor \cdot q}$.
On the other hand, if we repeatedly go from $s_k = \frac{p}{q}$ to its parent in the Calkin-Wilf tree when $p > q$, we will end up in $\frac{p \mod q}{q} = \frac{1}{s_{k+1}}$. If we continue doing so, we will end up in $s_{k+2}$, then $\frac{1}{s_{k+3}}$ and so on. From this we can deduce that:
1. When $a_0> 0$, the direct parent of $[a_0; a_1, \dots, a_k]$ in the Calkin-Wilf tree is $\frac{p-q}{q}=[a_0 - 1; a_1, \dots, a_k]$.
2. When $a_0 = 0$ and $a_1 > 1$, its direct parent is $\frac{p}{q-p} = [0; a_1 - 1, a_2, \dots, a_k]$.
3. And when $a_0 = 0$ and $a_1 = 1$, its direct parent is $\frac{p}{q-p} = [a_2; a_3, \dots, a_k]$.
Correspondingly, children of $\frac{p}{q} = [a_0; a_1, \dots, a_k]$ are
1. $\frac{p+q}{q}=1+\frac{p}{q}$, which is $[a_0+1; a_1, \dots, a_k]$,
2. $\frac{p}{p+q} = \frac{1}{1+\frac{q}{p}}$, which is $[0, 1, a_0, a_1, \dots, a_k]$ for $a_0 > 0$ and $[0, a_1+1, a_2, \dots, a_k]$ for $a_0=0$.
Noteworthy, if we enumerate vertices of the Calkin-Wilf tree in the breadth-first search order (that is, the root has a number $1$, and the children of the vertex $v$ have indices $2v$ and $2v+1$ correspondingly), the index of the rational number in the Calkin-Wilf tree would be the same as in the Stern-Brocot tree.
Thus, numbers on the same levels of the Stern-Brocot tree and the Calkin-Wilf tree are the same, but their ordering differs through the [bit-reversal permutation](https://en.wikipedia.org/wiki/Bit-reversal_permutation).
## Convergence
For the number $r$ and its $k$-th convergent $r_k=\frac{p_k}{q_k}$ the following formula stands:
$$r_k = a_0 + \sum\limits_{i=1}^k \frac{(-1)^{i-1}}{q_i q_{i-1}}.$$
In particular, it means that
$$r_k - r_{k-1} = \frac{(-1)^{k-1}}{q_k q_{k-1}}$$
and
$$p_k q_{k-1} - p_{k-1} q_k = (-1)^{k-1}.$$
From this we can conclude that
$$\left| r-\frac{p_k}{q_k} \right| \leq \frac{1}{q_{k+1}q_k} \leq \frac{1}{q_k^2}.$$
The latter inequality is due to the fact that $r_k$ and $r_{k+1}$ are generally located on different sides of $r$, thus
$$|r-r_k| = |r_k-r_{k+1}|-|r-r_{k+1}| \leq |r_k - r_{k+1}|.$$
??? tip "Detailed explanation"
To estimate $|r-r_k|$, we start by estimating the difference between adjacent convergents. By definition,
$$\frac{p_k}{q_k} - \frac{p_{k-1}}{q_{k-1}} = \frac{p_k q_{k-1} - p_{k-1} q_k}{q_k q_{k-1}}.$$
Replacing $p_k$ and $q_k$ in the numerator with their recurrences, we get
$$\begin{align} p_k q_{k-1} - p_{k-1} q_k &= (a_k p_{k-1} + p_{k-2}) q_{k-1} - p_{k-1} (a_k q_{k-1} + q_{k-2})
\\&= p_{k-2} q_{k-1} - p_{k-1} q_{k-2},\end{align}$$
thus the numerator of $r_k - r_{k-1}$ is always the negated numerator of $r_{k-1} - r_{k-2}$. It, in turn, equals to $1$ for
$$r_1 - r_0=\left(a_0+\frac{1}{a_1}\right)-a_0=\frac{1}{a_1},$$
thus
$$r_k - r_{k-1} = \frac{(-1)^{k-1}}{q_k q_{k-1}}.$$
This yields an alternative representation of $r_k$ as a partial sum of infinite series:
$$r_k = (r_k - r_{k-1}) + \dots + (r_1 - r_0) + r_0
= a_0 + \sum\limits_{i=1}^k \frac{(-1)^{i-1}}{q_i q_{i-1}}.$$
From the recurrent relation it follows that $q_k$ monotonously increases at least as fast as Fibonacci numbers, thus
$$r = \lim\limits_{k \to \infty} r_k = a_0 + \sum\limits_{i=1}^\infty \frac{(-1)^{i-1}}{q_i q_{i-1}}$$
is always well-defined, as the underlying series always converge. Noteworthy, the residual series
$$r-r_k = \sum\limits_{i=k+1}^\infty \frac{(-1)^{i-1}}{q_i q_{i-1}}$$
has the same sign as $(-1)^k$ due to how fast $q_i q_{i-1}$ decreases. Hence even-indexed $r_k$ approach $r$ from below while odd-indexed $r_k$ approach it from above:
<figure><img src="https://upload.wikimedia.org/wikipedia/commons/b/b4/Golden_ration_convergents.svg" width="600px"/>
<figcaption>_Convergents of $r=\phi = \frac{1+\sqrt{5}}{2}=[1;1,1,\dots]$ and their distance from $r$._</figcaption></figure>
From this picture we can see that
$$|r-r_k| = |r_k - r_{k+1}| - |r-r_{k+1}| \leq |r_k - r_{k+1}|,$$
thus the distance between $r$ and $r_k$ is never larger than the distance between $r_k$ and $r_{k+1}$:
$$\left|r-\frac{p_k}{q_k}\right| \leq \frac{1}{q_k q_{k+1}} \leq \frac{1}{q_k^2}.$$
!!! example "Extended Euclidean?"
You're given $A, B, C \in \mathbb Z$. Find $x, y \in \mathbb Z$ such that $Ax + By = C$.
??? hint "Solution"
Although this problem is typically solved with the [extended Euclidean algorithm](../algebra/extended-euclid-algorithm.md), there is a simple and straightforward solution with continued fractions.
Let $\frac{A}{B}=[a_0; a_1, \dots, a_k]$. It was proved above that $p_k q_{k-1} - p_{k-1} q_k = (-1)^{k-1}$. Substituting $p_k$ and $q_k$ with $A$ and $B$, we get
$$Aq_{k-1} - Bp_{k-1} = (-1)^{k-1} g,$$
where $g = \gcd(A, B)$. If $C$ is divisible by $g$, then the solution is $x = (-1)^{k-1}\frac{C}{g} q_{k-1}$ and $y = (-1)^{k}\frac{C}{g} p_{k-1}$.
=== "Python"
```py
# return (x, y) such that Ax+By=C
# assumes that such (x, y) exists
def dio(A, B, C):
p, q = convergents(fraction(A, B))
C //= A // p[-1] # divide by gcd(A, B)
t = (-1) if len(p) % 2 else 1
return t*C*q[-2], -t*C*p[-2]
```
## Linear fractional transformations
Another important concept for continued fractions are the so-called [linear fractional transformations](https://en.wikipedia.org/wiki/Linear_fractional_transformation).
!!! info "Definition"
A **linear fractional transformation** is a function $f : \mathbb R \to \mathbb R$ such that $f(x) = \frac{ax+b}{cx+d}$ for some $a,b,c,d \in \mathbb R$.
A composition $(L_0 \circ L_1)(x) = L_0(L_1(x))$ of linear fractional transforms $L_0(x)=\frac{a_0 x + b_0}{c_0 x + d_0}$ and $L_1(x)=\frac{a_1 x + b_1}{c_1 x + d_1}$ is itself a linear fractional transform:
$$\frac{a_0\frac{a_1 x + b_1}{c_1 x + d_1} + b_0}{c_0 \frac{a_1 x + b_1}{c_1 x + d_1} + d_0} = \frac{a_0(a_1 x + b_1) + b_0 (c_1 x + d_1)}{c_0 (a_1 x + b_1) + d_0 (c_1 x + d_1)} = \frac{(a_0 a_1 + b_0 c_1) x + (a_0 b_1 + b_0 d_1)}{(c_0 a_1 + d_0 c_1) x + (c_0 b_1 + d_0 d_1)}.$$
Inverse of a linear fractional transform, is also a linear fractional transform:
$$y = \frac{ax+b}{cx+d} \iff y(cx+d) = ax + b \iff x = -\frac{dy-b}{cy-a}.$$
!!! example "[DMOPC '19 Contest 7 P4 - Bob and Continued Fractions](https://dmoj.ca/problem/dmopc19c7p4)"
You're given an array of positive integers $a_1, \dots, a_n$. You need to answer $m$ queries. Each query is to compute $[a_l; a_{l+1}, \dots, a_r]$.
??? hint "Solution"
We can solve this problem with the segment tree if we're able to concatenate continued fractions.
It's generally true that $[a_0; a_1, \dots, a_k, b_0, b_1, \dots, b_k] = [a_0; a_1, \dots, a_k, [b_1; b_2, \dots, b_k]]$.
Let's denote $L_{k}(x) = [a_k; x] = a_k + \frac{1}{x} = \frac{a_k\cdot x+1}{1\cdot x + 0}$. Note that $L_k(\infty) = a_k$. In this notion, it holds that
$$[a_0; a_1, \dots, a_k, x] = [a_0; [a_1; [\dots; [a_k; x]]]] = (L_0 \circ L_1 \circ \dots \circ L_k)(x) = \frac{p_k x + p_{k-1}}{q_k x + q_{k-1}}.$$
Thus, the problem boils down to the computation of
$$(L_l \circ L_{l+1} \circ \dots \circ L_r)(\infty).$$
Composition of transforms is associative, so it's possible to compute in each node of a segment tree the composition of transforms in its subtree.
!!! example "Linear fractional transformation of a continued fraction"
Let $L(x) = \frac{ax+b}{cx+d}$. Compute the continued fraction representation $[b_0; b_1, \dots, b_m]$ of $L(A)$ for $A=[a_0; a_1, \dots, a_n]$.
_This allows to compute $A + \frac{p}{q} = \frac{qA + p}{q}$ and $A \cdot \frac{p}{q} = \frac{p A}{q}$ for any $\frac{p}{q}$._
??? hint "Solution"
As we noted above, $[a_0; a_1, \dots, a_k] = (L_{a_0} \circ L_{a_1} \circ \dots \circ L_{a_k})(\infty)$, hence $L([a_0; a_1, \dots, a_k]) = (L \circ L_{a_0} \circ L_{a_1} \circ \dots L_{a_k})(\infty)$.
Hence, by consequentially adding $L_{a_0}$, $L_{a_1}$ and so on we would be able to compute
$$(L \circ L_{a_0} \circ \dots \circ L_{a_k})(x) = L\left(\frac{p_k x + p_{k-1}}{q_k x + q_{k-1}}\right)=\frac{a_k x + b_k}{c_k x + d_k}.$$
Since $L(x)$ is invertible, it is also monotonous in $x$. Therefore, for any $x \geq 0$ it holds that $L(\frac{p_k x + p_{k-1}}{q_k x + q_{k-1}})$ is between $L(\frac{p_k}{q_k}) = \frac{a_k}{c_k}$ and $L(\frac{p_{k-1}}{q_{k-1}}) = \frac{b_k}{d_k}$.
Moreover, for $x=[a_{k+1}; \dots, a_n]$ it is equal to $L(A)$. Hence, $b_0 = \lfloor L(A) \rfloor$ is between $\lfloor L(\frac{p_k}{q_k}) \rfloor$ and $\lfloor L(\frac{p_{k-1}}{q_{k-1}}) \rfloor$. When they're equal, they're also equal to $b_0$.
Note that $L(A) = (L_{b_0} \circ L_{b_1} \circ \dots \circ L_{b_m})(\infty)$. Knowing $b_0$, we can compose $L_{b_0}^{-1}$ with the current transform and continue adding $L_{a_{k+1}}$, $L_{a_{k+2}}$ and so on, looking for new floors to agree, from which we would be able to deduce $b_1$ and so on until we recover all values of $[b_0; b_1, \dots, b_m]$.
!!! example "Continued fraction arithmetics"
Let $A=[a_0; a_1, \dots, a_n]$ and $B=[b_0; b_1, \dots, b_m]$. Compute the continued fraction representations of $A+B$ and $A \cdot B$.
??? hint "Solution"
Idea here is similar to the previous problem, but instead of $L(x) = \frac{ax+b}{cx+d}$ you should consider bilinear fractional transform $L(x, y) = \frac{axy+bx+cy+d}{exy+fx+gy+h}$.
Rather than $L(x) \mapsto L(L_{a_k}(x))$ you would change your current transform as $L(x, y) \mapsto L(L_{a_k}(x), y)$ or $L(x, y) \mapsto L(x, L_{b_k}(y))$.
Then, you check if $\lfloor \frac{a}{e} \rfloor = \lfloor \frac{b}{f} \rfloor = \lfloor \frac{c}{g} \rfloor = \lfloor \frac{d}{h} \rfloor$ and if they all agree, you use this value as $c_k$ in the resulting fraction and change the transform as
$$L(x, y) \mapsto \frac{1}{L(x, y) - c_k}.$$
!!! info "Definition"
A continued fraction $x = [a_0; a_1, \dots]$ is said to be **periodic** if $x = [a_0; a_1, \dots, a_k, x]$ for some $k$.
A continued fraction $x = [a_0; a_1, \dots]$ is said to be **eventually periodic** if $x = [a_0; a_1, \dots, a_k, y]$, where $y$ is periodic.
For $x = [1; 1, 1, \dots]$ it holds that $x = 1 + \frac{1}{x}$, thus $x^2 = x + 1$. There is a generic connection between periodic continued fractions and quadratic equations. Consider the following equation:
$$ x = [a_0; a_1, \dots, a_k, x].$$
On one hand, this equation means that the continued fraction representation of $x$ is periodic with the period $k+1$.
On the other hand, using the formula for convergents, this equation means that
$$x = \frac{p_k x + p_{k-1}}{q_k x + q_{k-1}}.$$
That is, $x$ is a linear fractional transformation of itself. It follows from the equation that $x$ is a root of the second degree equation:
$$q_k x^2 + (q_{k-1}-p_k)x - p_{k-1} = 0.$$
Similar reasoning stands for continued fractions that are eventually periodic, that is $x = [a_0; a_1, \dots, a_k, y]$ for $y=[b_0; b_1, \dots, b_k, y]$. Indeed, from first equation we derive that $x = L_0(y)$ and from second equation that $y = L_1(y)$, where $L_0$ and $L_1$ are linear fractional transformations. Therefore,
$$x = (L_0 \circ L_1)(y) = (L_0 \circ L_1 \circ L_0^{-1})(x).$$
One can further prove (and it was first done by Lagrange) that for arbitrary quadratic equation $ax^2+bx+c=0$ with integer coefficients, its solution $x$ is an eventually periodic continued fraction.
!!! example "Quadratic irrationality"
Find the continued fraction of $\alpha = \frac{x+y\sqrt{n}}{z}$ where $x, y, z, n \in \mathbb Z$ and $n > 0$ is not a perfect square.
??? hint "Solution"
For the $k$-th complete quotient $s_k$ of the number it generally holds that
$$\alpha = [a_0; a_1, \dots, a_{k-1}, s_k] = \frac{s_k p_{k-1} + p_{k-2}}{s_k q_{k-1} + q_{k-2}}.$$
Therefore,
$$s_k = -\frac{\alpha q_{k-1} - p_{k-1}}{\alpha q_k - p_k} = -\frac{q_{k-1} y \sqrt n + (x q_{k-1} - z p_{k-1})}{q_k y \sqrt n + (xq_k-zp_k)}.$$
Multiplying the numerator and denominator by $(xq_k - zp_k) - q_k y \sqrt n$, we'll get rid of $\sqrt n$ in the denominator, thus the complete quotients are of form
$$s_k = \frac{x_k + y_k \sqrt n}{z_k}.$$
Let's find $s_{k+1}$, assuming that $s_k$ is known.
First of all, $a_k = \lfloor s_k \rfloor = \left\lfloor \frac{x_k + y_k \lfloor \sqrt n \rfloor}{z_k} \right\rfloor$. Then,
$$s_{k+1} = \frac{1}{s_k-a_k} = \frac{z_k}{(x_k - z_k a_k) + y_k \sqrt n} = \frac{z_k (x_k - y_k a_k) - y_k z_k \sqrt n}{(x_k - y_k a_k)^2 - y_k^2 n}.$$
Thus, if we denote $t_k = x_k - y_k a_k$, it will hold that
\begin{align}x_{k+1} &=& z_k t_k, \\ y_{k+1} &=& -y_k z_k, \\ z_{k+1} &=& t_k^2 - y_k^2 n.\end{align}
Nice thing about such representation is that if we reduce $x_{k+1}, y_{k+1}, z_{k+1}$ by their greatest common divisor, the result would be unique. Therefore, we may use it to check whether the current state has already been repeated and also to check where was the previous index that had this state.
Below is the code to compute the continued fraction representation for $\alpha = \sqrt n$:
=== "Python"
```py
# compute the continued fraction of sqrt(n)
def sqrt(n):
n0 = math.floor(math.sqrt(n))
x, y, z = 1, 0, 1
a = []
def step(x, y, z):
a.append((x * n0 + y) // z)
t = y - a[-1]*z
x, y, z = -z*x, z*t, t**2 - n*x**2
g = math.gcd(x, math.gcd(y, z))
return x // g, y // g, z // g
used = dict()
for i in range(n):
used[x, y, z] = i
x, y, z = step(x, y, z)
if (x, y, z) in used:
return a
```
Using the same `step` function but different initial $x$, $y$ and $z$ it is possible to compute it for arbitrary $\frac{x+y \sqrt{n}}{z}$.
!!! example "[Tavrida NU Akai Contest - Continued Fraction](https://timus.online/problem.aspx?space=1&num=1814)"
You're given $x$ and $k$, $x$ is not a perfect square. Let $\sqrt x = [a_0; a_1, \dots]$, find $\frac{p_k}{q_k}=[a_0; a_1, \dots, a_k]$ for $0 \leq k \leq 10^9$.
??? hint "Solution"
After computing the period of $\sqrt x$, it is possible to compute $a_k$ using binary exponentiation on the linear fractional transformation induced by the continued fraction representation. To find the resulting transformation, you compress the period of size $T$ into a single transformation and repeat it $\lfloor \frac{k-1}{T}\rfloor$ times, after which you manually combine it with the remaining transformations.
=== "Python"
```py
x, k = map(int, input().split())
mod = 10**9+7
# compose (A[0]*x + A[1]) / (A[2]*x + A[3]) and (B[0]*x + B[1]) / (B[2]*x + B[3])
def combine(A, B):
return [t % mod for t in [A[0]*B[0]+A[1]*B[2], A[0]*B[1]+A[1]*B[3], A[2]*B[0]+A[3]*B[2], A[2]*B[1]+A[3]*B[3]]]
A = [1, 0, 0, 1] # (x + 0) / (0*x + 1) = x
a = sqrt(x)
T = len(a) - 1 # period of a
# apply ak + 1/x = (ak*x+1)/(1x+0) to (Ax + B) / (Cx + D)
for i in reversed(range(1, len(a))):
A = combine([a[i], 1, 1, 0], A)
def bpow(A, n):
return [1, 0, 0, 1] if not n else combine(A, bpow(A, n-1)) if n % 2 else bpow(combine(A, A), n // 2)
C = (0, 1, 0, 0) # = 1 / 0
while k % T:
i = k % T
C = combine([a[i], 1, 1, 0], C)
k -= 1
C = combine(bpow(A, k // T), C)
C = combine([a[0], 1, 1, 0], C)
print(str(C[1]) + '/' + str(C[3]))
```
## Geometric interpretation
Let $\vec r_k = (q_k;p_k)$ for the convergent $r_k = \frac{p_k}{q_k}$. Then, the following recurrence holds:
$$\vec r_k = a_k \vec r_{k-1} + \vec r_{k-2}.$$
Let $\vec r = (1;r)$. Then, each vector $(x;y)$ corresponds to the number that is equal to its slope coefficient $\frac{y}{x}$.
With the notion of [pseudoscalar product](../geometry/basic-geometry.md) $(x_1;y_1) \times (x_2;y_2) = x_1 y_2 - x_2 y_1$, it can be shown (see the explanation below) that
$$s_k = -\frac{\vec r_{k-2} \times \vec r}{\vec r_{k-1} \times \vec r} = \left|\frac{\vec r_{k-2} \times \vec r}{\vec r_{k-1} \times \vec r}\right|.$$
The last equation is due to the fact that $r_{k-1}$ and $r_{k-2}$ lie on the different sides of $r$, thus pseudoscalar products of $\vec r_{k-1}$ and $\vec r_{k-2}$ with $\vec r$ have distinct signs. With $a_k = \lfloor s_k \rfloor$ in mind, formula for $\vec r_k$ now looks like
$$\vec r_k = \vec r_{k-2} + \left\lfloor \left| \frac{\vec r \times \vec r_{k-2}}{\vec r \times \vec r_{k-1}}\right|\right\rfloor \vec r_{k-1}.$$
Note that $\vec r_k \times r = (q;p) \times (1;r) = qr - p$, thus
$$a_k = \left\lfloor \left| \frac{q_{k-1}r-p_{k-1}}{q_{k-2}r-p_{k-2}} \right| \right\rfloor.$$
??? hint "Explanation"
As we have already noted, $a_k = \lfloor s_k \rfloor$, where $s_k = [a_k; a_{k+1}, a_{k+2}, \dots]$. On the other hand, from the convergent recurrence we derive that
$$r = [a_0; a_1, \dots, a_{k-1}, s_k] = \frac{s_k p_{k-1} + p_{k-2}}{s_k q_{k-1} + q_{k-2}}.$$
In vector form, it rewrites as
$$\vec r \parallel s_k \vec r_{k-1} + \vec r_{k-2},$$
meaning that $\vec r$ and $s_k \vec r_{k-1} + \vec r_{k-2}$ are collinear (that is, have the same slope coefficient). Taking the [pseudoscalar product](../geometry/basic-geometry.md) of both parts with $\vec r$, we get
$$0 = s_k (\vec r_{k-1} \times \vec r) + (\vec r_{k-2} \times \vec r),$$
which yields the final formula
$$s_k = -\frac{\vec r_{k-2} \times \vec r}{\vec r_{k-1} \times \vec r}.$$
!!! example "Nose stretching algorithm"
Each time you add $\vec r_{k-1}$ to the vector $\vec p$, the value of $\vec p \times \vec r$ is increased by $\vec r_{k-1} \times \vec r$.
Thus, $a_k=\lfloor s_k \rfloor$ is the maximum integer number of $\vec r_{k-1}$ vectors that can be added to $\vec r_{k-2}$ without changing the sign of the cross product with $\vec r$.
In other words, $a_k$ is the maximum integer number of times you can add $\vec r_{k-1}$ to $\vec r_{k-2}$ without crossing the line defined by $\vec r$:
<figure><img src="https://upload.wikimedia.org/wikipedia/commons/9/92/Continued_convergents_geometry.svg" width="700px"/>
<figcaption>_Convergents of $r=\frac{7}{9}=[0;1,3,2]$. Semiconvergents correspond to intermediate points between gray arrows._</figcaption></figure>
On the picture above, $\vec r_2 = (4;3)$ is obtained by repeatedly adding $\vec r_1 = (1;1)$ to $\vec r_0 = (1;0)$.
When it is not possible to further add $\vec r_1$ to $\vec r_0$ without crossing the $y=rx$ line, we go to the other side and repeatedly add $\vec r_2$ to $\vec r_1$ to obtain $\vec r_3 = (9;7)$.
This procedure generates exponentially longer vectors, that approach the line.
For this property, the procedure of generating consequent convergent vectors was dubbed the **nose stretching algorithm** by Boris Delaunay.
If we look on the triangle drawn on points $\vec r_{k-2}$, $\vec r_{k}$ and $\vec 0$ we will notice that its doubled area is
$$|\vec r_{k-2} \times \vec r_k| = |\vec r_{k-2} \times (\vec r_{k-2} + a_k \vec r_{k-1})| = a_k |\vec r_{k-2} \times \vec r_{k-1}| = a_k.$$
Combined with the [Pick's theorem](../geometry/picks-theorem.md), it means that there are no lattice points strictly inside the triangle and the only lattice points on its border are $\vec 0$ and $\vec r_{k-2} + t \cdot \vec r_{k-1}$ for all integer $t$ such that $0 \leq t \leq a_k$. When joined for all possible $k$ it means that there are no integer points in the space between polygons formed by even-indexed and odd-indexed convergent vectors.
This, in turn, means that $\vec r_k$ with odd coefficients form a convex hull of lattice points with $x \geq 0$ above the line $y=rx$, while $\vec r_k$ with even coefficients form a convex hull of lattice points with $x > 0$ below the line $y=rx$.
!!! info "Definition"
These polygons are also known as **Klein polygons**, named after Felix Klein who first suggested this geometric interpretation to the continued fractions.
## Problem examples
Now that the most important facts and concepts were introduced, it is time to delve into specific problem examples.
!!! example "Convex hull under the line"
Find the convex hull of lattice points $(x;y)$ such that $0 \leq x \leq N$ and $0 \leq y \leq rx$ for $r=[a_0;a_1,\dots,a_k]=\frac{p_k}{q_k}$.
??? hint "Solution"
If we were considering the unbounded set $0 \leq x$, the upper convex hull would be given by the line $y=rx$ itself.
However, with additional constraint $x \leq N$ we'd need to eventually deviate from the line to maintain proper convex hull.
Let $t = \lfloor \frac{N}{q_k}\rfloor$, then first $t$ lattice points on the hull after $(0;0)$ are $\alpha \cdot (q_k; p_k)$ for integer $1 \leq \alpha \leq t$.
However $(t+1)(q_k; p_k)$ can't be next lattice point since $(t+1)q_k$ is greater than $N$.
To get to the next lattice points in the hull, we should get to the point $(x;y)$ which diverges from $y=rx$ by the smallest margin, while maintaining $x \leq N$.
<figure><img src="https://upload.wikimedia.org/wikipedia/commons/b/b1/Lattice-hull.svg" width="500px"/>
<figcaption>Convex hull of lattice points under $y=\frac{4}{7}x$ for $0 \leq x \leq 19$ consists of points $(0;0), (7;4), (14;8), (16;9), (18;10), (19;10)$.</figcaption></figure>
Let $(x; y)$ be the last current point in the convex hull. Then the next point $(x'; y')$ is such that $x' \leq N$ and $(x'; y') - (x; y) = (\Delta x; \Delta y)$ is as close to the line $y=rx$ as possible. In other words, $(\Delta x; \Delta y)$ maximizes $r \Delta x - \Delta y$ subject to $\Delta x \leq N - x$ and $\Delta y \leq r \Delta x$.
Points like that lie on the convex hull of lattice points below $y=rx$. In other words, $(\Delta x; \Delta y)$ must be a lower semiconvergent of $r$.
That being said, $(\Delta x; \Delta y)$ is of form $(q_{i-1}; p_{i-1}) + t \cdot (q_i; p_i)$ for some odd number $i$ and $0 \leq t < a_i$.
To find such $i$, we can traverse all possible $i$ starting from the largest one and use $t = \lfloor \frac{N-x-q_{i-1}}{q_i} \rfloor$ for $i$ such that $N-x-q_{i-1} \geq 0$.
With $(\Delta x; \Delta y) = (q_{i-1}; p_{i-1}) + t \cdot (q_i; p_i)$, the condition $\Delta y \leq r \Delta x$ would be preserved by semiconvergent properties.
And $t < a_i$ would hold because we already exhausted semiconvergents obtained from $i+2$, hence $x + q_{i-1} + a_i q_i = x+q_{i+1}$ is greater than $N$.
Now that we may add $(\Delta x; \Delta y)$, to $(x;y)$ for $k = \lfloor \frac{N-x}{\Delta x} \rfloor$ times before we exceed $N$, after which we would try the next semiconvergent.
=== "C++"
```cpp
// returns [ah, ph, qh] such that points r[i]=(ph[i], qh[i]) constitute upper convex hull
// of lattice points on 0 <= x <= N and 0 <= y <= r * x, where r = [a0; a1, a2, ...]
// and there are ah[i]-1 integer points on the segment between r[i] and r[i+1]
auto hull(auto a, int N) {
auto [p, q] = convergents(a);
int t = N / q.back();
vector ah = {t};
vector ph = {0, t*p.back()};
vector qh = {0, t*q.back()};
for(int i = q.size() - 1; i >= 0; i--) {
if(i % 2) {
while(qh.back() + q[i - 1] <= N) {
t = (N - qh.back() - q[i - 1]) / q[i];
int dp = p[i - 1] + t * p[i];
int dq = q[i - 1] + t * q[i];
int k = (N - qh.back()) / dq;
ah.push_back(k);
ph.push_back(ph.back() + k * dp);
qh.push_back(qh.back() + k * dq);
}
}
}
return make_tuple(ah, ph, qh);
}
```
=== "Python"
```py
# returns [ah, ph, qh] such that points r[i]=(ph[i], qh[i]) constitute upper convex hull
# of lattice points on 0 <= x <= N and 0 <= y <= r * x, where r = [a0; a1, a2, ...]
# and there are ah[i]-1 integer points on the segment between r[i] and r[i+1]
def hull(a, N):
p, q = convergents(a)
t = N // q[-1]
ah = [t]
ph = [0, t*p[-1]]
qh = [0, t*q[-1]]
for i in reversed(range(len(q))):
if i % 2 == 1:
while qh[-1] + q[i-1] <= N:
t = (N - qh[-1] - q[i-1]) // q[i]
dp = p[i-1] + t*p[i]
dq = q[i-1] + t*q[i]
k = (N - qh[-1]) // dq
ah.append(k)
ph.append(ph[-1] + k * dp)
qh.append(qh[-1] + k * dq)
return ah, ph, qh
```
!!! example "[Timus - Crime and Punishment](https://timus.online/problem.aspx?space=1&num=1430)"
You're given integer numbers $A$, $B$ and $N$. Find $x \geq 0$ and $y \geq 0$ such that $Ax + By \leq N$ and $Ax + By$ is the maximum possible.
??? hint "Solution"
In this problem it holds that $1 \leq A, B, N \leq 2 \cdot 10^9$, so it can be solved in $O(\sqrt N)$. However, there is $O(\log N)$ solution with continued fractions.
For our convenience, we will invert the direction of $x$ by doing a substitution $x \mapsto \lfloor \frac{N}{A}\rfloor - x$, so that now we need to find the point $(x; y)$ such that $0 \leq x \leq \lfloor \frac{N}{A} \rfloor$, $By - Ax \leq N \;\bmod\; A$ and $By - Ax$ is the maximum possible. Optimal $y$ for each $x$ has a value of $\lfloor \frac{Ax + (N \bmod A)}{B} \rfloor$.
To treat it more generically, we will write a function that finds the best point on $0 \leq x \leq N$ and $y = \lfloor \frac{Ax+B}{C} \rfloor$.
Core solution idea in this problem essentially repeats the previous problem, but instead of using lower semiconvergents to diverge from line, you use upper semiconvergents to get closer to the line without crossing it and without violating $x \leq N$. Unfortunately, unlike the previous problem, you need to make sure that you don't cross the $y=\frac{Ax+B}{C}$ line while getting closer to it, so you should keep it in mind when calculating semiconvergent's coefficient $t$.
=== "Python"
```py
# (x, y) such that y = (A*x+B) // C,
# Cy - Ax is max and 0 <= x <= N.
def closest(A, B, C, N):
# y <= (A*x + B)/C <=> diff(x, y) <= B
def diff(x, y):
return C*y-A*x
a = fraction(A, C)
p, q = convergents(a)
ph = [B // C]
qh = [0]
for i in range(2, len(q) - 1):
if i % 2 == 0:
while diff(qh[-1] + q[i+1], ph[-1] + p[i+1]) <= B:
t = 1 + (diff(qh[-1] + q[i-1], ph[-1] + p[i-1]) - B - 1) // abs(diff(q[i], p[i]))
dp = p[i-1] + t*p[i]
dq = q[i-1] + t*q[i]
k = (N - qh[-1]) // dq
if k == 0:
return qh[-1], ph[-1]
if diff(dq, dp) != 0:
k = min(k, (B - diff(qh[-1], ph[-1])) // diff(dq, dp))
qh.append(qh[-1] + k*dq)
ph.append(ph[-1] + k*dp)
return qh[-1], ph[-1]
def solve(A, B, N):
x, y = closest(A, N % A, B, N // A)
return N // A - x, y
```
!!! example "[June Challenge 2017 - Euler Sum](https://www.codechef.com/problems/ES)"
Compute $\sum\limits_{x=1}^N \lfloor ex \rfloor$, where $e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, \dots, 1, 2n, 1, \dots]$ is the Euler's number and $N \leq 10^{4000}$.
??? hint "Solution"
This sum is equal to the number of lattice point $(x;y)$ such that $1 \leq x \leq N$ and $1 \leq y \leq ex$.
After constructing the convex hull of the points below $y=ex$, this number can be computed using [Pick's theorem](../geometry/picks-theorem.md):
=== "C++"
```cpp
// sum floor(k * x) for k in [1, N] and x = [a0; a1, a2, ...]
int sum_floor(auto a, int N) {
N++;
auto [ah, ph, qh] = hull(a, N);
// The number of lattice points within a vertical right trapezoid
// on points (0; 0) - (0; y1) - (dx; y2) - (dx; 0) that has
// a+1 integer points on the segment (0; y1) - (dx; y2).
auto picks = [](int y1, int y2, int dx, int a) {
int b = y1 + y2 + a + dx;
int A = (y1 + y2) * dx;
return (A - b + 2) / 2 + b - (y2 + 1);
};
int ans = 0;
for(size_t i = 1; i < qh.size(); i++) {
ans += picks(ph[i - 1], ph[i], qh[i] - qh[i - 1], ah[i - 1]);
}
return ans - N;
}
```
=== "Python"
```py
# sum floor(k * x) for k in [1, N] and x = [a0; a1, a2, ...]
def sum_floor(a, N):
N += 1
ah, ph, qh = hull(a, N)
# The number of lattice points within a vertical right trapezoid
# on points (0; 0) - (0; y1) - (dx; y2) - (dx; 0) that has
# a+1 integer points on the segment (0; y1) - (dx; y2).
def picks(y1, y2, dx, a):
b = y1 + y2 + a + dx
A = (y1 + y2) * dx
return (A - b + 2) // 2 + b - (y2 + 1)
ans = 0
for i in range(1, len(qh)):
ans += picks(ph[i-1], ph[i], qh[i]-qh[i-1], ah[i-1])
return ans - N
```
!!! example "[NAIPC 2019 - It's a Mod, Mod, Mod, Mod World](https://open.kattis.com/problems/itsamodmodmodmodworld)"
Given $p$, $q$ and $n$, compute $\sum\limits_{i=1}^n [p \cdot i \bmod q]$.
??? hint "Solution"
This problem reduces to the previous one if you note that $a \bmod b = a - \lfloor \frac{a}{b} \rfloor b$. With this fact, the sum reduces to
$$\sum\limits_{i=1}^n \left(p \cdot i - \left\lfloor \frac{p \cdot i}{q} \right\rfloor q\right) = \frac{pn(n+1)}{2}-q\sum\limits_{i=1}^n \left\lfloor \frac{p \cdot i}{q}\right\rfloor.$$
However, summing up $\lfloor rx \rfloor$ for $x$ from $1$ to $N$ is something that we're capable of from the previous problem.
=== "C++"
```cpp
void solve(int p, int q, int N) {
cout << p * N * (N + 1) / 2 - q * sum_floor(fraction(p, q), N) << "\n";
}
```
=== "Python"
```py
def solve(p, q, N):
return p * N * (N + 1) // 2 - q * sum_floor(fraction(p, q), N)
```
!!! example "[Library Checker - Sum of Floor of Linear](https://judge.yosupo.jp/problem/sum_of_floor_of_linear)"
Given $N$, $M$, $A$ and $B$, compute $\sum\limits_{i=0}^{N-1} \lfloor \frac{A \cdot i + B}{M} \rfloor$.
??? hint "Solution"
This is the most technically troublesome problem so far.
It is possible to use the same approach and construct the full convex hull of points below the line $y = \frac{Ax+B}{M}$.
We already know how to solve it for $B = 0$. Moreover, we already know how to construct this convex hull up to the closest lattice point to this line on $[0, N-1]$ segment (this is done in the "Crime and Punishment" problem above.
Now we should note that once we reached the closest point to the line, we can just assume that the line in fact passes through the closest point, as there are no other lattice points on $[0, N-1]$ in between the actual line and the line moved slightly below to pass through the closest point.
That being said, to construct the full convex hull below the line $y=\frac{Ax+B}{M}$ on $[0, N-1]$, we can construct it up to the closest point to the line on $[0, N-1]$ and then continue as if the line passes through this point, reusing algorithm for constructing convex hull with $B=0$:
=== "Python"
```py
# hull of lattice (x, y) such that C*y <= A*x+B
def hull(A, B, C, N):
def diff(x, y):
return C*y-A*x
a = fraction(A, C)
p, q = convergents(a)
ah = []
ph = [B // C]
qh = [0]
def insert(dq, dp):
k = (N - qh[-1]) // dq
if diff(dq, dp) > 0:
k = min(k, (B - diff(qh[-1], ph[-1])) // diff(dq, dp))
ah.append(k)
qh.append(qh[-1] + k*dq)
ph.append(ph[-1] + k*dp)
for i in range(1, len(q) - 1):
if i % 2 == 0:
while diff(qh[-1] + q[i+1], ph[-1] + p[i+1]) <= B:
t = (B - diff(qh[-1] + q[i+1], ph[-1] + p[i+1])) // abs(diff(q[i], p[i]))
dp = p[i+1] - t*p[i]
dq = q[i+1] - t*q[i]
if dq < 0 or qh[-1] + dq > N:
break
insert(dq, dp)
insert(q[-1], p[-1])
for i in reversed(range(len(q))):
if i % 2 == 1:
while qh[-1] + q[i-1] <= N:
t = (N - qh[-1] - q[i-1]) // q[i]
dp = p[i-1] + t*p[i]
dq = q[i-1] + t*q[i]
insert(dq, dp)
return ah, ph, qh
```
!!! example "[OKC 2 - From Modular to Rational](https://codeforces.com/gym/102354/problem/I)"
There is a rational number $\frac{p}{q}$ such that $1 \leq p, q \leq 10^9$. You may ask the value of $p q^{-1}$ modulo $m \sim 10^9$ for several prime numbers $m$. Recover $\frac{p}{q}$.
_Equivalent formulation:_ Find $x$ that delivers the minimum of $Ax \;\bmod\; M$ for $1 \leq x \leq N$.
??? hint "Solution"
Due to Chinese remainder theorem, asking the result modulo several prime numbers is the same as asking it modulo their product. Due to this, without loss of generality we'll assume that we know the remainder modulo sufficiently large number $m$.
There could be several possible solutions $(p, q)$ to $p \equiv qr \pmod m$ for a given remainder $r$. However, if $(p_1, q_1)$ and $(p_2, q_2)$ are both the solutions then it also holds that $p_1 q_2 \equiv p_2 q_1 \pmod m$. Assuming that $\frac{p_1}{q_1} \neq \frac{p_2}{q_2}$ it means that $|p_1 q_2 - p_2 q_1|$ is at least $m$.
In the statement we were told that $1 \leq p, q \leq 10^9$, so if both $p_1, q_1$ and $p_2, q_2$ are at most $10^9$, then the difference is at most $10^{18}$. For $m > 10^{18}$ it means that the solution $\frac{p}{q}$ with $1 \leq p, q \leq 10^9$ is unique, as a rational number.
So, the problem boils down, given $r$ modulo $m$, to finding any $q$ such that $1 \leq q \leq 10^9$ and $qr \;\bmod\; m \leq 10^9$.
This is effectively the same as finding $q$ that delivers the minimum possible $qr \bmod m$ for $1 \leq q \leq 10^9$.
For $qr = km + b$ it means that we need to find a pair $(q, m)$ such that $1 \leq q \leq 10^9$ and $qr - km \geq 0$ is the minimum possible.
Since $m$ is constant, we can divide by it and further restate it as find $q$ such that $1 \leq q \leq 10^9$ and $\frac{r}{m} q - k \geq 0$ is the minimum possible.
In terms of continued fractions it means that $\frac{k}{q}$ is the best diophantine approximation to $\frac{r}{m}$ and it is sufficient to only check lower semiconvergents of $\frac{r}{m}$.
=== "Python"
```py
# find Q that minimizes Q*r mod m for 1 <= k <= n < m
def mod_min(r, n, m):
a = fraction(r, m)
p, q = convergents(a)
for i in range(2, len(q)):
if i % 2 == 1 and (i + 1 == len(q) or q[i+1] > n):
t = (n - q[i-1]) // q[i]
return q[i-1] + t*q[i]
```
|
---
title
- Original
---
<!--?title Continued fractions -->
# Continued fractions
**Continued fraction** is a representation of a real number as a specific convergent sequence of rational numbers. They are useful in competitive programming because they are easy to compute and can be efficiently used to find the best possible rational approximation of the underlying real number (among all numbers whose denominator doesn't exceed a given value).
Besides that, continued fractions are closely related to Euclidean algorithm which makes them useful in a bunch of number-theoretical problems.
## Continued fraction representation
!!! info "Definition"
Let $a_0, a_1, \dots, a_k \in \mathbb Z$ and $a_1, a_2, \dots, a_k \geq 1$. Then the expression
$$r=a_0 + \frac{1}{a_1 + \frac{1}{\dots + \frac{1}{a_k}}},$$
is called the **continued fraction representation** of the rational number $r$ and is denoted shortly as $r=[a_0;a_1,a_2,\dots,a_k]$.
??? example
Let $r = \frac{5}{3}$. There are two ways to represent it as a continued fraction:
$$
\begin{align}
r = [1;1,1,1] &= 1+\frac{1}{1+\frac{1}{1+\frac{1}{1}}},\\
r = [1;1,2] &= 1+\frac{1}{1+\frac{1}{2}}.
\end{align}
$$
It can be proven that any rational number can be represented as a continued fraction in exactly $2$ ways:
$$r = [a_0;a_1,\dots,a_k,1] = [a_0;a_1,\dots,a_k+1].$$
Moreover, the length $k$ of such continued fraction is estimated as $k = O(\log \min(p, q))$ for $r=\frac{p}{q}$.
The reasoning behind this will be clear once we delve into the details of the continued fraction construction.
!!! info "Definition"
Let $a_0,a_1,a_2, \dots$ be an integer sequence such that $a_1, a_2, \dots \geq 1$. Let $r_k = [a_0; a_1, \dots, a_k]$. Then the expression
$$r = a_0 + \frac{1}{a_1 + \frac{1}{a_2+\dots}} = \lim\limits_{k \to \infty} r_k.$$
is called the **continued fraction representation** of the irrational number $r$ and is denoted shortly as $r = [a_0;a_1,a_2,\dots]$.
Note that for $r=[a_0;a_1,\dots]$ and integer $k$, it holds that $r+k = [a_0+k; a_1, \dots]$.
Another important observation is that $\frac{1}{r}=[0;a_0, a_1, \dots]$ when $a_0 > 0$ and $\frac{1}{r} = [a_1; a_2, \dots]$ when $a_0 = 0$.
!!! info "Definition"
In the definition above, rational numbers $r_0, r_1, r_2, \dots$ are called the **convergents** of $r$.
Correspondingly, individual $r_k = [a_0; a_1, \dots, a_k] = \frac{p_k}{q_k}$ is called the $k$-th **convergent** of $r$.
??? example
Consider $r = [1; 1, 1, 1, \dots]$. It can be proven by induction that $r_k = \frac{F_{k+2}}{F_{k+1}}$, where $F_k$ is the Fibonacci sequence defined as $F_0 = 0$, $F_1 = 1$ and $F_{k} = F_{k-1} + F_{k-2}$. From the Binet's formula, it is known that
$$r_k = \frac{\phi^{k+2} - \psi^{k+2}}{\phi^{k+1} - \psi^{k+1}},$$
where $\phi = \frac{1+\sqrt{5}}{2} \approx 1.618$ is the golden ratio and $\psi = \frac{1-\sqrt{5}}{2} = -\frac{1}{\phi} \approx -0.618$. Thus,
$$r = 1+\frac{1}{1+\frac{1}{1+\dots}}=\lim\limits_{k \to \infty} r_k = \phi = \frac{1+\sqrt{5}}{2}.$$
Note that in this specific case, an alternative way to find $r$ would be to solve the equation
$$r = 1+\frac{1}{r} \implies r^2 = r + 1. $$
!!! info "Definition"
Let $r_k = [a_0; a_1, \dots, a_{k-1}, a_k]$. The numbers $[a_0; a_1, \dots, a_{k-1}, t]$ for $1 \leq t \leq a_k$ are called **semiconvergents**.
We will typically refer to (semi)convergents that are greater than $r$ as **upper** (semi)convergents and to those that are less than $r$ as **lower** (semi)convergents.
!!! info "Definition"
Complementary to convergents, we define the **[complete quotients](https://en.wikipedia.org/wiki/Complete_quotient)** as $s_k = [a_k; a_{k+1}, a_{k+2}, \dots]$.
Correspondingly, we will call an individual $s_k$ the $k$-th complete quotient of $r$.
From the definitions above, one can conclude that $s_k \geq 1$ for $k \geq 1$.
Treating $[a_0; a_1, \dots, a_k]$ as a formal algebraic expression and allowing arbitrary real numbers instead of $a_i$, we obtain
$$r = [a_0; a_1, \dots, a_{k-1}, s_k].$$
In particular, $r = [s_0] = s_0$. On the other hand, we can express $s_k$ as
$$s_k = [a_k; s_{k+1}] = a_k + \frac{1}{s_{k+1}},$$
meaning that we can compute $a_k = \lfloor s_k \rfloor$ and $s_{k+1} = (s_k - a_k)^{-1}$ from $s_k$.
The sequence $a_0, a_1, \dots$ is well-defined unless $s_k=a_k$ which only happens when $r$ is a rational number.
Thus the continued fraction representation is uniquely defined for any irrational number $r$.
### Implementation
In the code snippets we will mostly assume finite continued fractions.
From $s_k$, the transition to $s_{k+1}$ looks like
$$s_k =\left\lfloor s_k \right\rfloor + \frac{1}{s_{k+1}}.$$
From this expression, the next complete quotient $s_{k+1}$ is obtained as
$$s_{k+1} = \left(s_k-\left\lfloor s_k\right\rfloor\right)^{-1}.$$
For $s_k=\frac{p}{q}$ it means that
$$
s_{k+1} = \left(\frac{p}{q}-\left\lfloor \frac{p}{q} \right\rfloor\right)^{-1} = \frac{q}{p-q\cdot \lfloor \frac{p}{q} \rfloor} = \frac{q}{p \bmod q}.
$$
Thus, the computation of a continued fraction representation for $r=\frac{p}{q}$ follows the steps of the Euclidean algorithm for $p$ and $q$.
From this also follows that $\gcd(p_k, q_k) = 1$ for $\frac{p_k}{q_k} = [a_0; a_1, \dots, a_k]$. Hence, convergents are always irreducible.
=== "C++"
```cpp
auto fraction(int p, int q) {
vector<int> a;
while(q) {
a.push_back(p / q);
tie(p, q) = make_pair(q, p % q);
}
return a;
}
```
=== "Python"
```py
def fraction(p, q):
a = []
while q:
a.append(p // q)
p, q = q, p % q
return a
```
## Key results
To provide some motivation for further study of continued fraction, we give some key facts now.
??? note "Recurrence"
For the convergents $r_k = \frac{p_k}{q_k}$, the following recurrence stands, allowing their fast computation:
$$\frac{p_k}{q_k}=\frac{a_k p_{k-1} + p_{k-2}}{a_k q_{k-1} + q_{k-2}},$$
where $\frac{p_{-1}}{q_{-1}}=\frac{1}{0}$ and $\frac{p_{-2}}{q_{-2}}=\frac{0}{1}$.
??? note "Deviations"
The deviation of $r_k = \frac{p_k}{q_k}$ from $r$ can be generally estimated as
$$\left|\frac{p_k}{q_k}-r\right| \leq \frac{1}{q_k q_{k+1}} \leq \frac{1}{q_k^2}.$$
Multiplying both sides with $q_k$, we obtain alternate estimation:
$$|p_k - q_k r| \leq \frac{1}{q_{k+1}}.$$
From the recurrence above it follows that $q_k$ grows at least as fast as Fibonacci numbers.
On the picture below you may see the visualization of how convergents $r_k$ approach $r=\frac{1+\sqrt 5}{2}$:

$r=\frac{1+\sqrt 5}{2}$ is depicted by blue dotted line. Odd convergents approach it from above and even convergents approach it from below.
??? note "Lattice hulls"
Consider convex hulls of points above and below the line $y=rx$.
Odd convergents $(q_k;p_k)$ are the vertices of the upper hull, while the even convergents $(q_k;p_k)$ are the vertices of the bottom hull.
All integers vertices on the hulls are obtained as $(q;p)$ such that
$$\frac{p}{q} = \frac{tp_{k-1} + p_{k-2}}{tq_{k-1} + q_{k-2}}$$
for integer $0 \leq t \leq a_k$. In other words, the set of lattice points on the hulls corresponds to the set of semiconvergents.
On the picture below, you may see the convergents and semiconvergents (intermediate gray points) of $r=\frac{9}{7}$.

??? note "Best approximations"
Let $\frac{p}{q}$ be the fraction to minimize $\left|r-\frac{p}{q}\right|$ subject to $q \leq x$ for some $x$.
Then $\frac{p}{q}$ is a semiconvergent of $r$.
The last fact allows to find the best rational approximations of $r$ by checking its semiconvergents.
Below you will find the further explanation and a bit of intuition and interpretation for these facts.
## Convergents
Let's take a closer look at the convergents that were defined earlier. For $r=[a_0, a_1, a_2, \dots]$, its convergents are
\begin{gather}
r_0=[a_0],\\r_1=[a_0, a_1],\\ \dots,\\ r_k=[a_0, a_1, \dots, a_k].
\end{gather}
Convergents are the core concept of continued fractions, so it is important to study their properties.
For the number $r$, its $k$-th convergent $r_k = \frac{p_k}{q_k}$ can be computed as
$$r_k = \frac{P_k(a_0,a_1,\dots,a_k)}{P_{k-1}(a_1,\dots,a_k)} = \frac{a_k p_{k-1} + p_{k-2}}{a_k q_{k-1} + q_{k-2}},$$
where $P_k(a_0,\dots,a_k)$ is [the continuant](https://en.wikipedia.org/wiki/Continuant_(mathematics)), a multivariate polynomial defined as
$$P_k(x_0,x_1,\dots,x_k) = \det \begin{bmatrix}
x_k & 1 & 0 & \dots & 0 \\
-1 & x_{k-1} & 1 & \dots & 0 \\
0 & -1 & x_2 & . & \vdots \\
\vdots & \vdots & . & \ddots & 1 \\
0 & 0 & \dots & -1 & x_0
\end{bmatrix}_{\textstyle .}$$
Thus, $r_k$ is a weighted [mediant](https://en.wikipedia.org/wiki/Mediant_(mathematics)) of $r_{k-1}$ and $r_{k-2}$.
For consistency, two additional convergents $r_{-1} = \frac{1}{0}$ and $r_{-2} = \frac{0}{1}$ are defined.
??? hint "Detailed explanation"
The numerator and the denominator of $r_k$ can be seen as multivariate polynomials of $a_0, a_1, \dots, a_k$:
$$r_k = \frac{P_k(a_0, a_1, \dots, a_k)}{Q_k(a_0,a_1, \dots, a_k)}.$$
From the definition of convergents,
$$r_k = a_0 + \frac{1}{[a_1;a_2,\dots, a_k]}= a_0 + \frac{Q_{k-1}(a_1, \dots, a_k)}{P_{k-1}(a_1, \dots, a_k)} = \frac{a_0 P_{k-1}(a_1, \dots, a_k) + Q_{k-1}(a_1, \dots, a_k)}{P_{k-1}(a_1, \dots, a_k)}.$$
From this follows $Q_k(a_0, \dots, a_k) = P_{k-1}(a_1, \dots, a_k)$. This yields the relation
$$P_k(a_0, \dots, a_k) = a_0 P_{k-1}(a_1, \dots, a_k) + P_{k-2}(a_2, \dots, a_k).$$
Initially, $r_0 = \frac{a_0}{1}$ and $r_1 = \frac{a_0 a_1 + 1}{a_1}$, thus
$$\begin{align}P_0(a_0)&=a_0,\\ P_1(a_0, a_1) &= a_0 a_1 + 1.\end{align}$$
For consistency, it is convenient to define $P_{-1} = 1$ and $P_{-2}=0$ and formally say that $r_{-1} = \frac{1}{0}$ and $r_{-2}=\frac{0}{1}$.
From numerical analysis, it is known that the determinant of an arbitrary tridiagonal matrix
$$T_k = \det \begin{bmatrix}
a_0 & b_0 & 0 & \dots & 0 \\
c_0 & a_1 & b_1 & \dots & 0 \\
0 & c_1 & a_2 & . & \vdots \\
\vdots & \vdots & . & \ddots & c_{k-1} \\
0 & 0 & \dots & b_{k-1} & a_k
\end{bmatrix}$$
can be computed recursively as $T_k = a_k T_{k-1} - b_{k-1} c_{k-1} T_{k-2}$. Comparing it to $P_k$, we get a direct expression
$$P_k = \det \begin{bmatrix}
x_k & 1 & 0 & \dots & 0 \\
-1 & x_{k-1} & 1 & \dots & 0 \\
0 & -1 & x_2 & . & \vdots \\
\vdots & \vdots & . & \ddots & 1 \\
0 & 0 & \dots & -1 & x_0
\end{bmatrix}_{\textstyle .}$$
This polynomial is also known as [the continuant](https://en.wikipedia.org/wiki/Continuant_(mathematics)) due to its close relation with continued fraction. The continuant won't change if the sequence on the main diagonal is reversed. This yields an alternative formula to compute it:
$$P_k(a_0, \dots, a_k) = a_k P_{k-1}(a_0, \dots, a_{k-1}) + P_{k-2}(a_0, \dots, a_{k-2}).$$
### Implementation
We will compute the convergents as a pair of sequences $p_{-2}, p_{-1}, p_0, p_1, \dots, p_k$ and $q_{-2}, q_{-1}, q_0, q_1, \dots, q_k$:
=== "C++"
```cpp
auto convergents(vector<int> a) {
vector<int> p = {0, 1};
vector<int> q = {1, 0};
for(auto it: a) {
p.push_back(p[p.size() - 1] * it + p[p.size() - 2]);
q.push_back(q[q.size() - 1] * it + q[q.size() - 2]);
}
return make_pair(p, q);
}
```
=== "Python"
```py
def convergents(a):
p = [0, 1]
q = [1, 0]
for it in a:
p.append(p[-1]*it + p[-2])
q.append(q[-1]*it + q[-2])
return p, q
```
## Trees of continued fractions
There are two major ways to unite all possible continued fractions into useful tree structures.
### Stern-Brocot tree
[The Stern-Brocot tree](../others/stern_brocot_tree_farey_sequences.md) is a binary search tree that contains all distinct positive rational numbers.
The tree generally looks as follows:
<figure>
<img src="https://upload.wikimedia.org/wikipedia/commons/3/37/SternBrocotTree.svg">
<figcaption>
<a href="https://commons.wikimedia.org/wiki/File:SternBrocotTree.svg">The image</a> by <a href="https://commons.wikimedia.org/wiki/User:Aaron_Rotenberg">Aaron Rotenberg</a> is licensed under <a href="https://creativecommons.org/licenses/by-sa/3.0/deed.en">CC BY-SA 3.0</a>
</figcaption>
</figure>
Fractions $\frac{0}{1}$ and $\frac{1}{0}$ are "virtually" kept on the left and right sides of the tree correspondingly.
Then the fraction in a node is a mediant $\frac{a+c}{b+d}$ of two fractions $\frac{a}{b}$ and $\frac{c}{d}$ above it.
The recurrence $\frac{p_k}{q_k}=\frac{a_k p_{k-1} + p_{k-2}}{a_k q_{k-1} + q_{k-2}}$ means that the continued fraction representation encodes the path to $\frac{p_k}{q_k}$ in the tree. To find $[a_0; a_1, \dots, a_{k}, 1]$, one has to make $a_0$ moves to the right, $a_1$ moves to the left, $a_2$ moves to the right and so on up to $a_k$.
The parent of $[a_0; a_1, \dots, a_k,1]$ then is the fraction obtained by taking one step back in the last used direction.
In other words, it is $[a_0; a_1, \dots, a_k-1,1]$ when $a_k > 1$ and $[a_0; a_1, \dots, a_{k-1}, 1]$ when $a_k = 1$.
Thus the children of $[a_0; a_1, \dots, a_k, 1]$ are $[a_0; a_1, \dots, a_k+1, 1]$ and $[a_0; a_1, \dots, a_k, 1, 1]$.
Let's index the Stern-Brocot tree. The root vertex is assigned an index $1$. Then for a vertex $v$, the index of its left child is assigned by changing the leading bit of $v$ from $1$ to $10$ and for the right child, it's assigned by changing the leading bit from $1$ to $11$:
<figure><img src="https://upload.wikimedia.org/wikipedia/commons/1/18/Stern-brocot-index.svg" width="500px"/></figure>
In this indexing, the continued fraction representation of a rational number specifies the [run-length encoding](https://en.wikipedia.org/wiki/Run-length_encoding) of its binary index.
For $\frac{5}{2} = [2;2] = [2;1,1]$, its index is $1011_2$ and its run-length encoding, considering bits in the ascending order, is $[2;1,1]$.
Another example is $\frac{2}{5} = [0;2,2]=[0;2,1,1]$, which has index $1100_2$ and its run-length encoding is, indeed, $[0;2,2]$.
It is worth noting that the Stern-Brocot tree is, in fact, a [treap](../data_structures/treap.md). That is, it is a binary search tree by $\frac{p}{q}$, but it is a heap by both $p$ and $q$.
!!! example "Comparing continued fractions"
You're given $A=[a_0; a_1, \dots, a_n]$ and $B=[b_0; b_1, \dots, b_m]$. Which fraction is smaller?
??? hint "Solution"
Assume for now that $A$ and $B$ are irrational and their continued fraction representations denote an infinite descent in the Stern-Brocot tree.
As we already mentioned, in this representation $a_0$ denotes the number of right turns in the descent, $a_1$ denotes the number of consequent left turns and so on. Therefore, when we compare $a_k$ and $b_k$, if $a_k = b_k$ we should just move on to comparing $a_{k+1}$ and $b_{k+1}$. Otherwise, if we're at right descents, we should check if $a_k < b_k$ and if we're at left descents, we should check if $a_k > b_k$ to tell whether $A < B$.
In other words, for irrational $A$ and $B$ it would be $A < B$ if and only if $(a_0, -a_1, a_2, -a_3, \dots) < (b_0, -b_1, b_2, -b_3, \dots)$ with lexicographical comparison.
Now, formally using $\infty$ as an element of continued fraction representation it is possible to emulate irrational numbers $A-\varepsilon$ and $A+\varepsilon$, that is, elements that are smaller (greater) than $A$, but greater (smaller) than any other real number. Specifically, for $A=[a_0; a_1, \dots, a_n]$, one of these two elements can be emulated as $[a_0; a_1, \dots, a_n, \infty]$ and the other can be emulated as $[a_0; a_1, \dots, a_n - 1, 1, \infty]$.
Which one corresponds to $A-\varepsilon$ and which one to $A+\varepsilon$ can be determined by the parity of $n$ or by comparing them as irrational numbers.
=== "Python"
```py
# check if a < b assuming that a[-1] = b[-1] = infty and a != b
def less(a, b):
a = [(-1)**i*a[i] for i in range(len(a))]
b = [(-1)**i*b[i] for i in range(len(b))]
return a < b
# [a0; a1, ..., ak] -> [a0, a1, ..., ak-1, 1]
def expand(a):
if a: # empty a = inf
a[-1] -= 1
a.append(1)
return a
# return a-eps, a+eps
def pm_eps(a):
b = expand(a.copy())
a.append(float('inf'))
b.append(float('inf'))
return (a, b) if less(a, b) else (b, a)
```
!!! example "Best inner point"
You're given $\frac{0}{1} \leq \frac{p_0}{q_0} < \frac{p_1}{q_1} \leq \frac{1}{0}$. Find the rational number $\frac{p}{q}$ such that $(q; p)$ is lexicographically smallest and $\frac{p_0}{q_0} < \frac{p}{q} < \frac{p_1}{q_1}$.
??? hint "Solution"
In terms of the Stern-Brocot tree it means that we need to find the LCA of $\frac{p_0}{q_0}$ and $\frac{p_1}{q_1}$. Due to the connection between Stern-Brocot tree and continued fraction, this LCA would roughly correspond to the largest common prefix of continued fraction representations for $\frac{p_0}{q_0}$ and $\frac{p_1}{q_1}$.
So, if $\frac{p_0}{q_0} = [a_0; a_1, \dots, a_{k-1}, a_k, \dots]$ and $\frac{p_1}{q_1} = [a_0; a_1, \dots, a_{k-1}, b_k, \dots]$ are irrational numbers, the LCA is $[a_0; a_1, \dots, \min(a_k, b_k)+1]$.
For rational $r_0$ and $r_1$, one of them could be the LCA itself which would require us to casework it. To simplify the solution for rational $r_0$ and $r_1$, it is possible to use continued fraction representation of $r_0 + \varepsilon$ and $r_1 - \varepsilon$ which was derived in the previous problem.
=== "Python"
```py
# finds lexicographically smallest (q, p)
# such that p0/q0 < p/q < p1/q1
def middle(p0, q0, p1, q1):
a0 = pm_eps(fraction(p0, q0))[1]
a1 = pm_eps(fraction(p1, q1))[0]
a = []
for i in range(min(len(a0), len(a1))):
a.append(min(a0[i], a1[i]))
if a0[i] != a1[i]:
break
a[-1] += 1
p, q = convergents(a)
return p[-1], q[-1]
```
!!! example "[GCJ 2019, Round 2 - New Elements: Part 2](https://codingcompetitions.withgoogle.com/codejam/round/0000000000051679/0000000000146184)"
You're given $N$ positive integer pairs $(C_i, J_i)$. You need to find a positive integer pair $(x, y)$ such that $C_i x + J_i y$ is a strictly increasing sequence.
Among such pairs, find the lexicographically minimum one.
??? hint "Solution"
Rephrasing the statement, $A_i x + B_i y$ must be positive for all $i$, where $A_i = C_i - C_{i-1}$ and $B_i = J_i - J_{i-1}$.
Among such equations we have four significant groups for $A_i x + B_i y > 0$:
1. $A_i, B_i > 0$ can be ignored since we're looking for $x, y > 0$.
2. $A_i, B_i \leq 0$ would provide "IMPOSSIBLE" as an answer.
3. $A_i > 0$, $B_i \leq 0$. Such constraints are equivalent to $\frac{y}{x} < \frac{A_i}{-B_i}$.
4. $A_i \leq 0$, $B_i > 0$. Such constraints are equivalent to $\frac{y}{x} > \frac{-A_i}{B_i}$.
Let $\frac{p_0}{q_0}$ be the largest $\frac{-A_i}{B_i}$ from the fourth group and $\frac{p_1}{q_1}$ be the smallest $\frac{A_i}{-B_i}$ from the third group.
The problem is now, given $\frac{p_0}{q_0} < \frac{p_1}{q_1}$, find a fraction $\frac{p}{q}$ such that $(q;p)$ is lexicographically smallest and $\frac{p_0}{q_0} < \frac{p}{q} < \frac{p_1}{q_1}$.
=== "Python"
```py
def solve():
n = int(input())
C = [0] * n
J = [0] * n
# p0/q0 < y/x < p1/q1
p0, q0 = 0, 1
p1, q1 = 1, 0
fail = False
for i in range(n):
C[i], J[i] = map(int, input().split())
if i > 0:
A = C[i] - C[i-1]
B = J[i] - J[i-1]
if A <= 0 and B <= 0:
fail = True
elif B > 0 and A < 0: # y/x > (-A)/B if B > 0
if (-A)*q0 > p0*B:
p0, q0 = -A, B
elif B < 0 and A > 0: # y/x < A/(-B) if B < 0
if A*q1 < p1*(-B):
p1, q1 = A, -B
if p0*q1 >= p1*q0 or fail:
return 'IMPOSSIBLE'
p, q = middle(p0, q0, p1, q1)
return str(q) + ' ' + str(p)
```
### Calkin-Wilf tree
A somewhat simpler way to organize continued fractions in a binary tree is the [Calkin-Wilf tree](https://en.wikipedia.org/wiki/Calkin–Wilf_tree).
The tree generally looks like this:
<figure>
<img src="https://upload.wikimedia.org/wikipedia/commons/8/82/Calkin–Wilf_tree.svg" width="500px"/>
<figcaption><a href="https://commons.wikimedia.org/wiki/File:Calkin–Wilf_tree.svg">The image</a> by <a href="https://commons.wikimedia.org/wiki/User:Olli_Niemitalo">Olli Niemitalo</a>, <a href="https://commons.wikimedia.org/wiki/User:Proz">Proz</a> is licensed under <a href="https://creativecommons.org/publicdomain/zero/1.0/deed.en">CC0 1.0</a></figcaption>
</figure>
In the root of the tree, the number $\frac{1}{1}$ is located. Then, for the vertex with a number $\frac{p}{q}$, its children are $\frac{p}{p+q}$ and $\frac{p+q}{q}$.
Unlike the Stern-Brocot tree, the Calkin-Wilf tree is not a binary _search_ tree, so it can't be used to perform rational binary search.
In the Calkin-Wilf tree, the direct parent of a fraction $\frac{p}{q}$ is $\frac{p-q}{q}$ when $p>q$ and $\frac{p}{q-p}$ otherwise.
For the Stern-Brocot tree, we used the recurrence for convergents. To draw the connection between the continued fraction and the Calkin-Wilf tree, we should recall the recurrence for complete quotients. If $s_k = \frac{p}{q}$, then $s_{k+1} = \frac{q}{p \mod q} = \frac{q}{p-\lfloor p/q \rfloor \cdot q}$.
On the other hand, if we repeatedly go from $s_k = \frac{p}{q}$ to its parent in the Calkin-Wilf tree when $p > q$, we will end up in $\frac{p \mod q}{q} = \frac{1}{s_{k+1}}$. If we continue doing so, we will end up in $s_{k+2}$, then $\frac{1}{s_{k+3}}$ and so on. From this we can deduce that:
1. When $a_0> 0$, the direct parent of $[a_0; a_1, \dots, a_k]$ in the Calkin-Wilf tree is $\frac{p-q}{q}=[a_0 - 1; a_1, \dots, a_k]$.
2. When $a_0 = 0$ and $a_1 > 1$, its direct parent is $\frac{p}{q-p} = [0; a_1 - 1, a_2, \dots, a_k]$.
3. And when $a_0 = 0$ and $a_1 = 1$, its direct parent is $\frac{p}{q-p} = [a_2; a_3, \dots, a_k]$.
Correspondingly, children of $\frac{p}{q} = [a_0; a_1, \dots, a_k]$ are
1. $\frac{p+q}{q}=1+\frac{p}{q}$, which is $[a_0+1; a_1, \dots, a_k]$,
2. $\frac{p}{p+q} = \frac{1}{1+\frac{q}{p}}$, which is $[0, 1, a_0, a_1, \dots, a_k]$ for $a_0 > 0$ and $[0, a_1+1, a_2, \dots, a_k]$ for $a_0=0$.
Noteworthy, if we enumerate vertices of the Calkin-Wilf tree in the breadth-first search order (that is, the root has a number $1$, and the children of the vertex $v$ have indices $2v$ and $2v+1$ correspondingly), the index of the rational number in the Calkin-Wilf tree would be the same as in the Stern-Brocot tree.
Thus, numbers on the same levels of the Stern-Brocot tree and the Calkin-Wilf tree are the same, but their ordering differs through the [bit-reversal permutation](https://en.wikipedia.org/wiki/Bit-reversal_permutation).
## Convergence
For the number $r$ and its $k$-th convergent $r_k=\frac{p_k}{q_k}$ the following formula stands:
$$r_k = a_0 + \sum\limits_{i=1}^k \frac{(-1)^{i-1}}{q_i q_{i-1}}.$$
In particular, it means that
$$r_k - r_{k-1} = \frac{(-1)^{k-1}}{q_k q_{k-1}}$$
and
$$p_k q_{k-1} - p_{k-1} q_k = (-1)^{k-1}.$$
From this we can conclude that
$$\left| r-\frac{p_k}{q_k} \right| \leq \frac{1}{q_{k+1}q_k} \leq \frac{1}{q_k^2}.$$
The latter inequality is due to the fact that $r_k$ and $r_{k+1}$ are generally located on different sides of $r$, thus
$$|r-r_k| = |r_k-r_{k+1}|-|r-r_{k+1}| \leq |r_k - r_{k+1}|.$$
??? tip "Detailed explanation"
To estimate $|r-r_k|$, we start by estimating the difference between adjacent convergents. By definition,
$$\frac{p_k}{q_k} - \frac{p_{k-1}}{q_{k-1}} = \frac{p_k q_{k-1} - p_{k-1} q_k}{q_k q_{k-1}}.$$
Replacing $p_k$ and $q_k$ in the numerator with their recurrences, we get
$$\begin{align} p_k q_{k-1} - p_{k-1} q_k &= (a_k p_{k-1} + p_{k-2}) q_{k-1} - p_{k-1} (a_k q_{k-1} + q_{k-2})
\\&= p_{k-2} q_{k-1} - p_{k-1} q_{k-2},\end{align}$$
thus the numerator of $r_k - r_{k-1}$ is always the negated numerator of $r_{k-1} - r_{k-2}$. It, in turn, equals to $1$ for
$$r_1 - r_0=\left(a_0+\frac{1}{a_1}\right)-a_0=\frac{1}{a_1},$$
thus
$$r_k - r_{k-1} = \frac{(-1)^{k-1}}{q_k q_{k-1}}.$$
This yields an alternative representation of $r_k$ as a partial sum of infinite series:
$$r_k = (r_k - r_{k-1}) + \dots + (r_1 - r_0) + r_0
= a_0 + \sum\limits_{i=1}^k \frac{(-1)^{i-1}}{q_i q_{i-1}}.$$
From the recurrent relation it follows that $q_k$ monotonously increases at least as fast as Fibonacci numbers, thus
$$r = \lim\limits_{k \to \infty} r_k = a_0 + \sum\limits_{i=1}^\infty \frac{(-1)^{i-1}}{q_i q_{i-1}}$$
is always well-defined, as the underlying series always converge. Noteworthy, the residual series
$$r-r_k = \sum\limits_{i=k+1}^\infty \frac{(-1)^{i-1}}{q_i q_{i-1}}$$
has the same sign as $(-1)^k$ due to how fast $q_i q_{i-1}$ decreases. Hence even-indexed $r_k$ approach $r$ from below while odd-indexed $r_k$ approach it from above:
<figure><img src="https://upload.wikimedia.org/wikipedia/commons/b/b4/Golden_ration_convergents.svg" width="600px"/>
<figcaption>_Convergents of $r=\phi = \frac{1+\sqrt{5}}{2}=[1;1,1,\dots]$ and their distance from $r$._</figcaption></figure>
From this picture we can see that
$$|r-r_k| = |r_k - r_{k+1}| - |r-r_{k+1}| \leq |r_k - r_{k+1}|,$$
thus the distance between $r$ and $r_k$ is never larger than the distance between $r_k$ and $r_{k+1}$:
$$\left|r-\frac{p_k}{q_k}\right| \leq \frac{1}{q_k q_{k+1}} \leq \frac{1}{q_k^2}.$$
!!! example "Extended Euclidean?"
You're given $A, B, C \in \mathbb Z$. Find $x, y \in \mathbb Z$ such that $Ax + By = C$.
??? hint "Solution"
Although this problem is typically solved with the [extended Euclidean algorithm](../algebra/extended-euclid-algorithm.md), there is a simple and straightforward solution with continued fractions.
Let $\frac{A}{B}=[a_0; a_1, \dots, a_k]$. It was proved above that $p_k q_{k-1} - p_{k-1} q_k = (-1)^{k-1}$. Substituting $p_k$ and $q_k$ with $A$ and $B$, we get
$$Aq_{k-1} - Bp_{k-1} = (-1)^{k-1} g,$$
where $g = \gcd(A, B)$. If $C$ is divisible by $g$, then the solution is $x = (-1)^{k-1}\frac{C}{g} q_{k-1}$ and $y = (-1)^{k}\frac{C}{g} p_{k-1}$.
=== "Python"
```py
# return (x, y) such that Ax+By=C
# assumes that such (x, y) exists
def dio(A, B, C):
p, q = convergents(fraction(A, B))
C //= A // p[-1] # divide by gcd(A, B)
t = (-1) if len(p) % 2 else 1
return t*C*q[-2], -t*C*p[-2]
```
## Linear fractional transformations
Another important concept for continued fractions are the so-called [linear fractional transformations](https://en.wikipedia.org/wiki/Linear_fractional_transformation).
!!! info "Definition"
A **linear fractional transformation** is a function $f : \mathbb R \to \mathbb R$ such that $f(x) = \frac{ax+b}{cx+d}$ for some $a,b,c,d \in \mathbb R$.
A composition $(L_0 \circ L_1)(x) = L_0(L_1(x))$ of linear fractional transforms $L_0(x)=\frac{a_0 x + b_0}{c_0 x + d_0}$ and $L_1(x)=\frac{a_1 x + b_1}{c_1 x + d_1}$ is itself a linear fractional transform:
$$\frac{a_0\frac{a_1 x + b_1}{c_1 x + d_1} + b_0}{c_0 \frac{a_1 x + b_1}{c_1 x + d_1} + d_0} = \frac{a_0(a_1 x + b_1) + b_0 (c_1 x + d_1)}{c_0 (a_1 x + b_1) + d_0 (c_1 x + d_1)} = \frac{(a_0 a_1 + b_0 c_1) x + (a_0 b_1 + b_0 d_1)}{(c_0 a_1 + d_0 c_1) x + (c_0 b_1 + d_0 d_1)}.$$
Inverse of a linear fractional transform, is also a linear fractional transform:
$$y = \frac{ax+b}{cx+d} \iff y(cx+d) = ax + b \iff x = -\frac{dy-b}{cy-a}.$$
!!! example "[DMOPC '19 Contest 7 P4 - Bob and Continued Fractions](https://dmoj.ca/problem/dmopc19c7p4)"
You're given an array of positive integers $a_1, \dots, a_n$. You need to answer $m$ queries. Each query is to compute $[a_l; a_{l+1}, \dots, a_r]$.
??? hint "Solution"
We can solve this problem with the segment tree if we're able to concatenate continued fractions.
It's generally true that $[a_0; a_1, \dots, a_k, b_0, b_1, \dots, b_k] = [a_0; a_1, \dots, a_k, [b_1; b_2, \dots, b_k]]$.
Let's denote $L_{k}(x) = [a_k; x] = a_k + \frac{1}{x} = \frac{a_k\cdot x+1}{1\cdot x + 0}$. Note that $L_k(\infty) = a_k$. In this notion, it holds that
$$[a_0; a_1, \dots, a_k, x] = [a_0; [a_1; [\dots; [a_k; x]]]] = (L_0 \circ L_1 \circ \dots \circ L_k)(x) = \frac{p_k x + p_{k-1}}{q_k x + q_{k-1}}.$$
Thus, the problem boils down to the computation of
$$(L_l \circ L_{l+1} \circ \dots \circ L_r)(\infty).$$
Composition of transforms is associative, so it's possible to compute in each node of a segment tree the composition of transforms in its subtree.
!!! example "Linear fractional transformation of a continued fraction"
Let $L(x) = \frac{ax+b}{cx+d}$. Compute the continued fraction representation $[b_0; b_1, \dots, b_m]$ of $L(A)$ for $A=[a_0; a_1, \dots, a_n]$.
_This allows to compute $A + \frac{p}{q} = \frac{qA + p}{q}$ and $A \cdot \frac{p}{q} = \frac{p A}{q}$ for any $\frac{p}{q}$._
??? hint "Solution"
As we noted above, $[a_0; a_1, \dots, a_k] = (L_{a_0} \circ L_{a_1} \circ \dots \circ L_{a_k})(\infty)$, hence $L([a_0; a_1, \dots, a_k]) = (L \circ L_{a_0} \circ L_{a_1} \circ \dots L_{a_k})(\infty)$.
Hence, by consequentially adding $L_{a_0}$, $L_{a_1}$ and so on we would be able to compute
$$(L \circ L_{a_0} \circ \dots \circ L_{a_k})(x) = L\left(\frac{p_k x + p_{k-1}}{q_k x + q_{k-1}}\right)=\frac{a_k x + b_k}{c_k x + d_k}.$$
Since $L(x)$ is invertible, it is also monotonous in $x$. Therefore, for any $x \geq 0$ it holds that $L(\frac{p_k x + p_{k-1}}{q_k x + q_{k-1}})$ is between $L(\frac{p_k}{q_k}) = \frac{a_k}{c_k}$ and $L(\frac{p_{k-1}}{q_{k-1}}) = \frac{b_k}{d_k}$.
Moreover, for $x=[a_{k+1}; \dots, a_n]$ it is equal to $L(A)$. Hence, $b_0 = \lfloor L(A) \rfloor$ is between $\lfloor L(\frac{p_k}{q_k}) \rfloor$ and $\lfloor L(\frac{p_{k-1}}{q_{k-1}}) \rfloor$. When they're equal, they're also equal to $b_0$.
Note that $L(A) = (L_{b_0} \circ L_{b_1} \circ \dots \circ L_{b_m})(\infty)$. Knowing $b_0$, we can compose $L_{b_0}^{-1}$ with the current transform and continue adding $L_{a_{k+1}}$, $L_{a_{k+2}}$ and so on, looking for new floors to agree, from which we would be able to deduce $b_1$ and so on until we recover all values of $[b_0; b_1, \dots, b_m]$.
!!! example "Continued fraction arithmetics"
Let $A=[a_0; a_1, \dots, a_n]$ and $B=[b_0; b_1, \dots, b_m]$. Compute the continued fraction representations of $A+B$ and $A \cdot B$.
??? hint "Solution"
Idea here is similar to the previous problem, but instead of $L(x) = \frac{ax+b}{cx+d}$ you should consider bilinear fractional transform $L(x, y) = \frac{axy+bx+cy+d}{exy+fx+gy+h}$.
Rather than $L(x) \mapsto L(L_{a_k}(x))$ you would change your current transform as $L(x, y) \mapsto L(L_{a_k}(x), y)$ or $L(x, y) \mapsto L(x, L_{b_k}(y))$.
Then, you check if $\lfloor \frac{a}{e} \rfloor = \lfloor \frac{b}{f} \rfloor = \lfloor \frac{c}{g} \rfloor = \lfloor \frac{d}{h} \rfloor$ and if they all agree, you use this value as $c_k$ in the resulting fraction and change the transform as
$$L(x, y) \mapsto \frac{1}{L(x, y) - c_k}.$$
!!! info "Definition"
A continued fraction $x = [a_0; a_1, \dots]$ is said to be **periodic** if $x = [a_0; a_1, \dots, a_k, x]$ for some $k$.
A continued fraction $x = [a_0; a_1, \dots]$ is said to be **eventually periodic** if $x = [a_0; a_1, \dots, a_k, y]$, where $y$ is periodic.
For $x = [1; 1, 1, \dots]$ it holds that $x = 1 + \frac{1}{x}$, thus $x^2 = x + 1$. There is a generic connection between periodic continued fractions and quadratic equations. Consider the following equation:
$$ x = [a_0; a_1, \dots, a_k, x].$$
On one hand, this equation means that the continued fraction representation of $x$ is periodic with the period $k+1$.
On the other hand, using the formula for convergents, this equation means that
$$x = \frac{p_k x + p_{k-1}}{q_k x + q_{k-1}}.$$
That is, $x$ is a linear fractional transformation of itself. It follows from the equation that $x$ is a root of the second degree equation:
$$q_k x^2 + (q_{k-1}-p_k)x - p_{k-1} = 0.$$
Similar reasoning stands for continued fractions that are eventually periodic, that is $x = [a_0; a_1, \dots, a_k, y]$ for $y=[b_0; b_1, \dots, b_k, y]$. Indeed, from first equation we derive that $x = L_0(y)$ and from second equation that $y = L_1(y)$, where $L_0$ and $L_1$ are linear fractional transformations. Therefore,
$$x = (L_0 \circ L_1)(y) = (L_0 \circ L_1 \circ L_0^{-1})(x).$$
One can further prove (and it was first done by Lagrange) that for arbitrary quadratic equation $ax^2+bx+c=0$ with integer coefficients, its solution $x$ is an eventually periodic continued fraction.
!!! example "Quadratic irrationality"
Find the continued fraction of $\alpha = \frac{x+y\sqrt{n}}{z}$ where $x, y, z, n \in \mathbb Z$ and $n > 0$ is not a perfect square.
??? hint "Solution"
For the $k$-th complete quotient $s_k$ of the number it generally holds that
$$\alpha = [a_0; a_1, \dots, a_{k-1}, s_k] = \frac{s_k p_{k-1} + p_{k-2}}{s_k q_{k-1} + q_{k-2}}.$$
Therefore,
$$s_k = -\frac{\alpha q_{k-1} - p_{k-1}}{\alpha q_k - p_k} = -\frac{q_{k-1} y \sqrt n + (x q_{k-1} - z p_{k-1})}{q_k y \sqrt n + (xq_k-zp_k)}.$$
Multiplying the numerator and denominator by $(xq_k - zp_k) - q_k y \sqrt n$, we'll get rid of $\sqrt n$ in the denominator, thus the complete quotients are of form
$$s_k = \frac{x_k + y_k \sqrt n}{z_k}.$$
Let's find $s_{k+1}$, assuming that $s_k$ is known.
First of all, $a_k = \lfloor s_k \rfloor = \left\lfloor \frac{x_k + y_k \lfloor \sqrt n \rfloor}{z_k} \right\rfloor$. Then,
$$s_{k+1} = \frac{1}{s_k-a_k} = \frac{z_k}{(x_k - z_k a_k) + y_k \sqrt n} = \frac{z_k (x_k - y_k a_k) - y_k z_k \sqrt n}{(x_k - y_k a_k)^2 - y_k^2 n}.$$
Thus, if we denote $t_k = x_k - y_k a_k$, it will hold that
\begin{align}x_{k+1} &=& z_k t_k, \\ y_{k+1} &=& -y_k z_k, \\ z_{k+1} &=& t_k^2 - y_k^2 n.\end{align}
Nice thing about such representation is that if we reduce $x_{k+1}, y_{k+1}, z_{k+1}$ by their greatest common divisor, the result would be unique. Therefore, we may use it to check whether the current state has already been repeated and also to check where was the previous index that had this state.
Below is the code to compute the continued fraction representation for $\alpha = \sqrt n$:
=== "Python"
```py
# compute the continued fraction of sqrt(n)
def sqrt(n):
n0 = math.floor(math.sqrt(n))
x, y, z = 1, 0, 1
a = []
def step(x, y, z):
a.append((x * n0 + y) // z)
t = y - a[-1]*z
x, y, z = -z*x, z*t, t**2 - n*x**2
g = math.gcd(x, math.gcd(y, z))
return x // g, y // g, z // g
used = dict()
for i in range(n):
used[x, y, z] = i
x, y, z = step(x, y, z)
if (x, y, z) in used:
return a
```
Using the same `step` function but different initial $x$, $y$ and $z$ it is possible to compute it for arbitrary $\frac{x+y \sqrt{n}}{z}$.
!!! example "[Tavrida NU Akai Contest - Continued Fraction](https://timus.online/problem.aspx?space=1&num=1814)"
You're given $x$ and $k$, $x$ is not a perfect square. Let $\sqrt x = [a_0; a_1, \dots]$, find $\frac{p_k}{q_k}=[a_0; a_1, \dots, a_k]$ for $0 \leq k \leq 10^9$.
??? hint "Solution"
After computing the period of $\sqrt x$, it is possible to compute $a_k$ using binary exponentiation on the linear fractional transformation induced by the continued fraction representation. To find the resulting transformation, you compress the period of size $T$ into a single transformation and repeat it $\lfloor \frac{k-1}{T}\rfloor$ times, after which you manually combine it with the remaining transformations.
=== "Python"
```py
x, k = map(int, input().split())
mod = 10**9+7
# compose (A[0]*x + A[1]) / (A[2]*x + A[3]) and (B[0]*x + B[1]) / (B[2]*x + B[3])
def combine(A, B):
return [t % mod for t in [A[0]*B[0]+A[1]*B[2], A[0]*B[1]+A[1]*B[3], A[2]*B[0]+A[3]*B[2], A[2]*B[1]+A[3]*B[3]]]
A = [1, 0, 0, 1] # (x + 0) / (0*x + 1) = x
a = sqrt(x)
T = len(a) - 1 # period of a
# apply ak + 1/x = (ak*x+1)/(1x+0) to (Ax + B) / (Cx + D)
for i in reversed(range(1, len(a))):
A = combine([a[i], 1, 1, 0], A)
def bpow(A, n):
return [1, 0, 0, 1] if not n else combine(A, bpow(A, n-1)) if n % 2 else bpow(combine(A, A), n // 2)
C = (0, 1, 0, 0) # = 1 / 0
while k % T:
i = k % T
C = combine([a[i], 1, 1, 0], C)
k -= 1
C = combine(bpow(A, k // T), C)
C = combine([a[0], 1, 1, 0], C)
print(str(C[1]) + '/' + str(C[3]))
```
## Geometric interpretation
Let $\vec r_k = (q_k;p_k)$ for the convergent $r_k = \frac{p_k}{q_k}$. Then, the following recurrence holds:
$$\vec r_k = a_k \vec r_{k-1} + \vec r_{k-2}.$$
Let $\vec r = (1;r)$. Then, each vector $(x;y)$ corresponds to the number that is equal to its slope coefficient $\frac{y}{x}$.
With the notion of [pseudoscalar product](../geometry/basic-geometry.md) $(x_1;y_1) \times (x_2;y_2) = x_1 y_2 - x_2 y_1$, it can be shown (see the explanation below) that
$$s_k = -\frac{\vec r_{k-2} \times \vec r}{\vec r_{k-1} \times \vec r} = \left|\frac{\vec r_{k-2} \times \vec r}{\vec r_{k-1} \times \vec r}\right|.$$
The last equation is due to the fact that $r_{k-1}$ and $r_{k-2}$ lie on the different sides of $r$, thus pseudoscalar products of $\vec r_{k-1}$ and $\vec r_{k-2}$ with $\vec r$ have distinct signs. With $a_k = \lfloor s_k \rfloor$ in mind, formula for $\vec r_k$ now looks like
$$\vec r_k = \vec r_{k-2} + \left\lfloor \left| \frac{\vec r \times \vec r_{k-2}}{\vec r \times \vec r_{k-1}}\right|\right\rfloor \vec r_{k-1}.$$
Note that $\vec r_k \times r = (q;p) \times (1;r) = qr - p$, thus
$$a_k = \left\lfloor \left| \frac{q_{k-1}r-p_{k-1}}{q_{k-2}r-p_{k-2}} \right| \right\rfloor.$$
??? hint "Explanation"
As we have already noted, $a_k = \lfloor s_k \rfloor$, where $s_k = [a_k; a_{k+1}, a_{k+2}, \dots]$. On the other hand, from the convergent recurrence we derive that
$$r = [a_0; a_1, \dots, a_{k-1}, s_k] = \frac{s_k p_{k-1} + p_{k-2}}{s_k q_{k-1} + q_{k-2}}.$$
In vector form, it rewrites as
$$\vec r \parallel s_k \vec r_{k-1} + \vec r_{k-2},$$
meaning that $\vec r$ and $s_k \vec r_{k-1} + \vec r_{k-2}$ are collinear (that is, have the same slope coefficient). Taking the [pseudoscalar product](../geometry/basic-geometry.md) of both parts with $\vec r$, we get
$$0 = s_k (\vec r_{k-1} \times \vec r) + (\vec r_{k-2} \times \vec r),$$
which yields the final formula
$$s_k = -\frac{\vec r_{k-2} \times \vec r}{\vec r_{k-1} \times \vec r}.$$
!!! example "Nose stretching algorithm"
Each time you add $\vec r_{k-1}$ to the vector $\vec p$, the value of $\vec p \times \vec r$ is increased by $\vec r_{k-1} \times \vec r$.
Thus, $a_k=\lfloor s_k \rfloor$ is the maximum integer number of $\vec r_{k-1}$ vectors that can be added to $\vec r_{k-2}$ without changing the sign of the cross product with $\vec r$.
In other words, $a_k$ is the maximum integer number of times you can add $\vec r_{k-1}$ to $\vec r_{k-2}$ without crossing the line defined by $\vec r$:
<figure><img src="https://upload.wikimedia.org/wikipedia/commons/9/92/Continued_convergents_geometry.svg" width="700px"/>
<figcaption>_Convergents of $r=\frac{7}{9}=[0;1,3,2]$. Semiconvergents correspond to intermediate points between gray arrows._</figcaption></figure>
On the picture above, $\vec r_2 = (4;3)$ is obtained by repeatedly adding $\vec r_1 = (1;1)$ to $\vec r_0 = (1;0)$.
When it is not possible to further add $\vec r_1$ to $\vec r_0$ without crossing the $y=rx$ line, we go to the other side and repeatedly add $\vec r_2$ to $\vec r_1$ to obtain $\vec r_3 = (9;7)$.
This procedure generates exponentially longer vectors, that approach the line.
For this property, the procedure of generating consequent convergent vectors was dubbed the **nose stretching algorithm** by Boris Delaunay.
If we look on the triangle drawn on points $\vec r_{k-2}$, $\vec r_{k}$ and $\vec 0$ we will notice that its doubled area is
$$|\vec r_{k-2} \times \vec r_k| = |\vec r_{k-2} \times (\vec r_{k-2} + a_k \vec r_{k-1})| = a_k |\vec r_{k-2} \times \vec r_{k-1}| = a_k.$$
Combined with the [Pick's theorem](../geometry/picks-theorem.md), it means that there are no lattice points strictly inside the triangle and the only lattice points on its border are $\vec 0$ and $\vec r_{k-2} + t \cdot \vec r_{k-1}$ for all integer $t$ such that $0 \leq t \leq a_k$. When joined for all possible $k$ it means that there are no integer points in the space between polygons formed by even-indexed and odd-indexed convergent vectors.
This, in turn, means that $\vec r_k$ with odd coefficients form a convex hull of lattice points with $x \geq 0$ above the line $y=rx$, while $\vec r_k$ with even coefficients form a convex hull of lattice points with $x > 0$ below the line $y=rx$.
!!! info "Definition"
These polygons are also known as **Klein polygons**, named after Felix Klein who first suggested this geometric interpretation to the continued fractions.
## Problem examples
Now that the most important facts and concepts were introduced, it is time to delve into specific problem examples.
!!! example "Convex hull under the line"
Find the convex hull of lattice points $(x;y)$ such that $0 \leq x \leq N$ and $0 \leq y \leq rx$ for $r=[a_0;a_1,\dots,a_k]=\frac{p_k}{q_k}$.
??? hint "Solution"
If we were considering the unbounded set $0 \leq x$, the upper convex hull would be given by the line $y=rx$ itself.
However, with additional constraint $x \leq N$ we'd need to eventually deviate from the line to maintain proper convex hull.
Let $t = \lfloor \frac{N}{q_k}\rfloor$, then first $t$ lattice points on the hull after $(0;0)$ are $\alpha \cdot (q_k; p_k)$ for integer $1 \leq \alpha \leq t$.
However $(t+1)(q_k; p_k)$ can't be next lattice point since $(t+1)q_k$ is greater than $N$.
To get to the next lattice points in the hull, we should get to the point $(x;y)$ which diverges from $y=rx$ by the smallest margin, while maintaining $x \leq N$.
<figure><img src="https://upload.wikimedia.org/wikipedia/commons/b/b1/Lattice-hull.svg" width="500px"/>
<figcaption>Convex hull of lattice points under $y=\frac{4}{7}x$ for $0 \leq x \leq 19$ consists of points $(0;0), (7;4), (14;8), (16;9), (18;10), (19;10)$.</figcaption></figure>
Let $(x; y)$ be the last current point in the convex hull. Then the next point $(x'; y')$ is such that $x' \leq N$ and $(x'; y') - (x; y) = (\Delta x; \Delta y)$ is as close to the line $y=rx$ as possible. In other words, $(\Delta x; \Delta y)$ maximizes $r \Delta x - \Delta y$ subject to $\Delta x \leq N - x$ and $\Delta y \leq r \Delta x$.
Points like that lie on the convex hull of lattice points below $y=rx$. In other words, $(\Delta x; \Delta y)$ must be a lower semiconvergent of $r$.
That being said, $(\Delta x; \Delta y)$ is of form $(q_{i-1}; p_{i-1}) + t \cdot (q_i; p_i)$ for some odd number $i$ and $0 \leq t < a_i$.
To find such $i$, we can traverse all possible $i$ starting from the largest one and use $t = \lfloor \frac{N-x-q_{i-1}}{q_i} \rfloor$ for $i$ such that $N-x-q_{i-1} \geq 0$.
With $(\Delta x; \Delta y) = (q_{i-1}; p_{i-1}) + t \cdot (q_i; p_i)$, the condition $\Delta y \leq r \Delta x$ would be preserved by semiconvergent properties.
And $t < a_i$ would hold because we already exhausted semiconvergents obtained from $i+2$, hence $x + q_{i-1} + a_i q_i = x+q_{i+1}$ is greater than $N$.
Now that we may add $(\Delta x; \Delta y)$, to $(x;y)$ for $k = \lfloor \frac{N-x}{\Delta x} \rfloor$ times before we exceed $N$, after which we would try the next semiconvergent.
=== "C++"
```cpp
// returns [ah, ph, qh] such that points r[i]=(ph[i], qh[i]) constitute upper convex hull
// of lattice points on 0 <= x <= N and 0 <= y <= r * x, where r = [a0; a1, a2, ...]
// and there are ah[i]-1 integer points on the segment between r[i] and r[i+1]
auto hull(auto a, int N) {
auto [p, q] = convergents(a);
int t = N / q.back();
vector ah = {t};
vector ph = {0, t*p.back()};
vector qh = {0, t*q.back()};
for(int i = q.size() - 1; i >= 0; i--) {
if(i % 2) {
while(qh.back() + q[i - 1] <= N) {
t = (N - qh.back() - q[i - 1]) / q[i];
int dp = p[i - 1] + t * p[i];
int dq = q[i - 1] + t * q[i];
int k = (N - qh.back()) / dq;
ah.push_back(k);
ph.push_back(ph.back() + k * dp);
qh.push_back(qh.back() + k * dq);
}
}
}
return make_tuple(ah, ph, qh);
}
```
=== "Python"
```py
# returns [ah, ph, qh] such that points r[i]=(ph[i], qh[i]) constitute upper convex hull
# of lattice points on 0 <= x <= N and 0 <= y <= r * x, where r = [a0; a1, a2, ...]
# and there are ah[i]-1 integer points on the segment between r[i] and r[i+1]
def hull(a, N):
p, q = convergents(a)
t = N // q[-1]
ah = [t]
ph = [0, t*p[-1]]
qh = [0, t*q[-1]]
for i in reversed(range(len(q))):
if i % 2 == 1:
while qh[-1] + q[i-1] <= N:
t = (N - qh[-1] - q[i-1]) // q[i]
dp = p[i-1] + t*p[i]
dq = q[i-1] + t*q[i]
k = (N - qh[-1]) // dq
ah.append(k)
ph.append(ph[-1] + k * dp)
qh.append(qh[-1] + k * dq)
return ah, ph, qh
```
!!! example "[Timus - Crime and Punishment](https://timus.online/problem.aspx?space=1&num=1430)"
You're given integer numbers $A$, $B$ and $N$. Find $x \geq 0$ and $y \geq 0$ such that $Ax + By \leq N$ and $Ax + By$ is the maximum possible.
??? hint "Solution"
In this problem it holds that $1 \leq A, B, N \leq 2 \cdot 10^9$, so it can be solved in $O(\sqrt N)$. However, there is $O(\log N)$ solution with continued fractions.
For our convenience, we will invert the direction of $x$ by doing a substitution $x \mapsto \lfloor \frac{N}{A}\rfloor - x$, so that now we need to find the point $(x; y)$ such that $0 \leq x \leq \lfloor \frac{N}{A} \rfloor$, $By - Ax \leq N \;\bmod\; A$ and $By - Ax$ is the maximum possible. Optimal $y$ for each $x$ has a value of $\lfloor \frac{Ax + (N \bmod A)}{B} \rfloor$.
To treat it more generically, we will write a function that finds the best point on $0 \leq x \leq N$ and $y = \lfloor \frac{Ax+B}{C} \rfloor$.
Core solution idea in this problem essentially repeats the previous problem, but instead of using lower semiconvergents to diverge from line, you use upper semiconvergents to get closer to the line without crossing it and without violating $x \leq N$. Unfortunately, unlike the previous problem, you need to make sure that you don't cross the $y=\frac{Ax+B}{C}$ line while getting closer to it, so you should keep it in mind when calculating semiconvergent's coefficient $t$.
=== "Python"
```py
# (x, y) such that y = (A*x+B) // C,
# Cy - Ax is max and 0 <= x <= N.
def closest(A, B, C, N):
# y <= (A*x + B)/C <=> diff(x, y) <= B
def diff(x, y):
return C*y-A*x
a = fraction(A, C)
p, q = convergents(a)
ph = [B // C]
qh = [0]
for i in range(2, len(q) - 1):
if i % 2 == 0:
while diff(qh[-1] + q[i+1], ph[-1] + p[i+1]) <= B:
t = 1 + (diff(qh[-1] + q[i-1], ph[-1] + p[i-1]) - B - 1) // abs(diff(q[i], p[i]))
dp = p[i-1] + t*p[i]
dq = q[i-1] + t*q[i]
k = (N - qh[-1]) // dq
if k == 0:
return qh[-1], ph[-1]
if diff(dq, dp) != 0:
k = min(k, (B - diff(qh[-1], ph[-1])) // diff(dq, dp))
qh.append(qh[-1] + k*dq)
ph.append(ph[-1] + k*dp)
return qh[-1], ph[-1]
def solve(A, B, N):
x, y = closest(A, N % A, B, N // A)
return N // A - x, y
```
!!! example "[June Challenge 2017 - Euler Sum](https://www.codechef.com/problems/ES)"
Compute $\sum\limits_{x=1}^N \lfloor ex \rfloor$, where $e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, \dots, 1, 2n, 1, \dots]$ is the Euler's number and $N \leq 10^{4000}$.
??? hint "Solution"
This sum is equal to the number of lattice point $(x;y)$ such that $1 \leq x \leq N$ and $1 \leq y \leq ex$.
After constructing the convex hull of the points below $y=ex$, this number can be computed using [Pick's theorem](../geometry/picks-theorem.md):
=== "C++"
```cpp
// sum floor(k * x) for k in [1, N] and x = [a0; a1, a2, ...]
int sum_floor(auto a, int N) {
N++;
auto [ah, ph, qh] = hull(a, N);
// The number of lattice points within a vertical right trapezoid
// on points (0; 0) - (0; y1) - (dx; y2) - (dx; 0) that has
// a+1 integer points on the segment (0; y1) - (dx; y2).
auto picks = [](int y1, int y2, int dx, int a) {
int b = y1 + y2 + a + dx;
int A = (y1 + y2) * dx;
return (A - b + 2) / 2 + b - (y2 + 1);
};
int ans = 0;
for(size_t i = 1; i < qh.size(); i++) {
ans += picks(ph[i - 1], ph[i], qh[i] - qh[i - 1], ah[i - 1]);
}
return ans - N;
}
```
=== "Python"
```py
# sum floor(k * x) for k in [1, N] and x = [a0; a1, a2, ...]
def sum_floor(a, N):
N += 1
ah, ph, qh = hull(a, N)
# The number of lattice points within a vertical right trapezoid
# on points (0; 0) - (0; y1) - (dx; y2) - (dx; 0) that has
# a+1 integer points on the segment (0; y1) - (dx; y2).
def picks(y1, y2, dx, a):
b = y1 + y2 + a + dx
A = (y1 + y2) * dx
return (A - b + 2) // 2 + b - (y2 + 1)
ans = 0
for i in range(1, len(qh)):
ans += picks(ph[i-1], ph[i], qh[i]-qh[i-1], ah[i-1])
return ans - N
```
!!! example "[NAIPC 2019 - It's a Mod, Mod, Mod, Mod World](https://open.kattis.com/problems/itsamodmodmodmodworld)"
Given $p$, $q$ and $n$, compute $\sum\limits_{i=1}^n [p \cdot i \bmod q]$.
??? hint "Solution"
This problem reduces to the previous one if you note that $a \bmod b = a - \lfloor \frac{a}{b} \rfloor b$. With this fact, the sum reduces to
$$\sum\limits_{i=1}^n \left(p \cdot i - \left\lfloor \frac{p \cdot i}{q} \right\rfloor q\right) = \frac{pn(n+1)}{2}-q\sum\limits_{i=1}^n \left\lfloor \frac{p \cdot i}{q}\right\rfloor.$$
However, summing up $\lfloor rx \rfloor$ for $x$ from $1$ to $N$ is something that we're capable of from the previous problem.
=== "C++"
```cpp
void solve(int p, int q, int N) {
cout << p * N * (N + 1) / 2 - q * sum_floor(fraction(p, q), N) << "\n";
}
```
=== "Python"
```py
def solve(p, q, N):
return p * N * (N + 1) // 2 - q * sum_floor(fraction(p, q), N)
```
!!! example "[Library Checker - Sum of Floor of Linear](https://judge.yosupo.jp/problem/sum_of_floor_of_linear)"
Given $N$, $M$, $A$ and $B$, compute $\sum\limits_{i=0}^{N-1} \lfloor \frac{A \cdot i + B}{M} \rfloor$.
??? hint "Solution"
This is the most technically troublesome problem so far.
It is possible to use the same approach and construct the full convex hull of points below the line $y = \frac{Ax+B}{M}$.
We already know how to solve it for $B = 0$. Moreover, we already know how to construct this convex hull up to the closest lattice point to this line on $[0, N-1]$ segment (this is done in the "Crime and Punishment" problem above.
Now we should note that once we reached the closest point to the line, we can just assume that the line in fact passes through the closest point, as there are no other lattice points on $[0, N-1]$ in between the actual line and the line moved slightly below to pass through the closest point.
That being said, to construct the full convex hull below the line $y=\frac{Ax+B}{M}$ on $[0, N-1]$, we can construct it up to the closest point to the line on $[0, N-1]$ and then continue as if the line passes through this point, reusing algorithm for constructing convex hull with $B=0$:
=== "Python"
```py
# hull of lattice (x, y) such that C*y <= A*x+B
def hull(A, B, C, N):
def diff(x, y):
return C*y-A*x
a = fraction(A, C)
p, q = convergents(a)
ah = []
ph = [B // C]
qh = [0]
def insert(dq, dp):
k = (N - qh[-1]) // dq
if diff(dq, dp) > 0:
k = min(k, (B - diff(qh[-1], ph[-1])) // diff(dq, dp))
ah.append(k)
qh.append(qh[-1] + k*dq)
ph.append(ph[-1] + k*dp)
for i in range(1, len(q) - 1):
if i % 2 == 0:
while diff(qh[-1] + q[i+1], ph[-1] + p[i+1]) <= B:
t = (B - diff(qh[-1] + q[i+1], ph[-1] + p[i+1])) // abs(diff(q[i], p[i]))
dp = p[i+1] - t*p[i]
dq = q[i+1] - t*q[i]
if dq < 0 or qh[-1] + dq > N:
break
insert(dq, dp)
insert(q[-1], p[-1])
for i in reversed(range(len(q))):
if i % 2 == 1:
while qh[-1] + q[i-1] <= N:
t = (N - qh[-1] - q[i-1]) // q[i]
dp = p[i-1] + t*p[i]
dq = q[i-1] + t*q[i]
insert(dq, dp)
return ah, ph, qh
```
!!! example "[OKC 2 - From Modular to Rational](https://codeforces.com/gym/102354/problem/I)"
There is a rational number $\frac{p}{q}$ such that $1 \leq p, q \leq 10^9$. You may ask the value of $p q^{-1}$ modulo $m \sim 10^9$ for several prime numbers $m$. Recover $\frac{p}{q}$.
_Equivalent formulation:_ Find $x$ that delivers the minimum of $Ax \;\bmod\; M$ for $1 \leq x \leq N$.
??? hint "Solution"
Due to Chinese remainder theorem, asking the result modulo several prime numbers is the same as asking it modulo their product. Due to this, without loss of generality we'll assume that we know the remainder modulo sufficiently large number $m$.
There could be several possible solutions $(p, q)$ to $p \equiv qr \pmod m$ for a given remainder $r$. However, if $(p_1, q_1)$ and $(p_2, q_2)$ are both the solutions then it also holds that $p_1 q_2 \equiv p_2 q_1 \pmod m$. Assuming that $\frac{p_1}{q_1} \neq \frac{p_2}{q_2}$ it means that $|p_1 q_2 - p_2 q_1|$ is at least $m$.
In the statement we were told that $1 \leq p, q \leq 10^9$, so if both $p_1, q_1$ and $p_2, q_2$ are at most $10^9$, then the difference is at most $10^{18}$. For $m > 10^{18}$ it means that the solution $\frac{p}{q}$ with $1 \leq p, q \leq 10^9$ is unique, as a rational number.
So, the problem boils down, given $r$ modulo $m$, to finding any $q$ such that $1 \leq q \leq 10^9$ and $qr \;\bmod\; m \leq 10^9$.
This is effectively the same as finding $q$ that delivers the minimum possible $qr \bmod m$ for $1 \leq q \leq 10^9$.
For $qr = km + b$ it means that we need to find a pair $(q, m)$ such that $1 \leq q \leq 10^9$ and $qr - km \geq 0$ is the minimum possible.
Since $m$ is constant, we can divide by it and further restate it as find $q$ such that $1 \leq q \leq 10^9$ and $\frac{r}{m} q - k \geq 0$ is the minimum possible.
In terms of continued fractions it means that $\frac{k}{q}$ is the best diophantine approximation to $\frac{r}{m}$ and it is sufficient to only check lower semiconvergents of $\frac{r}{m}$.
=== "Python"
```py
# find Q that minimizes Q*r mod m for 1 <= k <= n < m
def mod_min(r, n, m):
a = fraction(r, m)
p, q = convergents(a)
for i in range(2, len(q)):
if i % 2 == 1 and (i + 1 == len(q) or q[i+1] > n):
t = (n - q[i-1]) // q[i]
return q[i-1] + t*q[i]
```
## Practice problems
* [UVa OJ - Continued Fractions](https://onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=775)
* [ProjectEuler+ #64: Odd period square roots](https://www.hackerrank.com/contests/projecteuler/challenges/euler064/problem)
* [Codeforces Round #184 (Div. 2) - Continued Fractions](https://codeforces.com/contest/305/problem/B)
* [Codeforces Round #201 (Div. 1) - Doodle Jump](https://codeforces.com/contest/346/problem/E)
* [Codeforces Round #325 (Div. 1) - Alice, Bob, Oranges and Apples](https://codeforces.com/contest/585/problem/C)
* [POJ Founder Monthly Contest 2008.03.16 - A Modular Arithmetic Challenge](http://poj.org/problem?id=3530)
* [2019 Multi-University Training Contest 5 - fraction](http://acm.hdu.edu.cn/showproblem.php?pid=6624)
* [SnackDown 2019 Elimination Round - Election Bait](https://www.codechef.com/SNCKEL19/problems/EBAIT)
|
Continued fractions
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.