nvidia/AceMath-RL-Nemotron-7B

Introduction

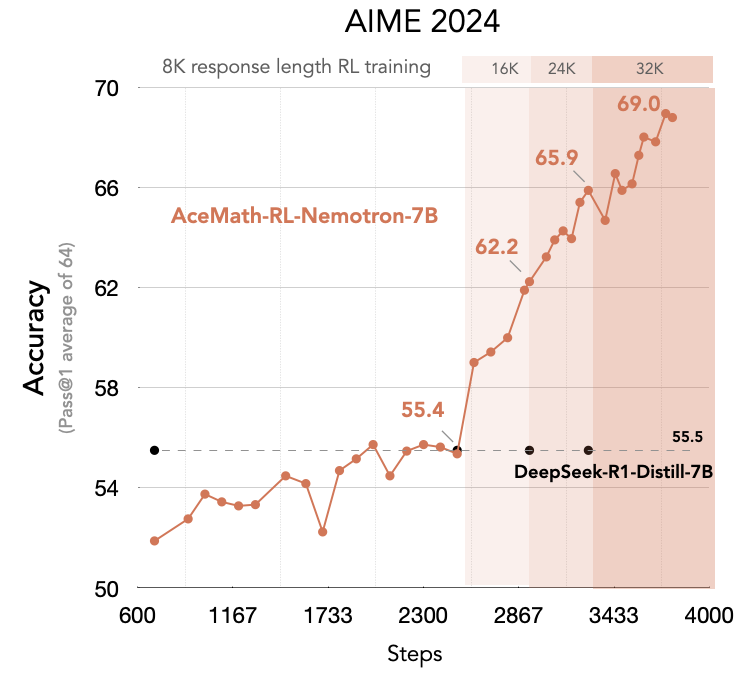
We’re thrilled to introduce AceMath-RL-Nemotron-7B, a math reasoning model trained entirely through reinforcement learning (RL), starting from the Deepseek-R1-Distilled-Qwen-7B. It delivers impressive results, achieving 69.0% Pass@1 accuracy on AIME 2024 (+13.5% gain) and 53.6% Pass@1 accuracy on AIME 2025 (+14.4% gain). Interestingly, this math-focused RL training also improves the model’s coding accuracy on LiveCodeBench, reaching 44.4% Pass@1 (+6.8% gain), demonstrating the generalization capabilities of scaled RL training.

We share our training recipe, training logs, and data curation details in our BLOG.

Results

We evaluate our model against competitive reasoning models of comparable size on AIME 2024, AIME 2025, and GPQA.

Model	AIME 2024 (AVG@64)	AIME 2025 (AVG@64)	GPQA-Diamond (AVG@8)
DeepSeek-R1-Distill-Qwen-7B	55.5	39.2	49.1
Light-R1-7B-DS	59.1	44.3	49.4
AReaL-boba-RL-7B	61.9	48.3	47.6
Llama-Nemotron-Nano-v1 (8B)	63.8	47.1	54.1
Skywork-OR1-Math-7B-Preview	69.8	52.3	-
AceMath-RL-Nemotron-7B 🤗	69.0	53.6	52.1

Additionally, we evaluate our models on additional math benchmarks and LiveCodeBench for a more comprehensive evaluation.

Model	GSM8K (AVG@1)	MATH500 (AVG@4)	Minerva Math (AVG@1)	GaoKao2023En (AVG@1)	Olympiad Bench (AVG@1)	College Math (AVG@1)	ACM23 (AVG@5)	LiveCodeBench (AVG@8)
DeepSeek-R1-Distill-Qwen-7B	92.7	92.8	57.4	82.3	58.2	56.7	89.0	37.6
AceMath-RL-Nemotron-7B 🤗	93.3	94.1	56.6	85.5	66.7	59.8	94.0	44.4

How to use

import torch
from transformers import AutoModelForCausalLM, AutoTokenizer

model_name = 'nvidia/AceMath-RL-Nemotron-7B'
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(model_name, torch_dtype="auto", device_map="auto")

prompt = "Jen enters a lottery by picking $4$ distinct numbers from $S=\\{1,2,3,\\cdots,9,10\\}.$ $4$ numbers are randomly chosen from $S.$ She wins a prize if at least two of her numbers were $2$ of the randomly chosen numbers, and wins the grand prize if all four of her numbers were the randomly chosen numbers. The probability of her winning the grand prize given that she won a prize is $\\tfrac{m}{n}$ where $m$ and $n$ are relatively prime positive integers. Find $m+n$."
messages = [{"role": "user", "content": prompt}]

text = tokenizer.apply_chat_template(
    messages,
    tokenize=False,
    add_generation_prompt=True
)
model_inputs = tokenizer([text], return_tensors="pt").to("cuda")

generated_ids = model.generate(
    **model_inputs,
    max_new_tokens=32768,
    temperature=0.6,
    top_p=0.95
)
generated_ids = [
    output_ids[len(input_ids):] for input_ids, output_ids in zip(model_inputs.input_ids, generated_ids)
]

response = tokenizer.batch_decode(generated_ids, skip_special_tokens=True)[0]

Usage Recommendations

1. Don't include a system prompt; instead, place all instructions directly in the user prompt.
2. We recommend using the following prompt format for math questions:
   <｜begin▁of▁sentence｜><｜User｜>{math_question}\nPlease reason step by step, and put your final answer within \boxed{}.<｜Assistant｜><think>\n

Correspondence to

Yang Chen ([email protected]),
Zihan Liu ([email protected]),
Chankyu Lee ([email protected]),
Wei Ping ([email protected])

License

Your use of this model is governed by the NVIDIA Open Model License.

Citation

@article{acemath2024,
  title={AceMath: Advancing Frontier Math Reasoning with Post-Training and Reward Modeling},
  author={Liu, Zihan and Chen, Yang and Shoeybi, Mohammad and Catanzaro, Bryan and Ping, Wei},
  journal={arXiv preprint},
  year={2024}
}