problem
stringlengths 1
7.47k
| solution
stringlengths 0
13.5k
| answer
stringlengths 1
272
| problem_type
stringclasses 8
values | question_type
stringclasses 3
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 7
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
XXXIII OM - I - Problem 9
In a chessboard created by dividing a square of side length $ n $ into unit squares using lines parallel to the sides of the square, we consider all squares whose sides are contained in the lines forming the chessboard. Let $ 1 \leq k \leq n $ and $ P(k,n) $ denote the number of these squares whose side lengths do not exceed $ k $. Let $ k(n) $ be the largest of such numbers $ k $ for which $ P(k, n) \leq \frac{1}{2} P(n, n) $. Calculate $ \lim_{n\to \infty} \frac{k(n)}{n} $. | On the side of the chessboard, there are $ n - k + 1 $ segments of length $ k $ with endpoints at the division points. Hence, the total number of squares of side length $ k $ contained in the lines forming the chessboard is $ (n - k + 1)^2 $. Therefore, we have the following formulas:
The number $ k(n) $ satisfies the inequality
Thus
Multiplying by $ - \frac{1}{n^3} $ the difference of the obtained inequality and $ n(n + 1)(2n + 1) $, we have:
The above inequality takes the form
where $ a_n = 1 - \frac{k(n)}{n} $.
We will prove that the sequence $ \left( 2a_n \left( a_n + \frac{1}{n} \right) \left( a_n + \frac{1}{2n} \right) \right) $ converges to the number $ 1 $. If this were not the case, then in view of inequality (*) and the fact that $ \displaystyle \lim_{n \to \infty} \left( 1 + \frac{1}{n} \right) \left( 1 + \frac{1}{2n} \right) = 1 $, we would have
Let us take $ n_0 $ so large that for every $ n \geq n_0 $ the conditions
are satisfied.
Since
we have the inequality
Based on the last inequality and (***), we obtain
This is contradictory to condition (**). The contradiction arose from the assumption that the number $ 1 $ is not the limit of the sequence $ 2a_n \left( a_n + \frac{1}{n} \right) \left( a_n + \frac{1}{2n} \right) $. Therefore, the limit of this sequence exists and is equal to $ 1 $. Similarly, we conclude that the sequence $ \left( 2a_n \left( a_n - \frac{1}{n} \right) \left( a_n - \frac{1}{2n} \right) \right) $ also converges to $ 1 $. Given the obvious inequality
we obtain, based on the theorem of three sequences, that
Since $ \frac{k(n)}{n} = 1 - a_n $ and $ \displaystyle \lim_{n \to \infty} a_n = \frac{1}{\sqrt[3]{2}} $, we have | \frac{\sqrt[3]{4}}{2} | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
XXXIX OM - III - Problem 6
Calculate the maximum volume of a tetrahedron contained within a hemisphere of radius 1. | Let us denote the given hemisphere by $H$, the whole sphere by $K$, and the circle forming the flat part of the boundary of $H$ by $E$. Let $O$ be any tetrahedron contained in $H$. Its interior is the intersection of four open half-spaces determined by the planes of the faces. The center of the sphere $K$ does not belong to the interior of the tetrahedron; hence it does not belong to at least one of these half-spaces. Therefore, there is a face $S$ of the tetrahedron $Q$ such that the opposite vertex of the tetrahedron and the center of the sphere $K$ lie on opposite sides of the plane of this face (or, in the limiting case, the center of the sphere lies on this plane).
Thus, $Q$ is contained in the smaller of the two parts (or in one of the two equal parts) into which the plane of the face $S$ divides the sphere $K$. Therefore, the height of the tetrahedron $Q$ dropped onto the face $S$ has a length not greater than $1$, so the volume of $Q$ does not exceed one third of the area of this face. The area of the face $S$, being a triangle, is not greater than the area of an equilateral triangle inscribed in the circle which is the section of the sphere $K$ by the plane of this face (see Note); and even more so, it is not greater than the area of an equilateral triangle inscribed in the great circle $E$. The latter area equals $3\sqrt{3}/4$. Therefore, the volume of $Q$ is less than or equal to $\sqrt{3}/4$.
In all the estimates mentioned, we can achieve equality by taking $O$ to be a tetrahedron whose base is an equilateral triangle inscribed in $E$, and the fourth vertex is placed at the farthest point from $E$ on the hemisphere $H$ (at the "north pole").
The number $\sqrt{3}/4$ is the sought maximum.
Note: For completeness, we will provide an elementary proof of the fact that among all triangles inscribed in a fixed circle of radius $r$, the one with the largest area is the equilateral triangle.
Let $ABC$ be any such triangle. By placing point $C$ at the midpoint of the larger of the two arcs into which points $A$ and $B$ divide the circle circumscribed around triangle $ABC$, we obtain an isosceles triangle $ABC$, acute or right, with an area not less than that of triangle $ABC$. Therefore, in searching for a triangle with the maximum area (inscribed in a given circle), we can limit our attention to the class of isosceles triangles without obtuse angles (inscribed in this circle).
If now $ABC$ is a triangle from this class ($|AC| = |BC|$), then denoting by $x$ the distance from side $AB$ to the center of the circle, we get the relationships: $|AB| = 2\sqrt{r^2 - x^2}$, $h_C = r + x$ (the height dropped from vertex $C$), and thus
We have used here the inequality between the geometric mean and the arithmetic mean of four numbers: $a_1 = a_2 = a_3 = r + x$, $a_4 = 3r - 3x$. This inequality becomes an equality if and only if these numbers are equal, i.e., for $x = r/2$. It remains to note that the last equality means that triangle $ABC$ is equilateral. | \frac{\sqrt{3}}{4} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
XLV OM - II - Task 4
Each vertex of a cube is assigned the number $ 1 $ or $ -1 $, and each face is assigned the product of the numbers assigned to the vertices of that face. Determine the set of values that the sum of the $ 14 $ numbers assigned to the faces and vertices can take. | Let's consider an arbitrary assignment of the numbers $1$ and $-1$ to the vertices of a cube; denote the sum of these numbers by $S_1$. Assign numbers to the faces according to a given rule; denote the sum of these numbers by $S_2$. The sum of all $14$ considered numbers is $S_1 + S_2$.
If we change the number at one vertex (it doesn't matter which one), this will affect the numbers assigned to three faces. The value of the sum $S_1$ will increase or decrease by $2$. The value of the sum $S_2$ will increase or decrease by $2$ or $6$. The total sum $S = S_1 + S_2$ will increase or decrease by $4$ or $8$, or remain unchanged.
If all vertices are assigned the number $1$, then all faces are also assigned the number $1$, and in this case $S = 8 + 6 = 14$. (This is, of course, the maximum possible value of the sum $S$.) From this configuration, any other can be reached by changing the numbers at the vertices one by one. According to the previous observation, at each step of this procedure, the sum $S$ will change by $\pm 4$, $\pm 8$, or $0$. Therefore, the values taken by the sum $S$ will differ from the initial value $14$ by multiples of the number $4$. The set of possible values is thus a subset of the set $\{14, 10, 6, 2, -2, -6, -10, -14\}$.
The number $-14$ can be immediately eliminated: we would need to have $-1$ at all vertices and all faces, but this is contradictory to the conditions of the problem.
It is also not possible to achieve the value $S = 10$. This would require $12$ ones to appear with a positive sign and two with a negative sign. If all vertices were assigned a positive one, then all faces would also be assigned a positive one. If exactly one vertex were assigned a negative one, then three faces would receive a negative sign. If, finally, exactly two vertices were assigned a negative sign, then some faces would also receive a negative sign. Therefore, the configuration "10 positives, 2 negatives" is not achievable in any way.
The range of possible values for $S$ is thus limited to the set
Of these six values, each can be achieved in various ways. Here are examples of configurations that realize these values:
If all vertices of the cube are assigned the number $+1$, then $S_1 = 8$, $S_2 = 6$, and $S = 14$.
If all vertices of the cube are assigned the number $-1$, then $S_1 = -8$, $S_2 = 6$, and $S = -2$.
If one vertex is assigned the number $+1$ and the rest $-1$, then $S_1 = -6$, $S_2 = 0$, and $S = -6$.
If one vertex is assigned the number $-1$ and the rest $+1$, then $S_1 = 6$, $S_2 = 0$, and $S = 6$.
If two opposite vertices of the cube are assigned the number $+1$ and the rest $-1$, then $S_1 = -4$, $S_2 = -6$, and $S = -10$.
If two opposite vertices of one face are assigned the number $-1$ and the rest of the vertices of the cube are assigned the number $+1$, then $S_1 = 4$, $S_2 = -2$, and $S = 2$. | {14,10,6,2,-2,-6,-10,-14}\setminus{10,-14}={14,6,2,-2,-6,-10} | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
XLVI OM - I - Zadanie 1
Wyznaczyć wszystkie pary $ (x,y) $ liczb naturalnych, dla których liczby $ \frac{x+1}{y} $ oraz $ \frac{y+1}{x} $ są naturalne.
|
Niech $ (x,y) $ będzie jedną z szukanych par. Liczby naturalne $ y \geq 1 $ oraz $ x \geq 1 $ są odpowiednio dzielnikami liczb $ x + 1 $ oraz $ y + 1 $. Zatem iloczyn $ xy $ jest dzielnikiem iloczynu $ (x + 1)(y+ 1) $, równego sumie $ xy + x + y + 1 $. Jest więc też dzielnikiem sumy $ x + y + 1 $, a zatem zachodzi nierówność $ xy \leq x + y + 1 $, czyli $ (x-1)(y -1) \leq 2 $. Wartość iloczynu $ (x-1)(y-1) $ może być w takim razie równa tylko $ 2 $, $ 1 $ lub $ 0 $.
W pierwszym przypadku jeden z czynników $ (x - 1) $ i $ (y- 1) $ jest równy $ 2 $, a drugi $ 1 $, czyli para $ (x,y) $ jest jedną z par $ (3,2) $ i $ (2,3) $.
W drugim przypadku mamy $ x -1 = y -1 = 1 $, czyli $ x = y = 2 $. Jednak para $ (x,y) = (2,2) $ nie spełnia warunku zadania (iloraz $ 3/2 $ nie jest liczbą naturalną).
W trzecim przypadku co najmniej jeden z czynników $ (x - 1) $ i $ (y- 1) $ jest zerem. Jeśli na przykład $ y - 1 = 0 $, czyli $ y = 1 $, to liczba $ x $, jako dzielnik sumy $ y + 1 = 2 $, musi być równa $ 1 $ lub $ 2 $; tak więc $ x = y = 1 $ lub $ y = 1 $, $ x = 2 $ lub - przez symetrię - $ x = 1 $, $ y = 2 $.
Rekapitulując, widzimy, że tylko następujące pary $ (x,y) $ mogą spełniać postawione warunki: $ (3,2) $, $ (2,3) $, $ (1,1) $, $ (2,1) $, $ (1,2) $ - i istotnie je spełniają; sprawdzenie jest natychmiastowe.
| (3,2),(2,3),(1,1),(2,1),(1,2) | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
XVIII OM - I - Zadanie 10
Trójka liczb całkowitych tworzy postęp geometryczny o ilorazie całkowitym. Gdy najmniejszą z nich zwiększymy o 9, powstanie postęp arytmetyczny. Jakie to liczby?
|
Poszukiwana trójka liczb ma postać $ (a, aq, aq^2) $, gdzie $ a $ i $ q $ są liczbami całkowitymi różnymi od zera. Rozróżnimy dwa przypadki.
a) Najmniejszą z liczb tej trójki jest $ a $ lub $ aq^2 $. Nową trójką liczb jest wtedy $ (a+9, aq, aq^2) $ lub $ (a, aq, aq^2+9) $; warunek, aby to był postęp arytmetyczny, wyraża równość $ 2aq = aq^2+a+9 $, którą możemy napisać w postaci
Stąd wynika, że
bądź też
Otrzymujemy trójki liczb: $ ( - 1, -4, -16) $, $ ( - 1, 2, -4) $, $ ( - 9, -18, -36) $; stwierdzamy, że są one istotnie rozwiązaniami zadania.
b) Najmniejszą z liczb $ a, aq, aq^2 $ jest $ aq $. Nową trójkę tworzą wtedy liczby $ a, aq+ 9, aq^2 $; warunek, aby to był postęp arytmetyczny wyraża równość $ 2(aq+9) = aq^2+a $, której nadamy postać
Z tej równości wynika, że
bądź też
Otrzymujemy trójki liczb: $ (2, 8, 32) $, $ (2, -4, 8) $, $ (18, 36, 72) $, z których tylko druga spełnia warunki zadania.
Zadanie ma więc cztery rozwiązania: $ ( - 1, -4, -16) $, $ ( -1,2, -4) $, $ (-9, -18, -36) $, $ (2, -4, 8) $.
| (-1,-4,-16),(-1,2,-4),(-9,-18,-36),(2,-4,8) | Algebra | math-word-problem | Yes | Yes | olympiads | false |
LV OM - II - Task 4
Determine all positive integers $ n $ that have exactly $ \sqrt{n} $ positive divisors. | The number $ n = 1 $ satisfies the conditions of the problem. Let's assume, for the rest of the solution, that $ n > 1 $.
From the conditions of the problem, it follows that $ n = k^2 $ for some positive integer $ k $. The number of positive divisors of $ n $ that are less than $ k $ is equal to the number of its divisors that are greater than $ k $. Indeed: to each divisor $ d < k $ of $ n $, there corresponds a divisor $ n/d $ of $ n $, which is greater than $ k $. Additionally, the number $ k $ itself is a divisor of $ n $, which implies that $ n $ has an odd number of divisors. Therefore, $ k $, and thus $ n $, is an odd number.
The problem thus reduces to finding such odd numbers $ n = k^2 $ $ (n > 1) $, for which the number of divisors less than $ k $ is equal to $ \frac{1}{2} (k-1) $.
Since $ k^2 $ is an odd number, no even number is a divisor of $ k^2 $. Therefore, for the number of divisors less than $ k $ of $ k^2 $ to be equal to $ \frac{1}{2} (k-1) $, every odd number less than $ k $ must be a divisor of $ k^2 $. In particular, $ k^2 $ must be divisible by $ k-2 $. Since $ k^2 = (k-2)(k+2)+4 $, the number $ k-2 $ is an odd divisor of 4. This means that $ k - 2 = 1 $, or $ k = 3 $.
We directly verify that the number $ n = 3^2 = 9 $ satisfies the conditions of the problem. Therefore, the sought numbers are $ n = 1 $ and $ n = 9 $. | n=1n=9 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
XXVII OM - I - Zadanie 4
Samolot leci bez zatrzymywania się po najkrótszej drodze z Oslo do miasta $ X $ leżącego na równiku w Ameryce Południowej. Z Oslo startuje dokładnie w kierunku zachodnim. Wiedząc, że współrzędne geograficzne Oslo są : $ 59^{\circ}55 szerokości północnej i $ 10^{\circ}43 długości wschodniej, obliczyć współrzędne geograficzne miasta $ X $. Jakie to miasto? Obliczyć długość drogi samolotu z dokładnością do 100 km. Zakładamy, że Ziemia jest idealną kulą o długości równika 40 000 km oraz, że samolot leci na wysokości nie większej niż 10 km.
|
Najkrótsza droga na powierzchni kuli łącząca dwa punkty tej kuli jest łukiem koła wielkiego, tzn. łukiem okręgu, którego środkiem jest środek kuli. Zatem samolot leci po łuku koła wielkiego przechodzącego przez Oslo. Przy tym Oslo jest najbardziej na północ wysuniętym punktem tego koła wielkiego, ponieważ samolot startuje w kierunku zachodnim. Wynika stąd, że łuk o końcach w Oslo i mieście $ X $ jest czwartą częścią koła wielkiego. Długość tego łuku jest więc równa $ 10 000 $ km, a długości geograficzne miasta $ X $ i Osio różnią się o $ 90^\circ $. Zatem miasto $ X $ leży na równiku w punkcie mającym $ 79^\circ 17 długości zachodniej. Przekonujemy się za pomocą mapy, że jedynym większym miastem posiadającym lotnisko, w pobliżu tego punktu jest stolica Ekwadoru Quito.
Jeżeli uwzględnimy, że droga samolotu znajduje się nie na powierzchni ziemi, lecz np. $ 10 $ km nad ziemią, to otrzymamy, że długość tej drogi jest równa $ \frac{1}{4} [2\pi (R + 10)] = \frac{1}{4} 2\pi R + 5\pi \approx 10 000 + 15 $ km, gdzie $ R $ jest długością promienia Ziemi.
Uwaga: Szerokość geograficzna Oslo nie ma wpływu na rozwiązanie. Gdyby więc samolot startował z dowolnego punktu Ziemi, o długości geograficznej wschodniej $ 10^\circ 43 i spełnione były pozostałe warunki zadania, to wylądowałby w Quito po przebyciu drogi długości około $ 10 000 $ km.
| Quito,10000 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
XLIII OM - I - Problem 2
In square $ABCD$ with side length $1$, point $E$ lies on side $BC$, point $F$ lies on side $CD$, the measures of angles $EAB$ and $EAF$ are $20^{\circ}$ and $45^{\circ}$, respectively. Calculate the height of triangle $AEF$ drawn from vertex $A$. | The measure of angle $ FAD $ is $ 90^\circ - (20^\circ + 45^\circ) = 25^\circ $. From point $ A $, we draw a ray forming angles of $ 20^\circ $ and $ 25^\circ $ with rays $ AE $ and $ AF $, respectively, and we place a segment $ AG $ of length $ 1 $ on it (figure 2).
From the equality $ |AG| =|AB| = 1 $, $ | \measuredangle EAG| = | \measuredangle EAB| = 20^\circ $, it follows that triangle $ EAG $ is congruent to $ EAB $.
Similarly, from the equality $ |AG| = |AD| = 1 $, $ | \measuredangle FAG| = | \measuredangle FAD| = 25^\circ $, it follows that triangle $ FAG $ is congruent to $ FAD $.
This means that
point $ G $ lies on segment $ EF $ and is the foot of the altitude of triangle $ AEF $ drawn from vertex $ A $. Its length $ |AG| = 1 $. | 1 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
I OM - B - Task 3
Someone has an unbalanced two-pan scale (i.e., a scale
whose arms are unequal). Wanting to weigh 2 kg of sugar, they proceed
as follows: they place a 1 kg weight on the left pan of the scale,
and pour sugar onto the right pan until it balances; then:
after emptying both pans, they place the 1 kg weight on the right pan, and pour sugar onto the left pan until it balances. Do the two
amounts of sugar weighed in this way together weigh less, or more, or exactly
2 kg? | Let's denote the amount of sugar weighed for the first time by $ x $, and for the second time by $ y $. The lengths of the arms of the balance are $ p $ and $ q $, where $ p \neq q $.
According to the lever law (Fig. l) we have:
Therefore,
since
Answer: More than 2 kg of sugar was weighed in total. | More\than\2\ | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
XIX OM - III - Problem 1
What is the largest number of regions into which a plane can be divided by $ n $ pairs of parallel lines? | Let $ f(n) $ denote the greatest number of regions into which $ n $ pairs of parallel lines can divide the plane.
Consider $ k + 1 $ pairs of parallel lines on the plane.
Suppose that $ (p_1, q_1), (p_1, q_2),\ldots (p_k,q_k) $ divide the plane into $ l $ regions, and that the line $ p_{k+1} $ intersects the lines of these $ k $ pairs at $ r $ points, and the line $ q_{k+1} $ at $ s $ points. Then $ 0 \leq r \leq 2k $, $ 0 \leq s \leq 2k $, with the equalities $ r = 2k $, $ s = 2k $ holding precisely when both the line $ p_{k+1} $ and the line $ q_{k+1} $ intersect each of the lines $ p_1, q_1, p_2, q_2, \ldots, p_k,q_k $ but do not pass through any of the intersection points of these lines.
These $ r $ points divide the line $ p_{k+1} $ into $ r+1 $ segments. Each of these segments is either a line segment or a ray, and when $ r = 0 $ - the entire line, lies in one of the $ l $ regions into which the lines $ p_1, q_1, p_2, q_2, \ldots, p_k, q_k $ divide the plane (with each segment lying in a different region) and splits it into two regions. The lines $ p_1, q_1, p_2, q_2,\ldots,p_k, q_k $ and $ p_{k+1} $ thus divide the plane into $ l + r + 1 $ regions. Similarly, the $ s $ points on the line $ q_{k+1} $ divide this line into $ s + 1 $ segments, each of which splits one of the previous $ l + r + 1 $ regions into two regions. All the lines $ p_1, q_1, p_2, q_2, \ldots, p_k, q_k, p_{k+1}, q_{k + 1} $ thus divide the plane into $ l + r + s + 2 $ regions.
This number is greatest when the values of $ l $, $ r $, and $ s $ are greatest, i.e., when $ l=f(k) $, $ r = 2k $, $ s = 2k $. Therefore,
Indeed, $ f(1) = 3 $; from formula (1) we obtain the subsequent values $ f(2) = 3 + 4 + 2=9 $, $ f(3) = 9 + 8 + 2= 19 $, etc.
The value of $ f(n) $ for any natural number $ n $ can be calculated by substituting into (1) $ k = 1, 2, \ldots, n - 1 $ and adding the resulting equations
From this we obtain
and after simplification
| 2n^2-n+1 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
XLV OM - II - Task 1
Determine all polynomials $ P(x) $ of degree at most fifth with real coefficients, having the property that the polynomial $ P(x) + 1 $ is divisible by $ (x - 1)^3 $ and the polynomial $ P(x) - 1 $ is divisible by $ (x + 1)^3 $. | Suppose that the polynomial $ P(x) $ satisfies the given conditions. By assumption, there exist polynomials $ Q(x) $ and $ R(x) $, of degree at most two, satisfying for all real values of the variable $ x $ the equations
The coefficient of $ x^2 $ in each of the polynomials $ Q(x) $, $ R(x) $ is equal to the coefficient of $ x^5 $ in the polynomial $ P(x) $ (we do not exclude the possibility that it is zero). The polynomials $ Q(x) $ and $ R(x) $ therefore have the form
Transforming the first of the above equations,
Transforming the second, we obtain, analogously,
Subtracting the obtained relations (the second from the first), we get a constant on the left side, equal to $ 2 $. Therefore, the polynomials on the right sides of the above relations must have equal coefficients for each of the positive powers of the variable $ x $, and their constant terms must differ by $ 2 $:
We thus have a system of $ 5 $ equations with $ 5 $ unknowns. From the second and fifth equations, we get the relationship
and from the third and fifth -
Therefore, by adding and subtracting the sides,
From the first equation of the system, we have $ b - p = 6a $. Thus, $ 2a - 6 = 3(b - p) = 18a $, from which
Substituting these expressions into the fourth equation of the system, we determine $ c = -1 $. Therefore,
If the polynomial $ P(x) $ exists, then it must be given by each of the following two formulas:
Multiplying out, we obtain, from each of these formulas,
From the form of these formulas, it follows that the obtained polynomial indeed satisfies the conditions set in the problem.
Note 1. When solving the system of equations by elimination, we did not worry about writing an equivalent system of equations at each step. Therefore, at the end of the solution, it was necessary to verify that both proposed formulas indeed give the same polynomial $ P(x) $. | P(x)=-\frac{1}{8}x^5+\frac{5}{8}x^3-\frac{15}{8}x | Algebra | math-word-problem | Yes | Yes | olympiads | false |
XVIII OM - I - Problem 5
Find such natural numbers $ p $ and $ q $, so that the roots of the equations $ x^2 - qx + p = 0 $ and $ x^2 - px + q = 0 $ are natural numbers. | Let $ x_1 $, $ x_2 $ and $ y_1 $, $ y_2 $ denote the roots of the given equations, respectively. Then the following equalities hold:
From equalities (1) and (2), it follows that
Hence
Since each of the numbers $ x_1-1 $, $ x_2-1 $, $ y_1-1 $, $ y_2-1 $ is $ \geq 0 $, one of the following cases must hold:
a) $ (x_1-1)(x_2-1) = 1,\ (y_1-1)(y_2-1) = 1; $
in this case, $ x_1-1 = x_2-1 = 1 $, so $ x_1 = x_2 = 2 $, and thus $ p = q = 4 $.
b) $ (x_1-1)(x_2-1) = 2,\ (y_1-1)(y_2-1) = 1; $
then $ x_1-1 = 1 $, $ x_2-1 = 2 $ or $ x_1-1 = 2 $, $ x_2-1 = 1 $, i.e., $ x_1 = 2 $, $ x_2 = 3 $ or $ x_1 = 3 $, $ x_2 = 2 $.
Hence $ p = 6 $, $ q = 5 $.
c) $ (x_1-1)(x_2-1) = 0, \ (y_1-1)(y_2-1) = 2; $
similarly to b), we obtain $ y_1 = 2 $, $ y_2 = 3 $ or $ y_1 = 3 $, $ y_2 = 2 $, and thus $ p = 5 $, $ q = 6 $. | p=4,\p= | Algebra | math-word-problem | Yes | Yes | olympiads | false |
LIX OM - I - Task 12
Given an integer $ m \geqslant 2 $. Determine the smallest such integer
$ n \geqslant m $, such that for any partition of the set $ \{m,m+1,\dots ,n\} $ into two subsets, at least one of
these subsets contains numbers $ a, b, c $ (not necessarily distinct), such that $ ab = c $. | Answer: $ n = m^5 $.
Assume that there is a partition of the set $ \{m,m+1,\dots ,m^5\} $ into two subsets $ S $ and $ T $,
neither of which contains two numbers (not necessarily distinct) along with their product. Suppose,
moreover, that $ m \in S $. The number $ m^2 = m \cdot m $ is the product of two elements of the set $ S $, so we must have
$ m^2 \in T $. From this, $ m^4= m^2\cdot m^2 \in S $. We see that $ m, m^4 \in S $, which means that the number
$ m^5= m \cdot m^4 $ belongs to the set $ T $. On the other hand, the numbers $ m, m^4 $ are elements of the set $ S $,
so the number $ m^3 $ cannot belong to this set. Therefore, $ m, m^3, m^5 \in T $.
Thus, we have $ m^2, m^3, m^5 \in T $, which is a contradiction.
On the other hand, if we divide the set $ \{m,m+1,\dots ,m^5 -1\} $ into the following two subsets:
then the product of two elements (not necessarily distinct) of each of these subsets is not an element of that
subset. Indeed, the set $ T $ contains numbers not less than $ m^2 $, so the product of any two
of them is at least $ m^4 $, while the largest element of this set is the number $ m^4 -1 $. Meanwhile, the set $ S $ contains numbers not less than $ m $, so the product of any two is at least $ m $.
This product is less than $ m^4 $ if both numbers are less than $ m^2 $, or is at least
$ m^5 $ if one of the numbers is at least $ m^4 $, and in both cases it does not belong to the set $ S $.
We see, therefore, that the number $ n = m^5 -1 $ does not satisfy the conditions of the problem. Even more so, numbers
$ n < m^5 - 1 $ do not satisfy these conditions, as it is sufficient to remove from each of the sets $ S, T $ formed for the value
$ m^5 - 1 $ the numbers greater than $ n $. Therefore, the sought smallest value is $ n = m^5 $. | ^5 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
XV OM - I - Problem 10
Find the $ n $-th term of the sequence of numbers $ a_1, a_2, a_n, \ldots $, where $ a_1 = 1 $, $ a_2 = 3 $, $ a_3 = 6 $, and for every natural number $ k $ | We can write equality (1) in the form
Let's denote $ a_{i+1} - a_i = r_i $ for $ i = 1, 2, 3, \ldots $; according to the above equality, $ r_{k+2} - 2r_{k+1} + r_k = 0 $, from which $ r_{k+2} - r_{k+1}= r_{k+1} - r_k $.
The sequence of differences $ r_k $ is therefore an arithmetic progression. Since $ r_1 = a_2 - a_1 = 2 $ and $ r_2 = a_3 - a_2 = 3 $, the difference of this progression is $ r_2 - r_1 = 1 $. Hence, for every natural $ k $, we have $ r_k = r_1 + (k - 1) \cdot 1 = k + 1 $, thus
for every natural $ k $. From this, it easily follows (e.g., by induction) that $ a_n $ is the sum of natural numbers from $ 1 $ to $ n $:
| \frac{n(n+1)}{2} | Algebra | math-word-problem | Yes | Yes | olympiads | false |
XLVI OM - III - Problem 1
Determine the number of subsets of the set $ \{1,2, \ldots , 2n\} $ in which the equation $ x + y = 2n+1 $ has no solutions. | A set $ A $, contained in the set $ \{1,2,\ldots,2n\} $, will be called good if it has the required property; that is, if the equation $ x + y = 2n + 1 $ has no solution $ x,y \in A $.
The set $ \{1,2,\ldots,2n\} $ is the union of the following disjoint two-element subsets (i.e., pairs of numbers):
the symbol $ P_j $ denotes the pair $ \{j, 2n+1-j\} $.
A subset $ A $ of the set $ \{1,2,\ldots,2n\} $ is good if and only if it does not contain any pair $ P_j $, or equivalently, if for every number $ j \in \{1,2,\ldots,n\} $ the intersection $ P_j \cap A $ is either the empty set, or the one-element set $ \{j\} $, or the one-element set $ \{2n+1-j\} $. A good set $ A $ is thus uniquely determined by choosing one of these three options for each $ j \in \{1,2,\ldots,n\} $. Hence, the number of good sets is $ 3^n $. | 3^n | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
XLIX OM - I - Problem 4
Given a positive number $ a $. Determine all real numbers $ c $ that have the following property: for every pair of positive numbers $ x $, $ y $, the inequality $ (c-1)x^{a+1} \leq (cy - x)y^a $ is satisfied. | Assume that a real number $ c $ has the considered property:
Substituting $ y=tx $ and dividing both sides by $ x^{a+1} $, we obtain the relation
Notice that the converse is also true: condition (2) implies (1). Suppose that $ c $ is a real number satisfying condition (2). Let $ x $, $ y $ be any positive numbers. In inequality (2), substitute $ t = y/x $, multiply both sides by $ x^{a+1} $, and we get inequality (1).
Therefore, conditions (1) and (2) are equivalent. Fix a real number $ c $ and consider the function $ f:(0,\ \infty)\to \mathbb{R} $ given by
of course $ f(1) = c - 1 $ and
If condition (2) (equivalent to condition (1)) is satisfied for the considered number $ c $, then the function $ f $ has a minimum at the point $ t = 1 $, so $ f'(1) = 0 $, which means $ c(a+1)-a= 0 $; hence $ c=\frac{a}{a+1} $.
Conversely, if in the definition of the function $ f $ we take $ c= \frac{a}{a+1} $, then
therefore, the function $ f $ is decreasing in the interval $ (0;\ 1 \rangle $ and increasing in the interval $ \langle 1;\ \infty) $. At the point $ t = 1 $, it therefore attains its minimum value. In other words, $ f(t)\geq f(1) $ for $ t>0 $, which means that condition (2) (equivalent to condition (1)) is satisfied.
Conclusion: for a given positive number $ a $, the only number $ c $ having the postulated property is $ c=\frac{a}{a+1} $. | \frac{}{+1} | Inequalities | math-word-problem | Yes | Yes | olympiads | false |
L OM - I - Problem 11
In an urn, there are two balls: a white one and a black one. Additionally, we have 50 white balls and 50 black balls at our disposal. We perform the following action 50 times: we draw a ball from the urn, and then return it to the urn along with one more ball of the same color as the drawn ball. After completing these actions, we have 52 balls in the urn. What is the most probable number of white balls in the urn? | Let $ P(k,n) $, where $ 1 \leq k\leq n-1 $, denote the probability of the event that when there are $ n $ balls in the urn, exactly $ k $ of them are white. Then
Using the above relationships, we prove by induction (with respect to $ n $) that $ P(k,n) = 1/(n-1) $ for $ k = 1,2,\ldots,n-1 $. In particular
Therefore, each possible number of white balls after $ 50 $ draws (from $ 1 $ to $ 51 $) is equally likely. | 51 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
XLVI OM - III - Problem 2
The diagonals of a convex pentagon divide this pentagon into a pentagon and ten triangles. What is the maximum possible number of triangles with equal areas? | om46_3r_img_12.jpg
Let's denote the considered pentagon by $ABCDE$, and the pentagon formed by the intersection points of the diagonals by $KLMNP$ so that the following triangles are those mentioned in the problem:
$\Delta_0$: triangle $LEM$; $\quad \Delta_1$: triangle $EMA$;
$\Delta_2$: triangle $MAN$; $\quad \Delta_3$: triangle $ANB$;
$\Delta_4$: triangle $NBP$; $\quad \Delta_5$: triangle $BPC$;
$\Delta_6$: triangle $PCK$; $\quad \Delta_7$: triangle $CKD$;
$\Delta_8$: triangle $KDL$; $\quad \Delta_9$: triangle $DLE$
(figure 12). We will start by proving the implication:
We assume that the numbering of the triangles is cyclic (that is, we assume: $\Delta_{-1} = \Delta_9$; $\Delta_{10} = \Delta_0$).
Suppose, for example, that triangles $\Delta_4$, $\Delta_5$, and $\Delta_6$ have equal areas. From the equality of the areas of triangles $NBP$ and $BPC$, it follows that segment $BP$ is a median in triangle $BCN$; from the equality of the areas of triangles $BPC$ and $PCK$, it follows that segment $CP$ is a median in triangle $BCK$. Point $P$ would then be the common midpoint of diagonals $BK$ and $CN$ of quadrilateral $BCKN$, which should therefore be a parallelogram - but the lines $BN$ and $CK$ intersect at point $E$. This is a contradiction; implication (1) is proven.
We proceed to the main solution. The example of a regular pentagon shows that it is possible to obtain five triangles $\Delta_i$ with equal areas. We will prove that it is not possible to obtain seven such triangles.
Suppose, therefore, that there exists a seven-element set $Z$, contained in the set $\{0,1,\ldots,9\}$, such that triangles $\Delta_i$ with indices $i \in Z$ have equal areas. Let $k$, $l$, $m$ be three numbers from the set $\{0,1,\ldots,9\}$, not belonging to $Z$. Consider all triples of consecutive indices:
where, as before, the addition $i \pm 1$ should be understood modulo $10$. Each number from the set $\{0,1,\ldots,9\}$ belongs to exactly three triples $T_i$. This applies, in particular, to each of the numbers $k$, $l$, $m$. Therefore, the three-element set $\{k,l,m\}$ has a non-empty intersection with at most nine triples $T_i$. At least one triple $T_j$ remains that does not contain any of the numbers $k$, $l$, $m$, and is therefore contained in the set $Z$. The number $j$ must be even, according to observation (1).
Without loss of generality, assume that $j = 2$. This means that the numbers $1$, $2$, $3$ belong to the set $Z$. Therefore, the numbers $0$ and $4$ cannot belong to it (since, again by observation (1), the triples $\{0,1,2\}$ and $\{2,3,4\}$ are excluded); thus, one of the numbers $k$, $l$, $m$ equals $0$, and another equals $4$. The third of these numbers must be part of the triple $\{6,7,8\}$ (which otherwise would be contained in the set $Z$, contrary to implication (1)). The roles of the numbers $6$ and $8$ are symmetric in this context. We therefore have to consider two essentially different cases:
The set $Z$, respectively, has one of the following forms:
Let $S_i$ be the area of triangle $\Delta_i$ (for $i = 0,1,\ldots,9$). We will show that the implications hold:
This will be a proof that none of the seven-element sets $Z$ listed above can be the set of indices of triangles with equal areas. According to earlier statements, this will also justify the conclusion that among the ten triangles $\Delta_i$, there are never seven triangles with the same area.
Proof of implication (2). From the given equalities of areas:
and
it follows (respectively) that points $N$ and $P$ are the midpoints of segments $BM$ and $BK$, and points $M$ and $L$ are the midpoints of segments $EN$ and $EK$ (figure 13).
Thus, segment $NP$ connects the midpoints of two sides of triangle $BMK$, and segment $ML$ connects the midpoints of two sides of triangle $ENK$, and therefore
- and
The obtained parallelism relations show that quadrilateral $AMKN$ is a parallelogram; hence $|MK| = |AN|$. Line $MK$ is parallel to $NC$, so triangles $ENC$ and $EMK$ are similar in the ratio $|EN| : |EM| = 2$. Therefore, $|NC| = 2 \cdot |MK|$, and consequently
The segments $PC$ and $AN$, lying on the same line, are the bases of triangles $ANB$ and $BPC$ with a common vertex $B$. The ratio of the lengths of these bases is therefore also the ratio of the areas of the triangles: area($BPC$) : area($ANB$) = $3 : 2$, i.e., $S_5 : S_3 = 3 : 2$. The conclusion of implication (2) is thus proven.
om46_3r_img_13.jpg
om46_3r_img_14.jpg
Proof of implication (3). The given equalities of the areas of triangles:
and
show that points $M$ and $N$ divide segment $EB$ into three equal parts, and similarly, points $L$ and $K$ divide segment $EC$ into three equal parts. Therefore, line $BC$ is parallel to $ML$ (i.e., to $AM$). Since $N$ is the midpoint of segment $BM$, triangles $AMN$ and $CBN$ are similar in the ratio $-1$ (figure 14). Hence, area($AMN$) = area($CBN$) $> $ area($CBP$), i.e., $S_2 > S_5$. This completes the proof of implication (3), and thus also the proof of the general theorem: it is not possible to have seven triangles $\Delta_i$ with equal areas.
The reasoning conducted in the last case (proof of (3)) also provides a hint on how to obtain six triangles $\Delta_i$ with equal areas. We take any isosceles triangle $BCE$ where $|EB| = |EC|$. On the sides $EB$ and $EC$, we find points $M$ and $N$ and $L$ and $K$, dividing these sides into three equal parts:
The intersection points of line $ML$ with lines $CN$ and $BK$ are denoted by $A$ and $D$, respectively (figure 14 can still serve as an illustration; one only needs to imagine moving point $E$ to the perpendicular bisector of side $BC$ and appropriately repositioning the other points). The equalities (4) and (5) then hold; and thanks to the assumption that triangle $BCE$ is isosceles (and the resulting symmetry of the entire configuration), all areas appearing in relations (4) and (5) are equal.
Conclusion: six of the triangles $\Delta_i$ can have equal areas, and this number cannot be increased. | 6 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
XXVII OM - III - Task 5
A fishing vessel is fishing in the territorial waters of a foreign state without permission. Each cast of the net results in a catch of the same value. During each subsequent cast, the probability of the vessel being intercepted by the border guard is $ \frac{1}{k} $, where $ k $ is a fixed natural number. We assume that the event of the vessel being intercepted or not intercepted during each subsequent cast is independent of the previous course of the fishing. If intercepted by the border guard, the entire catch is confiscated, and further fishing is impossible. The captain plans to return after the $ n $-th cast. Considering the risk of interception, the profit from fishing is a random variable. Find the number $ n $ for which the expected value of the profit is maximized. | The probability of an event where a ship is not caught with a certain cast of the net is $1 - \frac{1}{k}$. Since events involving catching or not catching a ship with each subsequent cast of the net are independent, the probability of the event where the ship is not caught after $m$-times casting the net is $\left(1 - \frac{1}{k}\right)^n$. The expected value of the profit from $n$-times casting the net is therefore equal to
where $w$ is the value of the profit from one cast of the net.
The task is to investigate for which natural number $n$ the function $f$ attains its maximum value.
From (1), it follows that
Since the inequality $\displaystyle 1 + \frac{(k-1)-n}{kn} \geq 1$ is equivalent to the inequality $(k - 1) - n \geq 0$, which is $n \leq k - 1$, we have
Therefore, the function $f$ attains its maximum value twice at $n = k - 1$ and $n = k$. | n=k-1n=k | Algebra | math-word-problem | Yes | Yes | olympiads | false |
XXXVI OM - I - Problem 6
Calculate the lengths of the parallel sides of a trapezoid given the lengths of the other sides and the diagonals. | Let $ABCD$ be the considered trapezoid, $AB\parallel CD$, $|AB| = a$, $|BC| = b$, $|CD| = c$, $|DA| = d$, $|AC| = p$, $|BD| = q$ (Figure 2). Given $b$, $d$, $p$, $q$, we need to find $a$ and $c$.
om36_1r_img_2.jpg
First, note that if $p = q$, then it must be $b = d < p$ and in this case, the problem does not have a unique solution: there are infinitely many isosceles trapezoids with side length $b$ and diagonal length $p$. More precisely, if $a$ is any number satisfying the inequality $p - b < a < p + b$, then there exists a triangle $ABC$ where $|AB| = a$, $|BC| = b$, $|CA| = p$, and the desired trapezoid $ABCD$ is obtained by taking as vertex $D$ the image of point $C$ under the axial symmetry with respect to the perpendicular bisector of segment $AB$. Denoting by $C'$ the projection of point $C$ onto line $AB$ and setting $x = |AC'|$, $y = |BC'|$, $h = |CC'|$, we see (Figure 3) that if $C' < A$, then $a = x - y$, $c = x + y$, and if $C' > A$, then $a = x - y$, $c = x + y$. In both cases, $ac = x^2 - y^2 = (p^2 - h^2) - (b^2 - h^2) = p^2 - b^2$. Thus, when $b = d < p = q$, the solution to the problem is any pair of numbers $a, c$ such that $p - b < a < p + b$, $c = (p^2 - b^2) / a$.
om36_1r_img_3.jpg
Let us assume from now on that $p \neq q$ (the trapezoid is not isosceles). Triangles $ABC$ and $ABD$ have a common base and equal heights, and thus equal areas. We express these areas in terms of the side lengths, using Heron's formula:
\[
\text{Area of } \triangle ABC = \sqrt{s(s-a)(s-b)(s-p)}
\]
where $s = \frac{a + b + p}{2}$, and similarly,
\[
\text{Area of } \triangle ABD = \sqrt{t(t-a)(t-d)(t-q)}
\]
where $t = \frac{a + d + q}{2}$.
Equating the right-hand sides of the obtained equalities, we see that
\[
\sqrt{s(s-a)(s-b)(s-p)} = \sqrt{t(t-a)(t-d)(t-q)}
\]
If the expression in the parentheses on the left side were zero, then one of the factors on the right side would have to be zero; we would then have the alternative system of equations:
\[
\begin{cases}
s - a = 0 \\
s - b = 0 \\
s - p = 0
\end{cases}
\quad \text{or} \quad
\begin{cases}
t - a = 0 \\
t - d = 0 \\
t - q = 0
\end{cases}
\]
In the first case, adding and subtracting the equations of the system, we get $b = d$ and $p = q$, contrary to the previous assumption. In the second case, we get $b = q$ and $d = p$, which is not possible (points $C$ and $D$ would have to coincide). Therefore, $b^2 - d^2 + p^2 - q^2 \neq 0$, so
\[
\frac{(s-a)(s-b)(s-p)}{s} = \frac{(t-a)(t-d)(t-q)}{t}
\]
The left side is a positive number, so the right side is also positive, and thus ultimately
\[
a = \frac{2(p^2 - q^2)}{b^2 - d^2 + p^2 - q^2}
\]
We find the value of $c$ by swapping $p$ and $q$ in the obtained formula for $a$ (this corresponds to repeating the conducted reasoning, starting from the equality of the areas of triangles $CDA$ and $CDB$, with sides $c$, $d$, $p$ and $c$, $b$, $q$, respectively). Thus,
\[
c = \frac{2(q^2 - p^2)}{b^2 - d^2 + q^2 - p^2}
\]
Note. From the formulation of the problem, it follows implicitly that the considered trapezoid actually exists. Therefore, there is no need to seek conditions that the given quantities $b$, $d$, $p$, $q$ should satisfy for the found solution to make geometric sense. | \frac{2(p^2-q^2)}{b^2-^2+p^2-q^2},\quad\frac{2(q^2-p^2)}{b^2-^2+q^2-p^2} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
XXXVI OM - II - Problem 3
Let $ L $ be the set of all broken lines $ ABCDA $, where $ A, B, C, D $ are distinct vertices of a fixed regular 1985-gon. A broken line is randomly chosen from the set $ L $. Calculate the probability that it is the boundary of a convex quadrilateral. | Let $ W $ be the set of all vertices of a given regular polygon. Each broken line from the set $ L $ can be associated with a set of its vertices, i.e., a certain four-point subset of the set $ W $. Conversely, every four points from $ W $ are the set of vertices of exactly three different broken lines from the set $ L $ (Figure 6 shows three possible ways to connect these points with segments); of these three broken lines, one is the boundary of a convex quadrilateral. Thus, all broken lines in the set $ L $ can be grouped into triples such that in each triple one and only one is the boundary of a convex quadrilateral. The sought probability is therefore $ 1/3 $. | \frac{1}{3} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
XXVIII - II - Task 6
What is the maximum number of parts that the edges of $ n $ squares can divide a plane into? | The common part of the boundaries of two squares is either a finite set of points (and in this case, there are at most $8$ points, since each side of one square can intersect the boundary of the other square in at most two points), or it contains a segment (and in this case, it is a segment, the union of two segments - parallel or perpendicular, or is the union of a segment and a point - see Fig. 11). In each case, this common part consists of at most eight connected parts, each of which is a point, a segment, or the union of two segments with a common end.
Let there be $n$ squares $K_1, K_2, \ldots, K_n$ on the plane, where $n$ is some natural number. Suppose the boundaries of these squares divide the plane into $a_n$ parts. We now draw the $(n + 1)$-th square $K_{n+1}$. The boundary of each of the $n$ given squares $K_i$ defines on the boundary of the square $K_{n+1}$ a figure $F_i$ composed of at most eight connected parts. The figure $F = F_1 \cup F_2 \cup \ldots \cup F_n$ thus consists of at most $8n$ connected parts (which are points, segments, or unions of segments with common ends). Therefore, the difference between the boundary of the square $K_{n+1}$ and the figure $F$ consists of at most $8n$ connected parts, which are segments or unions of segments. Each such part of the boundary of the square $K_{n+1}$ divides into two parts one of the parts of the plane obtained after drawing the squares $K_1, K_2, \ldots, K_n$. Therefore, the number $a_{n+1}$ of parts into which the boundaries of the squares $K_1, K_2, \ldots, K_n, K_{n+1}$ divide the plane satisfies
We obviously have $a_1 = 2$, since the boundary of one square divides the plane into two parts. Therefore, from formula (1), by easy induction, it follows that for any natural number $k$,
where $a_k$ is the number of parts into which the boundaries of some $k$ squares divide the plane. Transforming the right-hand side of this formula, we get
or, finally,
We will now prove that for any natural number $n$ there exist $n$ squares whose boundaries divide the plane into $(2n - 1)^2 + 1$ parts, i.e., equality holds in formula (2). Consider, for example, any $n + 1$ squares $K_1, K_2, \ldots, K_n, K_{n+1}$ inscribed in a fixed circle $O$. Note that there is no point that belongs simultaneously to the boundaries of three of the considered squares. The sides of these squares have the same lengths and are chords of the given circle. And through no point inside the circle (different from its center) do three chords of the same length pass.
On the arc of the circle $O$ connecting two consecutive vertices $A$ and $B$ of the square $K_{n+1}$, there lies exactly one vertex of the square $K_j$ for $1 \leq j \leq n$. Therefore, any side $\overline{AB}$ of the square $K_{n+1}$ intersects the boundary of the square $K_j$ in two points, and the boundary of the square $K_{n+1}$ intersects the boundary of the square $K_j$ in eight points. From the initial remark, it follows that for $j = 1, 2, \ldots, n$, we obtain pairwise disjoint eight-point sets in the intersection of the boundary of the square $K_j$ with the boundary of the square $K_{n+1}$. Thus, on the boundary of the square $K_{n+1}$, we have $8n$ points belonging to the union of the boundaries of the squares $K_1, K_2, \ldots, K_n$. These points determine $8n$ connected figures on the boundary of the square $K_{n+1}$, which are segments or unions of segments with a common end. Each of these figures divides into two parts one of the parts of the plane obtained after drawing the squares $K_1, K_2, \ldots, K_n$. Therefore, we have the relationship $a_{n+1} = a_n + 8n$. Hence, given $a_1 = 2$, by easy induction, it follows, similarly as before, that for any natural number $k$ and $k$ squares inscribed in a fixed circle, the formula
We have thus proved that the maximum number of parts into which the boundaries of $n$ squares can divide the plane is equal to $(2n - 1)^2 + 1$.
Note 1. In the given solution, we did not use the assumption that the considered figures are squares in an essential way. If they were rectangles or even any convex quadrilaterals, the reasoning would proceed in the same way. Therefore, the maximum number of parts into which the boundaries of $n$ convex quadrilaterals can divide the plane is equal to $(2n - 1)^2 + 1$. However, for concave quadrilaterals, this number is larger.
Note 2. One can analogously prove that the maximum number of parts into which the boundaries of $n$ triangles can divide the plane is equal to $3n^2 - 3n + 2$. We leave the detailed proof to the reader as an exercise. | (2n-1)^2+1 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
LIX OM - I - Task 9
Determine the smallest real number a with the following property:
For any real numbers $ x, y, z \geqslant a $ satisfying the condition $ x + y + z = 3 $
the inequality holds | Answer: $ a = -5 $.
In the solution, we will use the following identity:
Suppose that the number $ a \leqslant 1 $ has the property given in the problem statement. The numbers
$ x = a, y = z = 2\cdot (\frac{3-a}{2}) $ satisfy the conditions $ x, y, z \geqslant a $ and $ x+y+z = 3 $, thus
by virtue of (1), from which the inequality $ a \geqslant -5 $ follows.
We will now show that the number $ a = -5 $ satisfies the conditions of the problem. For this purpose, consider numbers
$ x, y, z \geqslant-5 $ such that $ x + y + z = 3 $. Without loss of generality, assume that
$ x \leqslant y \leqslant z $. The sum $ y + z $ is a positive number, because otherwise, given
$ y\leqslant z $, we would have $ x \leqslant y \leqslant 0 $, which would imply that $ x +y + z \leqslant y + z \leqslant 0 $,
contradicting the condition $ x+y+z = 3 $. Since $ y + z > 0 $, the inequality
holds, and from the identity (1) we finally obtain
(Note: The last part of the text seems to be incomplete or missing in the original Polish text, so the translation reflects that.) | -5 | Inequalities | math-word-problem | Yes | Yes | olympiads | false |
XLIV OM - I - Problem 11
In six different cells of an $ n \times n $ table, we place a cross; all arrangements of crosses are equally probable. Let $ p_n $ be the probability that in some row or column there will be at least two crosses. Calculate the limit of the sequence $ (np_n) $ as $ n \to \infty $. | Elementary events are determined by six-element subsets of the set of $n^2$ cells of the table; there are $\binom{n^2}{6}$ of them. Let $\mathcal{Z}$ be the complementary event to the event considered in the problem. The configurations favorable to event $\mathcal{Z}$ are obtained as follows: we place the first cross in any arbitrarily chosen cell: here we have $n^2$ possibilities. We then "cross out" the entire horizontal row and the entire vertical row intersecting at the cell where we placed the first cross, and place the second cross in any of the remaining cells: thus, we now have $(n-1)^2$ possibilities. We repeat this scheme four more times and obtain the number of possibilities equal to $n^2 (n -1 )^2 (n - 2)^2 (n - 3)^2 (n - 4 )^2 (n - 5)^2$. This number must still be divided by $6!$ (the number of permutations of a six-element set) to make the reasoning independent of the order of placing the crosses.
Thus, the probability of event $\mathcal{Z}$ (equal to $1 - p_n$) is
One should not multiply all these factors! Let us denote the numerator of the obtained fraction by $L_n$, and the denominator by $M_n$. It is enough to notice that
where $\phi(n)$ and $f(n)$ are polynomials (in the variable $n$), of degree (at most) 4 and 10, respectively; similarly,
where $\psi(n)$ and $g(n)$ are polynomials (in the variable $n$), of degree (at most) 8 and 10, respectively. Therefore,
Since the polynomials $f(n)$ and $g(n)$ are of degree (at most) tenth, then
and consequently, $\displaystyle \lim_{n\to \infty} np_n = 30$. | 30 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
XV OM - I - Problem 7
Given a circle and points $ A $ and $ B $ inside it. Find a point $ P $ on this circle such that the angle $ APB $ is subtended by a chord $ MN $ equal to $ AB $. Does the problem have a solution if the given points, or only one of them, lie outside the circle? | Suppose that point $ P $ of a given circle $ C $ with radius $ r $ is a solution to the problem (Fig. 7).
Since points $ A $ and $ B $ lie inside the circle $ C $, points $ M $ and $ N $ lie on the rays $ PA $ and $ PB $ respectively, and angle $ APB $ coincides with angle $ MPN $. Triangles $ APB $ and $ MPN $ have equal bases $ AB = MN = a $ and a common angle at the vertex $ \measuredangle APB = \measuredangle MPN = \alpha $; hence, the circles circumscribed around these triangles have the same radius $ r = \frac{a}{2 \sin \alpha} $, and point $ P $ lies on the circle with radius $ r $ passing through points $ A $ and $ B $. Therefore, the construction of the desired point is as follows (Fig. 7a). We construct circles with radius $ r $ passing through points $ A $ and $ B $. Since $ AB < 2r $, there are 2 such circles: $ K_1 $ and $ K_2 $. If $ P $ is a common point of circles $ K_1 $ and $ C $, or circles $ K_2 $ and $ C $, then $ P $ is a solution to the problem. Indeed, the rays $ PA $ and $ PB $ intersect the given circle $ C $ at points $ M $ and $ N $; from triangle $ MPN $ we have $ MN = 2r \sin \measuredangle MPN = 2r \sin \measuredangle APB $; but in triangle $ APB $ we have $ \sin \measuredangle APB = AB \colon 2r $, so $ MN = AB $.
Each of the circles $ K_1 $ and $ K_2 $ intersects the circle $ C $ at two points; if $ O_1 $ and $ O_2 $ are the centers of circles $ K_1 $ and $ K_2 $, then
since $ OA < r $, $ AO_1 = r $; similarly $ 0 < OO_2 < 2r $.
The problem thus has 4 solutions.
Let us examine whether the above reasoning remains valid for any position of points $ A $ and $ B $. If point $ P $ is a solution to the problem, then points $ M $ and $ N $ lie on the lines $ PA $ and $ PB $, but not necessarily on the rays $ PA $ and $ PB $, so angle $ MPN $ coincides either with angle $ APB $ or with the adjacent angle to angle $ APB $. The conclusion that triangles $ APB $ and $ MPN $ have the same circumradius remains valid, hence point $ P $ lies, as before, on the circle with radius $ r $ passing through $ A $ and $ B $. Conversely, if point $ P $ is a common point of the given circle and a circle $ K $ with radius $ r $ passing through $ A $ and $ B $, then this point, provided it is different from $ A $ and $ B $, is a solution to the problem, as we conclude in the same way as before.
For such a point $ P $ to exist, the following conditions must be met:
1. There must exist a circle with radius $ r $ passing through points $ A $ and $ B $; this is the case when $ AB \leq 2r $. If $ AB < 2r $, there are two such circles $ K_1 $ and $ K_2 $ with centers $ O_1 $ and $ O_2 $. If $ AB = 2r $, there is one such circle: $ K_1 = K_2 $, $ O_1 = O_2 $.
2. There must exist a common point of circle $ K_1 $ or $ K_2 $ with the given circle $ C $, different from $ A $ and $ B $.
The table below gives the number of solutions for different cases of the position of points $ A $ and $ B $.
We propose to the Reader to provide a detailed justification of the above data for each of the cases 2-6 and to make the appropriate drawings. | 4 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
VI OM - III - Task 6
Through points $ A $ and $ B $, two oblique lines $ m $ and $ n $ perpendicular to the line $ AB $ have been drawn. On line $ m $, a point $ C $ (different from $ A $) has been chosen, and on line $ n $, a point $ D $ (different from $ B $). Given the lengths of segments $ AB = d $ and $ CD = l $, and the angle $ \varphi $ formed by the oblique lines $ m $ and $ n $, calculate the radius of the sphere passing through points $ A $, $ B $, $ C $, $ D $. | Fig. 20 shows the considered figure in an orthogonal projection onto the plane determined by the lines $AB$ and $n$, hence on this drawing $AB \bot n$. For simplicity, we denote the projections of points and lines with the same letters as the points and lines themselves. Let us draw through point $A$ a line $p$ parallel to line $m$, and through point $C$ a line parallel to line $AB$; it will intersect line $p$ at point $E$. The sphere $\sigma$ denotes the surface of the sphere passing through points $ABCD$; since points $A$, $B$, $C$, $D$ do not lie in the same plane (lines $m$ and $n$ are skew), such a sphere exists and is unique. Quadrilateral $ABCE$ is a rectangle because $AB \bot m$, $CE \bot m$, and $AB \bot p$; since three vertices $A$, $B$, $C$ of this rectangle lie on the sphere $\sigma$, the fourth vertex $E$ also lies on $\sigma$. The sphere $\sigma$ intersects the plane of lines $n$ and $p$ according to a circle passing through points $A$, $D$, $E$; the center $S$ of this circle is thus the center of the circumcircle of triangle $ADE$; we will explain shortly how point $S$ was constructed on Fig. 20. The center $O$ of the sphere $\sigma$ lies on the line perpendicular to the plane $ADE$ at point $S$, and thus on a line parallel to $AB$ (since $AB \bot n$ and $AB \bot p$). On the other hand, point $O$, being equidistant from points $A$ and $B$, lies on the perpendicular bisector plane of segment $AB$, so its distance $OS$ from the plane $ADE$ is equal to $\frac{1}{2} AB$. We find point $O$ by drawing a line parallel to $AB$ through point $S$ and measuring $SO = \frac{1}{2} d$ in the direction from $A$ to $B$.
Consider triangle $ASO$; the angle at vertex $S$ is a right angle, the hypotenuse $OA$ equals the sought radius $r$ of the sphere $\sigma$, $OS = \frac{1}{2} d$, and $SA$ equals the radius of the circumcircle of triangle $ADE$, so $SA = \frac{DE}{2 \sin \measuredangle DAE}$. But from the right triangle $DEC$ ($CE$ is perpendicular to the plane $ADE$) $DE^2 = DC^2 - EC^2 = l^2 - d^2$, and angle $DAE$ equals the angle $\varphi$ between the skew lines $m$ and $n$, so $SA = \frac{\sqrt{l^2 - d^2}}{2 \sin \varphi}$.
Since in triangle $ASO$ we have $OA^2 = SO^2 + SA^2$,
and finally
The construction of point $S$ is indicated on Fig. 20 with dashed lines, and it proceeds as follows. We perform a lay of triangle $ADE$ onto the plane of the drawing, i.e., onto the plane $ABD$, meaning we rotate the plane $ADE$ around line $n$ so that point $E$ ends up at some point $(E)$ in the plane of the drawing. During such a rotation, the orthogonal projection of each point in the plane $ADE$ moves along a line perpendicular to $n$. Point $(E)$ is found at the intersection of the perpendicular dropped from point $E$ to line $n$ and the ray drawn from point $A$ forming an angle $\varphi$ (in its natural size) with the ray $AD$.
Let $(S)$ be the center of the circumcircle of triangle $AD(E)$ and let the line $A(S)$ intersect the line $D(E)$ at point $(M)$. Drawing a perpendicular from point $(M)$ to line $n$ to intersect at point $M$ with line $DE$, and then drawing a perpendicular from point $(S)$ to line $n$, we find the sought point $S$ at the intersection of this perpendicular with line $AM$.
Note that when points $A$ and $B$ and lines $m$ and $n$ are given, there are infinitely many segments $CD$ of a given length $l$ with endpoints lying on lines $m$ and $n$. There are therefore infinitely many spheres passing through $A$ and $B$ and intersecting lines $m$ and $n$ at points $C$ and $D$ such that $CD = l$. The result of our problem shows that the radii of all these spheres are equal. | \sqrt{(\frac{} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
I OM - B - Task 20
The sides of a right-angled triangle are expressed by natural numbers. One of the legs is expressed by the number 10. Calculate the remaining sides of this triangle. | Natural numbers $ x $ and $ y $ representing the length of the hypotenuse and the length of the other leg of the considered triangle satisfy, according to the Pythagorean theorem, the equation
Since $ 10^2 $ is an even number, it follows from equation (1) that the numbers $ x^2 $ and $ y^2 $ are either both even or both odd. Therefore, the numbers $ x $ and $ y $ are either both even or both odd.
From equation (1) it follows
Since the numbers $ x $ and $ y $ are of the same parity, the numbers $ (x + y) $ and $ (x-y) $ are both even; moreover, $ x + y > x-y $. The number $ 10^2 = 100 $ can be factored into the product of two unequal even factors in only one way: $ 100 = 50 \cdot 2 $. Therefore, from equation (2) it follows that
Thus $ x = 26 $, $ y = 24 $. | x=26,y=24 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
I OM - B - Task 4
Find two natural numbers $ a $ and $ b $ given their greatest common divisor
$ D=12 $ and least common multiple $ M=432 $. Provide a method for finding
solutions in the general case. | If the greatest common divisor of numbers $ a $ and $ b $ is 12, then
where numbers $ x $ and $ y $ are coprime. In this case, the least common multiple of numbers $ 12x $ and $ 12y $ is $ 12xy $, hence
Numbers $ x $ and $ y $ can be found by factoring 36 into a product of two coprime factors.
There are two such factorizations:
We obtain two solutions
The sought numbers are
In the general case, when the greatest common divisor of numbers
$ a $ and $ b $ is $ D $, and the least common multiple is
$ M $, we reason similarly and obtain the equations:
from which
The problem has as many solutions as there are ways to factor the natural number \frac{M}{D} into two coprime factors $ x $ and $ y $. One of the solutions is always the numbers $ D $ and $ M $. | (12, | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
XLV OM - III - Task 1
Determine all triples $ (x,y,z) $ of positive rational numbers for which the numbers $ x+y+z $, $ \frac{1}{x}+\frac{1}{y}+\frac{1}{z} $, $ xyz $ are natural. | Let $ (x,y,z) $ be a triple of rational numbers satisfying the given condition. The numbers
are natural; therefore, the product
is also a natural number. The numbers $ x $, $ y $, $ z $ are roots of the polynomial
whose all coefficients are integers, and the coefficient of the highest power of the variable $ t $ is $ 1 $. It is known (see: *Remark*), that every rational root of such a polynomial is an integer. The numbers $ x $, $ y $, $ z $ are rational by assumption; they must therefore be integers.
Of course, for any natural numbers $ x,y,z \geq 1 $, the numbers $ a $ and $ c $, defined by formulas (1), are also natural. The task thus reduces to finding all triples $ (x,y,z) $ of positive natural numbers for which
is a natural number.
Assume that $ (x,y,z) $ is such a triple. Without loss of generality, we can assume that $ x \geq y \geq z $. Then
which means $ 1 \leq z \leq 3 $. If the numbers $ x $, $ y $, $ z $ are equal, then the relation (2) takes the form $ bx = 3 $, hence
In the further part, we will consider the case when not all three numbers $ x $, $ y $, $ z $ are equal. Then the inequality (3) is strict and we get $ 1 \leq z < 3 $,
which means $ z = 1 $ or $ z = 2 $. Hence $ b =\frac{1}{x} + \frac{1}{y} + \frac{1}{z} \leq 1 + 1 + \frac{1}{2} < 3 $, and thus also $ b = 1 $ or $ b = 2 $.
Let us rewrite equation (2) in the following equivalent forms:
From the last form, it is clear that the factor $ (bz - 1) $ cannot be zero (which excludes the possibility $ b = z = 1 $). Multiplying both sides by this factor, we get
and by adding the term $ z^2 $ to both sides, we obtain the equation
As we stated above, the numbers $ b $ and $ z $ can only take the values $ 1 $ and $ 2 $, and they cannot be equal to 1 at the same time. We thus have three possibilities:
The equation (5) then takes the form
The first of these equations gives the solution
and the second — the solutions
(the third equation has no solutions in natural numbers $ x \geq y \geq z = 2 $).
Formulas (4) and (6) and (7) represent the general solution of the problem under the assumption that $ x \geq y \geq z $. Dropping this assumption, we obtain the following triples $ (x,y,z) $ as the complete solution of the problem:
*Remark.* Here is the justification of the fact that every rational root of a polynomial of the form
whose coefficients $ a_0, a_1, \ldots, a_{N-1} $ are integers, is also an integer. (In this problem, we are dealing with a polynomial of degree $ N = 3 $.) Let us write the rational root $ x $ of the polynomial $ P(t) $ in the form of an irreducible fraction $ x = r/q $ ($ q, r $ integers, $ q > 0 $). Multiplying the equality $ P(x) = 0 $ by $ q^N $ gives
All terms except $ r^N $ are integers divisible by $ q $. Therefore, $ r^N $ must also be divisible by $ q $. The fraction $ r/q $ is irreducible by assumption. Hence, we conclude that $ q = 1 $. | (1,1,1),(2,2,1),(2,1,2),(1,2,2) | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
XXVI - I - Task 1
At the ball, there were 42 people. Lady $ A_1 $ danced with 7 gentlemen, Lady $ A_2 $ danced with 8 gentlemen, ..., Lady $ A_n $ danced with all the gentlemen. How many gentlemen were at the ball? | The number of ladies at the ball is $ n $, so the number of gentlemen is $ 42-n $. The lady with number $ k $, where $ 1 \leq k \leq n $, danced with $ k+6 $ gentlemen. Therefore, the lady with number $ n $ danced with $ n+ 6 $ gentlemen. These were all the gentlemen present at the ball. Thus, $ 42-n = n + 6 $. Solving this equation, we get $ n = 18 $. The number of gentlemen at the ball is therefore $ 42-18 = 24 $. | 24 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
I OM - B - Task 5
A motorboat set off upstream at 9:00, and at the same moment, a ball was thrown from the motorboat into the river. At 9:15, the motorboat turned around and started moving downstream. At what time did the motorboat catch up with the ball? | On standing water, the motorboat would have returned to the ball within the next 15 minutes, i.e., at 9:30. The same would happen on the river, as the current equally carries the motorboat and the ball. The motorboat will catch up with the ball at 9:30.
If someone did not come up with the above simple reasoning, they could solve the problem using equations.
At first glance, it seems that there is not enough data in the problem, as the boat's own speed, i.e., its speed on standing water, and the speed of the river current were not specified.
Not being discouraged by this, let's denote by $ x $ the sought number of hours from 9 o'clock to the moment when the motorboat caught up with the ball. In addition to this, let's introduce the speed of the current $ u $ expressed in kilometers per hour and the speed $ v $ of the motorboat on standing water, also expressed in kilometers per hour. To set up the equation, we need to express the distance traveled by the ball and the distance traveled by the motorboat using these quantities.
In $ x $ hours, the ball drifted with the river current $ xu $ kilometers.
The motorboat first traveled for $ \frac{1}{4} $ of an hour against the current, its speed was then $ (v - u) $ kilometers per hour, the distance traveled was thus $ \frac{1}{4}(v - u) $ kilometers; in the remaining time $ (x - \frac{1}{4}) $ hours, the motorboat traveled with the current, so at a speed of $ (u + v) $ kilometers per hour and traveled $ (x - \frac{1}{4})(u + v) $ kilometers, covering in the opposite direction first the distance $ \frac{1}{4}(v - u) $ kilometers to the starting point, and then the distance $ xu $ kilometers traveled by the ball to the point where the motorboat caught up with the ball.
Therefore
When we transform this equation by opening the parentheses and collecting the terms containing $ x $ on one side and the remaining terms on the other side, we get the equation
Since the motorboat's own speed $ v $ is certainly not zero, we can divide both sides of the equation by $ v $, obtaining
Thus, the motorboat will catch up with the ball after $ \frac{1}{2} $ of an hour from the moment of departure, i.e., at 9:30.
It turned out that the unknown quantities $ u $ and $ v $ were needed only to set up the equation. When performing the calculations, these quantities disappeared, i.e., as is said in mathematics, they were eliminated. Such auxiliary quantities are sometimes called parameters. | 9:30 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
XXXV OM - III - Task 4
We toss a coin $ n $ times and record the result as a sequence $ (a_1, a_2, \ldots, a_n) $, where $ a_i = 1 $ or $ a_i = 2 $ depending on whether an eagle or a tail appeared in the $ i $-th toss. We assume $ b_j = a_1 + a_2 + \ldots + a_j $ for $ j = 1, 2, \ldots, n $, $ p(n) $ is the probability that the number $ n $ appears in the sequence $ (b_1, b_2, \ldots, b_n) $. Determine $ p(n) $ in terms of $ p(n-1) $ and $ p(n-2) $. | We directly observe that $ p(1) = \frac{1}{2} $, $ p(2) = \frac{1}{4} $. Suppose that $ n \geq 3 $. Notice that $ b_j \geq j $ for every $ j $. The number $ n $ can appear in the sequence $ (b_1, b_2, \ldots, b_n) $ in the following two cases:
1. Some term of this sequence is equal to $ n-1 $, for example, $ b_k = n-1 $ ($ k \leq n-1 $) and moreover $ a_{k+1} = 1 $,
2. Some term of this sequence is equal to $ n - 2 $, for example, $ b_r = n - 2 $ ($ r \leq n - 2 $) and moreover $ a_{r + 1} = 2 $.
The probability for the cases mentioned here is respectively $ p(n-1) \cdot \frac{1}{2} $ and $ p(n-2) \cdot \frac{1}{2} $, and these cases cannot occur simultaneously. Therefore | p(n)=\frac{1}{2}p(n-1)+\frac{1}{2}p(n-2) | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
XLIX OM - I - Zadanie 2
Proste zawierające wysokości trójkąta $ ABC $, wpisanego w okrąg o środku $ O $, przecinają się w punkcie $ H $, przy czym $ |AO| =|AH| $. Obliczyć miarę kąta $ CAB $.
|
Oznaczmy przez $ M $ środek boku $ BC $. Rozwiązanie zadania będzie oparte na równości
która zachodzi w każdym trójkącie, niezależnie od założenia, że $ |AO| =|AH| $. Oto jej dowód:
Role punktów $ B $ i $ C $ są symetryczne; można przyjąć, że $ |AB|\geq|AC| $ i wobec tego kąt ABC jest ostry. Każdy z dwóch pozostałych kątów trójkąta $ ABC $ może być ostry, prosty lub rozwarty. Gdy kąt $ CAB $ jest prosty, wówczas punkt $ H $ pokrywa się z $ A $, punkt $ O $ pokrywa się z $ M $, i po obu stronach dowodzonej równości mamy zera. Dalej zakładamy, że kąt $ CAB $ jest ostry lub rozwarty (rysunek 1 przedstawia różne możliwe sytuacje; prowadzone rozumowanie nie zależy od przypadku).
Prowadzimy średnicę $ CX $ okręgu $ \omega $ opisanego na trójkącie $ ABC $; oparte na niej kąty wpisane $ CAX $ i $ CBX $ są proste. Wysokości trójkąta $ ABC $, poprowadzone z wierzchołków $ A $ i $ B $, są zawarte w prostych $ AH $ i $ BH $. Spełnione są więc warunki prostopadłości: $ AX \bot AC $, $ AC \bot BH $, $ BX \bot BC $, $ BC\bot AH $. Wynika z nich, że $ AX \parallel BH $ oraz $ BX \parallel AH $. Czworokąt $ AHBX $ jest zatem równoległobokiem i zachodzi równość $ |AH| = |BX| $. Odcinek $ OM $ łączy środki boków $ CX $ i $ CB $ trójkąta $ CBX $. Stąd $ |BX| = 2\cdot |OM| $, co w połączeniu z równością poprzednią daje dowodzoną zależność (1).
Jeżeli teraz, zgodnie z treścią zadania, długość odcinka $ AH $ jest równa promieniowi okręgu $ \omega $, to długość odcinka $ OM $ jest równa połowie tego promienia: $ |OM| = \frac{1}{2}\cdot|OC| $. Stąd $ |\measuredangle MOC| = 60^\circ $, czyli $ |\measuredangle BOC| = 120^\circ $.
Wniosek: kąt $ CAB $, jako kąt wpisany w okrąg $ \omega $, oparty albo na krótszym albo na dłuższym łuku $ BC $, ma miarę $ 60^\circ $ lub $ 120^\circ $.
Każda z tych wartości istotnie może być przyjęta; przykłady: trójkąt równoboczny $ ABC $ oraz trójkąt równoramienny $ ABC $ z kątem $ 120^\circ $ przy wierzchołku $ A $.
Uwaga: Jak zauważyliśmy, równość (1) jest prawdziwa dla każdego trójkąta $ ABC $; w podanym rozwiązaniu stanowi ona lemat, a dokończenie rozwiązania na podstawie tego lematu jest krótkie i zupełnie proste.
Wspomnijmy jeszcze o innych metodach rozwiązania. Każda z nich opiera się na jakimś fakcie ogólnym, słusznym dla każdego trójkąta i stanowiącym lemat, z którego da się wydedukować odpowiedź na pytanie postawione w zadaniu.
Oto owe lematy:
$ \qquad (4) $ proste $ AO $ i $ AH $ są symetryczne względem dwusiecznej kąta $ CAB $;
$ \qquad (5) $ obraz punktu $ H $ w symetrii względem prostej $ BC $ leży na okręgu $ \omega $.
Czytelnikom, którzy nie znają którejkolwiek z tych własności, proponujemy znalezienie dowodu (dowodów) jako pożyteczne ćwiczenie. Dokończenie rozwiązania zadania na podstawie dowolnej z własności (2), (3), (4) lub (5)\nic{rf} jest nie tak natychmiastowe, jak przy wykorzystaniu własności (1) — wciąż jednak niezbyt trudne i też może być przyjemnym ćwiczeniem.
| 60or120 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
L OM - II - Task 5
Let $ S = \{1, 2,3,4, 5\} $. Determine the number of functions $ f: S \to S $ satisfying the equation $ f^{50} (x) = x $ for all $ x \in S $.
Note: $ f^{50}(x) = \underbrace{f \circ f \circ \ldots \circ f}_{50} (x) $. | Let $ f $ be a function satisfying the conditions of the problem. For numbers $ x \neq y $, we get $ f^{49}(f(x)) = x \neq y = f^{49}(f(y)) $, hence $ f(x) \neq f(y) $. Therefore, $ f $ is a permutation of the set $ S $. Denote by $ r(x) $ ($ x \in S $) the smallest positive integer such that $ f^{r(x)}(x) = x $. Then $ r(x) \leq 5 $ and $ r(x) \mid 50 $, so $ r(x) \in \{1, 2, 5\} $.
If there exists a number $ a \in S $ such that $ r(a) = 5 $, then the numbers $ a $, $ f(a) $, $ f^2(a) $, $ f^3(a) $, $ f^4(a) $ are distinct; they thus exhaust the set $ S $. Then for any number $ x \in S $, $ r(x) = 5 $. The function $ f $ is thus uniquely determined by the permutation $ (f(1), f^2(1), f^3(1), f^4(1)) $ of the set $ \{2, 3, 4, 5\} $; hence it can be defined in $ 4! = 24 $ ways.
If for all $ x \in S $, $ r(x) = 1 $, then $ f $ is the identity function. Such a function is unique.
The remaining case to consider is when the maximum value attained by the function $ r $ is $ 2 $. Let $ a $ be an element of the set $ S $ such that $ r(a) = 2 $. Then also $ r(b) = 2 $, where $ b = f(a) $.
If $ r(x) = 1 $ for all $ x \in S \setminus \{a, b\} $, then $ f $ is determined by the choice of a two-element subset $ \{a, b\} $ of the set $ S $, which can be done in $ {5 \choose 2} = 10 $ ways.
If, however, there exists a number $ c \in S \setminus \{a, b\} $ such that $ r(c) = 2 $, then by setting $ d = f(c) $ and denoting by $ e $ the unique element of the set $ S \setminus \{a, b, c, d\} $, we have
Such a function $ f $ is determined by the choice of the number $ e $ (which can be done in $ 5 $ ways) and the partition of the set $ S \setminus \{e\} $ into two two-element subsets $ \{a, b\} $ and $ \{c, d\} $ (there are $ 3 $ such partitions). We thus get $ 15 $ functions of the form (1).
In total, there are $ 50 $ functions satisfying the conditions of the problem. | 50 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
XXXIII OM - I - Problem 1
A regular 25-gon $ A_1, A_2, \ldots, A_{25} $ is inscribed in a circle with center $ O $ and radius of length $ r $. What is the maximum length of the vector that is the sum of some of the vectors $ \overrightarrow{OA_1}, \overrightarrow{OA_2}, \ldots, \overrightarrow{OA_{25}} $? | Consider a certain subset $X$ of the set of data vectors, for which the vector $\overrightarrow{a}$ will be equal to the sum of all vectors in the subset $X$. If the vector $\overrightarrow{OA_i}$ does not belong to $X$ and forms an acute angle with the vector $\overrightarrow{a}$, then the sum of all vectors in the set $X$ and the vector $\overrightarrow{OA_i}$ has a length greater than $a$. Assuming that $\overrightarrow{OB} = \overrightarrow{a}$, then $\overrightarrow{OC} = \overrightarrow{a} + \overrightarrow{OA_i}$ and $\overrightarrow{OC}^2 = \overrightarrow{OA_i}^2 + \overrightarrow{A_iC}^2 - 2OA_i A_i C \cos| \measuredangle OA_iC| > OA_i^2 + A_iC^2$ (since the angle $OA_iC$ is obtuse). Therefore, $OC_i^2 > a^2$, which means $OC > a$.
om33_1r_img_1.jpg
On the other hand, since the sum of all data vectors $\overrightarrow{OA_1} + \ldots + \overrightarrow{OA_{25}}$ is the zero vector, the sum of vectors of any fixed subset $\{\overrightarrow{OA_{i_2}}, \ldots, \overrightarrow{OA_{i_k}}\}$ is the vector opposite to the sum of the remaining $25-k$ vectors, and thus both these sums are vectors of equal length. It follows that the maximum sum length can be obtained by adding no more than $12$ vectors. We will show that the maximum sum is obtained by adding $12$ consecutive vectors. Let the vector $\overrightarrow{a} = \overrightarrow{OB}$ denote the sum of vectors of the chosen subset $X$. Without loss of generality, we can assume that the point $B$ lies in the angle $A_6OA_7$. If, therefore, any of the vectors $\overrightarrow{OA_i}$ for $i = 1,2,\ldots,12$ did not belong to $X$, then by the initial remark, adding this vector to $X$ would yield a subset of vectors whose sum would be longer than $a$. Ultimately, then, the maximum length is the sum of $12$ consecutive vectors (the sum of $13$ consecutive vectors has the same length). It will be more convenient to calculate the length of the sum of $13$ consecutive vectors. Since consecutive vectors form an angle of measure $\frac{2\pi}{25}$, the sum of the lengths of such $13$ vectors $\{\overrightarrow{OA_1}, \ldots, \overrightarrow{OA_{13}}\}$ is equal to the sum of the lengths of the projections of these vectors onto the ray $OA_7$. It is
since the vectors $\overrightarrow{OA_1}$ and $\overrightarrow{OA_{13}}$ form an angle of measure $6 \cdot \frac{2\pi}{25}$ with $\overrightarrow{OA_7}$, the vectors $\overrightarrow{OA_1}$ and $\overrightarrow{OA_{13}}$ form angles of measure $5 \cdot \frac{2\pi}{25}, \ldots,$ the vectors $\overrightarrow{OA_6}$ and $\overrightarrow{OA_{8}}$ form angles of measure $\frac{2\pi}{25}$ with $\overrightarrow{OA_7}$.
To calculate the value (*), we will use complex numbers. The number
is the real part of the complex number
Taking $z = \cos \frac{2\pi}{25} + i \sin \frac{2\pi}{25}$, by de Moivre's formula,
It follows that
thus
The real part of this number that we are interested in is
We have therefore calculated that
Therefore,
Ultimately, the maximum length of the vector being the sum of some of the vectors $\overrightarrow{OA_1}, \ldots, \overrightarrow{OA_{25}}$ is | 2r\cos\frac{6\pi}{25} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
XIII OM - III - Task 3
What condition should the angles of triangle $ ABC $ satisfy so that the angle bisector of $ A $, the median drawn from vertex $ B $, and the altitude drawn from vertex $ C $ intersect at one point? | The common point of the bisector $AD$, the median $BS$, and the altitude $CH$ of triangle $ABC$ can only be an internal point of the triangle, since $AD$ and $BS$ intersect inside the triangle. Such a point can therefore exist only if the line $CH$ contains a segment lying inside the triangle, i.e., if angles $A$ and $B$ are acute.
Suppose this condition is satisfied and that the altitude $CH$ intersects the bisector $AD$ at point $K$ (Fig. 35), and the median $BS$ at point $L$ (Fig. 36).
In triangles $AHC$ and $AHK$
therefore
In triangles $BHC$ and $BHL$
where $\lambda$ denotes the acute angle $HBL$, hence
The lines $AD$, $BS$, and $CH$ intersect at one point if and only if $HK = HL$, i.e., if
The desired condition can be obtained by transforming equation (1) in such a way as to obtain a relationship between the angles of the triangle.
Applying the Law of Sines to triangle $ASB$ we get
hence
therefore
From (1) and (2) it follows that
Substituting in equation (3) $a = 2R\sin A$, $b = 2R \sin B$, $c = 2R \sin C$, we get
We can simplify relation (4). Substituting $\tan \frac{A}{2} = \frac{\sin A}{1 + \cos A}$, dividing both sides by $\sin A$, and multiplying by the denominator, we get
Therefore
and finally
We have thus obtained the necessary conditions for the existence of a common point of the lines $AD$, $BS$, and $CH$: the inequalities $\angle A < 90^\circ$, $\angle B < 90^\circ$, and equation (5).
However, note that these inequalities already follow from condition (5). Since $\sin C > 0$, according to (5) $\tan A \cdot \cos B > 0$, and since the numbers $\tan A$ and $\cos B$ cannot both be negative, $\tan A > 0$ and $\cos B > 0$, and angles $A$ and $B$ are acute.
Reversing the reasoning, we conclude that if $A$, $B$, $C$ satisfy condition (5), then equation (1) holds, and $AD$, $BS$, and $CH$ pass through one point.
The answer to the posed question is therefore: In triangle $ABC$, the bisector, median, and altitude drawn from vertices $A$, $B$, $C$ respectively intersect at one point if and only if the angles $A$, $B$, $C$ satisfy equation (5). | \tanA\cdot\cosB=\sinC | Geometry | math-word-problem | Yes | Yes | olympiads | false |
LIII OM - III - Task 1
Determine all such triples of natural numbers $ a $, $ b $, $ c $, such that the numbers $ a^2 +1 $ and $ b^2 +1 $ are prime and | Without loss of generality, we can assume that $ a \leq b $. Let $ p = b^2 +1 $. Then the number $ (c^2 +1) - (b^2 + 1) = (c - b)(c + b) $ is divisible by $ p $. From the given equation in the problem, it follows that $ b < c $. Furthermore,
Thus $ c - b < p $ and $ c + b < 2p $. Since $ p | (c - b)(c + b) $, it must be that $ c + b = p $, which means
The numbers $ a = b = 1 $ do not satisfy the conditions of the problem; we can therefore assume that $ b > 1 $. In this case, $ p $ is an odd prime number. From the relationship (1), it follows that $ c $ is odd, which in turn proves the evenness of the numbers $ c^2 + 1 $ and $ a^2 + 1 $. The number $ a^2 + 1 $ is prime, so $ a^2 + 1 = 2 $, from which $ a = 1 $. Thus, the given equation in the problem takes the form
Combining equations (1) and (2), we get $ 2b^2 + 2 = b^2(b - 1)^2 + 2b(b - 1) + 2 $, which simplifies to $ 2b = b(b - 1)^2 + 2b - 2 $. From this, $ b $ is a divisor of the number $ 2 $, and since $ b > 1 $, it must be that $ b = 2 $. This implies $ c = 3 $.
It remains to state that the triplet $ (a,b,c) = (1,2,3) $ satisfies the conditions of the problem.
Releasing the assumption $ a \leq b $, we obtain two triplets $ (a,b,c) $ that satisfy the conditions of the problem. They are: $ (1, 2, 3) $ and $ (2, 1, 3) $. | (1,2,3)(2,1,3) | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
XII OM - III - Task 6
Someone wrote six letters to six people and addressed six envelopes to them. In how many ways can the letters be placed into the envelopes so that no letter ends up in the correct envelope? | Let $ F (n) $ denote the number of all ways of placing $ n $ letters $ L_1, L_2, \ldots, L_n $ into $ n $ envelopes $ K_1, K_2, \ldots, K_n $ so that no letter $ L_i $ ends up in the correct envelope $ K_i $, or more simply, so that there is no "hit". We need to calculate $ F (6) $.
Suppose we incorrectly place all letters by putting letter $ L_1 $ in envelope $ K_i $ ($ i \ne 1 $). There are $ 2 $ cases:
a) Letter $ L_i $ ends up in envelope $ K_1 $. The remaining $ 4 $ letters must then be incorrectly placed in the remaining $ 4 $ envelopes, which can be done in $ F (4) $ ways. Since $ K_i $ can be any of the $ 5 $ envelopes $ K_2 $, $ K_3 $, $ K_4 $, $ K_5 $, $ K_6 $, case a) can occur $ 5 \cdot F (4) $ times.
b) Letter $ L_i $ does not end up in envelope $ K_1 $. By assigning envelope $ K_1 $ to letter $ L_i $ as its "pseudo-correct" envelope, we can say that none of the letters $ L_2 $, $ L_3 $, $ L_4 $, $ L_5 $, $ L_6 $ end up in their correct envelopes, which can be done in $ F (5) $ ways. Since $ K_i $ can be any of the $ 5 $ envelopes, case b) can occur $ 5 \cdot F (5) $ times.
Since cases a) and b) cover all possibilities, therefore
Analogously
\[ F (5) = 4F (4) + 4F (3) \]
\[ F (4) = 3F (3) + 3F (2) \]
\[ F (3) = 2F (2) + 2F (1). \]
But of course
\[ F (2) = 1 \]
\[ F (1) = 0 \]
Therefore, from the above equations, we obtain sequentially,
\[ F (3) = 2 \cdot 1 + 2 \cdot 0 = 2 \]
\[ F (4) = 3 \cdot 2 + 3 \cdot 1 = 9 \]
\[ F (5) = 4 \cdot 9 + 4 \cdot 2 = 44 \]
Note. In the above solutions, the number $ 6 $ does not play any significant role. The same methods can be applied to $ n $ letters and $ n $ envelopes. Method I leads to the formula
\[ F (n) = (n - 1) [F (n - 1) + F (n - 2)] \]
This is the so-called recursive or reduction formula, which allows us to calculate $ F (n) $ if the values of $ F (n - 1) $ and $ F (n - 2) $ are known. Similarly, Method II leads to the recursive formula
\[ F (n) = nF (n - 1) + (-1)^n \]
Formula (1) allows us to calculate $ F (n) $ in terms of $ n $. We can write this formula as
\[ F (n) = nF (n - 1) + (-1)^n \]
From formula (3), we see that the function $ F (k) - kF (k - 1) $ has the same absolute value for every natural number $ k > 1 $, but changes sign when transitioning from $ k $ to $ k + 1 $. And since
\[ F (2) - 2F (1) = 1 \]
we have
\[ F (3) - 3F (2) = -1 \]
\[ F (4) - 4F (3) = 1 \]
\[ \ldots \]
From equality (4), we get
\[ F (n) - nF (n - 1) = (-1)^n \]
We introduce the notation
\[ \varphi (k) = \frac{F (k)}{k!} \]
Formula (5) becomes
\[ \varphi (k) - \varphi (k - 1) = \frac{(-1)^k}{k!} \]
Analogously
\[ \varphi (n) - \varphi (n - 1) = \frac{(-1)^n}{n!} \]
\[ \varphi (n - 1) - \varphi (n - 2) = \frac{(-1)^{n-1}}{(n-1)!} \]
\[ \ldots \]
\[ \varphi (2) - \varphi (1) = \frac{1}{2}. \]
Adding these formulas and considering that $ \varphi (1) = \frac{F (1)}{1} = 0 $, we get
\[ \varphi (n) = \sum_{k=1}^{n} \frac{(-1)^k}{k!} \]
Therefore,
\[ F (n) = n! \sum_{k=1}^{n} \frac{(-1)^k}{k!} \]
The problem we solved is known as the Bernoulli-Euler problem of the mislaid letters. | 265 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
IV OM - III - Task 5
A car departs from point $ O $ and drives along a straight road at a constant speed $ v $. A cyclist, who is at a distance $ a $ from point $ O $ and at a distance $ b $ from the road, wishes to deliver a letter to the car. What is the minimum speed at which the cyclist should ride to achieve his goal? | We assume that $ b > 0 $; let the Reader formulate the answer to the question in the case when $ b = 0 $, i.e., when the cyclist is on the road.
Let $ M $ be the point where the cyclist is located, $ S $ - the meeting point, $ \alpha $ - the angle $ MOS $, $ t $ - the time that will elapse from the initial moment to the moment of the meeting, and $ x $ - the speed of the cyclist. Note that
and hence, according to the Law of Sines (Fig. 48),
From this equality, it follows that $ x $ reaches its minimum value when $ \sin \beta $ is the largest. If $ \alpha < 90^\circ $, this occurs for the value $ \beta = 90^\circ $, thus
If $ \alpha \geq 90^\circ $ (Fig. 49), then the angle $ \beta $ is acute; the maximum value of $ \sin \beta $ does not exist, and the speed $ x $ is smaller the closer the angle $ \beta $ is to the acute angle $ 180^\circ - \alpha $. As the angle $ \beta $ increases and approaches $ 180^\circ - \alpha $, the speed $ x $ decreases and approaches $ v $.
Note. In the above solution, trigonometry can be avoided by reasoning as follows:
If $ \alpha < 90^\circ $ (Fig. 50) and $ MS \bot OM $, we draw $ TH \bot OM $ and $ RK \bot OM $. Then
thus, in point $ S $ on the road, the ratio of distances from points $ M $ and $ O $ is the smallest.
If $ \alpha \geq 90^\circ $ and point $ T $ is farther from point $ O $ than point $ S $ (Fig. 51), then by drawing $ NS \parallel MT $ we have
from which it is clear that the sought minimum does not exist. | v\sin\alpha | Algebra | math-word-problem | Yes | Yes | olympiads | false |
XXIII OM - I - Problem 9
How many natural numbers less than $ 10^n $ have a decimal representation whose digits form a non-decreasing sequence? | Let $ A $ be the set of natural numbers less than $ 10^n $, having a decimal representation whose digits form a non-decreasing sequence. Let's agree to place as many zeros at the beginning of the representation of each number in the set $ A $ so that the representation of this number has $ n $ digits in total.
Let $ B $ be the set of natural numbers less than $ 10^{n+10} $ having a decimal representation (with zeros at the beginning), whose digits form a non-decreasing sequence and in which each of the ten digits appears.
To each representation of a number in the set $ A $, we assign a representation in which each digit $ 0, 1, 2, \ldots, 9 $ appears one more time and the digits form a non-decreasing sequence. This assignment defines a mapping $ f $ from the set $ A $ to the set $ B $. At the same time, the number $ x = \underbrace{00\ldots 0}_{n+1} 12\ldots 9 $ belonging to $ B $ does not correspond to any number in the set $ A $.
The mapping $ f \colon A \to B - \{x\} $ is bijective; the inverse mapping involves deleting one digit of each kind in the representation of a number in the set $ B - \{x\} $. Therefore, the number of elements in the set $ B $ is one greater than the number of elements in the set $ A $.
The representation of any number in the set $ B $ consists of $ n + 10 $ digits. There are thus $ n + 9 $ places between consecutive digits. Let's agree to place a dash between digits in such a representation if they are different. There are $ 9 $ such dashes, since there are $ 10 $ different digits and each of them appears in the representation of a number in the set $ B $.
To determine the number of elements in the set $ B $, note that the representation of a number in the set $ B $ is uniquely determined by any placement of $ 9 $ dashes in $ n+9 $ places. Therefore, the set $ B $ has $ \displaystyle \binom{n+9}{9} $ elements, and the set $ A $ has $ \displaystyle \binom{n+9}{9}-1 $ elements. | \binom{n+9}{9}-1 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
XLIII OM - II - Problem 5
Determine the supremum of the volumes of spheres contained in tetrahedra with all altitudes no longer than $1$. | Suppose a sphere with center $ Q $ and radius $ r $ is contained within a tetrahedron with all altitudes no longer than $ 1 $. Let the volume of the tetrahedron be denoted by $ V $, and the areas of its faces by $ S_1 $, $ S_2 $, $ S_3 $, $ S_4 $; we arrange them such that $ S_1 \leq S_2 \leq S_3 \leq S_4 $.
The height of the tetrahedron perpendicular to the $ i $-th face has a length of $ 3V/S_i $ (by the formula: the volume of a pyramid is $ 1/3 $ of the product of the base area and the height). According to the given condition, these lengths do not exceed $ 1 $. In particular, $ 3V/S_1 \leq 1 $.
Notice that $ V $ is the sum of the volumes of four tetrahedra, whose bases are the faces of the given tetrahedron, and the common vertex is the point $ Q $ (i.e., the center of the considered sphere). The height of each of these four tetrahedra, drawn from the point $ Q $, has a length of at least $ r $.
From this, we conclude that
Therefore,
When the tetrahedron is regular and the sphere is inscribed in it, all the inequalities written above become equalities. Hence, the upper bound of possible values of $ r $ is $ 1/4 $. A sphere with radius $ 1/4 $ has a volume of $ \pi/48 $, and this number is the upper bound of the volumes of all considered spheres. | \pi/48 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
LI OM - III - Task 5
For a given natural number $ n \geq 2 $, find the smallest number $ k $ with the following property. From any $ k $-element set of fields of the $ n \times n $ chessboard, one can select a non-empty subset such that the number of fields of this subset in each row and each column of the chessboard is even. | We will prove the following two statements:
From any set composed of $ m + n $ squares of a chessboard with dimensions $ m \times n $ ($ m,n \geq 2 $), one can select a non-empty subset having an even number of squares in each row and each column of the chessboard.
There exists a set of $ m+n-1 $ squares of a chessboard with dimensions $ m \times n $, from which it is not possible to select a non-empty subset having an even number of squares in each row and each column of the chessboard.
From the above statements applied for $ m = n $, we conclude that the smallest number satisfying the conditions of the problem is $ k = 2n $.
Proof of statement 1.
We will conduct an inductive proof with respect to $ m + n $. For $ m = 2 $, $ n = 2 $, the statement 1 is true.
Let us fix two natural numbers $ m $, $ n $ with a sum greater than $ 4 $ and assume that statement 1 is true for any chessboard with a sum of dimensions less than $ m + n $. Consider any set $ A $ composed of $ m + n $ squares of a chessboard $ S $ with dimensions $ m \times n $. The following three cases are possible:
there exists a row or column of the chessboard $ S $ that does not contain any square from the set $ A $;
there exists a row or column of the chessboard $ S $ that contains exactly one square from the set $ A $;
in each row and each column, there are at least two squares from the set $ A $.
om51_3r_img_4.jpg
In case (a), we remove from the chessboard $ S $ that column (or row) which does not contain any square from the set $ A $. We then remove any square from the set $ A $ (in the figure, the squares of set $ A $ are marked with circles). In this way, we obtain a new chessboard that contains a certain set $ A $ composed of $ m + n - 1 $ squares and whose sum of dimensions is equal to $ m + n - 1 $ (fig. 2). Hence, each of the dimensions of the obtained chessboard is not less than $ 2 $. Therefore, by the inductive assumption, one can select from the set $ A $ a non-empty subset having an even number of squares in each row and each column. By reinserting the removed column or removed row back into its place (fig. 3), we obtain the desired subset of the set $ A $.
om51_3r_img_5.jpg
We proceed similarly in case (b): we first find a column (or row) that contains exactly one square from the set $ A $, and then remove that column from the chessboard $ S $ (fig. 4). As a result, we obtain a new chessboard that contains a certain set $ A' $ composed of $ m + n - 1 $ squares and whose sum of dimensions is equal to $ m + n - 1 $ (fig. 5). As above, we apply the inductive assumption, and then reinsert the removed column or removed row (fig. 6).
Consider case (c). Let $ k_1,k_2,\ldots,k_n, w_1,w_2,\ldots,w_m $ denote, respectively, the numbers of squares of the set $ A $ in the individual columns and rows. Then
Moreover, $ k_i,w_j \geq 2 $ for all $ i $, $ j $. Hence, $ k_i = w_j = 2 $. This means that the set $ A $ has exactly two squares in each column and each row. This implies that the number of squares of the set $ A $ in each row and each column is even.
The inductive proof, and thus the proof of statement 1, is complete.
Proof of statement 2.
om51_3r_img_6.jpg
Consider the set $ A $ composed of all $ m + n - 1 $ squares of a chessboard with dimensions $ m \times n $ located in the bottom row and the first column (fig. 7). To obtain an even number of squares in the columns from the second to the last, we must remove from the set $ A $ the squares that are in those columns. After their removal, we see that for the same reason, we must remove the remaining squares of the set $ A $. This completes the proof of statement 2. | 2n | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
XXII OM - III - Task 3
How many locks at least need to be placed on the treasury so that with a certain distribution of keys among the 11-member committee authorized to open the treasury, any 6 members can open it, but no 5 can? Determine the distribution of keys among the committee members with the minimum number of locks. | Suppose that for some natural number $ n $ there exists a key distribution to $ n $ locks among an 11-member committee such that the conditions of the problem are satisfied. Let $ A_i $ denote the set of locks that the $ i $-th member of the committee can open, where $ i = 1, 2, \ldots, 11 $, and let $ A $ denote the set of all locks. Then from the conditions of the problem, we have
for any five-element subset $ \{ i_1, \ldots, i_5\} $ of the set $ \{1, 2, \ldots, 11\} $ and
for any six-element subset $ \{j_1, \ldots, j_6\} $ of the set $ \{1,2,\ldots, 11\} $.
From (1), it follows that the set $ A - (A_{i_1} \cup \ldots \cup A_{i_5}) $ is non-empty. Let $ x_{i_1}, \ldots, x_{i_5} $ be one of its elements, i.e., a lock that the group of committee members numbered $ i_1, \ldots, i_5 $ cannot open. From (2), it follows that for every $ j \not \in \{i_1, \ldots, i_5 \} $ we have $ x_{i_1 , \ldots, i_5} \in A_j $.
Suppose that $ x_{i_1,\ldots,i_5} = x_{k_1, \ldots, k_5} $ for some subsets $ \{i_1, \ldots, i_5\} $ and $ \{k_1, \ldots, k_5\} $. If these subsets were different, then, for example, $ i_t \not \in \{ k_1, \ldots, k_5 \} $. Therefore, $ x_{k_1, \ldots, k_5} \in A_{i_t} $; but on the other hand, this leads to a contradiction. The obtained contradiction proves that $ \{i_1, \ldots,i_5\} = \{ k_1, \ldots, k_5 \} $.
In other words, different five-element subsets $ \{i_1, \ldots, i_5\} $ correspond to different locks. Therefore, the number of locks is not less than the number of five-element subsets of an 11-element set, i.e., $ n \geq \binom{11}{5} = 462 $.
We will now prove that if we install $ \binom{11}{5} $ locks on the treasury, then we can distribute the keys to them among the members of the 11-member committee in such a way that the conditions of the problem are satisfied.
Let us associate each of the $ \binom{11}{5} $ locks with a five-element subset of the set $ \{1, 2, \ldots, 11\} $ in a one-to-one manner. If a lock corresponds to the subset $ \{i_1, \ldots, i_5\} $, then the keys to it are given to all members of the committee whose numbers are different from $ i_1, \ldots, i_5 $.
We will show that no five members of the committee can open a certain lock, and therefore the treasury. Indeed, the members of the committee numbered $ i_1, \ldots, i_5 $ do not have the key to the lock corresponding to the subset $ \{i_1, \ldots, i_5\} $.
We will show that any six members of the committee can open any lock, and therefore the treasury. If the members of the committee have numbers $ j_1, \ldots, j_6 $ and want to open a lock corresponding to the subset $ \{i_1, \ldots, i_5\} $, then one of the six numbers $ j_1, \ldots, j_6 $ does not belong to this five-element subset, say $ j_t \not \in \{i_1, \ldots, i_5 \} $. Therefore, the member of the committee numbered $ j_t $ has the key to the lock corresponding to the subset $ \{i_1, \ldots, i_5\} $.
Thus, the smallest number satisfying the conditions of the problem is $ \binom{11}{5} = 462 $. | 462 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
LVIII OM - I - Problem 4
For each natural number $ n\ge 3 $, determine the number of sequences $ (c_1,c_2,\ldots,c_n) $, where $ {c_i\in\{0,1,\ldots,9\}} $, with the following property:\break in every triple of consecutive terms, there are at least two terms that are equal. | Let $ z_n $ be the number of $ n $-term sequences having the desired properties (we will further call them {\it good} sequences). Let $ x_n $ be the number of good sequences $ (c_1,c_2,\ldots,c_n) $, whose last two terms $ c_{n-1} $ and $ c_n $ are equal, and let $ y_n $ denote the number of good sequences $ (c_1,c_2,\ldots,c_n) $, in which $ c_{n-1}\ne c_n $. Of course, the equation $ z_n=x_n+y_n $ is satisfied.
Every good $ (n+1) $-term sequence $ (c_1,c_2,\ldots,c_{n+1}) $, in which the last two terms $ c_n $ and $ c_{n+1} $ are equal, arises from exactly one good sequence $ (c_1,c_2,\ldots,c_n) $ by adding the condition $ c_{n+1}=c_n $. Therefore, the following relationship holds:
On the other hand, a good $ (n+1) $-term sequence $ (c_1,c_2,\ldots,c_{n+1}) $, in which the last two terms $ c_n $ and $ c_{n+1} $ are different, can be obtained in two ways. In the first way, we take a good $ n $-term sequence $ (c_1,c_2,\ldots,c_n) $, in which $ c_{n-1}=c_n $, and take $ c_{n+1} $ to be any number from the set $ \{0,1,\ldots,9\} $ different from $ c_n $. This way we will obtain $ 9x_n $ different good $ (n+1) $-term sequences. In the second way, we choose a good $ n $-term sequence $ (c_1,c_2, \ldots,c_n) $, in which $ c_{n-1}\ne c_n $ and set $ c_{n+1}=c_{n-1} $. This time we will obtain $ y_n $ different sequences. Moreover, no sequence can be obtained in both ways. It follows that the following equation holds:
From equations (1) and (2) we get
for $ n=4,5,6,\ldots $. We will now apply the method of solving linear recurrences (see L Olimpiada Matematyczna, Sprawozdanie Komitetu Głównego, Warszawa 2000, Appendix A, p. 103). The characteristic equation of recurrence (3) is $ t^2=2t+8 $, which has two distinct real roots: $ t=4 $ and $ t=-2 $. Therefore, there exist real numbers $ a $, $ b $, such that the following equation holds:
To complete the solution, it remains to determine the values of $ a $, $ b $. For this purpose, we will calculate the numbers $ z_3 $, $ z_4 $. From equations (1) and (2) it follows that
The number of good sequences $ (c_1,c_2,c_3) $, in which $ c_2=c_3 $, is $ 10^2=100 $, since the values of $ c_1 $, $ c_2 $ can be chosen arbitrarily, while the number of good sequences $ (c_1,c_2,c_3) $, in which $ c_2\ne c_3 $, is $ 2\cdot 10\cdot 9=180 $, because the pair of different numbers $ (c_2,c_3) $ can be chosen arbitrarily and $ c_1 $ must be equal to $ c_2 $ or $ c_3 $. Therefore,
Combining the values calculated above with condition (4) we obtain the system of equations
whose solution are the numbers $ a=b=5 $.
Answer: The sought number of sequences is $ 5\cdot(4^n+(-2)^n) $.
Note: After obtaining dependencies (1) and (2), the solution of the problem can be completed without using the method of solving linear recurrences (although this requires guessing the correct coefficients). Namely, from dependencies (1) and (2) we get
Assuming now the notation
we have therefore
We also calculate that $ x_3=100 $, $ y_3=180 $, so $ u_3=480 $, $ v_3=120 $; therefore, from dependency (5) by induction we obtain the formulas
Hence, ultimately,
The final answer is: The sought number of sequences is $ 5\cdot(4^n+(-2)^n) $. | 5\cdot(4^n+(-2)^n) | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
1. Let $\log _{2} x=m \in Z, m>0, \log _{6} y=n \in Z, n>0$.
Then $x=2^{m}, y=6^{n}$. As a result, we have
$$
\text { GCD }(x, y)=\text { GCD }\left(2^{m}, 6^{n}\right)=\text { GCD }\left(2^{m}, 2^{n} \cdot 3^{n}\right)=8=2^{3} .
$$
Case 1. $m \geq n$. Then $n=3, \quad y=6^{3}=216$,
GCD $\left(\log _{2} x, 3\right)=3$. From this, we find $\log x=B k=$ or $x=8^{k}, k \in Z$.
Case 2. $m0$ or $y=216^{s}, s \in Z, s>0$. | Answer: 1) $x=8^{k}, k=1,2, \ldots ; y=216$;
2) $x=8, y=216^{s}, s=1,2, \ldots$ | 8^{k},k=1,2,\ldots;216\text | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. Since the right side of the equation $(x+y)^{2}=49(3 x+5 y)$ is divisible by 49, then $x+y=7 k$. Substituting this into the equation, we get $49 k^{2}=49(3 x+5 y)$ or $3 x+5 y=k^{2}$. Solving the system
$$
\left\{\begin{array}{c}
3 x+5 y=k^{2} \\
x+y=7 k
\end{array}\right.
$$
we find
$$
\left\{\begin{array}{l}
x=\frac{k(35-k)}{2} \\
y=\frac{k(k-21)}{2}
\end{array} k \in Z\right.
$$
From the obtained solutions, we need to select those for which $x$ and $y$ are integers. Since the numbers $k$ and $35-k$ and $k$ and $k-21$ have different parities, the numerators of both fractions are even for any integer $k$, and therefore, the fractions themselves are integers. | Answer: : $\left\{\begin{array}{l}x=\frac{k(35-k)}{2}, \\ y=\frac{k(k-21)}{2},\end{array} k \in Z\right.$. | {\begin{pmatrix}\frac{k(35-k)}{2},\\\frac{k(k-21)}{2},\end{pmatrix}k\inZ.} | Algebra | math-word-problem | Yes | Yes | olympiads | false |
4. Each experience of throwing the circle corresponds to a point $M-$ the position of the center of the circle on the vertical segment $[A ; B]$ of length 1.
Let's introduce the following notations: $R$ - the radius of the circle, $O$ - the midpoint of the segment $[A ; B], \quad O M=x \in[0 ; 0.5]$ - a random variable uniformly distributed on this segment, $\alpha$ - the angle indicated in the figure, $A M=h=\frac{\cos \alpha}{2}$.
The area of the circular segment $S_{1}$ of a circle with radius $R$ is given by the formula:
$$
S_{1}=\left|\alpha R^{2}-\frac{1}{2} R^{2} \sin 2 \alpha\right|
$$
In our case, $R=\frac{1}{2}$, so,
$$
S_{1}=\frac{\alpha}{4}-\frac{\sin 2 \alpha}{8} .
$$
From the problem statement, it follows that
$$
\left\{\begin{array}{c}
S_{1}: S_{2}=(\pi-2):(3 \pi+2) \\
S_{1}+S_{2}=\frac{\pi}{4}
\end{array}\right.
$$
Then $S_{1}=k(\pi-2)$, and $S_{2}=k(3 \pi+2)$. Substituting this into the second equality, we get: $S_{1}+S_{2}=k \cdot 4 \pi=\frac{\pi}{4}$. Therefore, $k=\frac{1}{16}$. Then, $S_{1}=\frac{\alpha}{4}-\frac{\sin 2 \alpha}{8}=\frac{1}{16}(\pi-2)$. From this, we find $\alpha=\frac{\pi}{4}$. Thus, the conditions of the problem correspond to the central angle $P M Q$ equal to $\frac{\pi}{2}$. Then $h=\frac{\sqrt{2}}{4}$ and the favorable outcome of the experiment corresponds to points $M$ that are no more than $\frac{1}{2}-h=\frac{2-\sqrt{2}}{4}$ away from point $O$. Since the probability of the desired event is the ratio of the length of the segment of "favorable" outcomes, i.e., $\frac{2-\sqrt{2}}{2}$ to the length of the segment $[A ; B]$, i.e., to one, the desired probability $P(A)=\frac{2-\sqrt{2}}{2} \approx 0.29$ | Answer: $P(A)=\frac{2-\sqrt{2}}{2} \approx 0.29$. | P(A)=\frac{2-\sqrt{2}}{2}\approx0.29 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
6. Let's introduce the following notations: $S$ - the area of the trapezoid, $S_{1}$ - the area of triangle $ABC$, $S_{2}$ - the area of triangle $ACD$, $h$ - the height of the trapezoid, $\gamma=\frac{q}{p}$, $\mu=\frac{n}{m}$.
We have $S_{1}: S_{2}=\frac{n}{m}$ because these triangles have the same height. Therefore, $S_{1}=\frac{n}{n+m} \cdot S$. From the similarity of triangles $AND$ and $CNT$, it follows that $\frac{TC}{AD}=\frac{q}{p}$. From this equality, we get: $TC=\frac{q}{p} AD$. Then $TB=TC-BC=\frac{q}{p} AD-\frac{n}{m} AD=\left(\frac{q}{p}-\frac{n}{m}\right) AD$. From the similarity of triangles $AMD$ and $BTM$, it follows that
$$
\mathrm{BM}: \mathrm{AM}=TB: AD=\left(\frac{q}{p}-\frac{n}{m}\right)
$$
Therefore,
$$
\frac{AM}{AB}=\frac{AM}{AM+MB}=\frac{1}{1+BM: AM}=\frac{1}{1+\frac{q}{p}-\frac{n}{m}}
$$
Then
$$
S_{AMN}=\frac{AM}{AB} \cdot \frac{p}{p+q} \cdot S_{1}=\frac{1}{1+\frac{q}{p}-\frac{n}{m}} \cdot \frac{1}{1+\frac{q}{p}} \cdot S_{1}=\frac{1}{1+\gamma-\mu} \cdot \frac{1}{1+\gamma} \cdot S_{1}
$$
From this, we get
$$
\begin{gathered}
S_{MBCN}=S_{1}-S_{AMN}=\left(1-\frac{1}{1+\gamma-\mu} \cdot \frac{1}{1+\gamma}\right) S_{1}= \\
=\left(1-\frac{1}{1+\gamma-\mu} \cdot \frac{1}{1+\gamma}\right) \frac{\mu}{1+\mu} S
\end{gathered}
$$
In our problem, $\gamma=2, \mu=\frac{1}{3}$, so $S_{MBCN}: S=7: 32$. | Answer: $\quad S_{\text {MVCN }}: S=7: 32$. | S_{MBCN}:S=7:32 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
3. Find all pairs of integers $(x ; y)$ that satisfy the equation $(x-y)^{2}=25(2 x-3 y)$. | Answer: $\left\{\begin{array}{l}x=m(15-m), \\ y=m(10-m),\end{array} m \in Z\right.$. | (15-),(10-),\inZ | Algebra | math-word-problem | Yes | Yes | olympiads | false |
4. On a plane, an infinite number of parallel lines are drawn, each separated from the next by a distance of 1. A circle with a diameter of 1 is randomly thrown onto the plane. Find the probability that a line intersecting the circle divides it into parts such that the ratio of the areas (of the smaller to the larger part) does not exceed the number \((4 \pi - 3 \sqrt{3}) : (8 \pi + 3 \sqrt{3})\). | Answer: $P(A)=\frac{1}{2}$. | \frac{1}{2} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
5. For what values of $a$ does the system of equations $\left\{\begin{array}{c}(x+2+2 \sqrt{2} \cos a)^{2}+(y-1-2 \sqrt{2} \sin a)^{2}=2 \\ (x-y+3)(x+y+1)=0\end{array}\right.$ have three
solutions? | Answer: $a_{1}=\frac{7 \pi}{12}+\pi k, a_{2}=\frac{11 \pi}{12}+\pi k, k \in Z$. | a_{1}=\frac{7\pi}{12}+\pik,a_{2}=\frac{11\pi}{12}+\pik,k\inZ | Algebra | math-word-problem | Yes | Yes | olympiads | false |
1. Natural numbers $x$ and $y$ are such that their LCM $(x, y)=3^{6} \cdot 2^{8}$, and GCD $\left(\log _{3} x, \log _{12} y\right)=2$. Find these numbers. | Answer: $x=3^{6}=729, y=12^{4}=20736$. | 3^{6}=729,12^{4}=20736 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. Find all pairs of integers $(x ; y)$ that satisfy the equation $(x+2 y)^{2}=9(x+y)$. | Answer: $\left\{\begin{array}{l}x=m(2 m-3), \\ y=m(3-m),\end{array} m \in Z\right.$. | (2-3),(3-),\inZ | Algebra | math-word-problem | Yes | Yes | olympiads | false |
4. On a plane, an infinite number of parallel lines are drawn, each separated from the next by a distance of 1. A circle with a diameter of 1 is randomly thrown onto the plane. Find the probability that a line intersecting the circle divides it into parts such that the ratio of the areas (of the smaller to the larger part) does not exceed the number \((2 \pi - 3 \sqrt{3}) : (10 \pi + 3 \sqrt{3})\). | Answer: $P(A)=\frac{2-\sqrt{3}}{2} \approx 0.13$. | \frac{2-\sqrt{3}}{2} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
5. For what values of $a$ does the system of equations $\left\{\begin{array}{c}(x-2-\sqrt{5} \cos a)^{2}+(y+1-\sqrt{5} \sin a)^{2}=\frac{5}{4} \text { have two solutions? } \\ (x-2)(x-y-3)=0\end{array}\right.$ | Answer: $a \in\left(\frac{\pi}{12}+\pi k ; \frac{\pi}{3}+\pi k\right) \cup\left(\frac{5 \pi}{12}+\pi k ; \frac{2 \pi}{3}+\pi k\right), k \in Z$. | \in(\frac{\pi}{12}+\pik;\frac{\pi}{3}+\pik)\cup(\frac{5\pi}{12}+\pik;\frac{2\pi}{3}+\pik),k\inZ | Algebra | math-word-problem | Yes | Yes | olympiads | false |
6. Point $N$ divides the diagonal $A C$ of trapezoid $A B C D$ in the ratio $C N: N A=4$. The lengths of the bases $B C$ and $A D$ of the trapezoid are in the ratio $2: 3$. A line is drawn through point $N$ and vertex $D$, intersecting the lateral side $A B$ at point $M$. What fraction of the area of the trapezoid is the area of quadrilateral $M B C N$? | Answer: $S_{\text {MBCN }}: S=124: 325$.
# | 124:325 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
4. On a plane, an infinite number of parallel lines are drawn, each at a distance of 1 from each other. A circle with a diameter of 1 is randomly thrown onto the plane. Find the probability that a line intersecting the circle divides it into parts, the ratio of the areas of which (the smaller to the larger) does not exceed the number \((5 \pi - 3):(7 \pi + 3)\) | Answer: $P(A)=\frac{2-\sqrt{2-\sqrt{3}}}{2} \approx 0.74$ | P(A)=\frac{2-\sqrt{2-\sqrt{3}}}{2}\approx0.74 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
5. For what values of $a$ does the system of equations $\left\{\begin{array}{c}(x-2-3 \cos a)^{2}+(y+2-3 \sin a)^{2}=1 \\ (y+2)(x+y)=0\end{array}\right.$ have a unique solution? | Answer: $a_{1}= \pm \arcsin \frac{1}{3}+\pi k, a_{2}=-\frac{\pi}{4} \pm \arcsin \frac{1}{3}+\pi k, k \in Z$. | a_{1}=\\arcsin\frac{1}{3}+\pik,a_{2}=-\frac{\pi}{4}\\arcsin\frac{1}{3}+\pik,k\inZ | Algebra | math-word-problem | Yes | Yes | olympiads | false |
1. Let $m$ be the number of coins in the treasure. Then the number of remaining coins $N$ in the morning is
$$
\begin{gathered}
N=\frac{2}{3}\left(\frac{2}{3}\left(\frac{2}{3}(m-1)-1\right)-1\right)=\frac{2^{3}}{3^{3}}(m-1)-\frac{2}{3}-\frac{2^{2}}{3^{2}} \\
N=\frac{2^{3}}{3^{3}}(m-1)-\frac{10}{9}=3 n \\
8(m-1)-30=81 k, \text { then }\left\{\begin{array}{c}
m-1=3 t, \\
8 t-27 k=10
\end{array},\left\{\begin{array}{c}
m=3 t+1 \\
k=2 s \\
4 t-27 s=5
\end{array}\right.\right. \\
\left\{\begin{array}{c}
m=3 t+1 \\
k=2 s, \\
t=8+27 u, \\
s=1+4 u
\end{array}\right.
\end{gathered}
$$
Considering the constraints
$$
\begin{gathered}
110 \leq 81 u+25 \leq 200, \text { so } u=2, m=187 . \\
m_{1}=1+\frac{187-1}{3}=63, \quad \widetilde{m}_{1}=63+18=81 \\
- \text { the money of the first pirate; } \\
m_{2}=1+\frac{187-63-1}{3}=42, \quad \widetilde{m}_{2}=42+18=60 \\
m_{3}=1+\frac{187-63-42-1}{3}=28, \quad \widetilde{m}_{3}=28+18=46 \\
- \text { the money of the third pirate; } \\
m_{0}=\frac{187-63-42-28}{3}=18 \\
\text {- the money each received in the morning. }
\end{gathered}
$$ | Answer: the first pirate 81 coins, the second pirate 60 coins, the third pirate 46 coins. | 81,60,46 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. For which natural numbers $n$ can the fraction $\frac{3}{n}$ be represented as a periodic decimal fraction of the form $0.1\left(a_{1} a_{2}\right)$ with a period containing two different digits? | Answer: $n=22 ; a_{1}=3, a_{2}=6$. | n=22;a_{1}=3,a_{2}=6 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. Consider the set $M$ of integers $n \in[-100 ; 500]$, for which the expression $A=n^{3}+2 n^{2}-5 n-6$ is divisible by 11. How many integers are contained in $M$? Find the largest and smallest of them? | Answer: 1) 164 numbers; 2) $n_{\text {min }}=-100, n_{\text {max }}=497$. | 164 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. For which natural numbers $n$ can the fraction $\frac{4}{n}$ be represented as a periodic decimal fraction of the form $0.1\left(a_{1} a_{2} a_{3}\right)$ with a period containing at least two different digits? | Answer: $n=27 ; a_{1}=4, a_{2}=8, a_{3}=1$;
$
n=37 ; a_{1}=0, a_{2}=8, a_{3}=2
$ | n=27;a_{1}=4,a_{2}=8,a_{3}=1n=37;a_{1}=0,a_{2}=8,a_{3}=2 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. Consider the set $M$ of integers $n \in[-30 ; 100]$, for which the expression $A=n^{3}+4 n^{2}+n-6$ is divisible by 5. How many integers are contained in $M$? Find the largest and smallest of them. | Answer: 1) 78 numbers; 2) $n_{\min }=-29, n_{\max }=98$. | 78,n_{\}=-29,n_{\max}=98 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. For which natural numbers $n$ can the fraction $\frac{5}{n}$ be represented as a periodic decimal fraction of the form $0.1\left(a_{1} a_{2} a_{3}\right)$ with a period containing at least two different digits? | Answer: $n=27 ; a_{1}=8, a_{2}=5, a_{3}=1$;
$$
n=37 ; a_{1}=3, a_{2}=5, a_{3}=1
$$ | n=27;a_{1}=8,a_{2}=5,a_{3}=1orn=37;a_{1}=3,a_{2}=5,a_{3}=1 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. Consider the set $M$ of integers $n \in[-50 ; 250]$, for which the expression $A=n^{3}-2 n^{2}-13 n-10$ is divisible by 13. How many integers are contained in $M$? Find the largest and smallest of them? | Answer: 1) 69 numbers; 2) $n_{\min }=-47, n_{\max }=246$. | 69,n_{\}=-47,n_{\max}=246 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
1. Solution. According to the problem, the sum of the original numbers is represented by the expression:
$$
\begin{aligned}
& \left(a_{1}+2\right)^{2}+\left(a_{2}+2\right)^{2}+\ldots+\left(a_{50}+2\right)^{2}=a_{1}^{2}+a_{2}^{2}+\ldots+a_{50}^{2} \rightarrow \\
& {\left[\left(a_{1}+2\right)^{2}-a_{1}^{2}\right]+\left[\left(a_{2}+2\right)^{2}-a_{2}^{2}\right]+\ldots\left[\left(a_{50}+2\right)^{2}-a_{50}^{2}\right]=0 \rightarrow} \\
& \rightarrow 4\left(a_{1}+1\right)+4\left(a_{2}+1\right)+\ldots+4\left(a_{50}+1\right)=0 \rightarrow a_{1}+a_{2}+\ldots+a_{50}=-50
\end{aligned}
$$
Then, if we add 3, we get:
$$
\begin{aligned}
& \left(a_{1}+3\right)^{2}+\left(a_{2}+3\right)^{2}+\ldots+\left(a_{50}+3\right)^{2}-\left(a_{1}^{2}+a_{2}^{2}+\ldots+a_{50}^{2}\right)= \\
& =\left[\left(a_{1}+3\right)^{2}-a_{1}^{2}\right]+\left[\left(a_{2}+3\right)^{2}-a_{2}^{2}\right]+\ldots\left[\left(a_{50}+3\right)^{2}-a_{50}^{2}\right]= \\
& =3\left(2 a_{1}+3\right)+3\left(2 a_{2}+3\right)+\ldots+3\left(2 a_{50}+3\right)=6\left(a_{1}+a_{2}+\ldots+a_{50}\right)+9 \cdot 50= \\
& =-300+450=150
\end{aligned}
$$ | Answer: will increase by 150. | 150 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
1. A set of 60 numbers is such that adding 3 to each of them does not change the value of the sum of their squares. By how much will the sum of the squares of these numbers change if 4 is added to each number? | Answer: will increase by 240. | 240 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
1. A set of 70 numbers is such that adding 4 to each of them does not change the magnitude of the sum of their squares. By how much will the sum of the squares of these numbers change if 5 is added to each number? | Answer: will increase by 350. | 350 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
1. A set of 80 numbers is such that adding 5 to each of them does not change the magnitude of the sum of their squares. By how much will the sum of the squares of these numbers change if 6 is added to each number? | Answer: will increase by 480. | 480 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
5. Find the fraction $\frac{p}{q}$ with the smallest possible natural denominator, for which $\frac{1}{2014}<\frac{p}{q}<\frac{1}{2013}$. Enter the denominator of this fraction in the provided field | 5. Find the fraction $\frac{p}{q}$ with the smallest possible natural denominator, for which
$\frac{1}{2014}<\frac{p}{q}<\frac{1}{2013}$. Enter the denominator of this fraction in the provided field
Answer: 4027 | 4027 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
8. The residents of the village Razumevo, located 3 km away from the river, love to visit the village Vkusnotevo, situated 3.25 km downstream on the opposite bank of the river, 1 km away from the shore. The width of the river is 500 m, the speed of the current is 1 km/h, and the banks are parallel straight lines. The residents of Razumevo have laid out the shortest route, taking into account that they always cross the river in a direction perpendicular to the shore with their own speed of 2 km/h. How long does this route take if the speed on land does not exceed 4 km/h? Enter the answer in hours in the provided field. | 8. The residents of the village Razumevo, located 3 km away from the river, love to visit the village Vkusnotevo, situated 3.25 km downstream on the opposite bank of the river, 1 km away from the shore. The width of the river is 500 m, the speed of the current is 1 km/h, and the banks are parallel straight lines. The residents of Razumevo have laid out the shortest route, taking into account that they always cross the river in a direction perpendicular to the shore at their own speed of 2 km/h. How long does this route take if the land travel speed does not exceed 4 km/h? Enter the answer in hours in the provided field.
Answer: 1.5 | 1.5 | Other | math-word-problem | Yes | Yes | olympiads | false |
6. Answer: $\Sigma_{\max }=\frac{\pi}{4}\left((\sqrt{2 a}-\sqrt{b})^{4}+6(3-2 \sqrt{2}) b^{2}\right)=4 \pi(19-12 \sqrt{2}) \approx 25.5$
Option 0
In rectangle $ABCD$ with sides $AD=a, AB=b(b<a<2b)$, three circles $K, K_{1}$, and $K_{2}$ are placed. Circle $K$ is externally tangent to circles $K_{1}$ and $K_{2}$, and also to the lines $AD$ and $BC$. Circles $K_{1}$ and $K_{2}$ are also tangent to the sides $AD, AB$ and $AD, CD$ respectively. Find the maximum and minimum possible value of the sum of the areas of the three circles. | Answer: $\quad S_{\max }=\pi\left(R^{2}+\rho^{2}+r^{2}\right)_{\max }=\frac{\pi}{4}\left(6(3-2 \sqrt{2}) b^{2}+(\sqrt{2 a}-\sqrt{b})^{4}\right)$
$$
S_{\min }=\pi\left(R^{2}+\rho^{2}+r^{2}\right)=\pi\left(\frac{b^{2}}{4}+\frac{(\sqrt{a+b}-\sqrt{b})^{4}}{2}\right)
$$
Solution.
Let $\rho, r, R$ be the radii of circles $K_{1}, K_{2}, K$. $b=2 R$.
$A E=x-$ variable, $x \in[R ; a-R], T E=P N=x-\rho=2 \sqrt{R \rho}$,
$E L=Q M=2 \sqrt{R r}=a-x-r, O P=R+\rho, O Q=R+r, O M=R-r, O N=R-\rho$.
The conditions $\left\{\begin{array}{c}\rho+2 \sqrt{R} \cdot \sqrt{\rho}-x=0 \\ r+2 \sqrt{R} \cdot \sqrt{r}-a+x=0 \\ \rho^{2}+r^{2} \rightarrow \max \end{array}\right.$ lead to the dependence of $r$ and $\rho$ on $x$ in the form $\left\{\begin{array}{c}\rho=(\sqrt{x+R}-\sqrt{R})^{2} \\ \rho=(\sqrt{a-x+R}-\sqrt{R})^{2}\end{array}\right.$. Denoting $\varphi(x)=(\sqrt{x+R}-\sqrt{R})^{4}$, we arrive at $\rho^{2}+r^{2}=\varphi(x)+\varphi(a-x)$.
Properties of the function $\varphi(x): 1) \varphi(x) \uparrow$ on the interval $[R ; a-R]$
2) $\varphi^{\prime}(x)=\frac{2(\sqrt{x+R}-\sqrt{R})^{3}}{\sqrt{x+R}}>0, x \in[R ; a-R]$
$\varphi^{\prime}(x) \uparrow$ on the interval $[R ; a-R]$.
3) $\varphi^{\prime \prime}=\frac{(\sqrt{x+R}-\sqrt{R})^{2}(2 \sqrt{x+R}+\sqrt{R})}{(\sqrt{x+R})^{3}}>0, x \in[R ; a-R]$, i.e., the function
Critical points of the function:
$\left(\rho^{2}+r^{2}\right)^{\prime}=\varphi^{\prime}(x)-\varphi^{\prime}(a-x)=0 \rightarrow \varphi^{\prime}(x)=\varphi^{\prime}(a-x) \rightarrow x=a-x \rightarrow x^{*}=\frac{a}{2}$
At the endpoints of the interval, the values of the function $\rho^{2}+r^{2}=\varphi(x)+\varphi(a-x)$ are the same and equal to
$\varphi(R)+\varphi(a-R)=(\sqrt{2 R}-\sqrt{R})^{4}+(\sqrt{a}-\sqrt{R})^{4}=\frac{b^{2}}{4}(\sqrt{2}-1)^{4}+\frac{1}{4}(\sqrt{2 a}-\sqrt{b})^{4}$. This value is the greatest for $\rho^{2}+r^{2}$ when $b \leq a \leq 2 b$. Under the same conditions, the minimum value of $\rho^{2}+r^{2}$ is achieved at $x=a / 2$ and it is equal to $2 \varphi\left(\frac{a}{2}\right)=\frac{(\sqrt{a+b}-\sqrt{b})^{4}}{2}$. Then the maximum value of the sum of the areas of the circles
$$
S_{\max }=\pi\left(R^{2}+\rho^{2}+r^{2}\right)_{\max }=\frac{\pi}{4}\left(6(3-2 \sqrt{2}) b^{2}+(\sqrt{2 a}-\sqrt{b})^{4}\right)
$$
and the minimum value
$$
S_{\min }=\pi\left(R^{2}+\rho^{2}+r^{2}\right)=\pi\left(\frac{b^{2}}{4}+\frac{(\sqrt{a+b}-\sqrt{b})^{4}}{2}\right)(* *)
$$ | S_{\max}=\frac{\pi}{4}(6(3-2\sqrt{2})b^{2}+(\sqrt{2}-\sqrt{b})^{4}) | Geometry | math-word-problem | Yes | Yes | olympiads | false |
3. Let $c_{n}=11 \ldots 1$ be a number with $n$ ones in its decimal representation. Then $c_{n+1}=10 \cdot c_{n}+1$. Therefore,
$$
c_{n+1}^{2}=100 \cdot c_{n}^{2}+22 \ldots 2 \cdot 10+1
$$
For example,
$c_{2}^{2}=11^{2}=(10 \cdot 1+1)^{2}=100+2 \cdot 10+1=121$,
$c_{3}^{2}=111^{2}=100 \cdot 11^{2}+220+1=12100+220+1=12321$,
$c_{4}^{2}=1111^{2}=100 \cdot 111^{2}+2220+1=1232100+2220+1=1234321$, and so on.
Notice that for all the listed numbers $c_{2}^{2}, c_{3}^{2}, c_{4}^{2}$, the digit around which these numbers are symmetric (2 in the case of $c_{2}^{2}$, 3 in the case of $c_{3}^{2}$, 4 in the case of $c_{4}^{2}$) matches the number of ones in the number being squared. The number $c=123456787654321$ given in the problem is also symmetric around the digit 8, i.e., it can be assumed that it is the square of the number $c_{8}=11111111$. This can be verified by column multiplication or using the recursive relation (*). | Answer: 1) $a^{2}=121 ;$ 2) $b^{2}=12321 ;$ 3) $\sqrt{c}=11111111$. | \sqrt{}=11111111 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. If $\quad a=\overline{a_{1} a_{2} a_{3} a_{4} a_{5} a_{6}}, \quad$ then $\quad P(a)=\overline{a_{6} a_{1} a_{2} a_{3} a_{4} a_{5}}$, $P(P(a))=\overline{a_{5} a_{6} a_{1} a_{2} a_{3} a_{4}} \quad$ with $\quad a_{5} \neq 0, a_{6} \neq 0, a_{1} \neq 0 . \quad$ From the equality $P(P(a))=a$ it follows that $a_{1}=a_{5}, a_{2}=a_{6}, a_{3}=a_{1}$, $a_{4}=a_{2}, a_{5}=a_{3}, a_{6}=a_{4}$, that is, $a_{1}=a_{3}=a_{5}=t, t=1,2, \ldots, 9$ and $a_{2}=a_{4}=a_{6}=u, u=1,2, \ldots, 9$. Thus, the sought $a=\overline{\text { tututu }}$ and there are 81 such different numbers ( $t$ and $u$ can take any values of the decimal system digits from 1 to 9).
Let $n>2-$ be a prime number, $a=\overline{a_{1} a_{2} a_{3} a_{4} \ldots a_{n-3} a_{n-2} a_{n-1} a_{n}}$. Then
$$
\begin{gathered}
P(a)=\overline{a_{n} a_{1} a_{2} a_{3} a_{4} \ldots a_{n-3} a_{n-2} a_{n-1}} \\
P(P(a))=\overline{a_{n-1} a_{n} a_{1} a_{2} a_{3} a_{4} \ldots a_{n-3} a_{n-2}}
\end{gathered}
$$
The property $P(P(a))=a$ gives the relations $a_{1}=a_{n-1}=a_{n-3}=\ldots=a_{1}$. For a prime $n>2$, all the digits of the number $a$ are involved in the chain, so they are all equal to each other. | Answer: 1) 81 is the number; 2) $a=\overline{t u t u t u}, t, u$, where $t, u$ - are any digits, not equal to zero. | 81 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. A cyclic permutation $P(a)$ of a natural number $a=\overline{a_{1} a_{2} \ldots a_{n}}, a_{n} \neq 0$ is the number $b=\overline{a_{n} a_{1} a_{2} \ldots a_{n-1}}$ written with the same digits but in a different order: the last digit becomes the first, and the rest are shifted one position to the right. How many eight-digit numbers $a$ exist for which $P(P(P(P(a))))=a$? Find these numbers. Prove that for a prime $n>3$, the equation $P(P(P(P(a))))=a$ has no solutions $a$ with distinct digits. | Answer: 1) $9^{4} \quad$ number; 2) $a=\overline{t u \gamma w t u \gamma w}, t, u, v, w \quad-$ arbitrary digits, not equal to zero. | 9^4 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. Square the numbers $a=10001, b=100010001$. Extract the square root of the number $c=1000200030004000300020001$. | 1) $a^{2}=100020001$; 2) $b^{2}=10002000300020001$; 3) $\sqrt{c}=1000100010001$. | 1000100010001 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. Let $a > b$, denote $x, y, z$ as digits. Consider several cases for the decimal representation of the desired numbers.
Case 1. Let $a = x \cdot 10 + y, b = y \cdot 10 + z$.
a) Write the conditions of the problem for these notations
$$
\left\{\begin{array} { c }
{ 1 0 x + y = 3 ( 1 0 y + z ) , } \\
{ x + y = y + z + 3 , }
\end{array} \left\{\begin{array}{c}
10 x - 29 y = 3 z, \\
z = x - 3
\end{array} 7 x - 29 y = -9, \left\{\begin{array}{c}
x = 7 \\
y = 2 \\
z = 4
\end{array}\right.\right.\right.
$$
Thus, $a = 72, b = 24$.
b) $\left\{\begin{array}{c}10 x + y = 3(10 y + z), \\ x + y = y + z - 3,\end{array}\left\{\begin{array}{c}10 x - 29 y = 3 z \\ z = x + 3,\end{array}\right.\right.$
$7 x - 29 y = 9$, there are no digits satisfying the condition of the problem.
Case 2. Let $a = x \cdot 10 + y, b = z \cdot 10 + x$.
$$
\left\{\begin{array} { c }
{ 1 0 x + y = 3 ( 1 0 z + x ) , } \\
{ x + y = x + z \pm 3 }
\end{array} \left\{\begin{array}{c}
7 x + y = 30 z, \\
z = y \pm 3,
\end{array} \quad 7 x - 29 y = \pm 90, \emptyset\right.\right.
$$
Case 3. Let $a = x \cdot 10 + y, b = x \cdot 10 + z$, there are no digits satisfying the condition of the problem.
Case 4. Let $a = x \cdot 10 + y, b = z \cdot 10 + y$.
$$
\begin{aligned}
& \left\{\begin{array} { c }
{ 1 0 x + y = 3 ( 1 0 z + y ) , } \\
{ x + y = z + y \pm 3 , }
\end{array} \left\{\begin{array}{c}
10 x - 2 y = 30 z, \\
z = x \pm 3,
\end{array} \quad 10 x + y = \pm 45\right.\right. \\
& \left\{\begin{array}{l}
x = 4 \\
y = 5 \\
z = 1
\end{array}\right.
\end{aligned}
$$
Thus, $a = 45, \quad b = 15$. | Answer: $a=72, b=24 ; \quad a=45, b=15$. | =72,b=24;\quad=45,b=15 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
5. Point $P$ is located on side $AB$ of square $ABCD$ such that $AP: PB=2: 3$. Point $Q$ lies on side $BC$ of the square and divides it in the ratio $BQ: QC=3$. Lines $DP$ and $AQ$ intersect at point $E$. Find the ratio of the lengths $AE: EQ$. | Answer: $A E: E Q=4: 9$.
# | AE:EQ=4:9 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
3. For two two-digit, integer, positive numbers $a$ and $b$, it is known that 1) one of them is 14 greater than the other; 2) in their decimal representation, one digit is the same; 3) the sum of the digits of one number is twice the sum of the digits of the other. Find these numbers. | Answer: $a_{1}=37, b_{1}=23 ; a_{2}=31, b_{2}=17$. | a_{1}=37,b_{1}=23;a_{2}=31,b_{2}=17 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
5. Point $P$ is located on side $AB$ of square $ABCD$ such that $AP: PB=1: 2$. Point $Q$ lies on side $BC$ of the square and divides it in the ratio $BQ: QC=2$. Lines $DP$ and $AQ$ intersect at point $E$. Find the ratio of the lengths $PE: ED$. | Answer: $P E: E D=2: 9$.
# | PE:ED=2:9 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
3. For two two-digit, positive integers $a$ and $b$, it is known that 1) one of them is 12 greater than the other; 2) in their decimal representation, one digit is the same; 3) the sum of the digits of one number is 3 greater than the sum of the digits of the other. Find these numbers. | Answer: $a=11 t+10, b=11 t-2, t=2,3, \ldots, 8$;
$$
\tilde{a}=11 s+1, \quad \tilde{b}=11 s+13, \quad s=1,2,3, \ldots, 6
$$ | =11+10,b=11-2,=2,3,\ldots,8;\quad\tilde{}=11+1,\quad\tilde{b}=11+13,\quad=1 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
5. Point $P$ is located on side $AB$ of square $ABCD$ such that $AP: PB=1: 4$. Point $Q$ lies on side $BC$ of the square and divides it in the ratio $BQ: QC=5$. Lines $DP$ and $AQ$ intersect at point $E$. Find the ratio of the lengths $AE: EQ$. | Answer: $A E: E Q=6: 29$. | AE:EQ=6:29 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
Problem 5. Answer: 1.
## Variant 0
Circles $K_{1}$ and $K_{2}$ have a common point $A$. Through point $A$, three lines are drawn: two pass through the centers of the circles and intersect them at points $B$ and $C$, the third is parallel to $BC$ and intersects the circles at points $M$ and $N$. Find the length of segment $MN$, if the length of segment $BC$ is $a$. | Answer: $a$
Solution.
Notations: $\alpha$ - angle $B A M, \beta-$ angle $C A N$
Angle $A B C=\alpha$, angle $A C B=\beta$ (vertical angles).
Angle $A M B=90^{\circ}$, angle $A N C=90^{\circ}$ (subtend the diameter).
Angle $A B M=90^{\circ}-\alpha$, angle $A C N=90^{\circ}-\beta$ (acute angles in right triangles)
Conclusion: angles $M B C$ and $N C B$ are right angles, quadrilateral $M B C N$ is a rectangle and $M N=B C=a$
## Variant 2 | a | Geometry | math-word-problem | Yes | Yes | olympiads | false |
2. Let's find the greatest common divisor (GCD) of the numerator and the denominator. By the properties of GCD:
$$
\begin{aligned}
& \text { GCD }(5 n-7,3 n+2)=\text { GCD }(5 n-7-(3 n+2), 3 n+2)= \\
& =\text { GCD }(2 n-9,3 n+2)=\text { GCD }(2 n-9, n+11)= \\
& \quad=\text { GCD }(n-20, n+11)=\text { GCD }(31, n+11) .
\end{aligned}
$$
Since 31 is a prime number, we get that GCD $(31, n+11)=1$ or GCD $(31, n+11)=31$. The first case does not apply, as it does not lead to the reduction of the fraction. The second case is realized only if $n+11$ is divisible by 31, that is, for $n=31 k-11, k \in \mathbb{Z}$. In this case, the fraction is reduced only by 31. No other common divisors of the numerator and the denominator are possible, since 31 is a prime number. | Answer: it can be reduced by 31 when $n=31k-11, k \in Z$. | 31k-11,k\in\mathbb{Z} | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. Let $x_{1}, x_{2}$ be the integer solutions of the equation $x^{2} + p x + 3 q = 0$ with prime numbers $p$ and $q$. Then, by Vieta's theorem,
$$
x_{1} + x_{2} = -p
$$
From this, we conclude that both roots must be negative. Further, since the roots are integers and the numbers $q, 3$ are prime, there are only two possible cases:
$$
x_{1} = -1, x_{2} = -3 q \text{ or } x_{1} = -3, x_{2} = -q.
$$
Consider the first case. If $x_{1} = -1, x_{2} = -3 q$, then $1 + 3 q = p$. Thus, $p$ and $q$ have different parities. The only even prime number is 2. If $p = 2$, then the equation $1 + 3 q = 2$ has no solution in prime numbers, so this case is impossible. If $p$ is odd, then $q$ is even. The only possible value is $q = 2$. In this case, $p = 1 + 2 \cdot 3 = 7$ is a prime number. We have the solution $p = 7, q = 2$. In this case, $x_{1} = -1, x_{2} = -6$.
Consider the second case. If $x_{1} = -3, x_{2} = -q$, then $3 + q = p$. Again, $p$ and $q$ have different parities. If $p = 2$, then the equation $3 + q = 2$ has no solution in prime numbers, so this case is impossible. If $p$ is odd, then $q$ is even. For $q = 2$, $p = 3 + 2 = 5$ is a prime number. We have another solution $p = 5, q = 2$. In this case, $x_{1} = -3, x_{2} = -2$.
We have considered all possible cases. There are no other solutions. | Answer: there are two pairs of solutions: $p=5, q=2 ; p=7, q=2$. | p=5,q=2;p=7,q=2 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2. By what natural number can the numerator and denominator of the ordinary fraction of the form $\frac{5 n+3}{7 n+8}$ be reduced? For which integers $n$ can this occur? | Answer: it can be reduced by 19 when $n=19k+7, k \in Z$. | 19 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
2. By what natural number can the numerator and denominator of the ordinary fraction of the form $\frac{4 n+3}{5 n+2}$ be reduced? For which integers $n$ can this occur? | Answer: can be reduced by 7 when $n=7 k+1, k \in Z$. | 7 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
5. Based on the base $AC$ of the isosceles triangle $ABC$, a circle is constructed with $AC$ as its diameter, intersecting the side $BC$ at point $N$ such that $BN: NC = 7: 2$. Find the ratio of the lengths of the segments $AN$ and $BC$. | Answer: $\frac{A N}{B C}=\frac{4 \sqrt{2}}{9}$.
# | \frac{AN}{BC}=\frac{4\sqrt{2}}{9} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
2. By what natural number can the numerator and denominator of the ordinary fraction of the form $\frac{3 n+2}{8 n+1}$ be reduced? For which integers $n$ can this occur? | Answer: it can be reduced by 13 when $n=13k-5, k \in Z$. | 13k-5,k\inZ | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
5. Based on the base $AC$ of the isosceles triangle $ABC$, a circle is constructed with $AC$ as its diameter, intersecting the side $BC$ at point $N$ such that $BN: NC = 5: 2$. Find the ratio of the lengths of the medians $NO$ and $BO$ of triangles $ANC$ and $ABC$. | Answer: $\frac{N O}{B O}=\frac{1}{\sqrt{6}}$. | \frac{NO}{BO}=\frac{1}{\sqrt{6}} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
5. The angle at vertex $B$ of triangle $A B C$ is $130^{\circ}$. Through points $A$ and $C$, lines perpendicular to line $A C$ are drawn and intersect the circumcircle of triangle $A B C$ at points $E$ and $D$. Find the acute angle between the diagonals of the quadrilateral with vertices at points $A, C, D$ and $E$.
Problem 1 Answer: 12 students. | Solution. Let $a$ be the number of students in the first category, $c$ be the number of students in the third category, and $b$ be the part of students from the second category who will definitely lie in response to the first question (and say "YES" to all three questions), while the rest of the students from this category will answer "NO" to all three questions. Then, "YES" to the first question will be given by $a+b+c=25$ students. "YES" to the second question will be given by $b+c=21$ students. "YES" to the third question will be given by $b=6$ students. Solving the system, we get: $a=4, b=6, c=15$. Then, to the second category, we should assign $31-a-c=12$ students.
Problem 2 Answer: $a= \pm 5-2 \sqrt{6}$.
Solution. By Vieta's theorem, the roots of the equation are $m=(a+2 \sqrt{6})$ and $n=\left(\frac{1}{a}-2 \sqrt{6}\right)$.
Then we have:
$$
\left[\begin{array}{l}
a=m-2 \sqrt{6} \\
\frac{1}{a}=n+2 \sqrt{6}
\end{array} \rightarrow 1=m n+2 \sqrt{6}(m-n)-24 \rightarrow 2 \sqrt{6}(m-n)=25-m n\right.
$$
If $m, n \in Z, m \neq n$, then $2 \sqrt{6}=\frac{25-m n}{m-n}$ is a rational number, which is incorrect. Therefore, $m=n$ and then $m^{2}=25 \rightarrow m= \pm 5 \rightarrow a= \pm 5-2 \sqrt{6}$.
Problem 3 Answer: 5400 numbers.
Solution. Write $496125=3^{4} \cdot 5^{3} \cdot 7^{2}$. There are a total of $3^{4} \cdot 5^{3}=10125$ multiples of 49. Among them, $3^{3} \cdot 5^{3}=3375$ numbers are divisible by 3, $3^{4} \cdot 5^{2}=2025$ numbers are divisible by 5, and $3^{3} \cdot 5^{2}=675$ numbers are divisible by 15. Then, among the numbers that are multiples of 49, there are $3375+2025-675=4725$ numbers that are divisible by either 3 or 5. Therefore, the numbers that are not divisible by either 3 or 5 will be $10125-4775=$ 5400 desired numbers.
Problem 4 Answer: $n=210$.
Solution. According to the problem, $n=7 k$ and the expression
$$
n^{2}+25 n+100=(n+5)(n+20)=(7 k+5)(7 k+20)
$$
must be divisible by 5 and 23. Note that if one of the factors is divisible by 5, then the other is also divisible by 5 and vice versa, so:
$$
7 k+5=5 m \rightarrow 7 k=5(m-1) \rightarrow\left\{\begin{array}{c}
k=5 t \\
m=7 t+1
\end{array} \rightarrow n=35 t, t \in Z\right.
$$
Case 1. $7 k+5$ is divisible by 23:
$$
35 t+5=23 u \rightarrow\left\{\begin{array}{l}
t=23 v-10 \\
u=35 v-15
\end{array} \rightarrow n=35 t=35(23 v-10) \rightarrow n_{\min }=455\right.
$$
Case 2. $7 k+20$ is divisible by 23:
$$
35 t+20=23 u \rightarrow\left\{\begin{array}{c}
t=23 v+6 \\
u=35 v+10
\end{array} \rightarrow n=35 t=35(23 v+6) \rightarrow n_{\min }=210\right.
$$
Choosing the smallest of the found $n_{\min }$, we get $n_{\min }=210$.
Problem 5 Answer: $80^{\circ}$.
Solution. Figures 1 and 2 show the possible geometric configurations.
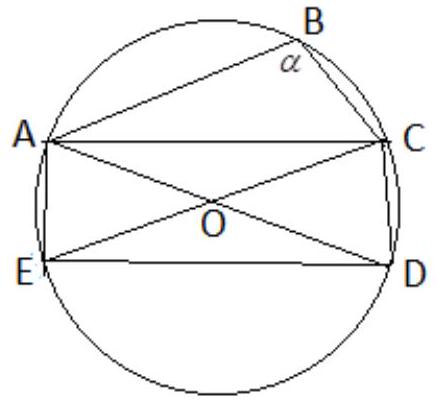
Fig 1
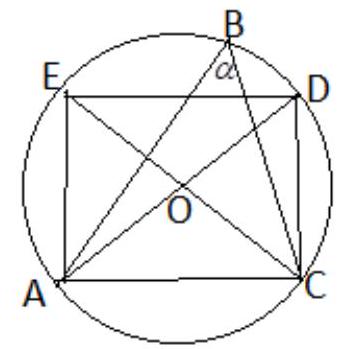
Fig 2
In the figures, point $O$ is the center of the circle $K$ circumscribed around triangle $A B C$.
Case 1. $\alpha>90^{\circ}$ (Fig. 1). Quadrilateral $A B C D$ is inscribed in circle $K$ by construction, so point $O$ is equidistant from points $C$ and $D$ at a distance equal to the radius of circle $K$. Similarly, point $O$ is equidistant from points $A$ and $E$ at the same distance. Therefore, point $O$ is the intersection point of the diagonals of rectangle $A C D E$. The angle $C D O$, as the opposite angle to $\alpha$ in the inscribed quadrilateral $A B C D$, is equal to $180^{\circ}-\alpha$. The desired angle between the diagonals of rectangle $A C D E$ is: $180^{\circ}-2\left(180^{\circ}-\alpha\right)=2\left(\alpha-90^{\circ}\right)$.
Case 2. $\alpha<90^{\circ}$ (Fig. 2). Point $O$ is equidistant from points $A, C, D$ and $E$, so it is the intersection point of the diagonals of rectangle $A C D E$ with these vertices. The angle $A D C$ is equal to $\alpha$, as it is inscribed and subtends the same arc of circle $K$ as angle $A B C$. Then the desired angle $D O C$ is: $180^{\circ}-2 \alpha=2\left(90^{\circ}-\alpha\right)$.
In case 1, $\alpha=130^{\circ}$, so case 1 applies, and $2\left(\alpha-90^{\circ}\right)=80^{\circ}$. | 80 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
2. For what values of $a$ are the roots of the equation $x^{2}-\left(a+\frac{1}{a}\right) x+(a+\sqrt{35})\left(\frac{1}{a}-\sqrt{35}\right)=0$ integers? | Answer: $a= \pm 6-\sqrt{35}$. | \6-\sqrt{35} | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2. For what values of $a$ are the roots of the equation $x^{2}-\left(a+\frac{1}{a}\right) x+(a+4 \sqrt{3})\left(\frac{1}{a}-4 \sqrt{3}\right)=0$ integers? | Answer: $a= \pm 7-4 \sqrt{3}$. | \7-4\sqrt{3} | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2. For what values of $a$ are the roots of the equation $x^{2}-\left(a+\frac{1}{a}\right) x+(a+4 \sqrt{5})\left(\frac{1}{a}-4 \sqrt{5}\right)=0$ integers? | Answer: $a= \pm 9-4 \sqrt{5}$. | \9-4\sqrt{5} | Algebra | math-word-problem | Yes | Yes | olympiads | false |
5. The angle at vertex $B$ of triangle $A B C$ is $58^{0}$. Through points $A$ and $C$, lines perpendicular to line $A C$ are drawn and intersect the circumcircle of triangle $A B C$ at points $D$ and $E$. Find the angle between the diagonals of the quadrilateral with vertices at points $A, C, D$ and $E$. | Answer: $64^{0}$
## Grading Criteria for the Final Round of the Rosatom Olympiad 04.03.2023 8th Grade
In all problems, the correct answer without justification $\quad 0$ | 64^{0} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
5. For which $a$ does the set of solutions of the inequality $x^{2}+(|y|-a)^{2} \leq a^{2}$ contain all pairs of numbers $(x ; y)$ for which $(x-4)^{2}+(y-2)^{2} \leq 1$?
Problem 5 Answer: $a \in\left[\frac{19}{2} ;+\infty\right)$ | Solution.
Case 1. $a \leq 0$. The first inequality is satisfied by a single point (0, 0), so the situation where the solutions of the second inequality (points of the circle of radius 1) are contained in the solutions of the first inequality is impossible.
Case 2. $a>0$. The solutions of the first inequality are the points of circles $K_{1}$ and $K_{2}$, where $K_{1}$ is a circle of radius $a$ centered at point $O_{1}(0 ; a)$, and $K_{2}$ is a circle of radius $a$ centered at point $O_{2}(0 ;-a)$. The solutions of the second inequality are the points of circle $K_{3}$ of radius 1 centered at point $O(4 ; 2)$. The conditions of the problem will be satisfied if circle $K_{3}$ is inside circle $K_{1}$. This situation occurs when $O_{1} O \leq a-1$. We obtain the inequality:
$$
\sqrt{4^{2}+(a-2)^{2}} \leq a-1
$$
This is equivalent to the system
$$
\left\{\begin{array}{l}
a-1 \geq 0 \\
4^{2}+(a-2)^{2} \leq(a-1)^{2}
\end{array}\right.
$$
Solving this system, we find $a \geq \frac{19}{2}$.
Problem 6 Answer: $s=7.5$
Solution.
Let the chords $B C$ and $A B$ subtend central angles $\alpha$ and $\beta$ respectively. Then, due to the perpendicularity of the diagonals, the chords $A D$ and $C D$ subtend central angles $\pi-\alpha$ and $\pi-\beta$. The sum of the areas of triangles $B C O$ and $A B O$ is:
$$
S_{B C O}+S_{A B O}=\frac{1}{2} R^{2}(\sin \alpha+\sin \beta)
$$
where $R$ is the radius of the circumscribed circle.
The sum of the areas of triangles $A D O$ and $C D O$ is:
$$
S_{A D O}+S_{C D O}=\frac{1}{2} R^{2}(\sin (\pi-\alpha)+\sin (\pi-\beta))=\frac{1}{2} R^{2}(\sin \alpha+\sin \beta)=S_{B C O}+S_{A B O}
$$
Thus, the area of quadrilateral $A B C O$ is half the area of quadrilateral $A B C D$, which is $\frac{1}{2} d_{1} \cdot d_{2}=\frac{1}{2} \cdot 5 \cdot 6=15$.
## Variant 2
Problem 1 Answer: 1) 6 pairs; 2) (3;5), (27;5), (243;5), (2187;5), (6561, 25),(1;625).
Problem 2 Answer: $S_{\text {min }}=\frac{\pi^{2}}{14}$
Problem 3 Answer: 24 circles (15+9)
Problem 4 Answer: $P(A)=\frac{\operatorname{arctg} 2-\operatorname{arctg}(1 / 2)}{\pi}=\frac{\operatorname{arctg} 2-\operatorname{arcctg} 2}{\pi}=\frac{2 \operatorname{arctg} 2}{\pi}-\frac{1}{2}$
Problem 5 Answer: $a \geq \frac{5}{2}$
Problem 6 Answer: $s=7$
## Variant 3
Problem 1 Answer: 1) 2 pairs; 2) (4;49), (1024;49)
Problem 2 Answer: $S_{\min }=\frac{\pi^{2}}{6}$
Problem 3 Answer: 30 circles. (18+12)
Problem 4 Answer: $P(A)=\frac{\operatorname{arctg}\left(\frac{4}{3}\right)-\operatorname{arctg}\left(\frac{3}{4}\right)}{\pi}=\frac{\operatorname{arctg}\left(\frac{4}{3}\right)-\operatorname{arctg}\left(\frac{4}{3}\right)}{\pi}=\frac{2 \operatorname{arctg}(4 / 3)}{\pi}-\frac{1}{2}$
Problem 5 Answer: $a<\frac{7}{3}$
Problem 6 Answer: $s=1.5$
## Variant 4
Problem 1 Answer: 1) 2 pairs; 2) (8;125), (64;125)
Problem 2 Answer: $S_{\min }=\frac{\pi^{2}}{10}$
Problem 3 Answer: 9 circles. (9+0)
Problem 4 Answer: $P(A)=\frac{\operatorname{arctg}\left(\frac{3}{2}\right)-\operatorname{arctg}\left(\frac{2}{3}\right)}{\pi}=\frac{\operatorname{arctg}\left(\frac{3}{2}\right)-\operatorname{arcctg}\left(\frac{3}{2}\right)}{\pi}=\frac{2 \operatorname{arctg}(3 / 2)}{\pi}-\frac{1}{2}$
Problem 5 Answer: $a=-\frac{8}{5}$
Problem 6 Answer: $s=12$ | \in[\frac{19}{2};+\infty) | Inequalities | math-word-problem | Yes | Yes | olympiads | false |
6. Answer: 1) $S_{1}=\frac{3 \sqrt{3}}{2}$ 2) $S_{2}=6 \sqrt{6}$
Option 0
In a cube $A B C D A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ with edge $a$, a section is made by a plane parallel to the plane $B D A^{\prime}$ and at a distance $b$ from it. Find the area of the section. | Answer: 1) $S_{1}=\frac{\sqrt{3}}{2}(a-b \sqrt{3})^{2}$ for $a>b \sqrt{3}$ 2) $S_{2}=\frac{\sqrt{3}}{2}\left(a^{2}+2 a b \sqrt{6}-12 b^{2}\right)$ for $a>b \sqrt{6}$ Solution.
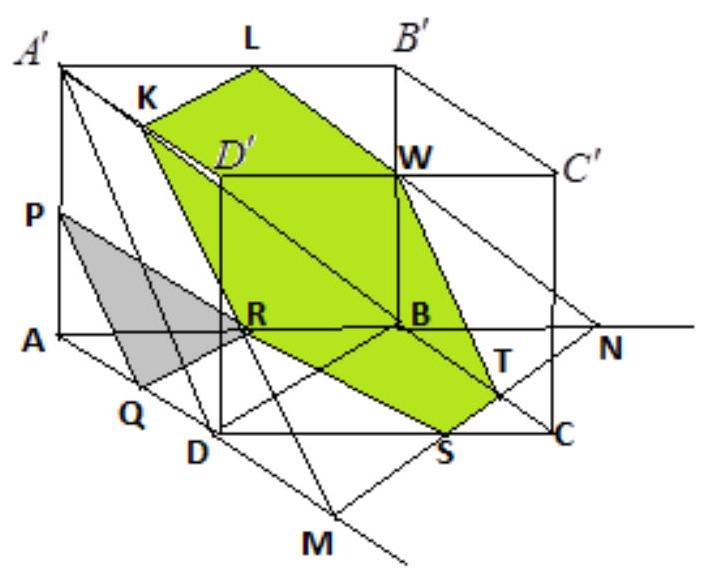
Fig. 1
Fig. 2
Case 1. The section passes through point $P$ on edge $A A^{\prime}, A P=n a, 0<b \sqrt{3}$. Triangle $P Q R$ of the section is similar to triangle $A^{\prime} D B$ with a similarity coefficient of $n$, so $S_{P Q R}=n^{2} \cdot S_{A^{\prime} D B}=\frac{(a-b \sqrt{3})^{2}}{a^{2}} \cdot \frac{\sqrt{3}}{4} 2 a^{2}=\frac{\sqrt{3}}{2}(a-b \sqrt{3})^{2}$.
In the case where $1 a=2 \sqrt{3}, b=1$, the area of the section $S_{1}$ in Case 1 is $S_{1}=\frac{3 \sqrt{3}}{2}$
Case 2. The section passes through point $G$ on diagonal $A^{\prime} C^{\prime}$, at a distance $b$ from the plane $B D A^{\prime}$.
The perpendicular $G U$ (Fig. 2), dropped from point $G$ to the plane $B D A^{\prime}$, has a length of $b$:
$A^{\prime} G=\frac{b}{\cos \alpha}=b \sqrt{3}$. Through point $G$, we draw a line $K L$ (see Fig. 1) parallel to the diagonal $B^{\prime} D^{\prime}$. $A^{\prime} K=\sqrt{2} \cdot A^{\prime} G=b \sqrt{6}$. Through point $K$, we draw a line parallel to the diagonal $A^{\prime} D$ of the face until it intersects the extension of edge $A D$ at point $M$. Similar actions are performed with line $L N$ (Fig. 1). We connect points $M$ and $N$, which intersects the edges of the base of the cube at points $S$ and $T$.
Calculations:
$$
D M=A^{\prime} K=b \sqrt{6}, M S=D M \sqrt{2}=2 b \sqrt{3}
$$
$A M=a+D M=a+b \sqrt{6}, M N=\sqrt{2} \cdot A M=a \sqrt{2}+2 b \sqrt{3}$.
$S T=M N-2 \cdot M S=a \sqrt{2}+2 b \sqrt{3}-4 b \sqrt{3}=a \sqrt{2}-2 b \sqrt{3}>0 \rightarrow a>b \sqrt{6}$.
The area $S_{2}^{*}$ of the projection of the section in Case 2 is $S_{2}^{*}=a^{2}-S_{A^{\prime} K L}-S_{T S C}=a^{2}-3 b^{2}-\frac{1}{4} T S^{2}=a^{2}-3 b^{2}-\frac{(a \sqrt{2}-2 b \sqrt{3})^{2}}{4}=\frac{a^{2}+2 a b \sqrt{6}-12 b^{2}}{2}$.
The area of the section $S_{2}=\frac{S_{2}^{*}}{\cos \alpha}=\frac{\sqrt{3}}{2}\left(a^{2}+2 a b \sqrt{6}-12 b^{2}\right)$.
In the case where $1 a=2 \sqrt{3}, b=1$, i.e., $S_{2}=6 \sqrt{6}$. | S_{1}=\frac{\sqrt{3}}{2}(-b\sqrt{3})^{2} | Geometry | math-word-problem | Yes | Yes | olympiads | false |
5. Answer: 1) $\alpha_{1}=\operatorname{arctg} \frac{24}{7}+2 \pi k, k \in Z \quad$ 2) $\alpha_{2}=\pi+2 \pi k, k \in Z$
$$
\text { 3) } \alpha_{3}=\operatorname{arctg} \frac{4+3 \sqrt{24}}{4 \sqrt{24}-3}+2 \pi k, k \in Z \quad \text { 4) } \alpha_{4}=\operatorname{arctg} \frac{3 \sqrt{24}-4}{4 \sqrt{24}+3}+2 \pi k, k \in Z
$$
(Other forms of the answers are possible: using other inverse trigonometric functions). | Solution (Geometric)
The line with the equation $x \cos a + y \sin a - 2 = 0$ is tangent to a circle of radius 2 centered at the origin. The system has a unique solution if it is tangent (common tangent) to the circle with the equation $x^{2} + y^{2} + 6x - 8y + 24 = 0 \leftrightarrow (x + 3)^{2} + (y - 4)^{2} = 1$, radius 1, and center at point $P(-3; 4)$. There are four cases of common tangents for two non-intersecting circles. Case 1.
Fig 1
In Fig 1, $L_{1}$ is the common tangent of the circles, $PQ$ is parallel to $L_{1}$, Triangle $OPQ$ is a right triangle with legs 3 and 4, equal to triangle $OPM$. The angle $POQ$ is $\beta, \operatorname{tg} \beta = 4 / 3$.
From the equality $\alpha + 2\beta = \pi$, we conclude that $\operatorname{tg} \alpha = -\operatorname{tg} 2\beta = -\frac{2 \operatorname{tg} \beta}{1 - \operatorname{tg}^{2} \beta} = \frac{24}{7}$, and the first series of solutions is $\alpha_{1} = \operatorname{arctg} \frac{24}{7} + 2\pi k, k \in \mathbb{Z}$.
Case 2. The second common tangent $L_{2}$ (see Fig. 1) is perpendicular to the x-axis and corresponds to the values of the parameter from the second series $\alpha_{2} = \pi + 2\pi k, k \in \mathbb{Z}$.
Case 3. The common tangent $L_{3}$ (does not intersect the segment $OP$)
Fig 2
The angle $POM$ is $\beta, \operatorname{tg} \beta = 4 / 3$, the length of the segment $PQ = \sqrt{24}$, the angle $POQ$ is $\gamma, \operatorname{tg} \gamma = \sqrt{24}$.
From the equality $\alpha + \beta + \gamma = \pi$, it follows that $\operatorname{tg} \alpha = -\operatorname{tg}(\beta + \gamma) = -\frac{4 / 3 + \sqrt{24}}{1 - 4 \sqrt{24} / 3} = \frac{4 + 3 \sqrt{24}}{4 \sqrt{24} - 3}$.
This value corresponds to the third series of solutions: $\alpha_{3} = \operatorname{arctg} \frac{4 + 3 \sqrt{24}}{4 \sqrt{24} - 3} + 2\pi k, k \in \mathbb{Z}$.
Case 4. The common tangent $L_{4}$ is symmetric to the tangent $L_{3}$ with respect to the line $PO$, so (see Fig. 2) $\alpha_{4} = \alpha_{3} + 2\gamma, \operatorname{tg} \alpha_{4} = \frac{\operatorname{tg} \alpha_{3} + \operatorname{tg} 2\gamma}{1 - \operatorname{tg} \alpha_{3} \cdot \operatorname{tg} 2\gamma} = \frac{3 \sqrt{24} - 4}{4 \sqrt{24} + 3}$.
Then the fourth series of solutions is $\alpha_{4} = \operatorname{arctg} \frac{3 \sqrt{24} - 4}{4 \sqrt{24} + 3} + 2\pi k, k \in \mathbb{Z}$. | \alpha_{1}=\operatorname{arctg}\frac{24}{7}+2\pik,k\inZ\quad\alpha_{2}=\pi+2\pik,k\inZ\quad\alpha_{3}=\operatorname{arctg}\frac{4+3\sqrt{24}}{4\sqrt{24}-3}+2\pik,k\inZ\ | Algebra | math-word-problem | Yes | Yes | olympiads | false |
1. According to the problem, Sasha makes one step in 1 second, while Dan makes one step in $\frac{6}{7}$ seconds. Therefore, after 6 seconds, both Sasha and Dan will have made an integer number of steps, specifically, Sasha will have made 6 steps, and Dan will have made 7 steps. Consequently, we need to consider moments of time that are multiples of 6 seconds, i.e., $t=6k, k=1,2, \ldots$. Since Sasha's step length is 0.4 meters and Dan's step length is 0.6 meters, in $t=6k$ seconds, Sasha will have walked $6 \cdot k \cdot 0.4 = 2.4k$ meters, and Dan will have walked $7 \cdot k \cdot 0.6 = 4.2k$ meters. The distance between Sasha and Dan on the road at such moments of time is:
$$
d(k)=|200-2.4k|+|300-4.2k|.
$$
Consider the function $d(x), x \in \mathbb{R}$. For $x \leq x_{1}=\frac{300}{4.2}=71.42 \ldots$
$$
d(x)=200-2.4x+300-4.2x=500-6.6x
$$
For $x_{1} \leq x \leq x_{2}=\frac{200}{2.4}=83$,(3)
$$
d(x)=200-2.4x-300+4.2x=1.8x-100
$$
For $x \geq x_{2}$
$$
d(x)=-200+2.4x-300+4.2x=6.6x-500
$$
We have obtained that for $x \leq x_{1}$ the function $d(x)$ is decreasing, and for $x \geq x_{1}$ it is increasing. This means that at the point $x=x_{1}$ the function $d(x)$ attains its minimum value. To find the minimum of the function $d(k)$, consider the nearest integer values of $k$ to $x=x_{1}$: $k_{1}=\left[x_{1}\right]=71$ and $k_{2}=\left[x_{1}\right]+1=72$. Calculate $d(71)=500-6.6 \cdot 71=31.4$ and $d(72)=1.8 \cdot 72-100=29.6$. Therefore, the smallest possible distance between Sasha and Dan is 29.6 meters. Since this distance is achieved at $k=72$, the number of steps Sasha has taken by this time is $6 \cdot 72=432$, and the number of steps Dan has taken is $7 \cdot 72=504$. | Answer: 1) $d_{\min }=29.6$ m; 2) Sasha made 432 steps, Dania made 504 steps. | 29.6 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
3. Rewrite the original equation in the form
$$
16 z^{2}+4 x y z+\left(y^{2}-3\right)=0
$$
This is a quadratic equation in terms of z. It has a solution if $D / 4=4 x^{2} y^{2}-16\left(y^{2}-3\right) \geq 0$. After transformations, we obtain the inequality
$$
y^{2}\left(x^{2}-4\right)+12 \geq 0
$$
If $x^{2}-4 \geq 0$, then the first term on the left side of the inequality is non-negative, and consequently, the left side is greater than or equal to 12 for any $y$. If $x^{2}-4<0$, then the first term on the left side of the inequality is negative, and by choosing $y$, we can make the left side of the inequality negative. Therefore, the condition of the problem is satisfied by $x$ for which $x^{2}-4 \geq 0$. From this, we find $x \in(-\infty ;-2] \cup[2 ;+\infty)$. | Answer: $\quad x \in(-\infty ;-2] \cup[2 ;+\infty)$. | x\in(-\infty;-2]\cup[2;+\infty) | Algebra | math-word-problem | Yes | Yes | olympiads | false |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.