Gromov series [GRPO]
Collection
Specific datasets particulary effective in GRPO
•
8 items
•
Updated
•
1
id
stringlengths 12
21
| en
stringlengths 1
2.05k
| answer
stringlengths 21
1.24k
| problem
stringlengths 4
2.1k
|
|---|---|---|---|
numina_1.5_0
|
Problem 4. A $5 \times 100$ table is divided into 500 unit square cells, where $n$ of them are coloured black and the rest are coloured white. Two unit square cells are called adjacent if they share a common side. Each of the unit square cells has at most two adjacent black unit square cells. Find the largest possible value of $n$.
|
{"ground_truth": "302"}
|
Таблица размером $5 \times 100$ разделена на 500 единичных квадратных ячеек, из которых $n$ окрашены в черный цвет, а остальные — в белый. Две единичные квадратные ячейки называются соседними, если у них есть общая сторона. Каждая из единичных квадратных ячеек имеет не более двух соседних ячеек, окрашенных в черный цвет. Найдите наибольшее возможное значение $n$.
|
numina_1.5_4
|
## Problem 4
Find all positive integers $x, y, z$ and $t$ such that
$$
2^{x} \cdot 3^{y}+5^{z}=7^{t}
$$
|
{"ground_truth": "3,1,=2"}
|
Найдите все положительные целые числа $x, y, z$ и $t$ такие, что
$$
2^{x} \cdot 3^{y}+5^{z}=7^{t}
$$
|
numina_1.5_8
|
Problem 2. Consider an acute triangle $A B C$ with area S. Let $C D \perp A B \quad(D \in A B)$, $D M \perp A C \quad(M \in A C)$ and $\quad D N \perp B C \quad(N \in B C)$. Denote by $H_{1}$ and $H_{2}$ the orthocentres of the triangles $M N C$ and $M N D$ respectively. Find the area of the quadrilateral $\mathrm{AH}_{1} \mathrm{BH}_{2}$ in terms of $S$.
|
{"ground_truth": "S"}
|
Рассмотрим острый треугольник $A B C$ с площадью $S$. Пусть $C D \perp A B \quad(D \in A B)$, $D M \perp A C \quad(M \in A C)$ и $\quad D N \perp B C \quad(N \in B C)$. Обозначим через $H_{1}$ и $H_{2}$ ортоцентры треугольников $M N C$ и $M N D$ соответственно. Найдите площадь четырехугольника $\mathrm{AH}_{1} \mathrm{BH}_{2}$ в терминах $S$.
|
numina_1.5_12
|
## Problem 1.
Find all pairs $(a, b)$ of positive integers such that $a!+b$ and $b!+a$ are both powers of 5 .
|
{"ground_truth": "(1,4),(4,1),(5,5)"}
|
Найдите все пары $(a, b)$ положительных целых чисел такие, что $a!+b$ и $b!+a$ являются степенями 5.
|
numina_1.5_16
|
Problem 1. Find all prime numbers $a, b, c$ and positive integers $k$ which satisfy the equation
$$
a^{2}+b^{2}+16 \cdot c^{2}=9 \cdot k^{2}+1
$$
|
{"ground_truth": "(37,3,3,13),(17,3,3,7),(3,37,3,13),(3,17,3,7),(3,3,2,3)"}
|
Найдите все простые числа $a, b, c$ и положительные целые числа $k$, удовлетворяющие уравнению
$$
a^{2}+b^{2}+16 \cdot c^{2}=9 \cdot k^{2}+1
$$
|
numina_1.5_20
|
C2. Consider a regular $2 n$-gon $P$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We want to color the sides of $P$ in 3 colors, such that every side is colored in exactly one color, and each color must be used at least once. Moreover, from every point in the plane external to $P$, at most 2 different colors on $P$ can be seen (ignore the vertices of $P$, we consider them colorless). Find the number of distinct such colorings of $P$ (two colorings are considered distinct if at least one side is colored differently).
|
{"ground_truth": "6n"}
|
Рассмотрим правильный $2n$-угольник $P$ на плоскости, где $n$ — положительное целое число. Мы говорим, что точка $S$ на одной из сторон $P$ видна из точки $E$, внешней для $P$, если отрезок $S E$ не содержит других точек, лежащих на сторонах $P$, кроме $S$. Требуется раскрасить стороны $P$ в 3 цвета так, чтобы каждая сторона была окрашена ровно в один цвет, и каждый цвет должен быть использован хотя бы один раз. Более того, из любой точки плоскости, внешней для $P$, можно увидеть не более 2 различных цветов на $P$ (вершины $P$ игнорируются, считаем их бесцветными). Найдите количество различных таких раскрасок $P$ (две раскраски считаются различными, если хотя бы одна сторона окрашена по-разному).
|
numina_1.5_24
|
A4. Solve the following equation for $x, y, z \in \mathbb{N}$
$$
\left(1+\frac{x}{y+z}\right)^{2}+\left(1+\frac{y}{z+x}\right)^{2}+\left(1+\frac{z}{x+y}\right)^{2}=\frac{27}{4}
$$
|
{"ground_truth": "z"}
|
Решите следующее уравнение для $x, y, z \in \mathbb{N}$
$$
\left(1+\frac{x}{y+z}\right)^{2}+\left(1+\frac{y}{z+x}\right)^{2}+\left(1+\frac{z}{x+y}\right)^{2}=\frac{27}{4}
$$
|
numina_1.5_28
|
A1. Find all ordered triples $(x, y, z)$ of real numbers satisfying the following system of equations:
$$
\begin{aligned}
x^{3} & =\frac{z}{y}-2 \frac{y}{z} \\
y^{3} & =\frac{x}{z}-2 \frac{z}{x} \\
z^{3} & =\frac{y}{x}-2 \frac{x}{y}
\end{aligned}
$$
|
{"ground_truth": "(1,1,-1),(1,-1,1),(-1,1,1),(-1,-1,-1)"}
|
Найдите все упорядоченные тройки $(x, y, z)$ действительных чисел, удовлетворяющие следующей системе уравнений:
$$
\begin{aligned}
x^{3} & =\frac{z}{y}-2 \frac{y}{z} \\
y^{3} & =\frac{x}{z}-2 \frac{z}{x} \\
z^{3} & =\frac{y}{x}-2 \frac{x}{y}
\end{aligned}
$$
|
numina_1.5_32
|
N6. Find all ordered triples $(x, y, z)$ of integers satisfying the following system of equations:
$$
\begin{aligned}
x^{2}-y^{2} & =z \\
3 x y+(x-y) z & =z^{2}
\end{aligned}
$$
|
{"ground_truth": "(0,0,0),(1,0,1),(0,1,-1),(1,2,-3),(2,1,3)"}
|
Найдите все упорядоченные тройки $(x, y, z)$ целых чисел, удовлетворяющие следующей системе уравнений:
$$
\begin{aligned}
x^{2}-y^{2} & =z \\
3 x y+(x-y) z & =z^{2}
\end{aligned}
$$
|
numina_1.5_36
|
## C1 BUL
A board $n \times n(n \geq 3)$ is divided into $n^{2}$ unit squares. Integers from 0 to $n$ included are written down: one integer in each unit square, in such a way that the sums of integers in each $2 \times 2$ square of the board are different. Find all $n$ for which such boards exist.
|
{"ground_truth": "3\\leqn\\leq6"}
|
Доска $n \times n (n \geq 3)$ разделена на $n^{2}$ единичных квадратов. В каждый единичный квадрат записаны целые числа от 0 до $n$ включительно, таким образом, чтобы суммы чисел в каждом квадрате $2 \times 2$ доски были различны. Найдите все $n$, для которых такие доски существуют.
|
numina_1.5_40
|
G2 Let $A B C D$ be a convex quadrilateral with $\varangle D A C=\varangle B D C=36^{\circ}, \varangle C B D=18^{\circ}$ and $\varangle B A C=72^{\circ}$. If $P$ is the point of intersection of the diagonals $A C$ and $B D$, find the measure of $\varangle A P D$.
|
{"ground_truth": "108"}
|
Пусть $A B C D$ — выпуклый четырехугольник, с $\varangle D A C=\varangle B D C=36^{\circ}, \varangle C B D=18^{\circ}$ и $\varangle B A C=72^{\circ}$. Если $P$ — точка пересечения диагоналей $A C$ и $B D$, найдите величину $\varangle A P D$.
|
numina_1.5_44
|
## C3
For a given positive integer n, two players $A$ and B play the following game: Given is pile of $\boldsymbol{\Omega}$ stones. The players take turn alternatively with A going first. On each turn the player is allowed to take one stone, a prime number of stones, or a multiple of $n$ stones. The winner is the one who takes the last stone. Assuming perfect play, find the number of values for $S_{\infty}$, for which A cannot win.
|
{"ground_truth": "n-1"}
|
Для заданного положительного целого числа $n$, два игрока $A$ и $B$ играют в следующую игру: Дана куча из $\boldsymbol{\Omega}$ камней. Игроки ходят по очереди, начиная с игрока $A$. На каждом ходу игрок может взять один камень, простое число камней или кратное $n$ камней. Победителем является тот, кто берет последний камень. Предполагая оптимальную игру, найдите количество значений для $S_{\infty}$, для которых игрок $A$ не может выиграть.
|
numina_1.5_48
|
N3
Find the integer solutions of the equation
$$
x^{2}=y^{2}\left(x+y^{4}+2 y^{2}\right)
$$
|
{"ground_truth": "(x,y)=(0,0),(12,-2),(12,2),(-8,-2),(-8,2)"}
|
Найдите целочисленные решения уравнения
$$
x^{2}=y^{2}\left(x+y^{4}+2 y^{2}\right)
$$
|
numina_1.5_52
|
C4. We have a group of $n$ kids. For each pair of kids, at least one has sent a message to the other one. For each kid $A$, among the kids to whom $A$ has sent a message, exactly $25 \%$ have sent a message to $A$. How many possible two-digit values of $n$ are there?
|
{"ground_truth": "26"}
|
У нас есть группа из $n$ детей. Для каждой пары детей хотя бы один из них отправил сообщение другому. Для каждого ребенка $A$, среди детей, которым $A$ отправил сообщение, ровно $25 \%$ отправили сообщение $A$. Сколько существует возможных двузначных значений $n$?
|
numina_1.5_56
|
N6. Find all triples $(a, b, c)$ of nonnegative integers that satisfy
$$
a!+5^{b}=7^{c}
$$
|
{"ground_truth": "(,b,)\\in{(3,0,1),(1,2,1),(4,2,2)}"}
|
Найдите все тройки $(a, b, c)$ неотрицательных целых чисел, удовлетворяющие уравнению
$$
a!+5^{b}=7^{c}
$$
|
numina_1.5_60
|
NT3 Find all positive integers $n$ such that the equation $y^{2}+x y+3 x=n\left(x^{2}+x y+3 y\right)$ has at least a solution $(x, y)$ in positive integers.
|
{"ground_truth": "n\\in{1,3,4,9}"}
|
Найдите все положительные целые числа $n$, такие что уравнение $y^{2}+x y+3 x=n\left(x^{2}+x y+3 y\right)$ имеет хотя бы одно решение $(x, y)$ в положительных целых числах.
|
numina_1.5_64
|
G3 Let $A B C$ be a triangle in which ( $B L$ is the angle bisector of $\widehat{A B C}(L \in A C), A H$ is an altitude of $\triangle A B C(H \in B C)$ and $M$ is the midpoint of the side $[A B]$. It is known that the midpoints of the segments $[B L]$ and $[M H]$ coincides. Determine the internal angles of triangle $\triangle A B C$.
|
{"ground_truth": "60"}
|
Пусть $A B C$ — треугольник, в котором ($B L$ — биссектриса угла $\widehat{A B C}(L \in A C)$, $A H$ — высота $\triangle A B C(H \in B C)$ и $M$ — середина стороны $[A B]$. Известно, что середины отрезков $[B L]$ и $[M H]$ совпадают. Определите внутренние углы треугольника $\triangle A B C$.
|
numina_1.5_68
|
Problem A3. Find all pairs $(x, y)$ of real numbers such that $|x|+|y|=1340$ and $x^{3}+y^{3}+2010 x y=670^{3}$.
|
{"ground_truth": "(-670,-670),(1005,-335),(-335,1005)"}
|
Найдите все пары $(x, y)$ действительных чисел, такие что $|x|+|y|=1340$ и $x^{3}+y^{3}+2010 x y=670^{3}$.
|
numina_1.5_72
|
Problem N2. Find all positive integers $n$ such that $36^{n}-6$ is a product of two or more consecutive positive integers.
|
{"ground_truth": "1"}
|
Найдите все положительные целые числа $n$, такие что $36^{n}-6$ является произведением двух или более последовательных положительных целых чисел.
|
numina_1.5_76
|
C3. Consider any four pairwise distinct real numbers and write one of these numbers in each cell of a $5 \times 5$ array so that each number occurs exactly once in every $2 \times 2$ subarray. The sum over all entries of the array is called the total sum of that array. Determine the maximum number of distinct total sums that may be obtained in this way.
|
{"ground_truth": "60"}
|
Рассмотрим любые четыре попарно различных действительных числа и запишем одно из этих чисел в каждую ячейку массива $5 \times 5$ так, чтобы каждое число встречалось ровно один раз в каждом подмассиве $2 \times 2$. Сумма по всем элементам массива называется полной суммой этого массива. Определите максимальное количество различных полных сумм, которые можно получить таким образом.
|
numina_1.5_80
|
N4. Find all triples of integers $(a, b, c)$ such that the number
$$
N=\frac{(a-b)(b-c)(c-a)}{2}+2
$$
is a power of 2016 .
|
{"ground_truth": "(,b,)=(k+2,k+1,k),k\\in\\mathbb{Z}"}
|
Найдите все тройки целых чисел $(a, b, c)$ такие, что число
$$
N=\frac{(a-b)(b-c)(c-a)}{2}+2
$$
является степенью 2016.
|
numina_1.5_84
|
A 3. Find all triples of positive real numbers $(a, b, c)$ so that the expression
$$
M=\frac{(a+b)(b+c)(a+b+c)}{a b c}
$$
gets its least value.
|
{"ground_truth": "==\\sqrt[3]{\\frac{1+\\sqrt{5}}{2}},b=\\frac{1}{}"}
|
Найдите все тройки положительных вещественных чисел $(a, b, c)$ такие, что выражение
$$
M=\frac{(a+b)(b+c)(a+b+c)}{a b c}
$$
достигает своего наименьшего значения.
|
numina_1.5_88
|
A 2. Find the maximum positive integer $k$ such that for any positive integers $m, n$ such that $m^{3}+n^{3}>$ $(m+n)^{2}$, we have
$$
m^{3}+n^{3} \geq(m+n)^{2}+k
$$
|
{"ground_truth": "10"}
|
Найдите максимальное положительное целое число $k$, такое что для любых положительных целых чисел $m, n$, удовлетворяющих условию $m^{3}+n^{3}>$ $(m+n)^{2}$, выполняется
$$
m^{3}+n^{3} \geq(m+n)^{2}+k
$$
|
numina_1.5_92
|
C 2. A set $T$ of $n$ three-digit numbers has the following five properties:
(1) No number contains the digit 0 .
(2) The sum of the digits of each number is 9 .
(3) The units digits of any two numbers are different.
(4) The tens digits of any two numbers are different.
(5) The hundreds digits of any two numbers are different.
Find the largest possible value of $n$.
|
{"ground_truth": "5"}
|
Множество $T$ состоит из $n$ трехзначных чисел и обладает следующими пятью свойствами:
(1) Ни одно число не содержит цифру 0.
(2) Сумма цифр каждого числа равна 9.
(3) Цифры единиц любых двух чисел различны.
(4) Цифры десятков любых двух чисел различны.
(5) Цифры сотен любых двух чисел различны.
Найдите наибольшее возможное значение $n$.
|
numina_1.5_96
|
A2 Find the maximum value of $z+x$, if $(x, y, z, t)$ satisfies the conditions:
$$
\left\{\begin{array}{l}
x^{2}+y^{2}=4 \\
z^{2}+t^{2}=9 \\
x t+y z \geq 6
\end{array}\right.
$$
|
{"ground_truth": "\\sqrt{13}"}
|
Найдите максимальное значение $z+x$, если $(x, y, z, t)$ удовлетворяет условиям:
$$
\left\{\begin{array}{l}
x^{2}+y^{2}=4 \\
z^{2}+t^{2}=9 \\
x t+y z \geq 6
\end{array}\right.
$$
|
numina_1.5_100
|
G2 In a right trapezoid $A B C D(A B \| C D)$ the angle at vertex $B$ measures $75^{\circ}$. Point $H$ is the foot of the perpendicular from point $A$ to the line $B C$. If $B H=D C$ and $A D+A H=8$, find the area of $A B C D$.
|
{"ground_truth": "8"}
|
В прямоугольной трапеции $A B C D(A B \| C D)$ угол при вершине $B$ равен $75^{\circ}$. Точка $H$ — основание перпендикуляра, опущенного из точки $A$ на прямую $B C$. Если $B H=D C$ и $A D+A H=8$, найдите площадь $A B C D$.
|
numina_1.5_104
|
NT4 Determine all prime numbers $p_{1}, p_{2}, \ldots, p_{12}, p_{13}, p_{1} \leq p_{2} \leq \ldots \leq p_{12} \leq p_{13}$, such that
$$
p_{1}^{2}+p_{2}^{2}+\ldots+p_{12}^{2}=p_{13}^{2}
$$
and one of them is equal to $2 p_{1}+p_{9}$.
|
{"ground_truth": "(2,2,2,2,2,2,2,3,3,5,7,7,13),(2,2,2,2,2,2,2,3,3,5,7,13,17),(2,2,2,2,2,2,2,3,3,5,7,29,31)"}
|
Определите все простые числа $p_{1}, p_{2}, \ldots, p_{12}, p_{13}, p_{1} \leq p_{2} \leq \ldots \leq p_{12} \leq p_{13}$, такие что
$$
p_{1}^{2}+p_{2}^{2}+\ldots+p_{12}^{2}=p_{13}^{2}
$$
и одно из них равно $2 p_{1}+p_{9}$.
|
numina_1.5_108
|
C7 Consider a rectangle whose lengths of sides are natural numbers. If someone places as many squares as possible, each with area 3 , inside of the given rectangle, such that
the sides of the squares are parallel to the rectangle sides, then the maximal number of these squares fill exactly half of the area of the rectangle. Determine the dimensions of all rectangles with this property.
|
{"ground_truth": "(2,3);(3,4);(3,6);(3,8);(3,10);(3,12)"}
|
Рассмотрим прямоугольник, длины сторон которого являются натуральными числами. Если кто-то помещает в данный прямоугольник максимально возможное количество квадратов, каждый площадью 3, так, чтобы стороны квадратов были параллельны сторонам прямоугольника, то максимальное количество этих квадратов заполняет ровно половину площади прямоугольника. Определите размеры всех прямоугольников, обладающих этим свойством.
|
numina_1.5_112
|
A5. Solve the equation
$$
8 x^{3}+8 x^{2} y+8 x y^{2}+8 y^{3}=15\left(x^{2}+y^{2}+x y+1\right)
$$
in the set of integers.
|
{"ground_truth": "(x,y)=(1,2)(x,y)=(2,1)"}
|
Решите уравнение
$$
8 x^{3}+8 x^{2} y+8 x y^{2}+8 y^{3}=15\left(x^{2}+y^{2}+x y+1\right)
$$
в множестве целых чисел.
|
numina_1.5_116
|
NT2. Find all natural numbers $n$ such that $5^{n}+12^{n}$ is perfect square.
|
{"ground_truth": "2"}
|
Найдите все натуральные числа $n$, такие что $5^{n}+12^{n}$ является полным квадратом.
|
numina_1.5_120
|
A5 Determine the positive integers $a, b$ such that $a^{2} b^{2}+208=4\{l c m[a ; b]+g c d(a ; b)\}^{2}$.
|
{"ground_truth": "(,b)\\in{(2,12);(4,6);(6,4);(12;2)}"}
|
Определите положительные целые числа $a, b$, такие что $a^{2} b^{2}+208=4\{l c m[a ; b]+g c d(a ; b)\}^{2}$.
|
numina_1.5_124
|
A3 Let the real parameter $p$ be such that the system
$$
\left\{\begin{array}{l}
p\left(x^{2}-y^{2}\right)=\left(p^{2}-1\right) x y \\
|x-1|+|y|=1
\end{array}\right.
$$
has at least three different real solutions. Find $p$ and solve the system for that $p$.
|
{"ground_truth": "p=1orp=-1,0\\leqx\\leq1,withy=\\x"}
|
Пусть вещественный параметр $p$ таков, что система
$$
\left\{\begin{array}{l}
p\left(x^{2}-y^{2}\right)=\left(p^{2}-1\right) x y \\
|x-1|+|y|=1
\end{array}\right.
$$
имеет по крайней мере три различных вещественных решения. Найдите $p$ и решите систему для этого $p$.
|
numina_1.5_128
|
G3 The vertices $A$ and $B$ of an equilateral $\triangle A B C$ lie on a circle $k$ of radius 1 , and the vertex $C$ is inside $k$. The point $D \neq B$ lies on $k, A D=A B$ and the line $D C$ intersects $k$ for the second time in point $E$. Find the length of the segment $C E$.
|
{"ground_truth": "1"}
|
Вершины $A$ и $B$ равностороннего $\triangle A B C$ лежат на окружности $k$ радиуса 1, а вершина $C$ находится внутри $k$. Точка $D \neq B$ лежит на $k$, $A D=A B$ и прямая $D C$ пересекает $k$ во второй раз в точке $E$. Найдите длину отрезка $C E$.
|
numina_1.5_132
|
NT4 Find all integers $n$ such that $n^{4}+8 n+11$ is a product of two or more consecutive integers.
|
{"ground_truth": "1"}
|
Найдите все целые числа $n$, такие что $n^{4}+8 n+11$ является произведением двух или более последовательных целых чисел.
|
numina_1.5_136
|
NT9 Let $p$ be a prime number. Find all positive integers $a$ and $b$ such that:
$$
\frac{4 a+p}{b}+\frac{4 b+p}{a}
$$
and
$$
\frac{a^{2}}{b}+\frac{b^{2}}{a}
$$
are integers.
|
{"ground_truth": "(,b)={(1,1),(2,2),(p,p),(2p,2p),(5,25),(6,18),(18,6),(25,5),(30,150),(150,30)}"}
|
Пусть $p$ — простое число. Найдите все положительные целые числа $a$ и $b$, такие что:
$$
\frac{4 a+p}{b}+\frac{4 b+p}{a}
$$
и
$$
\frac{a^{2}}{b}+\frac{b^{2}}{a}
$$
являются целыми числами.
|
numina_1.5_140
|
87.3. Let $f$ be a strictly increasing function defined in the set of natural numbers satisfying the conditions $f(2)=a>2$ and $f(m n)=f(m) f(n)$ for all natural numbers $m$ and $n$. Determine the smallest possible value of $a$.
|
{"ground_truth": "4"}
|
Пусть $f$ — строго возрастающая функция, определенная на множестве натуральных чисел, удовлетворяющая условиям $f(2)=a>2$ и $f(m n)=f(m) f(n)$ для всех натуральных чисел $m$ и $n$. Определите наименьшее возможное значение $a$.
|
numina_1.5_144
|
91.1. Determine the last two digits of the number
$$
2^{5}+2^{5^{2}}+2^{5^{3}}+\cdots+2^{5^{1991}}
$$
written in decimal notation.
|
{"ground_truth": "12"}
|
Определите последние две цифры числа
$$
2^{5}+2^{5^{2}}+2^{5^{3}}+\cdots+2^{5^{1991}}
$$
записанного в десятичной системе счисления.
|
numina_1.5_148
|
93.3. Find all solutions of the system of equations
$$
\left\{\begin{aligned}
s(x)+s(y) & =x \\
x+y+s(z) & =z \\
s(x)+s(y)+s(z) & =y-4
\end{aligned}\right.
$$
where $x, y$, and $z$ are positive integers, and $s(x), s(y)$, and $s(z)$ are the numbers of digits in the decimal representations of $x, y$, and $z$, respectively.
|
{"ground_truth": "(2,8,12)"}
|
Найдите все решения системы уравнений
$$
\left\{\begin{aligned}
s(x)+s(y) & =x \\
x+y+s(z) & =z \\
s(x)+s(y)+s(z) & =y-4
\end{aligned}\right.
$$
где $x, y$ и $z$ – положительные целые числа, а $s(x), s(y)$ и $s(z)$ – количество цифр в десятичных представлениях чисел $x, y$ и $z$ соответственно.
|
numina_1.5_152
|
97.1. Let A be a set of seven positive numbers. Determine the maximal number of triples $(x, y, z)$ of elements of A satisfying $x<y$ and $x+y=z$.
|
{"ground_truth": "9"}
|
Пусть A — множество из семи положительных чисел. Определите максимальное количество троек $(x, y, z)$ элементов A, удовлетворяющих условиям $x<y$ и $x+y=z$.
|
numina_1.5_156
|
99.1. The function $f$ is defined for non-negative integers and satisfies the condition
$$
f(n)= \begin{cases}f(f(n+11)), & \text { if } n \leq 1999 \\ n-5, & \text { if } n>1999\end{cases}
$$
Find all solutions of the equation $f(n)=1999$.
|
{"ground_truth": "1999=f(6n),ifonlyifn=1,2,\\ldots,334"}
|
Функция $f$ определена для неотрицательных целых чисел и удовлетворяет условию
$$
f(n)= \begin{cases}f(f(n+11)), & \text { если } n \leq 1999 \\ n-5, & \text { если } n>1999\end{cases}
$$
Найдите все решения уравнения $f(n)=1999$.
|
numina_1.5_160
|
01.3. Determine the number of real roots of the equation
$$
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2}=0
$$
|
{"ground_truth": "0"}
|
Определите количество действительных корней уравнения
$$
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2}=0
$$
|
numina_1.5_164
|
03.4. Let $\mathbb{R}^{*}=\mathbb{R} \backslash\{0\}$ be the set of non-zero real numbers. Find all functions $f: \mathbb{R}^{*} \rightarrow \mathbb{R}^{*}$ satisfying
$$
f(x)+f(y)=f(x y f(x+y))
$$
for $x, y \in \mathbb{R}^{*}$ and $x+y \neq 0$.
|
{"ground_truth": "f(x)=\\frac{1}{x}"}
|
Пусть $\mathbb{R}^{*}=\mathbb{R} \backslash\{0\}$ — множество ненулевых вещественных чисел. Найдите все функции $f: \mathbb{R}^{*} \rightarrow \mathbb{R}^{*}$ удовлетворяющие равенству
$$
f(x)+f(y)=f(x y f(x+y))
$$
для $x, y \in \mathbb{R}^{*}$ и $x+y \neq 0$.
|
numina_1.5_168
|
06.3. A sequence of positive integers $\left\{a_{n}\right\}$ is given by
$$
a_{0}=m \quad \text { and } \quad a_{n+1}=a_{n}^{5}+487
$$
for all $n \geq 0$. Determine all values of $m$ for which the sequence contains as many square numbers as possible.
|
{"ground_truth": "9"}
|
Задана последовательность положительных целых чисел $\left\{a_{n}\right\}$ следующим образом:
$$
a_{0}=m \quad \text { и } \quad a_{n+1}=a_{n}^{5}+487
$$
для всех $n \geq 0$. Определите все значения $m$, для которых последовательность содержит максимально возможное количество квадратов.
|
numina_1.5_172
|
09.2. On a faded piece of paper it is possible, with some effort, to discern the following:
$$
\left(x^{2}+x+a\right)\left(x^{15}-\ldots\right)=x^{17}+x^{13}+x^{5}-90 x^{4}+x-90
$$
Some parts have got lost, partly the constant term of the first factor of the left side, partly the main part of the other factor. It would be possible to restore the polynomial forming the other factor, but we restrict ourselves to asking the question: What is the value of the constant term a? We assume that all polynomials in the statement above have only integer coefficients.
|
{"ground_truth": "2"}
|
(x^{2}+x+a)(x^{15}-\ldots)=x^{17}+x^{13}+x^{5}-90 x^{4}+x-90
Некоторые части были утеряны, отчасти постоянный член первого множителя левой части, отчасти основная часть другого множителя. Чему равно значение постоянного члена $a$? Мы предполагаем, что все многочлены в вышеизложенном имеют только целочисленные коэффициенты.
|
numina_1.5_176
|
## Problem 3
Find all $a \in \mathbb{R}$ for which there exists a function $f: \mathbb{R} \rightarrow \mathbb{R}$, such that
(i) $f(f(x))=f(x)+x$, for all $x \in \mathbb{R}$,
(ii) $f(f(x)-x)=f(x)+$ ax, for all $x \in \mathbb{R}$.
|
{"ground_truth": "\\frac{1\\\\sqrt{5}}{2}"}
|
Найдите все $a \in \mathbb{R}$, для которых существует функция $f: \mathbb{R} \rightarrow \mathbb{R}$, такая что
(i) $f(f(x))=f(x)+x$, для всех $x \in \mathbb{R}$,
(ii) $f(f(x)-x)=f(x)+$ ax, для всех $x \in \mathbb{R}$.
|
numina_1.5_180
|
Problem 4. The number 1 is written on the blackboard. After that a sequence of numbers is created as follows: at each step each number $a$ on the blackboard is replaced by the numbers $a-1$ and $a+1$; if the number 0 occurs, it is erased immediately; if a number occurs more than once, all its occurrences are left on the blackboard. Thus the blackboard will show 1 after 0 steps; 2 after 1 step; 1,3 after 2 steps; 2, 2, 4 after 3 steps, and so on. How many numbers will there be on the blackboard after $n$ steps?
|
{"ground_truth": "\\binom{n}{\\lfloor\\frac{n}{2}\\rfloor}"}
|
На доске написано число 1. После этого создается последовательность чисел следующим образом: на каждом шаге каждое число $a$ на доске заменяется числами $a-1$ и $a+1$; если появляется число 0, оно немедленно стирается; если число встречается более одного раза, все его вхождения остаются на доске. Таким образом, на доске будет 1 после 0 шагов; 2 после 1 шага; 1, 3 после 2 шагов; 2, 2, 4 после 3 шагов и так далее. Сколько чисел будет на доске после $n$ шагов?
|
numina_1.5_184
|
LIV OM - II - Task 3
Given is the polynomial $ W(x) = x^4 - 3x^3 + 5x^2 - 9x $. Determine all pairs of different integers $ a $, $ b $ satisfying the equation
|
{"ground_truth": "(-1,0),(0,-1),(1,2),(2,1)"}
|
Дан полином $ W(x) = x^4 - 3x^3 + 5x^2 - 9x $. Определите все пары различных целых чисел $ a $, $ b $, удовлетворяющие уравнению.
|
numina_1.5_188
|
XLVI OM - I - Problem 11
Given are natural numbers $ n > m > 1 $. From the set $ \{1,2, \ldots ,n\} $, we draw $ m $ numbers without replacement. Calculate the expected value of the difference between the largest and the smallest drawn number.
|
{"ground_truth": "\\frac{(n-1)}{n-+1}"}
|
Даны натуральные числа $ n > m > 1 $. Из множества $ \{1,2, \ldots ,n\} $ мы вытягиваем $ m $ чисел без возвращения. Вычислите математическое ожидание разности между наибольшим и наименьшим вытянутым числом.
|
numina_1.5_192
|
XXV - I - Task 1
During World War I, a battle took place near a certain castle. One of the shells destroyed a statue of a knight with a spear standing at the entrance to the castle. This happened on the last day of the month. The product of the day of the month, the month number, the length of the spear expressed in feet, half the age of the battery commander firing at the castle expressed in years, and half the time the statue stood expressed in years equals 451,066. In which year was the statue erected?
|
{"ground_truth": "1714"}
|
Произведение числа дня месяца, номера месяца, длины копья в футах, половины возраста командира батареи, стрелявшей по замку в годах, и половины времени, в течение которого стояла статуя в годах, равно 451 066. В каком году была воздвигнута статуя?
|
numina_1.5_196
|
XXII OM - I - Problem 10
Given is a table with $ n $ rows and $ n $ columns. The number located in the $ m $-th column and $ k $-th row is equal to $ n(k - 1) + m $. How should $ n $ numbers be chosen, one from each row and each column, so that the product of these numbers is the largest?
|
{"ground_truth": "a_{1n}a_{2n-1}\\ldotsa_{n1}=n(2n-1)(3n-2)(4n-3)\\ldots(n^2-(n-1))"}
|
Дана таблица размером $ n \times n $. Число, расположенное в $ m $-м столбце и $ k $-й строке, равно $ n(k - 1) + m $. Как следует выбрать $ n $ чисел, по одному из каждой строки и каждого столбца, чтобы произведение этих чисел было наибольшим?
|
numina_1.5_200
|
XL OM - I - Task 5
For a given natural number $ n $, determine the number of sequences $ (a_1, a_2, \ldots , a_n) $ whose terms $ a_i $ belong to the set $ \{0,1,2,3,4\} $ and satisfy the condition $ |a_i - a_{i+1}| = 1 $ for $ i = 1,2,\ldots,n-1 $.
|
{"ground_truth": "notfound"}
|
Для заданного натурального числа $ n $, определите количество последовательностей $ (a_1, a_2, \ldots , a_n) $, члены $ a_i $ которых принадлежат множеству $ \{0,1,2,3,4\} $ и удовлетворяют условию $ |a_i - a_{i+1}| = 1 $ для $ i = 1,2,\ldots,n-1 $.
|
numina_1.5_204
|
XXIV OM - I - Problem 12
In a class of n students, a Secret Santa event was organized. Each student draws the name of the person for whom they are to buy a gift, so student $ A_1 $ buys a gift for student $ A_2 $, $ A_2 $ buys a gift for $ A_3 $, ..., $ A_k $ buys a gift for $ A_1 $, where $ 1 \leq k \leq n $. Assuming that all drawing outcomes are equally probable, calculate the probability that $ k = n $.
|
{"ground_truth": "\\frac{1}{n}"}
|
В классе из $n$ учеников был организован обмен подарками «Тайный Санта». Каждый ученик вытягивает имя человека, которому он должен купить подарок, так что ученик $A_1$ покупает подарок ученику $A_2$, $A_2$ покупает подарок ученику $A_3$, ..., $A_k$ покупает подарок ученику $A_1$, где $1 \leq k \leq n$. Предполагая, что все возможные исходы розыгрыша равновероятны, вычислите вероятность того, что $k = n$.
|
numina_1.5_208
|
LI OM - II - Problem 4
Point $ I $ is the center of the circle inscribed in triangle $ ABC $, where $ AB \neq AC $. Lines $ BI $ and $ CI $ intersect sides $ AC $ and $ AB $ at points $ D $ and $ E $, respectively. Determine all possible measures of angle $ BAC $ for which the equality $ DI = EI $ can hold.
|
{"ground_truth": "60"}
|
Точка $I$ является центром окружности, вписанной в треугольник $ABC$, где $AB \neq AC$. Прямые $BI$ и $CI$ пересекают стороны $AC$ и $AB$ в точках $D$ и $E$ соответственно. Определите все возможные величины угла $BAC$, для которых может выполняться равенство $DI = EI$.
|
numina_1.5_212
|
LVII OM - III - Problem 6
Determine all pairs of integers $ a $, $ b $, for which there exists a polynomial $ P(x) $ with integer coefficients, such that the product $ (x^2 + ax + b)\cdot P(x) $ is a polynomial of the form
where each of the numbers $ c_0,c_1,\dots ,c_{n-1} $ is equal to 1 or -1.
|
{"ground_truth": "(-2,1),(-1,-1),(-1,1),(0,-1),(0,1),(1,-1),(1,1),(2,1)"}
|
Определите все пары целых чисел $a$, $b$, для которых существует многочлен $P(x)$ с целыми коэффициентами, такой что произведение $(x^2 + ax + b)\cdot P(x)$ является многочленом вида $c_0 + c_1 x + \dots + c_{n-1} x^{n-1}$, где каждое из чисел $c_0, c_1, \dots, c_{n-1}$ равно 1 или -1.
|
numina_1.5_216
|
VI OM - II - Task 3
What should be the angle at the vertex of an isosceles triangle so that a triangle can be constructed with sides equal to the height, base, and one of the remaining sides of this isosceles triangle?
|
{"ground_truth": "106"}
|
Под каким углом при вершине равнобедренного треугольника следует построить треугольник, чтобы можно было построить треугольник со сторонами, равными высоте, основанию и одной из оставшихся сторон этого равнобедренного треугольника?
|
numina_1.5_220
|
XXXVI OM - III - Problem 1
Determine the largest number $ k $ such that for every natural number $ n $ there are at least $ k $ natural numbers greater than $ n $, less than $ n+17 $, and coprime with the product $ n(n+17) $.
|
{"ground_truth": "1"}
|
Определите наибольшее число $ k $, такое что для любого натурального числа $ n $ существует по крайней мере $ k $ натуральных чисел, больших $ n $, меньших $ n+17 $ и взаимно простых с произведением $ n(n+17) $.
|
numina_1.5_224
|
XXXVIII OM - III - Zadanie 5
Wyznaczyć najmniejszą liczbę naturalną $ n $, dla której liczba $ n^2-n+11 $ jest iloczynem czterech liczb pierwszych (niekoniecznie różnych).
|
{"ground_truth": "132"}
|
Определить наименьшее натуральное число $ n $, для которого число $ n^2-n+11 $ является произведением четырех простых чисел (не обязательно различных).
|
numina_1.5_228
|
XXXII - I - Problem 10
Determine all functions $ f $ mapping the set of all rational numbers $ \mathbb{Q} $ to itself that satisfy the following conditions:
a) $ f(1)=2 $,
b) $ f(xy) = f(x)f(y)-f(x+y)+1 $ for $ x, y \in \mathbb{Q} $.
|
{"ground_truth": "f(x)=x+1"}
|
Определите все функции $f$, отображающие множество всех рациональных чисел $ \mathbb{Q} $ в себя, которые удовлетворяют следующим условиям:
a) $ f(1)=2 $,
b) $ f(xy) = f(x)f(y)-f(x+y)+1 $ для $ x, y \in \mathbb{Q} $.
|
numina_1.5_232
|
XXXVIII OM - II - Zadanie 4
Wyznaczyć wszystkie pary liczb rzeczywistych $ a, b $, dla których wielomiany $ x^4 + 2ax^2 + 4bx + a^2 $ i $ x^3 + ax - b $ mają dwa różne wspólne pierwiastki rzeczywiste.
|
{"ground_truth": "(,0),where0"}
|
Определить все пары действительных чисел $a, b$, для которых многочлены $x^4 + 2ax^2 + 4bx + a^2$ и $x^3 + ax - b$ имеют два различных общих действительных корня.
|
numina_1.5_236
|
XXXIII OM - III - Problem 1
Indicate such a way of arranging $ n $ girls and $ n $ boys around a round table so that the number $ d_n - c_n $ is maximized, where $ d_n $ is the number of girls sitting between two boys, and $ c_n $ is the number of boys sitting between two girls.
|
{"ground_truth": "[\\frac{n}{2}]-1"}
|
Укажите такой способ рассадки $n$ девочек и $n$ мальчиков вокруг круглого стола, чтобы число $d_n - c_n$ было максимальным, где $d_n$ – количество девочек, сидящих между двумя мальчиками, а $c_n$ – количество мальчиков, сидящих между двумя девочками.
|
numina_1.5_240
|
LI OM - I - Task 5
Determine all pairs $ (a,b) $ of natural numbers for which the numbers $ a^3 + 6ab + 1 $ and $ b^3 + 6ab + 1 $ are cubes of natural numbers.
|
{"ground_truth": "(1,1)"}
|
Определите все пары $ (a,b) $ натуральных чисел, для которых числа $ a^3 + 6ab + 1 $ и $ b^3 + 6ab + 1 $ являются кубами натуральных чисел.
|
numina_1.5_244
|
L OM - I - Task 3
In an isosceles triangle $ ABC $, angle $ BAC $ is a right angle. Point $ D $ lies on side $ BC $, such that $ BD = 2 \cdot CD $. Point $ E $ is the orthogonal projection of point $ B $ onto line $ AD $. Determine the measure of angle $ CED $.
|
{"ground_truth": "45"}
|
В равнобедренном треугольнике $ ABC $ угол $ BAC $ является прямым. Точка $ D $ лежит на стороне $ BC $, так что $ BD = 2 \cdot CD $. Точка $ E $ является ортогональной проекцией точки $ B $ на прямую $ AD $. Определите величину угла $ CED $.
|
numina_1.5_248
|
XXXI - I - Task 1
Determine for which values of the parameter $ a $ a rhombus with side length $ a $ is a cross-section of a cube with edge length 2 by a plane passing through the center of the cube.
|
{"ground_truth": "[2,\\sqrt{5}]"}
|
Определите, при каких значениях параметра $a$ ромб со стороной $a$ является сечением куба с ребром длиной 2 плоскостью, проходящей через центр куба.
|
numina_1.5_252
|
I OM - B - Task 1
Determine the coefficients $ a $ and $ b $ of the equation $ x^2 + ax + b=0 $ such that the values of $ a $ and $ b $ themselves are roots of this equation.
|
{"ground_truth": "1,0"}
|
Определите коэффициенты $a$ и $b$ уравнения $x^2 + ax + b = 0$ таким образом, чтобы значения $a$ и $b$ сами являлись корнями этого уравнения.
|
numina_1.5_256
|
XIX OM - I - Problem 4
In the plane, given are parallel lines $ a $ and $ b $ and a point $ M $ lying outside the strip bounded by these lines. Determine points $ A $ and $ B $ on lines $ a $ and $ b $, respectively, such that segment $ AB $ is perpendicular to $ a $ and $ b $, and the angle $ AMB $ is the largest.
|
{"ground_truth": "ABlieonthecirclewithdiameterMN"}
|
На плоскости даны параллельные прямые $a$ и $b$ и точка $M$, лежащая вне полосы, ограниченной этими прямыми. Определите точки $A$ и $B$ на прямых $a$ и $b$ соответственно, такие, чтобы отрезок $AB$ был перпендикулярен прямым $a$ и $b$, а угол $AMB$ был наибольшим.
|
numina_1.5_260
|
XXIII OM - I - Problem 4
Points $ A $ and $ B $ do not belong to the plane $ \pi $. Find the set of all points $ M \in \pi $ with the property that the lines $ AM $ and $ BM $ form equal angles with the plane $ \pi $.
|
{"ground_truth": "notfound"}
|
Точки $A$ и $B$ не принадлежат плоскости $ \pi $. Найдите множество всех точек $M \in \pi$ со свойством, что прямые $AM$ и $BM$ образуют равные углы с плоскостью $ \pi $.
|
numina_1.5_264
|
XXXVIII OM - II - Problem 5
Determine all prime numbers $ p $ and natural numbers $ x, y $, for which $ p^x - y^3 = 1 $.
|
{"ground_truth": "(2,1,1)(3,2,2)"}
|
Определите все простые числа $ p $ и натуральные числа $ x, y $, для которых $ p^x - y^3 = 1 $.
|
numina_1.5_268
|
XXXVI OM - I - Zadanie 9
W urnie jest 1985 kartek z napisanymi liczbami 1,2,3,..., 1985, każda lczba na innej kartce. Losujemy bez zwracania 100 kartek. Znaleźć wartość oczekiwaną sumy liczb napisanych na wylosowanych kartkach.
|
{"ground_truth": "99300"}
|
В урне находится 1985 карточек с написанными числами 1, 2, 3, ..., 1985, каждое число на отдельной карточке. Мы вынимаем без возвращения 100 карточек. Найти математическое ожидание суммы чисел, написанных на вытянутых карточках.
|
numina_1.5_272
|
VIII OM - I - Problem 8
In the rectangular prism $ ABCDA_1B_1C_1D_1 $, the lengths of the edges are given as $ AA_1 = a $, $ AB = b $, $ AD = c $. On the face $ A_1B_1C_1D_1 $, a point $ M $ is chosen at a distance $ p $ from the side $ A_1B_1 $, and at a distance $ q $ from the side $ A_1D_1 $, and a parallelepiped is constructed with the base $ ABCD $ and the lateral edge $ AM $. Calculate the area of the lateral faces of this parallelepiped.
|
{"ground_truth": "\\sqrt{^2+}"}
|
В прямоугольном параллелепипеде $ ABCDA_1B_1C_1D_1 $ заданы длины рёбер: $ AA_1 = a $, $ AB = b $, $ AD = c $. На грани $ A_1B_1C_1D_1 $ выбрана точка $ M $, находящаяся на расстоянии $ p $ от стороны $ A_1B_1 $ и на расстоянии $ q $ от стороны $ A_1D_1 $, и построен параллелепипед с основанием $ ABCD $ и боковым ребром $ AM $. Вычислите площадь боковых граней этого параллелепипеда.
|
numina_1.5_276
|
XV OM - I - Problem 8
On three pairwise skew edges of a cube, choose one point on each in such a way that the sum of the squares of the sides of the triangle formed by them is minimized.
|
{"ground_truth": "\\frac{9}{2}^2"}
|
На трех попарно скрещивающихся ребрах куба выберите по одной точке на каждом из них таким образом, чтобы сумма квадратов сторон треугольника, образованного ими, была минимальной.
|
numina_1.5_280
|
XII OM - I - Problem 3
On a plane, a circle $ K $ and a point $ A $ are given. Draw a circle $ L $ passing through point $ A $, so that the lens, which is the common part of both circles, has a given diameter $ a $ and a given thickness $ b $.
|
{"ground_truth": "notfound"}
|
На плоскости заданы окружность $K$ и точка $A$. Постройте окружность $L$, проходящую через точку $A$, так, чтобы линза, являющаяся общей частью обеих окружностей, имела заданный диаметр $a$ и заданную толщину $b$.
|
numina_1.5_284
|
XIII OM - I - Problem 7
Given on a plane are segments $ AB $ and $ CD $. Find on this plane a point $ M $ such that triangles $ AMB $ and $ CMD $ are similar, and at the same time, angle $ AMB $ is equal to angle $ CMD $.
|
{"ground_truth": "notfound"}
|
На плоскости даны отрезки $AB$ и $CD$. Найдите на этой плоскости точку $M$ так, чтобы треугольники $AMB$ и $CMD$ были подобны, и при этом угол $AMB$ был равен углу $CMD$.
|
numina_1.5_288
|
V OM - I - Task 2
Investigate when the sum of the cubes of three consecutive natural numbers is divisible by $18$.
|
{"ground_truth": "3"}
|
Исследуйте, когда сумма кубов трех последовательных натуральных чисел делится на $18$.
|
numina_1.5_292
|
XXXV OM - III - Problem 1
Determine the number of functions $ f $ mapping an $ n $-element set to itself such that $ f^{n-1} $ is a constant function, while $ f^{n-2} $ is not a constant function, where $ f^k = f\circ f \circ \ldots \circ f $, and $ n $ is a fixed natural number greater than 2.
|
{"ground_truth": "n!"}
|
Определите количество функций $f$, отображающих $n$-элементное множество на себя, таких что $f^{n-1}$ является постоянной функцией, а $f^{n-2}$ не является постоянной функцией, где $f^k = f\circ f \circ \ldots \circ f$, и $n$ – фиксированное натуральное число, большее 2.
|
numina_1.5_296
|
XL OM - II - Task 3
Given is a trihedral angle $ OABC $ with vertex $ O $ and a point $ P $ inside it. Let $ V $ be the volume of the parallelepiped with two vertices at points $ O $ and $ P $, whose three edges are contained in the rays $ OA^{\rightarrow} $, $ OB^{\rightarrow} $, $ OC^{\rightarrow} $. Calculate the minimum volume of the tetrahedron, whose three faces are contained in the faces of the trihedral angle $ OABC $, and the fourth face contains the point $ P $.
|
{"ground_truth": "\\frac{9}{2}V"}
|
Дан трехгранный угол $ OABC $ с вершиной $ O $ и точка $ P $ внутри него. Пусть $ V $ — объем параллелепипеда с двумя вершинами в точках $ O $ и $ P $, три ребра которого лежат на лучах $ OA^{\rightarrow} $, $ OB^{\rightarrow} $, $ OC^{\rightarrow} $. Вычислите минимальный объем тетраэдра, три грани которого содержатся в гранях трехгранного угла $ OABC $, а четвертая грань содержит точку $ P $.
|
numina_1.5_300
|
LIX OM - II - Task 1
Determine the maximum possible length of a sequence of consecutive integers, each of which can be expressed in the form $ x^3 + 2y^2 $ for some integers $ x, y $.
|
{"ground_truth": "5"}
|
Определите максимальную возможную длину последовательности последовательных целых чисел, каждое из которых может быть выражено в виде $ x^3 + 2y^2 $ для некоторых целых чисел $ x, y $.
|
numina_1.5_304
|
XVI OM - I - Problem 7
On the side $ AB $ of triangle $ ABC $, a point $ K $ is chosen, and points $ M $ and $ N $ are determined on the lines $ AC $ and $ BC $ such that $ KM \perp AC $, $ KN \perp BC $. For what position of point $ K $ is the area of triangle $ MKN $ the largest?
|
{"ground_truth": "KisthemidpointofsideAB"}
|
На стороне $AB$ треугольника $ABC$ выбрана точка $K$, и точки $M$ и $N$ определены на прямых $AC$ и $BC$ соответственно так, что $KM \perp AC$, $KN \perp BC$. При каком положении точки $K$ площадь треугольника $MKN$ наибольшая?
|
numina_1.5_308
|
XXVIII - II - Task 3
In a hat, there are 7 slips of paper. On the $ n $-th slip, the number $ 2^n-1 $ is written ($ n = 1, 2, \ldots, 7 $). We draw slips randomly until the sum exceeds 124. What is the most likely value of this sum?
|
{"ground_truth": "127"}
|
В шляпе находится 7 бумажных записок. На $n$-й записке написано число $2^n-1$ ($n = 1, 2, \ldots, 7$). Мы случайным образом вытягиваем записки до тех пор, пока сумма не превысит 124. Какое наиболее вероятное значение этой суммы?
|
numina_1.5_312
|
XI OM - I - Task 3
Each side of a triangle with a given area $ S $ is divided into three equal parts, and the points of division are connected by segments, skipping one point to form two triangles. Calculate the area of the hexagon that is the common part of these triangles.
|
{"ground_truth": "\\frac{2}{9}S"}
|
Каждая сторона треугольника с заданной площадью $S$ делится на три равные части, и точки деления соединяются отрезками, пропуская одну точку, чтобы образовать два треугольника. Вычислите площадь шестиугольника, являющегося общей частью этих треугольников.
|
numina_1.5_316
|
XXV - I - Problem 11
Let $ X_n $ and $ Y_n $ be independent random variables with the same distribution $ \left{ \left(\frac{k}{2^n}, \frac{1}{2^n}\right) : k = 0, 1, \ldots, 2^n-1\right} $. Denote by $ p_n $ the probability of the event that there exists a real number $ t $ satisfying the equation $ t^2 + X_n \cdot t + Y_n = 0 $. Calculate $ \lim_{n\to\infty} p_n $.
|
{"ground_truth": "\\frac{1}{12}"}
|
Пусть $ X_n $ и $ Y_n $ — независимые случайные величины с одинаковым распределением $ \left{ \left(\frac{k}{2^n}, \frac{1}{2^n}\right) : k = 0, 1, \ldots, 2^n-1\right} $. Обозначим через $ p_n $ вероятность события, что существует действительное число $ t $, удовлетворяющее уравнению $ t^2 + X_n \cdot t + Y_n = 0 $. Вычислите $ \lim_{n\to\infty} p_n $.
|
numina_1.5_320
|
X OM - II - Task 2
Under what relationship between the sides of a triangle is it similar to the triangle formed by its medians?
|
{"ground_truth": "^2=2b^2-^2"}
|
При каком соотношении между сторонами треугольника он подобен треугольнику, образованному его медианами?
|
numina_1.5_324
|
XXXII - II - Task 4
Given are natural numbers $ k, n $. We define inductively two sequences of numbers $ (a_j) $ and $ (r_j) $ as follows:
First step: divide $ k $ by $ n $ and obtain the quotient $ a_1 $ and the remainder $ r_1 $,
j-th step: divide $ k + r_{j-1} $ by $ n $ and obtain the quotient $ a_j $ and the remainder $ r_j $. Calculate the sum $ a_1 + \ldots + a_n $.
|
{"ground_truth": "k"}
|
Даны натуральные числа $ k, n $. Определим индуктивно две последовательности чисел $ (a_j) $ и $ (r_j) $ следующим образом:
Первый шаг: разделите $ k $ на $ n $ и получите частное $ a_1 $ и остаток $ r_1 $,
j-й шаг: разделите $ k + r_{j-1} $ на $ n $ и получите частное $ a_j $ и остаток $ r_j $. Вычислите сумму $ a_1 + \ldots + a_n $.
|
numina_1.5_328
|
XXII OM - III - Problem 5
Find the largest integer $ A $ such that for every permutation of the set of natural numbers not greater than 100, the sum of some 10 consecutive terms is at least $ A $.
|
{"ground_truth": "505"}
|
Найдите наибольшее целое число $A$, такое что для любой перестановки множества натуральных чисел, не превосходящих 100, сумма каких-либо 10 последовательных членов не меньше $A$.
|
numina_1.5_332
|
XXXVIII OM - I - Problem 6
Which of the quadrilaterals having three sides of length 1 has the largest area?
|
{"ground_truth": "notfound"}
|
Какой из четырехугольников с тремя сторонами длиной 1 имеет наибольшую площадь?
|
numina_1.5_336
|
XVIII OM - I - Zadanie 10
Trójka liczb całkowitych tworzy postęp geometryczny o ilorazie całkowitym. Gdy najmniejszą z nich zwiększymy o 9, powstanie postęp arytmetyczny. Jakie to liczby?
|
{"ground_truth": "(-1,-4,-16),(-1,2,-4),(-9,-18,-36),(2,-4,8)"}
|
Тройка целых чисел образует геометрическую прогрессию с целым знаменателем. Если наименьшее из них увеличить на 9, получится арифметическая прогрессия. Какие это числа?
|
numina_1.5_340
|
XLIII OM - I - Problem 2
In square $ABCD$ with side length $1$, point $E$ lies on side $BC$, point $F$ lies on side $CD$, the measures of angles $EAB$ and $EAF$ are $20^{\circ}$ and $45^{\circ}$, respectively. Calculate the height of triangle $AEF$ drawn from vertex $A$.
|
{"ground_truth": "1"}
|
В квадрате $ABCD$ со стороной длиной $1$, точка $E$ лежит на стороне $BC$, точка $F$ лежит на стороне $CD$, величины углов $EAB$ и $EAF$ равны $20^{\circ}$ и $45^{\circ}$ соответственно. Вычислите высоту треугольника $AEF$, опущенную из вершины $A$.
|
numina_1.5_344
|
XIX OM - III - Problem 1
What is the largest number of regions into which a plane can be divided by $ n $ pairs of parallel lines?
|
{"ground_truth": "2n^2-n+1"}
|
Какое наибольшее количество областей, на которые плоскость может быть разделена $ n $ парами параллельных прямых?
|
numina_1.5_348
|
LIX OM - I - Task 12
Given an integer $ m \geqslant 2 $. Determine the smallest such integer
$ n \geqslant m $, such that for any partition of the set $ \{m,m+1,\dots ,n\} $ into two subsets, at least one of
these subsets contains numbers $ a, b, c $ (not necessarily distinct), such that $ ab = c $.
|
{"ground_truth": "^5"}
|
Дано целое число $ m \geqslant 2 $. Определите наименьшее такое целое число $ n \geqslant m $, такое что для любого разбиения множества $ \{m,m+1,\dots ,n\} $ на два подмножества, по крайней мере в одном из этих подмножеств содержатся числа $ a, b, c $ (не обязательно различные), такие что $ ab = c $.
|
numina_1.5_352
|
L OM - I - Problem 11
In an urn, there are two balls: a white one and a black one. Additionally, we have 50 white balls and 50 black balls at our disposal. We perform the following action 50 times: we draw a ball from the urn, and then return it to the urn along with one more ball of the same color as the drawn ball. After completing these actions, we have 52 balls in the urn. What is the most probable number of white balls in the urn?
|
{"ground_truth": "51"}
|
В урне находятся два шара: белый и черный. Кроме того, в нашем распоряжении имеется 50 белых и 50 черных шаров. Мы выполняем следующее действие 50 раз: мы вытягиваем шар из урны, а затем возвращаем его в урну вместе с одним дополнительным шаром того же цвета, что и вытянутый шар. После завершения этих действий в урне находится 52 шара. Какое наиболее вероятное количество белых шаров в урне?
|
numina_1.5_356
|
XXVII OM - III - Task 5
A fishing vessel is fishing in the territorial waters of a foreign state without permission. Each cast of the net results in a catch of the same value. During each subsequent cast, the probability of the vessel being intercepted by the border guard is $ \frac{1}{k} $, where $ k $ is a fixed natural number. We assume that the event of the vessel being intercepted or not intercepted during each subsequent cast is independent of the previous course of the fishing. If intercepted by the border guard, the entire catch is confiscated, and further fishing is impossible. The captain plans to return after the $ n $-th cast. Considering the risk of interception, the profit from fishing is a random variable. Find the number $ n $ for which the expected value of the profit is maximized.
|
{"ground_truth": "n=k-1n=k"}
|
Рыболовное судно ведет промысел в территориальных водах иностранного государства без разрешения. Каждый заброс сети приносит улов одинаковой ценности. Во время каждого последующего заброса вероятность перехвата судна пограничной охраной составляет $ \frac{1}{k} $, где $ k $ – фиксированное натуральное число. Предполагается, что событие перехвата или неперехвата судна во время каждого последующего заброса не зависит от предыдущего хода промысла. В случае перехвата пограничной охраной весь улов конфискуется, и дальнейший промысел становится невозможным. Капитан планирует вернуться после $ n $-го заброса. Учитывая риск перехвата, прибыль от промысла является случайной величиной. Найдите число $ n $, для которого математическое ожидание прибыли максимизируется.
|
numina_1.5_360
|
LIX OM - I - Task 9
Determine the smallest real number a with the following property:
For any real numbers $ x, y, z \geqslant a $ satisfying the condition $ x + y + z = 3 $
the inequality holds
|
{"ground_truth": "-5"}
|
Определите наименьшее действительное число $a$ со следующим свойством:
Для любых действительных чисел $x, y, z \geqslant a$, удовлетворяющих условию $x + y + z = 3$,
выполняется неравенство
|
numina_1.5_364
|
VI OM - III - Task 6
Through points $ A $ and $ B $, two oblique lines $ m $ and $ n $ perpendicular to the line $ AB $ have been drawn. On line $ m $, a point $ C $ (different from $ A $) has been chosen, and on line $ n $, a point $ D $ (different from $ B $). Given the lengths of segments $ AB = d $ and $ CD = l $, and the angle $ \varphi $ formed by the oblique lines $ m $ and $ n $, calculate the radius of the sphere passing through points $ A $, $ B $, $ C $, $ D $.
|
{"ground_truth": "\\sqrt{(\\frac{}"}
|
Через точки $A$ и $B$ проведены две наклонные линии $m$ и $n$, перпендикулярные линии $AB$. На линии $m$ выбрана точка $C$ (отличная от $A$), а на линии $n$ – точка $D$ (отличная от $B$). Даны длины отрезков $AB = d$ и $CD = l$, а также угол $ \varphi $ между наклонными линиями $m$ и $n$. Вычислите радиус сферы, проходящей через точки $A$, $B$, $C$, $D$.
|
numina_1.5_368
|
XXVI - I - Task 1
At the ball, there were 42 people. Lady $ A_1 $ danced with 7 gentlemen, Lady $ A_2 $ danced with 8 gentlemen, ..., Lady $ A_n $ danced with all the gentlemen. How many gentlemen were at the ball?
|
{"ground_truth": "24"}
|
На балу присутствовало 42 человека. Леди $A_1$ танцевала с 7 джентльменами, леди $A_2$ танцевала с 8 джентльменами, ..., леди $A_n$ танцевала со всеми джентльменами. Сколько джентльменов было на балу?
|
numina_1.5_372
|
L OM - II - Task 5
Let $ S = \{1, 2,3,4, 5\} $. Determine the number of functions $ f: S \to S $ satisfying the equation $ f^{50} (x) = x $ for all $ x \in S $.
Note: $ f^{50}(x) = \underbrace{f \circ f \circ \ldots \circ f}_{50} (x) $.
|
{"ground_truth": "50"}
|
Пусть $ S = \{1, 2,3,4, 5\} $. Определите количество функций $ f: S \to S $, удовлетворяющих уравнению $ f^{50} (x) = x $ для всех $ x \in S $.
Примечание: $ f^{50}(x) = \underbrace{f \circ f \circ \ldots \circ f}_{50} (x) $.
|
numina_1.5_376
|
LIII OM - III - Task 1
Determine all such triples of natural numbers $ a $, $ b $, $ c $, such that the numbers $ a^2 +1 $ and $ b^2 +1 $ are prime and
|
{"ground_truth": "(1,2,3)(2,1,3)"}
|
Определите все такие тройки натуральных чисел $a$, $b$, $c$, такие что числа $a^2 + 1$ и $b^2 + 1$ являются простыми и
|
numina_1.5_380
|
XLIII OM - II - Problem 5
Determine the supremum of the volumes of spheres contained in tetrahedra with all altitudes no longer than $1$.
|
{"ground_truth": "\\pi/48"}
|
Определите супремум объемов сфер, содержащихся в тетраэдрах, все высоты которых не превышают $1$.
|
numina_1.5_384
|
LVIII OM - I - Problem 4
For each natural number $ n\ge 3 $, determine the number of sequences $ (c_1,c_2,\ldots,c_n) $, where $ {c_i\in\{0,1,\ldots,9\}} $, with the following property:\break in every triple of consecutive terms, there are at least two terms that are equal.
|
{"ground_truth": "5\\cdot(4^n+(-2)^n)"}
|
Для каждого натурального числа $ n\ge 3 $, определите количество последовательностей $ (c_1,c_2,\ldots,c_n) $, где $ {c_i\in\{0,1,\ldots,9\}} $, обладающих следующим свойством: в каждой тройке последовательных членов есть по крайней мере два равных члена.
|
numina_1.5_388
|
4. Each experience of throwing the circle corresponds to a point $M-$ the position of the center of the circle on the vertical segment $[A ; B]$ of length 1.
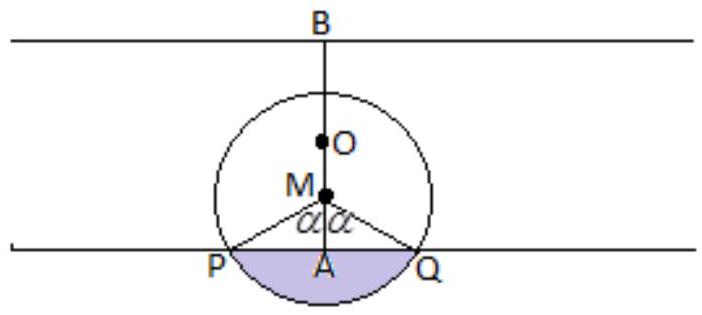
Let's introduce the following notations: $R$ - the radius of the circle, $O$ - the midpoint of the segment $[A ; B], \quad O M=x \in[0 ; 0.5]$ - a random variable uniformly distributed on this segment, $\alpha$ - the angle indicated in the figure, $A M=h=\frac{\cos \alpha}{2}$.
The area of the circular segment $S_{1}$ of a circle with radius $R$ is given by the formula:
$$
S_{1}=\left|\alpha R^{2}-\frac{1}{2} R^{2} \sin 2 \alpha\right|
$$
In our case, $R=\frac{1}{2}$, so,
$$
S_{1}=\frac{\alpha}{4}-\frac{\sin 2 \alpha}{8} .
$$
From the problem statement, it follows that
$$
\left\{\begin{array}{c}
S_{1}: S_{2}=(\pi-2):(3 \pi+2) \\
S_{1}+S_{2}=\frac{\pi}{4}
\end{array}\right.
$$
Then $S_{1}=k(\pi-2)$, and $S_{2}=k(3 \pi+2)$. Substituting this into the second equality, we get: $S_{1}+S_{2}=k \cdot 4 \pi=\frac{\pi}{4}$. Therefore, $k=\frac{1}{16}$. Then, $S_{1}=\frac{\alpha}{4}-\frac{\sin 2 \alpha}{8}=\frac{1}{16}(\pi-2)$. From this, we find $\alpha=\frac{\pi}{4}$. Thus, the conditions of the problem correspond to the central angle $P M Q$ equal to $\frac{\pi}{2}$. Then $h=\frac{\sqrt{2}}{4}$ and the favorable outcome of the experiment corresponds to points $M$ that are no more than $\frac{1}{2}-h=\frac{2-\sqrt{2}}{4}$ away from point $O$. Since the probability of the desired event is the ratio of the length of the segment of "favorable" outcomes, i.e., $\frac{2-\sqrt{2}}{2}$ to the length of the segment $[A ; B]$, i.e., to one, the desired probability $P(A)=\frac{2-\sqrt{2}}{2} \approx 0.29$
|
{"ground_truth": "P(A)=\\frac{2-\\sqrt{2}}{2}\\approx0.29"}
|
Каждый опыт бросания круга соответствует точке $M$ – положению центра круга на вертикальном отрезке $[A ; B]$ длиной 1.
Введем следующие обозначения: $R$ – радиус круга, $O$ – середина отрезка $[A ; B], \quad O M=x \in[0 ; 0.5]$ – случайная величина, равномерно распределенная на этом отрезке, $\alpha$ – угол, указанный на рисунке, $A M=h=\frac{\cos \alpha}{2}$.
Площадь кругового сегмента $S_{1}$ круга радиуса $R$ задается формулой:
$$
S_{1}=\left|\alpha R^{2}-\frac{1}{2} R^{2} \sin 2 \alpha\right|
$$
В нашем случае, $R=\frac{1}{2}$, следовательно,
$$
S_{1}=\frac{\alpha}{4}-\frac{\sin 2 \alpha}{8} .
$$
Из условия задачи следует, что
$$
\left\{\begin{array}{c}
S_{1}: S_{2}=(\pi-2):(3 \pi+2) \\
S_{1}+S_{2}=\frac{\pi}{4}
\end{array}\right.
$$
Тогда $S_{1}=k(\pi-2)$, а $S_{2}=k(3 \pi+2)$. Подставляя это во второе равенство, получаем: $S_{1}+S_{2}=k \cdot 4 \pi=\frac{\pi}{4}$. Следовательно, $k=\frac{1}{16}$. Тогда, $S_{1}=\frac{\alpha}{4}-\frac{\sin 2 \alpha}{8}=\frac{1}{16}(\pi-2)$. Отсюда находим $\alpha=\frac{\pi}{4}$. Таким образом, условиям задачи соответствует центральный угол $P M Q$, равный $\frac{\pi}{2}$. Тогда $h=\frac{\sqrt{2}}{4}$ и благоприятный исход эксперимента соответствует точкам $M$, находящимся на расстоянии не более $\frac{1}{2}-h=\frac{2-\sqrt{2}}{4}$ от точки $O$. Поскольку вероятность искомого события является отношением длины сегмента «благоприятных» исходов, т.е. $\frac{2-\sqrt{2}}{2}$, к длине сегмента $[A ; B]$, т.е. к единице, то искомая вероятность $P(A)=\frac{2-\sqrt{2}}{2} \approx 0.29$
|
numina_1.5_392
|
5. For what values of $a$ does the system of equations $\left\{\begin{array}{c}(x+2+2 \sqrt{2} \cos a)^{2}+(y-1-2 \sqrt{2} \sin a)^{2}=2 \\ (x-y+3)(x+y+1)=0\end{array}\right.$ have three
solutions?
|
{"ground_truth": "a_{1}=\\frac{7\\pi}{12}+\\pik,a_{2}=\\frac{11\\pi}{12}+\\pik,k\\inZ"}
|
При каких значениях $a$ система уравнений $\left\{\begin{array}{c}(x+2+2 \sqrt{2} \cos a)^{2}+(y-1-2 \sqrt{2} \sin a)^{2}=2 \\ (x-y+3)(x+y+1)=0\end{array}\right.$ имеет три решения?
|
numina_1.5_396
|
5. For what values of $a$ does the system of equations $\left\{\begin{array}{c}(x-2-\sqrt{5} \cos a)^{2}+(y+1-\sqrt{5} \sin a)^{2}=\frac{5}{4} \text { have two solutions? } \\ (x-2)(x-y-3)=0\end{array}\right.$
|
{"ground_truth": "\\in(\\frac{\\pi}{12}+\\pik;\\frac{\\pi}{3}+\\pik)\\cup(\\frac{5\\pi}{12}+\\pik;\\frac{2\\pi}{3}+\\pik),k\\inZ"}
|
При каких значениях $a$ система уравнений $\left\{\begin{array}{c}(x-2-\sqrt{5} \cos a)^{2}+(y+1-\sqrt{5} \sin a)^{2}=\frac{5}{4} \\ (x-2)(x-y-3)=0\end{array}\right.$ имеет два решения?
|
Cleaned and translated version of INTELLECT-2
(https://huggingface.co/datasets/PrimeIntellect/INTELLECT-2-RL-Dataset)
The original IDs and ground_truth answers are kept as is.
Only rows with task_type=verifiable_math are used.
Applied LLM processing to drop task numbers and other metadata.
Applied LLM processing to find if problems contain solutions, please refer to 'ERROR' string, marking solutions